UNIVERZITA KOMENSKÉHO V BRATISLAVE. Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ Veronika Kleinová
|
|
|
- Phoebe Sherman
- 5 years ago
- Views:
Transcription
1 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová
2 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Zaistené a poistené stratégie Bakalárska práca Evidenčné číslo: f1ddf9f-88f-438d-94f7-c754737af8b Študijný program: Ekonomická a finančná matematika Študijný odbor: Aplikovaná matematika Školiace pracovisko: Katedra aplikovanej matematiky a štatistiky Vedúci bakalárskej práce: Mgr. Igor Melicherčík, PhD. Bratislava 011 Veronika Kleinová
3
4 Prehlásenie Čestne prehlasujem, že túto prácu som vypracovala samostatne s použitím uvedenej literatúry a d alších informačných zdrojov. V Bratislave,. júna podpis autora práce
5 Pod akovanie Týmto sa chcem pod akovat vedúcemu práce Mgr. Igorovi Melicherčíkovi, PhD., za cenné rady, pripomienky a pomoc pri realizácii bakalárskej práce. Ďalej chcem pod akovat Michalovi Tomleinovi za pomoc pri práci s L A TEX-om a v neposlednom rade Štefanovi Mitríkovi za grafickú úpravu použitých obrázkov.
6 Abstrakt Kleinová, Veronika: Zaistené a poistené stratégie [Bakalárska práca], Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky, Katedra aplikovanej matematiky a štatistiky; školitel : Mgr. Igor Melicherčík, PhD. Spoločným znakom zaistených a poistených stratégií je kontrola rizika. Zaistené stratégie sa snažia o čo najvyšší zisk pri garantovaní čiastky, ktorá sa stanoví ako určité percento z počiatočnej investície. Pri poistených stratégiách je riziko kontrolované výškou poistenia dosiahnutia určitej hodnoty. Táto bakalárska práca sa zaoberá optimálnym prerozdelením aktív investora podl a štyroch rôznych metód a to zo zaistených stratégií metódou CPPI (Constant Proportion Portfolio Insurance) a metódou OBPI (Obtion Based Portfolio Insurance), z poistených stratégií metódou OBPI bez zrealizovania poistenia a stratégiou VAR (Value at Risk). Vysvetlíme podstatu jednotlivých metód a na záver vykonáme ich porovnania. Kl účové slová: CPPI (Constant Proportion Portfolio Insurance), OBPI (Obtion Based Portfolio Insurance), VAR (Value at Risk), riziko, poistenie.
7 Abstract Kleinová, Veronika: The portfolio insurance strategies and hedging strategies [Bachelor thesis], Comenius University Bratislava, Faculty of Mathematics, Physics, and Informatics, Department of Applied Mathematics and Statistics; Thesis Consultant: Mgr. Igor Melicherčík, PhD. A common feature of hedging strategies and insured strategies is a control of risk. The hedging strategies seek to maximize profit while the particular amount of the initial investment is guaranteed. The insured strategies control a risk by the cost of the insurance to achieve a certain value. This thesis deals with the optimal reallocation of investor assets by the four different methods. From the area of the hedging strategies we concentrate on the CPPI (Constant Proportion Portfolio Insurance) and the OBPI strategy (Obtion Based Portfolio Insurance) and from the domain of the insured strategies the OBPI strategy without realization of the insurance and the strategy VAR (Value at Risk). We describe the essence of these methods and finally we make a comparison. Key words: CPPI (Constant Proportion Portfolio Insurance), OBPI (Obtion Based Portfolio Insurance), VAR (Value at Risk), risk, insurance.
8 Obsah Úvod 3 1 Opcie Súčasná hodnota opcií Black - Scholesove vzorce Predajno-kúpna parita Zaistené stratégie 14.1 CPPI OBPI Porovnanie CPPI a OBPI Stratégie založené na metóde OBPI, CPPI, VAR Metóda OBPI Metóda OBPI bez kúpy opcie Metóda CPPI Metóda VAR Porovnania Záver 3 Zoznam obrázkov 1 Hodnota kúpnej opcie Hodnota predajnej opcie Jednokrokový binárny stromový model Jeden krok v binárnom modeli pre odvodenie ceny akcie Vankúš a dno v CPPI metóde Porovnanie OBPI a CPPI metódy metóda - OBPI Závislost podielu v akciách od garancie metóda - OBPI bez kúpy opcie metóda - CPPI (s multiplikátorom 1)
9 11 4. metóda - VAR (Value at risk) Podiel v akciách (VAR) Histogramy pre jednotlivé stratégie investovania Zoznam tabuliek 1 Hodnoty zodpovedajúce histogramom na Obr Porovnanie popisných ukazovatel ov jednotlivých metód Hodnoty funkcie užitočnosti vzhl adom na averziu k riziku
10 Úvod Je všeobnecne známe, že ak pri investovaní chceme dosiahnut vyšší zisk, musíme rátat so zvýšeným rizikom. Ako však obmedzit riziko a napriek tomu dosiahnut väčšie zhodnotenie v porovnaní napríklad s investíciou do bezrizikového aktíva? Jednou z odpovedí na túto otázku sú zaistené a poistené stratégie, ktoré nám ponúkajú možnost čiastočne sa podielat na zisku akcií v prípade rastúceho trhu a zároveň obmedzujú riziko. Zaistené stratégie nám garantujú, že hodnota portfólia neklesne pod nami vopred stanovenú hranicu, poistenými stratégiami kontrolujeme riziko výškou poistenia dosiahnutia určitej hranice. Ďalším spôsobom kontroly rizika je stanovit si, akú najväčšiu stratu sme ochotní akceptovat s určitou pravdepodobnost ou. Ciel om tejto bakalárskej práce je porovnat spomenuté metódy, vd aka ktorým môžeme obmedzit riziko. Bakalárska práca je rozdelená do troch kapitol. V prvej kapitole sa zameriame na opcie, ktoré sú nevyhnutným finančným nástrojom pre niektoré zo zaistených a poistených stratégií, konkrétne pre metódu OBPI (Obtion Based Portfolio Insurance) a metódu OBPI bez zrealizovania poistenia. Je vel mi dôležité porozumiet im, aby sme si uvedomili, ako je riziko obmedzované práve pri týchto dvoch spomenutých stratégiách. Uvedieme základnú charakteristiku opcií, odvodenie výpočtu ich súčasnej hodnoty a predajno-kúpnu paritu, ktorá určuje vzt ah medzi dvoma druhmi opcií. Druhá kapitola je venovaná práve dvom najrozšírenejším metódam zaistených stratégií, metóde CPPI a metóde OBPI. Okrem matematického modelu a popisu, ako je pri jednotlivých metódach zaručená garantovaná hranica, pod ktorú v čase splatnosti neklesne hodnota portfólia, ponúkneme aj porovnanie týchto metód. V poslednej časti budeme analyzovat štyri metódy ako rozdelit kapitál medzi rizikové a bezrizikové aktívum, aby sme určitým spôsobom obmedzili riziko a na druhej strane mohli dosiahnut čo najvyšší zisk. Porovnáme tieto metódy na základe popisných štatistík aj konkrétnej funkcie užitočnosti a vyhodnotíme, ktorá je vhodná pre rizikovo averzného investora, resp. ktorá je vhodná pre investora, ktorého postoj k riziku je neutrálny alebo kladný. 3
11 1 Opcie V nasledujúcej časti si vysvetlíme základnú charakteristiku opcií, vypočítame ich súčasnú hodnotu a odvodíme Black-Scholesov vzorec, pričom budeme vychádzat z [1]. Finančné deriváty sú finančné nástroje, ktoré sú odvodené od hodnoty podkladových aktív (akcie, dlhopisy), menových kurzov, úrokových mier, burzových indexov, resp. od iných nástrojov. Základnými typmi finančných derivátov sú opčné deriváty, forwardy, futurity a swapy. Opcie, ktoré sa zarad ujú medzi opčné deriváty, predstavujú právo (nie povinnost ) kúpit alebo predat podkladové aktívum za vopred dohodnutú cenu (realizačnú cenu) vo vopred dohodnutý deň splatnosti (maturita). Vypisovatel opcie od kupujúceho získava opčnú prémiu (trhová cena, za ktorú sa opcia predáva) a zároveň mu dáva právo požadovat od neho, aby podkladové aktívum kúpil alebo predal v závislosti od typu opcie. Ak držitel opcie získava právo na kúpu daného cenného papiera v danom čase za dohodnutú cenu ide o kúpnu opciu (call option). Predajná opcia (put option) predstavuje právo predat podkladové aktívum. Opcie môžu byt európskeho alebo amerického typu v závislosti od toho, kedy má vlastník opcie právo zrealizovat opčný kontrakt (kúpit alebo predat podkladové aktívum). Ak až v deň maturity, vtedy ide o opcie európskeho typu alebo ho môže zrealizovat kedykol vek do tohto dňa, vtedy je opcia amerického typu. Hodnota opcie je vyjadrená ako jej vnútorná hodnota, od ktorej je odpočítaná opčná prémia. Vnútorná hodnota je suma, ktorá by bola vyplatená držitel ovi opcie, ak by ju uplatnil. V prípade predajnej opcie je to max[(k S t ), 0] = (K S t ) +, pre kúpnu opciu max[(s t K), 0] = (S t K) +, kde K je realizačná cena opcie a S t je cena podkladového aktíva v čase t. Na Obr. 1 je znázornená hodnota kúpnej opcie (resp. hodnota predajnej opcie Obr. ) V v závislosti od ceny podkladového aktíva S. 4
12 Obr. 1: Hodnota kúpnej opcie. Obr. : Hodnota predajnej opcie. 1.1 Súčasná hodnota opcií Povedzme, že cena akcie je S 0 a za čas T stúpne jej hodnota na S 1 s pravdepodobnost ou p a s pravdepodobnost ou (1 p) klesne na S. Táto modelová situácia je znázornená jednokrokovým binárnym stromovým modelom na Obr. 3. Za predpokladu spojitého úročenia a bezrizikovej úrokovej miery r vypočítame, aká je súčasná hodnota opcie f 0 odvodenej od tejto akcie, ktorej realizačná cena je K. Obr. 3: Jednokrokový binárny stromový model. 5
13 Ak by akcia nadobudla hodnotu S 1, hodnota opcie v čase T by bola f 1, v druhom prípade f. Vytvoríme si portfólio tak, že si kúpime jednu opciu a predáme k kusov akcie. V čase 0 je hodnota portfólia rovná f 0 k.s 0. Potrebujeme eliminovat riziko, čiže určit počet kusov akcií tak, aby hodnota portfólia v čase T bola v oboch prípadoch rovnaká, čiže odtial f 1 k.s 1 = f k.s, k = f 1 f S 1 S. Čiže v každom prípade bude v čase T hodnota nášho portfólia f k.s, takže už stačí túto hodnotu len diskontovat do súčasnosti a získame, že Po vyjadrení f 0 a dosadení za k f 0 k.s 0 = e rt (f k.s ). f 0 = f 1 f S 0 + e rt (f f 1 f S ) S 1 S S 1 S ( ) = e rt f1 S 0 e rt f S 0 e rt + f S 1 f 1 S S 1 S ( ) = e rt (S1 S 0 e rt )f + (S 0 e rt S )f 1 S 1 S = e rt ((1 q)f + qf 1 ), kde q = S 0e rt S S 1 S sa nazýva rizikovo neutrálna pravdepodobnost. Všeobecne q = S nowe rδt S down S up S down, (1) kde S now je hodnota akcie na začiatku kroku, S up hodnota akcie pri zvýšení jej ceny za čas δt, S down hodnota akcie pri poklese jej ceny za čas δt. Dá sa ukázat, že q 0, 1, inak by nastala arbitráž. Môžeme teda povedat, že súčasná hodnota opcie je strednou hodnotou pri rizikovo neutrálnych pravdepodobnostiach. Pri viackrokovom binárnom strome by sme postupovali 6
14 odzadu a postupne riešili jednotlivé časti ako v jednokrokovom binárnom stromovom modeli. Súčasnú hodnotu opcie môžeme teda zapísat v tvare f 0 = E Q (e rt X), () kde E Q je stredná hodnota pri rizikovo neutrálnej pravdepodobnosti Q a X je náhodná premenná, ktorá vyjadruje hodnotu opcie v čase maturity T, napríklad pre kúpnu opciu X = (S T K) Black - Scholesove vzorce Na modelovanie ceny euróskej kúpnej opcie na akciu je dôležitý vývoj ceny akcie. Budeme predpokladat, že totálny výnos akcie je náhodný výber z lognormálneho rozdelenia. Čiže S t S t 1 pre t = 1,,..., T sú nezávislé rovnako rozdelené náhodné premenné, ktoré majú lognormálne rozdelenie s parametrami µ a σ. Náhodná premenná Y t = ln St S t 1 má potom normálne rozdelenie s tými istými parametrami. Využijeme poznatok, že ak každé Y t N(µ, σ ) a sú nezávislé pre všetky t = 1,,..., T, tak vektor (Y 1, Y,..., Y T ) T má µ µ µ µ T - rozmerné normálne rozdelenie N T, σ I, kde je T 1 rozmerný vektor a I je jednotková matica rozmeru T T. Náhodná.. µ µ premenná Y 1 ( ) T t=1 Y Y t = 1, 1,, 1 má normálne rozdelenie so strednou hodnotou. Y T µ ( ) µ 1, 1,, 1 = µt a disperziou. µ Teda T T P = Y t = t=1 t=1 ( ) 1, 1,, 1 σ I ln St S t 1 = ln T t=1 1 1 = σ T.. 1 St S t 1 = ln S T S 0 má normálne rozdelenie so strednou hodnotou µt a disperziou σ T. Odtial S T = S 0 e P. 7
15 Ked že P N(µT, σ T ), P môžeme napísat v tvare µt + σ T V, kde V N(0, 1), teda S T = S 0 e µt +σ T V, (3) pričom S 0 - cena akcie v čase 0, µ - stredná hodnota, σ - volatilita akcie, V - náhodná premenná, ktorá má normálne rozdelenie so strednou hodnotou 0 a disperziou 1. Teraz si vytvoríme binárny stromový model, ktorý bude zodpovedat vývoju akcie opísanej predchádzajúcou rovnicou. Časový interval 0, T rozdelíme na n rovnakých dielov δt = T. Za každý časový okamih δt sa cena akcie vyvi- n nie nasledovne: s pravdepodobnost ou 1 jej hodnota stúpne na S.eµδt+σ δt a s pravdepodobnost ou 1 klesne na S.eµδt σ δt. Jeden krok popísanej situácie je znázornený na Obr.4. Obr. 4: Jeden krok v binárnom modeli pre odvodenie ceny akcie. Na vyjadrenie hodnoty S T využijeme náhodnú premennú X n, ktorá má binomické rozdelenie s parametrami n a p = 1. Môžeme ju zapísat v tvare X n = T U i, i=1 kde Y i sú náhodné nezávislé premenné s alternatívnym rozdelením s parametrom p = 1. Čiže každé U i nám generuje hodnotu 0 alebo 1, obe s pravdepodobnost ou 1. My však potrebujeme hodnoty 1 alebo -1 a to docielime tak, že vytvoríme premennú Ũi = U i 1, teda X n = T i=1 Ũi = T i=1 (U i 1) = X n n vygeneruje n-krát hodnotu 1 alebo -1 vždy s pravdepodobnost ou 1 a sčíta tieto 8
16 hodnoty. Hodnotu akcie v čase T môžeme teraz vyjadrit nasledovne: S T = S 0.e µnδt+(x n n)σ δt = S 0.e µt + X n n n σ T = S 0.e µt +Zσ T. (4) Aby sme dokázali, že rovnica (4) je ekvivalentná vzt ahu (3), musíme ukázat, že náhodná premenná Z = Xn n n má rozdelenie N(0, 1). Ked že X n Bin(n, 1 ) E(X n ) = E(X n ) = np = n 1 = n, D(X n ) = 4D(X n ) = 4np(1 p) = 4n 1 (1 1 ) = n. Podl a Moivreovej-Laplaceovej centrálnej limitnej vety, ak má náhodná premenná X binomické rozdelenie, normovaná náhodná veličina X E(X) má pre vel ké D(X) n približne rozdelenie N(0, 1). Túto vetu aplikujeme na našu premennú X n, teda Z = X n E(X n ) = Xn n D(Xn ) n má aproximatívne normované normálne rozdelenie, čiže sme dokázali, že nami zostrojený binárny stromový model zodpovedá vývoju hodnoty akcie zo vzt ahu (3). Na určenie súčasnej hodnoty opcie potrebujeme okrem modelu vývoja hodnoty akcie vypočítat aj rizikovo neutrálnu pravdepodobnost q. Dosadením do vzt ahu (1) na strane 6 Po substitúcii δt = x : q = Serδt Se µδt σ δt Se µδt+σ δt Se. µδt σ δt q = erx e µx σx e µx +σx e. (5) µx σx Pomocou Taylorovej vety rozvinieme funkciu e x v okolí bodu 0: e x = 1 + x + x! + x3 3! + + xn n! + O(xn+1 ), kde v O(x n+1 ) sú zahrnuté len členy stupňa n + 1 a vyššieho. Po dosadení rozvoja do vzt ahu (5) a zanedbaní členov stupňa vyššieho ako q = = (1 + rx ) (1 + (µx σx) + σ x ) + O(x 3 )! (1 + (µx + σx) + σ x ) (1 + (µx! σx) + σ x ) + O(x! 3 ) rx µx+σ σ x! + O(x ) σ. 1 + O(x ) Po spätnej substitúcii x = δt = T n ( 1 q = 1 T n ) µ+ σ r σ 1 + O ( T n 9 + O ( ) T n ).
17 V pravdepodobnostnej miere Q si náhodnú premennú Z = X n n n označíme Z Q a vypočítame jej strednú hodnotu a disperziu, aby sme mohli v tejto pravdepodobnostnej miere vyjadrit hodnotu akcie v čase T. ( ) Xn n E(Z Q ) = E = nq n n n = n T n µ+ σ r + O(T ) n O(T ) σ ( ( n 1 + O T )) n = Pre vel ké n potom platí = 4 T µ+ σ r σ 1 + O ( T n ( ) + O T n ). E(Z Q ) =. T µ + σ r. σ L ahko sa dá ukázat, že disperzia Z Q je 1: ( ) Xn n D(Z Q ) = D = 4 n n D(X n) = 4 nq(1 q) n ( ) 1 T µ+ 1 σ r + O ( ) T 1 n σ n Pre vel ké n 1 + O ( T n D(Z Q ) =. ( 1 4 ) 1 ) ( (1 0) ( T 1 n ) µ+ σ r σ 1 + O ( T n ) (1 0) + 0 = 1. 1 Teraz už môžeme napísat hodnotu akcie v čase T nasledovne kde Z Q N( T µ+ σ r σ, 1). Teda ekvivalentne pre hodnotu akcie v pravdepodobnostnej miere Q platí S T = S 0 e µt +Z Qσ T, ) + O ( T n ) S T = S 0 e µt T µ+ σ = S 0 e σ T Z+T r σ T +σ T Z σ ) (r σ, kde Z N(0, 1). Podl a vzt ahu () zo strany 7 vypočítame súčasnú hodnotu európskej kúpnej opcie Call 0 Call 0 = E Q (e rt X) = E Q (e rt (S T K) + ) = E Q (e rt (S 0 e σ T Z+T (r σ ) K) + ) = E Q ((S 0 e σ T Z T σ Ke rt ) + ).. 10
18 Ak X je náhodná premenná, tak strednú hodnotu E(g(x)) vypočítame ako g(x)f(x)dx, kde g(x) je funkcia premennej x a f(x) je jej hustota. V našom prípade počítame strednú hodnotu výrazu E Q ((S 0 e σ T Z T σ Ke rt ) + ), kde Z je náhodná premenná, čiže g(z) = (S 0 e σ T Z T σ Ke rt ) + a hustota f(z) = 1 Π e z, pretože Z N(0, 1). Pre súčasnú hodnotu európskej kúpnej opcie Call 0 teda platí Call 0 = Po zavedení substitúcie σ T z T σ = y Call 0 = 1 Πσ T (S 0 e σ T z T σ Ke rt ) + 1 e z dz. Π Funkcia (S 0 e y Ke rt ) + bude nenulová, iba ak Ak ln K S 0 rt označíme M, potom Call 0 = = S 0 Πσ T S 0 Πσ T M M (S 0 e y Ke rt ) + e (y+ 1 σ T ) σ T S 0 e y > e rt Ke rt y > ln K S 0 rt. e y (y+ 1 σ T ) σ T dy e (y 1 σ T ) σ T dy = S 0 P (Y 1 M) Ke rt P (Y M), 1 Πσ T Ke rt M 1 Πσ T Ke rt M dy. e (y+ 1 σ T ) σ T dy e (y+ 1 σ T ) σ T dy kde Y 1 N( 1 σ T, σ T ) a Y N( 1 σ T, σ T ). Po znormovaní dostávame ( Y1 1 Call 0 = S 0 P σ T σ M 1 ) ( σ T T σ Ke rt Y + 1 P σ T T σ M + 1 σ T T σ T Ak X N(0, 1) platí, že P (X a) = 1 P (X a) = 1 ϕ(a), kde ϕ(a) je distribučná funkcia normovaného normálneho rozdelenia v bode a. V dôsledku toho, že funkcia hustoty normovaného normálneho rozdelenia je párna, platí, že 1 ϕ(a) = ϕ( a), dostávame ( M + 1 ) Call 0 = S 0 ϕ σ T σ T ( M 1 ) Ke rt ϕ σ T σ. T Dosadením za M = ln K S 0 rt vyjadríme hodnotu európskej kúpnej opcie v čase maturity T nasledovne: ( ln S 0 K Call 0 = S 0 ϕ + rt + ) ( 1 σ T ln S 0 σ Ke rt ϕ + rt ) 1 K σ T T σ. T ). 11
19 Pre l ubovol ný čas t 0, T potom platí: ( ln S t K Call t = S t ϕ + r(t t) + ) 1 σ (T t) σ T t ( ln S t Ke r(t t) K ϕ + r(t t) ) (6) 1 σ (T t) σ T t a tento vzt ah sa nazýva Black-Scholesov vzorec pre hodnotu európskej kúpnej opcie v čase t na akciu, ktorej hodnota v čase t je S t, pričom realizačná cena je K a maturita T. 1.3 Predajno-kúpna parita Predajno-kúpna parita je vzt ah, ktorý platí medzi hodnotou európskej kúpnej a európskej predajnej opcie, ktoré majú rovnaký čas splatnosti T, majú rovnakú realizačnú cenu K a ktorých podkladovým aktívom je tá istá akcia. Vzt ah v čase T má tvar: S T + P ut T Call T = K. O platnosti tohto vzt ahu sa presvedčíme tak, že sa pozrieme na 3 situácie, ktoré môžu nastat : 1. K > S T S T +P ut T Call T = S T +(K S T ) + (S T K) + = S T +(K S T ) 0 = K,. K < S T S T +P ut T Call T = S T +(K S T ) + (S T K) + = S T +0 (S T K) = K, 3. K = S T S T + P ut T Call T = S T + (K S T ) + (S T K) + = S T = K. Vo všeobecnosti pre čas t 0, T platí: S t + P ut t Call t = Ke r(t t). 1
20 Využitím predajno-kúpnej parity a Black-Scholesovho vzorca pre hodnotu európskej kúpnej opcie získavame vzorec pre výpočet hodnoty európskej predajnej opcie P ut t = Ke r(t t) S t + Call t ( ln S t K = S t (ϕ + r(t t) + ) ) 1 σ (T t) σ 1 T t ( ln S t + Ke (1 r(t t) K ϕ + r(t t) )) 1 σ (T t) σ. T t (7) 13
21 Zaistené stratégie Odjakživa je túžbou človeka zbohatnút a zhodnotit svoj majetok. Jednou z možností naplnenia tohto ciel a je investovanie vol ných finančných prostriedkov do cenných papierov. Investícia na akciových trhoch je vel mi lákavou ponukou z dôvodu možnosti vel kého zárobku, ale prináša so sebou aj riziko, že v prípade nepriaznivého vývoja na trhu, nemusí priniest žiadny zisk, dokonca môžeme o čast alebo aj celú počiatočnú investíciu príst. Naopak, investícia do dlhopisov, ktorú využívajú najmä rizikovo averzní investori, so sebou nenesie takmer žiadne riziko, ale aj zisk je tomu úmerný - minimálny. Je tu však aj iné riešenie, ktorým sú zaistené investície. Na rozdiel od akcií, nám zaistené investície nikdy neprinesú na konci obchodovatel ného obdobia stratu a v porovnaní s dlhopismi môžeme vd aka nim dosiahnut vyšší zisk. Ponúkajú nám možnost participovat na rastúcich trhoch a zároveň nám garantujú čiastku, pod ktorú hodnota našej investície neklesne, čiže nás chránia pred stratami spôsobenými klesaním cien akcií. Zaistenie však určite nie je zadarmo. Cenou pre investora je to, že sa musí vzdat časti svojho potenciálneho zisku, ktorý by mu plynul z investície do akciového trhu v prípade pozitívneho vývoja na trhu. Zaistené investície sú vel mi obl úbenou formou investovania v Európe, v menšej miere v Amerike a v niektorých krajinách Ázie a existuje ich už viacero druhov. Medzi najrozšírenejšie patria CPPI (Constant Proportion Portfolio Insurance) a OBPI (Option Based Portfolio Insurance)..1 CPPI V nasledujúcej časti sa bližšie pozrieme na metódu CPPI (Constant Proportion Portfolio Insurance), jej podstatu a taktiež matematický popis, pričom budeme vychádzat z [6]. CPPI je metóda investovania, pri ktorej má investor zaručené, že hodnota jeho portfólia bude vždy nad stanovenou hranicou (dnom). Hranicu si určí ako určité percento jeho pôvodného kapitálu, o ktoré nechce na konci investičného obdobia za žiadnu cenu príst. V čase sa dno bude vyvíjat podl a vzt ahu: dp t = P t rdt, 14
22 čiže P t = P 0 e rt, kde P t je hodnota dna v čase t, P 0 hodnota dna v čase 0, r je bezriziková úroková miera. Rozdiel medzi hodnotou portfólia a dnom sa nazýva vankúš, graficky znázornený na Obr. 5. Platí: C t = V t P t, (8) C t - hodnota vankúša v čase t, V t - hodnota portfólia v čase t, P t - hodnota dna v čase t. Obr. 5: Vankúš a dno v CPPI metóde. Investor rozdelí kapitál do akcií (riziková čast ) a dlhopisov (bezriziková čast ). Hodnota investovaná do akcií (E t ), nazývaná tiež vystavenie, je rovná konštantnému násobku vankúša a platí E t = mc t. Multiplikátor m > 1, ale v prípade, že m = 1, ide o stratégiu Buy & Hold, pri ktorej portfólio nemusíme rebalancovat (menit hodnotu investovanú v akciách a dlhopisoch), ale vystavenie sa nastaví len na začiatku a potom sa už s portfóliom do maturity nemanipuluje. Určí sa v závislosti od miery averzie ku riziku. Čím je multiplikátor väčší, tým viac môže portfólio participovat na raste cien akcií, na druhej strane, v prípade poklesu cien akcií sa vystavenie rýchlejšie zmenšuje 15
23 a t ažšie zachytí prípadný obrat vo vývoji cien. Zvyšok, čiže (V t E t ) je investovaný do dlhopisov. Podl a vzt ahu (8) vyjadríme hodnotu portfólia: Pre hodnotu vankúša C platí: kde V t E t V t = C t + P t = C t + P 0 e rt dc t = d(v t P t ) = db t B t (V t E t ) + ds t S t E t dp t, je hodnota investovaná v bezrizikovom aktíve B (dlhopisoch), ktorého hodnota je opísaná vzt ahom db t = B t rdt a E t je vystavenie do rizikového aktíva S (akcií), ktoré sa vyvíja podl a rovnice ds t = S t (µ + σdw t ), (9) pričom W t je štandardný Brownov pohyb, µ a σ sú kladné konštanty. Čiže platí: dc t = db t B t (C t + P t mc t ) + ds t S t mc t dp t = r.dt(c t + P t mc t ) + (µ + σdw t )mc t r.p t dt = C t [(r(1 m) + mµ)dt + mσdw t ] = C t [(m(µ r) + r)dt + mσdw t ] a teda C t = C 0 e (m(µ r)+r m σ )t+mσw t. (10) Zo vzt ahu (9) vyjadríme hodnotu akcie v čase t: S t = S 0 e (µ 1 σ )t+σw t, (11) potom a odtial ln S t S 0 = (µ 1 σ )t + σw t W t = 1 σ [ ln S t (µ 1 ) ] S σ t. 0 16
24 Ak dosadíme tento výraz do vzt ahu (10), dostávame [ ] C t = C 0 e (m(µ r)+r m σ )t+mσ 1 ln S t (µ 1 σ S 0 σ )t = C 0 e (r m(r 1 σ ) m σ ) t ( St S 0 ) m = α t S m t, kde α t = C 0 e β t, β = r m (r 1 ) S0 m σ m σ. Takže hodnotu portfólia môžeme zapísat ako V t = α t S m t + P 0 e rt. (1) Všimnime si, že hodnota portfólia nezávisí od počtu akcií v portfóliu.. OBPI Odvolávajúc sa na [4] metóda OBPI (Option Based Portfolio Insurance) je založená na zaistení portfólia vd aka opciám. Stratégia spočíva v investovaní do rizikového aktíva a put opcie vypísanej na toto aktívum. Hodnota portfólia tak bude v každom prípade nad realizačnou cenou put opcie. Ak cena rizikového aktíva bude v čase maturity pod realizačnou cenou put opcie, investor si uplatní túto opciu a predá akciu. V opačnom prípade opciu nebude realizovat. Čiže hodnotu portfólia v čase T vyjadríme nasledovne: V T = S T + P ut T = S T + max{k S T, 0}, kde S T je hodnota akcie v čase T, P ut T je hodnota put opcie v čase T na akciu S s maturitou T, K je realizačná cena opcie. Ak využijeme predajno-kúpnu paritu, predchádzajúci vzt ah bude mat tvar: V T = K + Call T (13) = K + max{s T K, 0}. Takže V T K S T K S T S T > K. 17
25 Vidíme, že garantovaná suma, o ktorú na konci investovania investor určite nepríde, je K. Pre hodnotu portfólia v každom čase t platí: V t = S t + P ut t = Ke r(t t) + Call t, kde P ut t a Call t sú hodnoty opcií s podkladovým aktívom S, realizačnou cenou K, maturitou T počítané Black-Scholesovými vzorcami..3 Porovnanie CPPI a OBPI Hodnotu portfólia v čase t pre metódu CPPI označíme V CP P I t a pre metódu OBPI Vt OBP I. Predpokladajme, že investujeme podl a obidvoch metód na rovnaký čas T, podkladovým aktívom je tá istá akcia S a na začiatku máme rovnaký kapitál, teda V CP P I 0 = V OBP I 0. Vychádzajúc z [3] platí, že ani jedna z týchto stratégií nie je výhodnejšia ako tá druhá pre všetky koncové hodnoty rizikového aktíva, pretože ich výplatné funkcie sa navzájom pretínajú. Pomocou vzt ahu (1) vyjadreného v čase T (pre CPPI) a vzt ahu (13) (pre OBPI) vypočítame hodnotu portfólia pre rôzne hodnoty akcie v čase maturity. Situácia je znázornená na Obr. 6 pre nasledujúce hodnoty: V 0 = 100, K = 100, S 0 = 100, T =, r = 0, 05, sigma = 0,. Z grafu vidíme, že konečná hodnota portfólia (V T ) je pri malom zvýšení hodnoty akcie najvyššia pri metóde OBPI, pri väčších výkyvoch hodnoty akcie je výnosnejšia metóda CPPI. Podl a [3] si ukážeme, že metóda OBPI je zovšeobecnenou metódou CPPI. V prípade metódy CPPI je v čase T garantovanou hodnotou P T a pri metóde OBPI určite neklesne hodnota portfólia pod hladinu K. Z toho vyplýva, že platí: P T = K, v čase t nastáva rovnost : P t = Ke r(t t). Pripomeňme si, že hodnota portfólia pre metódu OBPI vyzerá nasledovne: V OBP I t = Ke r(t t) + Call t. 18
26 CPPI (m=1) CPPI (m=) CPPI (m=6) CPPI (m=8) OBPI V T S T Obr. 6: Porovnanie OBPI a CPPI metódy. Ako sme si ukázali, Ke r(t t) môžeme nazvat dnom a zvyšok, teda Call t potom zodpovedá hodnote vankúša z metódy CPPI. Preto vo vzt ahu pre multiplikátor metódy CPPI, pre ktorý platí m t = E t C t môžeme vankúš C t nahradit kúpnou opciou (E t je vystavenie do rizikového aktíva). Dostávame: m OBP I t = S tn t Call t, kde S t je hodnota akcie v čase t, N t je počet týchto akcií nakúpených v čase t (S t N t = E t ), Call t je hodnota európskej kúpnej opcie, ktorej podkladovým aktívom je S a realizačnou cenou je K. Metóda OBPI je teda ekvivalentná metóde CPPI s multiplikátorom m OBP t I. Všimnime si však, že zatial čo pri metóde CPPI bol multiplikátor konštantný po celý čas investovania, pri metóde OBPI sa jeho hodnota v čase mení. 19
27 3 Stratégie založené na metóde OBPI, CPPI, VAR V tejto časti sa pozrieme na 4 rôzne prístupy ako rozdelit kapitál medzi rizikové a bezrizikové aktívum s ohraničením rizika. Nech V t hodnota portfólia v čase t, T dĺžka investovania (maturita), g garantovaná hranica, S hodnota v rizikovom aktíve, B hodnota v bezrizikovom aktíve, r bezrizikový úrok. 3.1 Metóda OBPI V prvom prípade zabezpečíme garanciu predajnou opciou, ktorej podkladovým aktívom bude rizikové aktívum z nášho portfólia. Opciou si vlastne poistíme pád hodnoty portfólia pod garantovanú hranicu. Táto stratégia je ekvivalentná už spomínanej metóde OBPI. Portfólio bude obsahovat okrem investície do rizikovej (S) a bezrizikovej časti (B) aj poistenie portfólia. Cena poistenia, ktorá nechceme aby presiahla nami stanovenú čast počiatočného kapitálu, bude vlastne hodnota tejto predajnej opcie (P ut). Situácia je graficky znázornená na Obr. (7). Zhodnotenie časti v bezrizikovom aktíve vieme určit už na začiatku, pretože poznáme bezrizikový úrok. Ak na začiatku investovania je táto hodnota B 0, na konci sa zúročí na B 0 e rt. Vývoj rizikovej časti už však vôbec nie je istý, preto nie je na obrázku znázornený plnou čiarou. Put 0 S 0 S T g B 0 B T Obr. 7: 1. metóda - OBPI. 0
28 Ak celková hodnota, ktorá je investovaná v akciách a dlhopisoch bude v čase maturity nižšia ako garantovaná hranica (čo je aj prípad na obrázku), uplatní sa predajná opcia. Realizačná cena tejto opcie (K), čiže cena, za ktorú sa akcia predá, musí byt rovná rozdielu medzi garantovanou hranicou a hodnotou v bezrizikovom aktíve v čase maturity. Matematicky K = g B T = g B 0 e rt, (14) kde K je realizačná cena opcie. Tak sa dosiahne, že pod garantovanú hranicu sa hodnota portfólia určite nedostane. Ak hodnota v rizikovej časti a bezrizikovej časti bude v súčte vyššia ako je garantovaná hranica, opcia sa neuplatní. Platí: g S T + B T g V T S T + B T S T + B T > g. Všimnime si, že využitím predajno-kúpnej parity pre počiatočnú hodnotu portfólia platí: V 0 = B 0 + S 0 + P ut 0 = B 0 + Ke rt + Call 0. Ked že hodnota Ke rt sa v čase správa rovnako ako hodnota, ktorá je investovaná do dlhopisu, môžeme napísat : V 0 = B 0 + Call 0, kde B 0 = B 0 + Ke rt. Úloha ako prerozdelit počiatočný kapitál, ak za poistenie sme ochotní zaplatit sumu εv 0, spočíva v maximalizácii hodnoty investovanej v rizikovej časti, pretože pri tej istej cene poistenia máme dolnú hranicu konečnej hodnoty portfólia takú istú (v prípade priaznivého aj nepriaznivého vývoja ceny akcie na trhu), ale v prípade priaznivého vývoja ceny rizikového aktíva dosiahneme vyšší výnos, ak do akcií investujeme vyššiu sumu. Našou úlohou je teda maxs 0 za podmienky cena poistenia εv 0. 1
29 Ako už bolo spomenuté, poistenie je rovné hodnote európskej predajnej opcie, z toho vyplýva: cena poistenia εv 0 P ut 0 εv 0, kde P ut 0 je hodnota európskej predajnej opcie vyjadrená Black-Scholesovým vzorcom. Čím bude cena poistenia vyššia, tým vyššia hodnota môže byt investovaná v rizikovom aktíve, preto riešenie úlohy bude spĺňat rovnost P ut 0 = εv 0. Následne vyjadríme realizačnú cenu opcie zo vzt ahu (14): K = g (V 0 εv 0 S 0 )e rt. (15) Využitím vzt ahu (7) pre hodnotu európskej kúpnej opcie riešime úlohu za podmienky S 0 (ϕ ( ln S 0 K +rt + 1 σ T σ T ) maxs 0 ) ( ( )) 1 + Ke rt ln 1 ϕ S 0 K +rt 1 σ T σ εv T 0, kde K je dané vzt ahom (15). Na Obr. 8 je znázornené, aká čast portfólia (p) môže byt investovaná v rizikovom aktíve v závislosti od pomeru garantovanej hodnoty k celkovej hodnote počiatočného kapitálu. Červenou farbou je táto závislost vyjadrená pri podmienke, že sme za poistenie ochotní zaplatit 5% vstupného kapitálu a modrou farbou je znázornená závislost pri maximálnej výške poistenia 1% kapitálu podiel v akciách p Obr. 8: Závislost podielu v akciách od garancie.
30 3. Metóda OBPI bez kúpy opcie Nasledujúca metóda je vel mi podobná predošlej, avšak prerozdelenie kapitálu medzi rizikové a bezrizikové aktívum určíme tak, aby prípadná cena poistenia portfólia proti pádu jeho hodnoty pod garantovanú hranicu nepresiahla nami stanovenú čast počiatočného kapitálu. Ako sme ukázali pri predošlej metóde, cena poistenia je rovná hodnote európskej predajnej opcie na akciu v portfóliu s realizačnou cenou K, ktorá je rovná rozdielu medzi garantovanou hranicou a hodnotou investovanou v bezrizikovom aktíve v čase maturity. Na rozdiel od predchádzajúcej metódy si predajnú opciu v tomto prípade nekúpime, čiže portfólio nebude poistené. Výhodou je, že máme k dispozícii viac prostriedkov na investíciu do akcií a dlhopisov a tým aj potenciálne vyšší výnos, ale garantovanú hranicu nemáme zaručenú. Takže rozdelíme počiatočný kapitál tak, že jeho poistenie by nebolo drahšie ako εv 0. Hodnota investície v čase maturity bude V T = S T + B T v každom prípade, čiže aj vtedy, ked S T + B T g. Na nasledujúcom obrázku je znázornená možná situácia investovania a vývoj portfólia. S 0 S T B 0 B T g Obr. 9:. metóda - OBPI bez kúpy opcie. Výpočet na určenie prerozdelenia kapitálu bude spočívat vo vyriešení rovnakej maximalizačnej úlohy ako pri predošlej metóde OBPI: 3
31 za podmienky S 0 (ϕ ( ln S 0 K +rt + 1 σ T σ T ) maxs 0 ) ( ( )) 1 + Ke rt ln 1 ϕ S 0 K +rt 1 σ T σ εv T 0, ale realizačná cena K = g B T = g B 0 e rt = g (V 0 S 0 )e rt. 3.3 Metóda CPPI Ďalšou z možností ako určit hodnotu investovanú do rizikového aktíva a do bezrizikového aktíva tak, aby sme dosiahli garantovanú hranicu je metóda CPPI, ktorej multiplikátor nastavíme na hodnotu 1. Takže počiatočná investícia v dlhopisoch musí byt rovná diskontovanej garantovanej hodnote, matematicky B 0 = ge rt, aby na konci investovania bola hodnota v dlhopisoch rovná práve garantovanej hodnote a zvyšok investovaný v akciách môže priniest zisk navyše, avšak aj v najhoršom prípade, ak by hodnota akcií klesla na 0, hodnota portfólia neklesne pod garantovanú hodnotu. Vieme, že garantovaná hodnota sa stanoví ako určité percento (p) počiatočného kapitálu a teda v akciách je hodnota S 0 = B 0 V 0 = ge rt V 0 = V 0 (pe rt 1). Rozdelenie portfólia pre túto metódu vidíme graficky na Obr. 10. S 0 S T B 0 rt g(=b e ) B T 0 Obr. 10: 3. metóda - CPPI (s multiplikátorom 1). 4
32 3.4 Metóda VAR Posledná stratégia, ktorú opíšeme je totožná s predchádzajúcou metódou CPPI s multiplikátorom 1, teraz však garantovanú hodnotu nemusíme dosiahnut s určitost ou, ale požadujeme iba 100(1 α)%-nú pravdepodobnost dosiahnutia tejto hranice. Je samozrejmé, že v rizikovom aktíve bude vyššia hodnota ako v predošlej metóde, tým aj možnost lepšieho zhodnotenia, ale na druhej strane, nie vždy dosiahneme garantovanú hodnotu, teda je tu možnost väčšej straty. Táto stratégia sa nazýva VAR (Value at risk), čiže je pri nej stanovená možná najhoršia strata, ktorá nebude prekročená s určitou pravdepodobnost ou ([5]). Rozloženie portfólia vidíme na Obr. 11. S 0 S T B 0 B T g(p(v >g)=90%) T Obr. 11: 4. metóda - VAR (Value at risk). Aby sme prišli na to, akú hodnotu môžeme investovat do rizikového aktíva, musíme vyriešit nasledovnú úlohu: Vieme, že V T = S T + B T a teda P (V T g) = 1 α. P (S 0 e (µ 1 σ )T +σw T + (V 0 S 0 )e rt g) = 1 α. Po úprave sa dostaneme k vyriešeniu úlohy ( W T P ln( ) g V 0+S 0 ert S 0 ) (µ 1 σ )T T σ = 1 α, T kde W T T N(0, 1), pretože W T N(0, T ). Musí platit ln( g V 0+S 0 e rt S 0 ) (µ 1 σ )T σ T = c α, 5
33 kde c α je 100α-percentná kritická hodnota normovaného normálneho rozdelenia. Po vyjadrení S 0, čo je vlastne hodnota v rizikovom aktíve a určení garantovanej hodnoty ako určitej časti počiatočného kapitálu dostávame S 0 = pv 0 V 0 e rt e c ασ T +(µ 1 σ )T e rt. Ak by sme chceli zabezpečit 100%-nú garanciu (c α ) S 0 = V 0 (pe rt 1), čo je presne hodnota, ktorú sme dostali pri predchádzajúcej metóde CPPI s multiplikátorom podiel v akciách alfa Obr. 1: Závislost podielu v akciách od pravdepodobnosti dosiahnutia garant. hranice. Na Obr. 1 je znázornená závislost podielu z celkového počiatočného kapitálu v akciách od pravdepodobnosti s akou chceme dosiahnut garantovanú hodnotu. Modrou farbou je táto závislost vyjadrená pre garantovanú hranicu rovnú výške počiatočného kapitálu (p = 1) a červenou pre garantovanú hodnotu, ktorá tvorí 90% počiatočného kapitálu (p = 0.9). Znak vyjadruje podiel v akciách ak garantovaná hodnota sa rovná počiatočnému kapitálu a chceme ju dosiahnut so 100%-nou pravdepodobnost ou a znakom je vyjadrený tento podiel pre 100%-nú garanciu návratu 90% zo vstupného kapitálu. 6
34 3.5 Porovnania V nasledujúcej časti sa pozrieme na porovnanie všetkých 4 spomenutých stratégií investovania do rizikového a bezrizikového aktíva. Prvú spomenutú metódu nazveme OBPI, druhú OBPI bez kúpy opcie, s tret ou budeme pracovat ako s metódou CPPI a pre štvrtú zavedieme názov VAR. V každej z metód sme vyjadrili počiatočnú investíciu v rizikovom aktíve a aj pomocou vzt ahu (11) vypočítame očakávanú hodnotu portfólia v momente splatnosti. Na určenie konečnej celkovej hodnoty portfólia je potrebné určit hodnotu v akciovej časti, ktorá záleží od náhodnej premennej W T N(0, T ). Budeme generovat náhodné čísla z tohto rozdelenia a tak získame rôzne hodnoty portfólia v čase maturity a na základe nich znázorníme histogramy, kvantily a iné popisné štatistiky. Pre modelovú situáciu si vstupné parametre, ktoré môžu zodpovedat reálnym hodnotám na finančnom trhu zvolíme nasledovne: bezrizikový úrok r = 0.03, stredná hodnota µ = 0.07, volatilita ceny akcie σ = 0., splatnost T = 10 rokov, cena poistenia ϵ = 1% vstupného kapitálu, garantovaná hodnota p = 90% vstupného kapitálu, pravdepodobnost dosiahnutia garantovanej hodnoty (pri metóde VAR) = 90%(α = 0.1). Na Obr. 13 sú znázornené histogramy pre všetky 4 stratégie. Na x-ovej ( V osi je totálny výnos portfólia T V0 ), na y-ovej osi kol kokrát bol daný totálny výnos portfólia dosiahnutý z 1000 náhodných simulácií. Červenou farbou sú znázornené tie stĺpce histogramu, ktoré vyjadrujú počet portfólií, ktoré nedosiahli garantovanú hodnotu. Pre dôkladnejšiu analýzu sa v Tab. 1 nachádzajú početnosti totálneho výnosu portfólia pre jednotlivé metódy v daných rozpätiach. Bolo už spomenuté, že obe metódy CPPI a OBPI garantujú, že hodnota celkového portfólia neklesne pod garantovanú hranicu, čo je takisto vidiet z histogramov a stĺpcov tabul ky prislúchajúcim týmto dvom metódam. V prípade OBPI bez kúpy opcie hodnota portfólia klesla pod hodotu 90% vstupného kapitál (garantovaná hodnota pri OBPI a CPPI) v, 7% prípadov a metódou 7
35 VAR sme danú hodnotu nedosiahli v 7, 3% prípadov. Z tabul ky d alej vidíme, že početnost totálnych výnosov je pri metóde VAR rovnomernejšie rozdelená ako pri zvyšných, takže je tu vyššia pravdepodobnost dosiahnutia vel kých výnosov ale i strát. Naopak pri metóde CPPI, sú simulované dáta viac koncentrované, dokonca hodnoty 1., 1.5) sú dosiahnuté s pravdepodobnost ou až 41, 6%. 150 OBPI 150 OBPI bez kúpy opcie CPPI VAR Obr. 13: Histogramy pre jednotlivé stratégie investovania. Ako je na prvý pohl ad zrejmé, pri metóde CPPI nie je rozptyl dát taký vel ký ako pri zvyšných metódach. Pri metóde OBPI sa javí byt tento ukazovatel o čosi väčší a najväčší rozptyl dát môžeme pozorovat pri investovaní metódou VAR. Tento predpoklad sme overili spočítaním príslušných variancií σ (vid Tab. ). Na základe tohto ukazovatel a môžeme povedat, že najmenej riziková je CPPI a najrizikovejšou je metóda VAR. Je však všeobecne známe, že pri riskantnejších stratégiách je s väčšou pravdepodobnost ou možné dosiahnut vyšší zisk. Môžeme to dokázat výpočtom strednej hodnoty očakávaného totálneho výnosu (R) (vid Tab.). Najvyšší očakávaný výnos poskytuje metóda s najväčšou varianciou, teda metóda VAR a naopak najnižší metóda CPPI, ktorej variancia je najmenšia zo všetkých skúmaných stratégií. 8
36 Tabul ka 1: Hodnoty zodpovedajúce histogramom na Obr. 13. Rozpätie R Početnost hodnôt v danom rozpätí (v %) OBPI OBPI bez CPPI VAR kúpy opcie 0, 0.9) 0,0,7 0,0 7,3 0.9, 1.) 1, 17,9 10,4 19,5 1., 1.5) 5,3,9 41,6 16,5 1.5, 1.8) 17,8 18, 3,8 15,0 1.8,.1) 1,5 1,5 1,6 10,9.1,.4) 8,3 7, 5,8 9,3.4,.7) 4,4 6,,4 6,1.7, 3.0) 3,8 4,5 1,3 4,3 3.0, 3.3) 1,9, 0,8,8 3.3, 3.6) 1, 1,7 0,5,0 3.6, 3.9) 0,7 0,7 0,4 1,6 3.9, 4.) 1,1 0,8 0,1 0,9 4., 4.5) 0,1 0,9 0, 0,5 4.5, 4.8) 0,5 0,6 0,0 0, , 1,0 0,1 5,0 Ďalšou porovnávacou štatistikou, ktorú môžeme sledovat sú kvantily. Pre jednotlivé metódy sme vypočítali príslušné 5%, 10%, 0%, 40%, 60%, 80%-né kvantily. α%-ný kvantil nám udáva totálny výnos, ktorý je vyšší ako α% totálnych výnosov, ktoré sme náhodne vygenerovali pre konkrétnu stratégiu. Môžeme ho chápat taktiež ako hodnotu, pod ktorú neklesne totálny výnos s pravdepodobnost ou α alebo hodnotu, nad ktorú sa môže dostat s pravdepodobnost ou 1 α. Vidíme, že pri metóde OBPI bez kúpy opcie môže totálny výnos klesnút pod hodnotu 0, 88 s pravdepodobnost ou 5%, pri metóde VAR až pod hodnotu 0, 78. Ak sa pozrieme bližšie na metódu VAR, vidíme, že s rovnakou pravdepodobnost ou môžeme klesnút vždy pod nižšiu hodnotu v porovnaní so zvyšnými metódami až po pravdepodobnost 40%. Avšak naopak s tou istou pravdepodobnost ou 40% dosiahneme už vyšší výnos ako v ostatných stratégiách a rozdiel vo výnosoch sa stále zväčšuje, čím je menšia pravdepodobnost prekročenia určitej hodnoty. Vidíme, že je spnená podmienka, ktorú 9
37 sme požadovali od tejto metódy a to, že garantovanú hranicu stačí dosiahnut s pravdepodobnost ou 90%, pretože 10%-ný kvantil má hodnotu 0, 8966 =. 0, 9. Taktiež si môžeme všimnút, že CPPI je najkonzervatívnejšia spomedzi ostatných a vyšší totálny výnos ako 1, 81 dosiahneme len s 0%-nou pravdepodobnost ou, zatial čo pri druhej najkonzervatívnejšej metóde (OBPI) s touto pravdepodobnost ou dosiahneme totálny výnos vyšší ako, 15. Tabul ka : Porovnanie popisných ukazovatel ov jednotlivých metód OBPI OBPI bez CPPI VAR kúpy opcie σ 0,478 0,7770 0,485 1,041 R 1,6610 1,7873 1,5857 1,8510 kvantil (5%) 0,9000 0,8836 1,1009 0,776 kvantil (10%) 0,9789 0,9780 1,1508 0,8996 kvantil (0%) 1,1110 1,173 1,356 1,0399 kvantil (40%) 1,3817 1,387 1,3630 1,3554 kvantil (60%) 1,6784 1,755 1,5587 1,8445 kvantil (80%),1515,39 1,8149,365 Porovnania budeme realizovat aj na základe funkcie užitočnosti, ktorej tvar je nasledovný: U(x) = x1 α 1 1 α, kde α reprezentuje investorovu mieru averzie k riziku, čiže čím vyššie α, tým je jeho averzia vyššia. Investor si volí svoje portfólio tak, aby maximalizoval strednú hodnotu funkcie užitočnosti, teda maxe(u(x)). V Tab. 3 sa nachádzajú stredné hodnoty funkcie užitočnosti v závislosti od averzie k riziku (α) pre jednotlivé metódy. Vždy červenou farbou sú znázornené najvyššie hodnoty v príslušnom stĺpci. V prvom stĺpci sú zaznamenané hodnoty pre investora, ktorému riziko do vel kej miery neprekáža a aby maximalizoval svoju užitočnost zvolí si metódu VAR. Vidíme, že v poslednom stĺpci, v ktorom sú hodnoty pre investora, ktorý je vel mi averzný voči riziku, sa 30
38 najvyššia hodnota nachádza pri investovaní podl a stratégie CPPI a najnižšia pri VAR, takže sme si overili, že metódu CPPI môžeme považovat za najkonzervatívnejšiu a metódu VAR naopak za najriskantnejšiu, menej vhodnú pre riziko averzného investora. Tabul ka 3: Hodnoty funkcie užitočnosti vzhl adom na averziu k riziku. Metóda α = α = 4 α = 6 α = 8 α = 10 OBPI OBPI bez kúpy opcie CPPI VAR Samozrejme, pri inom nastavení vstupných parametrov by situácia mohla dopadnút inak. Ak by sme si napríklad pri metóde CPPI stanovili nižšiu garantovanú hranicu, stratégia by mohla dosahovat vysoké hodnoty s väčšou pravdepodobnost ou ako pri metóde VAR, avšak strácal by sa význam garancie iba nízkeho pádu hodnoty portfólia. Naopak, pri stratégii VAR, čím by sme požadovali vyššiu pravdepodobnost dosiahnutia určitej hranice, tým viac by sa táta metóda podobala metóde CPPI (pri pravdepodobnosti 100% sú tieto metódy totožné). Ak v stratégii OBPI bez kúpy opcie obmedzíme výšku poistenia na, 93% hodnoty vstupného kapitálu (ϵ = 0, 093), dosiahneme, že do rizikového aktíva vložíme takú čast kapitálu, ktorú sme doň vložili pri metóde VAR s požiadavkou, že garantovanú hranicu, tvoriacu 90% kapitálu, dosiahneme s pravdepodobnost ou 90%. Takže v každej situácii by sa dali nastavit vstupné parametre tak, aby VAR a OBPI bez kúpy opcie boli ekvivalentné. 31
39 Záver Ciel om tejto bakalárskej práce bolo porovnat zaistené stratégie, ktoré pri garancii určitej čiastky na horizonte sl ubujú pokial možno čo najvyšší zisk so stratégiou, kde je riziko kontrolované vel kost ou poistenia dosiahnutia určitej hranice. V prvej časti bakalárskej práce sme sa zamerali na opcie a vd aka poznatkom z tejto časti sme mali možnost porozumiet, na akom princípe je založená metóda OBPI (Option Based Portfolio Insurance), ktorá patrí spolu s metódou CPPI (Constant Proportion Portfolio Insurance) medzi zaistené stratégie. Tieto dve metódy sme podrobnejšie analyzovali a zároveň sme ich navzájom porovnali. Metóda CPPI spočíva v prerozdelení kapitálu medzi rizikové a bezrizikové aktívum, zatial čo pri metóde OBPI sa investuje do rizikového aktíva a naň naviazanej predajnej opcie. Ukázali sme, že ani jedna z týchto stratégií nedominuje nad druhou pre všetky konečné hodnoty rizikového aktíva a vysvetlili sme vzt ah medzi týmito metódami. Nosnou čast ou tejto práce bolo porovnanie štyroch rôznych metód prerozdelenia počiatočného kapitálu medzi rizikové a bezrizikové aktívum, pričom v každej z metód bolo riziko ohraničené iným spôsobom. Prvou metódou bola už spomenutá metóda CPPI. Jej podstata spočívala v investovaní do bezrizikového aktíva takej čiastky, aby na konci investičného obdobia zabezpečila určenú garantovanú hodnotu a rizikové aktívum tak mohlo priniest už len zisk navyše. Pri hlbšej analýze CPPI sme sa zamysleli nad otázkou, ako by vyzeralo prerozdelenie kapitálu, ak by sme nepožadovali, aby garantovaná hodnota bola dosiahnutá so 100%-nou pravdepodobnost ou, ale menšou. Táto stratégia sa nazýva VAR (Value at risk) a takisto bola jednou s porovnávaných metód. Na stratégiu OBPI sme sa pozreli ako na stratégiu, pri ktorej sa poistíme proti pádu pod garantovanú hranicu a zároveň žiadame, aby poistenie nebolo drahšie ako určitá čast vstupného kapitálu. Ak by sa toto poistenie nekúpilo, k dispozícii zostane viac prostriedkov na investovanie a riziko je aj v tomto prípade ohraničené. Nevýhodou však je, že garantovaná hranica nebude vždy dosiahnutá, ale aj táto stratégia je zaujímavou príležitost ou ako investovat, a tak sme ju zahrnuli do porovnania. Pre rôzne postoje ku riziku sme stanovili 3
40 vždy najvýhodnejšiu stratégiu. Výhodnost však závisí od nastavení vstupných údajov ako napríklad výšky garantovanej hranice, ceny poistenia alebo pravdepodobnosti, s ktorou má byt garantovaná hranica dosiahnutá. Je tak na samotnom investorovi ako si určí vstupné parametre a pre ktorú zo spomínaných metód sa rozhodne. 33
41 Literatúra [1] MELICHERČÍK, I. - OLŠAROVÁ, L. - ÚRADNÍČEK, V. 005 Kapitoly z finančnej matematiky. Bratislava: EPOS, 005. ISBN [] PEROLD, A.F. - SHARPE, W.F Dynamic strategies for asset allocation. In Financial Analysts Journal. ISSN: X, 1988, vol.44, no.1, p [3] BERTRAND, P. - PRIGENT, J. 001 Portfolio Insurance Strategies: Obpi Versus Cppi. University of CERGY: Working Paper No ; GREQAM Working Paper, 001. Dostupné na internete: [4] BOUYÉ, E. 009 Portfolio Insurance: A Short Introduction. Warwick Business School, 009. Dostupné na internete: [5] JORION, P. 1996: Risk : Measuring the Risk in Value at Risk. In Financial Analysts Journal. ISSN: X, 1996, vol.5, no.6, p [6] BALDER, S. - BRANDL, M. - MAHAYNI, A. 009: Effectiveness of CPPI Strategies under Discrete Time Trading. In The Journal of Economic Dynamics and Control. ISSN: , 009, vol. 33, no. 1, p [7] BOULIER, J-F. - KANNIGANTI, A. 005: Expected performance and risks of various portfolio insurance strategies. Paris: 5 th AFIR International Colloquium, 005. Dostupné na internete: Kanniganti.pdf 34
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky
 fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Zaistené stratégie. Bc. Tomáš Miklošovič.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie
 I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio
 Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY
 International Scientific Conference YOUNG SCIENTISTS 2011 HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY Marko LALIĆ Technická Univerzita v Košiciach, Ekonomická fakulta Katedra financií
International Scientific Conference YOUNG SCIENTISTS 2011 HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY Marko LALIĆ Technická Univerzita v Košiciach, Ekonomická fakulta Katedra financií
Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií
 UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put opcií: Aplikácia na akcie SPDR Gold Shares
 Ing. Martina Rusnáková Katedra financií, Ekonomická fakulta echnická univerzita v Košiciach E-mail: martina.rusnakova@tuke.sk Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put
Ing. Martina Rusnáková Katedra financií, Ekonomická fakulta echnická univerzita v Košiciach E-mail: martina.rusnakova@tuke.sk Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put
OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE
 NATIONAL AND REGIONAL ECONOMICS VIII OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE Ing. Radoslav BLAHOVEC Technická univerzita v Košiciach Ekonomická fakulta Katedra regionálnych vied a manažmentu Radoslav.Blahovec@tuke.sk
NATIONAL AND REGIONAL ECONOMICS VIII OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE Ing. Radoslav BLAHOVEC Technická univerzita v Košiciach Ekonomická fakulta Katedra regionálnych vied a manažmentu Radoslav.Blahovec@tuke.sk
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ. Currency risk hedging in Flash Steel, a. s.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ Zajištění proti kurzovému riziku ve společnosti Flash Steel, a. s. Currency risk hedging in Flash Steel, a. s. company
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ Zajištění proti kurzovému riziku ve společnosti Flash Steel, a. s. Currency risk hedging in Flash Steel, a. s. company
OPČNÉ STRATÉGIE A MOŽNOSTI ICH VYUŽITIA
 Masarykova univerzita Ekonomicko-správní fakulta Studijní obor: Finance OPČNÉ STRATÉGIE A MOŽNOSTI ICH VYUŽITIA Option strategies and their application Diplomová práce Vedoucí práce: Ing. Peter MOKRIČKA,
Masarykova univerzita Ekonomicko-správní fakulta Studijní obor: Finance OPČNÉ STRATÉGIE A MOŽNOSTI ICH VYUŽITIA Option strategies and their application Diplomová práce Vedoucí práce: Ing. Peter MOKRIČKA,
Opčné spektrum. Neutrálne trhové očakávania. Vypísanie kužela Vypísanie brzdy. Kúpa časového rozpätia
 Opčné stratégie. Realizácia opčných stratégií sa uskutočňuje prostredníctvom zaujatia pozície v jednej alebo viacerých opciách. Opcie pri tom môžu mať rozdielne realizačné ceny alebo dátumy splatnosti.
Opčné stratégie. Realizácia opčných stratégií sa uskutočňuje prostredníctvom zaujatia pozície v jednej alebo viacerých opciách. Opcie pri tom môžu mať rozdielne realizačné ceny alebo dátumy splatnosti.
9 Oceňovanie derivátov
 9 Oceňovanie derivátov Finančné deriváty (financial derivatives) sú nástroje, ktorých hodnota je odvodená od ceny podkladového aktíva (underlying). Týmto môže byť komodita, akcia, dlhopis, menový kurz,
9 Oceňovanie derivátov Finančné deriváty (financial derivatives) sú nástroje, ktorých hodnota je odvodená od ceny podkladového aktíva (underlying). Týmto môže byť komodita, akcia, dlhopis, menový kurz,
Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš
 Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš Abstract Cieľ článku: Cieľom tohto článku je priblížiť zmeny hodnoty rizikovej prémie, identifikovať ktoré determinanty ju ovplyvňujú a ako
Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš Abstract Cieľ článku: Cieľom tohto článku je priblížiť zmeny hodnoty rizikovej prémie, identifikovať ktoré determinanty ju ovplyvňujú a ako
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. modelu úrokových mier
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová UNIVERZITA
Pokročilé metody kalibrace modelů
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Pokročilé metody kalibrace modelů úrokových sazeb Dominika Holotňáková Katedra pravděpodobnosti a matematické statistiky Vedoucí
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Pokročilé metody kalibrace modelů úrokových sazeb Dominika Holotňáková Katedra pravděpodobnosti a matematické statistiky Vedoucí
FDI development during the crisis from 2008 till now
 VŠB-TU Ostrava, Ekonomická fakulta, katedra Financí 8. -. září FDI development during the crisis from 8 till now Michal Fabuš, Miroslav Kohuťár Abstract Investments represent an important resource of country
VŠB-TU Ostrava, Ekonomická fakulta, katedra Financí 8. -. září FDI development during the crisis from 8 till now Michal Fabuš, Miroslav Kohuťár Abstract Investments represent an important resource of country
Raiffeisen Centrobank AG WEBEX - 1.ČASŤ PRE TATRA BANKA PREMIUM BANKING. Jún, Certifikáty od
 Raiffeisen Centrobank AG WEBEX - 1.ČASŤ PRE TATRA BANKA PREMIUM BANKING Jún, 2018 Certifikáty od WEBEX OBSAH 1. Nové Emisie 2. Podkladový index - aktualizácia vývoja na akciových trhoch 3. Premium garantované
Raiffeisen Centrobank AG WEBEX - 1.ČASŤ PRE TATRA BANKA PREMIUM BANKING Jún, 2018 Certifikáty od WEBEX OBSAH 1. Nové Emisie 2. Podkladový index - aktualizácia vývoja na akciových trhoch 3. Premium garantované
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks
 Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
Produkty finančných trhov a ich riziká. Ostatné (vrátane produktov viazaných na komodity, úver, či majetkové podiely)
 Produkty finančných trhov a ich riziká Ostatné (vrátane produktov viazaných na komodity, úver, či majetkové podiely) Obsah Úvod... 1 Popis rizík... 2 Všeobecné... 2 Charakteristiky opcií... 3 Riziko straty
Produkty finančných trhov a ich riziká Ostatné (vrátane produktov viazaných na komodity, úver, či majetkové podiely) Obsah Úvod... 1 Popis rizík... 2 Všeobecné... 2 Charakteristiky opcií... 3 Riziko straty
Pouºitie metódy Monte Carlo vo nanciách
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
Problémy oceňovania Startupov v súčasnosti. The problems with valuation of startups at present
 Problémy oceňovania Startupov v súčasnosti. The problems with valuation of startups at present Ján Bukoven Abstrakt: V súčasnosti je ekonomický rast a konkurencieschopnosť rozvinutých krajín poháňaný hlavne
Problémy oceňovania Startupov v súčasnosti. The problems with valuation of startups at present Ján Bukoven Abstrakt: V súčasnosti je ekonomický rast a konkurencieschopnosť rozvinutých krajín poháňaný hlavne
Kapitola 14. Výmenné kurzy a devízový trh: meny ako aktíva
 Kapitola 14 Výmenné kurzy a devízový trh: meny ako aktíva Obsah Čo sú výmenné kurzy Výmenné kurzy a ceny tovarov Devízový trh Dopyt po mene a ostatných aktívach Model devízového trhu: vplyv úrokových sadzieb
Kapitola 14 Výmenné kurzy a devízový trh: meny ako aktíva Obsah Čo sú výmenné kurzy Výmenné kurzy a ceny tovarov Devízový trh Dopyt po mene a ostatných aktívach Model devízového trhu: vplyv úrokových sadzieb
Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom
 Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom Príloha č. 1 k opatreniu Pozície štandardných derivátov sa konvertujú na ich ekvivalentnú pozíciu podkladového
Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom Príloha č. 1 k opatreniu Pozície štandardných derivátov sa konvertujú na ich ekvivalentnú pozíciu podkladového
BAKALÁŘSKÁ PRÁCE. Eva Mináriková Analýza akciového trhu
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Eva Mináriková Analýza akciového trhu Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr. Jan
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Eva Mináriková Analýza akciového trhu Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr. Jan
Analytické aproximácie pri modelovaní cien opcií
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
Attachment No. 1 Employees authorized for communication
 On behalf of Market Operator: Attachment No. 1 Employees authorized for communication Employees authorized for invoicing and payments: Head of billing Dana Vinická +421 917 931 470 dana.vinicka@okte.sk
On behalf of Market Operator: Attachment No. 1 Employees authorized for communication Employees authorized for invoicing and payments: Head of billing Dana Vinická +421 917 931 470 dana.vinicka@okte.sk
DÔLEŽITOSŤ INVESTOVANIA VOĽNÝCH PEŇAŽNÝCH PROSTRIEDKOV DO PODIELOVÝCH FONDOV THE IMPORTANCE OF INVESTING FREE FUNDS IN MUTUAL FUNDS
 DÔLEŽITOSŤ INVESTOVANIA VOĽNÝCH PEŇAŽNÝCH PROSTRIEDKOV DO PODIELOVÝCH FONDOV THE IMPORTANCE OF INVESTING FREE FUNDS IN MUTUAL FUNDS MONIKA LIČKOVÁ JUDr. Monika Ličková, Katedra obchodného a hospodárskeho
DÔLEŽITOSŤ INVESTOVANIA VOĽNÝCH PEŇAŽNÝCH PROSTRIEDKOV DO PODIELOVÝCH FONDOV THE IMPORTANCE OF INVESTING FREE FUNDS IN MUTUAL FUNDS MONIKA LIČKOVÁ JUDr. Monika Ličková, Katedra obchodného a hospodárskeho
Effectiveness of CPPI Strategies under Discrete Time Trading
 Effectiveness of CPPI Strategies under Discrete Time Trading S. Balder, M. Brandl 1, Antje Mahayni 2 1 Department of Banking and Finance, University of Bonn 2 Department of Accounting and Finance, Mercator
Effectiveness of CPPI Strategies under Discrete Time Trading S. Balder, M. Brandl 1, Antje Mahayni 2 1 Department of Banking and Finance, University of Bonn 2 Department of Accounting and Finance, Mercator
Modelovanie nan ných trhov a risku metódou Monte Carlo
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Modelovanie nan ných trhov a risku metódou Monte Carlo 211 Luká² Kunert UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Modelovanie nan ných trhov a risku metódou Monte Carlo 211 Luká² Kunert UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
HODNOTENIE INVESTÍCIÍ POMOCOU ČISTEJ SÚČASNEJ HODNOTY A VPLYV ZMENY FAKTOROV NA INVESTIČNÉ ROZHODOVANIE. Ing. Veronika Uličná 89
 HODNOTENIE INVESTÍCIÍ POMOCOU ČISTEJ SÚČASNEJ HODNOTY A VPLYV ZMENY FAKTOROV NA INVESTIČNÉ ROZHODOVANIE Ing. Veronika Uličná 89 Abstrakt: Príspevok je venovaný hodnoteniu investícií pomocou čistej súčasnej
HODNOTENIE INVESTÍCIÍ POMOCOU ČISTEJ SÚČASNEJ HODNOTY A VPLYV ZMENY FAKTOROV NA INVESTIČNÉ ROZHODOVANIE Ing. Veronika Uličná 89 Abstrakt: Príspevok je venovaný hodnoteniu investícií pomocou čistej súčasnej
Globálne optimálne gama zaisťovanie s transakčnými nákladmi
 Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
Financial Accelerator and Interest Rate in Selected Countries
 COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA Martin Lauko
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA 2009 Martin Lauko Numerické a analytické aproximácie hranice predčasného uplatnenia americkej put opcie DIPLOMOVÁ
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA 2009 Martin Lauko Numerické a analytické aproximácie hranice predčasného uplatnenia americkej put opcie DIPLOMOVÁ
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky. Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová UNIVERZITA KOMENSKÉHO
Produkty finančných trhov a ich riziká. Produkty kapitálových trhov
 Produkty finančných trhov a ich riziká Produkty kapitálových trhov Obsah Úvod... 1 rizík... 2 Všeobecné... 2 Charakteristiky opcií... 4 Riziko straty investovanej čiastky... 5 Daňové dopady... 5 finančných
Produkty finančných trhov a ich riziká Produkty kapitálových trhov Obsah Úvod... 1 rizík... 2 Všeobecné... 2 Charakteristiky opcií... 4 Riziko straty investovanej čiastky... 5 Daňové dopady... 5 finančných
Produkty finančných trhov a ich riziká. Produkty devízových a peňažných transakcií
 Produkty finančných trhov a ich riziká Produkty devízových a peňažných transakcií Obsah Úvod... 1 rizík... 2 Všeobecné... 2 Charakteristiky opcií... 3 Riziko straty investovanej čiastky... 4 Daňové dopady...
Produkty finančných trhov a ich riziká Produkty devízových a peňažných transakcií Obsah Úvod... 1 rizík... 2 Všeobecné... 2 Charakteristiky opcií... 3 Riziko straty investovanej čiastky... 4 Daňové dopady...
Oceňovanie spoločností
 Oceňovanie spoločností Ivan Chodák invest forum 22. november 2006, Bratislava Obsah hlavné okruhy Koncept oceňovania Cash Flow, Assets... Dôležité pojmy Value vs. Price... Hlavné metódy oceňovania Acc,
Oceňovanie spoločností Ivan Chodák invest forum 22. november 2006, Bratislava Obsah hlavné okruhy Koncept oceňovania Cash Flow, Assets... Dôležité pojmy Value vs. Price... Hlavné metódy oceňovania Acc,
Diverzifikácia rizika pri investičnom rozhodovaní s využitím alternatívnych foriem investovania
 Bankovní institut vysoká škola Praha zahraničná vysoká škola Banská Bystrica Katedra ekonómie a financií Diverzifikácia rizika pri investičnom rozhodovaní s využitím alternatívnych foriem investovania
Bankovní institut vysoká škola Praha zahraničná vysoká škola Banská Bystrica Katedra ekonómie a financií Diverzifikácia rizika pri investičnom rozhodovaní s využitím alternatívnych foriem investovania
Problematické stránky štandardných metód Value at Risk 1
 Problematické stránky štandardných metód Value at Risk 1 Martin ŠORF Abstrakt Príspevok sa venuje hodnoteniu štandardných metód merania Value at Risk z koncepčného hľadiska. Model historickej simulácie,
Problematické stránky štandardných metód Value at Risk 1 Martin ŠORF Abstrakt Príspevok sa venuje hodnoteniu štandardných metód merania Value at Risk z koncepčného hľadiska. Model historickej simulácie,
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
INSURANCE PORTFOLIO. CSc.
 Ekonomická univerzita, Fakulta hospodárskej informatiky Dolnozemská cesta, 85 35 Bratislava INSURANCE PORTFOLIO Doc. RNDr. Ľudovít t Pinda, CSc. FHI EU, Katedra matematiky mail: pinda@euba.sk Marec 00
Ekonomická univerzita, Fakulta hospodárskej informatiky Dolnozemská cesta, 85 35 Bratislava INSURANCE PORTFOLIO Doc. RNDr. Ľudovít t Pinda, CSc. FHI EU, Katedra matematiky mail: pinda@euba.sk Marec 00
Alternatívne investičné kritériá- pokr. NPV a plánovanie investícií
 20. október 2003 Alternatívne investičné kritériá- pokr. NPV a plánovanie investícií Literatúra: Brealey R. A., Myers S.C.: Principles of Corporate Finance Chapter 6 Ross A. R., Westerfield R.W., Jaffe
20. október 2003 Alternatívne investičné kritériá- pokr. NPV a plánovanie investícií Literatúra: Brealey R. A., Myers S.C.: Principles of Corporate Finance Chapter 6 Ross A. R., Westerfield R.W., Jaffe
Odhady parametrov modelov
 Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
Oznam pre akcionárov World Investment Opportunities Funds
 WORLD INVESTMENT OPPORTUNITIES FUNDS ( Spoločnosť ) Société d investissement à capital variable Sídlo: 11, rue Aldringen, L-1118 Luxembourg R.C.S. Luxembourg B-68.606 Oznam pre akcionárov World Investment
WORLD INVESTMENT OPPORTUNITIES FUNDS ( Spoločnosť ) Société d investissement à capital variable Sídlo: 11, rue Aldringen, L-1118 Luxembourg R.C.S. Luxembourg B-68.606 Oznam pre akcionárov World Investment
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
KATALÓG FONDOV V PONUKE VÚB BANKY 1. POLROK 2018
 KATALÓG FONDOV V PONUKE VÚB BANKY 1. POLROK 2018 VŠETKO, ČO JE MOŽNÉ www.vub.sk, 0850 123 000 Bank of JEDNOTLIVÉ TRHY V DETAILOCH Vážení klienti, rast globálnej ekonomiky zotrval veľmi solídny aj počas
KATALÓG FONDOV V PONUKE VÚB BANKY 1. POLROK 2018 VŠETKO, ČO JE MOŽNÉ www.vub.sk, 0850 123 000 Bank of JEDNOTLIVÉ TRHY V DETAILOCH Vážení klienti, rast globálnej ekonomiky zotrval veľmi solídny aj počas
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ UNIVERZITA KOMENSKÉHO V
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ UNIVERZITA KOMENSKÉHO V
Oceňovanie CMS Spread Range Accrual
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a štatistiky Oceňovanie CMS Spread Range Accrual Diplomová práca Matej Stračiak Vedúci práce:
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a štatistiky Oceňovanie CMS Spread Range Accrual Diplomová práca Matej Stračiak Vedúci práce:
Moderné metódy ohodnocovania akcií 1
 148 Ekonomický časopis, 59, 2011, č. 2, s. 148 162 Moderné metódy ohodnocovania akcií 1 Božena HRVOĽOVÁ* Jana MARKOVÁ** Lucia ZACHAR NINČÁK* 1 Modern Methods of Valuation of Shares Abstract The current
148 Ekonomický časopis, 59, 2011, č. 2, s. 148 162 Moderné metódy ohodnocovania akcií 1 Božena HRVOĽOVÁ* Jana MARKOVÁ** Lucia ZACHAR NINČÁK* 1 Modern Methods of Valuation of Shares Abstract The current
Maticové algoritmy II systém lineárnych rovníc riešenie SLR pomocou Gaussovej eliminačnej metódy (GEM) determinanty výpočet determinantu pomocou GEM
 Maticové algoritmy II systém lineárnych rovníc riešenie SLR pomocou Gaussovej eliminačnej metódy (GEM) determinanty výpočet determinantu pomocou GEM Priesvitka 1 M. C. Escher: Relativity Priesvitka 2 Systém
Maticové algoritmy II systém lineárnych rovníc riešenie SLR pomocou Gaussovej eliminačnej metódy (GEM) determinanty výpočet determinantu pomocou GEM Priesvitka 1 M. C. Escher: Relativity Priesvitka 2 Systém
Modelovanie postojov k riziku pri investovaní v domácnostiach SR
 Modelovanie postojov k riziku pri investovaní v domácnostiach SR doc. Ing. Iveta Stankovičová, PhD. Mgr. Katarína Kuľková Univerzita Komenského v Bratislave Investovanie domácností SR - problém 1 Otázka
Modelovanie postojov k riziku pri investovaní v domácnostiach SR doc. Ing. Iveta Stankovičová, PhD. Mgr. Katarína Kuľková Univerzita Komenského v Bratislave Investovanie domácností SR - problém 1 Otázka
Charles University in Prague Faculty of Social Sciences. Forecasting realized volatility: Do jumps in prices matter?
 Charles University in Prague Faculty of Social Sciences Institute of Economic Studies RIGOROSIS DIPLOMA THESIS ing realized volatility: Do jumps in prices matter? Author: Mgr. Štefan Lipták Supervisor:
Charles University in Prague Faculty of Social Sciences Institute of Economic Studies RIGOROSIS DIPLOMA THESIS ing realized volatility: Do jumps in prices matter? Author: Mgr. Štefan Lipták Supervisor:
HEDGING A FORMY ZAJIŠTĚNÍ ÚROKOVÉHO RIZIKA
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA PODNIKATELSKÁ ÚSTAV EKONOMIKY FACULTY OF BUSINESS AND MANAGEMENT INSTITUTE OF ECONOMICS HEDGING A FORMY ZAJIŠTĚNÍ ÚROKOVÉHO RIZIKA THE
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA PODNIKATELSKÁ ÚSTAV EKONOMIKY FACULTY OF BUSINESS AND MANAGEMENT INSTITUTE OF ECONOMICS HEDGING A FORMY ZAJIŠTĚNÍ ÚROKOVÉHO RIZIKA THE
Správcovská spoločnosť: IAD Investments, správ. spol., a.s., Malý trh 2/A, Bratislava 1
 Správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde za kalendárny rok 2014 podľa 187 zákona č. 203/2011 Z.z. o kolektívnom investovaní v znení neskorších predpisov (ZKI) Správcovská
Správa o hospodárení správcovskej spoločnosti s majetkom v podielovom fonde za kalendárny rok 2014 podľa 187 zákona č. 203/2011 Z.z. o kolektívnom investovaní v znení neskorších predpisov (ZKI) Správcovská
VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY
 VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY THE DEVELOPMENT OF THE AMOUNT OF LOANS GRANTED AND THEIR APPROPRIATE
VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY THE DEVELOPMENT OF THE AMOUNT OF LOANS GRANTED AND THEIR APPROPRIATE
PROSPEKT HORIZON 19/05/2014
 PROSPEKT Verejná investičná spoločnosť variabilného kapitálu podľa belgického práva (bevek) pre investície v súlade s podmienkami smernice 2009/65/EC UCITS HORIZON 19/05/2014 Prospekt sa skladá z: Informácií
PROSPEKT Verejná investičná spoločnosť variabilného kapitálu podľa belgického práva (bevek) pre investície v súlade s podmienkami smernice 2009/65/EC UCITS HORIZON 19/05/2014 Prospekt sa skladá z: Informácií
KATALÓG FONDOV V PONUKE VÚB BANKY 1. POLROK 2017
 KATALÓG FONDOV V PONUKE VÚB BANKY 1. POLROK 2017 VŠETKO, ČO JE MOŽNÉ www.vub.sk, *0200 Bank of JEDNOTLIVÉ TRHY V DETAILOCH PROGNÓZY VÝVOJA Vážení klienti, rast ekonomiky na začiatku roku 2017 v Európe
KATALÓG FONDOV V PONUKE VÚB BANKY 1. POLROK 2017 VŠETKO, ČO JE MOŽNÉ www.vub.sk, *0200 Bank of JEDNOTLIVÉ TRHY V DETAILOCH PROGNÓZY VÝVOJA Vážení klienti, rast ekonomiky na začiatku roku 2017 v Európe
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA
Valuing Stock Options: The Black-Scholes-Merton Model. Chapter 13
 Valuing Stock Options: The Black-Scholes-Merton Model Chapter 13 1 The Black-Scholes-Merton Random Walk Assumption l Consider a stock whose price is S l In a short period of time of length t the return
Valuing Stock Options: The Black-Scholes-Merton Model Chapter 13 1 The Black-Scholes-Merton Random Walk Assumption l Consider a stock whose price is S l In a short period of time of length t the return
How good are Portfolio Insurance Strategies?
 How good are Portfolio Insurance Strategies? S. Balder and A. Mahayni Department of Accounting and Finance, Mercator School of Management, University of Duisburg Essen September 2009, München S. Balder
How good are Portfolio Insurance Strategies? S. Balder and A. Mahayni Department of Accounting and Finance, Mercator School of Management, University of Duisburg Essen September 2009, München S. Balder
CVaR Portfolio Models for Electricity Generating Capacities
 CVaR Portfolio Models for Electricity Generating Capacities Dizertačná práca Mgr. Jana Szolgayová Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky
CVaR Portfolio Models for Electricity Generating Capacities Dizertačná práca Mgr. Jana Szolgayová Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky
VYUŽITIE FINANČNEJ PÁKY V PODMIENKACH SLOVENSKÉHO POĽNOHOSPODÁRSTVA
 VYUŽITIE FINANČNEJ PÁKY V PODMIENKACH SLOVENSKÉHO POĽNOHOSPODÁRSTVA Tomáš Rábek, Zuzana Čierna, Marián Tóth ÚVOD Cieľom príspevku je poukázať na výsledky výskumu v oblasti finančnej analýzy súboru poľnohospodárskych
VYUŽITIE FINANČNEJ PÁKY V PODMIENKACH SLOVENSKÉHO POĽNOHOSPODÁRSTVA Tomáš Rábek, Zuzana Čierna, Marián Tóth ÚVOD Cieľom príspevku je poukázať na výsledky výskumu v oblasti finančnej analýzy súboru poľnohospodárskych
Sadzobník kartových poplatkov firemné platobné karty / Schedule of Card Charges company payment cards
 Sadzobník kartových poplatkov firemné platobné karty / Schedule of Card Charges company payment cards Citibank Europe plc., so sídlom Dublin, North Wall Quay 1, Írsko, registrovaná v registri spoločností
Sadzobník kartových poplatkov firemné platobné karty / Schedule of Card Charges company payment cards Citibank Europe plc., so sídlom Dublin, North Wall Quay 1, Írsko, registrovaná v registri spoločností
Fakulta matematiky, fyziky a informatiky. Katedra aplikovanej matematiky a štatistiky EXOTICKÝCH OPCIÍ. Diplomová práca.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
GLOBAL PROPERTY FUND A-EURO 31. JÚL 2014
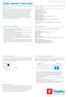 Prístup a štýl Základnou filozofiou Dirka Philippu je investovať do majetkových cenných papierov s atraktívnym ocenením. Vyhľadáva anomálie ocenenia vzhľadom na históriu, kolegov alebo v porovnaní s inými
Prístup a štýl Základnou filozofiou Dirka Philippu je investovať do majetkových cenných papierov s atraktívnym ocenením. Vyhľadáva anomálie ocenenia vzhľadom na históriu, kolegov alebo v porovnaní s inými
Incorporating Managerial Cash-Flow Estimates and Risk Aversion to Value Real Options Projects. The Fields Institute for Mathematical Sciences
 Incorporating Managerial Cash-Flow Estimates and Risk Aversion to Value Real Options Projects The Fields Institute for Mathematical Sciences Sebastian Jaimungal sebastian.jaimungal@utoronto.ca Yuri Lawryshyn
Incorporating Managerial Cash-Flow Estimates and Risk Aversion to Value Real Options Projects The Fields Institute for Mathematical Sciences Sebastian Jaimungal sebastian.jaimungal@utoronto.ca Yuri Lawryshyn
Finančné nástroje pre oblasť smart cities & regions. Január 2018
 Finančné nástroje pre oblasť smart cities & regions Január 2018 Čo sú to vlastne finančné nástroje? Návratná / splatná forma finančnej pomoci Základné typy finančných nástrojov Úverové nástroje Garančné
Finančné nástroje pre oblasť smart cities & regions Január 2018 Čo sú to vlastne finančné nástroje? Návratná / splatná forma finančnej pomoci Základné typy finančných nástrojov Úverové nástroje Garančné
ZRÁŽKA ZA NÍZKU LIKVIDITU
 ZRÁŽKA ZA NÍZKU LIKVIDITU Stela Beslerová, Juraj Tobák, Petra Tutková ÚVOD V slovenskom a rovnako aj v českom podnikateľskom prostredí sú väčšinou oceňované podniky, ktoré nie sú kótované na burze cenných
ZRÁŽKA ZA NÍZKU LIKVIDITU Stela Beslerová, Juraj Tobák, Petra Tutková ÚVOD V slovenskom a rovnako aj v českom podnikateľskom prostredí sú väčšinou oceňované podniky, ktoré nie sú kótované na burze cenných
Premium Harmonic TB. Komentár portfólio manažéra % 29%
 Mesačný report Viac o fonde Výkonnosť fondu Dokumenty www.tam.sk 31. august 2018 strana 1/5 Základné údaje Čistá hodnota aktív 139 142 134 Historická výkonnosť 12, 5, -6,9% 6, 5, -3,7% 2, 5, -1,9% Kurz
Mesačný report Viac o fonde Výkonnosť fondu Dokumenty www.tam.sk 31. august 2018 strana 1/5 Základné údaje Čistá hodnota aktív 139 142 134 Historická výkonnosť 12, 5, -6,9% 6, 5, -3,7% 2, 5, -1,9% Kurz
CROSS SECTIONAL FORECASTS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
Application of CAPM for investment decisions in emerging countries
 Application of CAPM for investment decisions in emerging countries Peter Krištofík 1 Abstract The paper is focused on investment decisions of companies with a diversified shareholder base in emerging countries.
Application of CAPM for investment decisions in emerging countries Peter Krištofík 1 Abstract The paper is focused on investment decisions of companies with a diversified shareholder base in emerging countries.
KATALÓG FONDOV V PONUKE VÚB BANKY 2. POLROK 2017
 KATALÓG FONDOV V PONUKE VÚB BANKY 2. POLROK 2017 VŠETKO, ČO JE MOŽNÉ www.vub.sk, 0850 123 000 Bank of JEDNOTLIVÉ TRHY V DETAILOCH Vážení klienti, rok 2017 bol pre svetovú ekonomiku ďalším rokom solídneho
KATALÓG FONDOV V PONUKE VÚB BANKY 2. POLROK 2017 VŠETKO, ČO JE MOŽNÉ www.vub.sk, 0850 123 000 Bank of JEDNOTLIVÉ TRHY V DETAILOCH Vážení klienti, rok 2017 bol pre svetovú ekonomiku ďalším rokom solídneho
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Identifikácia trhových neefektívností na základe makroekonomických veličín
 Identifikácia trhových neefektívností na základe makroekonomických veličín Eduard BAUMÖHL Mária FARKAŠOVSKÁ Úvod Prvá komplexná publikácia zaoberajúca sa trhovými neefektívnosťami na akciovom trhu pochádza
Identifikácia trhových neefektívností na základe makroekonomických veličín Eduard BAUMÖHL Mária FARKAŠOVSKÁ Úvod Prvá komplexná publikácia zaoberajúca sa trhovými neefektívnosťami na akciovom trhu pochádza
Horizon Prospekt 01/06/2016
 Horizon Prospekt Verejná investičná spoločnosť s variabilným kapitálom podľa belgického práva s premenlivým počtom podielových listov zastúpených v investíciách, ktoré sú v súlade s podmienkami Smernice
Horizon Prospekt Verejná investičná spoločnosť s variabilným kapitálom podľa belgického práva s premenlivým počtom podielových listov zastúpených v investíciách, ktoré sú v súlade s podmienkami Smernice
PACIFIC FUND A-USD 31. JÚL 2014
 PACIFIC FUND AUSD Prístup a štýl Dale Nicholls využíva prístup výberu akcií metódou zdola nahor, pričom sa zameriava na spoločnosti ponúkajúce najlepšie hodnoty vo vzťahu k ich dlhodobým vyhliadkam rastu,
PACIFIC FUND AUSD Prístup a štýl Dale Nicholls využíva prístup výberu akcií metódou zdola nahor, pričom sa zameriava na spoločnosti ponúkajúce najlepšie hodnoty vo vzťahu k ich dlhodobým vyhliadkam rastu,
Financial Economics & Insurance
 Financial Economics & Insurance Albert Cohen Actuarial Sciences Program Department of Mathematics Department of Statistics and Probability A336 Wells Hall Michigan State University East Lansing MI 48823
Financial Economics & Insurance Albert Cohen Actuarial Sciences Program Department of Mathematics Department of Statistics and Probability A336 Wells Hall Michigan State University East Lansing MI 48823
The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations
 The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations Stan Stilger June 6, 1 Fouque and Tullie use importance sampling for variance reduction in stochastic volatility simulations.
The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations Stan Stilger June 6, 1 Fouque and Tullie use importance sampling for variance reduction in stochastic volatility simulations.
KONEČNÉ PODMIENKY. 31. mája Slovenská sporiteľňa, a.s.
 KONEČNÉ PODMIENKY 31. mája 2018 Slovenská sporiteľňa, a.s. Celkový objem emisie: 2 000 000 EUR Názov Investičných certifikátov: Investičné certifikáty SLSP RC Sanofi 2019 I ktoré budú vydané na základe
KONEČNÉ PODMIENKY 31. mája 2018 Slovenská sporiteľňa, a.s. Celkový objem emisie: 2 000 000 EUR Názov Investičných certifikátov: Investičné certifikáty SLSP RC Sanofi 2019 I ktoré budú vydané na základe
Univerzita Karlova v Praze. Fakulta sociálních věd. Institut ekonomických studií. Bakalárska práca Vladimír Šťastný
 Univerzita Karlova v Praze Fakulta sociálních věd Institut ekonomických studií Bakalárska práca 2008 Vladimír Šťastný Univerzita Karlova v Praze Fakulta sociálních věd Institut ekonomických studií Bakalárska
Univerzita Karlova v Praze Fakulta sociálních věd Institut ekonomických studií Bakalárska práca 2008 Vladimír Šťastný Univerzita Karlova v Praze Fakulta sociálních věd Institut ekonomických studií Bakalárska
Neistota pri oceňovaní technických rezerv poisťovní
 Neistota pri oceňovaní technických rezerv poisťovní Peter Marko 1 Abstrakt Technické rezervy sú dôležité z hľadiska schopnosti poisťovne plniť svoje záväzky vyplývajúce z poistných zmlúv v budúcnosti.
Neistota pri oceňovaní technických rezerv poisťovní Peter Marko 1 Abstrakt Technické rezervy sú dôležité z hľadiska schopnosti poisťovne plniť svoje záväzky vyplývajúce z poistných zmlúv v budúcnosti.
Lecture 17. The model is parametrized by the time period, δt, and three fixed constant parameters, v, σ and the riskless rate r.
 Lecture 7 Overture to continuous models Before rigorously deriving the acclaimed Black-Scholes pricing formula for the value of a European option, we developed a substantial body of material, in continuous
Lecture 7 Overture to continuous models Before rigorously deriving the acclaimed Black-Scholes pricing formula for the value of a European option, we developed a substantial body of material, in continuous
Malovecká, I. 1, Papargyris, K. 1, Mináriková, D. 1, Foltán V. 1, Jankovská, A. 2
 ISSN 1338-6786 (online) and ISSN 0301-2298 (print version), DOI: 10.1515/afpuc-2015-0015 ACTA FACULTATIS PHARMACEUTICAE UNIVERSITATIS COMENIANAE Prosperity of community pharmacy evaluated by gross and
ISSN 1338-6786 (online) and ISSN 0301-2298 (print version), DOI: 10.1515/afpuc-2015-0015 ACTA FACULTATIS PHARMACEUTICAE UNIVERSITATIS COMENIANAE Prosperity of community pharmacy evaluated by gross and
HODNOCENÍ VÝNOSNOSTI RŮZNÝCH FOREM INVESTIC DO NEMOVITOSTÍ
 VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA PODNIKATELSKÁ ÚSTAV EKONOMIKY FACULTY OF BUSINESS AND MANAGEMENT INSTITUTE OF ECONOMICS HODNOCENÍ VÝNOSNOSTI RŮZNÝCH FOREM INVESTIC DO
VYSOKÉ UČENÍ TECHNICKÉ V BRNĚ BRNO UNIVERSITY OF TECHNOLOGY FAKULTA PODNIKATELSKÁ ÚSTAV EKONOMIKY FACULTY OF BUSINESS AND MANAGEMENT INSTITUTE OF ECONOMICS HODNOCENÍ VÝNOSNOSTI RŮZNÝCH FOREM INVESTIC DO
Black-Scholes-Merton Model
 Black-Scholes-Merton Model Weerachart Kilenthong University of the Thai Chamber of Commerce c Kilenthong 2017 Weerachart Kilenthong University of the Thai Chamber Black-Scholes-Merton of Commerce Model
Black-Scholes-Merton Model Weerachart Kilenthong University of the Thai Chamber of Commerce c Kilenthong 2017 Weerachart Kilenthong University of the Thai Chamber Black-Scholes-Merton of Commerce Model
Some useful optimization problems in portfolio theory
 Some useful optimization problems in portfolio theory Igor Melicherčík Department of Economic and Financial Modeling, Faculty of Mathematics, Physics and Informatics, Mlynská dolina, 842 48 Bratislava
Some useful optimization problems in portfolio theory Igor Melicherčík Department of Economic and Financial Modeling, Faculty of Mathematics, Physics and Informatics, Mlynská dolina, 842 48 Bratislava
Chapter 9 - Mechanics of Options Markets
 Chapter 9 - Mechanics of Options Markets Types of options Option positions and profit/loss diagrams Underlying assets Specifications Trading options Margins Taxation Warrants, employee stock options, and
Chapter 9 - Mechanics of Options Markets Types of options Option positions and profit/loss diagrams Underlying assets Specifications Trading options Margins Taxation Warrants, employee stock options, and
( ) since this is the benefit of buying the asset at the strike price rather
 Review of some financial models for MAT 483 Parity and Other Option Relationships The basic parity relationship for European options with the same strike price and the same time to expiration is: C( KT
Review of some financial models for MAT 483 Parity and Other Option Relationships The basic parity relationship for European options with the same strike price and the same time to expiration is: C( KT
Univerzita Karlova v Praze Matematicko fyzikální fakulta
 Univerzita Karlova v Praze Matematicko fyzikální fakulta DIPLOMOVÁ PRÁCE Jana Garajová Modely úrokových měr ve spojitém čase Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Prof.
Univerzita Karlova v Praze Matematicko fyzikální fakulta DIPLOMOVÁ PRÁCE Jana Garajová Modely úrokových měr ve spojitém čase Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Prof.
Premium Strategic TB
 Mesačný report Viac o fonde Výsledky fondov Dokumenty www.tam.sk 31. august 2018 strana 1/5 Základné údaje Čistá hodnota aktív 35 974 481 Historická výkonnosť 16,1% 6, -9, 9,1% 8, 1, -4, 2, 7, -2,1% Kurz
Mesačný report Viac o fonde Výsledky fondov Dokumenty www.tam.sk 31. august 2018 strana 1/5 Základné údaje Čistá hodnota aktív 35 974 481 Historická výkonnosť 16,1% 6, -9, 9,1% 8, 1, -4, 2, 7, -2,1% Kurz
Bubliny na finančných trhoch
 Kristína Klátiková Peter Korduliak Bubliny na finančných trhoch 3.časť Z histórie Tulipmánia Jednou z prvých zdokumentovaných bublín bola takzvaná Tulipmánia (1636-1637) v Holandsku. Počas nej sa z obchodovania
Kristína Klátiková Peter Korduliak Bubliny na finančných trhoch 3.časť Z histórie Tulipmánia Jednou z prvých zdokumentovaných bublín bola takzvaná Tulipmánia (1636-1637) v Holandsku. Počas nej sa z obchodovania
VaR Estimation under Stochastic Volatility Models
 VaR Estimation under Stochastic Volatility Models Chuan-Hsiang Han Dept. of Quantitative Finance Natl. Tsing-Hua University TMS Meeting, Chia-Yi (Joint work with Wei-Han Liu) December 5, 2009 Outline Risk
VaR Estimation under Stochastic Volatility Models Chuan-Hsiang Han Dept. of Quantitative Finance Natl. Tsing-Hua University TMS Meeting, Chia-Yi (Joint work with Wei-Han Liu) December 5, 2009 Outline Risk
The Black-Scholes Equation using Heat Equation
 The Black-Scholes Equation using Heat Equation Peter Cassar May 0, 05 Assumptions of the Black-Scholes Model We have a risk free asset given by the price process, dbt = rbt The asset price follows a geometric
The Black-Scholes Equation using Heat Equation Peter Cassar May 0, 05 Assumptions of the Black-Scholes Model We have a risk free asset given by the price process, dbt = rbt The asset price follows a geometric
Obsah č. 4/2013 (Table of Contents No. 4/2013)
 Obsah č. 4/2013 (Table of Contents No. 4/2013) Vedecké práce (Scientific Papers) Stanislav Buchta Sociálne zmeny poľnohospodárskej populácie proces postupného statusového pádu Social changes of agricultural
Obsah č. 4/2013 (Table of Contents No. 4/2013) Vedecké práce (Scientific Papers) Stanislav Buchta Sociálne zmeny poľnohospodárskej populácie proces postupného statusového pádu Social changes of agricultural
VÝBER VHODNEJ METÓDY OCENENIA INVESTÍCIÍ 1.
 VÝBER VHODNEJ METÓDY OCENENIA INVESTÍCIÍ 1. Veronika Frnková ÚVOD V ekonomickej teórií možno nájsť rôzne metódy hodnotenia efektívnosti investícií, ktoré kopírujú požiadavky investorov na výstupnú informáciu
VÝBER VHODNEJ METÓDY OCENENIA INVESTÍCIÍ 1. Veronika Frnková ÚVOD V ekonomickej teórií možno nájsť rôzne metódy hodnotenia efektívnosti investícií, ktoré kopírujú požiadavky investorov na výstupnú informáciu
Charles University in Prague. Faculty of Social Sciences. Institute of Economic Studies. Bachelor Thesis Diana Žigraiová
 Charles University in Prague Faculty of Social Sciences Institute of Economic Studies Bachelor Thesis 2010 Diana Žigraiová Charles University in Prague Faculty of Social Sciences Institute of Economic
Charles University in Prague Faculty of Social Sciences Institute of Economic Studies Bachelor Thesis 2010 Diana Žigraiová Charles University in Prague Faculty of Social Sciences Institute of Economic
Partial differential approach for continuous models. Closed form pricing formulas for discretely monitored models
 Advanced Topics in Derivative Pricing Models Topic 3 - Derivatives with averaging style payoffs 3.1 Pricing models of Asian options Partial differential approach for continuous models Closed form pricing
Advanced Topics in Derivative Pricing Models Topic 3 - Derivatives with averaging style payoffs 3.1 Pricing models of Asian options Partial differential approach for continuous models Closed form pricing
Zuzana ILKOVÁ * simple joint stock company, common shares, shares with special rights, shareholder agreements /eual
 10.1515/eual-2017-0009 LEGAL FRAMEWORK FOR ESTABLISHING AND FUNCTIONING OF START UPS IN THE CONDITIONS OF SLOVAK LEGISLATION PRÁVNY RÁMEC PRE ZAKLADANIE A FUNGOVANIE STARTUPOV V PODMIENKACH PRÁVNEJ ÚPRAVY
10.1515/eual-2017-0009 LEGAL FRAMEWORK FOR ESTABLISHING AND FUNCTIONING OF START UPS IN THE CONDITIONS OF SLOVAK LEGISLATION PRÁVNY RÁMEC PRE ZAKLADANIE A FUNGOVANIE STARTUPOV V PODMIENKACH PRÁVNEJ ÚPRAVY
