UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
|
|
|
- Brandon Phillip Gaines
- 6 years ago
- Views:
Transcription
1 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA 017 Bc. Ivan MAGDOLEN
2 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA tudijný program: tudijný odbor: koliace pracovisko: Vedúci práce: Ekonomicko-nan ná matematika a modelovanie Aplikovaná matematika Katedra aplikovanej matematiky a ²tatistiky prof. RNDr. Daniel ev ovi, CSc. Bratislava 017 Bc. Ivan MAGDOLEN
3 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky ZADANIE ZÁVEREČNEJ PRÁCE Meno a priezvisko študenta: Študijný program: Študijný odbor: Typ záverečnej práce: Jazyk záverečnej práce: Sekundárny jazyk: Bc. Ivan Magdolen ekonomicko-finančná matematika a modelovanie (Jednoodborové štúdium, magisterský II. st., denná forma) aplikovaná matematika diplomová slovenský anglický Názov: Cieľ: Analýza riešení nelineárnych rovníc pre oceňovanie finančných derivátov s premenlivými transakčnými nákladmi. Analysis of solutions of nonlinear equations for pricing derivative securities with variable transaction costs. Cieľom práce bude kvalitatívna a numerická analýza riešení nelineárnych rovníc pre oceňovanie finančných derivátov s premenlivými transakčnými nákladmi. Vedúci: Katedra: Vedúci katedry: Dátum zadania: prof. RNDr. Daniel Ševčovič, CSc. FMFI.KAMŠ - Katedra aplikovanej matematiky a štatistiky prof. RNDr. Daniel Ševčovič, CSc. Dátum schválenia: prof. RNDr. Daniel Ševčovič, CSc. garant študijného programu študent vedúci práce
4 Po akovanie Na tomto mieste by som sa chcel po akova môjmu ²kolite ovi prof. RNDr. Danielovi ev ovi ovi, CSc. za cenné rady a pripomienky k práci a za as venovaný vedeniu mojej práce. Tieº by som sa chcel po akova pánovi Rafaelovi Companymu z Polytechnickej Univerzity vo Valencii za plodnú diskusiu a cenné rady po as môjho pobytu v panielsku. akujem aj mojej rodine a priate om za podporu a porozumenie po as písania práce.
5 Abstrakt v ²tátnom jazyku MAGDOLEN, Ivan: Analýza rie²ení nelineárnych rovníc pre oce ovanie nan ných derivátov s premenlivými transak nými nákladmi [Diplomová práca], Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky, Katedra aplikovanej matematiky a ²tatistiky; ²kolite : prof. RNDr. Daniel ev ovi, CSc., Bratislava, 017, 57 s. Modely na oce ovanie nan ných derivátov uvaºujúce transak né náklady sú charakterizované rôznymi nelineárnymi volatilitami v difúznom lene parabolickej Black- Scholesovej rovnice. Tieto rovnice vyºadujú numerické rie²enia, ke ºe presné rie²enia nie sú známe. V tejto práci analyzujeme rovnicu s difúznym koecientom z modelu s variabilnými transak nými nákladmi, ktorý bol navrhnutý autormi ev ovi a šit anská. Je navrhnutá efektívna numerická schéma na rie²enie plne nelineárnej rovnice metódou kone ných diferencií s vyuºitím explicitnej a Crank-Nicholsonovej metódy. Rovnicu týmto spôsobom rie²ime a výsledky podrobujeme analýze. Aplikujeme testy konvergencie rie²enia a presnosti schémy. Overujeme platnos horných a dolných ohrani ení pre toto rie²enie a porovnávame numerické výsledky s výsledkami autorov modelu. K ú ové slová: Nelineárna Black-Scholesova rovnica, variabilné transak né náklady, numerické rie²enie, metóda kone ných diferencií.
6 Abstract MAGDOLEN, Ivan: Analysis of solutions of nonlinear equations for pricing derivative securities with variable transaction costs [Master Thesis], Comenius University in Bratislava, Faculty of Mathematics, Physics and Informatics, Department of Applied Mathematics and Statistics; Supervisor: prof. RNDr. Daniel ev ovi, CSc., Bratislava, 017, 57 p. Models for pricing nancial derivatives that consider transaction costs are characterized by dierent nonlinear volatilities in the diusion term of the parabolic Black- Scholes equation. These equations require numerical solutions since exact solutions are not known. In this thesis, we analyze an equation with the diusion coecient coming from the model with variable transaction costs, proposed by authors ev ovi and šit- anská. We create an eective numerical scheme for solving fully nonlinear equation using nite dierence method, namely explicit and Crank-Nicholson methods. We solve the equation this way and analyze the results. We apply convergence tests on the solution and tests of accuracy of the scheme. We also check validity of upper and lower bounds of the solution and compare results with those of the authors of the model. Keywords: Nonlinear Black-Scholes equation, variable transaction costs, numerical solution, nite dierence method.
7 OBSAH Obsah Zoznam obrázkov 9 Zoznam tabuliek 10 Úvod 11 1 Úvod do derivátov Trh s derivátmi História derivátov Typy derivátov Futurity a forwardy Opcie Swapy Oce ovanie opcií 0.1 Stochastické procesy Itova lema Black-Scholesova rovnica Lelandov model al²ie modely s transak nými nákladmi Model likvidity Model s preferenciami investora Risk Adjusted Pricing Methodology Model s lineárne klesajúcimi transak nými nákladmi Model s variabilnými transak nými nákladmi Návrh numerickej schémy Transformácia pôvodnej rovnice Návrh numerickej schémy pre explicitnú metódu Návrh numerickej schémy pre Crank-Nicholsonovu metódu Analýza rie²ení Rie²enie metódou kone ných diferencií
8 OBSAH 4. Testovanie konvergencie Diskusia k výsledkom Záver 49 Zoznam pouºitej literatúry 51 Príloha 54 8
9 ZOZNAM OBRÁZKOV Zoznam obrázkov 1 Vývoj objemu obchodovaných derivátov Payo call a put opcie Tok platieb Hodnoty call opcie pre rôzne asy t Porovnanie metód Porovnanie rie²enia s lineárnym modelom pre t = Porovnanie rie²enia s lineárnym modelom pre S = Porovnanie schémy pri pôvodnom a novom asovom kroku Schéma znázor ujúca ideu testovania konvergencie Chyba numerického rie²enia rovnice s rezíduom
10 ZOZNAM TABULIEK Zoznam tabuliek 1 Rozdiely medzi futuritami a forwardmi Aktíva a pasíva banky a inej nan nej in²titúcie Vstupy do numerickej schémy Porovnanie výsledkov Hodnoty explicitnej schémy s hlad²ou aproximáciou druhej derivácie v nelineárnom lene Vypo ítané hodnoty α a výpo tová náro nos Hodnoty α pre xné a variabilné m
11 ÚVOD Úvod Teória oce ovania nan ných derivátov je záleºitos ou nieko kých posledných desa ro í. Od publikovania lánku Blacka a Scholesa v roku 1973, v ktorom uviedli v²eobecný návod na oce ovanie vanilla opcií, boli roz²írenia ich modelu záujmom i uº akademickej obce ako aj nan ných expertov. Jednou z nevýhod Black-Scholesovho modelu sú limitujúce predpoklady pre jeho platnos. Takýmto predpokladom sú aj nulové transak né náklady pri obchodovaní, ktoré prirodzene v reálnom svete nulové nie sú. Teória oce ovania opcií na trhoch s nenulovými transak nými nákladmi sa za ala rozvíja po roku 1985, ke Leland publikoval lánok [17], v ktorom uvaºoval kon²tantné transak né náklady C. al²ie modely boli odvodené v nasledujúcich rokoch, pri om rôzni autori volili rôzne prístupy priblí- ºenia sa podmienkam reálneho sveta. Spolo ným znakom týchto modelov je upravená volatilita, ktorá vystupuje ako difúzny koecient v nelineárnej parabolickej parciálnej diferenciálnej rovnici (upravená Black-Scholesova rovnica) a je funkciou gammy opcie, t.j. má tvar σ (V SS ). Bakstein a Howison v práci [5] brali do úvahy efekty likvidity pri obchodovaní aktív. Napríklad zníºená likvidita na trhu môºe spôsobi, ºe investor nekúpi v²etky akcie za rovnakú cenu, o vytvára transak né náklady. Barles a Soner v [7] uvaºovali preferencie investora vyuºijúc jeho faktor averzie k riziku. RAPM model navrhnutý Kratkom a roz²írený autormi Janda ka a ev ovi minimalizuje riziká vyplývajúce z vysokých transak ných nákladov a nechráneného portfólia [15]. Amster et al. v [1] predpokladali na rozdiel od Lelandovho modelu nekon²tantnú, lineárne klesajúcu funkciu transak ných nákladov a ev ovi a šit anská v [1] vytvorili model so v²eobecnou funkciou transak ných nákladov. V nedávnom lánku [] Amster a Mogni pouºili ideu variabilných transak ných nákladov na ocenenie opcií s viacerými podkladovými aktívami. V tejto práci budeme analyzova rie²enie nelineárnej rovnice vyplývajúcej z modelu ev ovi a a šit anskej [1]. Autori v tomto modeli výslednú rovnicu rie²ili transformáciou na kvázilineárnu Gamma rovnicu. Tento prístup v²ak znamená problém s po iato nou podmienkou, ktorá je Diracova δ funkcia, ktorá sa aºko aproximuje. V na²om prístupe budeme rie²i priamo plne nelineárnu rovnicu. Vyuºijeme metódu kone ných diferencií a explicitnú a Crank-Nicholsonovu metódu. Tieto schémy potom 11
12 ÚVOD naprogramujeme a získané výsledky následne porovnáme s výsledkami z práce [1]. alej podrobíme uvedené numerické schémy rôznym testom presnosti, nako ko presné rie²enie pri nelineárnej rovnici nie je známe. V prvej kapitole stru ne zhrnieme históriu derivátov, spôsoby ich obchodovania a opí²eme základné tri typy derivátov. V druhej kapitole uvedieme základnú teóriu oce ovania derivátov a predstavíme niektoré roz²írenia Black-Scholesovho modelu spomínané vy²²ie. V tretej kapitole navrhneme numerickú schému metódou kone ných diferencií na rie²enie problému vychádzajúceho z lánku [1] a vo ²tvrtej kapitole prezentujeme numerické výsledky. 1
13 1 ÚVOD DO DERIVÁTOV 1 Úvod do derivátov Vo svete nancií rozli²ujeme tri základné typy nan ných nástrojov. Sú to dlhopisy, akcie a nan né deriváty. Zatia o idey oce ovania prvých dvoch typov sú relatívne priamo iare, teória oce ovania derivátov je ve mi rozsiahla a neustále je predmetom ²túdia i uº akademickou obcou ako aj profesionálmi z investi ných bánk. V úvodnej kapitole krátko zhrnieme históriu obchodovania s derivátmi a predstavíme tri základné typy derivátov. Bliº²ie ich charakterizujeme a popí²eme spôsoby ich vyuºitia pri obchodovaní. 1.1 Trh s derivátmi Pod a denície, deriváty sú nan né nástroje, ktorých hodnota je ur itým spôsobom odvodená (angl. derived) od iného tzv. podkladového aktíva. Medzi základné typy derivátov patria: ˆ futurity a forwardy, ˆ opcie, ˆ swapy. Existuje v²ak aj ve ké mnoºstvo rôznych variácii týchto derivátov História derivátov Napriek tomu, ºe za prvé deriváty môºeme povaºova uº niektoré staroveké obchody, najvä ²í rozmach dosiahli aº v nieko kých posledných desa ro iach. Ako pí²e Chance v knihe [11], v Biblii v knihe Genezis (predpokladá sa, ºe bola písaná okolo roku 1700 pnl.) sa spomína príbeh Jákoba. Ten pri²iel slúºi k Labánovi, ktorý mu za 7 rokov slúºenia pris úbil svoju dcéru Ráchel. "Jákob si zamiloval Ráchel a povedal: Za tvoju mlad²iu dcéru ti budem slúºi sedem rokov." Gen 9:18. Labán tento prís ub nesplnil, prinútil ho zobra si za ºenu dcéru Leu, o môºe by povaºované za vôbec prvý default (tzn. nesplnenie kontraktu). Kontrakt medzi týmito dvomi môºeme povaºova i uº za opciu alebo forward v závislosti od toho i mal Jákob len právo alebo povinnos vzia 13
14 1 ÚVOD DO DERIVÁTOV si Ráchel. Tak i tak, ide o kontrakt pri ktorom Jákob za cenu 7 rokov práce mal dosta v ase splatnosti (maturity) za ºenu Ráchel. Novodobý rozvoj derivátov nastal v Chicagu, kde v roku 1848 vznikla Chicago Board of Trade (CBT). Na tejto burze obchodníci s po nohospodárskymi produktmi, najmä obilím, kupovali forwardové kontrakty aby sa poistili proti kolísavým cenám obilia. Burza v²ak bola zárove plná ²pekulantov snaºiacich sa zarobi na cenových výkyvoch. Zárove existovalo vysoké riziko, ºe emitent nevyplatil dohodnutú iastku, o sa ozna uje ako riziko protistrany (angl. counter-party risk ). V roku 1865, CBT vytvorila prvé ²tandardizované kontrakty s oh adom na kvalitu, kvantitu, miesto a as dodania, ktoré môºeme ozna i ako prvé futures kontrakty. Takisto vytvorila tzv. clearing house, ktorý bol zodpovedný za sprostredkovávanie transakcií a zniºoval riziko protistrany [18]. V roku 1919 z pôvodnej Chicago Butter and Egg Board, ktorá obchodoval len s kontraktmi na maslo a vajcia, vznikla Chicago Mercantile Exchange. Táto sa v roku 007 spojila s CBT a vytvorili CME Group, ktorá je najvä ²ou burzou derivátov na svete, s viac ako 3,5 miliardou kontraktov v roku 015 []. Najvä ²í rozmach derivátov nastal v 70-tych rokoch jednak kvôli pokrokom vo výpo tovej technike (nov²ie po íta e zvládali komplikované výpo ty na po ítanie pravdepodobností a odhadovanie budúcej hodnoty) a zárove v aka práci Fishera Blacka a Myrona Scholesa. Títo americkí ekonómovia publikovali v roku 1973 lánok s názvom The pricing of options and corporate liabilities [8], v ktorom odvodili vzorec na oce ovanie opcií, ktorý je výsledkom parciálnej diferenciálnej rovnice známej ako Black- Scholesova. Tento lánok vytvoril základ oce ovania opcií a otvoril cestu obchodovaniu s derivátmi najrôznej²ích typov. Na Obrázku 1 môºeme vidie enormný nárast objemu obchodovaných derivátov mien a úrokových mier na tzv. OTC (Over The Counter) trhoch 1. Zárove si môºeme uvedomi aká obrovská je táto suma, nieko ko-násobne vä ²ia ako celosvetové HDP. Niektorí ekonómovia v²ak tieto odhady spochyb ujú a povaºujú ich za nadhodnotené. 1 Za OTC obchodovanie sa ozna uje priame obchodovanie medzi dvoma stranami bez ºiadneho sprostredkovate a. 14
15 1 ÚVOD DO DERIVÁTOV Deriváty mien a úrokovej miery Obchodované množstvo (v miliardách $) Obr. 1: Vývoj objemu obchodovaných derivátov Zdroj: 1. Typy derivátov Cie om tejto práce je analyzova oce ovanie derivátov na trhoch s transak nými nákladmi. Ako sme spomínali, existujú tri základné typy derivátov a v tejto asti ich stru ne popí²eme. Transak né náklady môºu ma pri obchodovaní rôzne formy, pri om najvä ²í vplyv majú na oce ovanie opcií Futurity a forwardy V Kapitole sme spomínali biblický príbeh prvých derivátov a spomenuli sme pojem forward. Tieto deriváty sú podobné futuritám, nako ko oba nástroje predstavujú povinnos kupujúceho kúpi resp. preda podkladové aktívum za vopred dohodnutú cenu v ase splatnosti v budúcnosti. Sú v²ak medzi nimi ur ité rozdiely, ako môºeme vidie v Tabu ke 1. Ceny forwardov sa dajú relatívne ahko odvodi a nebudeme ich tu uvádza. Pokia predpokladáme úrokové miery kon²tantné, sú ceny futurít rovnaké ako ceny forwardov. V skuto nosti sa v²ak môºu lí²i berúc do úvahy dane, transak né náklady alebo riziko protistrany. Vo v²eobecnosti v²ak môºeme povaºova ceny za rovnaké [14]. 15
16 1 ÚVOD DO DERIVÁTOV Tabu ka 1: Rozdiely medzi futuritami a forwardmi Futurity obchodované na burze ²tandardizované denné vyplácanie Forwardy obchodované na OTC trhoch ne²tandardizované vyplatenie na konci kontraktu 1.. Opcie Ako sme spomínali vy²²ie, futurity resp. forwardy predstavujú povinnos dohodnutý kontrakt uskuto ni. Naopak opcia dáva kupujúcemu právo rozhodnú sa, i kontrakt vykoná alebo nie. Teda kupujúci má právo preda resp. kúpi podkladové aktívum za vopred dohodnutú cenu (angl. strike price). Opcie sa delia na klasické tzv. vanilla opcie a exotické opcie. Vanilla opcie rozde ujeme na európske a americké v závislosti od toho i sa opcia môºe vykona len v ase exspirácie alebo po as celej doby platnosti. Vanilla opcie tieº rozde ujeme pod a toho i má kupujúci právo kúpi - vtedy hovoríme o call opcii - alebo preda, vtedy ide o put opciu. Ak ozna íme cenu podkladového aktíva S a strike price K, payo call opcie je max(s K, 0) a payo put opcie max(k S, 0). Tieto sú znázornené na Obrázku. Obr. : Payo call a put opcie Exotických opcií existuje ve a typov. Uvedieme si niektoré z nich. Ázijské opcie Sú to opcie, ktorých payo závisí od priemeru ceny podkladového aktíva po as platnosti kontraktu. Rozde ujeme ich pod a pouºitia aritmetického alebo geometrického priemeru. Taktieº tieto opcie delíme na average rate, resp. average strike 16
17 1 ÚVOD DO DERIVÁTOV pod a toho akú premennú zastupuje priemer v payo funkcii. Tieto funkcie vyzerajú nasledovne (A ozna uje priemer): max(a K, 0) pre average rate call, max(k A, 0) pre average rate put, max(s A, 0) pre average strike call, max(a S, 0) pre average strike put. Binárne opcie Tieto opcie vyplácajú v ase splatnosti bu xnú iastku alebo ni v závislosti od toho i opcia skon í in-the-money resp. out-of-the-money. Iný typ binárnej opcie vypláca namiesto xnej iastky hodnotu podkladového aktíva. Bariérové opcie Opcia je splatná v momente ak cena podkladového aktíva dosiahne hodnotu ur- itej bariérovej funkcie. Rozli²ujeme i opcia dosiahne bariéru zhora alebo zdola. Lookback opcie Tento typ je podobný average rate opcii s tým rozdielom, ºe namiesto funkcie priemeru sa pouºíva funkcia maxima alebo minima. T.j. v payoe nahrádzame funkciou A(S, t) funkciu M max (S, t) = max(s, t (T 0, T )). Pri minime nahradíme funkciu minimom. Ko²íkové opcie Sú to opcie na vä ²í po et podkladových aktív, ktoré sú váºené ur itými váhami. Bermudské opcie Tento typ je podobný vanilla opciám s tým rozdielom, ºe opcia môºe by vykonaná iba v ur itých asových intervaloch po as doby splatnosti. Takýto spôsob vykonávania ich stavia medzi európske a americké opcie (názov plynie z polohy Bermudských ostrovov, ktoré patria Ve kej Británii ale leºia v blízkosti USA). Hovoríme ºe opcia je in-the-money ak platí, ºe cena podkladového aktíva je vä ²ia ako strike price S > K. Podobne out-of-the-money ak S < K 17
18 1 ÚVOD DO DERIVÁTOV Poznamenajme, ºe tento zoznam je iba zlomkom existujúcich exotických opcií. Mohol by by roz²írený al²ími viac- i-menej pouºívanými typmi, ktoré môºe itate nájs napr. v lánku [19]. Základným teóriam oce ovania opcií sa budeme venova v Kapitole Swapy Tretím základným typom derivátov sú swapy (z angl. swap = vymeni ). Je to dohoda medzi dvoma stranami o výmene cash-ows v budúcnosti. Táto dohoda ur uje za akých podmienok majú tieto výmeny prebehnú, s oh adom na as a výpo et cash- ow. Zvy ajne sa po ítajú z budúcich úrokových mier, výmenných kurzov alebo iných trhových premenných [14]. Z aleka najviac pouºívaným 3 typom swapu je interest rate swap (IRS). Pri tomto kontrakte si dve strany vzájomne vymie ajú cash-ows, pri om jedna strana platí xnú iastku a druhá plávajúcu v závislosti od aktuálnej hodnoty úrokovej miery. Naj astej²ie pouºívanou referen nou hodnotou úrokovej miery je LI- BOR 4. Strany sa na za iatku dohodnú na hodnote istiny, z ktorej sa platby po ítajú a následne vyplácajú iba percentuálne asti tejto istiny. Ako príklad môºeme uvies banku, ktorá uzatvorí IRS kontrakt s inou nan nou in²titúciou. Ke ºe sa úrokové miery menia a banka musí plati svojím klientom rôzne úroky z krátkodobých vkladov, je pre u výhodné poisti sa proti vysokým úrokovým mieram práve pomocou IRS s tým, ºe banka bude plati xnú sadzbu a dostáva plávajúcu. Naopak nan ná in²titúcia, ktorá musí spláca dlh s xnou úrokovou sadzbou vstúpi do kontraktu aby mohla dostáva xnú sadzbu s tým, ºe bude vypláca plávajúcu sadzbu, ktorú môºe nancova z krátkodobých pôºi iek svojich klientov. Situáciu ilustrujú Tabu ka a Obrázok 3: Týmto spôsobom si obe strany zabezpe ia nanco- Obr. 3: Tok platieb 3 OTC derivatives statistics at end-december 014 [6] 4 London Interbank Oered Rate 18
19 1 ÚVOD DO DERIVÁTOV Tabu ka : Aktíva a pasíva banky a inej nan nej in²titúcie Banka Finana ná in²titúcia Aktíva Pasíva Aktíva Pasíva Dlhopisy xný úrok Vklady klientov plávajúci úrok Pôºi ky klientom plávajúci úrok Dlhodobý dlh xný úrok vanie svojich pasív svojimi aktívami, ke ºe IRS prevedie xné sadzby na plávajúce a naopak. V praxi sa IRS nedohadujú priamo medzi dvoma stranami, ale rolu sprostredkovate a preberá tretia strana, ktorá zárove zabezpe uje riadne plnenie dohodnutého kontraktu. Okrem IRS existujú al²ie typy swapov ako napríklad commodity swaps, volatility swaps alebo credit default swaps. Uviedli sme teda tri základné typy nan ných derivátov a stru ne sme opísali princípy fungovania futurít a swapov. V al²ích astiach tejto práce sa budeme zaobera oce ovaním opcií. 19
20 OCEŒOVANIE OPCIÍ Oce ovanie opcií V tejto asti uvedieme niektoré známe poznatky z teórie oce ovania nan ných derivátov. Uvedieme základné denície stochastických procesov, Itovu lemu a odvodíme Black-Scholesovu rovnicu na oce ovanie opcií. Následne odvodíme Lelandovu rovnicu, ktorá taktieº slúºi na oce ovanie opcií ale berie do úvahy aj transak né náklady a zhrnieme niektoré modely na oce ovanie opcií s nekon²tantnou volatilitou. V Kapitolách pritom vychádzame z knihy [0]..1 Stochastické procesy Ceny akcií sa nedajú popísa nejakou jednoduchou matematickou závislos ou, pretoºe ich vývoj je viac-menej náhodný. Pokia chceme modelova ceny akcií, potrebujeme uvaºova aj náhodnú zloºku. Takýto vývoj, ktorý zah a náhodnos, nazývame stochastický proces a denujeme ho nasledovne: Denícia.1. Stochastickým procesom nazývame súbor náhodných premenných {X(t), t I} s mnoºinou indexov I, ktorá môºe by diskrétna alebo spojitá. Dôleºitou vlastnos ou, ktorú budeme vyºadova je tzv.markovovská vlastnos. Ak je táto vlastnos splnená, potom hodnoty stochastického procesu X(t) v ase s nezávisia od predo²lých hodnôt v asoch u < s. Stochastickým procesom je aj Brownov pohyb. Denícia.. Brownov pohyb {X(t), t 0} je súbor náhodných premenných, ktoré sp ajú nasledovné tri vlastnosti: 1. v²etky prírastky X(t + ) X(t) kde > 0 sú normálne rozdelené náhodné premenné so strednou hodnotou µ a disperziou σ,. pre kaºdé delenie t 0 = 0 < t 1 < t < t 3 <... < t n intervalu (0, t n ), v²etky prírastky, X(t ) X(t 1 ),..., X(t n ) X(t n 1 ) sú nezávislé náhodné premenné s parametrami z bodu 1, 3. X(0) = 0 a funkcia t X(t) je s pravdepodobnos ou 1 spojitá pre kaºdé t. Brownov pohyb s µ = 0, σ = 1 nazývame Wienerov proces. 0
21 OCEŒOVANIE OPCIÍ V predo²lej denícii nazývame µ drift a σ volatilita. Zmenu Brownovho pohybu môºeme chápa ako sú et zmeny deterministického komponentu µdt a stochastického komponentu σdw(t). Dostávame teda rovnicu, ktorú nazývame stochastická diferenciálna rovnica (SDR): dx(t) = µdt + σdw(t). (1) Z tejto rovnice môºeme odvodi rovnicu opisujúcu pohyb cien akcií. Av²ak musíme zobra do úvahy, ºe pri zmene ceny akcie nemôºeme uvaºova kon²tantný drift. Majitelia akcií totiº neo akávajú rast ceny akcie v absolútnych íslach ale v relatívnej percentuálnej miere. Ak investor o akáva zisk akcie 10%, ktorá stojí 10$, bude o akáva 10% aj ke bude táto akcia stá 50$. Preto namiesto kon²tantného driftu musíme pouºi kon²tantný výnos vyjadrený v tvare µs, kde µ vyjadruje výnos akcie. Potom za as dt vzrastie cena akcie o µsdt. Rovnako aj náhodná as musí by proporcionálna hodnote akcie a teda pre modelovanie ceny akcie pouºívame nasledovnú SDR: ds(t) = µsdt + σsdw(t). () Teda výnosy akcie ds(t)/s sa správajú pod a Brownovho pohybu. Neskôr pomocou Itovej lemy ukáºeme odvodenie rovnice pre vývoj ceny akcie.. Itova lema Rovnica (1) sa dá prepísa ak drift a volatilitu nepovaºujeme za kon²tantné, ale povaºujeme ich za funkcie asu t a stochastickej premennej X. Takúto SDR potom nazývame Itov proces a zapisujeme v nasledovnom diferenciálnom tvare: dx(t) = µ(t, X)dt + σ(t, X)dw(t). (3) Ako sme uº spomínali SDR opisujú ceny akcií. Nako ko ceny derivátov závisia jednak od vývoja ceny akcie a taktieº od asovej premennej, funkcie typu f(x, t), kde x je stochastická premenná sp ajúca SDR a t je as, sú pri oce ovaní derivátov k ú ové. Ve mi významnú vlastnos takýchto funkcii - diferencovate nos - opisuje tzv. Itova lema, ktorú spolu s ná rtom dôkazu uvádzame pod a knihy [0]. Veta.1. Nech f(x,t) je hladká funkcia dvoch premenných, pri om premenná x je rie²ením stochastickej diferenciálnej rovnice (3). Potom prvý diferenciál funkcie f je 1
22 OCEŒOVANIE OPCIÍ daný vz ahom df = f ( f x dx + t + 1 ) σ (x, t) f dt, (4) x dôsledkom oho funkcia f vyhovuje stochastickej diferenciálnej rovnici df = ( f t + µ(x, t) f x + 1 ) σ (x, t) f dt + σ(x, t) f dw. (5) x x Dôkaz. Uvádzame ho pod a knihy [0]. Po rozvinutí funkcie f do Taylorovho radu máme df = f f dx + x t dt + 1 f x (dx) + f x t dxdt + 1 f t (dt) +... (6) Po umocnení SDR (3) dostávame (dx) = µ (dt) + µ dt σ dw + σ (dw). (7) Ke ºe pod a Denície. platí E(dw(t)) = 0 a V ar(dw(t)) = dt, môºeme napísa dw = Φ dt (dw) dt. Po dosadení do (7) dostávame (dx) = σ dt + leny vy²²ieho rádu v dt, teda leny pri (dx) v rovnici (6) nemôºeme zanedba. alej v rovnici (6) máme (dt) a dwdt (dt) 3/, ktoré sú vy²²ieho rádu v dt a môºeme ich zanedba. Z rovnice (6) dostávame df = f f dx + x t dt + 1 f σ x dt teda rovnicu (4) a po dosadení (3) aj rovnicu (5). Tento výsledok je podobný klasickému pravidlu derivovania funkcie dvoch premenných. Rozdielom je dodato ný tretí len, ktorý vyplýva z povahy stochastickej premennej x. Itova lema je k ú ovým prvkom pri odvodení Black-Scholesovej rovnice. Ako sme uº uviedli, výnosy akcií sa správajú pod a SDR (). Pod a Itovej lemy platí, ºe diferenciál funkcie g(s, t) = ln(s) je rovný dg = 1 S ds σ S ( 1 S )dt.
23 OCEŒOVANIE OPCIÍ Po dosadení rovnice () za ds a integrovaní dostávame dg = µdt 1 σ dt + σdw g = g(s 0, 0) + µt 1 σ t + σw(t). Spätným dosadením g = ln(s) ln S = ln S 0 + µt 1 σ t + σw(t) S = S 0 exp((µ 1/σ )t + σw(t)). (8) Rovnica (8) vyjadruje vývoj ceny akcie v ase t. Funkciu S(t, w(t)) nazývame geometrický Brownov pohyb a denujeme ho nasledovne: Denícia.3. Ak {X(t), t 0} je Brownov pohyb s parametrami µ, σ a y 0 > 0 R +, tak systém náhodných premenných {Y (t), t 0}, Y (t) = y 0 e X(t), t 0, (9) nazývame geometrický Brownov pohyb..3 Black-Scholesova rovnica Ako sme uviedli v kapitole 1.1.1, významným mí nikom v histórii derivátov bolo odvodenie Black-Scholesovej rovnice v roku Black so Scholesom pouºili na odvodenie tejto rovnice my²lienku CAPM 5. Robert C. Merton 6 vyuºil iný prístup a odvodenie zaloºil na idey vytvorenia samonancujúceho portfólia. Tento prístup je v²eobecnej²í, nako ko nie je limitovaný predpokladmi CAPM modelu. V tejto kapitole odvodíme Black-Scholesovu rovnicu Mertonovým prístupom pod a knihy [0]. Pri tomto modeli predpokladáme, ºe sú splnené nasledovné poºiadavky (Black- Scholesov svet): 1. existuje bezriziková úrokové miera r,. akcie nevyplácajú dividendy, 5 Capital Asset Pricing Model 6 Merton je americký ekonóm, ktorý ako prvý publikoval lánok objas ujúci matematickú podstatu Black-Scholesoveho modelu. 3
24 OCEŒOVANIE OPCIÍ 3. ceny akcií vyhovujú SDR (), 4. na trhu neexistuje arbitráº, 5. je moºné kúpi alebo preda ubovo né mnoºstvo akcií a dlhopisov, 6. na trhu neexistujú transak né náklady alebo dane. alej ozna me funkciu stochastickej premennej S (ceny aktíva) a asu, ktorá prezentuje hodnotu nan ného derivátu ako V (S, t). Ak aplikujeme Itovu lemu na túto funkciu, s vyuºitím podmienky 3. môºeme jej diferenciál napísa ako ( V V dv = + µs t S + 1 ) σ S V dt + σs V dw. (10) S S Teraz vytvoríme samonancujúce portfólio z akcií, opcií na tieto akcie a dlhopisov. Podmienka samonancovate nosti znamená, ºe na udrºanie hodnoty portfólia nie je potrebné pridáva al²ie prostriedky a ºe kúpa/predaj jednej asti portfólia je vyvá- ºený kúpou/predajom inej asti. alej od portfólia vyºadujeme aby sp alo predpoklad nulových investícií, t.j. jeho celková hodnota je nulová. Takéto portfólio môºeme zapísa ako SQ S + V Q V + B = 0, (11) kde premenné znamenajú v poradí: cena akcie, mnoºstvo akcií v portfóliu, cena opcie, mnoºstvo opcií v portfóliu, hodnota dlhopisov v portfóliu. Ke ºe zmena hodnoty portfólia má by nulová (samonancovate nos ), platí SdQ S + V dq V + δb = 0. (1) Od dlhopisov o akávame, ºe sú úro ené spojitou bezrizikovou úrokovou mierou r a nevyplácajú kupóny. Zmena hodnoty dlhopisov v portfóliu sa dá vyjadri ako sú et úrokov a mnoºstva kúpených/predaných dlhopisov na nancovanie portfólia db = rbdt + δb. (13) Diferencovaním rovnice (11) a vyuºitím (1) a (13) dostávame Q S ds + Q V dv r(sq S + V Q V )dt = 0 / Q V Q S Q V ds + dv Q S Q V rsdt rv dt = 0. (14) 4
25 OCEŒOVANIE OPCIÍ Ke ozna íme pomer Q S Q V ( V V + µs t S + 1 σ S V S = a dosadíme predpoklady (10) a () do (14) dostávame ) rv µs + rs dt + σs ( ) V S dw = 0. (15) Na avej strane rovnice je deterministická a stochastická as. Rizikovo averzný investor chce prirodzene eliminova rizikovos zo svojho portfólia, ktorá je predstavovaná lenmi pri dw. Volí teda = V. Po dosadení tejto vo by do (15) dostávame S V t + 1 σ S V V + rs S S rv = 0. (16) Táto parciálna diferenciálna rovnica sa nazýva Black-Scholesova rovnica a ide o parabolickú rovnicu druhého rádu. Opisuje vývoj ceny derivátu, ktorého podkladovým aktívom je akcia. Pre výpo et ceny ²pecického druhu derivátu ako napríklad európskej call opcie, je potrebné prida k rovnici (16) koncovú podmienku. Táto podmienka bude v tvare payo-u derivátu, pre európsku call opciu teda V (S, T ) = max(s K, 0)..4 Lelandov model Ako sme uviedli v Kapitole.3, Black-Scholesov model vychádza z ur itých predpokladov, ktoré nie sú v reálnom svete splnené. Pre lep²ie priblíºenie sa realite existujú rôzne roz²írenia tohto modelu. Predpoklad nulových transak ných nákladov je príkladom nereálneho predpokladu, nako ko pri obchodovaní sú obchodníci vystavení takýmto nákladom i uº z dôvodu nedostato nej likvidity a z toho vyplývajúcim rôznym bid a ask 7 cenám alebo poplatkom za transakcie. V roku 1985 publikoval americký profesor H. Leland lánok [17], v ktorom odvodil upravenú Black-Scholesovu rovnicu berúc do úvahy transak né náklady v tvare C = S ask S bid S = S ask S bid S ask + S bid, teda C ozna uje náklady investora na nákup a následný predaj jednej akcie. Výsledná rovnica je v podstate klasická Black-Scholesova rovnica s upravenou volatilitou, ktorá je 7 Bid cena sa pouºíva na ozna enie najvy²²ej ceny, za ktorú je kupujúci ochotný kúpi aktívum na burze. Ask cena je najniº²ia cena, za ktorú je predávajúci ochotný aktívum na burze preda. Kvôli princípu arbitráºe musí plati P bid P ask. 5
26 OCEŒOVANIE OPCIÍ funkciou gammy 8 opcie σ (V SS ). V nasledujúcej asti ukáºeme odvodenie Lelandovho modelu. Toto odvodenie je podobné Black-Scholesovemu modelu. Opä máme portfólio P z opcie a akcií, ktorých po et je daný pod a δ = V S. V tomto prípade v²ak pri zmene portfólia uvaºujeme transak né náklady, teda platí P = V + δ S S C δ. (17) Predpokladáme, ºe ceny opcie a akcie vyhovujú rovniciam (10) resp. (). Ke ºe udr- ºujeme po et akcií rovný delte opcie, platí δ = δ S S = V SS S = V SS (µs t + σs w). Leland ukázal, ºe leny pri t môºeme zanedba a w môºeme aproximova strednou hodnotou. Taktieº platí E( w ) = t, pretoºe w Φ t a Φ má π strednú hodnotu. Teda π δ = V S σs t. (18) π Dosadením (18), (10) a () do (17), vyuºijúc fakt, ºe od portfólia o akávame, ºe bude ma výnos rovný bezrizikovej miere, teda P = rp t = r(v V S S) t a úpravou dostávame V t + 1 ( σ S V 1 S π V tejto rovnici sa asto ozna uje Le = ( )) C σ t sign V S π je to Black-Scholesova rovnica s upravenou volatilitou v tvare ( )) σ (V SS ) = σ (1 V Le sign. S + rs V S rv = 0. C σ ako Lelandovo íslo. Ako sme spomínali, t Pre európske opcie platí V SS > 0 a teda upravená volatilita má tvar σ (V SS ) = (1 Le). Poznamenajme, ºe v prípade V SS > 0 platí kvôli kladnosti volatility obmedzenie Le < 1, o dáva ohrani enie na najmen²í moºný asový interval úpravy portfólia t. Musí teda plati t > π C σ. Naopak, ak V SS rovnica uº nie je lineárna kvôli lenu sign(v SS ). < 0, v prípade ºe t 0, σ. Lelandova 8 Parciálne derivácie funkcie V (S, t) sa ozna ujú gréckymi písmenami. Napr. delta a V S ozna ujeme ako gamma. V S ozna ujeme ako 6
27 OCEŒOVANIE OPCIÍ.5 al²ie modely s transak nými nákladmi V predchádzajúcej asti sme odvodili Lelandov model, ktorý je roz²írením Black- Scholesovho modelu a berie do úvahy aj transak né náklady. Rozdielom je nekon²tantná volatilita v Lelandovom modeli, ktorá je závislá od gammy opcie. Tento model bol alej roz²írený v lánku [13] pre portfólia opcií. al²ie modely berúce do úvahy transak né náklady boli odvodené v lánkoch [1], [5], [7], [15], [1]. Spolo ným znakom týchto modelov je nelinearita výsledných rovníc v dôsledku nekon²tantnej volatility, ktorá je v tvare σ (SV SS ). V al²ej asti budeme tieto modely analyzova..5.1 Model likvidity Bakstein a Howison v [5] vytvorili parametrizovaný model, ktorý berie do úvahy efekty likvidity pri obchodovaní aktív. Likvidita je denovaná ako kombinácia transak ných nákladov investora a vplyvu cenových zmien. Zníºená likvidita na trhu môºe spôsobi, ºe investor kupujúci vä ²ie mnoºstvo aktív nekúpi v²etky tieto aktíva za rovnakú cenu pretoºe po et aktív ponúkaných na burze za najniº²iu ask cenu je men²í ako po et poºadovaných aktív. Investor potom dokúpi al²ie aktíva za druhú (tretiu, at.) najniº²iu ask cenu. Podobne to platí pre predávajúceho a bid ceny. Teda platí, ºe ím vä ²í objem transakcií, tým vä ²ia odchýlka od priemernej ceny (S ask S bid )/. Taktieº, ve ké obchody môºu z knihy objednávok (order book) vymaza viaceré ponuky napr. kúpením v²etkých ponúkaných aktív za nieko ko najniº²ích ask cien o spôsobí zmenu ceny. Táto obmedzená likvidita tak vedie k transak ným nákladom. Autori odvodili rovnicu, ktorá môºe by chápaná ako Black-Scholesova rovnica s volatilitou σ (SV SS ) = σ ( 1 + γ (1 α) + λsv SS + λ (1 α) ( SV SS ) + π γ sign( ) SV SS + π λ(1 α) γ ) SV SS. Parameter λ ozna uje h bku trhu a parameter γ = γσ δt modeluje bid-ask spready..5. Model s preferenciami investora Autormi tohto modelu sú Barles a Soner [7], pri om tento model berie do úvahy preferencie investora vyuºijúc jeho funkciu uºito nosti. Autori sa zaoberajú funkciou 7
28 OCEŒOVANIE OPCIÍ uºito nosti v tvare U ɛ (ξ) = 1 exp( ξ/ɛ), ξ R s kladným parametrom ɛ. Tento parameter sp a vz ah 1 = γn, pri om γ je faktor averzie k riziku a N je po et ɛ predávaných opcií. alej skúmajú správanie sa hodnoty opcie V pre parameter ɛ 0 a taktieº µ 0, kde v tomto prípade µ ozna uje propor né transak né náklady. Vz ah investora k riziku je ur ený parametrom a, pri om a = µ γn. Teda hodnota tohto parametra v rovnici závisí od toho aké riziko je investor ochotný podstúpi. Pre vy²²ie uvedené parametre idúce do nuly potom cena opcie V sp a nelineárnu Black- Scholesovú rovnicu s nasledovnou volatilitou: σ = σ ( 1 + ψ[exp(r(t t)a S V SS )] ), kde funkcia ψ je rie²ením oby ajnej diferenciálnej rovnice ψ (A) = ψ(a) + 1, ψ(0) = 0. Aψ(A) A.5.3 Risk Adjusted Pricing Methodology V roku 1998 navrhol Kratka [16] RAPM (Risk Adjusted Pricing Methodology) model. Janda ka a ev ovi v lánku [15] ho alej rozoberali a vylep²ili ho. Odstránili nedostatky Kratkovho modelu, ktorý nebol dobre navrhnutý a invariantný na ²kále [3]. Podstatou tohto modelu je minimalizovanie rizika plynúceho jednak z transak ných nákladov a takisto z nechráneného portfólia. Investor prirodzene preferuje niº²ie transak né náklady. Tie môºe dosiahnu volením vä ²ieho intervalu úpravy portfólia, ím sa v²ak vystavuje vä ²iemu riziku, nako ko takéto portfólio uº nezodpovedá pohybom ceny akcie. Transak né náklady sú tu kon²tantné podobne ako v Lelandovom modeli. Volatilita tohto modelu má tvar σ (SV SS ) = σ (1 µ(sv SS ) 1 3 ), µ = 3 ( C R π ) 1 3. Kon²tanty C a R predstavujú transak né náklady a koecient rizikovej prémie..5.4 Model s lineárne klesajúcimi transak nými nákladmi Amster, Averbuj, Mariani a Rial v tomto modeli [1], na rozdiel od Lelandovho modelu, uvaºovali transak né náklady, ktoré nie sú kon²tantné, ale ich vý²ka závisí od 8
29 OCEŒOVANIE OPCIÍ mnoºstva vykonaných transakcií. Nerastúcos transak ných nákladov môºe by chápaná ako ur itá mnoºstevná z ava pre investora, t.j. ím vä ²í objem transakcií vykoná, tým budú jeho jednotkové náklady na transakciu niº²ie. Moºno ich popísa lineárnou nerastúcou funkciou transak ných nákladov v tvare h(x) = a bx, a, b > 0. Autori alej v lánku [1] aplikujú metódu horných a dolných rie²ení na získanie rie²enia stacionárneho problému. alej uviedli podmienky existencie a jednozna nosti rie²enia rovnice. Volatilita tohto modelu je σ (SV SS ) = σ (1 π a σ t sign(sv SS) + bsv SS Jedným problémom tohto modelu je fakt, ºe umoº uje nereálny prípad zápornosti transak ných nákladov. )..5.5 Model s variabilnými transak nými nákladmi al²í model bol odvodený autormi ev ovi a šit anská v lánku [1] a umoº uje funkciu variabilných transak ných nákladov. Tento model vychádza z Lelandovho modelu, kde sú uvaºované kon²tantné transak né náklady a taktieº z vy²²ie spomínaného modelu s lineárne klesajúcimi transak nými nákladmi. Má volatilitu v tvare σ (SV SS ) = σ (1 π C(σS V SS t) sign(sv ) SS) σ, (19) t kde C(σS V SS t) predstavuje mean-value modikáciu funkcie transak ných nákladov C(ξ) = 0 C(ξx)xe x / dx. Autori v lánku transformovali nelineárnu parabolickú rovnicu s vy²²ie uvedenou volatilitou na kvázilineárnu parabolickú rovnicu a dokázali existenciu klasických hladkých rie²ení. Taktieº uviedli ohrani enia, ktoré rie²enie tejto rovnice sp a. Jedným typom transak nej funkcie navrhnutým v lánku, je po astiach lineárna neklesajúca funkcia C 0, pre 0 ξ ξ, C(ξ) = C 0 κ(ξ ξ ), pre ξ ξ ξ +, (0) C 0, pre ξ ξ +. Na rozdiel od lineárnej neklesajúcej transak nej funkcie z predchádzajúceho modelu má táto funkcia výhodu, ºe nenadobúda záporné hodnoty. Môºeme ju chápa v tom 9
30 OCEŒOVANIE OPCIÍ zmysle, ºe pri men²ích objemoch transakcií sú poplatky za transakciu kon²tantné C 0. Ke ich mnoºstvo prekro í ur itú hranicu ξ, dostane investor z avu. Pri prekro ení hodnoty ξ + uº náklady za transakciu alej neklesajú ale zostanú kon²tantné s hodnotou C 0. Pre mean-value modikáciu tejto funkcie potom pod a rovnice (4) z lánku [1] platí C(ξ) = C 0 κξ ξ + ξ ξ ξ e x / dx, pre ξ 0. (1) Druhá funkcia uvaºovaná v lánku je exponenciálne klesajúca transak ná funkcia. Má tvar C(ξ) = C 0 exp( κξ), pre ξ 0, kde C 0 > 0 a κ > 0 sú dané kon²tanty. Autori v lánku odvodili aj jej mean-value modikáciu. Numerická schéma, ktorú autori v lánku vyuºili, rie²ila transformovanú Gamma rovnicu a nie priamo nelineárnu Black-Scholesovu rovnicu s volatilitou (19). V al²ej asti práce budeme rie²i túto rovnicu priamo, bez transformácie, s vyuºitím numerickej metódy kone ných diferencií a rie²enia porovnáme s rie²eniami uvedenými v lánku. 30
31 3 NÁVRH NUMERICKEJ SCHÉMY 3 Návrh numerickej schémy Ako sme uviedli v predchádzajúcej asti v Kapitole.5.5, model navrhnutý v lánku [1] má volatilitu v tvare (19). V tejto asti navrhneme numerickú schému na výpo et nelineárnej Black-Scholesovej rovnice s touto volatilitou. Zvolená metóda rie²enia tejto rovnice je metóda kone ných diferencií za pouºitia explicitnej ako aj Crank- Nicholsonovej metódy. Výhodou pouºitia druhej schémy je jej vy²²í rád lokálnej diskretiza nej chyby, ktorý je O(k ) + O(h ) ( v asovej a v priestorovej premennej) oproti explicitnej schéme, ktorá ma chybu rádu O(k) + O(h ). Rovnicu budeme rie²i pre európsku call opciu a okrem koncovej podmienky v tvare payo-u budeme potrebova aj okrajové podmienky, ktoré ur ujú hodnoty opcie v krajných bodoch intervalu S [0, + ). Ke je cena akcie rovná nule, znamená to, ºe táto akcia je bezcenná, iºe aj hodnota call opcie na takúto akciu je rovná nule. Platí teda V (0, t) = 0. V prípade, ºe cena akcie rastie do +, call opcia bude ur ite uplatnená a drºite ov payo bude cena akcie mínus diskontovaná strike price a teda lim S V (S, t) = S Ke r(t t). Budeme teda rie²i nasledovnú úlohu: V t + 1 σ (SV SS )S V V + rs S S rv = 0, () kde funkcia σ (SV SS ) je modikovaná volatilita denovaná pod a rovnice (19) a pri koncovej a okrajových podmienkach S [0, ), t (0, T ) : V (S, T ) = max(s K, 0), lim S V (0, t) = 0, V (S, t) = 1. S Ke r(t t) 3.1 Transformácia pôvodnej rovnice V prvom kroku urobíme tieto dve transformácie pôvodnej rovnice: 1. τ = T t, pomocou ktorej bude as plynú opa ným smerom, t.j. od koncovej podmienky aº po as t = 0 a. x = ln( S K ). 31
32 3 NÁVRH NUMERICKEJ SCHÉMY Máme teda novú funkciu W (x, τ) = V (Ke x, T τ). Pre derivácie platí: V t = W τ, V S = W x V S = W 1 x S W x Po prvej transformácii dostávame a po druhej 1 S S V S = W x, 1 S V S S = W x W x. W τ + 1 σ (SV SS )S V V + rs S S rv = 0 W τ + 1 ( W σ x W τ 1 σ W x + W ) + r W x x rw = 0 ) ( σ W r + rw = 0, x pri om τ [0, T ], x (, + ). Funkcia volatility je potom v tvare σ (K 1 e x (W xx W x )) = σ (1 π C(σKe x (Ke x ) (W xx W x ) t ) ) sign(k 1 e x (W xx W x )) σ. t Koncová podmienka sa zmení na za iato nú W (x, 0) = max(ke x K, 0) a okrajové podmienky sú v tvare W (, τ) = 0 a W (+, τ) = Ke x Ke rτ. Teda nová transformovaná úloha, ktorú budeme numericky rie²i je v tvare W τ 1 ) W ( σ W σ x + r + rw = 0, (4) x kde volatilita σ je denovaná rovnicou (3) a pre x R, τ (0, T ) platí po iato ná a okrajové podmienky W (x, 0) = max(k(e x 1), 0), (3) lim W (x, τ) = 0, (5) x lim W (x, τ) = x K(ex e rτ ). 3. Návrh numerickej schémy pre explicitnú metódu Pre vytvorenie numerickej schémy za neme s denovaním mrieºky, na ktorej sa budú jednotlivé hodnoty po íta. Pre ohrani enie premennej x denujme priestorový interval 3
33 3 NÁVRH NUMERICKEJ SCHÉMY x ( L, L), L > 0. Pretoºe S = Ke x, na dostato né pokrytie významných hodnôt ceny akcie S posta uje zobra L. Rozde me asový interval τ [0, T ] na m deliacich bodov s krajnými bodmi τ 0 a τ m+1 = T. Dostaneme tak m + 1 deliacich intervalov. D ºku kaºdého intervalu ozna me k. Priestorový interval rozde me na n uzlových bodov, pri om krajné body intervalu sú x 0 a x n+1. Máme teda n+1 ekvidi²tan ných intervalov, kaºdý s d ºkou h, teda (n + 1)h = L. Ozna me x i = L + ih, i = 0,..., n + 1, alej τ j = jk, j = 0,..., m + 1 a W j i ako aproximáciu funkcie W v bode x = x i a τ = τ j, teda W j i W (x i, τ j ). Na aproximáciu prvej priestorovej derivácie pouºijeme centrálnu diferenciu W x (x i, τ j ) W j i+1 W j h na aproximáciu druhej priestorovej derivácie diferenciu i 1 W x (x i, τ j ) W j i 1 W j i + W j i+1, h a na aproximáciu asovej derivácie doprednú diferenciu W τ (x i, τ j ) W j+1 i W j i. k Prepí²eme rovnicu (4) v bode (x i, τ j ) a volatilitu ozna íme ( σ j i ), W j+1 i k W j i 1 W j ( σj i ) i 1 W j i + W j ) i+1 ( σ W j + h r i+1 W j h i 1 + rw j i = 0. Po vynásobení výrazom h k a usporiadaní máme ( ) h W j+1 i W j i 1 ( ) ( σj i ) k W j i 1 W j i + W j i ( ( σ j )( ) hk i ) r W j i+1 W j i 1 + rh kw j i = 0 h W j+1 i + ( h + ( σ j i ) k + rh k ) W j [( 1 W j+1 i = k ( σj i ) h + 1 k h i + ( 1 ( σji ) k 1 ( ( σ j hk i ) ( + 1 ( σji ) k + 1 ( ( σ j hk ( ( σ j )) i ) r W j ( 1 + i ) r )) r W j i 1 )) ( i ( σ j k ) i ) h rk k ( σj i ) h 1 k h 33 W j i+1 = 0 W j i ( ( σ j )) i ) r W j i+1 ].
34 3 NÁVRH NUMERICKEJ SCHÉMY Volatilitu ( σ j i ) budeme na kaºdej asovej vrstve j a v kaºdom bode x i po íta a jej tvar je kde ( σ j i ) (K 1 e x (W xx W x )) = σ (1 ( W j i 1 sign(...) = sign W j i + W j i+1 ( C(...) = C σke x i K e x i Podmienky (5) nadobudnú tvar h π C(...) sign(...) σ t W j i+1 W j h ( W j i 1 W j i + W j i+1 W j h W 0 i = max(k(e x i 1), 0), i 1 i+1 W j h ), i 1 ), (6) ) t ). W j 0 = 0, (7) W j n+1 = K(e x n+1 e rτ j ). Pre zjednodu²enie ozna me koecienty pri W j i 1, W j i, W j i+1 ako αj i, βj i, γj i. Explicitnú schému metódou kone ných diferencií môºeme potom zapísa v tvare W j+1 i = α j i W j i 1 + βj i W j i + γ j i W j i+1, (8) kde α j i = 1 k ( σj i ) h + 1 ( k ( σ j ) i ) r, h β j i = 1 k ( σj i ) h rk, γ j i = 1 k ( σj i ) h 1 ( k ( σ j ) i ) r, h kde ( σ j i ) je daná rovnicou (6) a podmienky sú v tvare (7). 3.3 Návrh numerickej schémy pre Crank-Nicholsonovu metódu Táto metóda je kombináciou explicitnej a implicitnej metódy a ako sme spomínali, má vy²²í rád lokálnej diskretiza nej chyby ako explicitná metóda. Uvaºujme mrieºku v rovine xτ rovnakú ako pri explicitnej metóde. Na odvodenie Crank-Nicholsonovej metódy prepí²eme rovnicu (4) v bode (x, τ j+ 1 ) = (x, τ j + k ). Derivácie majú potom tvar W τ (x, τ j+ 1 ) = W (x, τ j+1) W (x, τ j ) + O(k ), k 34
35 3 NÁVRH NUMERICKEJ SCHÉMY a po dosadení dostávame W j+1 i k W j i W xx (x, τ j+ 1 ) = W xx(x, τ j ) + W xx (x, τ j+1 ) + O(k ), W x (x, τ j+ 1 ) = W x(x, τ j ) + W x (x, τ j+1 ) + O(k ) 1 4 ( σj i ) ( W j i 1 W j i + W j i+1 ( ( σ j i ) ( ) h W j+1 i W j i 1 4 ( σj i ) k = W j i ( ( σ j i ) W j+1 i k 4h ( σj i ) Ak ozna íme k 4h ( σj i ) ( )( W j i+1 r W j i 1 ( + W j+1 j+1 i 1 Wi + W j+1 ) i+1 h h + W j+1 i+1 W j+1 ) i 1 + rw j i = 0, h h ) W j i 1 W j i + W j i+1 + W j+1 j+1 i 1 Wi + W j+1 i+1 ) ) ( r kh W j i+1 W j i 1 + W j+1 i+1 W j+1 i 1 W j+1 i 1 ( W j i 1 W j i + W j i+1 ) j+1 Wi + W j+1 i+1 + k 4h ) k 4h ( ( σ j i ) r α = k ( ( σ j ) i ) r, 4h môºeme Crank-Nicholsonovu metódu zapísa ako kde ( ( σ j i ) )( + rkh W j i = 0, )( ) r W j+1 i+1 W j+1 i 1 ) W j i+1 W j i 1 A j i W j+1 i 1 + Bj i W j+1 i + C j i W j+1 i+1 = Dj i W j i 1 + Ej i W j i + F j i W j i+1, A j i = k 4h ( σj i ) α, B j i = 1 + k h ( σj i ), D j i = k 4h ( σj i ) + α, E j i = 1 k h ( σj i ) rk, C j i = k 4h ( σj i ) + α, F j i = k 4h ( σj i ) α rkw j i. a po iato né a okrajové podmienky sú (7). Volatilita ( σ j i ) je daná rovnicou (6), rovnako ako pri explicitnej metóde. ƒasovú vrstvu j + 1 uº nemôºeme vypo íta priamo z diferen nej rovnice nako ko nepoznáme hodnoty W j+1 i 1 a W j+1 i+1. Z okrajových podmienok v²ak poznáme hodnoty W j 0, a W j n+1 j. Vieme teda rie²i systém n rovníc (9). Ozna me tento systém XW j+1 = YW j + y. Na kaºdej asovej vrstve j najprv vypo ítame hodnoty volatility ( σ j i ) i, ktoré vstupujú do koecientov A j i aº E j i. Tým vyplníme matice X, Y a vektor y. Následne vypo ítame tento systém s n rovnicami a 35
36 3 NÁVRH NUMERICKEJ SCHÉMY n neznámymi, ím dostaneme hodnoty W i v novej asovej vrstve j + 1. B j 1 C j A j B j C j 0 0 A j 3 B j 3 C j A j n 1 B j n 1 C j n 1 0 A j n B j n W j+1 1 W j+1. W j+1 n = E j 1 F j 1 D j E j 0 D j E j n 1 F j n 1 D j n F j n W j 1 W j. W j n + D j 1W j 0 A j 1W j F j nw j n+1 C j nw j+1 n+1. (9) Poznamenajme, ºe pre kaºdú asovú vrstvu j platí B j i = h + 1 ( σj i ) k > 1 4 ( σj i ) k α 1 4 ( σj i ) k+α = 1 ( σj i ) k = 1 ( σj i ) k = Cj i +Aj i pre i, teda matica X je diagonálne dominantná a teda regulárna, predo²lý systém má teda vºdy rie²enie. 36
37 4 ANALÝZA RIE ENÍ 4 Analýza rie²ení V predchádzajúcej kapitole sme odvodili numerické schémy na rie²enie nelineárnej Black-Scholesovej rovnice s difúznym koecientom (19). Táto rovnica vystupuje v modeli na oce ovanie derivátov uvaºujúc variabilné transak né náklady pod a lánku [1]. V tejto kapitole prezentujeme výsledky numerických schém, analyzujeme ich presnos a porovnáme ich s výsledkami autorov modelu. 4.1 Rie²enie metódou kone ných diferencií Na rie²enie numerických systémov sme pouºili program MATLAB. Ako funkciu transak ných nákladov C sme pouºili mean-value modikáciu po astiach lineárnej nerastúcej funkcie (1). Na jej numerické vy íslenie sme vyuºili fakt, ºe b ( ( ) b a erf erf( a e x dx = π kde erf(x) je chybová funkcia, ktorá je v MATLAB-e vstavaná. )), (30) V prvej asti programu sme denovali kon²tanty numerickej schémy: rozsah priestorového intervalu L, po et priestorových deliacich bodov n, po et asových deliacich bodov m a kone ný as T. alej kon²tanty týkajúce sa opcie: strike price K, historickú volatilitu σ, bezrizikovú úrokovú mieru r a interval úpravy portfólia t. Tretími kon²tantami boli kon²tanty k funkcii transak ných nákladov z Kapitoly.5.5: C 0, κ, ξ +, ξ. Spôsob výpo tu jednotlivých asových vrstiev sa v daných metódach lí²il. Pri explicitnej metóde sa pre kaºdú asovú vrstvu a kaºdý bod x i vypo ítala príslu²ná volatilita ( σ j i ), v aka ktorej sa vypo ítali koecienty α j i, βj i, γj i W j+1 i a potom hodnota v novej asovej vrstve j + 1. Pri Crack-Nicholsonovej metóde sa takisto najprv vypo ítali volatility, pomocou ktorých sa získali koecienty A j i aº Ej i pre asovú vrstvu j, ktorými sa vyplnili riedke trojdiagonálne matice X, Y a vektor y. Následne sa vyrie²il systém rovníc XW j+1 = YW j + y a získal sa neznámy vektor W j+1. V Tabu ke 3 sú uvedené vstupy do numerickej schémy v závislosti od ich typu pouºité pri výpo te. Na Obrázku 4 sú znázornené rie²enia V (S, t) pre call opciu s hodnotami t = 0, t = 1/3 a t = /3 Crank-Nicholsonovou metódou. Tieº je znázornený payo call opcie, teda V (S, T ). 37
38 4 ANALÝZA RIE ENÍ Tabu ka 3: Vstupy do numerickej schémy Numerická schéma Parametre opcie Funkcia transak ných nákladov L=1,5 σ = 0, 3 κ = 0, 3 n=51 r=0,011 C 0 = 0, 0 m=1000 t = 1/61 ξ = 0, 05 T=1 K=5 ξ + = 0, t=0 t=1/3 t=/3 t=t 5 cena opcie V S Obr. 4: Hodnoty call opcie pre rôzne asy t V Tabu ke 4 sú hodnoty opcie v ase 0 pre niektoré hodnoty akcie S získané oboma metódami pomocou kubického splajnu a na Obrázku 5 sú tieto metódy porovnané. Rozdiel je vypo ítaný ako V Crank Nicholsonova V explicitna. Pri explicitnej metóde sme Tabu ka 4: Porovnanie výsledkov S Explicitná metóda C-N metóda Výsledky v lánku [1] 0 0,1547 0,1547 0,17 3 0,93 0,934 0, ,8610 1,861 1, ,855 3,857 3, ,5045 5,5046 5,37 38
39 4 ANALÝZA RIE ENÍ 1.8 x rozdiel S Obr. 5: Porovnanie metód pouºili m = 7056, takºe k h. Tieto výsledky sa lí²ia od výsledkov v práci [1], tieº uvedené v Tabu ke 4. Pripome me, ºe v spomínanej práci nerie²ili autori priamo rovnicu (). Túto rovnicu najskôr transformovali a rie²ili kvázilineárnu tzv. Gamma rovnicu, kde po iato ná podmienka je Diracova δ funkcia. Túto autori aproximovali funkciou f(d)/( σ τ ), kde f(d) je hustota normálneho rozdelenia. Zjednodu²enie nelineárnej parabolickej PDR na kvázilineárnu znamenalo zmenu po iato nej (resp. koncovej) podmienky, ktorá je v rovnici () jednoducho payo derivátu v ase maturity. Problém nelinearity rovnice sa teda ur itým spôsobom presunul do po iato nej podmienky, ktorú je potrebné aproximova. Rie²enie teda neza ína v ase τ = 0 ale v nejakom malom ase τ > 0. Pre porovnanie sme ako po iato nú podmienku pouºili spojité rie²enie v ase τ = s volatilitou σ(0). Tento prístup v²ak rozdiely nevysvetlil nako ko výsledky boli podobné ako v predo²lých prípadoch. Jednou vlastnos ou modelu s variabilnými transak nými nákladmi je platnos vz ahu V σmin (S, t) V T C (S, t) V σmax (S, t) S > 0, t [0, T ], (31) kde V σmin a V σmax sú ceny opcií z Black-Scholesoveho ( modelu s danými volatilitami ( σ min a σ max, ktoré sú denované ako σmax = σ 1 C 0 ), σ min = σ 1 π 1 σ t 39
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky
 fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky. Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová UNIVERZITA KOMENSKÉHO
Pouºitie metódy Monte Carlo vo nanciách
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
CROSS SECTIONAL FORECASTS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ UNIVERZITA KOMENSKÉHO V
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ UNIVERZITA KOMENSKÉHO V
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Univerzita Komenského v Bratislave
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Mgr. Magdaléna Žitňanská Autoreferát dizertačnej práce KVALITATÍVNA A KVANTITATÍVNA ANALÝZA MODELOV OCEŇOVANIA DERIVÁTOV AKTÍV
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Mgr. Magdaléna Žitňanská Autoreferát dizertačnej práce KVALITATÍVNA A KVANTITATÍVNA ANALÝZA MODELOV OCEŇOVANIA DERIVÁTOV AKTÍV
Modelovanie nan ných trhov a risku metódou Monte Carlo
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Modelovanie nan ných trhov a risku metódou Monte Carlo 211 Luká² Kunert UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Modelovanie nan ných trhov a risku metódou Monte Carlo 211 Luká² Kunert UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio
 Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
Analytické aproximácie pri modelovaní cien opcií
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE. Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ Veronika Kleinová
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CALIBRATION OF A MODEL FOR OPTION PRICES WITH FEEDBACK EFFECT
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CALIBRATION OF A MODEL FOR OPTION PRICES WITH FEEDBACK EFFECT DIPLOMA THESIS 017 Zuzana FRONCOVÁ COMENIUS UNIVERSITY IN
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CALIBRATION OF A MODEL FOR OPTION PRICES WITH FEEDBACK EFFECT DIPLOMA THESIS 017 Zuzana FRONCOVÁ COMENIUS UNIVERSITY IN
9 Oceňovanie derivátov
 9 Oceňovanie derivátov Finančné deriváty (financial derivatives) sú nástroje, ktorých hodnota je odvodená od ceny podkladového aktíva (underlying). Týmto môže byť komodita, akcia, dlhopis, menový kurz,
9 Oceňovanie derivátov Finančné deriváty (financial derivatives) sú nástroje, ktorých hodnota je odvodená od ceny podkladového aktíva (underlying). Týmto môže byť komodita, akcia, dlhopis, menový kurz,
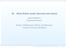
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie
 I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií
 UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA Martin Lauko
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA 2009 Martin Lauko Numerické a analytické aproximácie hranice predčasného uplatnenia americkej put opcie DIPLOMOVÁ
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA 2009 Martin Lauko Numerické a analytické aproximácie hranice predčasného uplatnenia americkej put opcie DIPLOMOVÁ
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. modelu úrokových mier
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová UNIVERZITA
Globálne optimálne gama zaisťovanie s transakčnými nákladmi
 Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
Black-Scholes model: Derivation and solution
 III. Black-Scholes model: Derivation and solution Beáta Stehlíková Financial derivatives Faculty of Mathematics, Physics and Informatics Comenius University, Bratislava III. Black-Scholes model: Derivation
III. Black-Scholes model: Derivation and solution Beáta Stehlíková Financial derivatives Faculty of Mathematics, Physics and Informatics Comenius University, Bratislava III. Black-Scholes model: Derivation
Chapter 3: Black-Scholes Equation and Its Numerical Evaluation
 Chapter 3: Black-Scholes Equation and Its Numerical Evaluation 3.1 Itô Integral 3.1.1 Convergence in the Mean and Stieltjes Integral Definition 3.1 (Convergence in the Mean) A sequence {X n } n ln of random
Chapter 3: Black-Scholes Equation and Its Numerical Evaluation 3.1 Itô Integral 3.1.1 Convergence in the Mean and Stieltjes Integral Definition 3.1 (Convergence in the Mean) A sequence {X n } n ln of random
Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing
 Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing We shall go over this note quickly due to time constraints. Key concept: Ito s lemma Stock Options: A contract giving
Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing We shall go over this note quickly due to time constraints. Key concept: Ito s lemma Stock Options: A contract giving
PAijpam.eu ANALYTIC SOLUTION OF A NONLINEAR BLACK-SCHOLES EQUATION
 International Journal of Pure and Applied Mathematics Volume 8 No. 4 013, 547-555 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.173/ijpam.v8i4.4
International Journal of Pure and Applied Mathematics Volume 8 No. 4 013, 547-555 ISSN: 1311-8080 (printed version); ISSN: 1314-3395 (on-line version) url: http://www.ijpam.eu doi: http://dx.doi.org/10.173/ijpam.v8i4.4
Lecture 3: Review of mathematical finance and derivative pricing models
 Lecture 3: Review of mathematical finance and derivative pricing models Xiaoguang Wang STAT 598W January 21th, 2014 (STAT 598W) Lecture 3 1 / 51 Outline 1 Some model independent definitions and principals
Lecture 3: Review of mathematical finance and derivative pricing models Xiaoguang Wang STAT 598W January 21th, 2014 (STAT 598W) Lecture 3 1 / 51 Outline 1 Some model independent definitions and principals
HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY
 International Scientific Conference YOUNG SCIENTISTS 2011 HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY Marko LALIĆ Technická Univerzita v Košiciach, Ekonomická fakulta Katedra financií
International Scientific Conference YOUNG SCIENTISTS 2011 HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY Marko LALIĆ Technická Univerzita v Košiciach, Ekonomická fakulta Katedra financií
Binomial model: numerical algorithm
 Binomial model: numerical algorithm S / 0 C \ 0 S0 u / C \ 1,1 S0 d / S u 0 /, S u 3 0 / 3,3 C \ S0 u d /,1 S u 5 0 4 0 / C 5 5,5 max X S0 u,0 S u C \ 4 4,4 C \ 3 S u d / 0 3, C \ S u d 0 S u d 0 / C 4
Binomial model: numerical algorithm S / 0 C \ 0 S0 u / C \ 1,1 S0 d / S u 0 /, S u 3 0 / 3,3 C \ S0 u d /,1 S u 5 0 4 0 / C 5 5,5 max X S0 u,0 S u C \ 4 4,4 C \ 3 S u d / 0 3, C \ S u d 0 S u d 0 / C 4
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Zaistené stratégie. Bc. Tomáš Miklošovič.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Attachment No. 1 Employees authorized for communication
 On behalf of Market Operator: Attachment No. 1 Employees authorized for communication Employees authorized for invoicing and payments: Head of billing Dana Vinická +421 917 931 470 dana.vinicka@okte.sk
On behalf of Market Operator: Attachment No. 1 Employees authorized for communication Employees authorized for invoicing and payments: Head of billing Dana Vinická +421 917 931 470 dana.vinicka@okte.sk
BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS
 BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS PRICING EMMS014S7 Tuesday, May 31 2011, 10:00am-13.15pm
BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS PRICING EMMS014S7 Tuesday, May 31 2011, 10:00am-13.15pm
VII. Incomplete Markets. Tomas Björk
 VII Incomplete Markets Tomas Björk 1 Typical Factor Model Setup Given: An underlying factor process X, which is not the price process of a traded asset, with P -dynamics dx t = µ (t, X t ) dt + σ (t, X
VII Incomplete Markets Tomas Björk 1 Typical Factor Model Setup Given: An underlying factor process X, which is not the price process of a traded asset, with P -dynamics dx t = µ (t, X t ) dt + σ (t, X
Lecture 11: Ito Calculus. Tuesday, October 23, 12
 Lecture 11: Ito Calculus Continuous time models We start with the model from Chapter 3 log S j log S j 1 = µ t + p tz j Sum it over j: log S N log S 0 = NX µ t + NX p tzj j=1 j=1 Can we take the limit
Lecture 11: Ito Calculus Continuous time models We start with the model from Chapter 3 log S j log S j 1 = µ t + p tz j Sum it over j: log S N log S 0 = NX µ t + NX p tzj j=1 j=1 Can we take the limit
Financial Accelerator and Interest Rate in Selected Countries
 COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ. Currency risk hedging in Flash Steel, a. s.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ Zajištění proti kurzovému riziku ve společnosti Flash Steel, a. s. Currency risk hedging in Flash Steel, a. s. company
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ Zajištění proti kurzovému riziku ve společnosti Flash Steel, a. s. Currency risk hedging in Flash Steel, a. s. company
COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS The risk sensitive dynamic accumulation model and optimal pension saving management DISSERTATION THESIS 2014 Mgr. Zuzana
COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS The risk sensitive dynamic accumulation model and optimal pension saving management DISSERTATION THESIS 2014 Mgr. Zuzana
Black-Scholes-Merton Model
 Black-Scholes-Merton Model Weerachart Kilenthong University of the Thai Chamber of Commerce c Kilenthong 2017 Weerachart Kilenthong University of the Thai Chamber Black-Scholes-Merton of Commerce Model
Black-Scholes-Merton Model Weerachart Kilenthong University of the Thai Chamber of Commerce c Kilenthong 2017 Weerachart Kilenthong University of the Thai Chamber Black-Scholes-Merton of Commerce Model
Bluff Your Way Through Black-Scholes
 Bluff our Way Through Black-Scholes Saurav Sen December 000 Contents What is Black-Scholes?.............................. 1 The Classical Black-Scholes Model....................... 1 Some Useful Background
Bluff our Way Through Black-Scholes Saurav Sen December 000 Contents What is Black-Scholes?.............................. 1 The Classical Black-Scholes Model....................... 1 Some Useful Background
1.1 Basic Financial Derivatives: Forward Contracts and Options
 Chapter 1 Preliminaries 1.1 Basic Financial Derivatives: Forward Contracts and Options A derivative is a financial instrument whose value depends on the values of other, more basic underlying variables
Chapter 1 Preliminaries 1.1 Basic Financial Derivatives: Forward Contracts and Options A derivative is a financial instrument whose value depends on the values of other, more basic underlying variables
4. Black-Scholes Models and PDEs. Math6911 S08, HM Zhu
 4. Black-Scholes Models and PDEs Math6911 S08, HM Zhu References 1. Chapter 13, J. Hull. Section.6, P. Brandimarte Outline Derivation of Black-Scholes equation Black-Scholes models for options Implied
4. Black-Scholes Models and PDEs Math6911 S08, HM Zhu References 1. Chapter 13, J. Hull. Section.6, P. Brandimarte Outline Derivation of Black-Scholes equation Black-Scholes models for options Implied
Quadratic hedging in affine stochastic volatility models
 Quadratic hedging in affine stochastic volatility models Jan Kallsen TU München Pittsburgh, February 20, 2006 (based on joint work with F. Hubalek, L. Krawczyk, A. Pauwels) 1 Hedging problem S t = S 0
Quadratic hedging in affine stochastic volatility models Jan Kallsen TU München Pittsburgh, February 20, 2006 (based on joint work with F. Hubalek, L. Krawczyk, A. Pauwels) 1 Hedging problem S t = S 0
Economathematics. Problem Sheet 1. Zbigniew Palmowski. Ws 2 dw s = 1 t
 Economathematics Problem Sheet 1 Zbigniew Palmowski 1. Calculate Ee X where X is a gaussian random variable with mean µ and volatility σ >.. Verify that where W is a Wiener process. Ws dw s = 1 3 W t 3
Economathematics Problem Sheet 1 Zbigniew Palmowski 1. Calculate Ee X where X is a gaussian random variable with mean µ and volatility σ >.. Verify that where W is a Wiener process. Ws dw s = 1 3 W t 3
STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL
 STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL YOUNGGEUN YOO Abstract. Ito s lemma is often used in Ito calculus to find the differentials of a stochastic process that depends on time. This paper will introduce
STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL YOUNGGEUN YOO Abstract. Ito s lemma is often used in Ito calculus to find the differentials of a stochastic process that depends on time. This paper will introduce
Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom
 Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom Príloha č. 1 k opatreniu Pozície štandardných derivátov sa konvertujú na ich ekvivalentnú pozíciu podkladového
Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom Príloha č. 1 k opatreniu Pozície štandardných derivátov sa konvertujú na ich ekvivalentnú pozíciu podkladového
Calibration Lecture 4: LSV and Model Uncertainty
 Calibration Lecture 4: LSV and Model Uncertainty March 2017 Recap: Heston model Recall the Heston stochastic volatility model ds t = rs t dt + Y t S t dw 1 t, dy t = κ(θ Y t ) dt + ξ Y t dw 2 t, where
Calibration Lecture 4: LSV and Model Uncertainty March 2017 Recap: Heston model Recall the Heston stochastic volatility model ds t = rs t dt + Y t S t dw 1 t, dy t = κ(θ Y t ) dt + ξ Y t dw 2 t, where
Inflation rate prediction a statistical approach
 Abstract Inflation rate prediction a statistical approach Předpověď míry inflace - statistický přístup František Vávra 1, Tomáš Ťoupal 2, Eva Wagnerová 3, Patrice Marek 4, Zdeněk Hanzal 5 This paper deals
Abstract Inflation rate prediction a statistical approach Předpověď míry inflace - statistický přístup František Vávra 1, Tomáš Ťoupal 2, Eva Wagnerová 3, Patrice Marek 4, Zdeněk Hanzal 5 This paper deals
Pricing American Call Options by the Black-Scholes Equation with a Nonlinear Volatility Function
 Pricing American Call Options by the Black-Scholes Equation with a Nonlinear Volatility Function Maria do Rosário Grossinho, Yaser Faghan Kord Daniel Ševčovič February 0, 018 arxiv:1707.00358v [q-fin.cp]
Pricing American Call Options by the Black-Scholes Equation with a Nonlinear Volatility Function Maria do Rosário Grossinho, Yaser Faghan Kord Daniel Ševčovič February 0, 018 arxiv:1707.00358v [q-fin.cp]
Credit Burden of Households in Slovakia
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Credit Burden of Households in Slovakia Diploma Thesis Adam Biro² Bratislava 2011 525ee80a-3c15-4902-b736-9cfdd96015d6
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Credit Burden of Households in Slovakia Diploma Thesis Adam Biro² Bratislava 2011 525ee80a-3c15-4902-b736-9cfdd96015d6
Hedging of swaptions in a Lévy driven Heath-Jarrow-Morton framework
 Hedging of swaptions in a Lévy driven Heath-Jarrow-Morton framework Kathrin Glau, Nele Vandaele, Michèle Vanmaele Bachelier Finance Society World Congress 2010 June 22-26, 2010 Nele Vandaele Hedging of
Hedging of swaptions in a Lévy driven Heath-Jarrow-Morton framework Kathrin Glau, Nele Vandaele, Michèle Vanmaele Bachelier Finance Society World Congress 2010 June 22-26, 2010 Nele Vandaele Hedging of
AN ANALYTICALLY TRACTABLE UNCERTAIN VOLATILITY MODEL
 AN ANALYTICALLY TRACTABLE UNCERTAIN VOLATILITY MODEL FABIO MERCURIO BANCA IMI, MILAN http://www.fabiomercurio.it 1 Stylized facts Traders use the Black-Scholes formula to price plain-vanilla options. An
AN ANALYTICALLY TRACTABLE UNCERTAIN VOLATILITY MODEL FABIO MERCURIO BANCA IMI, MILAN http://www.fabiomercurio.it 1 Stylized facts Traders use the Black-Scholes formula to price plain-vanilla options. An
Financial Economics & Insurance
 Financial Economics & Insurance Albert Cohen Actuarial Sciences Program Department of Mathematics Department of Statistics and Probability A336 Wells Hall Michigan State University East Lansing MI 48823
Financial Economics & Insurance Albert Cohen Actuarial Sciences Program Department of Mathematics Department of Statistics and Probability A336 Wells Hall Michigan State University East Lansing MI 48823
Advanced Topics in Derivative Pricing Models. Topic 4 - Variance products and volatility derivatives
 Advanced Topics in Derivative Pricing Models Topic 4 - Variance products and volatility derivatives 4.1 Volatility trading and replication of variance swaps 4.2 Volatility swaps 4.3 Pricing of discrete
Advanced Topics in Derivative Pricing Models Topic 4 - Variance products and volatility derivatives 4.1 Volatility trading and replication of variance swaps 4.2 Volatility swaps 4.3 Pricing of discrete
The Derivation and Discussion of Standard Black-Scholes Formula
 The Derivation and Discussion of Standard Black-Scholes Formula Yiqian Lu October 25, 2013 In this article, we will introduce the concept of Arbitrage Pricing Theory and consequently deduce the standard
The Derivation and Discussion of Standard Black-Scholes Formula Yiqian Lu October 25, 2013 In this article, we will introduce the concept of Arbitrage Pricing Theory and consequently deduce the standard
Konvergen né modely úrokových mier
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Konvergen né moely úrokových mier Diplomová práca Veúci iplomovej práce: RNDr. Beáta Stehlíková, PhD. Autor: Bc. Zuzana Zíková
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Konvergen né moely úrokových mier Diplomová práca Veúci iplomovej práce: RNDr. Beáta Stehlíková, PhD. Autor: Bc. Zuzana Zíková
MSc Financial Engineering CHRISTMAS ASSIGNMENT: MERTON S JUMP-DIFFUSION MODEL. To be handed in by monday January 28, 2013
 MSc Financial Engineering 2012-13 CHRISTMAS ASSIGNMENT: MERTON S JUMP-DIFFUSION MODEL To be handed in by monday January 28, 2013 Department EMS, Birkbeck Introduction The assignment consists of Reading
MSc Financial Engineering 2012-13 CHRISTMAS ASSIGNMENT: MERTON S JUMP-DIFFUSION MODEL To be handed in by monday January 28, 2013 Department EMS, Birkbeck Introduction The assignment consists of Reading
Lecture 4. Finite difference and finite element methods
 Finite difference and finite element methods Lecture 4 Outline Black-Scholes equation From expectation to PDE Goal: compute the value of European option with payoff g which is the conditional expectation
Finite difference and finite element methods Lecture 4 Outline Black-Scholes equation From expectation to PDE Goal: compute the value of European option with payoff g which is the conditional expectation
Partial differential approach for continuous models. Closed form pricing formulas for discretely monitored models
 Advanced Topics in Derivative Pricing Models Topic 3 - Derivatives with averaging style payoffs 3.1 Pricing models of Asian options Partial differential approach for continuous models Closed form pricing
Advanced Topics in Derivative Pricing Models Topic 3 - Derivatives with averaging style payoffs 3.1 Pricing models of Asian options Partial differential approach for continuous models Closed form pricing
last problem outlines how the Black Scholes PDE (and its derivation) may be modified to account for the payment of stock dividends.
 224 10 Arbitrage and SDEs last problem outlines how the Black Scholes PDE (and its derivation) may be modified to account for the payment of stock dividends. 10.1 (Calculation of Delta First and Finest
224 10 Arbitrage and SDEs last problem outlines how the Black Scholes PDE (and its derivation) may be modified to account for the payment of stock dividends. 10.1 (Calculation of Delta First and Finest
Pokročilé metody kalibrace modelů
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Pokročilé metody kalibrace modelů úrokových sazeb Dominika Holotňáková Katedra pravděpodobnosti a matematické statistiky Vedoucí
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Pokročilé metody kalibrace modelů úrokových sazeb Dominika Holotňáková Katedra pravděpodobnosti a matematické statistiky Vedoucí
Fakulta matematiky, fyziky a informatiky. Katedra aplikovanej matematiky a štatistiky EXOTICKÝCH OPCIÍ. Diplomová práca.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
M5MF6. Advanced Methods in Derivatives Pricing
 Course: Setter: M5MF6 Dr Antoine Jacquier MSc EXAMINATIONS IN MATHEMATICS AND FINANCE DEPARTMENT OF MATHEMATICS April 2016 M5MF6 Advanced Methods in Derivatives Pricing Setter s signature...........................................
Course: Setter: M5MF6 Dr Antoine Jacquier MSc EXAMINATIONS IN MATHEMATICS AND FINANCE DEPARTMENT OF MATHEMATICS April 2016 M5MF6 Advanced Methods in Derivatives Pricing Setter s signature...........................................
A Moment Matching Approach To The Valuation Of A Volume Weighted Average Price Option
 A Moment Matching Approach To The Valuation Of A Volume Weighted Average Price Option Antony Stace Department of Mathematics and MASCOS University of Queensland 15th October 2004 AUSTRALIAN RESEARCH COUNCIL
A Moment Matching Approach To The Valuation Of A Volume Weighted Average Price Option Antony Stace Department of Mathematics and MASCOS University of Queensland 15th October 2004 AUSTRALIAN RESEARCH COUNCIL
Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put opcií: Aplikácia na akcie SPDR Gold Shares
 Ing. Martina Rusnáková Katedra financií, Ekonomická fakulta echnická univerzita v Košiciach E-mail: martina.rusnakova@tuke.sk Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put
Ing. Martina Rusnáková Katedra financií, Ekonomická fakulta echnická univerzita v Košiciach E-mail: martina.rusnakova@tuke.sk Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put
An Overview of Volatility Derivatives and Recent Developments
 An Overview of Volatility Derivatives and Recent Developments September 17th, 2013 Zhenyu Cui Math Club Colloquium Department of Mathematics Brooklyn College, CUNY Math Club Colloquium Volatility Derivatives
An Overview of Volatility Derivatives and Recent Developments September 17th, 2013 Zhenyu Cui Math Club Colloquium Department of Mathematics Brooklyn College, CUNY Math Club Colloquium Volatility Derivatives
AMH4 - ADVANCED OPTION PRICING. Contents
 AMH4 - ADVANCED OPTION PRICING ANDREW TULLOCH Contents 1. Theory of Option Pricing 2 2. Black-Scholes PDE Method 4 3. Martingale method 4 4. Monte Carlo methods 5 4.1. Method of antithetic variances 5
AMH4 - ADVANCED OPTION PRICING ANDREW TULLOCH Contents 1. Theory of Option Pricing 2 2. Black-Scholes PDE Method 4 3. Martingale method 4 4. Monte Carlo methods 5 4.1. Method of antithetic variances 5
A distributed Laplace transform algorithm for European options
 A distributed Laplace transform algorithm for European options 1 1 A. J. Davies, M. E. Honnor, C.-H. Lai, A. K. Parrott & S. Rout 1 Department of Physics, Astronomy and Mathematics, University of Hertfordshire,
A distributed Laplace transform algorithm for European options 1 1 A. J. Davies, M. E. Honnor, C.-H. Lai, A. K. Parrott & S. Rout 1 Department of Physics, Astronomy and Mathematics, University of Hertfordshire,
Sadzobník kartových poplatkov firemné platobné karty / Schedule of Card Charges company payment cards
 Sadzobník kartových poplatkov firemné platobné karty / Schedule of Card Charges company payment cards Citibank Europe plc., so sídlom Dublin, North Wall Quay 1, Írsko, registrovaná v registri spoločností
Sadzobník kartových poplatkov firemné platobné karty / Schedule of Card Charges company payment cards Citibank Europe plc., so sídlom Dublin, North Wall Quay 1, Írsko, registrovaná v registri spoločností
Convexity Theory for the Term Structure Equation
 Convexity Theory for the Term Structure Equation Erik Ekström Joint work with Johan Tysk Department of Mathematics, Uppsala University October 15, 2007, Paris Convexity Theory for the Black-Scholes Equation
Convexity Theory for the Term Structure Equation Erik Ekström Joint work with Johan Tysk Department of Mathematics, Uppsala University October 15, 2007, Paris Convexity Theory for the Black-Scholes Equation
LOGNORMAL MIXTURE SMILE CONSISTENT OPTION PRICING
 LOGNORMAL MIXTURE SMILE CONSISTENT OPTION PRICING FABIO MERCURIO BANCA IMI, MILAN http://www.fabiomercurio.it Daiwa International Workshop on Financial Engineering, Tokyo, 26-27 August 2004 1 Stylized
LOGNORMAL MIXTURE SMILE CONSISTENT OPTION PRICING FABIO MERCURIO BANCA IMI, MILAN http://www.fabiomercurio.it Daiwa International Workshop on Financial Engineering, Tokyo, 26-27 August 2004 1 Stylized
Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš
 Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš Abstract Cieľ článku: Cieľom tohto článku je priblížiť zmeny hodnoty rizikovej prémie, identifikovať ktoré determinanty ju ovplyvňujú a ako
Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš Abstract Cieľ článku: Cieľom tohto článku je priblížiť zmeny hodnoty rizikovej prémie, identifikovať ktoré determinanty ju ovplyvňujú a ako
Continuous Time Finance. Tomas Björk
 Continuous Time Finance Tomas Björk 1 II Stochastic Calculus Tomas Björk 2 Typical Setup Take as given the market price process, S(t), of some underlying asset. S(t) = price, at t, per unit of underlying
Continuous Time Finance Tomas Björk 1 II Stochastic Calculus Tomas Björk 2 Typical Setup Take as given the market price process, S(t), of some underlying asset. S(t) = price, at t, per unit of underlying
Likelihood Estimation of Jump-Diffusions
 Likelihood Estimation of Jump-Diffusions Extensions from Diffusions to Jump-Diffusions, Implementation with Automatic Differentiation, and Applications Berent Ånund Strømnes Lunde DEPARTMENT OF MATHEMATICS
Likelihood Estimation of Jump-Diffusions Extensions from Diffusions to Jump-Diffusions, Implementation with Automatic Differentiation, and Applications Berent Ånund Strømnes Lunde DEPARTMENT OF MATHEMATICS
All Investors are Risk-averse Expected Utility Maximizers. Carole Bernard (UW), Jit Seng Chen (GGY) and Steven Vanduffel (Vrije Universiteit Brussel)
 All Investors are Risk-averse Expected Utility Maximizers Carole Bernard (UW), Jit Seng Chen (GGY) and Steven Vanduffel (Vrije Universiteit Brussel) First Name: Waterloo, April 2013. Last Name: UW ID #:
All Investors are Risk-averse Expected Utility Maximizers Carole Bernard (UW), Jit Seng Chen (GGY) and Steven Vanduffel (Vrije Universiteit Brussel) First Name: Waterloo, April 2013. Last Name: UW ID #:
On Using Shadow Prices in Portfolio optimization with Transaction Costs
 On Using Shadow Prices in Portfolio optimization with Transaction Costs Johannes Muhle-Karbe Universität Wien Joint work with Jan Kallsen Universidad de Murcia 12.03.2010 Outline The Merton problem The
On Using Shadow Prices in Portfolio optimization with Transaction Costs Johannes Muhle-Karbe Universität Wien Joint work with Jan Kallsen Universidad de Murcia 12.03.2010 Outline The Merton problem The
OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE
 NATIONAL AND REGIONAL ECONOMICS VIII OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE Ing. Radoslav BLAHOVEC Technická univerzita v Košiciach Ekonomická fakulta Katedra regionálnych vied a manažmentu Radoslav.Blahovec@tuke.sk
NATIONAL AND REGIONAL ECONOMICS VIII OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE Ing. Radoslav BLAHOVEC Technická univerzita v Košiciach Ekonomická fakulta Katedra regionálnych vied a manažmentu Radoslav.Blahovec@tuke.sk
Lecture 8: The Black-Scholes theory
 Lecture 8: The Black-Scholes theory Dr. Roman V Belavkin MSO4112 Contents 1 Geometric Brownian motion 1 2 The Black-Scholes pricing 2 3 The Black-Scholes equation 3 References 5 1 Geometric Brownian motion
Lecture 8: The Black-Scholes theory Dr. Roman V Belavkin MSO4112 Contents 1 Geometric Brownian motion 1 2 The Black-Scholes pricing 2 3 The Black-Scholes equation 3 References 5 1 Geometric Brownian motion
Structural Models of Credit Risk and Some Applications
 Structural Models of Credit Risk and Some Applications Albert Cohen Actuarial Science Program Department of Mathematics Department of Statistics and Probability albert@math.msu.edu August 29, 2018 Outline
Structural Models of Credit Risk and Some Applications Albert Cohen Actuarial Science Program Department of Mathematics Department of Statistics and Probability albert@math.msu.edu August 29, 2018 Outline
Rohini Kumar. Statistics and Applied Probability, UCSB (Joint work with J. Feng and J.-P. Fouque)
 Small time asymptotics for fast mean-reverting stochastic volatility models Statistics and Applied Probability, UCSB (Joint work with J. Feng and J.-P. Fouque) March 11, 2011 Frontier Probability Days,
Small time asymptotics for fast mean-reverting stochastic volatility models Statistics and Applied Probability, UCSB (Joint work with J. Feng and J.-P. Fouque) March 11, 2011 Frontier Probability Days,
Sample Path Large Deviations and Optimal Importance Sampling for Stochastic Volatility Models
 Sample Path Large Deviations and Optimal Importance Sampling for Stochastic Volatility Models Scott Robertson Carnegie Mellon University scottrob@andrew.cmu.edu http://www.math.cmu.edu/users/scottrob June
Sample Path Large Deviations and Optimal Importance Sampling for Stochastic Volatility Models Scott Robertson Carnegie Mellon University scottrob@andrew.cmu.edu http://www.math.cmu.edu/users/scottrob June
OPČNÉ STRATÉGIE A MOŽNOSTI ICH VYUŽITIA
 Masarykova univerzita Ekonomicko-správní fakulta Studijní obor: Finance OPČNÉ STRATÉGIE A MOŽNOSTI ICH VYUŽITIA Option strategies and their application Diplomová práce Vedoucí práce: Ing. Peter MOKRIČKA,
Masarykova univerzita Ekonomicko-správní fakulta Studijní obor: Finance OPČNÉ STRATÉGIE A MOŽNOSTI ICH VYUŽITIA Option strategies and their application Diplomová práce Vedoucí práce: Ing. Peter MOKRIČKA,
Math489/889 Stochastic Processes and Advanced Mathematical Finance Solutions to Practice Problems
 Math489/889 Stochastic Processes and Advanced Mathematical Finance Solutions to Practice Problems Steve Dunbar No Due Date: Practice Only. Find the mode (the value of the independent variable with the
Math489/889 Stochastic Processes and Advanced Mathematical Finance Solutions to Practice Problems Steve Dunbar No Due Date: Practice Only. Find the mode (the value of the independent variable with the
Risk Neutral Valuation
 copyright 2012 Christian Fries 1 / 51 Risk Neutral Valuation Christian Fries Version 2.2 http://www.christian-fries.de/finmath April 19-20, 2012 copyright 2012 Christian Fries 2 / 51 Outline Notation Differential
copyright 2012 Christian Fries 1 / 51 Risk Neutral Valuation Christian Fries Version 2.2 http://www.christian-fries.de/finmath April 19-20, 2012 copyright 2012 Christian Fries 2 / 51 Outline Notation Differential
Completeness and Hedging. Tomas Björk
 IV Completeness and Hedging Tomas Björk 1 Problems around Standard Black-Scholes We assumed that the derivative was traded. How do we price OTC products? Why is the option price independent of the expected
IV Completeness and Hedging Tomas Björk 1 Problems around Standard Black-Scholes We assumed that the derivative was traded. How do we price OTC products? Why is the option price independent of the expected
Kapitola 14. Výmenné kurzy a devízový trh: meny ako aktíva
 Kapitola 14 Výmenné kurzy a devízový trh: meny ako aktíva Obsah Čo sú výmenné kurzy Výmenné kurzy a ceny tovarov Devízový trh Dopyt po mene a ostatných aktívach Model devízového trhu: vplyv úrokových sadzieb
Kapitola 14 Výmenné kurzy a devízový trh: meny ako aktíva Obsah Čo sú výmenné kurzy Výmenné kurzy a ceny tovarov Devízový trh Dopyt po mene a ostatných aktívach Model devízového trhu: vplyv úrokových sadzieb
Financial Risk Management
 Risk-neutrality in derivatives pricing University of Oulu - Department of Finance Spring 2018 Portfolio of two assets Value at time t = 0 Expected return Value at time t = 1 Asset A Asset B 10.00 30.00
Risk-neutrality in derivatives pricing University of Oulu - Department of Finance Spring 2018 Portfolio of two assets Value at time t = 0 Expected return Value at time t = 1 Asset A Asset B 10.00 30.00
Exploring Volatility Derivatives: New Advances in Modelling. Bruno Dupire Bloomberg L.P. NY
 Exploring Volatility Derivatives: New Advances in Modelling Bruno Dupire Bloomberg L.P. NY bdupire@bloomberg.net Global Derivatives 2005, Paris May 25, 2005 1. Volatility Products Historical Volatility
Exploring Volatility Derivatives: New Advances in Modelling Bruno Dupire Bloomberg L.P. NY bdupire@bloomberg.net Global Derivatives 2005, Paris May 25, 2005 1. Volatility Products Historical Volatility
arxiv: v1 [q-fin.cp] 1 Nov 2016
![arxiv: v1 [q-fin.cp] 1 Nov 2016 arxiv: v1 [q-fin.cp] 1 Nov 2016](/thumbs/76/73518072.jpg) Essentially high-order compact schemes with application to stochastic volatility models on non-uniform grids arxiv:1611.00316v1 [q-fin.cp] 1 Nov 016 Bertram Düring Christof Heuer November, 016 Abstract
Essentially high-order compact schemes with application to stochastic volatility models on non-uniform grids arxiv:1611.00316v1 [q-fin.cp] 1 Nov 016 Bertram Düring Christof Heuer November, 016 Abstract
Extended Libor Models and Their Calibration
 Extended Libor Models and Their Calibration Denis Belomestny Weierstraß Institute Berlin Vienna, 16 November 2007 Denis Belomestny (WIAS) Extended Libor Models and Their Calibration Vienna, 16 November
Extended Libor Models and Their Calibration Denis Belomestny Weierstraß Institute Berlin Vienna, 16 November 2007 Denis Belomestny (WIAS) Extended Libor Models and Their Calibration Vienna, 16 November
FDI development during the crisis from 2008 till now
 VŠB-TU Ostrava, Ekonomická fakulta, katedra Financí 8. -. září FDI development during the crisis from 8 till now Michal Fabuš, Miroslav Kohuťár Abstract Investments represent an important resource of country
VŠB-TU Ostrava, Ekonomická fakulta, katedra Financí 8. -. září FDI development during the crisis from 8 till now Michal Fabuš, Miroslav Kohuťár Abstract Investments represent an important resource of country
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
Aspects of Financial Mathematics:
 Aspects of Financial Mathematics: Options, Derivatives, Arbitrage, and the Black-Scholes Pricing Formula J. Robert Buchanan Millersville University of Pennsylvania email: Bob.Buchanan@millersville.edu
Aspects of Financial Mathematics: Options, Derivatives, Arbitrage, and the Black-Scholes Pricing Formula J. Robert Buchanan Millersville University of Pennsylvania email: Bob.Buchanan@millersville.edu
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks
 Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
A Controlled Optimal Stochastic Production Planning Model
 Theoretical Mathematics & Applications, vol.3, no.3, 2013, 107-120 ISSN: 1792-9687 (print), 1792-9709 (online) Scienpress Ltd, 2013 A Controlled Optimal Stochastic Production Planning Model Godswill U.
Theoretical Mathematics & Applications, vol.3, no.3, 2013, 107-120 ISSN: 1792-9687 (print), 1792-9709 (online) Scienpress Ltd, 2013 A Controlled Optimal Stochastic Production Planning Model Godswill U.
RMSC 4005 Stochastic Calculus for Finance and Risk. 1 Exercises. (c) Let X = {X n } n=0 be a {F n }-supermartingale. Show that.
 1. EXERCISES RMSC 45 Stochastic Calculus for Finance and Risk Exercises 1 Exercises 1. (a) Let X = {X n } n= be a {F n }-martingale. Show that E(X n ) = E(X ) n N (b) Let X = {X n } n= be a {F n }-submartingale.
1. EXERCISES RMSC 45 Stochastic Calculus for Finance and Risk Exercises 1 Exercises 1. (a) Let X = {X n } n= be a {F n }-martingale. Show that E(X n ) = E(X ) n N (b) Let X = {X n } n= be a {F n }-submartingale.
Jean-Paul Murara, Västeras, 26-April Mälardalen University, Sweden. Pricing EO under 2-dim. B S PDE by. using the Crank-Nicolson Method
 Prcng EO under Mälardalen Unversty, Sweden Västeras, 26-Aprl-2017 1 / 15 Outlne 1 2 3 2 / 15 Optons - contracts that gve to the holder the rght but not the oblgaton to buy/sell an asset sometmes n the
Prcng EO under Mälardalen Unversty, Sweden Västeras, 26-Aprl-2017 1 / 15 Outlne 1 2 3 2 / 15 Optons - contracts that gve to the holder the rght but not the oblgaton to buy/sell an asset sometmes n the
Monte Carlo Simulations
 Monte Carlo Simulations Lecture 1 December 7, 2014 Outline Monte Carlo Methods Monte Carlo methods simulate the random behavior underlying the financial models Remember: When pricing you must simulate
Monte Carlo Simulations Lecture 1 December 7, 2014 Outline Monte Carlo Methods Monte Carlo methods simulate the random behavior underlying the financial models Remember: When pricing you must simulate
Odhady parametrov modelov
 Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
Introduction to Financial Mathematics
 Department of Mathematics University of Michigan November 7, 2008 My Information E-mail address: marymorj (at) umich.edu Financial work experience includes 2 years in public finance investment banking
Department of Mathematics University of Michigan November 7, 2008 My Information E-mail address: marymorj (at) umich.edu Financial work experience includes 2 years in public finance investment banking
Portfolio optimization for an exponential Ornstein-Uhlenbeck model with proportional transaction costs
 Portfolio optimization for an exponential Ornstein-Uhlenbeck model with proportional transaction costs Martin Forde King s College London, May 2014 (joint work with Christoph Czichowsky, Philipp Deutsch
Portfolio optimization for an exponential Ornstein-Uhlenbeck model with proportional transaction costs Martin Forde King s College London, May 2014 (joint work with Christoph Czichowsky, Philipp Deutsch
LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives
 Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
