UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky. Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli.
|
|
|
- Kenneth Murphy
- 5 years ago
- Views:
Transcription
1 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová
2 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca tudijný program: Ekonomická a nan ná matematika tudijný odbor: Aplikovaná matematika, 1114 koliace pracovisko: Katedra aplikovanej matematiky a ²tatistiky, FMFI UK, Mlynská dolina, Bratislava kolite : RNDr. Beáta Stehlíková, PhD. Bratislava 2012 Bc. Radka Sele éniová
3 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky ZADANIE ZÁVEREČNEJ PRÁCE Meno a priezvisko študenta: Študijný program: Študijný odbor: Typ záverečnej práce: Jazyk záverečnej práce: Bc. Radka Selečéniová ekonomická a finančná matematika (Jednoodborové štúdium, magisterský II. st., denná forma) aplikovaná matematika diplomová slovenský Názov: Cieľ: Rýchla časová škála volatility vo Fong-Vašíčkovom modeli Fong-Vašíčkov model patrí medzi modely so stochastickou volatilitou. To znamená, že máme stochastickú diferenciálnu rovnicu pre okamžitú úrokovu mieru, v ktorej je volatilita náhodná a riadi sa ďalšou stochastickou diferenciálnou rovnicou. Dlhopisy, z ktorých sa počítajú výnosove krivky, sú potom riešenim parabolickej PDR (premenné sú čas, okamžitá úroková miera, volatilita). Volatilita sa však pohybuje v inej časovej škále ako úrokova miera. Tymto sa zaobera článok B. Stehlíková, D. Ševčovič: On the singular limit of solutions to the Cox-Ingersoll-Ross interest rate model with stochastic volatility pdf, kde je spravená všeobecná analýza. V diplomovej praci sa zoberie Fong- Vašíčkov model (kvôli možnosti jednoduchšieho výpočtu cien dlhopisov), kde je predpoklad, že sa toho o cenách dlhopisov dá odvodiť viac, aproximácie sa môžu porovnávať s presným riešením atď. Motiváciou je, že takéto výsledky pre konkrétny model sú užitočné pri analýze zložitejsích alebo všeobecnejších modelov. Vedúci: Katedra: Dátum zadania: RNDr. Mgr. Beáta Stehlíková, PhD. FMFI.KAMŠ - Katedra aplikovanej matematiky a štatistiky Dátum schválenia: prof. RNDr. Daniel Ševčovič, CSc. garant študijného programu študent vedúci práce
4 ƒestné prehlásenie ƒestne prehlasujem, ºe som diplomovú prácu vypracovala samostatne, s pomocou literatúry uvedenej v zozname, konzultácií s vedúcou diplomovej práce a s vyuºitím teoretických vedomostí. V Bratislave, apríl Radka Sele éniová
5 Po akovanie Touto cestou by som sa rada po akovala vedúcej diplomovej práce RNDr. Beáte Stehlíkovej, PhD. za cenné rady a pripomienky, za poskytnutie literatúry ale hlavne za podporu a motiváciu pri písaní diplomovej práce.
6 SELEƒÉNIOVÁ, Radka: Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli [diplomová práca]. Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky, Katedra aplikovanej matematiky a ²tatistiky. Vedúca diplomovej práce: RNDr. Beáta Stehlíková, PhD., Bratislava, 2012, 59 s. Abstrakt Medzi významné oblasti modernej nan nej matematiky patrí modelovanie úrokových mier. Hodnota úrokovej miery je nevyhnutnou sú as ou ocenenia mnohých nan ných derivátov. Jeden zo spôsobov ako opísa dynamiku krátkodobej úrokovej miery je pomocou dvojfaktorových modelov so stochastickou volatilitou. Medzi takéto modely patrí aj Fong- Va²í kov model. V diplomovej práci uvádzame jeho podrobný opis, výpo et ceny dlhopisov, výnosových kriviek a tieº kalibráciu trhových cien rizika. Proces volatility krátkodobej úrokovej miery sa pohybuje v rýchlej²ej asovej ²kále ako samotná úroková miera ([6]). Zoh adnením tejto informácie a pouºitím asymptotickej metódy odvodíme aproximáciu ceny dlhopisu. Závislos tejto aproximácie od parametrov skrytého procesu volatility bude v porovnaní s presnou cenou dlhopisu zredukovaná, ím sa napríklad eliminuje náro ná kalibrácia aktuálnej hodnoty volatility úrokovej miery potrebnej na výpo et presnej ceny dlhopisu. Od cien dlhopisu sa odvíjajú výnosové krivky. Porovnanie aproximácie ceny dlhopisu s presnou cenou a porovnanie príslu²ných výnosových kriviek prinesie moºnos predstavy o presnosti a kvalite aproximácie. K ú ové slová: stochastická volatilita, rýchla asová ²kála, Fong-Va²í kov model, asymptotická metóda, aproximácia ceny dlhopisu
7 SELEƒÉNIOVÁ, Radka: Fast time scale of volatility in the Fong-Vasicek model [master thesis]. Comenius University in Bratislava, Faculty of Mathematics, Physics and Informatics, Department of Applied Mathematics and Statistics. Supervisor of the thesis: RNDr. Beáta Stehlíková, PhD., Bratislava, 2012, 59 p. Abstract Modeling short-rate process is one of the most important part of modern nancial mathematics. It is necessary to know the value of interest rate in pricing nancial derivatives. There are several ways of modeling instantaneous interest rate. Two-factor model with stochastic volatility is one of them. In this master thesis we focus our attention on the Fong-Vasicek model for which we calculate the bond price, yield curves and we calibrate the market prices of risk. It was observed that stochastic volatility evolves in a dierent time scale, which is faster than the scale of short rate ([6]). We present an asymptotic analysis which corrects the classic formula for bond price. The key assumption of this method is fast time scale of volatility. The approximation reduces the dependence of bond price on the details of underlying volatility process, which is unknown. The present volatility level is not need to be calibrated yet. The yield curves are derived from the bond prices. A comparison of classic bond price and yield curves with approximations given by asymptotic method give us an idea of quality and accuracy of approximation. Key words: stochastic volatility, fast time scale, Fong-Vasicek model, asymptotic analysis, correction of bond price
8 Obsah Úvod 1 1 Modelovanie okamºitej úrokovej miery a ocenenie dlhopisov Základné pojmy Stochastický kalkulus Modely okamºitej úrokovej miery Jednofaktorové modely Cena dlhopisu v jednofaktorovom modeli Dvojfaktorové modely Cena dlhopisu v dvojfaktorovom modeli Pojem stochastickej volatility a Fong-Va²í kov model Hustota rozdelenia stochastického procesu Stochastická volatilita Modelovanie stochastickej volatility Rýchla asová ²kála volatility Fong-Va²í kov model so stochastickou volatilitou Ceny dlhopisov a výnosové krivky Limita výnosových kriviek Kalibrácia trhových cien rizika Asymptotická metóda a odvodenie aproximácie ceny dlhopisu Asymptotická metóda Odvodenie aproximovanej ceny dlhopisu Výpo et kon²tanty yφ Zhrnutie
9 4 Porovnanie aproximácie rie²enia s presným rie²ením Porovnanie cien dlhopisov Porovnanie výnosových kriviek Záver 54 Literatúra 55 Príloha 58
10 Úvod V posledných desa ro iach nastala výrazná expanzia trhu s úrokovými derivátmi. K ú ovú úlohu v správnom oce ovaní týchto derivátov hrá hodnota okamºitej úrokovej miery. Jej stochastický charakter podnietil vznik mnohých modelov. Spo iatku to boli jednofaktorové modely, av²ak ²kála výnosových kriviek, ktorú nimi bolo moºné popísa nebola posta ujúca. Tak vznikli dvojfaktorové modely, medzi ktoré patria aj modely so stochastickou volatilitou. V práci sa budeme venova Fong-Va²í kovmu modelu. V om je dynamika úrokovej miery popísaná dvojicou stochastických diferenciálnych rovníc pre samotnú úrokovú mieru a pre volatilitu úrokovej miery. Proces volatility nie je na trhu pozorovate ný, preto je kalibrácia jeho parametrov náro ná. Cena dlhopisu je v²ak od aktuálnej hodnoty volatility a parametrov popisujúcich jej vývoj závislá. Jedným z rie²ení ako sa vyhnú kalibrácii aktuálnej hodnoty volatility je pomocou asymptotickej metódy odvodi aproximáciu ceny dlhopisu, ktorej závislos od volatility bude oproti klasickej cene zredukovaná. Základným prvkom tejto metódy je predpoklad o rýchlej asovej ²kále volatility. Aplikáciami tohto konceptu na viaceré typy dvojfaktorových modelov sa zaoberajú lánky [1], [6], [12], [26]. V diplomovej práci odvodíme aproximáciu ceny dlhopisu pre Fong-Va²í kov model. Vzh adom na existenciu explicitného rie²enia tohto modelu, budeme ma moºnos porovnania aproximácie s presným rie²ením a tým získame predstavu o presnosti aproximácie. Výsledky pre konkrétny model môºu by uºito né pri analýzach zloºitej²ích modelov. Práca je rozdelená na ²tyri kapitoly. V prvej kapitole sa venujeme stru nému úvodu do problematiky modelovania okamºitej úrokovej miery a oce ovaniu dlhopisov. V druhej kapitole rozoberieme proces stochastickej volatility a vysvetlíme pojem rýchlej asovej ²kály. Podrobne sa budeme venova aj Fong-Va²í kovmu modelu, pre ktorý odvodíme cenu dlhopisu, výnosové krivky a rôznymi metódami odhadneme trhové ceny rizika. Detailným odvodením aproximácie ceny dlhopisu pomocou asymptotickej metódy sa zaoberá tretia kapitola. Nakoniec v ²tvrtej kapitole pre konkrétne hodnoty parametrov porovnáme aproximácie ceny dlhopisov a výnosových kriviek s presným rie²ením.
11 Kapitola 1 Modelovanie okamºitej úrokovej miery a ocenenie dlhopisov Na úvod zadenujeme základné pojmy ako dlhopis, asová ²truktúra úrokových mier, okamºitá úroková miera a stru ne spomenieme teóriu stochastického kalkulu. Budeme vychádza z [17], [18] a [27]. V al²ej asti kapitoly predstavíme jeden zo spôsobov modelovania vývoja úrokových mier, a to short-rate modely. V skratke uvedieme aj ocenenia dlhopisov, pre ktoré je okamºitá úroková miera podkladovým aktívom. 1.1 Základné pojmy Dlhopis je dlhodobý cenný papier obchodovate ný na burze. Dlºník sa v om zaväzuje, ºe v stanovenom termíne vyplatí nominálnu hodnotu a v dohodnutých intervaloch bude vypláca pravidelný kupón. Dlhopis, ktorého nominálna hodnota je rovná 1 nazývame diskontný dlhopis. Dlhopisy rozde ujeme na dva typy, kupónové a bezkupónové, pod a toho, i kupóny vyplácajú alebo nie. My sa alej budeme zaobera najjednoduch²ím typom dlhopisu a to bezkupónovým diskontným dlhopisom. Pri spojitom úro ení sa sú asná cena dlhopisu P (t, T ) vypo íta pod a vzorca P (t, T ) = e R(t,T )(T t), (1.1) kde t je okamºitý as a T je doba splatnosti dlhopisu, tzv. maturita. Výrazom R(t, T ) ozna ujeme úrokovú mieru, ktorá vyjadruje mieru zhodnotenia dlhopisu oproti kúpnej cene. Vyjadrením R(t, T ) z uvedeného vz ahu môºeme na základe známych cien dlhopisov
12 1.1 Základné pojmy 3 ur i asovú ²truktúru úrokových mier R(t, T ) = 1 ln P (t, T ). (1.2) T t Tá vyjadruje funk nú závislos medzi asom do maturity a výnosom R(t, T ). Graf, zobrazujúci jednotlivé R(t, T ) pre xný as t, sa nazýva výnosová krivka. Tvary výnosových kriviek sú predmetom rozsiahleho skúmania. V praxi sa ukazuje, ºe môºu by rôzne, rozli²ujú sa v²ak ²tyri základné typy: rastúca, klesajúca, plochá a tzv. humped 1 krivka. Rastúca (normálna) výnosová krivka sa vyskytuje, ak trh neo akáva významné zmeny, alebo ak o akáva rast trhových úrokových mier (vtedy jej sklon rastie). Klesajúca (inverzná) krivka sa na trhu vyskytuje relatívne vzácne, napr. ke centrálna banka z ur itých dôvodov výrazne zvý²i hodnoty úrokových sadzieb. Plochá výnosová krivka je tzv. prechodovou krivkou medzi klesajúcou a rastúcou krivkou a spravidla o akáva pokles úrokových mier. Humped krivka môºe signalizova prechod ku inverznej, ale aj opa ne, návrat k normálnej výnosovej krivke. V²etky ²tyri tvary sú zobrazené na obr.1.1. Výnos (%) 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 US Treasury Maturita (v rokoch) Výnos (%) 5 4,5 4 3,5 3 2,5 2 1,5 1 0,5 0 Kanada Maturita (v rokoch) Grécko Brazília , ,7 Výnos (%) Výnos (%) 12,6 12,5 12,4 8 12,3 7 12, Maturita (v rokoch) Maturita (v rokoch) Obr. 1.1: Rôzne tvary kriviek asovej ²truktúry úrokových mier. Zdroj: krivka s práve jedným lokálnym maximom a bez minima na intervale (0, )
13 1.2 Stochastický kalkulus 4 Úroková miera pre dlhopis s okamºitou splatnos ou, t. j. T = t sa nazýva okamºitá úroková miera, alebo aj short rate. Získame ju pomocou vz ahu r t = lim R(t, T ) = R(t, t). (1.3) T t + Short rate predstavuje za iatok výnosovej krivky a poskytuje informáciu o jej al²om priebehu. Je teoretickou veli inou, v praxi má k nej najbliº²ie tzv. overnight, t. j. jednod ová úroková miera, za ktorú si medzi sebou poºi iavajú banky. ƒasový vývoj úrokovej miery má stochastický charakter. Na nasledujúcom obrázku je znázornený reálny priebeh referen nej sadzby EONIA, ktorá je sadzbou pre skuto ne zrealizované jednod ové obchody v mene euro. 1,80 1,65 1,50 1,35 EONIA (%) 1,20 1,05 0,90 0,75 0,60 0,45 0, Mesiac Obr. 1.2: ƒasový priebeh okamºitej úrokovej miery EONIA v roku Zdroj: Z obrázka je zrejmý náhodný charakter úrokovej miery, ktorá sa v priebehu roku 2011 pohybovala v ²kále medzi 0.347% a 1.715%. V nasledujúcej asti uvedieme základné informácie týkajúce sa teórie stochastického kalkulu. 1.2 Stochastický kalkulus Stochastický proces je t-parametrický systém náhodných premenných {X(t), t I}, kde I je interval alebo diskrétna mnoºina indexov. Medzi základné stochastické procesy patria Markovovské náhodné procesy, ktorých charakteristickou rtou je fakt, ºe budúca hodnota procesu závisí len od sú asnej hodnoty, nie minulej. peciálnym typom Markovovského
14 1.2 Stochastický kalkulus 5 procesu je vo nan nej matematike ²iroko vyuºívaný proces - Wienerov proces a jeho zov²eobecnenie Brownov pohyb. Uvedieme ich denície. Denícia 1. ([27], str. 22) Brownov pohyb {X(t), t 0} je t-parametrický systém náhodných veli ín, pri om (i) v²etky prírastky X(t + ) X(t) majú normálne rozdelenie so strednou hodnotou µ a disperziou σ 2, (ii) pre kaºdé delenie t 0 = 0 < t 1 < t 2 < t 3 <... t n sú prírastky X(t 1 ) X(t 0 ), X(t 2 ) X(t 1 ),..., X(t n ) X(t n 1 ) nezávislé náhodné premenné s parametrami pod a bodu (i), (iii) X(0) = 0. Brownov pohyb s parametrami µ = 0, σ 2 = 1 nazývame Wienerov proces. Náhodný proces zvy ajne modelujeme ako rie²enie stochastickej diferenciálnej rovnice dx(t) = µ(x, t)dt + σ(x, t)dw, (1.4) kde w je Wienerov proces, zabezpe ujúci stochastickos procesu. Napr. okamºitá úroková miera sa modeluje ako stochastický proces r(t). Na ocenenie jej derivátov, funkcií okamºitej úrokovej miery, potrebujeme nástroj stochastickej analýzy - Itóovu lemu. Itóova lema je k ú ovou v teórii oce ovania nan ných derivátov. Lema 1. (Itóova lema)([27], str. 27) Nech f(x, t) je hladká funkcia dvoch premenných, pri om premenná x je rie²ením stochastickej diferenciálnej rovnice dx = µ(x, t)dt + σ(x, t)dw, kde w je Wienerov proces. Potom prvý diferenciál funkcie f je daný vz ahom df = f ( f x dx + t + 1 ) 2 σ2 (x, t) 2 f dt, x 2 dôsledkom oho funkcia f vyhovuje stochastickej diferenciálnej rovnici df = ( f t + µ(x, t) f x σ2 (x, t) 2 f x 2 ) dt + σ(x, t) f x dw.
15 1.3 Modely okamºitej úrokovej miery 6 Roz²írenie Itóovej lemy pre vektorové náhodné premenné, ktoré budeme neskôr pri oce ovaní dlhopisov v dvojfaktorových modeloch vyuºíva nebudeme uvádza, ale itate ho nájde v knihe [27]. V nasledujúcej asti si stru ne predstavíme jedno a dvojfaktorové modely, ktoré sa pouºívajú pri modelovaní okamºitej úrokovej miery. Uvedieme aj postup odvodenia ceny dlhopisu. 1.3 Modely okamºitej úrokovej miery Modely okamºitej, resp. krátkodobej úrokovej miery opisujú vývoj okamºitej úrokovej miery a závislos výnosovej krivky od nej. Okamºitú úrokovú mieru budeme v jednofaktorových modeloch modelova ako rie²enie stochastickej diferenciálnej rovnice, v dvojfaktorových modeloch ako rie²enie systému dvoch takýchto rovníc Jednofaktorové modely V jednofaktorových modeloch je dynamika okamºitej úrokovej miery opísaná len pomocou jedného faktora, jedného zdroja náhodnosti. Týmto zdrojom je samotná okamºitá úroková miera r. Jej vývoj sa modeluje pomocou stochastickej diferenciálnej rovnice, ktorá má vo v²eobecnosti tvar dr = µ(r, t)dt + σ(r, t)dw, (1.5) kde w je ²tandardný Wienerov proces. V teórii modelovania okamºitej úrokovej miery rozli²ujeme dve hlavné triedy modelov, a to rovnováºne a bezarbitráºne modely. Kaºdý z týchto prístupov modelovania vyuºíva iný typ informácie. Zatia o v rovnováºnych modeloch je výstupom asová ²truktúra úrokových mier, v bezarbitráºnych je táto krivka vstupom. Rovnováºne modely nedokáºu presne zachyti sú asnú výnosovú krivku, pretoºe obsahujú len nieko ko parametrov modelu. Bezarbitáºne modely sú skon²truované tak, aby presne opisovali dennú asovú ²truktúru úrokových mier. Av²ak cena za takúto vlastnos sa prejaví v potrebe zavedenia asovo závislých koecientov - driftu a volatility. V mnohých modeloch potom nastáva nemarkovovos a aj preto sú astokrát analyticky nerie²ite né. Bezarbitráºnymi modelmi sa v tejto práci zaobera nebudeme, a preto len v krátkosti vymenujeme tie najznámej²ie. Patria medzi ne Ho-Leeho model z roku 1986 a Hull-Whiteov model z roku alej sa budeme zaobera len rovnováºnymi modelmi. Proces (1.5) obsahuje dve zloºky. Deterministická as procesu - drift µ(r, t) reprezentuje trend vývoja short rate, stochastická as - volatilita σ(r, t) ur uje ve kos uktuácií v okolí deterministickej asti. Jedným z naj astej²ie pouºívaných tvarov driftovej asti je
16 1.3 Modely okamºitej úrokovej miery 7 tzv. mean reversion drift µ(r, t) = κ(θ r), (1.6) kde parametre κ, θ sú kladné kon²tanty. K ú ovou vlastnos ou takejto vo by je, ºe stredná hodnota úrokovej miery je pri ahovaná rýchlos ou κ ku rovnováºnej (limitnej) hodnote, ktorou je hodnota parametra θ. Takýto predpoklad o správaní sa úrokovej miery nie je síce istým javom pozorovaným na reálnych trhoch ale je v súlade s ekonomickou teóriou. Ak zaznamenáme nárast úrokových mier, ekonomika spomalí a nastane pokles dopytu po pôºi kách. Tým pádom majú úrokové miery opä tendenciu klesnú. Podobne v opa nom smere. Na obr.1.3 je znázornený priebeh úrokovej miery EURIBOR v rokoch 2010 aº Vidíme, ºe v prvej polovici roka 2010 je úroková miera takmer kon²tantná. Môºe teda nasta situácia, ºe vývoj úrokovej miery nie je moºné popísa mean reversion procesom. Av²ak pre niektoré sady parametrov mean reversion proces nie vºdy vyzerá ideálne a aj procesy, ktoré na prvý poh ad moºno nevyzerajú ako mean reversion nimi sú. Vývoj v roku 2011 uº viac pripomína proces, v ktorom je úroková miera pri ahovaná k limitnej hodnote. 1,60 1,40 1,20 1,00 1 týždňový EURIBOR(%) 0,80 0,60 0,40 0,20 0,00 04/01/ /05/ /09/ /01/ /05/ /09/2011 Obr. 1.3: ƒasový priebeh úrokovej miery EURIBOR v rokoch Zdroj: Stochastická as modelu je asto v tvare σ(r, t) = σr γ, (1.7) kde parametre σ > 0 a γ 0 sú kon²tanty. V závislosti od vo by parametrov potom rozoznávame rôzne modely.
17 1.3 Modely okamºitej úrokovej miery 8 Va²í kov model Vo bou γ = 0 dostávame jeden z prvých modelov okamºitej úrokovej miery - Va²í kov model. Bol publikovaný v roku 1977 v lánku [29]. Okamºitá úroková miera sa v om riadi stochastickou diferenciálnou rovnicou dr = κ(θ r)dt + σdw. (1.8) Proces v takomto tvare sa zvykne ozna ova ako Ornstein-Uhlenbeckov proces. Va²í kov model bol prvým modelom, ktorý dokázal popísa vlastnos mean reversion. Vzh adom na prvenstvo v oblasti modelovania úrokovej miery má v²ak model nieko ko nedostatkov. Prvým z nich je kon²tantná volatilita, ktorá nezávisí od hodnoty úrokovej miery. Druhým je, ºe rozdelenie úrokovej miery r je normálne a tým pádom dovo uje aj záporné hodnoty. Pozrime sa v²ak na to, i je tento nedostatok aº taký významný. Ve kos pravdepodobnosti nadobudnutia záporných hodnôt r závisí od vo by parametrov. Vypo ítajme jej hodnotu. 2 P (r t+ t < 0) = ) P (N (θ(1 e κt ) + r 0 e κt, σ2 2κ (1 e 2κt )) < 0 = P N (0, 1) < θ(1 e κt ) r 0 e κt σ 2 2κ e 2κt ) = Φ θ(1 e κt ) r 0 e κt σ 2 2κ e 2κt ) Funkcia Φ(.) je distribu nou funkciou normovaného normálneho rozdelenia. Na nasledujúcom obrázku je znázornený priebeh hodnoty pravdepodobnosti v závislosti od asu pre hodnoty parametrov κ = 0.109, θ = , σ = , prebraté z lánku [9] a pre po iato nú hodnotu r 0 = Vidíme, ºe pravdepodobnos, ºe krátkodobá úroková miera o rok pri daných parametroch nadobudne zápornú hodnotu je prakticky nulová (obrázok v avo). Aj ke pravdepodobnos s rastúcim asom rastie, je stále ve mi nízka. Nakoniec sa v²ak ustáli na limitnej hodnote, ktorá je pre na²e hodnoty parametrov rovná (obrázok vpravo). Problém nadobudnutia záporných hodnôt úrokovej miery nie je teda vºdy aº taký závaºný, ako sa na prvý poh ad môºe zda, nako ko pri vhodných hodnotách parametrov je táto pravdepodobnos ve mi nízka. 2 Pri výpo te je potrebné pozna podmienenú hustotu rozdelenia r a jej ²tatistiky - strednú hodnotu a disperziu. Týmto sa zaoberá kapitola 2.
18 1.3 Modely okamºitej úrokovej miery 9 Pravdepodobnost 4.5 x Cas Pravdepodobnost Cas Obr. 1.4: Priebeh pravdepodobnosti nadobudnutia zápornej hodnoty r pre Va²í kov model v ase s po iato nou hodnotou r 0 = 0.05 a parametrami κ = 0.109, θ = , σ = Cox-Ingersoll-Rossov model (CIR) Cox-Ingersoll-Rossov model bol prvýkrát publikovaný v roku 1985 v lánku [8]. Vo bou parametra γ = 1 2 dostávame stochastickú diferenciálnu rovnicu dr = κ(θ r)dt + σ rdw, (1.9) ktorej sa zvykne hovori aj Besselov odmocninový proces, z dôvodu, ºe stochastický len dw je násobený odmocninou z náhodnej premennej r. Významným prínosom CIR modelu je fakt, ºe ak proces okamºitej úrokovej miery za ína z kladnej po iato nej hodnoty r 0 a je splnený predpoklad o paramatroch modelu 2κθ σ 2, tak r t uº nikdy nenadobudne nulové alebo záporné hodnoty. Intuitívne, ak sa okamºitá úroková miera blíºi k nulovým hodnotám, jej volatilita je tieº malá a ak by r nadobudlo nulovú hodnotu, volatilita bude tieº nulová a al²í vývoj okamºitej úrokovej miery je riadený trendovou zloºkou, ktorá je v tomto prípade kladná. Preto sa hodnota r opä zvý²i ([27]). Medzi al²ie známe jednofaktorové modely patrí aj Dothanov model (1978), Black- Karasinského model (1991) a Chan-Karolyi-Longsta-Sandersov model (1992). O nich sa itate môºe do íta napr. aj v [4].
19 1.3 Modely okamºitej úrokovej miery Cena dlhopisu v jednofaktorovom modeli Okamºitá úroková miera slúºi ako podkladové aktívum pre bezkupónový dlhopis. Popí²eme si odvodenie parciálnej diferenciálnej rovnice (PDR) pre cenu dlhopisu P (t, r; T ), ktorá je závislá od asu t, okamºitej úrokovej miery r a parametra T, ktorý predstavuje as splatnosti. Uvádzame len stru né odvodenie bez príslu²ných konkrétnych výpo tov, podrobné odvodenie itate môºe nájs napríklad v [18]. Predpokladajme, ºe okamºitá úroková miera sa riadi jednofaktorovým modelom (1.5). Pod a Itóovej lemy pre cenu dlhopisu P (t, r; T ) platí dp = ( P t + µ P r + 1 ) 2 P 2 σ2 dt + σ P dw. (1.10) r 2 r Vytvorme portfólio Π = V 1 V 2 pozostávajúce z dvoch typov dlhopisov s rôznymi maturitami T 1 a T 2 v mnoºstvách V 1 a V 2. Zvo me hodnoty V 1 a V 2 tak, aby stochastický proces zmeny hodnoty portfólia dπ bol bezrizikový, t. j. aby obsahoval len deterministickú as. Vylú ením moºnosti arbitráºe a teda vyuºitím faktu, ºe výnos bezrizikového portfólia musí by rovný r, t. j. dπ = rπdt, dostávame parciálnu diferenciálnu rovnicu v tvare P t + (µ(r, t) λ(r, t)σ(r, t)) P r σ2 (r, t) 2 P rp = 0 (1.11) r2 s koncovou podmienkou P (T, r; T ) = 1. Funkcia λ(r, t) sa nazýva trhová cena rizika a vyjadruje o akávaný nárast výnosu dlhopisu na jednotku rizika, resp. dá sa interpretova ako prémia pre investora, z dôvodu podstupovania rizika. Ak teda ur íme parametre stochastickej rovnice pre r(t) a hodnotu trhovej ceny rizika λ(r, t), vyrie²ením parciálnej diferenciálnej rovnice (1.11) dostaneme cenu dlhopisu. V nasledujúcej asti uvedieme výpo et ceny dlhopisu pre Va²í kov model, ktorú budeme v al²ej asti práce potrebova.
20 1.3 Modely okamºitej úrokovej miery 11 Cena dlhopisu vo Va²í kovom modeli Cenu dlhopisu pre Va²í kov model (1.8) budeme h ada v tvare P (τ, r). Nová premenná τ = T t vyjadruje as zostávajúci do expirácie dlhopisu. V takomto zápise potom parciálna diferenciálna rovnica pre Va²í kov model s kon²tantnou trhovou cenou rizika λ(r, t) = λ má pod a (1.11) tvar P τ + (κ(θ r) λσ) P r P 2 σ2 rp = 0 (1.12) r2 s po iato nou podmienkou P (0, r) = 1. Predpokladajme rie²enie v separovanom tvare potom príslu²né derivácie vystupujúce v (1.12) sú P (τ, r) = A(τ)e B(τ)r, (1.13) P τ = A e Br AB e Br, P r = ABe Br, 2 P r 2 = AB 2 e Br. Dosadením derivácií do (1.12) dostávame systém oby ajných diferenciálnych rovníc pre funkcie A, B: B = 1 κb, (1.14) A = AB(λσ κθ) σ2 AB 2, (1.15) s po iato nými podmienkami A(0) = 1 a B(0) = 0. Rovnica pre funkciu B je oby ajnou lineárnou diferenciálnou rovnicou a preto s vyuºitím po iato nej podmienky po ahky dostávame B = 1 κ (1 e κτ ). (1.16) Dosadením explicitného tvaru funkcie B do rovnice (1.15), následnou integráciou a vyuºitím po iato nej podmienky dostávame ] A = exp [(B(τ) τ)r σ2 4κ B2 (τ), (1.17)
21 1.3 Modely okamºitej úrokovej miery 12 kde sme symbolom R ozna ili R = θ λσ κ σ2 2κ 2. (1.18) Toto ozna enie vychádza z toho, ºe hodnota R je limitou výnosových kriviek pre τ. Cena dlhopisu v CIR modeli Postup výpo tu ceny dlhopisu v CIR modeli je analogický postupu vo Va²í kovom modeli. Predpokladaním tvaru (1.13) pre cenu dlhopisu a hodnoty trhovej ceny rizika λ(r, t) = λ r s kon²tantou λ, vy íslením jednotlivých derivácií a dosadením do príslu²nej parciálnej diferenciálnej rovnice dostávame systém oby ajných diferenciálnych rovníc pre funkcie A, B. Explicitným rie²ením tohto systému je: A(τ) = B(τ) = [ ] 2φe τ 2 (φ+ψ) σ 2, (φ + ψ)[e φτ 1] + 2φ (1.19) 2(e φτ 1) (φ + ψ)[e φτ 1] + 2φ, (1.20) φ = ψ 2 + 2σ 2, ψ = κ + λσ. (1.21) Ve kou výhodou a aj jedným z dôvodov popularity Va²í kovho a CIR modelu je okrem iného aj fakt, ºe pre oba modely je moºné analyticky nájs explicitné rie²enie pre cenu dlhopisu. Niektoré modely, napr. exponenciálny Va²í kov model (1990), bezarbitráºny Black- Karasinského model (1991), CKLS model (1992) alebo Mercurio-Moraledov model (2000) takúto vlastnos nemajú. Cena dlhopisu sa dá vypo íta pomocou numerických metód, napr. pomocou Crank-Nicolsonovej schémy ([7]) alebo Box metódy ([22]), alebo pomocou aproximácií v analytickom tvare (napr. [15], [24]) Dvojfaktorové modely V predchádzajúcej asti práce sme si predstavili jednofaktorové modely. Dynamika úrokovej miery je v týchto modeloch opísaná len pomocou jedného stochastického faktora. Jednoduchos takéhoto modelovania na jednej strane môºe pre niektoré modely priná²a výhodu v moºnosti nájdenia explicitného rie²enia pre cenu dlhopisu, na strane druhej v²ak stojí nieko ko nedostatkov. Jedným z nich je fakt, ºe akonáhle je hodnota úrokovej miery známa,
22 1.3 Modely okamºitej úrokovej miery 13 celá krivka asovej ²truktúry úrokových mier je ur ená. Av²ak, aj v realite môºu výnosové krivky s rovnakým za iatkom nadobúda rôzne tvary. Takýto prístup modelovania je ve kým zjednodu²ením skuto ného správania sa úrokovej miery. Jedným z rie²ení týchto problémov je kon²trukcia dvojfaktorových modelov, ktoré priná²ajú vä ²iu vo nos pri modelovaní úrokovej miery. Pri pouºití takýchto modelov môºu výnosové krivky nadobúda ²ir²iu ²kálu tvarov. Úroková miera je v dvojfaktorových modeloch funkciou dvoch faktorov, t. j. r = r(x, y), a jej dynamika je potom vo v²eobecnom prípade opísaná pomocou systému dvoch stochastických rovníc: dx = µ x (x, y)dt + σ x (x, y)dw 1, dy = µ y (x, y)dt + σ y (x, y)dw 2. (1.22) Prírastky dw 1, dw 2 Wienerových procesov môºu by korelované, t. j. E(dw 1 dw 2 ) = ρdt. V závislosti od vo by faktorov potom rozli²ujeme rôzne typy dvojfaktorových modelov. Uvedieme len niektoré z nich, itate sa podrobnej²ie informácie môºe dozvedie napr. z [4] a [18]. Dvojfaktorový Va²í kov a CIR model V dvojfaktorovej verzii Va²í kovho a CIR modelu je okamºitá úroková miera sú tom dvoch nezávislých faktorov, t. j. r = r 1 + r 2, kde r 1, r 2 sú popísané stochastickou diferenciálnou rovnicou typu (1.8) vo Va²í kovom modeli a (1.9) v CIR modeli. Modely s inou ekonomickou veli inou V modeloch tohto typu je dynamika úrokovej miery popísaná dvomi stavovými premennými, ktoré môºu ale nemusia by na trhu pozorovate né, môºu alebo nemusia by korelované. V modeli Brennana a Schwartza (1982) sú týmito premennými krátkodobá a dlhodobá úroková miera. Model Corzovej a Schwartza (2003), patriaci do triedy konvergen ných modelov, bol vyvinutý pre krajiny vstupujúce do Európskej menovej únie. V tomto modeli je úroková miera krajiny vstupujúcej do Európskej únie závislá od európskej miery, pri om obe sú modelované pomocou stochastických diferenciálnych rovníc. Dvojfaktorové modely so stochastickou volatilitou Inou triedou dvojfaktorových modelov sú modely, v ktorých sa niektorý z kon²tantných parametrov jednofaktorového modelu modeluje ako náhodný proces. Týmto parametrom
23 1.3 Modely okamºitej úrokovej miery 14 môºe by napríklad trhová cena rizika alebo volatilita úrokovej miery. Medzi modely so stochastickou volatilitou patrí napríklad model Andersona a Lunda (1996) alebo Fong- Va²í kov model (1991). Druhým z nich sa budeme v tejto práci zaobera a jeho podrobnú analýzu uvádzame v nasledujúcej kapitole Cena dlhopisu v dvojfaktorovom modeli Odvodíme parciálnu diferenciálnu rovnicu pre cenu dlhopisu P (t, x, y; T ), kde t je as a T je as splatnosti. Odvodenie je analogické odvodeniu pre jednofaktorové modely. Uvádzame preto len stru ný postup bez uvedenia príslu²ných výpo tov. Podrobné odvodenie itate môºe nájs napr. v [18]. Predpokladajme, ºe vývoj úrokovej miery je popísaný dvojfaktorovým modelom (1.22). Vyuºitím viacrozmernej Itóovej lemy pre cenu dlhopisu P (t, x, y; T ) dostávame dp = µdt + σ 1 dw 1 + σ 2 dw 2, kde µ = P t + µ P x x + µ P y y + σ2 x 2 P 2 x + σ2 y 2 P 2 2 y + ρσ 2 P xσ 2 y x y, σ 1 = P σ x x, σ 2 = P σ y y. Zostrojme portfólio Π pozostávajúce z troch typov dlhopisov s rôznymi maturitami T 1, T 2 a T 3 v mnoºstvách V 1, V 2 a V 3. Zvo me hodnoty V 1, V 2 a V 3 tak, aby stochastický proces zmeny hodnoty portfólia dπ bol bezrizikový. Vylú ením moºnosti arbitráºe a teda vyuºitím faktu, ºe výnos bezrizikového portfólia musí by rovný r, t. j. dπ = rπdt, dostávame parciálnu diferenciálnu rovnicu v tvare
24 1.3 Modely okamºitej úrokovej miery 15 + σ2 x 2 P t + (µ x λ 1 σ x ) P x + (µ y λ 2 σ y ) P y + 2 P x + σ2 y 2 P 2 2 y + ρσ 2 P xσ 2 y r(x, y)p = 0 (1.23) x y s koncovou podmienkou P (T, x, y; T ) = 1. Funkcie λ 1 (x, y, t) a λ 1 (x, y, t) sú tzv. trhové ceny rizika príslu²ných faktorov a nezávisia od maturity T.
25 Kapitola 2 Pojem stochastickej volatility a Fong-Va²í kov model V kapitole 2 sa zoznámime s nieko kými pojmami, ktoré budeme potrebova v al²ej asti diplomovej práce. Ako prvé popí²eme Fokker-Planckovu rovnicu, pomocou ktorej je moºné ur i hustotu rozdelenia náhodnej premennej riadiacej sa stochastickou diferenciálnou rovnicou. Spomenieme dôleºitý koncept limitnej hustoty a predstavíme pojmy stochastická volatilita, vlastnos zhlukovania a rýchla asová ²kála volatility. Na záver podrobne opí²eme Fong-Va²í kov model, odvodíme cenu dlhopisu a zaobera sa budeme aj kalibráciou trhových cien rizika. 2.1 Hustota rozdelenia stochastického procesu Uvaºujme náhodnú premennú x = x(t), ktorá sa riadi v²eobecným stochastickým procesom v tvare dx(t) = µ(x, t)dt + σ(x, t)dw (2.1) a za ína v bode x(0) = x 0. Najprv si ukáºeme, ako ur i pravdepodobnostné rozdelenie takejto premennej a potom nás bude zaujíma rozdelenie pre ve ký as t, tzv. limitné rozdelenie premennej x. Ozna me hustotu pravdepodobnostného rozdelenia procesu x(t) v ase t ako f = f(x, t x(0) = x 0 ). (2.2) Funkcia hustoty okrem asu t závisí aj od po iato nej hodnoty x 0. alej, ak ozna íme
26 2.1 Hustota rozdelenia stochastického procesu 17 kumulatívnu distribu nú funkciu ako F = F (x, t) = P (x(t) < x x(0) = x 0 ), (2.3) potom na jej výpo et môºeme pouºi vz ah f = F. Funkcia hustoty sp a tzv. Fokker- x Planckovu rovnicu 1 f t = x 2 (σ2 f) (µf) (2.4) x s po iato nou podmienkou f(x, 0) = δ(x x 0 ). Funkciou δ(x x 0 ) sme ozna ili tzv. Diracovu delta funkciu v bode x 0. Diracova funkcia predstavuje distribúciu, t. j. nie je to funkcia v pravom slova zmysle. Platí δ(x x 0 ) = { 0 ak x x 0 + ak x = x 0 a δ(x x 0 )dx = 1, o pre proces x(t) v ase t = 0 znamená, ºe sa takmer isto nachádza v bode x 0. Z matematického h adiska je Fokker-Planckova rovnica lineárnou parciálnou diferenciálnou rovnicou druhého rádu parabolického typu. Okrem vyuºitia na výpo et pravdepodobnostného rozdelenia náhodnej premennej sa pomocou nej môºe opisova napr. pozícia a rýchlos malej astice pohybujúcej sa Brownovým pohybom, prúd v elektrickom obvode alebo elektrické pole v laseri ([21]). Je známe (pozri [18]), ºe napr. rozdelenie rie²enia r(t) Va²í kovho stochastického procesu (1.8) v ase t pri ²tartovacej hodnote r 0 pochádza z normálneho rozdelenia s parametrami 2 E(r t ) = θ(1 e κt ) + r 0 e κt, D(r t ) = σ2 2κ (1 e 2κt ). Hustotu f(x, t) je moºné explicitne vyjadri len pre niektoré ²peciálne tvary stochastického procesu. Av²ak, ak predpokladáme, ºe proces trvá dostato ne dlho, t. j. t je dostato ne ve ké, môºeme hustotu rozdelenia f(x, t) aproximova pomocou tzv. limitného rozdelenia. Toto limitné rozdelenie existuje ak existuje lim t f(t, x) a limitné rozdelenie je funkciou hustoty. Uvaºujme teda prípad, ke t a limitné rozdelenie existuje. O akávame, ºe v takomto prípade uº rozdelenie nebude závisie od ²tartovacej hodnoty x 0 a ºe hustota f(x, t) sa stabilizuje na limitnej hustote f(x). Ke ºe potom f = f(x) a f = 0, limitná t 1 Intuitívny dôkaz moºno nájs v [27]. 2 Výpo et zaloºený na Fokker-Planckovej rovnici je napr. uvedený v [27].
27 2.1 Hustota rozdelenia stochastického procesu 18 hustota sp a tzv. stacionárnu Fokker-Planckovu rovnicu x 2 (σ2 f) x (µ f) = 0 (2.5) a podmienku na hustotu rozdelenia pravdepodobnosti f(x)dx = 1. Limitným rozdelením Va²í kovho modelu je normálne rozdelenie r lim N (θ, σ2 ). V al²ej asti sa zame- R 2κ riame na rozdelenie pravdepodobnosti náhodnej premennej, ktorá je rie²ením Besselovho odmocninového procesu, t. j. dx = κ(θ x)dt + σ xdw. (2.6) Limitné rozdelenie náhodnej premennej, ktorá je rie²ením procesu (2.6) budeme vo ve kej miere vyuºíva v kapitole 3 pri odvádzaní aproximovanej ceny dlhopisu vo Fong-Va²í kovom modeli. Fokker-Planckova rovnica pre uvedenený proces má tvar f t = σ2 2 2 x (xf) (κ(θ x)f). (2.7) 2 x Autori v lánku [8] uvádzajú, ºe pravdepodobnostné rozdelenie x je necentralizovaný chíkvadrát. Parametre tohto rozdelenia nebudeme z dôvodu zloºitosti uvádza. V na²ej práci budeme vyuºíva len limitné rozdelenie, teda rozdelenie pre t. Stacionárna Fokker- Planckova rovnica má potom tvar σ x (x f) 2 x (κ(θ x) f) = 0. (2.8) Za podmienky 2κθ σ 2 rozdelenie v tvare > 1 integráciou (2.8) dostávame, ºe náhodná premenná x(t) má limitné f(x) = { β α Γ(α) e βx x α 1 ak x > 0 0 ak x 0 kde α = 2κθ σ 2, β = 2κ σ 2 a Γ je gama funkcia. Takéto pravdepodobnostné rozdelenie zodpovedá gama rozdeleniu Γ(α, β). Uvedieme aj základné ²tatistiky rozdelenia, t. j. strednú hodnotu
28 2.2 Stochastická volatilita 19 a disperziu ([31]). E(x) = α β = θ (2.9) D(x) = α β 2 = θσ2 2κ (2.10) Na nasledujúcom obrázku je zobrazené limitné rozdelenie náhodnej premennej riadiacej sa pod a Besselovho odmocninového procesu Obr. 2.1: Limitné rozdelenie Besselovho odmocninového procesu s hodnotami parametrov κ = 1.482, θ = 2.640, σ = Parametre prebraté z [9]. 2.2 Stochastická volatilita V roku 1973 bol prvýkrát publikovaný známy Black-Scholesov model na oce ovanie derivátov akcií. Stal sa základným kame om tejto teórie a aj napriek mnoºstvu re²triktívnych predpokladov je dodnes uznávaný a asto pouºívaným modelom. Jedným z predpokladov tohto modelu je aj predpoklad o kon²tantnej volatilite. Uº samotní autori v roku 1972 v asopise Journal of Political Economy 3 napísali:...there is evidence of non-stacionarity in the variance. More work must be done to predict variances using the information available. Premenlivos volatility stochastického procesu pre vývoj cien akcií v ase potvrdzujú aj al²ie známe fakty, napríklad volatility smile. Aj volatilita úrokovej miery má charakter náhodného procesu a tento fakt je známy uº nieko ko desa ro í. Longsta a Schwartz v lánku [20] hovoria o existencii empirických dôkazov o náhodnom charaktere volatility úrokovej miery a poukazujú na jej dôleºitos pri ur ovaní cien derivátov. Je známych mnoho modelov, v ktorých volatilita vystupuje ako al²í stochastický faktor. Patria medzi ne 3 BLACK, F., SCHOLES, M.: The Valuation of Option Contracts and Test of Market Eciency, Journal of Political Economy, Vol.27, No.2. p.416
29 2.2 Stochastická volatilita 20 napríklad v²eobecný dvojfaktorový CIR model, ktorý sa dá do tvaru modelu stochastickej volatility prepísa (Longsta a Schwartz 1992, Due a Kan 1996), stochastický Va²í kov model, model odvodený Trollem a Schwartzom ([28]) alebo Brennerov model ([3]). Chen ako prvý v lánku [14] uviedol trojfaktorový model so stochastickou volatilitou. Vznik modelov úrokovej miery so stochastickou volatilitou je astokrát motivovaný aj tým, ºe pomocou nich je moºné vysvetli tvar výnosových kriviek a ich pohyb ([20]) Modelovanie stochastickej volatility Vlastnos clustering Proces volatility úrokovej miery nie je priamo pozorovate ný na trhu. Predstavu o jeho priebehu si môºeme napríklad urobi z odhadov získaných z pozorovate ných cien dlhopisov. Ukazuje sa, ºe charakteristickou rtou procesu volatility je tzv. volatility clustering 4, niekedy známou aj pod názvom volatility burstiness 5 ([12]). V sloven ine by sme túto vlastnos mohli vo ne preloºi ako zhlukovanie volatility. Na obr. 2.2 sú znázornené dva simulované priebehy procesu volatility. Na vrchnom obrázku je proces volatility na za iatku nad limitnou hodnotu, potom v²ak dlhodobo nadobúda nízke hodnoty. Takýto priebeh nie je ve mi typický, na rozdiel od priebehu na spodnom obrázku. Tu je pozorovate ná vlastnos volatility clustering. Volatilita uktuuje medzi nízkymi a vysokými hodnotami, pri om ostáva na nízkych, resp. na vysokých hodnotách len nieko ko dní, potom sa rýchlo zmení. Zdá sa, ºe hodnoty volatility sú nízke ur itú (krátku) periódu, potom rýchlo, v návale nadobudnú vysoké hodnoty, opä ostanú vysokými nieko ko dní a vrátia sa spä na nízke hodnoty. Táto vlastnos je úzko spätá s pojmom mean reversion, ktorý sme spomínali v kapitole 1. Pripome me, ºe drift v tvare µ(x, t) = κ(θ x) stochastického procesu hovorí, ºe stredná hodnota náhodnej premennej x je rýchlos ou κ pri ahovaná k limitnej hodnote θ. Hodnota parametra 1 potom intuitívne súvisí s pojmom holding period, to znamená, s dobou, po as κ ktorej ostáva volatilita na pribliºne rovnakých hodnotách. ƒím je táto perióda men²ia, tým astej²ie sa volatilita vracia k strednej hodnote ([12]). Spojitos medzi vlastnos ami volatility clustering a mean reversion nazna uje, ºe spomínaný tvar driftu by mohol by správnou vo bou pre modelovanie stochastickej volatility. Je e²te potrebné spomenú, ºe v modeli, ktorý popisuje volatilitu by mala by zaru ená nezápornos tejto premennej. Je intuitívne zrejmé, ºe záporné hodnoty volatility nedávajú zmysel. Vzh adom na spomenuté 4 z ang. cluster- zhluk, zoskupenie 5 z ang. burst- nával, výbuch, prepuknutie
30 2.3 Rýchla asová ²kála volatility 21 poºiadavky sa ako vhodný kandidát na popis stochastického charakteru volatility ukazuje Besselov odmocninový proces (2.6). 8 x x Obr. 2.2: Simulácie priebehu procesu volatility, ktorý sa riadi stochastickou diferenciálnou rovnicou (2.6). Hodnoty parametrov sú: θ = , σ = , T = 10 rokov a parameter κ = 0.5 pre vrchný obrázok a κ = 10 pre spodný obrázok. 2.3 Rýchla asová ²kála volatility Empirické ²túdie ukazujú (pozri [6]), ºe na nan ných trhoch sa procesy úroková miera a volatilita úrokovej miery pohybujú v odli²ných asových ²kálach, presnej²ie, asová ²kála volatility je rýchlej²ia. Uvedieme dva rôzne prístupy, ako pojem rýchlej asovej ²kály zakomponova do modelu popisujúceho proces volatility. Predpokladajme, ºe proces volatility je modelovaný pomocou Besselovho odmocninového procesu (2.6) a nech pojem asovej ²kály reprezentuje hodnota parametra ɛ. Prvý zo spôsobov ²kálovania je prebratý z [26]. Pri tomto type ²kálovania sa akokeby volatilita úrokovej miery nepohybovala v asovej ²kále t ale v ²kále tɛ, kde hodnota parametra ɛ je malá a platí 0 < ɛ 1. kálovaním stochastickej diferenciálnej rovnice (2.6) dostaneme dy = κ(θ y) dt + σ y dw. (2.11) ɛ ɛ
31 2.4 Fong-Va²í kov model so stochastickou volatilitou 22 Parameter σ je ²kálovaný hodnotou ɛ z toho dôvodu, ºe pre stochastický len dw platí dw = Φ dt, kde Φ N (0, 1). Rýchla asová ²kála je potom reprezentovaná malými hodnotami ɛ a limitou ɛ 0. Druhý spôsob je prebratý z lánku [12]. Rýchla asová ²kála volatility zodpovedá ve kej hodnote parametra κ. Ak zadenujeme ɛ := 1, potom je κ opä rýchla asová ²kála reprezentovaná malými hodnotami ɛ a pre²kálovaný model vyzerá nasledovne: dy = 1 ɛ (θ y)dt + σ y ɛ dw. (2.12) Koecient pri volatilite procesu y sa ur í tak, aby sa dosiahla kon²tantná hodnota disperzie limitného rozdelenia y, ktorej hodnota potom je D(y) = θσ2 2. (2.13) 2.4 Fong-Va²í kov model so stochastickou volatilitou Fong-Va²í kov model bol prvýkrát publikovaný v lánku Fixed - Income Volatility Management ([11]) v roku 1991 autormi Fongom a Va²í kom. Patrí medzi dvojfaktorové modely so stochastickou volatilitou a vznikol roz²írením Va²í kovho jednofaktorového modelu. Je zaloºený na pozorovaniach týkajúcich sa volatility krátkodobej úrokovej miery. Ako sme spomenuli v predchádzajúcej podkapitole 2.2, volatilita krátkodobej úrokovej miery nie je nutne kon²tantná, tak ako napr. predpokladá Va²í kov model (1.8). Fong-Va²í kov model teda zah a stochastickos volatility a opisuje okamºitú úrokovú mieru prostredníctvom systému dvoch stochastických rovníc dr(t) = κ 1 (θ 1 r(t))dt + y(t)dw 1, dy(t) = κ 2 (θ 2 y(t))dt + υ y(t)dw 2, (2.14) kde prírastky dw 1 a dw 2 Wienerových procesov moºu by korelované, t. j. E(dw 1 dw 2 ) = ρdt. Pre korela ný koecient ρ platí ρ ( 1, 1). Parametre modelu κ 1, κ 2, θ 1, θ 2 a υ sú kladné kon²tanty. Dynamiku short rate teda popisujú dva faktory - okamºitá úroková miera a volatilita okamºitej úrokovej miery, ktoré sú modelované mean reversion procesmi. Na nasledujúcom obrázku je znázornená simulácia dvojrozmerného náhodného procesu {r(t), y(t), t [0, T ]}, ktorý sa riadi Fong-Va²í kovým modelom (2.14).
32 2.4 Fong-Va²í kov model so stochastickou volatilitou r(t) 3.1 x y(t) Obr. 2.3: Simulácia rie²enia (r, y) systému stochastických rovníc (2.14) s hodnotami parametrov z tab. 2.1 a T=10. Vidíme, ºe ako krátkodobá úroková miera, tak aj volatilita sú pri ahované k limitným hodnotám θ 1 = , resp. θ 2 = Naviac vidíme, ºe volatilita je nezáporná. Krátkodobá úroková miera z teoretického h adiska môºe nadobúda aj záporné hodnoty, av²ak zo simulácií sa zdá, ºe pravdepodobnos nadobudnutia záporných hodnôt je ve mi nízka Ceny dlhopisov a výnosové krivky V kapitole 1 sme odvodili oce ovaciu parciálnu diferenciálnu rovnicu (1.23) pre v²eobecný dvojfaktorový model. Predpokladajme, ºe trhové ceny rizika majú tvar λ 1 y, resp. λ2 y, kde λ 1, λ 2 sú kon²tanty. Potom PDR pre Fong-Va²í kov model pre cenu dlhopisu P (τ, r, y) má nasledovný tvar: P τ + (κ 1(θ 1 r) λ 1 y) P r + (κ 2(θ 2 y) λ 2 υy) P y + + y 2 2 P r 2 + υ2 y 2 2 P y + ρυy 2 P rp = 0, (2.15) 2 r y pri om po iato ná podmienka ceny dlhopisu je P (0, r, y) = 1. Rie²enie rovnice (2.15) sa dá vyjadri v separovanom tvare (pozri [11]) P (τ, r, y) = A(τ)e B(τ)r C(τ)y, (2.16)
33 2.4 Fong-Va²í kov model so stochastickou volatilitou 24 pri om, aby bola splnená po iato ná podmienka P (0, r, y) = 1, pre funkcie A, B a C musí plati A(0) = 1, B(0) = 0 a C(0) = 0. Vy íslením jednotlivých parciálnych derivácií vystupujúcich v rovnici (2.15), následným spätným dosadením do (2.15) a zlú ením jednotlivých výrazov prislúchajúcich k r a y dostávame, ºe P (τ, r, y) je rie²ením (2.15) v tvare (2.16) práve vtedy ke funkcie A(τ), B(τ) a C(τ) sp ajú systém oby ajných diferenciálnych rovníc A = A(κ 1 θ 1 B + κ 2 θ 2 C), (2.17) B = κ 1 B + 1, (2.18) C = λ 1 B κ 2 C λ 2 υc B2 2 υ2 C 2 υρbc, (2.19) 2 s po iato nými podmienkami A(0) = 1, B(0) = 0, C(0) = 0. Pozrime sa bliº²ie na tento systém rovníc. Oby ajná diferenciálna rovnica (2.18) pre funkciu B(τ) je lineárna a preto jej rie²enie sp ajúce po iato nú podmienku B(0) = 0 moºno ahko analyticky vypo íta. Explicitný tvar rie²enia je B = 1 κ 1 (1 e κ 1τ ). (2.20) V²imnime si, ºe funkcia B má presne taký istý tvar ako (1.16), vystupujúca vo Va²í kovom modeli. Rovnica (2.19) pre funkciu C(τ) má uº zloºitej²í tvar, av²ak ak dosadíme explicitný tvar rie²enia (2.20), C = υ2 2 C2 (κ 2 + λ 2 υ + υρb)c λ 1 B B2, C(0) = 0 (2.21) 2 vieme ju numericky, napríklad pomocou implementovanej explicitnej Runge-Kutta metódy ²tvrtého a piateho rádu 6, vypo íta. Potom uº len dosadením do poslednej rovnice (2.17) a následnou integráciou dostávame aj rie²enie pre funkciu A(τ), τ ) A = exp ( θ 1 τ + θ 1 B κ 2 θ 2 C(s)ds. (2.22) 0 Na obr. 2.4 sú zobrazené priebehy funkcií A, B a C pre hodnoty parametrov z tab E²te predtým, ako sa budeme zaobera samotnými vlastnos ami funkcií A, B a C, spomenieme jeden zásadný predpoklad týkajúci sa parametrov Fong-Va²í kovho modelu. Stehlíková a ev ovi sa v lánku [25] okrem iného zaoberajú aj prípustnos ou ceny dlhopisu P (τ, r, y). Presnej²ie, aby sme funkciu (2.16) mohli chápa ako cenu dlhopisu, mala 6 V Matlabe je to funkcia ode45.
34 2.4 Fong-Va²í kov model so stochastickou volatilitou 25 1 Funkcia A 7 Funkcia B 40 Funkcia C Maturita Maturita Maturita Obr. 2.4: Priebehy funkcií A, B a C pre hodnoty parametrov z tab. 2.1, λ 1 = 12, λ 2 = 5, τ (0, 10]. by sp a isté vlastnosti. Sú to: 1. 0 < P (τ, r, y) < 1 pre τ (0, T ], 2. funkcia r P (τ, r, y) je klesajúca, 3. funkcia y P (τ, r, y) je klesajúca. Prvá z vlastností hovorí o tom, ºe cena dlhopisu by mala by kladná a nemala by presiahnu svoju nominálnu hodnotu 7. V druhej vlastnosti poºadujeme, aby pri vy²²ích krátkodobých úrokových mierach bola hodnota dlhopisu niº²ia a pri poslednej, aby so zvä ²ujúcou sa volatilitou krátkodobej úrokovej miery klesala cena dlhopisu. V²etky tieto tri vlastnosti sú prirodzené a intuitívne a teda je rozumné, aby ich cena dlhopisu sp ala. V lánku [25] autori ukázali, ºe ak parametre modelu sp ajú nerovnos λ 1 1 2κ 1, (2.23) potom cena dlhopisu P (τ, r, y) sp a vlastnosti 1-3. Preto budeme v al²ej asti práce predpoklada, ºe parametre modelu sp ajú (2.23). V krátkosti spomenieme nieko ko vlastností funkcií A, B a C, ktoré sú podmienené ²trukturálnym predpokladom o parametroch modelu (2.23) a ktoré sa vyuºívajú pri odvodení vlastností cien dlhopisov a výnosových kriviek. 7 V na²om prípade sme uvaºovali diskontný dlhopis, touto hodnotou je teda 1.
35 2.4 Fong-Va²í kov model so stochastickou volatilitou 26 Veta 1. ([23], Veta 19.) Za predpokladu (2.23) funkcie A, B, a C majú nasledovné vlastnosti: 1. C (0) = 0, C (0) = λ 1, 2. τ > 0 : 0 < A(τ) < 1, B(τ) > 0, C(τ) > 0. Ukáºeme, ºe z podmienok uvedených vo Vete 1 vyplývajú vlastnosti 1-3. Pripome me, ºe cena dlhopisu je v tvare (2.16). Pretoºe pre funkciu A(τ) platí A(τ) (0, 1), τ > 0 dostávame P (τ, r, y) (0, 1) pre τ (0, T ]. Ak zderivujeme cenu dlhopisu P (τ, r, y) postupne pod a premenných r a y a vyuºijeme P (τ, r, y) (0, 1) a B(τ) > 0, C(τ) > 0, τ > 0 dostávame P r P y = B(τ)P (τ, r, y) < 0, = C(τ)P (τ, r, y) < 0. Záporné hodnoty derivácií dokazujú vlastnosti 2 a 3. Pozrime sa, aký tvar môºe nadobúda krivka asovej ²truktúry úrokových mier pri pouºití Fong-Va²í kovho modelu. Pouºijúc separovaný tvar rie²enia ceny dlhopisu (2.16) a vzorec (1.2) na výpo et úrokovej miery R(τ, r, y) dostávame R(τ, r, y) = 1 τ ln A(τ) + 1 τ B(τ)r + 1 C(τ)y. (2.24) τ Obrázok 2.5 zobrazuje krivky asovej ²truktúry úrokových mier. Výnos Maturita Výnos Maturita Obr. 2.5: Krivky asovej ²truktúry úrokových mier. Hodnoty parametrov modelu sú z tab. 2.1, λ 1 = 12, λ 2 = 5, τ (0, 30]. V avo: r = , y [0.0001, ]. Vpravo: y = , r [0.05, 0.10].
36 2.4 Fong-Va²í kov model so stochastickou volatilitou 27 Na obrázku v avo sú vykreslené výnosové krivky pre xnú hodnotu úrokovej miery r = a meniace sa hodnoty volatility. Vpravo je naopak zaxovaná hodnota volatility úrokovej miery na y = , zatia o úroková miera sa mení. Na záver si ukáºeme e²te jeden dôvod, pre o je ²trukturálna podmienka (2.23) dôleºitá. Predpokladajme na teraz, ºe parametre modelu nesp ajú predpoklad (2.23), konkrétne uvaºujme λ 1 > 0. Pod a prvej podmienky vo Vete 1 potom platí C (0) = λ 1 < 0, C (0) = 0 a naviac C(0) = 0. Preto pre nejaký malý as do expirácie τ > 0 nadobúda funkcia C záporné hodnoty, o má za následok fakt, ºe úrokové miery môºu by pre vysoké hodnoty volatility záporné. Túto situáciu ilustruje obr. 2.6, kde sme pre trhovú cenu rizika λ 1 zvolili hodnotu 15 a pre volatilitu hodnoty z intervalu [0.006, ]. Vidíme, ºe funkcia C je na celom intervale záporná a hodnoty úrokových mier nadobúdajú aj záporné hodnoty, o nie je v súlade s realitou. 0 Funkcia C 0.07 Výnosové krivky Výnos Maturita Maturita Obr. 2.6: Funkcia C a výnosové krivky pri poru²ení predpokladu (2.23). Hodnoty parametrov modelu sú z tab. 2.1, λ 1 = 15, λ 2 = 5, τ (0, 30] Limita výnosových kriviek Vrá me sa naspä k obr. 2.5, ktorý zobrazuje výnosové krivky. Pri poh ade na nás môºe napadnú otázka, i existuje limita výnosových kriviek pre τ a v prípade ak existuje, aká je jej hodnota. Touto otázkou sa teraz budeme zaobera. Hodnoty krivky asovej ²truktúry úrokových mier sa vypo ítajú pomocou vzorca (2.24), v ktorom vystupujú funkcie A, B a C. Pod a Vety 1 je funkcia A ohrani ená a z explicitného tvaru (2.20) funkcie B dostávame lim B(τ) = 1. (2.25) τ κ 1
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. modelu úrokových mier
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová UNIVERZITA
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky
 fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
Averaged bond prices for Fong-Vasicek and the generalized Vasicek interest rates models
 MATHEMATICAL OPTIMIZATION Mathematical Methods In Economics And Industry 007 June 3 7, 007, Herl any, Slovak Republic Averaged bond prices for Fong-Vasicek and the generalized Vasicek interest rates models
MATHEMATICAL OPTIMIZATION Mathematical Methods In Economics And Industry 007 June 3 7, 007, Herl any, Slovak Republic Averaged bond prices for Fong-Vasicek and the generalized Vasicek interest rates models
A THREE-FACTOR CONVERGENCE MODEL OF INTEREST RATES
 Proceedings of ALGORITMY 01 pp. 95 104 A THREE-FACTOR CONVERGENCE MODEL OF INTEREST RATES BEÁTA STEHLÍKOVÁ AND ZUZANA ZÍKOVÁ Abstract. A convergence model of interest rates explains the evolution of the
Proceedings of ALGORITMY 01 pp. 95 104 A THREE-FACTOR CONVERGENCE MODEL OF INTEREST RATES BEÁTA STEHLÍKOVÁ AND ZUZANA ZÍKOVÁ Abstract. A convergence model of interest rates explains the evolution of the
Konvergen né modely úrokových mier
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Konvergen né moely úrokových mier Diplomová práca Veúci iplomovej práce: RNDr. Beáta Stehlíková, PhD. Autor: Bc. Zuzana Zíková
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Konvergen né moely úrokových mier Diplomová práca Veúci iplomovej práce: RNDr. Beáta Stehlíková, PhD. Autor: Bc. Zuzana Zíková
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA
ON NON-EXISTENCE OF A ONE FACTOR INTEREST RATE MODEL FOR VOLATILITY AVERAGED GENERALIZED FONG VASICEK TERM STRUCTURES
 Proceedings of the Czech Japanese Seminar in Applied Mathematics 6 Czech Technical University in Prague, September 14-17, 6 pp. 1 8 ON NON-EXISTENCE OF A ONE FACTOR INTEREST RATE MODEL FOR VOLATILITY AVERAGED
Proceedings of the Czech Japanese Seminar in Applied Mathematics 6 Czech Technical University in Prague, September 14-17, 6 pp. 1 8 ON NON-EXISTENCE OF A ONE FACTOR INTEREST RATE MODEL FOR VOLATILITY AVERAGED
Pouºitie metódy Monte Carlo vo nanciách
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ UNIVERZITA KOMENSKÉHO V
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ UNIVERZITA KOMENSKÉHO V
CROSS SECTIONAL FORECASTS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
Analytické aproximácie pri modelovaní cien opcií
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Odhady parametrov modelov
 Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií
 UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CALIBRATION OF A MODEL FOR OPTION PRICES WITH FEEDBACK EFFECT
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CALIBRATION OF A MODEL FOR OPTION PRICES WITH FEEDBACK EFFECT DIPLOMA THESIS 017 Zuzana FRONCOVÁ COMENIUS UNIVERSITY IN
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CALIBRATION OF A MODEL FOR OPTION PRICES WITH FEEDBACK EFFECT DIPLOMA THESIS 017 Zuzana FRONCOVÁ COMENIUS UNIVERSITY IN
Modelovanie nan ných trhov a risku metódou Monte Carlo
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Modelovanie nan ných trhov a risku metódou Monte Carlo 211 Luká² Kunert UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Modelovanie nan ných trhov a risku metódou Monte Carlo 211 Luká² Kunert UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
Multi-dimensional Term Structure Models
 Multi-dimensional Term Structure Models We will focus on the affine class. But first some motivation. A generic one-dimensional model for zero-coupon yields, y(t; τ), looks like this dy(t; τ) =... dt +
Multi-dimensional Term Structure Models We will focus on the affine class. But first some motivation. A generic one-dimensional model for zero-coupon yields, y(t; τ), looks like this dy(t; τ) =... dt +
COMENIUS UNIVERSITY IN BRATISLAVA Faculty of Mathematics, Physics and Informatics Department of Applied Mathematics and Statistics
 COMENIUS UNIVERSITY IN BRATISLAVA Faculty of Mathematics, Physics and Informatics Department of Applied Mathematics and Statistics TWO-FACTOR CONVERGENCE MODEL OF COX-INGERSOLL-ROSS TYPE Master s Thesis
COMENIUS UNIVERSITY IN BRATISLAVA Faculty of Mathematics, Physics and Informatics Department of Applied Mathematics and Statistics TWO-FACTOR CONVERGENCE MODEL OF COX-INGERSOLL-ROSS TYPE Master s Thesis
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
dt+ ρσ 2 1 ρ2 σ 2 κ i and that A is a rather lengthy expression that we may or may not need. (Brigo & Mercurio Lemma Thm , p. 135.
 A 2D Gaussian model (akin to Brigo & Mercurio Section 4.2) Suppose where ( κ1 0 dx(t) = 0 κ 2 r(t) = δ 0 +X 1 (t)+x 2 (t) )( X1 (t) X 2 (t) ) ( σ1 0 dt+ ρσ 2 1 ρ2 σ 2 )( dw Q 1 (t) dw Q 2 (t) ) In this
A 2D Gaussian model (akin to Brigo & Mercurio Section 4.2) Suppose where ( κ1 0 dx(t) = 0 κ 2 r(t) = δ 0 +X 1 (t)+x 2 (t) )( X1 (t) X 2 (t) ) ( σ1 0 dt+ ρσ 2 1 ρ2 σ 2 )( dw Q 1 (t) dw Q 2 (t) ) In this
dt + ρσ 2 1 ρ2 σ 2 B i (τ) = 1 e κ iτ κ i
 A 2D Gaussian model (akin to Brigo & Mercurio Section 4.2) Suppose where dx(t) = ( κ1 0 0 κ 2 ) ( X1 (t) X 2 (t) In this case we find (BLACKBOARD) that r(t) = δ 0 + X 1 (t) + X 2 (t) ) ( σ1 0 dt + ρσ 2
A 2D Gaussian model (akin to Brigo & Mercurio Section 4.2) Suppose where dx(t) = ( κ1 0 0 κ 2 ) ( X1 (t) X 2 (t) In this case we find (BLACKBOARD) that r(t) = δ 0 + X 1 (t) + X 2 (t) ) ( σ1 0 dt + ρσ 2
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio
 Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
Investigation of Dependency between Short Rate and Transition Rate on Pension Buy-outs. Arık, A. 1 Yolcu-Okur, Y. 2 Uğur Ö. 2
 Investigation of Dependency between Short Rate and Transition Rate on Pension Buy-outs Arık, A. 1 Yolcu-Okur, Y. 2 Uğur Ö. 2 1 Hacettepe University Department of Actuarial Sciences 06800, TURKEY 2 Middle
Investigation of Dependency between Short Rate and Transition Rate on Pension Buy-outs Arık, A. 1 Yolcu-Okur, Y. 2 Uğur Ö. 2 1 Hacettepe University Department of Actuarial Sciences 06800, TURKEY 2 Middle
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
Counterparty Credit Risk Simulation
 Counterparty Credit Risk Simulation Alex Yang FinPricing http://www.finpricing.com Summary Counterparty Credit Risk Definition Counterparty Credit Risk Measures Monte Carlo Simulation Interest Rate Curve
Counterparty Credit Risk Simulation Alex Yang FinPricing http://www.finpricing.com Summary Counterparty Credit Risk Definition Counterparty Credit Risk Measures Monte Carlo Simulation Interest Rate Curve
Interest Rate Course Lecture 9. June
 Interest Rate Course Lecture 9 June 28 2010 Last days Want to find stochastic models consistent with observed i) yield curves and ii) dynamics of yield curve One factor models Two factor models Other approaches
Interest Rate Course Lecture 9 June 28 2010 Last days Want to find stochastic models consistent with observed i) yield curves and ii) dynamics of yield curve One factor models Two factor models Other approaches
25. Interest rates models. MA6622, Ernesto Mordecki, CityU, HK, References for this Lecture:
 25. Interest rates models MA6622, Ernesto Mordecki, CityU, HK, 2006. References for this Lecture: John C. Hull, Options, Futures & other Derivatives (Fourth Edition), Prentice Hall (2000) 1 Plan of Lecture
25. Interest rates models MA6622, Ernesto Mordecki, CityU, HK, 2006. References for this Lecture: John C. Hull, Options, Futures & other Derivatives (Fourth Edition), Prentice Hall (2000) 1 Plan of Lecture
Financial Accelerator and Interest Rate in Selected Countries
 COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing
 Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing We shall go over this note quickly due to time constraints. Key concept: Ito s lemma Stock Options: A contract giving
Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing We shall go over this note quickly due to time constraints. Key concept: Ito s lemma Stock Options: A contract giving
UNIVERZITA KOMENSKÉHO V BRATISLAVE. Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ Veronika Kleinová
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky
Pokročilé metody kalibrace modelů
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Pokročilé metody kalibrace modelů úrokových sazeb Dominika Holotňáková Katedra pravděpodobnosti a matematické statistiky Vedoucí
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Pokročilé metody kalibrace modelů úrokových sazeb Dominika Holotňáková Katedra pravděpodobnosti a matematické statistiky Vedoucí
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks
 Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
Pricing Barrier Options under Local Volatility
 Abstract Pricing Barrier Options under Local Volatility Artur Sepp Mail: artursepp@hotmail.com, Web: www.hot.ee/seppar 16 November 2002 We study pricing under the local volatility. Our research is mainly
Abstract Pricing Barrier Options under Local Volatility Artur Sepp Mail: artursepp@hotmail.com, Web: www.hot.ee/seppar 16 November 2002 We study pricing under the local volatility. Our research is mainly
APPROXIMATE FORMULAE FOR PRICING ZERO-COUPON BONDS AND THEIR ASYMPTOTIC ANALYSIS
 INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING Volume 1, Number 1, Pages 1 1 c 28 Institute for Scientific Computing and Information APPROXIMATE FORMULAE FOR PRICING ZERO-COUPON BONDS AND THEIR
INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING Volume 1, Number 1, Pages 1 1 c 28 Institute for Scientific Computing and Information APPROXIMATE FORMULAE FOR PRICING ZERO-COUPON BONDS AND THEIR
Lecture 18. More on option pricing. Lecture 18 1 / 21
 Lecture 18 More on option pricing Lecture 18 1 / 21 Introduction In this lecture we will see more applications of option pricing theory. Lecture 18 2 / 21 Greeks (1) The price f of a derivative depends
Lecture 18 More on option pricing Lecture 18 1 / 21 Introduction In this lecture we will see more applications of option pricing theory. Lecture 18 2 / 21 Greeks (1) The price f of a derivative depends
BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS
 BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS PRICING EMMS014S7 Tuesday, May 31 2011, 10:00am-13.15pm
BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS PRICING EMMS014S7 Tuesday, May 31 2011, 10:00am-13.15pm
Analytical and Numerical Approximative Methods for solving Multifactor Models for pricing of Financial Derivatives
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS DEPARTMENT OF APPLIED MATHEMATICS AND STATISTICS UNIVERSITY OF WUPPERTAL FACULTY OF MATHEMATICS AND NATURAL SCIENCES DEPARTMENT
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS DEPARTMENT OF APPLIED MATHEMATICS AND STATISTICS UNIVERSITY OF WUPPERTAL FACULTY OF MATHEMATICS AND NATURAL SCIENCES DEPARTMENT
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Zaistené stratégie. Bc. Tomáš Miklošovič.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
Credit Burden of Households in Slovakia
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Credit Burden of Households in Slovakia Diploma Thesis Adam Biro² Bratislava 2011 525ee80a-3c15-4902-b736-9cfdd96015d6
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Credit Burden of Households in Slovakia Diploma Thesis Adam Biro² Bratislava 2011 525ee80a-3c15-4902-b736-9cfdd96015d6
Calibration of Interest Rates
 WDS'12 Proceedings of Contributed Papers, Part I, 25 30, 2012. ISBN 978-80-7378-224-5 MATFYZPRESS Calibration of Interest Rates J. Černý Charles University, Faculty of Mathematics and Physics, Prague,
WDS'12 Proceedings of Contributed Papers, Part I, 25 30, 2012. ISBN 978-80-7378-224-5 MATFYZPRESS Calibration of Interest Rates J. Černý Charles University, Faculty of Mathematics and Physics, Prague,
7 pages 1. Premia 14
 7 pages 1 Premia 14 Calibration of Stochastic Volatility model with Jumps A. Ben Haj Yedder March 1, 1 The evolution process of the Heston model, for the stochastic volatility, and Merton model, for the
7 pages 1 Premia 14 Calibration of Stochastic Volatility model with Jumps A. Ben Haj Yedder March 1, 1 The evolution process of the Heston model, for the stochastic volatility, and Merton model, for the
M5MF6. Advanced Methods in Derivatives Pricing
 Course: Setter: M5MF6 Dr Antoine Jacquier MSc EXAMINATIONS IN MATHEMATICS AND FINANCE DEPARTMENT OF MATHEMATICS April 2016 M5MF6 Advanced Methods in Derivatives Pricing Setter s signature...........................................
Course: Setter: M5MF6 Dr Antoine Jacquier MSc EXAMINATIONS IN MATHEMATICS AND FINANCE DEPARTMENT OF MATHEMATICS April 2016 M5MF6 Advanced Methods in Derivatives Pricing Setter s signature...........................................
Credit Risk : Firm Value Model
 Credit Risk : Firm Value Model Prof. Dr. Svetlozar Rachev Institute for Statistics and Mathematical Economics University of Karlsruhe and Karlsruhe Institute of Technology (KIT) Prof. Dr. Svetlozar Rachev
Credit Risk : Firm Value Model Prof. Dr. Svetlozar Rachev Institute for Statistics and Mathematical Economics University of Karlsruhe and Karlsruhe Institute of Technology (KIT) Prof. Dr. Svetlozar Rachev
Globálne optimálne gama zaisťovanie s transakčnými nákladmi
 Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
(1) Consider a European call option and a European put option on a nondividend-paying stock. You are given:
 (1) Consider a European call option and a European put option on a nondividend-paying stock. You are given: (i) The current price of the stock is $60. (ii) The call option currently sells for $0.15 more
(1) Consider a European call option and a European put option on a nondividend-paying stock. You are given: (i) The current price of the stock is $60. (ii) The call option currently sells for $0.15 more
A Simple Model of Credit Spreads with Incomplete Information
 A Simple Model of Credit Spreads with Incomplete Information Chuang Yi McMaster University April, 2007 Joint work with Alexander Tchernitser from Bank of Montreal (BMO). The opinions expressed here are
A Simple Model of Credit Spreads with Incomplete Information Chuang Yi McMaster University April, 2007 Joint work with Alexander Tchernitser from Bank of Montreal (BMO). The opinions expressed here are
The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations
 The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations Stan Stilger June 6, 1 Fouque and Tullie use importance sampling for variance reduction in stochastic volatility simulations.
The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations Stan Stilger June 6, 1 Fouque and Tullie use importance sampling for variance reduction in stochastic volatility simulations.
Monte Carlo Simulations
 Monte Carlo Simulations Lecture 1 December 7, 2014 Outline Monte Carlo Methods Monte Carlo methods simulate the random behavior underlying the financial models Remember: When pricing you must simulate
Monte Carlo Simulations Lecture 1 December 7, 2014 Outline Monte Carlo Methods Monte Carlo methods simulate the random behavior underlying the financial models Remember: When pricing you must simulate
ON THE FOUR-PARAMETER BOND PRICING MODEL. Man M. Chawla X-027, Regency Park II, DLF City Phase IV Gurgaon , Haryana, INDIA
 International Journal of Applied Mathematics Volume 29 No. 1 216, 53-68 ISSN: 1311-1728 printed version); ISSN: 1314-86 on-line version) doi: http://dx.doi.org/1.12732/ijam.v29i1.5 ON THE FOUR-PARAMETER
International Journal of Applied Mathematics Volume 29 No. 1 216, 53-68 ISSN: 1311-1728 printed version); ISSN: 1314-86 on-line version) doi: http://dx.doi.org/1.12732/ijam.v29i1.5 ON THE FOUR-PARAMETER
Calibration of Different Interest Rate Models for a Good Fit of Yield Curves
 Delft University of Technology Faculty of Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics Calibration of Different Interest Rate Models for a Good Fit of
Delft University of Technology Faculty of Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics Calibration of Different Interest Rate Models for a Good Fit of
Introduction to Affine Processes. Applications to Mathematical Finance
 and Its Applications to Mathematical Finance Department of Mathematical Science, KAIST Workshop for Young Mathematicians in Korea, 2010 Outline Motivation 1 Motivation 2 Preliminary : Stochastic Calculus
and Its Applications to Mathematical Finance Department of Mathematical Science, KAIST Workshop for Young Mathematicians in Korea, 2010 Outline Motivation 1 Motivation 2 Preliminary : Stochastic Calculus
Advanced topics in continuous time finance
 Based on readings of Prof. Kerry E. Back on the IAS in Vienna, October 21. Advanced topics in continuous time finance Mag. Martin Vonwald (martin@voni.at) November 21 Contents 1 Introduction 4 1.1 Martingale.....................................
Based on readings of Prof. Kerry E. Back on the IAS in Vienna, October 21. Advanced topics in continuous time finance Mag. Martin Vonwald (martin@voni.at) November 21 Contents 1 Introduction 4 1.1 Martingale.....................................
Term Structure Models Workshop at AFIR-ERM Colloquium, Panama, 2017
 Term Structure Models Workshop at AFIR-ERM Colloquium, Panama, 2017 Michael Sherris CEPAR and School of Risk and Actuarial Studies UNSW Business School UNSW Sydney m.sherris@unsw.edu.au UNSW August 2017
Term Structure Models Workshop at AFIR-ERM Colloquium, Panama, 2017 Michael Sherris CEPAR and School of Risk and Actuarial Studies UNSW Business School UNSW Sydney m.sherris@unsw.edu.au UNSW August 2017
arxiv: v1 [q-fin.pr] 23 Feb 2014
![arxiv: v1 [q-fin.pr] 23 Feb 2014 arxiv: v1 [q-fin.pr] 23 Feb 2014](/thumbs/87/95850189.jpg) Time-dependent Heston model. G. S. Vasilev, Department of Physics, Sofia University, James Bourchier 5 blvd, 64 Sofia, Bulgaria CloudRisk Ltd (Dated: February 5, 04) This work presents an exact solution
Time-dependent Heston model. G. S. Vasilev, Department of Physics, Sofia University, James Bourchier 5 blvd, 64 Sofia, Bulgaria CloudRisk Ltd (Dated: February 5, 04) This work presents an exact solution
Univerzita Karlova v Praze Matematicko fyzikální fakulta
 Univerzita Karlova v Praze Matematicko fyzikální fakulta DIPLOMOVÁ PRÁCE Jana Garajová Modely úrokových měr ve spojitém čase Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Prof.
Univerzita Karlova v Praze Matematicko fyzikální fakulta DIPLOMOVÁ PRÁCE Jana Garajová Modely úrokových měr ve spojitém čase Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Prof.
Introduction to Financial Mathematics
 Department of Mathematics University of Michigan November 7, 2008 My Information E-mail address: marymorj (at) umich.edu Financial work experience includes 2 years in public finance investment banking
Department of Mathematics University of Michigan November 7, 2008 My Information E-mail address: marymorj (at) umich.edu Financial work experience includes 2 years in public finance investment banking
Dynamic Model of Pension Savings Management with Stochastic Interest Rates and Stock Returns
 Dynamic Model of Pension Savings Management with Stochastic Interest Rates and Stock Returns Igor Melicherčík and Daniel Ševčovič Abstract In this paper we recall and summarize results on a dynamic stochastic
Dynamic Model of Pension Savings Management with Stochastic Interest Rates and Stock Returns Igor Melicherčík and Daniel Ševčovič Abstract In this paper we recall and summarize results on a dynamic stochastic
Convexity Theory for the Term Structure Equation
 Convexity Theory for the Term Structure Equation Erik Ekström Joint work with Johan Tysk Department of Mathematics, Uppsala University October 15, 2007, Paris Convexity Theory for the Black-Scholes Equation
Convexity Theory for the Term Structure Equation Erik Ekström Joint work with Johan Tysk Department of Mathematics, Uppsala University October 15, 2007, Paris Convexity Theory for the Black-Scholes Equation
MLEMVD: A R Package for Maximum Likelihood Estimation of Multivariate Diffusion Models
 MLEMVD: A R Package for Maximum Likelihood Estimation of Multivariate Diffusion Models Matthew Dixon and Tao Wu 1 Illinois Institute of Technology May 19th 2017 1 https://papers.ssrn.com/sol3/papers.cfm?abstract
MLEMVD: A R Package for Maximum Likelihood Estimation of Multivariate Diffusion Models Matthew Dixon and Tao Wu 1 Illinois Institute of Technology May 19th 2017 1 https://papers.ssrn.com/sol3/papers.cfm?abstract
( ) since this is the benefit of buying the asset at the strike price rather
 Review of some financial models for MAT 483 Parity and Other Option Relationships The basic parity relationship for European options with the same strike price and the same time to expiration is: C( KT
Review of some financial models for MAT 483 Parity and Other Option Relationships The basic parity relationship for European options with the same strike price and the same time to expiration is: C( KT
Modern Dynamic Asset Pricing Models
 Modern Dynamic Asset Pricing Models Lecture Notes 7. Term Structure Models Pietro Veronesi University of Chicago Booth School of Business CEPR, NBER Pietro Veronesi Term Structure Models page: 2 Outline
Modern Dynamic Asset Pricing Models Lecture Notes 7. Term Structure Models Pietro Veronesi University of Chicago Booth School of Business CEPR, NBER Pietro Veronesi Term Structure Models page: 2 Outline
Multiscale Stochastic Volatility Models Heston 1.5
 Multiscale Stochastic Volatility Models Heston 1.5 Jean-Pierre Fouque Department of Statistics & Applied Probability University of California Santa Barbara Modeling and Managing Financial Risks Paris,
Multiscale Stochastic Volatility Models Heston 1.5 Jean-Pierre Fouque Department of Statistics & Applied Probability University of California Santa Barbara Modeling and Managing Financial Risks Paris,
Stochastic Volatility Modeling
 Stochastic Volatility Modeling Jean-Pierre Fouque University of California Santa Barbara 28 Daiwa Lecture Series July 29 - August 1, 28 Kyoto University, Kyoto 1 References: Derivatives in Financial Markets
Stochastic Volatility Modeling Jean-Pierre Fouque University of California Santa Barbara 28 Daiwa Lecture Series July 29 - August 1, 28 Kyoto University, Kyoto 1 References: Derivatives in Financial Markets
Volatility Time Scales and. Perturbations
 Volatility Time Scales and Perturbations Jean-Pierre Fouque NC State University, soon UC Santa Barbara Collaborators: George Papanicolaou Stanford University Ronnie Sircar Princeton University Knut Solna
Volatility Time Scales and Perturbations Jean-Pierre Fouque NC State University, soon UC Santa Barbara Collaborators: George Papanicolaou Stanford University Ronnie Sircar Princeton University Knut Solna
Lecture 5: Review of interest rate models
 Lecture 5: Review of interest rate models Xiaoguang Wang STAT 598W January 30th, 2014 (STAT 598W) Lecture 5 1 / 46 Outline 1 Bonds and Interest Rates 2 Short Rate Models 3 Forward Rate Models 4 LIBOR and
Lecture 5: Review of interest rate models Xiaoguang Wang STAT 598W January 30th, 2014 (STAT 598W) Lecture 5 1 / 46 Outline 1 Bonds and Interest Rates 2 Short Rate Models 3 Forward Rate Models 4 LIBOR and
The Lognormal Interest Rate Model and Eurodollar Futures
 GLOBAL RESEARCH ANALYTICS The Lognormal Interest Rate Model and Eurodollar Futures CITICORP SECURITIES,INC. 399 Park Avenue New York, NY 143 Keith Weintraub Director, Analytics 1-559-97 Michael Hogan Ex
GLOBAL RESEARCH ANALYTICS The Lognormal Interest Rate Model and Eurodollar Futures CITICORP SECURITIES,INC. 399 Park Avenue New York, NY 143 Keith Weintraub Director, Analytics 1-559-97 Michael Hogan Ex
Interest rate models in continuous time
 slides for the course Interest rate theory, University of Ljubljana, 2012-13/I, part IV József Gáll University of Debrecen Nov. 2012 Jan. 2013, Ljubljana Continuous time markets General assumptions, notations
slides for the course Interest rate theory, University of Ljubljana, 2012-13/I, part IV József Gáll University of Debrecen Nov. 2012 Jan. 2013, Ljubljana Continuous time markets General assumptions, notations
Pricing Pension Buy-ins and Buy-outs 1
 Pricing Pension Buy-ins and Buy-outs 1 Tianxiang Shi Department of Finance College of Business Administration University of Nebraska-Lincoln Longevity 10, Santiago, Chile September 3-4, 2014 1 Joint work
Pricing Pension Buy-ins and Buy-outs 1 Tianxiang Shi Department of Finance College of Business Administration University of Nebraska-Lincoln Longevity 10, Santiago, Chile September 3-4, 2014 1 Joint work
LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives
 Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Attachment No. 1 Employees authorized for communication
 On behalf of Market Operator: Attachment No. 1 Employees authorized for communication Employees authorized for invoicing and payments: Head of billing Dana Vinická +421 917 931 470 dana.vinicka@okte.sk
On behalf of Market Operator: Attachment No. 1 Employees authorized for communication Employees authorized for invoicing and payments: Head of billing Dana Vinická +421 917 931 470 dana.vinicka@okte.sk
WITH SKETCH ANSWERS. Postgraduate Certificate in Finance Postgraduate Certificate in Economics and Finance
 WITH SKETCH ANSWERS BIRKBECK COLLEGE (University of London) BIRKBECK COLLEGE (University of London) Postgraduate Certificate in Finance Postgraduate Certificate in Economics and Finance SCHOOL OF ECONOMICS,
WITH SKETCH ANSWERS BIRKBECK COLLEGE (University of London) BIRKBECK COLLEGE (University of London) Postgraduate Certificate in Finance Postgraduate Certificate in Economics and Finance SCHOOL OF ECONOMICS,
COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS The risk sensitive dynamic accumulation model and optimal pension saving management DISSERTATION THESIS 2014 Mgr. Zuzana
COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS The risk sensitive dynamic accumulation model and optimal pension saving management DISSERTATION THESIS 2014 Mgr. Zuzana
An Analytical Approximation for Pricing VWAP Options
 .... An Analytical Approximation for Pricing VWAP Options Hideharu Funahashi and Masaaki Kijima Graduate School of Social Sciences, Tokyo Metropolitan University September 4, 215 Kijima (TMU Pricing of
.... An Analytical Approximation for Pricing VWAP Options Hideharu Funahashi and Masaaki Kijima Graduate School of Social Sciences, Tokyo Metropolitan University September 4, 215 Kijima (TMU Pricing of
Multiscale Stochastic Volatility Models
 Multiscale Stochastic Volatility Models Jean-Pierre Fouque University of California Santa Barbara 6th World Congress of the Bachelier Finance Society Toronto, June 25, 2010 Multiscale Stochastic Volatility
Multiscale Stochastic Volatility Models Jean-Pierre Fouque University of California Santa Barbara 6th World Congress of the Bachelier Finance Society Toronto, June 25, 2010 Multiscale Stochastic Volatility
VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY
 VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY THE DEVELOPMENT OF THE AMOUNT OF LOANS GRANTED AND THEIR APPROPRIATE
VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY THE DEVELOPMENT OF THE AMOUNT OF LOANS GRANTED AND THEIR APPROPRIATE
Fixed-Income Options
 Fixed-Income Options Consider a two-year 99 European call on the three-year, 5% Treasury. Assume the Treasury pays annual interest. From p. 852 the three-year Treasury s price minus the $5 interest could
Fixed-Income Options Consider a two-year 99 European call on the three-year, 5% Treasury. Assume the Treasury pays annual interest. From p. 852 the three-year Treasury s price minus the $5 interest could
UNIVERSITY OF CALGARY. Theoretical and Computational Analysis and Comparison of Stochastic Models of Energy. and Interest Rate Markets
 UNIVERSITY OF CALGARY Theoretical and Computational Analysis and Comparison of Stochastic Models of Energy and Interest Rate Markets by Tatiana Bukharina A THESIS SUBMITTED TO THE FACULTY OF GRADUATE STUDIES
UNIVERSITY OF CALGARY Theoretical and Computational Analysis and Comparison of Stochastic Models of Energy and Interest Rate Markets by Tatiana Bukharina A THESIS SUBMITTED TO THE FACULTY OF GRADUATE STUDIES
Interest rate models in Solvency II
 Interest rate models in Solvency II Master Thesis in Statistics Kristine Sivertsen Department of Mathematics University of Bergen November 2016 Abstract The best estimate of liabilities is important in
Interest rate models in Solvency II Master Thesis in Statistics Kristine Sivertsen Department of Mathematics University of Bergen November 2016 Abstract The best estimate of liabilities is important in
Quadratic hedging in affine stochastic volatility models
 Quadratic hedging in affine stochastic volatility models Jan Kallsen TU München Pittsburgh, February 20, 2006 (based on joint work with F. Hubalek, L. Krawczyk, A. Pauwels) 1 Hedging problem S t = S 0
Quadratic hedging in affine stochastic volatility models Jan Kallsen TU München Pittsburgh, February 20, 2006 (based on joint work with F. Hubalek, L. Krawczyk, A. Pauwels) 1 Hedging problem S t = S 0
Pension Risk Management with Funding and Buyout Options
 Pension Risk Management with Funding and Buyout Options Samuel H. Cox, Yijia Lin and Tianxiang Shi Presented at Eleventh International Longevity Risk and Capital Markets Solutions Conference Lyon, France
Pension Risk Management with Funding and Buyout Options Samuel H. Cox, Yijia Lin and Tianxiang Shi Presented at Eleventh International Longevity Risk and Capital Markets Solutions Conference Lyon, France
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie
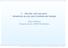 I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
Dynamic Hedging and PDE Valuation
 Dynamic Hedging and PDE Valuation Dynamic Hedging and PDE Valuation 1/ 36 Introduction Asset prices are modeled as following di usion processes, permitting the possibility of continuous trading. This environment
Dynamic Hedging and PDE Valuation Dynamic Hedging and PDE Valuation 1/ 36 Introduction Asset prices are modeled as following di usion processes, permitting the possibility of continuous trading. This environment
The stochastic calculus
 Gdansk A schedule of the lecture Stochastic differential equations Ito calculus, Ito process Ornstein - Uhlenbeck (OU) process Heston model Stopping time for OU process Stochastic differential equations
Gdansk A schedule of the lecture Stochastic differential equations Ito calculus, Ito process Ornstein - Uhlenbeck (OU) process Heston model Stopping time for OU process Stochastic differential equations
Oceňovanie CMS Spread Range Accrual
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a štatistiky Oceňovanie CMS Spread Range Accrual Diplomová práca Matej Stračiak Vedúci práce:
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a štatistiky Oceňovanie CMS Spread Range Accrual Diplomová práca Matej Stračiak Vedúci práce:
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
18. Diffusion processes for stocks and interest rates. MA6622, Ernesto Mordecki, CityU, HK, References for this Lecture:
 18. Diffusion processes for stocks and interest rates MA6622, Ernesto Mordecki, CityU, HK, 2006. References for this Lecture: P. Willmot, Paul Willmot on Quantitative Finance. Volume 1, Wiley, (2000) A.
18. Diffusion processes for stocks and interest rates MA6622, Ernesto Mordecki, CityU, HK, 2006. References for this Lecture: P. Willmot, Paul Willmot on Quantitative Finance. Volume 1, Wiley, (2000) A.
Option Pricing for a Stochastic-Volatility Jump-Diffusion Model with Log-Uniform Jump-Amplitudes
 Option Pricing for a Stochastic-Volatility Jump-Diffusion Model with Log-Uniform Jump-Amplitudes Floyd B. Hanson and Guoqing Yan Department of Mathematics, Statistics, and Computer Science University of
Option Pricing for a Stochastic-Volatility Jump-Diffusion Model with Log-Uniform Jump-Amplitudes Floyd B. Hanson and Guoqing Yan Department of Mathematics, Statistics, and Computer Science University of
Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš
 Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš Abstract Cieľ článku: Cieľom tohto článku je priblížiť zmeny hodnoty rizikovej prémie, identifikovať ktoré determinanty ju ovplyvňujú a ako
Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš Abstract Cieľ článku: Cieľom tohto článku je priblížiť zmeny hodnoty rizikovej prémie, identifikovať ktoré determinanty ju ovplyvňujú a ako
Linearity-Generating Processes, Unspanned Stochastic Volatility, and Interest-Rate Option Pricing
 Linearity-Generating Processes, Unspanned Stochastic Volatility, and Interest-Rate Option Pricing Liuren Wu, Baruch College Joint work with Peter Carr and Xavier Gabaix at New York University Board of
Linearity-Generating Processes, Unspanned Stochastic Volatility, and Interest-Rate Option Pricing Liuren Wu, Baruch College Joint work with Peter Carr and Xavier Gabaix at New York University Board of
Shape of the Yield Curve Under CIR Single Factor Model: A Note
 Shape of the Yield Curve Under CIR Single Factor Model: A Note Raymond Kan University of Chicago June, 1992 Abstract This note derives the shapes of the yield curve as a function of the current spot rate
Shape of the Yield Curve Under CIR Single Factor Model: A Note Raymond Kan University of Chicago June, 1992 Abstract This note derives the shapes of the yield curve as a function of the current spot rate
Calibration Lecture 4: LSV and Model Uncertainty
 Calibration Lecture 4: LSV and Model Uncertainty March 2017 Recap: Heston model Recall the Heston stochastic volatility model ds t = rs t dt + Y t S t dw 1 t, dy t = κ(θ Y t ) dt + ξ Y t dw 2 t, where
Calibration Lecture 4: LSV and Model Uncertainty March 2017 Recap: Heston model Recall the Heston stochastic volatility model ds t = rs t dt + Y t S t dw 1 t, dy t = κ(θ Y t ) dt + ξ Y t dw 2 t, where
Option Pricing for a Stochastic-Volatility Jump-Diffusion Model
 Option Pricing for a Stochastic-Volatility Jump-Diffusion Model Guoqing Yan and Floyd B. Hanson Department of Mathematics, Statistics, and Computer Science University of Illinois at Chicago Conference
Option Pricing for a Stochastic-Volatility Jump-Diffusion Model Guoqing Yan and Floyd B. Hanson Department of Mathematics, Statistics, and Computer Science University of Illinois at Chicago Conference
Affine term structures for interest rate models
 Stefan Tappe Albert Ludwig University of Freiburg, Germany UNSW-Macquarie WORKSHOP Risk: modelling, optimization and inference Sydney, December 7th, 2017 Introduction Affine processes in finance: R = a
Stefan Tappe Albert Ludwig University of Freiburg, Germany UNSW-Macquarie WORKSHOP Risk: modelling, optimization and inference Sydney, December 7th, 2017 Introduction Affine processes in finance: R = a
A New Class of Non-linear Term Structure Models. Discussion
 A New Class of Non-linear Term Structure Models by Eraker, Wang and Wu Discussion Pietro Veronesi The University of Chicago Booth School of Business Main Contribution and Outline of Discussion Main contribution
A New Class of Non-linear Term Structure Models by Eraker, Wang and Wu Discussion Pietro Veronesi The University of Chicago Booth School of Business Main Contribution and Outline of Discussion Main contribution
Locally risk-minimizing vs. -hedging in stochastic vola
 Locally risk-minimizing vs. -hedging in stochastic volatility models University of St. Andrews School of Economics and Finance August 29, 2007 joint work with R. Poulsen ( Kopenhagen )and K.R.Schenk-Hoppe
Locally risk-minimizing vs. -hedging in stochastic volatility models University of St. Andrews School of Economics and Finance August 29, 2007 joint work with R. Poulsen ( Kopenhagen )and K.R.Schenk-Hoppe
Ch 12. Interest Rate and Credit Models
 Ch. Interest Rate and Credit Models I. Equilibrium Interest Rate Models II. No-Arbitrage Interest Rate Models III. Forward Rate Models IV. Credit Risk Models This chapter introduces interest rate models
Ch. Interest Rate and Credit Models I. Equilibrium Interest Rate Models II. No-Arbitrage Interest Rate Models III. Forward Rate Models IV. Credit Risk Models This chapter introduces interest rate models
A More Detailed and Complete Appendix for Macroeconomic Volatilities and Long-run Risks of Asset Prices
 A More Detailed and Complete Appendix for Macroeconomic Volatilities and Long-run Risks of Asset Prices This is an on-line appendix with more details and analysis for the readers of the paper. B.1 Derivation
A More Detailed and Complete Appendix for Macroeconomic Volatilities and Long-run Risks of Asset Prices This is an on-line appendix with more details and analysis for the readers of the paper. B.1 Derivation
Stochastic Volatility (Working Draft I)
 Stochastic Volatility (Working Draft I) Paul J. Atzberger General comments or corrections should be sent to: paulatz@cims.nyu.edu 1 Introduction When using the Black-Scholes-Merton model to price derivative
Stochastic Volatility (Working Draft I) Paul J. Atzberger General comments or corrections should be sent to: paulatz@cims.nyu.edu 1 Introduction When using the Black-Scholes-Merton model to price derivative
Fakulta matematiky, fyziky a informatiky. Katedra aplikovanej matematiky a štatistiky EXOTICKÝCH OPCIÍ. Diplomová práca.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
