UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
|
|
|
- Jayson Hunter
- 5 years ago
- Views:
Transcription
1 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ
2 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA tudijný program: tudijný odbor: koliace pracovisko: Vedúci práce: Ekonomicko - nan ná matematika a modelovanie 1114 Aplikovaná matematika Katedra aplikovanej matematiky a ²tatistiky doc. Mgr. Igor Melicher ík, PhD. Bratislava 016 Bc. Ivana KRASULOVÁ
3 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky ZADANIE ZÁVEREČNEJ PRÁCE Meno a priezvisko študenta: Študijný program: Študijný odbor: Typ záverečnej práce: Jazyk záverečnej práce: Sekundárny jazyk: Bc. Ivana Krasulová ekonomicko-finančná matematika a modelovanie (Jednoodborové štúdium, magisterský II. st., denná forma) aplikovaná matematika diplomová slovenský anglický Názov: Cieľ: Využitie Meixnerovho procesu pri modelovaní finančných trhov Aplication of Meixner process in modeling financial markets V klasickom Black-Scholesovom modeli sa predpokladá normalita rozdelenia výnosov akcií. Štatistické testy však zvyčajne zamietajú túto hypotézu. Meixnerov proces patrí medzi Lévyho procesy. V práci pôjde o preskúmanie možnosti kvalitnejšieho modelovania finančných trhov pomocou tohto procesu. Vedúci: Katedra: Vedúci katedry: Dátum zadania: doc. Mgr. Igor Melicherčík, PhD. FMFI.KAMŠ - Katedra aplikovanej matematiky a štatistiky prof. RNDr. Daniel Ševčovič, CSc. Dátum schválenia: prof. RNDr. Daniel Ševčovič, CSc. garant študijného programu študent vedúci práce
4 Abstrakt KRASULOVÁ, Ivana: Vyuºitie Meixnerovho procesu pri modelovaní nan ných trhov [Diplomová práca], Univerzita Komenského v Bratislave, Fakulta matematiky, fyziky a informatiky, Katedra aplikovanej matematiky a ²tatistiky; Vedúci diplomovej práce: doc. Mgr. Igor Melicher ík, PhD., Bratislava, 016. V diplomovej práci sa zaoberáme Lévyho procesmi. Ide o porovnanie Black - Scholesovho modelu a modelu zaloºeného na Meixnerovom procese. Na základe testovania trhových dát, logaritmických výnosov akcií, poukazujeme na nedostatky Black - Scholesovho modelu, ktoré sú odstránené vyuºitím Meixnerovho procesu. Taktieº porovnávame trhové ceny opcií s cenami získanými pomocou Black - Scholesovho modelu aj modelu s Meixnerovým procesom. Pri Meixnerovom procese sú vyuºité dva prístupy získania ekvivalentnej martingalovej miery. K ú ové slová: nekone ne delite né rozdelenie, Lévyho procesy, Black - Scholesov model, Meixnerov proces, ekvivalentná martingalová miera, Esscherova transformácia
5 Abstract KRASULOVÁ, Ivana: Aplication of Meixner process in modeling nancial markets [Master s thesis], Comenius University in Bratislava, Faculty of Mathematics, Physics and Informatics, Department of Applied Mathematics and Statistics; Supervisor: doc. Mgr. Igor Melicher ík, PhD., Bratislava, 016. The thesis deals with Lévy processes. Compares the Black - Scholes model with the model based on the Meixner process. Based on empirical data testing, the asset log returns, we focus on the imperfections of the Black - Scholes model, which are removed using Meixner process. In the thesis we also compare market option prices with prices of Black - Scholes model and model with Meixner process. Two methods to optain an equivalent martingale meassure are used. Keywords: innitely divisible distribution, Lévy processes, Black - Scholes model, Meixner process, Equivalent Martingale Measure, Esscher transform
6 Obsah Úvod 8 1 Základné pojmy pri modelovaní nan ných trhov Stochastický proces, ltrácia Charakteristická funkcia Ekvivalentná martingalová miera, Oce ovacia formulka Wienerov proces, Brownov pohyb Lévyho procesy 17.1 V²eobecné charakteristiky Vlastnosti Lévyho procesov Vyuºitie na nan nom trhu Black - Scholesov model Nedostatky Black - Scholesovho modelu Normalita výnosov Stochastická volatilita Meixnerovo rozdelenie, Meixnerov proces Meixnerovo rozdelenie Kalibrovanie Meixnerovho rozdelenia na reálne dáta Gracké zobrazenie tatistické testy Simulácia cien podkladového aktíva Oce ovanie opcií Black - Scholesov model Meixnerov model Esscherova transformácia Ekvivalentná martingalová miera pomocou úpravy driftu Porovnanie Záver 59 6
7 Literatúra 61 Príloha 64 7
8 Úvod V posledných rokoch sa oraz viac teoretických ale aj praktických prác venuje problematike nesplnených predpokladov najznámej²ieho modelu oce ovania, Black - Scholesovho modelu. Model zaloºený na normálnom rozdelení je totiº len slabou aproximáciou reality, ke ºe logaritmické výnosy nan ných dát majú vä ²iu ²picatos neº je ²picatos normálneho rozdelenia. Taktieº sa astej²ie vyskytujú extremálnej²ie hodnoty, teda rozdelenie trhových dát je zo²ikmené. Práve pre tieto dôleºité vlastnosti empirických dát sa za ali vyuºíva na modelovanie nan ných trhov Lévyho procesy. Zaoberali sa nimi viacerí autori, spomenieme napríklad Cont a Tankov [], Schoutens [14]. Z týchto prác budeme vychádza aj v diplomovej práci. Medzi Lévyho procesy patrí aj Meixnerov proces. Vo nan nom svete bol vyuºitý v roku 1999 v práci [6], neskôr v roku 00 priniesol jeho nan nú aplikáciu v práci [16] aj Schoutens. Jedným z problémov pri Lévyho procesoch je nejednozna nos ekvivalentnej martingalovej miery. Jednou z moºností, ako ekvivalentnú martingalovú mieru získa, je Esscherova transformácia, ktorá pochádza uº z roku 193, kedy ju prvýkrát denoval Esccher. Pri oce ovaní nan ných derivátov je vhodné vyuºi deníciu pod a Gerber a Shiu [5] z roku Konkrétne parametre Esscherovej transformácie pre Meixnerov proces nájdeme napríklad v [6]. al²ou moºnos ou je ekvivalentná martingalová miera získaná pomocou úpravy driftu. Oba tieto prístupy vyuºijeme v diplomovej práci. Cie om diplomovej práce bolo overi predpoklady Black - Scholesovho modelu na trhových dátach a následne preskúma moºnosti lep²ieho modelovania nan ných trhov pomocou Meixnerovho procesu. V prvej kapitole uvedieme základné denície a princípy nan ného modelovania. Pripomenieme vlastnosti Wienerovho procesu, ktorý je základným stochastickým procesom. Druhá kapitola bude zameraná na Lévyho procesy. Priblíºime jednak ich spojitos s nekone ne delite nými rozdeleniami ale taktieº aj ich vlastnosti. Tretia kapitola bude obsahova okrem teoretických poznatkov o Black - Scholesovom modeli aj praktické overenie jeho predpokladov na trhových dátach, denných logaritmických výnosoch nieko kých akcií. V ²tvrtej kapitole sa budeme venova Meixnerovmu rozdeleniu a Meixnerovmu procesu, ktorý patrí medzi Lévyho procesy. Popí²eme dve metódy 8
9 odhadu parametrov pre Meixnerovo rozdelenie. Pomocou rovnakých metód ako v tretej kapitole otestujeme moºnos kvalitnej²ieho modelovania nan ných trhov v aka tomuto procesu. Závere ná, piata kapitola bude obsahova porovnanie Black - Scholesovho modelu a modelu s Meixnerovým procesom pri oce ovaní európskych kúpnych opcií akcie Yahoo. 9
10 1 Základné pojmy pri modelovaní nan ných trhov V prvej kapitole priblíºime nieko ko pojmov a základných princípov, ktoré sú dôleºité pri modelovaní nan ných trhov. Denície a vlastnosti uvedené v tejto kapitole môºeme nájs v [], [4], [9], [14], [18]. 1.1 Stochastický proces, ltrácia Denícia 1.1. (σ - algebra) Nech Ω je neprázdna mnoºina a nech F Ω. Usporiadanú dvojicu (Ω, F) nazývame σ - algebra, ak platí: Ω F A F Ω\A F Ak (A i ) i I je postupnos mnoºín patriacich do systému F, tak i I A i F kde Ω je mnoºina v²etkých podmnoºín mnoºiny Ω a postupnos ou máme na mysli kone nú alebo nekone nú spo ítate nú postupnos. [7] Uvaºujme mnoºinu v²etkých pozorovaní Ω a σ - algebru F. Pri nan nom modelovaní chápeme mnoºinu Ω ako mnoºinu scenárov, ktoré sa môºu na trhu udia. Napríklad ak chceme modelova cenu akcie v ase T ako náhodnú premennú X, ktorá je ovplyvnená mnohými faktormi ako sú dopyt a ponuka na trhu, ekonomické indikátory a mnohé al²ie, vplyv týchto faktorov môºeme celkovo popísa pomocou abstraktnej premennej ω. Budúca cena akcie pri daných udalostiach je teda vyjadrená pomocou X(ω). Pravdepodobnostná miera P na (Ω, F) je funkcia, ktorá kaºdej mnoºine A F nazývanej udalos, priradí pravdepodobnos z intervalu [0, 1]. (Ω, F, P) predstavuje pravdepodobnostný priestor. Nesmieme v²ak zabúda na fakt, ºe postupom asu získavame viac informácií, udalosti sú tým jasnej²ie. Preto je dôleºitý pojem ltrácie. 10
11 Denícia 1. (Filtrácia). Filtrácia alebo informa ný tok na pravdepodobnostnom priestore (Ω, F, P) je neklesajúci systém σ - algebier F = {F t } t 0, F t F takých, ºe 0 s < t F s F t (1) (F t ) je teda informácia prístupná v ase t. Pomocou nej môºeme rozlí²i, ktoré hodnoty ostávajú stále náhodné a ktoré sa pomocou dostupných informácií stávajú nenáhodnými. Pravdepodobnostný priestor (Ω, F, P) spolu s ltráciou (F t ) je ltrovaný pravdepodobnostný priestor. Namiesto toho, aby sme s asom menili pravdepodobnostnú mieru, zanecháme jú rovnakú a budeme modelova dopad informácií podmie- ovaním (F t ). Denícia 1.3 (Stochastický proces). Stochastický proces je súbor náhodných premenných X = {X t, 0 t < } = {X t (ω), 0 t <, ω Ω} na pravdepodobnostnom priestore (Ω, F, P) s hodnotami v R d. Stochastický proces je funkciou asovej premennej t, ktorá môºe by diskrétna alebo spojitá a premennej ω, ktorá popisuje neur itos v tom zmysle, ºe aj ke je známa po iato ná hodnota procesu, existuje mnoºstvo moºností, ako sa môºe proces vyvíja. pre t xné je X t (ω) náhodnou premennou, ω Ω je íslo pre xné ω je X t (ω) funkciou asu, nazývanou aj trajektória procesu priradená k ω peciálnym typom stochastického procesu je Markovov proces. Pri procesoch s Markovovou vlastnos ou je pre odhad budúcej hodnoty dôleºitá iba sú astná hodnota, minulos sa zabúda resp. je obsiahnutá v sú astnej hodnote. Denícia 1.4 (Adaptovaný proces). Stochastický proces je F t - adaptovaný, ak pre t [0, T ] hodnota X t je F t - merate ná. t.j. známa v ase t. Denícia 1.5 (Cadlag funkcia). Funkcia f : [0, T ] R d je cadlag funkciou, ak je spojitá sprava a má limitu z ava: t [0, T ] limity existujú a f(t) = f(t + ). f(t ) = lim f(s) f(t +) = lim f(s) () s t,s<t s t,s>t 11
12 Kaºdá spojitá funkcia je Cadlag funkciou. Denícia 1.6 (Martingal). Cadlag proces (X t ) t 0 je martingal vzh adom k ltrácii {F t } t 0 a miere P, ak X je F t - adaptovaný E[ X t ] je kone ná t 0 s > t, E[X s F t ] = X t Uvaºujme funkciu f : [a, b] R a delenie intervalu D = {a = t 0 < t 1 <... < t n = b}. Ozna me D = max (t k+1 t k ). k=0,...,n 1 Denícia 1.7 (Prvá variácia funkcie). Prvá variácia funkcie f vzh adom na delenie D je (ak limita existuje). n 1 V D (f) = lim D 0 f(t i+1 ) f(t i ) (3) i=0 Ak je sup V D (f) <, potom má f na [a, b] kone nú variáciu. V opa nom prípade hovoríme, ºe má nekone nú variáciu. Stochastický proces má kone nú variáciu, ak majú trajektórie kone nú variáciu s pravdepodobnos ou Charakteristická funkcia Významnú úlohu pri popise náhodnej premennej má charakteristická funkcia. Ke ºe z jej analytických vlastností vyplývajú vlastnosti náhodnej premennej. Charakteristická funkcia zárove jednozna ne identikuje rozdelenie náhodnej premennej, dve náhodné premenné s rovnakou charakteristickou funkciou sú rovnako rozdelené. Denícia 1.8 (Charakteristická funkcia). Charakteristická funkcia náhodnej premennej v R d je funkcia φ X : R d R denovaná ako z R d φ X (z) = E[e izx ] = e izx df (x) (4) R d pri om F (x) = P(X x). Charakteristická funkcia sp a φ(0) = 1, φ(z) = 1 z R d a je vºdy spojitá. 1
13 1.3 Ekvivalentná martingalová miera, Oce ovacia formulka Denícia 1.9 (Absolútna spojitos ). Nech P a Q sú pravdepodobnostné miery na (Ω, F). Potom Q je absolútne spojitá vzh adom na P, Q << P, vtedy a len vtedy, ak P(A) = 0 Q(A) = 0 A F. Denícia 1.10 (Ekvivalentné pravdepodobnostné miery). Nech P a Q sú pravdepodobnostné miery na (Ω, F). Ak Q je absolútne spojitá vzh adom na P a P je absolútne spojitá vzh adom na Q, potom P a Q sú ekvivalentné pravdepodobnostné miery, P Q. Denícia 1.11 (Ekvivalentná martingalová miera). Pravdepodobnostná miera Q je ekvivalentnou martingalovou mierou, ak Q je ekvivaletná vzh adom k P diskontovaný proces ceny akcie {e rt S t }, t 0 je martingalom pri Q Existencia ekvivalentnej martingalovej miery implikuje trh bez arbitráºnej príleºitosti. Trh je úplný, pokia pre kaºdý derivát existuje samonancovaná stratégia, ktorá ho replikuje. Úplnos trhu je spojená s jednozna nos ou ekvivalentnej martingalovej miery. Napríklad v prípade Black - Scholesovho modelu existuje jediná ekvivalentná martingalová miera. Av²ak vo vä ²ine modelov je trieda ekvivalentných mier vä ²ia. Pokia existuje viac ako jedna ekvivalentná miera trh je neúplný. Denícia 1.1 (Radon - Nikodymova derivácia). Nech P a Q sú pravdepodobnostné miery na (Ω, F) také ºe Q << P. Potom existuje jediná nezáporná funkcia Z : Ω R sp ajúca Z je F - merate ná Q(A) = Z(x) dp(x) A F A Q(A) < Potom Z = dq dp je Radon - Nikodymova derivácia Q vzh adom na P. (5) 13
14 Denícia 1.13 (Oce ovacia formulka európskych opcií). Uvaºujme výplatnú funkciu derivátu v ase expirácie ako G({S t, 0 t T }). Pri európskych kúpnych opciách platí G({S t, 0 t T }) = G(S T ) = (S T K) +, kde K predstavuje realiza nú cenu (strike price). Bezarbitráºna cena derivátu v ase t je V t = E Q [e r(t t) G({S u, 0 u T }) F t ] (6) pri om Q je ekvivalentná martingalová miera. 1.4 Wienerov proces, Brownov pohyb Na zachytenie stochastického vývoja podkladových aktív sa vyuºívajú Markovove náhodné procesy, medzi ktoré patrí aj Wienerov proces. Ten si popí²eme v tejto asti spolu s Brownovým pohybom, ktorý je jeho zov²eobecnením. Denícia 1.14 (Wienerov proces). Stochastický proces W = {W t, t 0} je Wienerov proces na pravdepodobnostnom priestore (Ω, F, P), ak sp a s pravdepodobnos ou 1 sú trajektórie W t (ω) spojité W 0 = 0 náhodná premenná W t má normálne rozlelenie N(0, t) W t+s W s má N(0, t) rozdelenie a prírastky W t1, W t W t1,..., W tk W tk 1 sú nezávislé pre 0 t 1 < t 1... < t k Z poslednej vlastnosti Wienerovho procesu vyplýva, ºe je Markovovým procesom. Zárove je Wienerov proces príkladom Lévyho procesov, ktoré si bliº²ie predstavíme v nasledujúcej kapitole. 14
15 Girsanovova veta Obr. 1: Wienerov proces Nech W t (ω), je Wienerov proces na (Ω, F, P). Nech γ t (ω) je F W t - adaptovaný proces, pre ktorý ( 1 T )) E P (exp γt dt <. (7) 0 Potom existuje miera Q na (Ω, F) taká, ºe P Q dq (ω) = exp( T γ dp 0 t(ω) dw t (ω) 1 T γ t t (ω)dt) W t (ω) = W t (ω) + t 0 γ s(ω)ds je Wienerov proces na (Ω, F, Q). Denícia 1.15 (Brownov pohyb). Nech W = {W t, t 0} je Wienerov proces. Pojmom Brownov pohyb sa ozna uje proces B t = µt + σw t t 0 (8) kde µ a σ > 0 sú kon²tanty. Wienerov proces je teda Brovnovým pohybom s driftom µ = 0 a volatilitou σ = 1. Denícia 1.16 (Geometrický Brownov pohyb). Nech B = {B t, t 0} je Brownov pohyb s parametrami µ a σ, nech Y 0 > 0. Potom proces Y t = Y 0 e Bt t 0 (9) 15
16 je Geometrický Brownov pohyb. Obr. : Brownov pohyb, µ = 3; σ = 0.5 Obr. 3: Geometrický Brownov pohyb, µ = 3; σ = 0.5; Y 0 =
17 Lévyho procesy Lévyho procesy nesú názov pod a jedného zo zakladate ov modernej teórie stochastických procesov, francúzskeho matematika Paula Lévyho ( ). Lévy taktieº významne prispel v ²túdiu teórie pravdepodobnosti, zaoberal sa napríklad Zákonom ve kých ísel, Centrálnou limitnou vetou a najmä procesmi s nezávislými a stacionárnymi prírastkami. [1] Vyuºívajú sa v rôznych odvetviach, i uº je to fyzika, strojárstvo, aktuárstvo, ekonomika a samozrejme nan ná matematika. Práve vo nan nej matematike na²li Lévyho procesy významné uplatnenie, ke ºe v aka svojim vlastnostiam dokáºu lep²ie zachyti empirické dáta nan ného trhu. Modely so skokmi totiº umoº ujú realistickej²ie zachytenie dynamiky cien na trhu a vä ²iu exibilitu. [11]. Pri spracovaní kapitoly o Lévyho procesoch sme vychádzali z [], [4], [11], [13]..1 V²eobecné charakteristiky Nech (Ω, F, P, F) je ltrovaný pravdepodobnostný priestor a T [0, ] je asový horizont. Denícia.1 (Lévyho proces). Cadlag adaptovaný stochastický proces s reálnymi hodnotami L = {L t, 0 t T } kde L 0 = 0 je Lévyho procesom, ak sú splnené nasledujúce podmienky: L má nezávislé prírastky, t.j. L t L s je nezávislé na F s pre v²etky 0 s < t T L má stacionárne prírastky, t.j. pre 0 s, t T rozdelenie L t+s L t nezávisí na t L je spojitý v pravdepodobnosti, t.j. pre t 0 a ɛ > 0; lim P ( L t L s > ɛ) = 0 s t Prvá a druhá podmienka implikujú, ºe Lévyho proces je Markovov proces. Lévyho procesy sú dôsledkom takmer istej spojitosti trajektórií sprava aj Silnými Markovovými procesmi. 17
18 Tretia podmienka vylu uje procesy so skokmi vyskytujúcimi sa v nenáhodných asoch, nehovorí o spojitosti trajektórií. V danom ase t je pravdepodobnos výskytu skoku nulová, pretoºe skoky sa v Lévyho procesoch vyskytujú v náhodných asoch. Medzi Lévyho procesy patrí napríklad lineárny drift (deterministický proces), ale aj Brownov pohyb, ktorý je jediným nedeterministickým Lévyho procesom so spojitými trajekóriami. Na Brownovom pohybe (a teda normálnom rozdelení) je postavený Black - Scholesov model, ktorý si bliº²ie popí²eme v nasledujúcej kapitole. Trieda Lévyho procesov je ve mi bohatá. Dokazuje to spojitos Lévyho procesov s nekone ne delite nými rozdeleniami, ktorú si teraz ukáºeme. Denícia. (Nekone ne delite né rozdelenie). Rozdelenie P X náhodnej premennej X je nekone ne delite né, ak pre v²etky n N existujú i.i.d. (nezávislé rovnako rozdelené) náhodné premenné X (1/n) 1,..., X (1/n) n tak, ºe teda platí rovnos v rozdelení. X d = X (1/n) X (1/n) n (10) Resp. alternatívna denícia cez charakteristickú funkciu. Denícia.3 (Nekone ne delite né rozdelenie). Rozdelenie P X náhodnej premennej X je nekone ne delite né, ak pre v²etky n N existuje náhodná premenná X (1/n) tak, ºe φ X (u) = (φ X (1/n)(u)) n (11) Uvedieme tri jednoduché príklady nekone ne delite ných rozdelení, pri om vyuºijeme deníciu pomocou charakteristickej funkcie. Normálne rozdelenie Nech X N(µ, σ ) ϕ X (u) = exp (iuµ 1 ) u σ a X (1/n) N = (ϕ X (1/n)(u)) n ( ) µ n, σ n ( = exp n (iu 18 )) µn 1 σ u = exp (iu n ) n µn 1 σ u n
19 Poissonovo rozdelenie Nech X P oisson(λ) a X (1/n) P oisson ϕ X (u) = exp(λ(e iu 1)) = exp ( ) λ n Meixnerovo rozdelenie = (ϕ X (1/n)(u)) n Nech X Meixner(a, b, d, m) ( ) ( d ( ϕ X (u) = e miu cos(b/) = e n( m n iu) cosh((au ib)/) = (ϕ X (1/n)(u)) n a X (1/n) Meixner ( a, b, d n, m ) n ( λ ( e iu 1 )) n n cos(b/) cosh((au ib)/) ) ) d n n Veta.1 (Lévy - Khintchine reprezentácia). Nech je D nekone ne delite né rozdelenie. Potom môºe by charakteristická funkcia vyjadrená ako φ D (u) = e ψ(u) u R (1) kde ψ je charakteristický exponent ψ(u) = iγu u σ + pri om γ R a ν je miera sp ajúca 1 x ν(dx) < ν(dx) < 1 x 1 (e iux 1 iux1 x 1 )ν(dx) (13) Trojica (γ, σ, ν) sa nazýva Lévyho alebo charakteristická trojica. γ je drift, σ Gaussovský alebo rozptylový koecient a ν je miera na R\{0} nazývaná Lévyho miera. Sp a ν({0}) = 0 a udáva o akávaný po et skokov ur itej ve kosti v danom asovom intervale d ºky t. Zárove hovorí o kone nosti momentov Lévyho procesu. Denícia.4 (Lévyho miera). Ak je Lévyho miera v tvare ν(dx) = u(x)dx (14) potom u(x) je Lévyho hustota. 19
20 Uvaºujme Lévyho proces (L t ) 0 t T, n N, pre ubovo né 0 t T L t = L t + (L t L t ) (L t L (n 1)t ) (15) n n n berúc do úvahy nezávislos a stacionaritu prírastkov Lévyho procesu, rozdelenie náhodnej premennej L t je nekone ne delite né. Pre kaºdý Lévyho proces platí E[e uil 1 ] = e tψ(u) (16) = exp {t (iγu u σ + n (e iux 1 iux1 x 1 )ν(dx))} (17) kde ψ(u) := ψ 1 (u) je Lévyho exponent L 1, náhodnej premennej s nekone ne delite ným rozdelením. Videli sme, ºe kaºdý Lévyho proces je spojený s nekone ne delite ným rozdelením, taktieº to platí aj opa ne. Teda pre kaºdé nekone ne delite né rozdelenie existuje Lévyho proces [4].. Vlastnosti Lévyho procesov Vlastnos.1. Nech L je Lévyho proces s charakteristickou trojicou (γ, σ, ν) ak ν(r) <, tak takmer v²etky trajektórie L majú na kaºdom kompaktnom intervale kone ný po et skokov, Lévyho proces má kone nú aktivitu ak ν(r) =, tak takmer v²etky trajektórie L majú na kaºdom kompaktnom intervale nekone ný po et skokov, Lévyho proces má nekone nú aktivitu Vlastnos.. Nech L je Lévyho proces s charakteristickou trojicou (γ, σ, ν) Nech σ = 0 a x ν(dx) <, tak takmer v²etky trajektórie L majú kone nú x 1 variáciu Nech σ 0 alebo x ν(dx) =, tak takmer v²etky trajektórie L majú x 1 nekone nú variáciu Vlastnos.3. Nech L je Lévyho proces s charakteristickou trojicou (γ, σ, ν), potom L t má kone ný p - ty moment pre p R + E L t p < vtedy a len vtedy, ak x 1 x p ν(dx) < 0
21 L t má kone ný p - ty exponenciálny moment pre p R E[e plt ] < vtedy a len vtedy, ak x 1 epx ν(dx) < Z vlastností vyplýva, ºe variácia Lévyho procesu závisí od malých skokov (a Brownovho pohybu), vlastnosti momentov od ve kých skokov a aktivita závisí od v²etkých skokov procesu. Vlastnos.4. Nech (L t ) 0 t T je Lévyho proces s charakteristickou trojicou (γ, σ, ν), pre u R x 1 eeu ν(dx) < a κ je kumulant L 1, t.j. κ(u) = log E[e ul 1 ]. Potom proces je martingal. M t = eult e tκ(u) (18).3 Vyuºitie na nan nom trhu Uvaºujme proces ceny akcie S t = S 0 e Lt 0 t T (19) kde L t je Lévyho proces s charakteristickou trojicou (γ, σ, ν) pri ekvivalentnej martingalovej miere Q. Logaritmické výnosy log( S t+s S t ) majú rozdelenie prislúchajúce prírastkom Lévyho procesu L t d ºky s. Ke ºe L 0 = 0, S 0 = S 0 e L 0 = S 0. Av²ak tým, ºe vyuºívame Lévyho proces, trh nie je úplný, a teda neexistuje len jedna ekvivalentná martingalová miera. Výnimkou sú iba modely s normálnym alebo Poissonovým rozdelením. [11] V piatej kapitole v²ak ukáºeme dva moºné prístupy, ako môºeme ekvivalentnú martingalovú mieru získa. Pri oce ovaní európskych kúpnych opcií s Lévyho procesmi sa dajú pouºi viaceré metódy. Je to jednak metóda transformácií, alej parciálna integrálno - diferenciálna rovnica a metóda Monte Carlo. Metóda transformácií je najjednoduch²ou a najrýchlej- ²ou metódou, nevýhodou v²ak je, ºe oce ovanie exotických derivátov nie je tak jednoduché. Metóda vyuºíva Fourierovu resp. Laplaceovu transformáciu, následne sa integrály dajú numericky ve mi rýchlo vypo íta. Pri parciálnej integrálno - diferenciálnej rovnici najskôr rovnicu odvodíme, potom ju numericky rie²ime. Výhodou oproti metóde transformácií je, ºe sa dajú uvaºova aj komplikovanej²ie výplatné funkcie (payoy), av- ²ak nevýhodou je výpo tová náro nos oproti predchádzajúcej metóde. Metóda Monte 1
22 Carlo simulácií je najvýhodnej²ia z poh adu rozmanitosti derivátov, ktoré môºu by jednoducho oce ované, av²ak práve pri tejto metóde je výpo tová náro nos najvä ²ia resp. metóda je najpomal²ia. Podstatou metódy je nasimulova cenu aktíva v ase T, S T = S 0 e L T, STk, k = 1,..., N sú jednotlivé simulácie. Cena európskej kúpnej akcie C T (S, K) je odhadnutá ako priemerná cena ĈT (S, K) a zo Zákona ve kých ísiel vyplýva Ĉ T (S, K) C T (S, K) (0) N V nasledujúcich dvoch kapitolách sa budeme bliº²ie venova najskôr Black - Scholesovmu modelu, ktorý je zaloºený na Brownovom pohybe a potom v ²tvrtej kapitole Meixnerovmu procesu. Pri oboch si najskôr bliº²ie popí²eme ich vlastnosti, jednak Lévyho charakteristiky, charakteristickú funkciu aj nekone ne delite né rozdelenie, ktoré je s daným procesom spojené. Taktieº budeme modelova denné logaritmické výnosy akcií pomocou týchto dvoch modelov.
23 3 Black - Scholesov model V tejto kapitole najskôr popí²eme najpouºívanej²í model oce ovania nan ných derivátov, Black - Scholesov model. Potom sa zameriame na jeho neodstatky, ktoré si overíme na trhových dátach. Pri spracovaní tretej kapitoly sme erpali z [9], [13], [14],[18]. Najznámej²ím a najviac pouºívaným modelom je Black - Scholesov model ( alej len BS model), ktorého základom je Geometrický Brownov pohyb. Dá sa poveda, ºe dosia ºiadny iný model nie je tak populárny a vyuºívaný ako BS model, o sa týka teórie aj praktického vyuºitia. Modely ktoré lep²ie zachytávajú realitu nan ného trhu sú zloºitej²ie v zmysle vä ²ieho po tu parametrov, tým sa v²ak stávajú náro nej²ími aj pri výpo toch a kalibrácii. Nech je S = {S t, t 0} proces ceny akcie. Ak ozna íme zmenu ceny akcie po as krátkeho asového intervalu t ako S t = S t+ t S t, potom výnos za tento interval je S t S t. Dá sa o akáva, ºe sa výnos skladá zo systematickej a náhodnej asti.µ je parameter predstavujúci priemerný výnos akcie a σ popisuje, ako ve mi cena akcie kolí²e, teda volatilitu. Náhodnos je zachytená pomocou Wienerovho procesu W t. Zmena ceny akcie je teda S t = S t (µ t + σ W t ) S 0 > 0 (1) a pre t 0 máme stochastickú diferenciálnu rovnicu ds t = S t (µdt + σdw t ) S 0 > 0 () ktorá má rie²enie v tvare S t = S 0 exp ) ) ((µ σ t + σw t (3) Tento (exponenciálny) funcionál Brownovho pohybu je Geometrický Brownov pohyb. Platí aj logs t logs 0 = ) (µ σ t + σw t. (4) Z vlastností Brownovho pohybu vyplýva, ºe logaritmický výnos má normálne rozdelenie N((µ σ )t, σ t). Toto je základným kame om BS modelu. 3
24 Ke ºe Brownov pohyb patrí medzi Lévyho procesy, uvedieme základné charakteristiky tohto procesu aj z poh adu vlastností a charakteristík Lévyho procesov, ktoré sme uviedli v druhej kapitole. Vyuºijeme ozna enie µ = µ σ. Hustota príslu²ného rozdelenia, normálneho rozdelenia, je charakteristická funkcia má tvar f L (x) = 1 σ µ) exp[ (x ], (5) π σ φ L (u) = exp[i µu σ u ], (6) kanonický rozklad L je L t = µt + σw t (7) a Lévyho charakteristiky sú ( µ, σ, 0). Brownov pohyb nemá monotónne trajektórie a tie majú neohrani enú variáciu na kone ných asových intervaloch. [8] Ako sme uº uviedli v druhej kapitole, pri BS modeli je trh úplný, existuje teda jediná ekvivalentná martingalová miera Q. Z Girsanovej vety vyplýva, ºe aj v rizikovo neutrálnej miere vývoj ceny akcie sleduje Geometrický Brownov pohyb. V rizikovo neutrálnom svete sa σ - parameter volatility nemení, mení sa v²ak drift. Vyuºijúc prístup získania ekvivalentnej martingalovej miery tzv. Mean - correcting equivalent martingale measure, teda len úpravou driftu, dostávame proces ceny akcie v tvare ) ) S t = S 0 exp ((r q σ t + σw t (8) kde r > 0 je spojitá miera úro enia dlhopisu a q 0 je dividendová miera. V nasledujúcej asti najskôr uvedieme Black - Scholesovu parabolickú parciálnu diferenciálnu rovnicu, ktorá opisuje vývoj ceny derivátu ako funkciu ceny podkladového aktíva a asu do expirácie. Taktieº explicitné formuly na oce ovanie vanilla opcií, teda kúpnych opcií a opcií na predaj európskeho typu. 4
25 Black - Scholesova parciálna diferenciálna rovnica na oce ovanie derivátov akcií (9) môºe by odvodená pomocou samonancovanej stratégie tvorby portfólia s nulovým rastom investícií, základom je snaha dosiahnu bezrizikové portfólio. Autorom tejto my²lienky je Merton. 1 V t V + (r q) S S + 1 σ S V rv = 0 (9) S V (S, t) je hodnota derivátu na dané aktívum, hladká funkcia dvoch premenných a T je as expirácie. Okrajovú podmienku môºeme získa, pokia je známa hodnota derivátu v ase jeho expirácie, teda V (S, T ). Hodnotu derivátu v ubovo nom ase do expirácie nájdeme rie²ením príslu²nej parciálnej diferenciálnej rovnice. Ke ºe poznáme koncovú podmienku pre európsku kúpnu opciu, pomocou nieko kých transformácií sa dá získa Black - Scholesova formula pre oce ovanie európskych kúpnych opcií V (S, t) = Se q(t t) Φ(d 1 ) Ke r(t t) Φ(d ) (30) kde Φ(.) je distribu ná funkcia normovaného normálneho rozdelenia a d 1, d sú v tvare d 1 = ln S K σ + (r q + )(T t) σ T t (31) d = d 1 σ T t (3) Následne vyuºitím put-call parity získame aj explicitnú formulu pre predajné opcie V (S, t) = Ke r(t t) Φ( d ) Se q(t t) Φ( d 1 ) (33) 1 V roku 1997 získali Myron Scholes a Robert Merton tzv. Cenu védskej banky za ekonómiu na pamiatku A. Nobela, ktorá je ozna ovaná aj ako Nobelova cena za ekonómiu. Bola tak ocenená dôleºitos a významnos Black - Scholesovho modelu, ktorý v 1970-tych rokoch priniesli do sveta oce ovania opcií Fischer Black, Myron Scholes a Robert Merton. 5
26 3.1 Nedostatky Black - Scholesovho modelu Táto podkapitola je zameraná na preskúmanie empirických vlastností nan ných dát a na nedostatky BS modelu. Budeme pracova s asovými radmi denných logaritmických výnosov nieko kých akcií s asovým rozpätím 1008 pracovných dní (9. september december 015). Dáta pochádzajú zo stránky Príklad takéhoto asového radu môºeme vidie na obrázku (Obr.4), ktorý zobrazuje denné logaritmické výnosy akcie Yahoo. Obr. 4: Denné logaritmické výnosy akcie Yahoo Pripomenieme, ºe platí: sú et k logaritmických výnosov za asové obdobie t je logaritmickým výnosom za obdobie k t. (ln(s t+ t ) ln(s t )) + (ln(s t+ t ) ln(s t+ t )) (ln(s t+k t ) ln(s t+(k 1) t )) = ln(s t+k t ) ln(s t ) (34) 6
27 Obr. 5: Histogram Yahoo. Obr. 6: Histogram Apple. Ako sme uº ukázali pri prezentovaní BS modelu, výnosy by mali by modelované pomocou prírastkov Brownovho pohybu, teda by mali by normálne rozdelené a nezávislé. Pri om parametre normálneho rozdelenia by sa nemali meni v ase. Tieto predpoklady si teraz overíme, vyuºijeme pri tom rôzne metódy Normalita výnosov Porovnanie momentov Pri porovnávaní teoretických momentov normálneho rozdelenia a odhadnutých momentov z dát sa zameriame na tretí a ²tvrtý moment. Budeme pracova s centrálnymi momentami. Tretí moment - ²ikmos, hovoriaca o symetrii rozdelenia, je v prípade normálneho rozdelenia nulová, teda toto pravdepodobnostné rozdelenie je symetrické. Záporná ( avostranná) ²ikmos v prípade vä ²iny nami pozorovaných akcií poukazuje na to, ºe vä ²ina hodnôt asového radu je vä ²ia ako priemer (v avo sa vyskytujú extrémnej²ie hodnoty, resp. v avo má dlh²í chvost). Rozdiel medzi pravostrannou a avostrannou ²ikmos ou znázor ujú obrázky Obr.5 a Obr.6. Odhadnuté ²tvrté momenty popisujúce ²picatos rozdelenia budeme porovnáva s hodnotou 3, ktorá predstavuje ²picatos normálneho rozdelenia. Ak má rozdelenie splo²tený vrchol, ²tvrtý moment je men²í ako 3. Pri poh ade na tabu ku (Tabu ka 1) teda môºeme usúdi, ºe dáta sú z rozdelení, ktoré majú ²picatej²í vrchol ako normálne 7
28 rozdelenie, a teda majú aº²ie chvosty. Z toho vyplýva, ºe ve ké rozdiely medzi cenami akcií sa vyskytujú astej²ie ako v modeli s normálne rozdelenými prírastkami. picatos totiº ur uje, aký priebeh má rozdelenie okolo stredu, resp. charakterizuje výskyt extremálnych hodnôt. Toto je jedným z hlavných dôvodov, pre o sa za ali pouºíva procesy so skokmi. stredná hodnota disperzia ²ikmos ²picatos normálne rozdelenie µ σ 0 3 GM 0, , ,0836 4,17577 KO 0, , ,34 3, Yahoo 0,0007 0, ,0836 5,80769 Intesa 0, , , ,98974 Tabu ka 1: Porovnanie momentov V tabu ke (Tabu ka 1) môºeme vidie odhad prvých ²tyroch momentov z nan ných dát ako aj teoretické momenty normálneho rozdelenia. Ako vidíme, ani jedny dáta pod a odhadov momentov nemajú normálne rozdelenie. Pre lep²í popis vlastností denných logaritmických výnosov by sme potrebovali rozdelenie, ktoré má viac parametrov ako normálne rozdelenie. Gracké porovnanie - QQ graf, jadrový odhad hustoty Pri overovaní normality denných logaritmických výnosov akcií pouºijeme pre názornos aj QQ - graf a porovnanie hustoty normálneho rozdelenia s empirickým odhadom hustoty, tzv. jadrovým odhadom hustoty. QQ-graf (the quantile-quantile plot) je kvalitatívne ve mi ú innou metódou testovania dobrej zhody. Porovnáva pre kaºdé j = 1,..., n (pri om n je rozsah súboru dát, v na²om prípade 1008 pozorovaní denných logaritmických výnosov) empirický j 1 n - kvantil s j 1 n - kvantilom daného rozdelenia, u nás normálneho rozdelenia. ƒím viac graf kopíruje iaru pod uhlom 45, tým je pravdepodobnej²ie, ºe dáta pochádzajú z daného rozdelenia. QQ - graf slúºi v²ak len na gracké znázornenie a priblíºenie, nepokladá sa za formálny test, pretoºe nie je jasne denované, kedy sa nulová hypotéza 8
29 zamieta. Obr. 7: QQ-graf denných logaritmických výnosov akcie Yahoo Normálne rozdelenie Ako vidíme na obrázku (Obr.7), zobrazené body sa od iary vz a ujú, a to hlavne na koncoch - chvostoch. Usudzujeme teda, ºe dáta nie sú z normálneho rozdelenia. Jadrový odhad hustoty je odhad hustoty f vypo ítaný z náhodného výberu x 1, x,..., x n ako f h = 1 nh n ( ) x xi K h i=1 (35) kde K(.) je funkcia sp ajúca K(x) dx = 1 (36) a h je zvolená ²írka okna. Existuje viacero moºností pre výber funkcie K(.). My sme pouºili tzv. Gaussovské jadro, K(.) je hustota normovaného normálneho rozdelenia N(0, 1) a h je zvolené pod a Silvermanovho pravidla palca ("Silverman's rule- ofthumb"), a teda má hodnotu h = 1.06σn 1 5. Na grafe (Obr.8) vidíme porovnanie jadrového odhadu hustoty denných logaritmických výnosov akcie Yahoo ako aj hustotu normálneho rozdelenia, ktoré má parametre zhodné s aritmetickým priemerom a výberovou disperziou odhadnutou z trhových dát. Aj pod a tohoto grackého porovnania môºeme usúdi, ºe normalita výnosov nie je splnená. 9
30 Obr. 8: Modrá je hustota normálneho rozdelenia s parametrami µ = 0, 0008 a σ = 0, , iernou je jadrový odhad hustoty denných logaritmických výnosov akcie Yahoo tatistické testy Tu²enie ºe denné logaritmické výnosy akcií nie sú normálne rozdelené potvrdíme aj ²tatistickými testami. Pri kaºdom z testov budeme na vopred zvolenej hladine významnosti α testova hypotézu, ºe denné logaritmické výnosy predstavujúce náhodný výber x 1, x,..., x n sú z rozdelenia daného kumulatívnou distribu nou funkciou F (x; θ). H 0 : F n (x) = F (x; θ) vs. H 1 : F n (x) F (x; θ) (37) kde F n (x) = 1 n n 1 xi x (38) je empirická kumulatívna distribu ná funkcia. Nulovú hypotézu na hladine významnosti α zamietame, ak je p - hodnota rovná alebo men²ia ako hladina významnosti α. P - hodnota udáva pravdepodobnos, ºe testovacia ²tatistika je e²te extrémnej²ia za predokladu, ºe platí nulová hypotéza. Vyuºili sme Pearsonov χ test, Kolmogorov - Smirnov test, Kuiperov test, Anderson Darling test a Crámer von Mises test. V nasledujúcej asti stru ne popí²eme pouºité testy a uvedieme testovaciu ²tatistiku. i=1 30
31 Pearson χ test (χ - test) je najznámej²ím testom dobrej zhody, ktorý porovnáva teoretické a empirické po etnosti. Testovacia ²tatistika χ = k i=1 n i np i np i (39) má pri n 50 za platnosti H 0 pribliºne Chí - kvadrát rozdelenie s k t 1 stup ami vo nosti. Pri om I 1, I,..., I k je rozklad reálnej osi na disjunktné intervaly, n i je po et pozorovaní spadajúcich do intervalu I i, p i je pravdepodobnostná miera I i ur ená distribu nou funkciou F (x; θ), np i je teoretická po etnos v intervale I i, k je po et tried a t po et odhadovaných parametrov. Kolmogorov Smirnov test (KS - test) Kolmogorova - Smirnova vzdialenos D n je denovaná ako maximálna vzdialenos medzi F n (x) a F (x; θ). Ak sú parametre θ známe, testovacia ²tatistika má tvar D n = sup F n (x) F (x; θ) (40) x Kuiper test je obdobou KS - testu, taktieº meria vzdialenos medzi empirickou a teoretickou distribu nou funkciou. Jeho testovacia ²tatistika má tvar [0] K = sup(f n (x) F (x; θ)) inf (F n(x) F (x; θ)) (41) x x Anderson Darling test (AD - test) je istou modikáciou KS - testu, ale dáva vä ²iu pozornos na chvosty resp. je citlivej²í na odchýlky na chvostoch, o je výhodou napr. pri aplikáciách v analýze rizík. Na rozdiel od KS - testu, pri ktorom kritické hodnoty nezávisia od testovaného rozdelenia, pri AD - teste sa kritické hodnoty po ítajú pre konkrétne rozdelenie, tým sa test stáva viac citlivým av²ak aj výpo tovo náro nej²ím. Testovacia ²tatistika má tvar A n = n 1 n (i 1) log (F (z i ; θ)(1 F (z n i+1 ; θ))) (4) n i=1 Ak chceme testova, i F (x; θ) je normálne rozdelenie so známymi parametrami N (µ,σ ), testovacia ²tatistika je v tvare A n = n 1 n (i 1) log (Φ(z i )(1 Φ(z n i+1 ))) (43) n i=1 31
32 kde z i = x i µ σ pre i = 1,,..., n a Φ(.) je distribu ná funkcia normálneho rozdelenia. Pokia sú parametre neznáme, pouºíva sa testovacia ²tatistika ( T n = A n n 5 ). (44) n Crámer von Mises test (CM - test) Testovacia ²tatistika tohto testu je v tvare W = 1 n ( ) i 1 1n + n F n(x i ) (45) i=1 χ test KS-test Kuiper-test AD-test CM-test GM 4, , , , KO, , , , Yahoo 5, , , , Intesa , , , Tabu ka : Výsledky testov Normálne rozdelenie V tabu ke (Tabu ka ) vidíme p - hodnoty v²etkých pouºitých testov na jednotlivé dáta predstavujúce denné logaritmické výnosy akcií. Ke ºe p - hodnoty sú men²ie ako 5%, o je nami zvolená hladina významnosti, nulovú hypotézu o normalite zamietame Stochastická volatilita Z dát môºeme taktieº pozorova, ºe odhadnutá volatilita sa stochasticky mení s asom, resp. mení sa prostredie. Potvrdzuje to jednak historická volatilita (Obr.9), ktorá popisuje, ako volatilné bolo aktívum v predchádzajúcom období. Historickú volatilitu akcie Yahoo zobrazenú na grafe sme získali pomocou odhadu ²tandardnej odchýlky denných logaritmických výnosov predchádzajúceho roka. Následne sme ju prenásobili odmocninou z 50, o predstavuje priemerný po et obchodných dní v kalendárnom roku. Vidíme, ºe historická volatilita kolí²e. Na druhom obrázku (Obr.10) môºeme vidie absolútnu hodnotu denných logaritmických výnosov akcie Yahoo. Je zjavné zhlukovanie volatility - sú vidite né obdobia s vysokým absolútnym výnosom a obdobia s nízkym absolútnym výnosom. Práve fakt, ºe po ve kých zmenách ceny akcie pravdepodobnej²ie nasleduje ve ká zmena motivuje k vyuºitiu modelu, kde je volatilita stochastická. 3
33 Obr. 9: Historická volatilita Obr. 10: Zhlukovanie volatility 33
34 4 Meixnerovo rozdelenie, Meixnerov proces Pre kvalitné oce ovanie derivátov, optimalizáciu portfólia i riadenie rizík, musíme ma aj kvalitný model podkladového aktíva. Je potrebné priblíºi sa o najviac modelom k realite, zachyti v²etky vlastnosti, ktoré vyplývajú z trhových dát. Na základe nesplnených predpokladov v Black - Scholesovom modeli sme sa rozhodli vyuºi Lévyho procesy, ktoré vhodne popisujú jednak skoky ale aj aºké chvosty pozorované pri trhových dátach. My sme sa zamerali na Meixnerov proces. V tejto kapitole najskôr popí²eme Meixnerovo rozdelenie a z neho odvodený Meixnerov proces. Potom ho podobne ako v predchádzajúcej kapitole otestujeme pomocou ²tatistických testov aj gracky. Budeme vychádza z [10], [13], [14], [15], [16]. 4.1 Meixnerovo rozdelenie Funkcia hustoty Meixnerovho rozdelenia M eixner(a, b, d, m) je f(x; a, b, d, m) = (cos(b/))d e b(x m) a aπγ(d) ( Γ d + ) i(x m) a (46) kde parametre sp ajú a > 0 π < b < π d > 0 m R (47) Γ(.) je Gamma funkcia a i = 1. V tabu ke (Tabu ka 3) vidíme vyjadrenie momentov Meixnerovho rozdelenia M eixner(a, b, d, m) pomocou parametrov. Je zrejmé, ºe ²picatos Meixnerovho rozdelenia, bude vºdy vä ²ia ako 3, o predstavuje ²picatos Normálneho rozdelenia. Meixnerovo rozdelenie stredná hodnota m + ad tg( b ) disperzia ²ikmos ²picatos sin(b) a d 1+cos(b) 1 d (1+cos(b)) 3 cos(b) d Tabu ka 3: Porovnanie momentov 34
35 Význam jednotlivých parametrov bliº²ie pribliºuje nasledujúci obrázok, ktorý porovnáva hustoty Meixnerovho rozdelenia s rôznymi parametrami. Taktieº uvádzame aj porovnanie kumulatívnych distribu ných funkcií týchto rozdelení. Parameter m je parametrom polohy, a a d ovplyv ujú ²picatos rozdelenia - a udáva, ako aºké sú chvosty; d ²kálu a parameter b ur uje ²ikmos. Obr. 11: Hustota Meixnerovho rozdelenia Obr. 1: Kumulatívna distribu ná funkcia Meixnerovho rozdelenia Pre názornos uvádzame aj obrázky s porovnaním dôsledkov zmeny len jedného z parametrov na hustotu Meixnerovho rozdelenia. 35
36 Obr. 13: Vplyv parametra a na hustotu Meixnerovho rozdelenia, a {0, 5; 1, 5; 3}; b = 0; d = 0, 1; m = 0 Obr. 14: Vplyv parametra b na hustotu Meixnerovho rozdelenia, b { 3, 0, 3}, a = 0, 5; d = 0, 1; m = 0 36
37 Obr. 15: Vplyv parametra d na hustotu Meixnerovho rozdelenia, d {0, 1; 0, 4; 0, 7}; a = 0, 5; b = 0; m = 0 Na odhad parametrov Meixnerovho rozdelenia sa pouºívajú dve metódy. Jednou z nich je Metóda momentov. Základnou my²lienkou Metódy momentov je odhad prvých ²tyroch momentov z trhových dát a následne vyuºitím vz ahov medzi parametrami a momentami, ktoré sme prezentovali v Tabu ke 3 ur i odhady parametrov Meixnerovho rozdelenia. V²eobecné vyjadrenie odhadnutých parametrov je potom d = 1 κ κ 1 3 (48) b = sign(κ 1 ) arcos( d (κ 3)) (49) a = S 1 + cos(b) d m = X ad tg ( ) b (50) (51) pri om musí by splnená podmienka κ κ (5) a vyuºili sme ozna enie X pre aritmetický priemer, S pre smerodajnú odchýlku. 37
38 κ 1 a κ sú odhady tretieho a ²tvrtého centrálneho momentu vypo ítané nasledovne µ k = 1 n n (x i X) k (53) i=1 κ 1 = µ 3 µ 3/ (54) κ 1 = µ 4 µ Presný postup odvodenia vz ahov uvádzame v prílohe. al²ou moºnos ou ako ur i parametre rozdelenia je Metóda maximálnej vierohodnosti. Podstatou tejto metódy je nájs také hodnoty parametrov, ktoré maximalizujú vierohodnostnú funkciu L(x; θ) = resp. logaritmickú vierohodnostnú funkciu l(x; θ) = log ( n f(x i ; θ)) i=1 ( n (cos(b/)) d = log aπγ(d) i=1 ( ) (cos(b/)) d = n log + b aπγ(d) a e b(x i m) a (55) n f(x i ; θ) (56) i=1 ( Γ d + i(x ) ) i m) a n n (x i m) + i=1 i=1 ( ( log Γ d + i(x ) ) i m) a S predpokladom, ºe existuje jediné maximum a l(x; θ) je hladká diferencovate ná funkcia, parametre získame rie²ením rovníc l θ i (x; θ) = 0 (57) Na urýchlenie výpo tov pri metóde Maximálnej vierohodnosti sa ako ²tartovací bod pouºíva odhad parametrov z Metódy momentov. 38
39 Charakteristická funkcia Meixnerovho rozdelenia M eixner(a, b, d, m) má tvar ( ) d φ(u; a, b, d, m) = e imu cos(b/) (58) cosh((au ib)/) z oho vyplýva, ºe toto rozdelenie je nekone ne delite né. Ako sme uº uviedli v. kapitole, pre kaºdé nekone ne delite né rozdelenie máme stochastický proces - Lévyho proces. Stochastický Meixnerov proces {M t, t 0} má nezávislé a stacionárne prírastky, M 0 = 0 a rozdelenie M t je dané Meixnerovým rozdelením Meixner(a, b, dt, mt). Lévyho triplet resp. trojica Lévyho charakteristík je v prípade Meixnerovho procesu (γ, 0, ν(dx)), t.j. nemá Brownovu as γ = a d tan ν(dx) = d e bx a xsinh( πx a ( ) b d 1 )dx (59) sinh( bx) a sinh( πx a )dx (60) Dôkaz môºeme nájs v ([10] str. 136). Ke ºe platí, ºe x ν(dx) = proces má nekone nú variáciu. [15] Existujú v²etky momenty tohto rozdelenia. [17] Kumulatívna vytvárajúca funkcia Meixnerovho rozdelenia je ( ( )) ( ( )) b at + b κ X (t) = d log cos d log cos + mt (61) kde M X (t) = E[e tx ] (6) je momentová generujúca funkcia a κ X (t) = log(m X (t)) (63) Presné odvodenie charakteristickej aj kumulatívnej vytvárajúcej funkcie Meixnerovho rozdelenia je v prílohe. Odvodenie bolo uvedené ako príklad pri denícii nekone ne delite ného rozdelenia v druhej kapitole. 39
40 4. Kalibrovanie Meixnerovho rozdelenia na reálne dáta Podobne ako v tretej kapitole aj v tejto kapitole vyºijeme asové rady denných logaritmických výnosov nieko kých akcií. Pomocou Metódy momentov odhadneme pre kaºdú z akcií parametre Meixnerovho rozdelenia. Následne otestujeme jednak gracky ako aj ²tatistickými testami, ºe práve Meixnerovo rozdelenie je v porovnaní s normálnym rozdelením lep²ie v zmysle, ºe lep²ie zachytáva vlastnosti denných logaritmických výnosov. Práve v aka ²tyrom parametrom Meixnerovho rozdelenia, dokáºeme lep²ie popísa aj aºké chvosty a ²ikmos trhových dát. V nasledujúcej tabu ke (Tabu ka 4) prezentujeme pre kaºdú zo ²tyroch akcií odhadnuté parametre Meixnerovho rozdelenia pomocou Metódy momentov. a b d m GM 0, ,0088 0, , KO 0, , , , Yahoo 0, , , , Intesa 0, ,4459 1, , Tabu ka 4: Odhadnuté parametre 4..1 Gracké zobrazenie Pri pozorovaní i empirické dáta pochádzajú z Meixnerovho rozdelenia vyuºijeme aj QQ-graf a porovnanie jadrového odhadu hustoty s hustotou príslu²ného Meixnerovho rozdelenia, t.j. Meixnerovho rozdelenia s odhadnutými parametrami jednotlivých akcií. Aby sme poukázali na zlep²enie oproti Normálnemu rozdeleniu, opätovne uvádzame aj obrázky z kapitoly o BS modeli. Ako vidíme na QQ-grafoch, Meixnerovo rozdelenie lep²ie zachytáva aº²ie chvosty. Porovnanie odhadov hustôt (Obr. 18) zas poukazuje na zlep²enie pri zachytení ²picatosti dát. 40
41 Obr. 16: QQ-graf denných logaritmických výnosov akcie Yahoo Normálne rozdelenie Obr. 17: QQ-graf denných logaritmických výnosov akcie Yahoo Meixnerovo rozdelenie Pri porovnaní hustoty sme alej vyuºili aj moºnos úpravy parametrov. A to v zmysle Metódy najmen²ích ²tvorcov, kedy sa vychádza z odhadov získaných pomocou metódy momentov, a potom sa parametre upravujú, aby sa získalo o najlep²ie zachytenie dát. Ke ºe vieme, ºe parameter d má vplyv na ²picatos rozdelenia a z porovnania jadrového odhadu hustoty a hustoty Meixnerovho rozdelenia vidíme, ºe ²picatos nie je dobre zachytená, rozhodli sme sa upravi práve parameter d. Uvádzame aj porovnanie hustôt práve po tejto zmene (Obr. 19). Nový parameter d odhadnutého Meixnerovho rozdelenia pre akciu Yahoo je d = 0,
42 Obr. 18: Porovnanie hustôt pre akciu Yahoo, modré je normálne rozdelenie, iernou jadrový odhad hustoty a ervenou hustota Meixnerovho rozdelenia Obr. 19: Porovnanie hustôt pre akciu Yahoo, modré je normálne rozdelenie, iernou jadrový odhad hustoty a ervenou hustota Meixnerovho rozdelenia so zmeneným parametrom d 4
43 4.. tatistické testy V tretej kapitole sme podrobne popísali ²tatistické testy, ktorými sme testovali zhodu empirických dát s normálnym rozdelením. V tejto asti vyuºijeme rovnaké testy, nulová hypotéza v²ak bude postavená v zmysle, i testované dáta pochádzajú z Meixnerovho rozdelenia s príslu²nými parametrami. Výsledky testov sme zhrnuli v tabu ke (Tabu ka 5). Uvádzame aj p - hodnoty testov zhody so zmeneným rozdelením, zmeneným parametrom d, iºe pre akciu Yahoo budeme ma dva výsledky. χ KS-test Kuiper-test AD-test CM-test GM 0, , ,0096 0, ,089 KO 0, , , ,3090 0, Yahoo 0, , , , ,9514 Yahoo zmena d 0, , ,497 0, ,49006 Intesa 0, , , , ,84810 Tabu ka 5: Výsledky testov Meixnerovo rozdelenie Na hladine významnosti 5% hypotézu o tom, ºe denné logaritmické výnosy sú z príslu²ného Meixnerovho rozdelenia pri vä ²ine testov nezamietame. Ako môºeme vidie, testy ukazujú, ºe pôvodne odhadnuté Meixnerovo rozdelenie pre akciu Yahoo je lep²ie, aj ke sa pri grackom porovnaní jadrového odhadu hustoty ako lep²ie zdalo práve upravené rozdelenie. To v²ak lep²ie zachytávalo len ²picatos rozdelenia. alej preto budeme pracova s pôvodným rozdelením odhadnutým pomocou Metódy momentov Simulácia cien podkladového aktíva V predchádzajúcich astiach sme si overili, ºe denné logaritmické výnosy majú Meixnerovo rozdelenie a hypotézu o Normálnom rozdelení sme zamietli. V al²om ukáºeme, ako sa empirický vývoj ceny podkladového aktíva lí²i od trajektórií Meixnerovho rozdelenia, ktoré má príslu²né odhadnuté paramatre. Taktieº uvedieme aj porovnanie s odhadnutým Normálnym rozdelením. Pri simuláciách sme pouºívali ²tatistický softvér R. Spravili sme 50 simulácií vývoja ceny akcie Yahoo od po.1.015, o predstavuje 1008 pracovných dní. Pri 43
44 Meixnerovom procese vieme, ºe M t je dané Meixnerovým rozdelením Meixner(a, b, dt, mt), preto sme parametre d, m pri simulovaní s postupujúcim asom menili. Získali sme tak 50 vývojov denných logaritmických výnosov a spätnými úpravami sme sa dostali k cenám podkladového aktíva. Pre získanie simulácií z normálneho rozdelenia sme vyuºili funkciu rnorm() a odhadnutý priemer a smerodajnú odchýlku. Na obrázku uvádzame reálny vývoj ceny akcie Yahoo v danom asovom intervale ako aj nasimulované trajéktórie z Meixnerovho rozdelenia (Obr.0) a Normálneho rozdelenia (Obr.1). Vychádzali sme z hodnoty 15,7 o predstavuje cenu akcie Obr. 0: ƒervenou je zobrazená realita, iernou sú simulácie z príslu²ného Meixnerovho rozdelenia al²í obrázok (Obr.) zobrazuje jednak reálny vývoj ako aj hranice dané extremálnymi hodnotami ur enými simuláciami. Ako môºeme vidie, Meixnerovo rozdelenie zachytáva lep²ie nielen spodnú hranicu reálneho vývoja ceny podkladového aktíva, ale taktieº aj horná hranica je presnej²ia, interval nie je aº taký ²iroký. Pozreli sme sa hlb²ie do histórie vývoja ceny akcie Yahoo, konkrétne na rovnako ve ké asové obdobie 1008 pracovných dní pred , aby sme si overili, i skuto ne môºe cena akcie tak poklesnú. Ke ºe d a bola hodnota akcie 6, a d a poklesla na úrove 8,95 (cca. 66% pokles) a v na²om pozorovaní je spodná hranica simulácií na úrovni 6,997, to znamená ºe z hodnoty 15,7 poklesla o cca. 56%, môºeme povaºova 44
45 výsledok získaný simuláciami za reálny. Obr. 1: ƒervenou je zobrazená realita, iernou sú simulácie z príslu²ného Normálneho rozdelenia Obr. : ƒervenou je zobrazená realita, modoru sú vyzna ené hranice simulácií Meixnerovho rozdelenia, zelené sú hranice Normálneho rozdelenia 45
46 5 Oce ovanie opcií Závere ná kapitola bude popisova praktické vyuºitie Meixnerovho procesu pri modelovaní nan ných derivátov, opcií. Porovnáme BS model s modelom zaloºeným na Meixnerovom procese. Uvedieme výsledky BS modelu, ktorého parametre budú odhadnuté na základe informácií o cenách opcií. Pri modeli s Meixnerovým procesom vyuºijeme dva prístupy získania ekvivalentnej martingalovej miery, ktoré porovnáme. Budeme pracova s 5 opciami na akciu Yahoo s rôznymi maturitami a realiza nými cenami. Dáta pochádzajú zo d a.1.015, kedy cena Adj.Close akcie Yahoo bola 35,65. Na obrázku (Obr.3) vidíme opcie s maturitou T = Je to jednak závislos trhovej last ceny opcie (poslednej obchodovanej) od realiza nej ceny, taktieº sme zobrazili mid ceny (priemer medzi bid a ask cenou opcie) v závislosti od realiza nej ceny. Obrázky pre opcie s inými maturitami sa nachádzajú v prílohe. V prílohe sa nachádza aj tabu ka so v²etkými opciami. Pri spracovaní piatej kapitoly budeme erpa z [], [3]. Obr. 3: Opcie akcie Yahoo s T = , ierne sú bid a ask ceny, ervená hviezdi ka mid cena a ervený krúºok last cena 46
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky
 fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky. Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová UNIVERZITA KOMENSKÉHO
Pouºitie metódy Monte Carlo vo nanciách
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA
CROSS SECTIONAL FORECASTS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií
 UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
Analytické aproximácie pri modelovaní cien opcií
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
Modelovanie nan ných trhov a risku metódou Monte Carlo
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Modelovanie nan ných trhov a risku metódou Monte Carlo 211 Luká² Kunert UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Modelovanie nan ných trhov a risku metódou Monte Carlo 211 Luká² Kunert UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY,
Normal Inverse Gaussian (NIG) Process
 With Applications in Mathematical Finance The Mathematical and Computational Finance Laboratory - Lunch at the Lab March 26, 2009 1 Limitations of Gaussian Driven Processes Background and Definition IG
With Applications in Mathematical Finance The Mathematical and Computational Finance Laboratory - Lunch at the Lab March 26, 2009 1 Limitations of Gaussian Driven Processes Background and Definition IG
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. modelu úrokových mier
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová UNIVERZITA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová UNIVERZITA
Lévy Processes. Antonis Papapantoleon. TU Berlin. Computational Methods in Finance MSc course, NTUA, Winter semester 2011/2012
 Lévy Processes Antonis Papapantoleon TU Berlin Computational Methods in Finance MSc course, NTUA, Winter semester 2011/2012 Antonis Papapantoleon (TU Berlin) Lévy processes 1 / 41 Overview of the course
Lévy Processes Antonis Papapantoleon TU Berlin Computational Methods in Finance MSc course, NTUA, Winter semester 2011/2012 Antonis Papapantoleon (TU Berlin) Lévy processes 1 / 41 Overview of the course
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY
 International Scientific Conference YOUNG SCIENTISTS 2011 HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY Marko LALIĆ Technická Univerzita v Košiciach, Ekonomická fakulta Katedra financií
International Scientific Conference YOUNG SCIENTISTS 2011 HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY Marko LALIĆ Technická Univerzita v Košiciach, Ekonomická fakulta Katedra financií
Change of Measure (Cameron-Martin-Girsanov Theorem)
 Change of Measure Cameron-Martin-Girsanov Theorem Radon-Nikodym derivative: Taking again our intuition from the discrete world, we know that, in the context of option pricing, we need to price the claim
Change of Measure Cameron-Martin-Girsanov Theorem Radon-Nikodym derivative: Taking again our intuition from the discrete world, we know that, in the context of option pricing, we need to price the claim
UNIVERZITA KOMENSKÉHO V BRATISLAVE. Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ Veronika Kleinová
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky
Quadratic hedging in affine stochastic volatility models
 Quadratic hedging in affine stochastic volatility models Jan Kallsen TU München Pittsburgh, February 20, 2006 (based on joint work with F. Hubalek, L. Krawczyk, A. Pauwels) 1 Hedging problem S t = S 0
Quadratic hedging in affine stochastic volatility models Jan Kallsen TU München Pittsburgh, February 20, 2006 (based on joint work with F. Hubalek, L. Krawczyk, A. Pauwels) 1 Hedging problem S t = S 0
Globálne optimálne gama zaisťovanie s transakčnými nákladmi
 Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
Financial Accelerator and Interest Rate in Selected Countries
 COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
A new approach to LIBOR modeling
 A new approach to LIBOR modeling Antonis Papapantoleon FAM TU Vienna Based on joint work with Martin Keller-Ressel and Josef Teichmann Istanbul Workshop on Mathematical Finance Istanbul, Turkey, 18 May
A new approach to LIBOR modeling Antonis Papapantoleon FAM TU Vienna Based on joint work with Martin Keller-Ressel and Josef Teichmann Istanbul Workshop on Mathematical Finance Istanbul, Turkey, 18 May
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Small-time asymptotics of stopped Lévy bridges and simulation schemes with controlled bias
 Small-time asymptotics of stopped Lévy bridges and simulation schemes with controlled bias José E. Figueroa-López 1 1 Department of Statistics Purdue University Computational Finance Seminar Purdue University
Small-time asymptotics of stopped Lévy bridges and simulation schemes with controlled bias José E. Figueroa-López 1 1 Department of Statistics Purdue University Computational Finance Seminar Purdue University
Odhady parametrov modelov
 Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
The stochastic calculus
 Gdansk A schedule of the lecture Stochastic differential equations Ito calculus, Ito process Ornstein - Uhlenbeck (OU) process Heston model Stopping time for OU process Stochastic differential equations
Gdansk A schedule of the lecture Stochastic differential equations Ito calculus, Ito process Ornstein - Uhlenbeck (OU) process Heston model Stopping time for OU process Stochastic differential equations
AN ANALYTICALLY TRACTABLE UNCERTAIN VOLATILITY MODEL
 AN ANALYTICALLY TRACTABLE UNCERTAIN VOLATILITY MODEL FABIO MERCURIO BANCA IMI, MILAN http://www.fabiomercurio.it 1 Stylized facts Traders use the Black-Scholes formula to price plain-vanilla options. An
AN ANALYTICALLY TRACTABLE UNCERTAIN VOLATILITY MODEL FABIO MERCURIO BANCA IMI, MILAN http://www.fabiomercurio.it 1 Stylized facts Traders use the Black-Scholes formula to price plain-vanilla options. An
Using Lévy Processes to Model Return Innovations
 Using Lévy Processes to Model Return Innovations Liuren Wu Zicklin School of Business, Baruch College Option Pricing Liuren Wu (Baruch) Lévy Processes Option Pricing 1 / 32 Outline 1 Lévy processes 2 Lévy
Using Lévy Processes to Model Return Innovations Liuren Wu Zicklin School of Business, Baruch College Option Pricing Liuren Wu (Baruch) Lévy Processes Option Pricing 1 / 32 Outline 1 Lévy processes 2 Lévy
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Zaistené stratégie. Bc. Tomáš Miklošovič.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
Financial Economics & Insurance
 Financial Economics & Insurance Albert Cohen Actuarial Sciences Program Department of Mathematics Department of Statistics and Probability A336 Wells Hall Michigan State University East Lansing MI 48823
Financial Economics & Insurance Albert Cohen Actuarial Sciences Program Department of Mathematics Department of Statistics and Probability A336 Wells Hall Michigan State University East Lansing MI 48823
Lecture 1: Lévy processes
 Lecture 1: Lévy processes A. E. Kyprianou Department of Mathematical Sciences, University of Bath 1/ 22 Lévy processes 2/ 22 Lévy processes A process X = {X t : t 0} defined on a probability space (Ω,
Lecture 1: Lévy processes A. E. Kyprianou Department of Mathematical Sciences, University of Bath 1/ 22 Lévy processes 2/ 22 Lévy processes A process X = {X t : t 0} defined on a probability space (Ω,
Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing
 Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing We shall go over this note quickly due to time constraints. Key concept: Ito s lemma Stock Options: A contract giving
Lecture Note 8 of Bus 41202, Spring 2017: Stochastic Diffusion Equation & Option Pricing We shall go over this note quickly due to time constraints. Key concept: Ito s lemma Stock Options: A contract giving
Continuous time; continuous variable stochastic process. We assume that stock prices follow Markov processes. That is, the future movements in a
 Continuous time; continuous variable stochastic process. We assume that stock prices follow Markov processes. That is, the future movements in a variable depend only on the present, and not the history
Continuous time; continuous variable stochastic process. We assume that stock prices follow Markov processes. That is, the future movements in a variable depend only on the present, and not the history
Chapter 3: Black-Scholes Equation and Its Numerical Evaluation
 Chapter 3: Black-Scholes Equation and Its Numerical Evaluation 3.1 Itô Integral 3.1.1 Convergence in the Mean and Stieltjes Integral Definition 3.1 (Convergence in the Mean) A sequence {X n } n ln of random
Chapter 3: Black-Scholes Equation and Its Numerical Evaluation 3.1 Itô Integral 3.1.1 Convergence in the Mean and Stieltjes Integral Definition 3.1 (Convergence in the Mean) A sequence {X n } n ln of random
AMH4 - ADVANCED OPTION PRICING. Contents
 AMH4 - ADVANCED OPTION PRICING ANDREW TULLOCH Contents 1. Theory of Option Pricing 2 2. Black-Scholes PDE Method 4 3. Martingale method 4 4. Monte Carlo methods 5 4.1. Method of antithetic variances 5
AMH4 - ADVANCED OPTION PRICING ANDREW TULLOCH Contents 1. Theory of Option Pricing 2 2. Black-Scholes PDE Method 4 3. Martingale method 4 4. Monte Carlo methods 5 4.1. Method of antithetic variances 5
MAS452/MAS6052. MAS452/MAS Turn Over SCHOOL OF MATHEMATICS AND STATISTICS. Stochastic Processes and Financial Mathematics
 t r t r2 r t SCHOOL OF MATHEMATICS AND STATISTICS Stochastic Processes and Financial Mathematics Spring Semester 2017 2018 3 hours t s s tt t q st s 1 r s r t r s rts t q st s r t r r t Please leave this
t r t r2 r t SCHOOL OF MATHEMATICS AND STATISTICS Stochastic Processes and Financial Mathematics Spring Semester 2017 2018 3 hours t s s tt t q st s 1 r s r t r s rts t q st s r t r r t Please leave this
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie
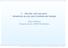 I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
Lecture 17. The model is parametrized by the time period, δt, and three fixed constant parameters, v, σ and the riskless rate r.
 Lecture 7 Overture to continuous models Before rigorously deriving the acclaimed Black-Scholes pricing formula for the value of a European option, we developed a substantial body of material, in continuous
Lecture 7 Overture to continuous models Before rigorously deriving the acclaimed Black-Scholes pricing formula for the value of a European option, we developed a substantial body of material, in continuous
NEWCASTLE UNIVERSITY SCHOOL OF MATHEMATICS, STATISTICS & PHYSICS SEMESTER 1 SPECIMEN 2 MAS3904. Stochastic Financial Modelling. Time allowed: 2 hours
 NEWCASTLE UNIVERSITY SCHOOL OF MATHEMATICS, STATISTICS & PHYSICS SEMESTER 1 SPECIMEN 2 Stochastic Financial Modelling Time allowed: 2 hours Candidates should attempt all questions. Marks for each question
NEWCASTLE UNIVERSITY SCHOOL OF MATHEMATICS, STATISTICS & PHYSICS SEMESTER 1 SPECIMEN 2 Stochastic Financial Modelling Time allowed: 2 hours Candidates should attempt all questions. Marks for each question
Inflation rate prediction a statistical approach
 Abstract Inflation rate prediction a statistical approach Předpověď míry inflace - statistický přístup František Vávra 1, Tomáš Ťoupal 2, Eva Wagnerová 3, Patrice Marek 4, Zdeněk Hanzal 5 This paper deals
Abstract Inflation rate prediction a statistical approach Předpověď míry inflace - statistický přístup František Vávra 1, Tomáš Ťoupal 2, Eva Wagnerová 3, Patrice Marek 4, Zdeněk Hanzal 5 This paper deals
Near-expiration behavior of implied volatility for exponential Lévy models
 Near-expiration behavior of implied volatility for exponential Lévy models José E. Figueroa-López 1 1 Department of Statistics Purdue University Financial Mathematics Seminar The Stevanovich Center for
Near-expiration behavior of implied volatility for exponential Lévy models José E. Figueroa-López 1 1 Department of Statistics Purdue University Financial Mathematics Seminar The Stevanovich Center for
FINANCIAL PRICING MODELS
 Page 1-22 like equions FINANCIAL PRICING MODELS 20 de Setembro de 2013 PhD Page 1- Student 22 Contents Page 2-22 1 2 3 4 5 PhD Page 2- Student 22 Page 3-22 In 1973, Fischer Black and Myron Scholes presented
Page 1-22 like equions FINANCIAL PRICING MODELS 20 de Setembro de 2013 PhD Page 1- Student 22 Contents Page 2-22 1 2 3 4 5 PhD Page 2- Student 22 Page 3-22 In 1973, Fischer Black and Myron Scholes presented
Credit Burden of Households in Slovakia
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Credit Burden of Households in Slovakia Diploma Thesis Adam Biro² Bratislava 2011 525ee80a-3c15-4902-b736-9cfdd96015d6
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Credit Burden of Households in Slovakia Diploma Thesis Adam Biro² Bratislava 2011 525ee80a-3c15-4902-b736-9cfdd96015d6
Credit Risk in Lévy Libor Modeling: Rating Based Approach
 Credit Risk in Lévy Libor Modeling: Rating Based Approach Zorana Grbac Department of Math. Stochastics, University of Freiburg Joint work with Ernst Eberlein Croatian Quants Day University of Zagreb, 9th
Credit Risk in Lévy Libor Modeling: Rating Based Approach Zorana Grbac Department of Math. Stochastics, University of Freiburg Joint work with Ernst Eberlein Croatian Quants Day University of Zagreb, 9th
The data-driven COS method
 The data-driven COS method Á. Leitao, C. W. Oosterlee, L. Ortiz-Gracia and S. M. Bohte Delft University of Technology - Centrum Wiskunde & Informatica Reading group, March 13, 2017 Reading group, March
The data-driven COS method Á. Leitao, C. W. Oosterlee, L. Ortiz-Gracia and S. M. Bohte Delft University of Technology - Centrum Wiskunde & Informatica Reading group, March 13, 2017 Reading group, March
LOGNORMAL MIXTURE SMILE CONSISTENT OPTION PRICING
 LOGNORMAL MIXTURE SMILE CONSISTENT OPTION PRICING FABIO MERCURIO BANCA IMI, MILAN http://www.fabiomercurio.it Daiwa International Workshop on Financial Engineering, Tokyo, 26-27 August 2004 1 Stylized
LOGNORMAL MIXTURE SMILE CONSISTENT OPTION PRICING FABIO MERCURIO BANCA IMI, MILAN http://www.fabiomercurio.it Daiwa International Workshop on Financial Engineering, Tokyo, 26-27 August 2004 1 Stylized
The data-driven COS method
 The data-driven COS method Á. Leitao, C. W. Oosterlee, L. Ortiz-Gracia and S. M. Bohte Delft University of Technology - Centrum Wiskunde & Informatica CMMSE 2017, July 6, 2017 Álvaro Leitao (CWI & TUDelft)
The data-driven COS method Á. Leitao, C. W. Oosterlee, L. Ortiz-Gracia and S. M. Bohte Delft University of Technology - Centrum Wiskunde & Informatica CMMSE 2017, July 6, 2017 Álvaro Leitao (CWI & TUDelft)
Valuing volatility and variance swaps for a non-gaussian Ornstein-Uhlenbeck stochastic volatility model
 Valuing volatility and variance swaps for a non-gaussian Ornstein-Uhlenbeck stochastic volatility model 1(23) Valuing volatility and variance swaps for a non-gaussian Ornstein-Uhlenbeck stochastic volatility
Valuing volatility and variance swaps for a non-gaussian Ornstein-Uhlenbeck stochastic volatility model 1(23) Valuing volatility and variance swaps for a non-gaussian Ornstein-Uhlenbeck stochastic volatility
Stochastic Differential equations as applied to pricing of options
 Stochastic Differential equations as applied to pricing of options By Yasin LUT Supevisor:Prof. Tuomo Kauranne December 2010 Introduction Pricing an European call option Conclusion INTRODUCTION A stochastic
Stochastic Differential equations as applied to pricing of options By Yasin LUT Supevisor:Prof. Tuomo Kauranne December 2010 Introduction Pricing an European call option Conclusion INTRODUCTION A stochastic
STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL
 STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL YOUNGGEUN YOO Abstract. Ito s lemma is often used in Ito calculus to find the differentials of a stochastic process that depends on time. This paper will introduce
STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL YOUNGGEUN YOO Abstract. Ito s lemma is often used in Ito calculus to find the differentials of a stochastic process that depends on time. This paper will introduce
Homework Assignments
 Homework Assignments Week 1 (p. 57) #4.1, 4., 4.3 Week (pp 58 6) #4.5, 4.6, 4.8(a), 4.13, 4.0, 4.6(b), 4.8, 4.31, 4.34 Week 3 (pp 15 19) #1.9, 1.1, 1.13, 1.15, 1.18 (pp 9 31) #.,.6,.9 Week 4 (pp 36 37)
Homework Assignments Week 1 (p. 57) #4.1, 4., 4.3 Week (pp 58 6) #4.5, 4.6, 4.8(a), 4.13, 4.0, 4.6(b), 4.8, 4.31, 4.34 Week 3 (pp 15 19) #1.9, 1.1, 1.13, 1.15, 1.18 (pp 9 31) #.,.6,.9 Week 4 (pp 36 37)
Short-time asymptotics for ATM option prices under tempered stable processes
 Short-time asymptotics for ATM option prices under tempered stable processes José E. Figueroa-López 1 1 Department of Statistics Purdue University Probability Seminar Purdue University Oct. 30, 2012 Joint
Short-time asymptotics for ATM option prices under tempered stable processes José E. Figueroa-López 1 1 Department of Statistics Purdue University Probability Seminar Purdue University Oct. 30, 2012 Joint
ASYMMETRICALLY TEMPERED STABLE DISTRIBUTIONS WITH APPLICATIONS TO FINANCE
 PROBABILITY AND MATHEMATICAL STATISTICS Vol. 0, Fasc. 0 (0000), pp. 000 000 doi: ASYMMETRICALLY TEMPERED STABLE DISTRIBUTIONS WITH APPLICATIONS TO FINANCE A. A R E F I (ALLAMEH TABATABA I UNIVERSITY) AND
PROBABILITY AND MATHEMATICAL STATISTICS Vol. 0, Fasc. 0 (0000), pp. 000 000 doi: ASYMMETRICALLY TEMPERED STABLE DISTRIBUTIONS WITH APPLICATIONS TO FINANCE A. A R E F I (ALLAMEH TABATABA I UNIVERSITY) AND
Time-changed Brownian motion and option pricing
 Time-changed Brownian motion and option pricing Peter Hieber Chair of Mathematical Finance, TU Munich 6th AMaMeF Warsaw, June 13th 2013 Partially joint with Marcos Escobar (RU Toronto), Matthias Scherer
Time-changed Brownian motion and option pricing Peter Hieber Chair of Mathematical Finance, TU Munich 6th AMaMeF Warsaw, June 13th 2013 Partially joint with Marcos Escobar (RU Toronto), Matthias Scherer
Limit Theorems for the Empirical Distribution Function of Scaled Increments of Itô Semimartingales at high frequencies
 Limit Theorems for the Empirical Distribution Function of Scaled Increments of Itô Semimartingales at high frequencies George Tauchen Duke University Viktor Todorov Northwestern University 2013 Motivation
Limit Theorems for the Empirical Distribution Function of Scaled Increments of Itô Semimartingales at high frequencies George Tauchen Duke University Viktor Todorov Northwestern University 2013 Motivation
Introduction to Financial Mathematics
 Department of Mathematics University of Michigan November 7, 2008 My Information E-mail address: marymorj (at) umich.edu Financial work experience includes 2 years in public finance investment banking
Department of Mathematics University of Michigan November 7, 2008 My Information E-mail address: marymorj (at) umich.edu Financial work experience includes 2 years in public finance investment banking
Binomial model: numerical algorithm
 Binomial model: numerical algorithm S / 0 C \ 0 S0 u / C \ 1,1 S0 d / S u 0 /, S u 3 0 / 3,3 C \ S0 u d /,1 S u 5 0 4 0 / C 5 5,5 max X S0 u,0 S u C \ 4 4,4 C \ 3 S u d / 0 3, C \ S u d 0 S u d 0 / C 4
Binomial model: numerical algorithm S / 0 C \ 0 S0 u / C \ 1,1 S0 d / S u 0 /, S u 3 0 / 3,3 C \ S0 u d /,1 S u 5 0 4 0 / C 5 5,5 max X S0 u,0 S u C \ 4 4,4 C \ 3 S u d / 0 3, C \ S u d 0 S u d 0 / C 4
M5MF6. Advanced Methods in Derivatives Pricing
 Course: Setter: M5MF6 Dr Antoine Jacquier MSc EXAMINATIONS IN MATHEMATICS AND FINANCE DEPARTMENT OF MATHEMATICS April 2016 M5MF6 Advanced Methods in Derivatives Pricing Setter s signature...........................................
Course: Setter: M5MF6 Dr Antoine Jacquier MSc EXAMINATIONS IN MATHEMATICS AND FINANCE DEPARTMENT OF MATHEMATICS April 2016 M5MF6 Advanced Methods in Derivatives Pricing Setter s signature...........................................
LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives
 Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Sato Processes in Finance
 Sato Processes in Finance Dilip B. Madan Robert H. Smith School of Business Slovenia Summer School August 22-25 2011 Lbuljana, Slovenia OUTLINE 1. The impossibility of Lévy processes for the surface of
Sato Processes in Finance Dilip B. Madan Robert H. Smith School of Business Slovenia Summer School August 22-25 2011 Lbuljana, Slovenia OUTLINE 1. The impossibility of Lévy processes for the surface of
Pricing in markets modeled by general processes with independent increments
 Pricing in markets modeled by general processes with independent increments Tom Hurd Financial Mathematics at McMaster www.phimac.org Thanks to Tahir Choulli and Shui Feng Financial Mathematics Seminar
Pricing in markets modeled by general processes with independent increments Tom Hurd Financial Mathematics at McMaster www.phimac.org Thanks to Tahir Choulli and Shui Feng Financial Mathematics Seminar
The Self-financing Condition: Remembering the Limit Order Book
 The Self-financing Condition: Remembering the Limit Order Book R. Carmona, K. Webster Bendheim Center for Finance ORFE, Princeton University November 6, 2013 Structural relationships? From LOB Models to
The Self-financing Condition: Remembering the Limit Order Book R. Carmona, K. Webster Bendheim Center for Finance ORFE, Princeton University November 6, 2013 Structural relationships? From LOB Models to
Univerzita Karlova v Praze Matematicko fyzikální fakulta
 Univerzita Karlova v Praze Matematicko fyzikální fakulta DIPLOMOVÁ PRÁCE Jana Garajová Modely úrokových měr ve spojitém čase Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Prof.
Univerzita Karlova v Praze Matematicko fyzikální fakulta DIPLOMOVÁ PRÁCE Jana Garajová Modely úrokových měr ve spojitém čase Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Prof.
Efficient valuation of exotic derivatives in Lévy models
 Efficient valuation of exotic derivatives in models Ernst Eberlein and Antonis Papapantoleon Department of Mathematical Stochastics and Center for Data Analysis and Modeling (FDM) University of Freiburg
Efficient valuation of exotic derivatives in models Ernst Eberlein and Antonis Papapantoleon Department of Mathematical Stochastics and Center for Data Analysis and Modeling (FDM) University of Freiburg
Statistical Analysis of Data from the Stock Markets. UiO-STK4510 Autumn 2015
 Statistical Analysis of Data from the Stock Markets UiO-STK4510 Autumn 2015 Sampling Conventions We observe the price process S of some stock (or stock index) at times ft i g i=0,...,n, we denote it by
Statistical Analysis of Data from the Stock Markets UiO-STK4510 Autumn 2015 Sampling Conventions We observe the price process S of some stock (or stock index) at times ft i g i=0,...,n, we denote it by
Stochastic modelling of electricity markets Pricing Forwards and Swaps
 Stochastic modelling of electricity markets Pricing Forwards and Swaps Jhonny Gonzalez School of Mathematics The University of Manchester Magical books project August 23, 2012 Clip for this slide Pricing
Stochastic modelling of electricity markets Pricing Forwards and Swaps Jhonny Gonzalez School of Mathematics The University of Manchester Magical books project August 23, 2012 Clip for this slide Pricing
Extended Libor Models and Their Calibration
 Extended Libor Models and Their Calibration Denis Belomestny Weierstraß Institute Berlin Vienna, 16 November 2007 Denis Belomestny (WIAS) Extended Libor Models and Their Calibration Vienna, 16 November
Extended Libor Models and Their Calibration Denis Belomestny Weierstraß Institute Berlin Vienna, 16 November 2007 Denis Belomestny (WIAS) Extended Libor Models and Their Calibration Vienna, 16 November
A Simple Model of Credit Spreads with Incomplete Information
 A Simple Model of Credit Spreads with Incomplete Information Chuang Yi McMaster University April, 2007 Joint work with Alexander Tchernitser from Bank of Montreal (BMO). The opinions expressed here are
A Simple Model of Credit Spreads with Incomplete Information Chuang Yi McMaster University April, 2007 Joint work with Alexander Tchernitser from Bank of Montreal (BMO). The opinions expressed here are
The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations
 The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations Stan Stilger June 6, 1 Fouque and Tullie use importance sampling for variance reduction in stochastic volatility simulations.
The Use of Importance Sampling to Speed Up Stochastic Volatility Simulations Stan Stilger June 6, 1 Fouque and Tullie use importance sampling for variance reduction in stochastic volatility simulations.
Financial Market Models with Lévy Processes and Time-Varying Volatility
 Financial Market Models with Lévy Processes and Time-Varying Volatility Young Shin Kim Department of Statistics, Econometrics and Mathematical Finance, School of Economics and Business Engineering, University
Financial Market Models with Lévy Processes and Time-Varying Volatility Young Shin Kim Department of Statistics, Econometrics and Mathematical Finance, School of Economics and Business Engineering, University
Pricing of some exotic options with N IG-Lévy input
 Pricing of some exotic options with N IG-Lévy input Sebastian Rasmus, Søren Asmussen 2 and Magnus Wiktorsson Center for Mathematical Sciences, University of Lund, Box 8, 22 00 Lund, Sweden {rasmus,magnusw}@maths.lth.se
Pricing of some exotic options with N IG-Lévy input Sebastian Rasmus, Søren Asmussen 2 and Magnus Wiktorsson Center for Mathematical Sciences, University of Lund, Box 8, 22 00 Lund, Sweden {rasmus,magnusw}@maths.lth.se
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio
 Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
Option pricing in the stochastic volatility model of Barndorff-Nielsen and Shephard
 Option pricing in the stochastic volatility model of Barndorff-Nielsen and Shephard Indifference pricing and the minimal entropy martingale measure Fred Espen Benth Centre of Mathematics for Applications
Option pricing in the stochastic volatility model of Barndorff-Nielsen and Shephard Indifference pricing and the minimal entropy martingale measure Fred Espen Benth Centre of Mathematics for Applications
Introduction to jump and Lévy processes. John Crosby
 Introduction to jump and Lévy processes John Crosby Glasgow University / Grizzly Bear Capital My website is: http://www.john-crosby.co.uk If you spot any typos or errors, please email me. My email address
Introduction to jump and Lévy processes John Crosby Glasgow University / Grizzly Bear Capital My website is: http://www.john-crosby.co.uk If you spot any typos or errors, please email me. My email address
Optimal Stopping for American Type Options
 Optimal Stopping for Department of Mathematics Stockholm University Sweden E-mail: silvestrov@math.su.se ISI 2011, Dublin, 21-26 August 2011 Outline of communication Multivariate Modulated Markov price
Optimal Stopping for Department of Mathematics Stockholm University Sweden E-mail: silvestrov@math.su.se ISI 2011, Dublin, 21-26 August 2011 Outline of communication Multivariate Modulated Markov price
Mgr. Jakub Petrásek 1. May 4, 2009
 Dissertation Report - First Steps Petrásek 1 2 1 Department of Probability and Mathematical Statistics, Charles University email:petrasek@karlin.mff.cuni.cz 2 RSJ Invest a.s., Department of Probability
Dissertation Report - First Steps Petrásek 1 2 1 Department of Probability and Mathematical Statistics, Charles University email:petrasek@karlin.mff.cuni.cz 2 RSJ Invest a.s., Department of Probability
Extended Libor Models and Their Calibration
 Extended Libor Models and Their Calibration Denis Belomestny Weierstraß Institute Berlin Haindorf, 7 Februar 2008 Denis Belomestny (WIAS) Extended Libor Models and Their Calibration Haindorf, 7 Februar
Extended Libor Models and Their Calibration Denis Belomestny Weierstraß Institute Berlin Haindorf, 7 Februar 2008 Denis Belomestny (WIAS) Extended Libor Models and Their Calibration Haindorf, 7 Februar
Portfolio optimization for an exponential Ornstein-Uhlenbeck model with proportional transaction costs
 Portfolio optimization for an exponential Ornstein-Uhlenbeck model with proportional transaction costs Martin Forde King s College London, May 2014 (joint work with Christoph Czichowsky, Philipp Deutsch
Portfolio optimization for an exponential Ornstein-Uhlenbeck model with proportional transaction costs Martin Forde King s College London, May 2014 (joint work with Christoph Czichowsky, Philipp Deutsch
Fakulta matematiky, fyziky a informatiky. Katedra aplikovanej matematiky a štatistiky EXOTICKÝCH OPCIÍ. Diplomová práca.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
arxiv: v2 [q-fin.pr] 3 Nov 2008
![arxiv: v2 [q-fin.pr] 3 Nov 2008 arxiv: v2 [q-fin.pr] 3 Nov 2008](/thumbs/76/73187014.jpg) AN INTODUCTION TO LÉVY POCESSES WITH APPLICATIONS IN FINANCE ANTONIS PAPAPANTOLEON arxiv:84.482v2 [q-fin.p] 3 Nov 28 Abstract. These lectures notes aim at introducing Lévy processes in an informal and
AN INTODUCTION TO LÉVY POCESSES WITH APPLICATIONS IN FINANCE ANTONIS PAPAPANTOLEON arxiv:84.482v2 [q-fin.p] 3 Nov 28 Abstract. These lectures notes aim at introducing Lévy processes in an informal and
Asset Pricing Models with Underlying Time-varying Lévy Processes
 Asset Pricing Models with Underlying Time-varying Lévy Processes Stochastics & Computational Finance 2015 Xuecan CUI Jang SCHILTZ University of Luxembourg July 9, 2015 Xuecan CUI, Jang SCHILTZ University
Asset Pricing Models with Underlying Time-varying Lévy Processes Stochastics & Computational Finance 2015 Xuecan CUI Jang SCHILTZ University of Luxembourg July 9, 2015 Xuecan CUI, Jang SCHILTZ University
QUANTITATIVE FINANCE RESEARCH CENTRE. A Modern View on Merton s Jump-Diffusion Model Gerald H. L. Cheang and Carl Chiarella
 QUANIAIVE FINANCE RESEARCH CENRE QUANIAIVE F INANCE RESEARCH CENRE QUANIAIVE FINANCE RESEARCH CENRE Research Paper 87 January 011 A Modern View on Merton s Jump-Diffusion Model Gerald H. L. Cheang and
QUANIAIVE FINANCE RESEARCH CENRE QUANIAIVE F INANCE RESEARCH CENRE QUANIAIVE FINANCE RESEARCH CENRE Research Paper 87 January 011 A Modern View on Merton s Jump-Diffusion Model Gerald H. L. Cheang and
Dynamic Protection for Bayesian Optimal Portfolio
 Dynamic Protection for Bayesian Optimal Portfolio Hideaki Miyata Department of Mathematics, Kyoto University Jun Sekine Institute of Economic Research, Kyoto University Jan. 6, 2009, Kunitachi, Tokyo 1
Dynamic Protection for Bayesian Optimal Portfolio Hideaki Miyata Department of Mathematics, Kyoto University Jun Sekine Institute of Economic Research, Kyoto University Jan. 6, 2009, Kunitachi, Tokyo 1
A GENERAL FORMULA FOR OPTION PRICES IN A STOCHASTIC VOLATILITY MODEL. Stephen Chin and Daniel Dufresne. Centre for Actuarial Studies
 A GENERAL FORMULA FOR OPTION PRICES IN A STOCHASTIC VOLATILITY MODEL Stephen Chin and Daniel Dufresne Centre for Actuarial Studies University of Melbourne Paper: http://mercury.ecom.unimelb.edu.au/site/actwww/wps2009/no181.pdf
A GENERAL FORMULA FOR OPTION PRICES IN A STOCHASTIC VOLATILITY MODEL Stephen Chin and Daniel Dufresne Centre for Actuarial Studies University of Melbourne Paper: http://mercury.ecom.unimelb.edu.au/site/actwww/wps2009/no181.pdf
Pension Risk Management with Funding and Buyout Options
 Pension Risk Management with Funding and Buyout Options Samuel H. Cox, Yijia Lin and Tianxiang Shi Presented at Eleventh International Longevity Risk and Capital Markets Solutions Conference Lyon, France
Pension Risk Management with Funding and Buyout Options Samuel H. Cox, Yijia Lin and Tianxiang Shi Presented at Eleventh International Longevity Risk and Capital Markets Solutions Conference Lyon, France
Lecture 3: Review of mathematical finance and derivative pricing models
 Lecture 3: Review of mathematical finance and derivative pricing models Xiaoguang Wang STAT 598W January 21th, 2014 (STAT 598W) Lecture 3 1 / 51 Outline 1 Some model independent definitions and principals
Lecture 3: Review of mathematical finance and derivative pricing models Xiaoguang Wang STAT 598W January 21th, 2014 (STAT 598W) Lecture 3 1 / 51 Outline 1 Some model independent definitions and principals
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
INSURANCE PORTFOLIO. CSc.
 Ekonomická univerzita, Fakulta hospodárskej informatiky Dolnozemská cesta, 85 35 Bratislava INSURANCE PORTFOLIO Doc. RNDr. Ľudovít t Pinda, CSc. FHI EU, Katedra matematiky mail: pinda@euba.sk Marec 00
Ekonomická univerzita, Fakulta hospodárskej informatiky Dolnozemská cesta, 85 35 Bratislava INSURANCE PORTFOLIO Doc. RNDr. Ľudovít t Pinda, CSc. FHI EU, Katedra matematiky mail: pinda@euba.sk Marec 00
Valuation of derivative assets Lecture 8
 Valuation of derivative assets Lecture 8 Magnus Wiktorsson September 27, 2018 Magnus Wiktorsson L8 September 27, 2018 1 / 14 The risk neutral valuation formula Let X be contingent claim with maturity T.
Valuation of derivative assets Lecture 8 Magnus Wiktorsson September 27, 2018 Magnus Wiktorsson L8 September 27, 2018 1 / 14 The risk neutral valuation formula Let X be contingent claim with maturity T.
Weierstrass Institute for Applied Analysis and Stochastics Maximum likelihood estimation for jump diffusions
 Weierstrass Institute for Applied Analysis and Stochastics Maximum likelihood estimation for jump diffusions Hilmar Mai Mohrenstrasse 39 1117 Berlin Germany Tel. +49 3 2372 www.wias-berlin.de Haindorf
Weierstrass Institute for Applied Analysis and Stochastics Maximum likelihood estimation for jump diffusions Hilmar Mai Mohrenstrasse 39 1117 Berlin Germany Tel. +49 3 2372 www.wias-berlin.de Haindorf
is a standard Brownian motion.
 Stochastic Calculus Final Examination Solutions June 7, 25 There are 2 problems and points each.. (Property of Brownian Bridge) Let Bt = {B t, t B = } be a Brownian bridge, and define dx t = Xt dt + db
Stochastic Calculus Final Examination Solutions June 7, 25 There are 2 problems and points each.. (Property of Brownian Bridge) Let Bt = {B t, t B = } be a Brownian bridge, and define dx t = Xt dt + db
Pricing American Options using Lévy Processes and Monte Carlo Simulations
 U.U.D.M. Project Report 2015:14 Pricing American Options using Lévy Processes and Monte Carlo Simulations Jonas Bergström Examensarbete i matematik, 30 hp Handledare och examinator: Maciej Klimek Juni
U.U.D.M. Project Report 2015:14 Pricing American Options using Lévy Processes and Monte Carlo Simulations Jonas Bergström Examensarbete i matematik, 30 hp Handledare och examinator: Maciej Klimek Juni
RMSC 4005 Stochastic Calculus for Finance and Risk. 1 Exercises. (c) Let X = {X n } n=0 be a {F n }-supermartingale. Show that.
 1. EXERCISES RMSC 45 Stochastic Calculus for Finance and Risk Exercises 1 Exercises 1. (a) Let X = {X n } n= be a {F n }-martingale. Show that E(X n ) = E(X ) n N (b) Let X = {X n } n= be a {F n }-submartingale.
1. EXERCISES RMSC 45 Stochastic Calculus for Finance and Risk Exercises 1 Exercises 1. (a) Let X = {X n } n= be a {F n }-martingale. Show that E(X n ) = E(X ) n N (b) Let X = {X n } n= be a {F n }-submartingale.
Statistical Analysis of Short-time Option Prices Based on a Levy Model
 Washington University in St. Louis Washington University Open Scholarship Arts & Sciences Electronic Theses and Dissertations Arts & Sciences Spring 5-2018 Statistical Analysis of Short-time Option Prices
Washington University in St. Louis Washington University Open Scholarship Arts & Sciences Electronic Theses and Dissertations Arts & Sciences Spring 5-2018 Statistical Analysis of Short-time Option Prices
Degree project. Pricing American and European options under the binomial tree model and its Black-Scholes limit model
 Degree project Pricing American and European options under the binomial tree model and its Black-Scholes limit model Author: Yuankai Yang Supervisor: Roger Pettersson Examiner: Astrid Hilbert Date: 2017-09-28
Degree project Pricing American and European options under the binomial tree model and its Black-Scholes limit model Author: Yuankai Yang Supervisor: Roger Pettersson Examiner: Astrid Hilbert Date: 2017-09-28
Charles University in Prague Faculty of Social Sciences. Forecasting realized volatility: Do jumps in prices matter?
 Charles University in Prague Faculty of Social Sciences Institute of Economic Studies RIGOROSIS DIPLOMA THESIS ing realized volatility: Do jumps in prices matter? Author: Mgr. Štefan Lipták Supervisor:
Charles University in Prague Faculty of Social Sciences Institute of Economic Studies RIGOROSIS DIPLOMA THESIS ing realized volatility: Do jumps in prices matter? Author: Mgr. Štefan Lipták Supervisor:
Hedging of swaptions in a Lévy driven Heath-Jarrow-Morton framework
 Hedging of swaptions in a Lévy driven Heath-Jarrow-Morton framework Kathrin Glau, Nele Vandaele, Michèle Vanmaele Bachelier Finance Society World Congress 2010 June 22-26, 2010 Nele Vandaele Hedging of
Hedging of swaptions in a Lévy driven Heath-Jarrow-Morton framework Kathrin Glau, Nele Vandaele, Michèle Vanmaele Bachelier Finance Society World Congress 2010 June 22-26, 2010 Nele Vandaele Hedging of
Deterministic Income under a Stochastic Interest Rate
 Deterministic Income under a Stochastic Interest Rate Julia Eisenberg, TU Vienna Scientic Day, 1 Agenda 1 Classical Problem: Maximizing Discounted Dividends in a Brownian Risk Model 2 Maximizing Discounted
Deterministic Income under a Stochastic Interest Rate Julia Eisenberg, TU Vienna Scientic Day, 1 Agenda 1 Classical Problem: Maximizing Discounted Dividends in a Brownian Risk Model 2 Maximizing Discounted
Valuing power options under a regime-switching model
 6 13 11 ( ) Journal of East China Normal University (Natural Science) No. 6 Nov. 13 Article ID: 1-5641(13)6-3-8 Valuing power options under a regime-switching model SU Xiao-nan 1, WANG Wei, WANG Wen-sheng
6 13 11 ( ) Journal of East China Normal University (Natural Science) No. 6 Nov. 13 Article ID: 1-5641(13)6-3-8 Valuing power options under a regime-switching model SU Xiao-nan 1, WANG Wei, WANG Wen-sheng
P VaR0.01 (X) > 2 VaR 0.01 (X). (10 p) Problem 4
 KTH Mathematics Examination in SF2980 Risk Management, December 13, 2012, 8:00 13:00. Examiner : Filip indskog, tel. 790 7217, e-mail: lindskog@kth.se Allowed technical aids and literature : a calculator,
KTH Mathematics Examination in SF2980 Risk Management, December 13, 2012, 8:00 13:00. Examiner : Filip indskog, tel. 790 7217, e-mail: lindskog@kth.se Allowed technical aids and literature : a calculator,
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks
 Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
