X = x p(x) 1 / 6 1 / 6 1 / 6 1 / 6 1 / 6 1 / 6. x = 1 x = 2 x = 3 x = 4 x = 5 x = 6 values for the random variable X
|
|
|
- Theodore Newman
- 6 years ago
- Views:
Transcription
1 Calculus II MAT 146 Integration Applications: Probability Calculating probabilities for discrete cases typically involves comparing the number of ways a chosen event can occur to the number of ways all possible events can occur. When the cases involve an infinite number of possibilities when the function associated with the probability is a continuous function we will need to call on the definite integral for help. Through these notes, we first review aspects of probability with which you ought to already be familiar. In so doing we introduce some terminology that we ll need for the continuous case, which is the primary focus of our study of probability as an application of integral calculus. Introduction: Probability for Discrete Cases Imagine rolling a typical 6-sided die. What are the probabilities associated with the outcomes of this action? We write that P(x = C) = 1 / 6, where C is from the set {1,2,3,4,5,6}. The variable X is called a random variable. Here, X can take on values 1, 2, 3, 4, 5, or 6, each equally likely to occur. We can represent this with a table and with a plot: p(x = x) X = x p(x) 1 / 6 1 / 6 1 / 6 1 / 6 1 / 6 1 / 6 1 / 6 x = 1 x = 2 x = 3 x = 4 x = 5 x = 6 values for the random variable X Each of these represents a probability distribution for the random variable X. The set of all possible outcomes in a probability situation is called the sample space.
2 Here is another example: A two-player game involving the tossing of two coins. If the two coins match, you pay me $2. If the two coins differ, I ll pay you $1. What could happen? Here are the possibilities for the coins, where H represents a coin landing head up and T represents a coin landing tail up. H and H H and T T and H T and T These are the outcomes that comprise the sample space. P(HH)=1/4 P(TT)=1/4 P(1H,1T)=1/2 a match not a match Here is a plot of the probability distribution for the game outcomes. Here, we have joined elements from the sample space to form events. What are the long-term expectations for this game? Who ll come out ahead, you or me? We can compute the expected value (here, average winnings) to answer this. The calculation of expected value weights each outcome according to its probability and its numerical result. We know, in our game, that P(2H) = ¼, P(2T) = ¼, and P(1T,1H) = ½. Now, use these probabilities as weights that affect my potential gain or loss: Expected gain / loss = ( P(2H ))( gain / loss if 2H ) + ( P(2T ))( gain / loss if 2T ) + ( P(1T,1H ))( gain / loss if one each) = 1 $ # & $2 " 4 % ( ) + 1 $ # " 4 & $2 % ( ) + 1 $ # " 2 & '$1 % = $ $ ('$0.50) = $0.50 ( ) This result is called the expected value, represented as E(X). In general, n E(X) = " p(x i ) x i. i=1
3 For our game, E(X) = $0.50. This indicates that if I continue to play this game forever, I m likely to average a gain of $0.50 per play. For the die roll situation, E(X) = 6 " i=1 p(x i ) x i = 1 6 (1)+ 1 6 (2)+ 1 6 (3)+ 1 6 (4)+ 1 6 (5)+ 1 6 (6) = 1 ( ) 6. = 21 6 = The die-roll and coin-toss situations illustrate discrete random variables. You can count outcomes and can use those counts to answer questions such as, What is the probability of rolling an even number with a fair die? or What is the probability of getting two heads and a tail when three coins are tossed? Other probability situations are continuous situations. These situations present an infinite number of outcomes. Situations involving measurement (height, weight, length, time, and so on) as well as questions asking, How much? are often of a continuous nature. Here are examples of some continuous random variables. descriptions of continuous random variables Probability distributions (plots) for these random variables the set of random numbers between 0 and 1 heights of ISU students (inches)
4 time waiting in line at a customer service counter (minutes) As shown here, we can represent these continuous random variables as functions on a two-dimensional coordinate system. In the context of probability, we call these probability density functions (pdf). f (x) 0 " Characteristics of a Probability Density Function f(x) The probability at a point can never be negative. # f (x) dx =1 All probabilities must sum to 1. " Because a continuous random variable has an infinite number of outcomes, we cannot simply carry out counting tasks and create ratios to generate probability statements. How, then, do we calculate probabilities for continuous random variables? We represent the probability as the area under a curve under some portion of the entire probability density function and then calculate that area. Example 1 Suppose we know that the heights of ISU students can be represented as a continuous random variable x where h(x) is the probability density function, with graphical representation shown here. Represent each probability using (i) appropriate probability notation, (ii) a definite integral and (iii) shading the corresponding area under a pdf. a) the probability that the height of an ISU student chosen at random is between 60 inches and 70 inches b) the probability that the height of an ISU student chosen at random is 84 inches or more c) the probability that the height of an ISU student chosen at random is less than 62 inches
5 Solutions Heights (inches) of ISU students: h(x) is the corresponding pdf 70 P(60 x 70) h(x)dx 60 P(x 84) P(x < 62) " h(x)dx # " h(x)dx Example 2 Here is a plot that Gervaise claims is of a probability density function. a) Verify that this plot shows the requirements of a pdf. b) Calculate the following probabilities. i. P(x 4) ii. P(4 x 6) iii. P(x > 7) iv. The value R such that " f (x)dx = 1. R is called the median of the 2 distribution. R Solutions a) This is a pdf, because the function is never negative and the area under the curve sums to 1. b) Probabilities determined by calculating areas: i. P(x 4) = ( 3 / 20 )(2) + ( 1 / 2 )(2)( 3 / / 20 ) = 1 / 2 ii. P(4 x 6) = ( 1 / 2 )(2)( 3 / / 20 ) = 1 / 5 iii. P(x > 7) = ( 3 / 20 )(1) = 3 / 20 iv. Because this is a symmetric distribution, the median is at its physical center. Therefore, R = 4.
6 Example 3 The function representing the wait time for a cable TV customer-service operator to answer your call has a mean µ (Greek letter, pronounced mu) of 6 minutes. a) Create a pdf for this situation. b) Calculate the following probabilities using your pdf. i. P(x 4) ii. P(3 x 7) iii. P(x > 10) iv. The smallest value t such that P(x > t) 1 / 100. Solutions a) possible pdf: p(x) = 1 6 e x 6 for x 0; you can verify that this is a pdf by showing that " p(x) dx =1and that the mean wait time is 0 " µ = E(x) = # x p(x) dx = 6. 0 b) Calculate the following probabilities using your pdf. 4 i. P(x 4) = p(x) dx " ii. P(3 x 7) = p(x) dx " iii. P(x > 10) = " p(x) dx # iv. P(x > t) 1 / 100 " p(x) dx # 0.01 t minutes t
7 A normal distribution is often used to represent characteristics of a population. It is a symmetric distribution, represented by a bellshaped curve. The mean of a normal distribution is signified using the lower-case Greek letter mu, µ. This represents the center of the distribution. The standard deviation describes chunks of the population centered around and eminating from the mean. Approximately 68% of a normally distributed population is within 1 standard deviation of the mean, and approximately 95% of a normally distributed population is within 2 standard deviations of the mean. We use the lower-case Greek letter sigma, σ, to represent the standard deviation of a population. A normal distribution has the following probability density function: p(x) = with mean µ and standard deviation σ. 1 2" e ( xµ ) Example 4 Suppose that the weights of boxes of Raisin Bran coming off an assembly line are normally distributed with µ = 240 grams and σ = 8 grams. Then w(x) = e ( x240) 2 2(8 2 ) represents this distribution. a) What is the probability that a randomly selected box of cereal from this assembly line will: i. weigh between 235 g and 240 g? ii. weigh at least 240 g? iii. weigh between 224 g and 256 g?
8 b) Based on the information provided and on your calculations: i. Is it appropriate for the boxes of cereal coming off the line to be labeled with a weight of 240 g? ii. How would you suggest altering the production parameters, µ and σ, so that these boxes of cereal could legitimately be labeled 240 g? Generate at least three different parameter pairs, µ and σ, so that your company can be at least 98% certain that a box will be filled with at least 240 g of cereal. Solutions a) Probabilities: 240 i. P(235 x 240) = w(x) dx " ii. P(x 240) = " w(x) dx # iii. P(224 x 256) = w(x) dx " b) Based on the information and on your calculations: i. Is it appropriate for the boxes of cereal coming off the line to be labeled with a weight of 240 g? No, because there is a 50% probability that the cereal in the box will weigh less than 240 g. ii. How would you suggest altering the production parameters, µ and σ, so that these boxes of cereal could legitimately be labeled 240 g? Generate at least three different parameter pairs, µ and σ, so that your company can be at least 98% certain that a box will be filled with at least 240 g of cereal. Best bet is to decrease the standard deviation (less variation in the weights) and increase the mean (move the center above 240 g to better assure the weights will be at least 240 g). Here are some possibilities. suggested µ and σ pairs µ = 250 g and σ = 4 g µ = 248 g and σ = 4 g µ = 249 g and σ = 4 g µ = g and σ = 4 g associated probability that cereal will weigh at least 240 g P(x 240) P(x 240) P(x 240) P(x 240)
Statistical Methods in Practice STAT/MATH 3379
 Statistical Methods in Practice STAT/MATH 3379 Dr. A. B. W. Manage Associate Professor of Mathematics & Statistics Department of Mathematics & Statistics Sam Houston State University Overview 6.1 Discrete
Statistical Methods in Practice STAT/MATH 3379 Dr. A. B. W. Manage Associate Professor of Mathematics & Statistics Department of Mathematics & Statistics Sam Houston State University Overview 6.1 Discrete
Chapter 7. Random Variables
 Chapter 7 Random Variables Making quantifiable meaning out of categorical data Toss three coins. What does the sample space consist of? HHH, HHT, HTH, HTT, TTT, TTH, THT, THH In statistics, we are most
Chapter 7 Random Variables Making quantifiable meaning out of categorical data Toss three coins. What does the sample space consist of? HHH, HHT, HTH, HTT, TTT, TTH, THT, THH In statistics, we are most
CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES
 CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES DISCRETE RANDOM VARIABLE: Variable can take on only certain specified values. There are gaps between possible data values. Values may be counting numbers or
CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES DISCRETE RANDOM VARIABLE: Variable can take on only certain specified values. There are gaps between possible data values. Values may be counting numbers or
Introduction to Business Statistics QM 120 Chapter 6
 DEPARTMENT OF QUANTITATIVE METHODS & INFORMATION SYSTEMS Introduction to Business Statistics QM 120 Chapter 6 Spring 2008 Chapter 6: Continuous Probability Distribution 2 When a RV x is discrete, we can
DEPARTMENT OF QUANTITATIVE METHODS & INFORMATION SYSTEMS Introduction to Business Statistics QM 120 Chapter 6 Spring 2008 Chapter 6: Continuous Probability Distribution 2 When a RV x is discrete, we can
Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a
 Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a Announcements: There are some office hour changes for Nov 5, 8, 9 on website Week 5 quiz begins after class today and ends at
Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a Announcements: There are some office hour changes for Nov 5, 8, 9 on website Week 5 quiz begins after class today and ends at
Example. Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables
 Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables You are dealt a hand of 5 cards. Find the probability distribution table for the number of hearts. Graph
Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables You are dealt a hand of 5 cards. Find the probability distribution table for the number of hearts. Graph
2011 Pearson Education, Inc
 Statistics for Business and Economics Chapter 4 Random Variables & Probability Distributions Content 1. Two Types of Random Variables 2. Probability Distributions for Discrete Random Variables 3. The Binomial
Statistics for Business and Economics Chapter 4 Random Variables & Probability Distributions Content 1. Two Types of Random Variables 2. Probability Distributions for Discrete Random Variables 3. The Binomial
Normal distribution. We say that a random variable X follows the normal distribution if the probability density function of X is given by
 Normal distribution The normal distribution is the most important distribution. It describes well the distribution of random variables that arise in practice, such as the heights or weights of people,
Normal distribution The normal distribution is the most important distribution. It describes well the distribution of random variables that arise in practice, such as the heights or weights of people,
Chapter 6: Random Variables
 Chapter 6: Random Variables Section 6.1 Discrete and Continuous Random Variables The Practice of Statistics, 4 th edition For AP* STARNES, YATES, MOORE Chapter 6 Random Variables 6.1 Discrete and Continuous
Chapter 6: Random Variables Section 6.1 Discrete and Continuous Random Variables The Practice of Statistics, 4 th edition For AP* STARNES, YATES, MOORE Chapter 6 Random Variables 6.1 Discrete and Continuous
Part 1 In which we meet the law of averages. The Law of Averages. The Expected Value & The Standard Error. Where Are We Going?
 1 The Law of Averages The Expected Value & The Standard Error Where Are We Going? Sums of random numbers The law of averages Box models for generating random numbers Sums of draws: the Expected Value Standard
1 The Law of Averages The Expected Value & The Standard Error Where Are We Going? Sums of random numbers The law of averages Box models for generating random numbers Sums of draws: the Expected Value Standard
continuous rv Note for a legitimate pdf, we have f (x) 0 and f (x)dx = 1. For a continuous rv, P(X = c) = c f (x)dx = 0, hence
 continuous rv Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f(x) such that for any two numbers a and b with a b, P(a X b) = b a f (x)dx.
continuous rv Let X be a continuous rv. Then a probability distribution or probability density function (pdf) of X is a function f(x) such that for any two numbers a and b with a b, P(a X b) = b a f (x)dx.
In a binomial experiment of n trials, where p = probability of success and q = probability of failure. mean variance standard deviation
 Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
Homework: Due Wed, Feb 20 th. Chapter 8, # 60a + 62a (count together as 1), 74, 82
 Announcements: Week 5 quiz begins at 4pm today and ends at 3pm on Wed If you take more than 20 minutes to complete your quiz, you will only receive partial credit. (It doesn t cut you off.) Today: Sections
Announcements: Week 5 quiz begins at 4pm today and ends at 3pm on Wed If you take more than 20 minutes to complete your quiz, you will only receive partial credit. (It doesn t cut you off.) Today: Sections
The normal distribution is a theoretical model derived mathematically and not empirically.
 Sociology 541 The Normal Distribution Probability and An Introduction to Inferential Statistics Normal Approximation The normal distribution is a theoretical model derived mathematically and not empirically.
Sociology 541 The Normal Distribution Probability and An Introduction to Inferential Statistics Normal Approximation The normal distribution is a theoretical model derived mathematically and not empirically.
TOPIC: PROBABILITY DISTRIBUTIONS
 TOPIC: PROBABILITY DISTRIBUTIONS There are two types of random variables: A Discrete random variable can take on only specified, distinct values. A Continuous random variable can take on any value within
TOPIC: PROBABILITY DISTRIBUTIONS There are two types of random variables: A Discrete random variable can take on only specified, distinct values. A Continuous random variable can take on any value within
AP Statistics Section 6.1 Day 1 Multiple Choice Practice. a) a random variable. b) a parameter. c) biased. d) a random sample. e) a statistic.
 A Statistics Section 6.1 Day 1 ultiple Choice ractice Name: 1. A variable whose value is a numerical outcome of a random phenomenon is called a) a random variable. b) a parameter. c) biased. d) a random
A Statistics Section 6.1 Day 1 ultiple Choice ractice Name: 1. A variable whose value is a numerical outcome of a random phenomenon is called a) a random variable. b) a parameter. c) biased. d) a random
Section Distributions of Random Variables
 Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
MA 1125 Lecture 14 - Expected Values. Wednesday, October 4, Objectives: Introduce expected values.
 MA 5 Lecture 4 - Expected Values Wednesday, October 4, 27 Objectives: Introduce expected values.. Means, Variances, and Standard Deviations of Probability Distributions Two classes ago, we computed the
MA 5 Lecture 4 - Expected Values Wednesday, October 4, 27 Objectives: Introduce expected values.. Means, Variances, and Standard Deviations of Probability Distributions Two classes ago, we computed the
Topic 6 - Continuous Distributions I. Discrete RVs. Probability Density. Continuous RVs. Background Reading. Recall the discrete distributions
 Topic 6 - Continuous Distributions I Discrete RVs Recall the discrete distributions STAT 511 Professor Bruce Craig Binomial - X= number of successes (x =, 1,...,n) Geometric - X= number of trials (x =,...)
Topic 6 - Continuous Distributions I Discrete RVs Recall the discrete distributions STAT 511 Professor Bruce Craig Binomial - X= number of successes (x =, 1,...,n) Geometric - X= number of trials (x =,...)
Expected Value of a Random Variable
 Knowledge Article: Probability and Statistics Expected Value of a Random Variable Expected Value of a Discrete Random Variable You're familiar with a simple mean, or average, of a set. The mean value of
Knowledge Article: Probability and Statistics Expected Value of a Random Variable Expected Value of a Discrete Random Variable You're familiar with a simple mean, or average, of a set. The mean value of
Section Distributions of Random Variables
 Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
NORMAL RANDOM VARIABLES (Normal or gaussian distribution)
 NORMAL RANDOM VARIABLES (Normal or gaussian distribution) Many variables, as pregnancy lengths, foot sizes etc.. exhibit a normal distribution. The shape of the distribution is a symmetric bell shape.
NORMAL RANDOM VARIABLES (Normal or gaussian distribution) Many variables, as pregnancy lengths, foot sizes etc.. exhibit a normal distribution. The shape of the distribution is a symmetric bell shape.
Section 7.5 The Normal Distribution. Section 7.6 Application of the Normal Distribution
 Section 7.6 Application of the Normal Distribution A random variable that may take on infinitely many values is called a continuous random variable. A continuous probability distribution is defined by
Section 7.6 Application of the Normal Distribution A random variable that may take on infinitely many values is called a continuous random variable. A continuous probability distribution is defined by
Problems from 9th edition of Probability and Statistical Inference by Hogg, Tanis and Zimmerman:
 Math 224 Fall 207 Homework 5 Drew Armstrong Problems from 9th edition of Probability and Statistical Inference by Hogg, Tanis and Zimmerman: Section 3., Exercises 3, 0. Section 3.3, Exercises 2, 3, 0,.
Math 224 Fall 207 Homework 5 Drew Armstrong Problems from 9th edition of Probability and Statistical Inference by Hogg, Tanis and Zimmerman: Section 3., Exercises 3, 0. Section 3.3, Exercises 2, 3, 0,.
Chapter 4 Random Variables & Probability. Chapter 4.5, 6, 8 Probability Distributions for Continuous Random Variables
 Chapter 4.5, 6, 8 Probability for Continuous Random Variables Discrete vs. continuous random variables Examples of continuous distributions o Uniform o Exponential o Normal Recall: A random variable =
Chapter 4.5, 6, 8 Probability for Continuous Random Variables Discrete vs. continuous random variables Examples of continuous distributions o Uniform o Exponential o Normal Recall: A random variable =
PROBABILITY DISTRIBUTIONS
 CHAPTER 3 PROBABILITY DISTRIBUTIONS Page Contents 3.1 Introduction to Probability Distributions 51 3.2 The Normal Distribution 56 3.3 The Binomial Distribution 60 3.4 The Poisson Distribution 64 Exercise
CHAPTER 3 PROBABILITY DISTRIBUTIONS Page Contents 3.1 Introduction to Probability Distributions 51 3.2 The Normal Distribution 56 3.3 The Binomial Distribution 60 3.4 The Poisson Distribution 64 Exercise
6.1 Discrete & Continuous Random Variables. Nov 4 6:53 PM. Objectives
 6.1 Discrete & Continuous Random Variables examples vocab Objectives Today we will... - Compute probabilities using the probability distribution of a discrete random variable. - Calculate and interpret
6.1 Discrete & Continuous Random Variables examples vocab Objectives Today we will... - Compute probabilities using the probability distribution of a discrete random variable. - Calculate and interpret
Section Random Variables and Histograms
 Section 3.1 - Random Variables and Histograms Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Section 3.1 - Random Variables and Histograms Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Normal Distribution. Definition A continuous rv X is said to have a normal distribution with. the pdf of X is
 Normal Distribution Normal Distribution Definition A continuous rv X is said to have a normal distribution with parameter µ and σ (µ and σ 2 ), where < µ < and σ > 0, if the pdf of X is f (x; µ, σ) = 1
Normal Distribution Normal Distribution Definition A continuous rv X is said to have a normal distribution with parameter µ and σ (µ and σ 2 ), where < µ < and σ > 0, if the pdf of X is f (x; µ, σ) = 1
TRUE-FALSE: Determine whether each of the following statements is true or false.
 Chapter 6 Test Review Name TRUE-FALSE: Determine whether each of the following statements is true or false. 1) A random variable is continuous when the set of possible values includes an entire interval
Chapter 6 Test Review Name TRUE-FALSE: Determine whether each of the following statements is true or false. 1) A random variable is continuous when the set of possible values includes an entire interval
1/3/12 AP STATS. WARM UP: How was your New Year? EQ: HW: Pg 381 #1, 2, 3, 6, 9, 10, 17, 18, 24, 25, 31. Chapter
 1/3/12 AP STATS WARM UP: How was your New Year? EQ: Name one way you can tell between discrete variables and continuous variables? HW: Pg 381 #1, 2, 3, 6, 9, 10, 17, 18, 24, 25, 31 1 Jan. 3, 2012 HW: Pg
1/3/12 AP STATS WARM UP: How was your New Year? EQ: Name one way you can tell between discrete variables and continuous variables? HW: Pg 381 #1, 2, 3, 6, 9, 10, 17, 18, 24, 25, 31 1 Jan. 3, 2012 HW: Pg
Probability. An intro for calculus students P= Figure 1: A normal integral
 Probability An intro for calculus students.8.6.4.2 P=.87 2 3 4 Figure : A normal integral Suppose we flip a coin 2 times; what is the probability that we get more than 2 heads? Suppose we roll a six-sided
Probability An intro for calculus students.8.6.4.2 P=.87 2 3 4 Figure : A normal integral Suppose we flip a coin 2 times; what is the probability that we get more than 2 heads? Suppose we roll a six-sided
The Uniform Distribution
 The Uniform Distribution EXAMPLE 1 The previous problem is an example of the uniform probability distribution. Illustrate the uniform distribution. The data that follows are 55 smiling times, in seconds,
The Uniform Distribution EXAMPLE 1 The previous problem is an example of the uniform probability distribution. Illustrate the uniform distribution. The data that follows are 55 smiling times, in seconds,
ECON 214 Elements of Statistics for Economists 2016/2017
 ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
Lecture 9. Probability Distributions. Outline. Outline
 Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
4 Random Variables and Distributions
 4 Random Variables and Distributions Random variables A random variable assigns each outcome in a sample space. e.g. called a realization of that variable to Note: We ll usually denote a random variable
4 Random Variables and Distributions Random variables A random variable assigns each outcome in a sample space. e.g. called a realization of that variable to Note: We ll usually denote a random variable
Density curves. (James Madison University) February 4, / 20
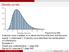 Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Chapter 4 and 5 Note Guide: Probability Distributions
 Chapter 4 and 5 Note Guide: Probability Distributions Probability Distributions for a Discrete Random Variable A discrete probability distribution function has two characteristics: Each probability is
Chapter 4 and 5 Note Guide: Probability Distributions Probability Distributions for a Discrete Random Variable A discrete probability distribution function has two characteristics: Each probability is
Example - Let X be the number of boys in a 4 child family. Find the probability distribution table:
 Chapter8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number
Chapter8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number
Chapter 7: Random Variables
 Chapter 7: Random Variables 7.1 Discrete and Continuous Random Variables 7.2 Means and Variances of Random Variables 1 Introduction A random variable is a function that associates a unique numerical value
Chapter 7: Random Variables 7.1 Discrete and Continuous Random Variables 7.2 Means and Variances of Random Variables 1 Introduction A random variable is a function that associates a unique numerical value
Lecture 9. Probability Distributions
 Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
Statistics 511 Supplemental Materials
 Gaussian (or Normal) Random Variable In this section we introduce the Gaussian Random Variable, which is more commonly referred to as the Normal Random Variable. This is a random variable that has a bellshaped
Gaussian (or Normal) Random Variable In this section we introduce the Gaussian Random Variable, which is more commonly referred to as the Normal Random Variable. This is a random variable that has a bellshaped
University of California, Los Angeles Department of Statistics. Normal distribution
 University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Normal distribution The normal distribution is the most important distribution. It describes
University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Normal distribution The normal distribution is the most important distribution. It describes
The Normal Distribution
 5.1 Introduction to Normal Distributions and the Standard Normal Distribution Section Learning objectives: 1. How to interpret graphs of normal probability distributions 2. How to find areas under the
5.1 Introduction to Normal Distributions and the Standard Normal Distribution Section Learning objectives: 1. How to interpret graphs of normal probability distributions 2. How to find areas under the
18.05 Problem Set 3, Spring 2014 Solutions
 8.05 Problem Set 3, Spring 04 Solutions Problem. (0 pts.) (a) We have P (A) = P (B) = P (C) =/. Writing the outcome of die first, we can easily list all outcomes in the following intersections. A B = {(,
8.05 Problem Set 3, Spring 04 Solutions Problem. (0 pts.) (a) We have P (A) = P (B) = P (C) =/. Writing the outcome of die first, we can easily list all outcomes in the following intersections. A B = {(,
Random Variables. 6.1 Discrete and Continuous Random Variables. Probability Distribution. Discrete Random Variables. Chapter 6, Section 1
 6.1 Discrete and Continuous Random Variables Random Variables A random variable, usually written as X, is a variable whose possible values are numerical outcomes of a random phenomenon. There are two types
6.1 Discrete and Continuous Random Variables Random Variables A random variable, usually written as X, is a variable whose possible values are numerical outcomes of a random phenomenon. There are two types
Example - Let X be the number of boys in a 4 child family. Find the probability distribution table:
 Chapter7 Probability Distributions and Statistics Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number of boys in
Chapter7 Probability Distributions and Statistics Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number of boys in
4.2 Probability Distributions
 4.2 Probability Distributions Definition. A random variable is a variable whose value is a numerical outcome of a random phenomenon. The probability distribution of a random variable tells us what the
4.2 Probability Distributions Definition. A random variable is a variable whose value is a numerical outcome of a random phenomenon. The probability distribution of a random variable tells us what the
Econ 6900: Statistical Problems. Instructor: Yogesh Uppal
 Econ 6900: Statistical Problems Instructor: Yogesh Uppal Email: yuppal@ysu.edu Lecture Slides 4 Random Variables Probability Distributions Discrete Distributions Discrete Uniform Probability Distribution
Econ 6900: Statistical Problems Instructor: Yogesh Uppal Email: yuppal@ysu.edu Lecture Slides 4 Random Variables Probability Distributions Discrete Distributions Discrete Uniform Probability Distribution
HHH HHT HTH THH HTT THT TTH TTT
 AP Statistics Name Unit 04 Probability Period Day 05 Notes Discrete & Continuous Random Variables Random Variable: Probability Distribution: Example: A probability model describes the possible outcomes
AP Statistics Name Unit 04 Probability Period Day 05 Notes Discrete & Continuous Random Variables Random Variable: Probability Distribution: Example: A probability model describes the possible outcomes
Test 7A AP Statistics Name: Directions: Work on these sheets.
 Test 7A AP Statistics Name: Directions: Work on these sheets. Part 1: Multiple Choice. Circle the letter corresponding to the best answer. 1. Suppose X is a random variable with mean µ. Suppose we observe
Test 7A AP Statistics Name: Directions: Work on these sheets. Part 1: Multiple Choice. Circle the letter corresponding to the best answer. 1. Suppose X is a random variable with mean µ. Suppose we observe
Discrete Random Variables
 Discrete Random Variables In this chapter, we introduce a new concept that of a random variable or RV. A random variable is a model to help us describe the state of the world around us. Roughly, a RV can
Discrete Random Variables In this chapter, we introduce a new concept that of a random variable or RV. A random variable is a model to help us describe the state of the world around us. Roughly, a RV can
Chapter ! Bell Shaped
 Chapter 6 6-1 Business Statistics: A First Course 5 th Edition Chapter 7 Continuous Probability Distributions Learning Objectives In this chapter, you learn:! To compute probabilities from the normal distribution!
Chapter 6 6-1 Business Statistics: A First Course 5 th Edition Chapter 7 Continuous Probability Distributions Learning Objectives In this chapter, you learn:! To compute probabilities from the normal distribution!
MATH 118 Class Notes For Chapter 5 By: Maan Omran
 MATH 118 Class Notes For Chapter 5 By: Maan Omran Section 5.1 Central Tendency Mode: the number or numbers that occur most often. Median: the number at the midpoint of a ranked data. Ex1: The test scores
MATH 118 Class Notes For Chapter 5 By: Maan Omran Section 5.1 Central Tendency Mode: the number or numbers that occur most often. Median: the number at the midpoint of a ranked data. Ex1: The test scores
Theoretical Foundations
 Theoretical Foundations Probabilities Monia Ranalli monia.ranalli@uniroma2.it Ranalli M. Theoretical Foundations - Probabilities 1 / 27 Objectives understand the probability basics quantify random phenomena
Theoretical Foundations Probabilities Monia Ranalli monia.ranalli@uniroma2.it Ranalli M. Theoretical Foundations - Probabilities 1 / 27 Objectives understand the probability basics quantify random phenomena
Some Characteristics of Data
 Some Characteristics of Data Not all data is the same, and depending on some characteristics of a particular dataset, there are some limitations as to what can and cannot be done with that data. Some key
Some Characteristics of Data Not all data is the same, and depending on some characteristics of a particular dataset, there are some limitations as to what can and cannot be done with that data. Some key
Chapter 5. Continuous Random Variables and Probability Distributions. 5.1 Continuous Random Variables
 Chapter 5 Continuous Random Variables and Probability Distributions 5.1 Continuous Random Variables 1 2CHAPTER 5. CONTINUOUS RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS Probability Distributions Probability
Chapter 5 Continuous Random Variables and Probability Distributions 5.1 Continuous Random Variables 1 2CHAPTER 5. CONTINUOUS RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS Probability Distributions Probability
Binomial Random Variables. Binomial Random Variables
 Bernoulli Trials Definition A Bernoulli trial is a random experiment in which there are only two possible outcomes - success and failure. 1 Tossing a coin and considering heads as success and tails as
Bernoulli Trials Definition A Bernoulli trial is a random experiment in which there are only two possible outcomes - success and failure. 1 Tossing a coin and considering heads as success and tails as
Chapter 3 - Lecture 5 The Binomial Probability Distribution
 Chapter 3 - Lecture 5 The Binomial Probability October 12th, 2009 Experiment Examples Moments and moment generating function of a Binomial Random Variable Outline Experiment Examples A binomial experiment
Chapter 3 - Lecture 5 The Binomial Probability October 12th, 2009 Experiment Examples Moments and moment generating function of a Binomial Random Variable Outline Experiment Examples A binomial experiment
ME3620. Theory of Engineering Experimentation. Spring Chapter III. Random Variables and Probability Distributions.
 ME3620 Theory of Engineering Experimentation Chapter III. Random Variables and Probability Distributions Chapter III 1 3.2 Random Variables In an experiment, a measurement is usually denoted by a variable
ME3620 Theory of Engineering Experimentation Chapter III. Random Variables and Probability Distributions Chapter III 1 3.2 Random Variables In an experiment, a measurement is usually denoted by a variable
Department of Quantitative Methods & Information Systems. Business Statistics. Chapter 6 Normal Probability Distribution QMIS 120. Dr.
 Department of Quantitative Methods & Information Systems Business Statistics Chapter 6 Normal Probability Distribution QMIS 120 Dr. Mohammad Zainal Chapter Goals After completing this chapter, you should
Department of Quantitative Methods & Information Systems Business Statistics Chapter 6 Normal Probability Distribution QMIS 120 Dr. Mohammad Zainal Chapter Goals After completing this chapter, you should
These Statistics NOTES Belong to:
 These Statistics NOTES Belong to: Topic Notes Questions Date 1 2 3 4 5 6 REVIEW DO EVERY QUESTION IN YOUR PROVINCIAL EXAM BINDER Important Calculator Functions to know for this chapter Normal Distributions
These Statistics NOTES Belong to: Topic Notes Questions Date 1 2 3 4 5 6 REVIEW DO EVERY QUESTION IN YOUR PROVINCIAL EXAM BINDER Important Calculator Functions to know for this chapter Normal Distributions
STUDY SET 2. Continuous Probability Distributions. ANSWER: Without continuity correction P(X>10) = P(Z>-0.66) =
 STUDY SET 2 Continuous Probability Distributions 1. The normal distribution is used to approximate the binomial under certain conditions. What is the best way to approximate the binomial using the normal?
STUDY SET 2 Continuous Probability Distributions 1. The normal distribution is used to approximate the binomial under certain conditions. What is the best way to approximate the binomial using the normal?
Chapter 7 Sampling Distributions and Point Estimation of Parameters
 Chapter 7 Sampling Distributions and Point Estimation of Parameters Part 1: Sampling Distributions, the Central Limit Theorem, Point Estimation & Estimators Sections 7-1 to 7-2 1 / 25 Statistical Inferences
Chapter 7 Sampling Distributions and Point Estimation of Parameters Part 1: Sampling Distributions, the Central Limit Theorem, Point Estimation & Estimators Sections 7-1 to 7-2 1 / 25 Statistical Inferences
Uniform Probability Distribution. Continuous Random Variables &
 Continuous Random Variables & What is a Random Variable? It is a quantity whose values are real numbers and are determined by the number of desired outcomes of an experiment. Is there any special Random
Continuous Random Variables & What is a Random Variable? It is a quantity whose values are real numbers and are determined by the number of desired outcomes of an experiment. Is there any special Random
MAS1403. Quantitative Methods for Business Management. Semester 1, Module leader: Dr. David Walshaw
 MAS1403 Quantitative Methods for Business Management Semester 1, 2018 2019 Module leader: Dr. David Walshaw Additional lecturers: Dr. James Waldren and Dr. Stuart Hall Announcements: Written assignment
MAS1403 Quantitative Methods for Business Management Semester 1, 2018 2019 Module leader: Dr. David Walshaw Additional lecturers: Dr. James Waldren and Dr. Stuart Hall Announcements: Written assignment
STAT 201 Chapter 6. Distribution
 STAT 201 Chapter 6 Distribution 1 Random Variable We know variable Random Variable: a numerical measurement of the outcome of a random phenomena Capital letter refer to the random variable Lower case letters
STAT 201 Chapter 6 Distribution 1 Random Variable We know variable Random Variable: a numerical measurement of the outcome of a random phenomena Capital letter refer to the random variable Lower case letters
Chapter Six Probability Distributions
 6.1 Probability Distributions Discrete Random Variable Chapter Six Probability Distributions x P(x) 2 0.08 4 0.13 6 0.25 8 0.31 10 0.16 12 0.01 Practice. Construct a probability distribution for the number
6.1 Probability Distributions Discrete Random Variable Chapter Six Probability Distributions x P(x) 2 0.08 4 0.13 6 0.25 8 0.31 10 0.16 12 0.01 Practice. Construct a probability distribution for the number
Chapter 7 1. Random Variables
 Chapter 7 1 Random Variables random variable numerical variable whose value depends on the outcome of a chance experiment - discrete if its possible values are isolated points on a number line - continuous
Chapter 7 1 Random Variables random variable numerical variable whose value depends on the outcome of a chance experiment - discrete if its possible values are isolated points on a number line - continuous
MATH 264 Problem Homework I
 MATH Problem Homework I Due to December 9, 00@:0 PROBLEMS & SOLUTIONS. A student answers a multiple-choice examination question that offers four possible answers. Suppose that the probability that the
MATH Problem Homework I Due to December 9, 00@:0 PROBLEMS & SOLUTIONS. A student answers a multiple-choice examination question that offers four possible answers. Suppose that the probability that the
Expectations. Definition Let X be a discrete rv with set of possible values D and pmf p(x). The expected value or mean value of X, denoted by E(X ) or
 Definition Let X be a discrete rv with set of possible values D and pmf p(x). The expected value or mean value of X, denoted by E(X ) or µ X, is E(X ) = µ X = x D x p(x) Definition Let X be a discrete
Definition Let X be a discrete rv with set of possible values D and pmf p(x). The expected value or mean value of X, denoted by E(X ) or µ X, is E(X ) = µ X = x D x p(x) Definition Let X be a discrete
Shifting our focus. We were studying statistics (data, displays, sampling...) The next few lectures focus on probability (randomness) Why?
 Probability Introduction Shifting our focus We were studying statistics (data, displays, sampling...) The next few lectures focus on probability (randomness) Why? What is Probability? Probability is used
Probability Introduction Shifting our focus We were studying statistics (data, displays, sampling...) The next few lectures focus on probability (randomness) Why? What is Probability? Probability is used
Chapter 6: Random Variables. Ch. 6-3: Binomial and Geometric Random Variables
 Chapter : Random Variables Ch. -3: Binomial and Geometric Random Variables X 0 2 3 4 5 7 8 9 0 0 P(X) 3???????? 4 4 When the same chance process is repeated several times, we are often interested in whether
Chapter : Random Variables Ch. -3: Binomial and Geometric Random Variables X 0 2 3 4 5 7 8 9 0 0 P(X) 3???????? 4 4 When the same chance process is repeated several times, we are often interested in whether
CHAPTER 8 PROBABILITY DISTRIBUTIONS AND STATISTICS
 CHAPTER 8 PROBABILITY DISTRIBUTIONS AND STATISTICS 8.1 Distribution of Random Variables Random Variable Probability Distribution of Random Variables 8.2 Expected Value Mean Mean is the average value of
CHAPTER 8 PROBABILITY DISTRIBUTIONS AND STATISTICS 8.1 Distribution of Random Variables Random Variable Probability Distribution of Random Variables 8.2 Expected Value Mean Mean is the average value of
Statistics 6 th Edition
 Statistics 6 th Edition Chapter 5 Discrete Probability Distributions Chap 5-1 Definitions Random Variables Random Variables Discrete Random Variable Continuous Random Variable Ch. 5 Ch. 6 Chap 5-2 Discrete
Statistics 6 th Edition Chapter 5 Discrete Probability Distributions Chap 5-1 Definitions Random Variables Random Variables Discrete Random Variable Continuous Random Variable Ch. 5 Ch. 6 Chap 5-2 Discrete
Consider the following examples: ex: let X = tossing a coin three times and counting the number of heads
 Overview Both chapters and 6 deal with a similar concept probability distributions. The difference is that chapter concerns itself with discrete probability distribution while chapter 6 covers continuous
Overview Both chapters and 6 deal with a similar concept probability distributions. The difference is that chapter concerns itself with discrete probability distribution while chapter 6 covers continuous
Chapter 3 Discrete Random Variables and Probability Distributions
 Chapter 3 Discrete Random Variables and Probability Distributions Part 2: Mean and Variance of a Discrete Random Variable Section 3.4 1 / 16 Discrete Random Variable - Expected Value In a random experiment,
Chapter 3 Discrete Random Variables and Probability Distributions Part 2: Mean and Variance of a Discrete Random Variable Section 3.4 1 / 16 Discrete Random Variable - Expected Value In a random experiment,
Chapter 4 Continuous Random Variables and Probability Distributions
 Chapter 4 Continuous Random Variables and Probability Distributions Part 2: More on Continuous Random Variables Section 4.5 Continuous Uniform Distribution Section 4.6 Normal Distribution 1 / 27 Continuous
Chapter 4 Continuous Random Variables and Probability Distributions Part 2: More on Continuous Random Variables Section 4.5 Continuous Uniform Distribution Section 4.6 Normal Distribution 1 / 27 Continuous
The Central Limit Theorem. Sec. 8.2: The Random Variable. it s Distribution. it s Distribution
 The Central Limit Theorem Sec. 8.1: The Random Variable it s Distribution Sec. 8.2: The Random Variable it s Distribution X p and and How Should You Think of a Random Variable? Imagine a bag with numbers
The Central Limit Theorem Sec. 8.1: The Random Variable it s Distribution Sec. 8.2: The Random Variable it s Distribution X p and and How Should You Think of a Random Variable? Imagine a bag with numbers
STAT Chapter 5: Continuous Distributions. Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s.
 STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
Prob and Stats, Nov 7
 Prob and Stats, Nov 7 The Standard Normal Distribution Book Sections: 7.1, 7.2 Essential Questions: What is the standard normal distribution, how is it related to all other normal distributions, and how
Prob and Stats, Nov 7 The Standard Normal Distribution Book Sections: 7.1, 7.2 Essential Questions: What is the standard normal distribution, how is it related to all other normal distributions, and how
Chapter 8. Variables. Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc.
 Chapter 8 Random Variables Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc. 8.1 What is a Random Variable? Random Variable: assigns a number to each outcome of a random circumstance, or,
Chapter 8 Random Variables Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc. 8.1 What is a Random Variable? Random Variable: assigns a number to each outcome of a random circumstance, or,
Bayes s Rule Example. defective. An MP3 player is selected at random and found to be defective. What is the probability it came from Factory I?
 Bayes s Rule Example A company manufactures MP3 players at two factories. Factory I produces 60% of the MP3 players and Factory II produces 40%. Two percent of the MP3 players produced at Factory I are
Bayes s Rule Example A company manufactures MP3 players at two factories. Factory I produces 60% of the MP3 players and Factory II produces 40%. Two percent of the MP3 players produced at Factory I are
Chapter 6 Continuous Probability Distributions. Learning objectives
 Chapter 6 Continuous s Slide 1 Learning objectives 1. Understand continuous probability distributions 2. Understand Uniform distribution 3. Understand Normal distribution 3.1. Understand Standard normal
Chapter 6 Continuous s Slide 1 Learning objectives 1. Understand continuous probability distributions 2. Understand Uniform distribution 3. Understand Normal distribution 3.1. Understand Standard normal
STA 320 Fall Thursday, Dec 5. Sampling Distribution. STA Fall
 STA 320 Fall 2013 Thursday, Dec 5 Sampling Distribution STA 320 - Fall 2013-1 Review We cannot tell what will happen in any given individual sample (just as we can not predict a single coin flip in advance).
STA 320 Fall 2013 Thursday, Dec 5 Sampling Distribution STA 320 - Fall 2013-1 Review We cannot tell what will happen in any given individual sample (just as we can not predict a single coin flip in advance).
Math Tech IIII, May 7
 Math Tech IIII, May 7 The Normal Probability Models Book Sections: 5.1, 5.2, & 5.3 Essential Questions: How can I use the normal distribution to compute probability? Standards: S.ID.4 Properties of the
Math Tech IIII, May 7 The Normal Probability Models Book Sections: 5.1, 5.2, & 5.3 Essential Questions: How can I use the normal distribution to compute probability? Standards: S.ID.4 Properties of the
CHAPTER 6 Random Variables
 CHAPTER 6 Random Variables 6.1 Discrete and Continuous Random Variables The Practice of Statistics, 5th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers Discrete and Continuous Random
CHAPTER 6 Random Variables 6.1 Discrete and Continuous Random Variables The Practice of Statistics, 5th Edition Starnes, Tabor, Yates, Moore Bedford Freeman Worth Publishers Discrete and Continuous Random
SECTION 4.4: Expected Value
 15 SECTION 4.4: Expected Value This section tells you why most all gambling is a bad idea. And also why carnival or amusement park games are a bad idea. Random Variables Definition: Random Variable A random
15 SECTION 4.4: Expected Value This section tells you why most all gambling is a bad idea. And also why carnival or amusement park games are a bad idea. Random Variables Definition: Random Variable A random
Central Limit Theorem, Joint Distributions Spring 2018
 Central Limit Theorem, Joint Distributions 18.5 Spring 218.5.4.3.2.1-4 -3-2 -1 1 2 3 4 Exam next Wednesday Exam 1 on Wednesday March 7, regular room and time. Designed for 1 hour. You will have the full
Central Limit Theorem, Joint Distributions 18.5 Spring 218.5.4.3.2.1-4 -3-2 -1 1 2 3 4 Exam next Wednesday Exam 1 on Wednesday March 7, regular room and time. Designed for 1 hour. You will have the full
Statistics and Probability
 Statistics and Probability Continuous RVs (Normal); Confidence Intervals Outline Continuous random variables Normal distribution CLT Point estimation Confidence intervals http://www.isrec.isb-sib.ch/~darlene/geneve/
Statistics and Probability Continuous RVs (Normal); Confidence Intervals Outline Continuous random variables Normal distribution CLT Point estimation Confidence intervals http://www.isrec.isb-sib.ch/~darlene/geneve/
5.1 Personal Probability
 5. Probability Value Page 1 5.1 Personal Probability Although we think probability is something that is confined to math class, in the form of personal probability it is something we use to make decisions
5. Probability Value Page 1 5.1 Personal Probability Although we think probability is something that is confined to math class, in the form of personal probability it is something we use to make decisions
Review of commonly missed questions on the online quiz. Lecture 7: Random variables] Expected value and standard deviation. Let s bet...
![Review of commonly missed questions on the online quiz. Lecture 7: Random variables] Expected value and standard deviation. Let s bet... Review of commonly missed questions on the online quiz. Lecture 7: Random variables] Expected value and standard deviation. Let s bet...](/thumbs/83/87696499.jpg) Recap Review of commonly missed questions on the online quiz Lecture 7: ] Statistics 101 Mine Çetinkaya-Rundel OpenIntro quiz 2: questions 4 and 5 September 20, 2011 Statistics 101 (Mine Çetinkaya-Rundel)
Recap Review of commonly missed questions on the online quiz Lecture 7: ] Statistics 101 Mine Çetinkaya-Rundel OpenIntro quiz 2: questions 4 and 5 September 20, 2011 Statistics 101 (Mine Çetinkaya-Rundel)
Value (x) probability Example A-2: Construct a histogram for population Ψ.
 Calculus 111, section 08.x The Central Limit Theorem notes by Tim Pilachowski If you haven t done it yet, go to the Math 111 page and download the handout: Central Limit Theorem supplement. Today s lecture
Calculus 111, section 08.x The Central Limit Theorem notes by Tim Pilachowski If you haven t done it yet, go to the Math 111 page and download the handout: Central Limit Theorem supplement. Today s lecture
No, because np = 100(0.02) = 2. The value of np must be greater than or equal to 5 to use the normal approximation.
 1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
5.2 Random Variables, Probability Histograms and Probability Distributions
 Chapter 5 5.2 Random Variables, Probability Histograms and Probability Distributions A random variable (r.v.) can be either continuous or discrete. It takes on the possible values of an experiment. It
Chapter 5 5.2 Random Variables, Probability Histograms and Probability Distributions A random variable (r.v.) can be either continuous or discrete. It takes on the possible values of an experiment. It
MAS187/AEF258. University of Newcastle upon Tyne
 MAS187/AEF258 University of Newcastle upon Tyne 2005-6 Contents 1 Collecting and Presenting Data 5 1.1 Introduction...................................... 5 1.1.1 Examples...................................
MAS187/AEF258 University of Newcastle upon Tyne 2005-6 Contents 1 Collecting and Presenting Data 5 1.1 Introduction...................................... 5 1.1.1 Examples...................................
Continuous Probability Distributions & Normal Distribution
 Mathematical Methods Units 3/4 Student Learning Plan Continuous Probability Distributions & Normal Distribution 7 lessons Notes: Students need practice in recognising whether a problem involves a discrete
Mathematical Methods Units 3/4 Student Learning Plan Continuous Probability Distributions & Normal Distribution 7 lessons Notes: Students need practice in recognising whether a problem involves a discrete
CHAPTER 4 DISCRETE PROBABILITY DISTRIBUTIONS
 CHAPTER 4 DISCRETE PROBABILITY DISTRIBUTIONS A random variable is the description of the outcome of an experiment in words. The verbal description of a random variable tells you how to find or calculate
CHAPTER 4 DISCRETE PROBABILITY DISTRIBUTIONS A random variable is the description of the outcome of an experiment in words. The verbal description of a random variable tells you how to find or calculate
Probability Basics. Part 1: What is Probability? INFO-1301, Quantitative Reasoning 1 University of Colorado Boulder. March 1, 2017 Prof.
 Probability Basics Part 1: What is Probability? INFO-1301, Quantitative Reasoning 1 University of Colorado Boulder March 1, 2017 Prof. Michael Paul Variables We can describe events like coin flips as variables
Probability Basics Part 1: What is Probability? INFO-1301, Quantitative Reasoning 1 University of Colorado Boulder March 1, 2017 Prof. Michael Paul Variables We can describe events like coin flips as variables
PRINTABLE VERSION. Quiz 6. Suppose that x is normally distributed with a mean of 20 and a standard deviation of 3. What is P(16.91 x 24.59)?
 PRINTABLE VERSION Quiz 6 Question 1 Suppose that x is normally distributed with a mean of 20 and a standard deviation of 3. What is P(16.91 x 24.59)? a) 0.348 b) 0.438 c) 0.353 d) 0.437 e) 0.785 Question
PRINTABLE VERSION Quiz 6 Question 1 Suppose that x is normally distributed with a mean of 20 and a standard deviation of 3. What is P(16.91 x 24.59)? a) 0.348 b) 0.438 c) 0.353 d) 0.437 e) 0.785 Question
