Using the Central Limit Theorem
|
|
|
- Jocelyn Walters
- 6 years ago
- Views:
Transcription
1 OpenStax-CNX module: m Using the Central Limit Theorem OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0 It is important for you to understand when to use the central limit theorem. If you are being asked to nd the probability of the mean, use the clt for the mean. If you are being asked to nd the probability of a sum or total, use the clt for sums. This also applies to percentiles for means and sums. : If you are being asked to nd the probability of an individual value, do not use the clt. Use the distribution of its random variable. 1 Examples of the Central Limit Theorem 1.1 Law of Large Numbers The law of large numbers says that if you take samples of larger and larger size from any population, then the mean x of the sample tends to get closer and closer to µ. From the central limit theorem, we know that as n gets larger and larger, the sample means follow a normal distribution. The larger n gets, the smaller σ the standard deviation gets. (Remember that the standard deviation for X is n.) This means that the sample mean x must be close to the population mean µ. We can say that µ is the value that the sample means approach as n gets larger. The central limit theorem illustrates the law of large numbers. 1.2 Central Limit Theorem for the Mean and Sum Examples Example 1 A study involving stress is conducted among the students on a college campus. The stress scores follow a uniform distribution with the lowest stress score equal to one and the highest equal to ve. Using a sample of 75 students, nd: a. The probability that the mean stress score for the 75 students is less than two. b. The 90 th percentile for the mean stress score for the 75 students. c. The probability that the total of the 75 stress scores is less than 200. d. The 90 th percentile for the total stress score for the 75 students. Let X = one stress score. Problems a and b ask you to nd a probability or a percentile for a mean. Problems c and d ask you to nd a probability or a percentile for a total or sum. The sample size, n, is equal to 75. Since the individual stress scores follow a uniform distribution, X U(1, 5) where a = 1 and b = 5 (See Continuous Random Variables for an explanation on the uniform distribution). µ X = a+b 2 = = 3 Version 1.5: Nov 23, :30 pm
2 OpenStax-CNX module: m (b a) 2 (5 1) 2 σ X = 12 = 12 = 1.15 For problems ( 1. ) and 2., let X = the mean stress score for the 75 students. Then, X N 3, where n = 75. Problem 1 a. Find P(x < 2). Draw the graph. Solution a. P(x < 2) = 0 The probability that the mean stress score is less than two is about zero. Figure 1 normalcdf ( ) 1,2,3, = 0 : The smallest stress score is one. Problem 2 b. Find the 90 th percentile for the mean of 75 stress scores. Draw a graph. Solution b. Let k = the 90 th precentile. Find k, where P(x < k) = k = 3.2
3 OpenStax-CNX module: m Figure 2 The 90 th percentile for the mean of 75 scores is about 3.2. This tells us that 90% of all the means of 75( stress scores ) are at most 3.2, and that 10% are at least 3.2. invnorm 0.90,3, = 3.2 For problems c and d, let ΣX = the sum of the 75 stress scores. Then, ΣX N[(75)(3), ( 75 ) (1.15)] Problem 3 c. Find P(Σx < 200). Draw the graph. Solution c. The mean of the sum of 75 stress scores is (75)(3) = 225 The standard deviation of the sum of 75 stress scores is ( 75 ) (1.15) = 9.96 P(Σx < 200) = 0 Figure 3 The probability that the total of 75 scores is less than 200 is about zero. normalcdf (75,200,(75)(3), ( 75 ) (1.15)).
4 OpenStax-CNX module: m : The smallest total of 75 stress scores is 75, because the smallest single score is one. Problem 4 d. Find the 90 th percentile for the total of 75 stress scores. Draw a graph. Solution d. Let k = the 90 th percentile. Find k where P(Σx < k) = k = Figure 4 The 90 th percentile for the sum of 75 scores is about This tells us that 90% of all the sums of 75 scores are no more than and 10% are no less than invnorm(0.90,(75)(3), ( 75 ) (1.15)) = : Exercise 5 (Solution on p. 26.) Use the information in Example 1, but use a sample size of 55 to answer the following questions. a.find P(x < 7). b.find P(Σx > 170). c.find the 80 th percentile for the mean of 55 scores. d.find the 85 th percentile for the sum of 55 scores.
5 OpenStax-CNX module: m Example 2 Suppose that a market research analyst for a cell phone company conducts a study of their customers who exceed the time allowance included on their basic cell phone contract; the analyst nds that for those people who exceed the time included in their basic contract, the excess time used follows an exponential distribution with a mean of 22 minutes. Consider a random sample of 80 customers who exceed the time allowance included in their basic cell phone contract. Let X = the excess time used by one INDIVIDUAL cell phone customer who exceeds his contracted time allowance. X ( 1 Exp 22). From previous chapters, we know that µ = 22 and σ = 22. Let X = the mean excess time used by a sample of n = 80 customers who exceed their contracted time allowance. ( ) 22 X N 22, 80 by the central limit theorem for sample means Problem 1 Using the clt to nd probability a. Find the probability that the mean excess time used by the 80 customers in the sample is longer than 20 minutes. This is asking us to nd P(x > 20). Draw the graph. b. Suppose that one customer who exceeds the time limit for his cell phone contract is randomly selected. Find the probability that this individual customer's excess time is longer than 20 minutes. This is asking us to nd P(x > 20). c. Explain why the probabilities in parts a and b are dierent. Solution a. Find: P(x > 20) ( ) P(x > 20) = using normalcdf 20,1E99,22, The probability is that the mean excess time used is more than 20 minutes, for a sample of 80 customers who exceed their contracted time allowance. Figure 5
6 OpenStax-CNX module: m : 1E99 = and 1E99 = Press the EE key for E. Or just use instead of 1E99. b. Find P(x > 20). Remember to use the exponential distribution for an individual:x Exp ( 1 22). P (x > 20) = e ( ( 1 22)(20)) or e ( (20)) = c. a. P(x > 20) = but P(x > 20) = b. The probabilities are not equal because we use dierent distributions to calculate the probability for individuals and for means. c. When asked to nd the probability of an individual value, use the stated distribution of its random variable; do not use the clt. Use the clt with the normal distribution when you are being asked to nd the probability for a mean. Problem 2 Using the clt to nd percentiles Find the 95 th percentile for the sample mean excess time for samples of 80 customers who exceed their basic contract time allowances. Draw a graph. Solution Let k = the 95 th percentile. ( Find k where ) P(x < k) = k = 26.0 using invnorm 0.95,22, 80 = 26.0 Figure 6 The 95 th percentile for the sample mean excess time used is about 26.0 minutes for random samples of 80 customers who exceed their contractual allowed time. Ninety ve percent of such samples would have means under 26 minutes; only ve percent of such samples would have means above 26 minutes.
7 OpenStax-CNX module: m : Exercise 8 (Solution on p. 26.) Use the information in Example 2, but change the sample size to 144. a.find P(20 < x < 30). b.find P(Σx is at least 3,000). c.find the 75 th percentile for the sample mean excess time of 144 customers. d.find the 85 th percentile for the sum of 144 excess times used by customers. Example 3 In the United States, someone is sexually assaulted every two minutes, on average, according to a number of studies. Suppose the standard deviation is 0.5 minutes and the sample size is 100. Problem a. Find the median, the rst quartile, and the third quartile for the sample mean time of sexual assaults in the United States. b. Find the median, the rst quartile, and the third quartile for the sum of sample times of sexual assaults in the United States. c. Find the probability that a sexual assault occurs on the average between 1.75 and 1.85 minutes. d. Find the value that is two standard deviations above the sample mean. e. Find the IQR for the sum of the sample times. Solution a. We have, µ x = µ = 2 and σ x = σ n = a. 50 th percentile = µ x = µ = 2 b. 25 th percentile = invnorm(0.25,2,0.05) = 1.97 c. 75 th percentile = invnorm(0.75,2,0.05) = 2.03 = Therefore: b. We have µ Σx = n(µ x ) = 100(2) = 200 and σ µx = n(σ x ) = 10(0.5) = 5. Therefore a. 50 th percentile = µ Σx = n(µ x ) = 100(2) = 200 b. 25 th percentile = invnorm(0.25,200,5) = c. 75 th percentile = invnorm(0.75,200,5) = c. P(1.75 < x < 1.85) = normalcdf(1.75,1.85,2,0.05) = d. Using the z-score equation, z = x µx σ x, and solving for x, we have x = 2(0.05) + 2 = 2.1 e. The IQR is 75 th percentile 25 th percentile = = 6.74 : Exercise 10 (Solution on p. 26.) Based on data from the National Health Survey, women between the ages of 18 and 24 have an average systolic blood pressures (in mm Hg) of with a standard deviation of Systolic blood pressure for women between the ages of 18 to 24 follow a normal distribution. a.if one woman from this population is randomly selected, nd the probability that her systolic blood pressure is greater than 120.
8 OpenStax-CNX module: m b.if 40 women from this population are randomly selected, nd the probability that their mean systolic blood pressure is greater than 120. c.if the sample were four women between the ages of 18 to 24 and we did not know the original distribution, could the central limit theorem be used? Example 4 A study was done about violence against prostitutes and the symptoms of the posttraumatic stress that they developed. The age range of the prostitutes was 14 to 61. The mean age was 30.9 years with a standard deviation of nine years. a. In a sample of 25 prostitutes, what is the probability that the mean age of the prostitutes is less than 35? b. Is it likely that the mean age of the sample group could be more than 50 years? Interpret the results. c. In a sample of 49 prostitutes, what is the probability that the sum of the ages is no less than 1,600? d. Is it likely that the sum of the ages of the 49 prostitutes is at most 1,595? Interpret the results. e. Find the 95 th percentile for the sample mean age of 65 prostitutes. Interpret the results. f. Find the 90 th percentile for the sum of the ages of 65 prostitutes. Interpret the results. Solution a. P(x < 35) = normalcdf(-e99,35,30.9,1.8) = b. P(x > 50) = normalcdf(50, E99,30.9,1.8) 0. For this sample group, it is almost impossible for the group's average age to be more than 50. However, it is still possible for an individual in this group to have an age greater than 50. c. P(Σx 1,600) = normalcdf(1600,e99, ,63) = d. P(Σx 1,595) = normalcdf(-e99,1595, ,63) = This means that there is a 90% chance that the sum of the ages for the sample group n = 49 is at most e. The 95th percentile = invnorm(0.95,30.9,1.1) = This indicates that 95% of the prostitutes in the sample of 65 are younger than 32.7 years, on average. f. The 90th percentile = invnorm(0.90,2008.5,72.56) = This indicates that 90% of the prostitutes in the sample of 65 have a sum of ages less than 2,101.5 years. : Exercise 12 (Solution on p. 26.) According to Boeing data, the 757 airliner carries 200 passengers and has doors with a mean height of 72 inches. Assume for a certain population of men we have a mean of 69.0 inches and a standard deviation of 2.8 inches. a.what mean doorway height would allow 95% of men to enter the aircraft without bending? b.assume that half of the 200 passengers are men. What mean doorway height satises the condition that there is a 0.95 probability that this height is greater than the mean height of 100 men?
9 OpenStax-CNX module: m c.for engineers designing the 757, which result is more relevant: the height from part a or part b? Why? : : Normal Approximation to the Binomial Historically, being able to compute binomial probabilities was one of the most important applications of the central limit theorem. Binomial probabilities with a small value for n(say, 20) were displayed in a table in a book. To calculate the probabilities with large values of n, you had to use the binomial formula, which could be very complicated. Using the normal approximation to the binomial distribution simplied the process. To compute the normal approximation to the binomial distribution, take a simple random sample from a population. You must meet the conditions for a binomial distribution: ˆthere are a certain number n of independent trials ˆthe outcomes of any trial are success or failure ˆeach trial has the same probability of a success p Recall that if X is the binomial random variable, then X B(n, p). The shape of the binomial distribution needs to be similar to the shape of the normal distribution. To ensure this, the quantities np and nq must both be greater than ve (np > 5 and nq > 5; the approximation is better if they are both greater than or equal to 10). Then the binomial can be approximated by the normal distribution with mean µ = np and standard deviation σ = npq. Remember that q = 1 p. In order to get the best approximation, add 0.5 to x or subtract 0.5 from x (use x or x 0.5). The number 0.5 is called the continuity correction factor and is used in the following example. Example 5 Suppose in a local Kindergarten through 12 th grade (K - 12) school district, 53 percent of the population favor a charter school for grades K through 5. A simple random sample of 300 is surveyed. a. Find the probability that at least 150 favor a charter school. b. Find the probability that at most 160 favor a charter school. c. Find the probability that more than 155 favor a charter school. d. Find the probability that fewer than 147 favor a charter school. e. Find the probability that exactly 175 favor a charter school. Let X = the number that favor a charter school for grades K trough 5. X B(n, p) where n = 300 and p = Since np > 5 and nq > 5, use the normal approximation to the binomial. The formulas for the mean and standard deviation are µ = np and σ = npq. The mean is 159 and the standard deviation is The random variable for the normal distribution is Y. Y N(159, ). See The Normal Distribution for help with calculator instructions. For part a, you include 150 so P(X 150) has normal approximation P(Y 149.5) = normalcdf(149.5,10^99,159,8.6447) = For part b, you include 160 so P(X 160) has normal appraximation P(Y 160.5) = normalcdf(0,160.5,159,8.6447) = For part c, you exclude 155 so P(X > 155) has normal approximation P(y > 155.5) = normalcdf(155.5,10^99,159,8.6447) = For part d, you exclude 147 so P(X < 147) has normal approximation P(Y < 146.5) = normalcdf(0,146.5,159,8.6447) = For part e,p(x = 175) has normal approximation P(174.5 < Y < 175.5) =
10 OpenStax-CNX module: m normalcdf(174.5,175.5,159,8.6447) = Because of calculators and computer software that let you calculate binomial probabilities for large values of n easily, it is not necessary to use the the normal approximation to the binomial distribution, provided that you have access to these technology tools. Most school labs have Microsoft Excel, an example of computer software that calculates binomial probabilities. Many students have access to the TI-83 or 84 series calculators, and they easily calculate probabilities for the binomial distribution. If you type in "binomial probability distribution calculation" in an Internet browser, you can nd at least one online calculator for the binomial. For Example 3, the probabilities are calculated using the following binomial distribution: ( n = 300 and p = 0.53). Compare the binomial and normal distribution answers. See Discrete Random Variables for help with calculator instructions for the binomial. P(X 150) :1 - binomialcdf(300,0.53,149) = P(X 160) :binomialcdf(300,0.53,160) = P(X > 155) :1 - binomialcdf(300,0.53,155) = P(X < 147) :binomialcdf(300,0.53,146) = P(X = 175) :(You use the binomial pdf.)binomialpdf(300,0.53,175) = : Exercise 13 (Solution on p. 26.) In a city, 46 percent of the population favor the incumbent, Dawn Morgan, for mayor. A simple random sample of 500 is taken. Using the continuity correction factor, nd the probability that at least 250 favor Dawn Morgan for mayor. : Class Time: Names: Student Learning Outcomes The student will demonstrate and compare properties of the central limit theorem. : This lab works best when sampling from several classes and combining data. Collect the Data 1.Count the change in your pocket. (Do not include bills.) 2.Randomly survey 30 classmates. Record the values of the change in Table 1. Table 1
11 OpenStax-CNX module: m Construct a histogram. Make ve to six intervals. Sketch the graph using a ruler and pencil. Scale the axes. Figure 7 4.Calculate the following (n = 1; surveying one person at a time): a.x = b.s = 5.Draw a smooth curve through the tops of the bars of the histogram. Use one to two complete sentences to describe the general shape of the curve. Collecting Averages of Pairs Repeat steps one through ve of the section Collect the Data. (Collect the Data, p. 10) with one exception. Instead of recording the change of 30 classmates, record the average change of 30 pairs. 1.Randomly survey 30 pairs of classmates. 2.Record the values of the average of their change in Table 2. Table 2 3.Construct a histogram. Scale the axes using the same scaling you used for the section titled Collect the Data (Collect the Data, p. 10). Sketch the graph using a ruler and a pencil.
12 OpenStax-CNX module: m Figure 8 4.Calculate the following (n = 2; surveying two people at a time): a.x = b.s = 5.Draw a smooth curve through tops of the bars of the histogram. Use one to two complete sentences to describe the general shape of the curve. Collecting Averages of Groups of Five Repeat steps one through ve (of the section titled Collect the Data (Collect the Data, p. 10)) with one exception. Instead of recording the change of 30 classmates, record the average change of 30 groups of ve. 1.Randomly survey 30 groups of ve classmates. 2.Record the values of the average of their change. Table 3 3.Construct a histogram. Scale the axes using the same scaling you used for the section titled Collect the Data (Collect the Data, p. 10). Sketch the graph using a ruler and a pencil.
13 OpenStax-CNX module: m Figure 9 4.Calculate the following (n = 5; surveying ve people at a time): a.x = b.s = 5.Draw a smooth curve through tops of the bars of the histogram. Use one to two complete sentences to describe the general shape of the curve. Discussion Questions 1.Why did the shape of the distribution of the data change, as n changed? Use one to two complete sentences to explain what happened. 2.In the section titled Collect the Data (Collect the Data, p. 10), what was the approximate distribution of the data? X (, ) 3.In the section titled Collecting Averages of Groups of Five (Collecting Averages of Groups of Five, p. 12), what was the approximate distribution of the averages? X (, ) 4.In one to two complete sentences, explain any dierences in your answers to the previous two questions. : Class Time: Names: Student Learning Outcomes The student will demonstrate and compare properties of the central limit theorem. Given X = length of time (in days) that a cookie recipe lasted at the Olmstead Homestead. (Assume that each of the dierent recipes makes the same quantity of cookies.)
14 OpenStax-CNX module: m Recipe # X Recipe # X Recipe # X Recipe # X Table 4 Calculate the following: a.µ x = b.σ x = Collect the Data Use a random number generator to randomly select four samples of size n = 5 from the given population. Record your samples in Table 5. Then, for each sample, calculate the mean to the nearest tenth. Record them in the spaces provided. Record the sample means for the rest of the class. 1.Complete the table: Sample 1 Sample 2 Sample 3 Sample 4 Sample means from other groups: continued on next page
15 OpenStax-CNX module: m Means: x = x = x = x = Table 5 2.Calculate the following: a.x = b.s x = 3.Again, use a random number generator to randomly select four samples from the population. This time, make the samples of size n = 10. Record the samples in Table 6. As before, for each sample, calculate the mean to the nearest tenth. Record them in the spaces provided. Record the sample means for the rest of the class. Sample 1 Sample 2 Sample 3 Sample 4 Sample means from other groups Means: x = x = x = x = Table 6 4.Calculate the following: a.x = b.s x = 5.For the original population, construct a histogram. Make intervals with a bar width of one day. Sketch the graph using a ruler and pencil. Scale the axes.
16 OpenStax-CNX module: m Figure 10 6.Draw a smooth curve through the tops of the bars of the histogram. Use one to two complete sentences to describe the general shape of the curve. Repeat the Procedure for n = 5 1.For the sample of n = 5 days averaged together, construct a histogram of the averages (your means together with the means of the other groups). Make intervals with bar widths of 1 2 a day. Sketch the graph using a ruler and pencil. Scale the axes. Figure 11 2.Draw a smooth curve through the tops of the bars of the histogram. Use one to two complete sentences to describe the general shape of the curve. Repeat the Procedure for n = 10 1.For the sample of n = 10 days averaged together, construct a histogram of the averages (your means together with the means of the other groups). Make intervals with bar widths of 1 2 a day. Sketch the graph using a ruler and pencil. Scale the axes.
17 OpenStax-CNX module: m Figure 12 2.Draw a smooth curve through the tops of the bars of the histogram. Use one to two complete sentences to describe the general shape of the curve. Discussion Questions 1.Compare the three histograms you have made, the one for the population and the two for the sample means. In three to ve sentences, describe the similarities and dierences. 2.State the theoretical (according to the clt) distributions for the sample means. a.n = 5: x (, ) b.n = 10: x (, ) 3.Are the sample means for n = 5 and n = 10 close to the theoretical mean, µ x? Explain why or why not. 4.Which of the two distributions of sample means has the smaller standard deviation? Why? 5.As n changed, why did the shape of the distribution of the data change? Use one to two complete sentences to explain what happened. 2 References Data from the Wall Street Journal. National Health and Nutrition Examination Survey. Center for Disease Control and Prevention. Available online at (accessed May 17, 2013). 3 Chapter Review The central limit theorem can be used to illustrate the law of large numbers. The law of large numbers states that the larger the sample size you take from a population, the closer the sample mean x gets to µ. 4 Use the following information to answer the next ten exercises: A manufacturer produces 25-pound lifting weights. The lowest actual weight is 24 pounds, and the highest is 26 pounds. Each weight is equally likely so the distribution of weights is uniform. A sample of 100 weights is taken. Exercise 14 (Solution on p. 26.) a. What is the distribution for the weights of one 25-pound lifting weight? What is the mean and standard deivation? b. What is the distribution for the mean weight of pound lifting weights? c. Find the probability that the mean actual weight for the 100 weights is less than 24.9.
18 OpenStax-CNX module: m Exercise 15 Draw the graph from Exercise Exercise 16 (Solution on p. 26.) Find the probability that the mean actual weight for the 100 weights is greater than Exercise 17 Draw the graph from Exercise Exercise 18 (Solution on p. 26.) Find the 90 th percentile for the mean weight for the 100 weights. Exercise 19 Draw the graph from Exercise Exercise 20 (Solution on p. 26.) a. What is the distribution for the sum of the weights of pound lifting weights? b. Find P(Σx < 2,450). Exercise 21 Draw the graph from Exercise Exercise 22 (Solution on p. 26.) Find the 90 th percentile for the total weight of the 100 weights. Exercise 23 Draw the graph from Exercise Use the following information to answer the next ve exercises: The length of time a particular smartphone's battery lasts follows an exponential distribution with a mean of ten months. A sample of 64 of these smartphones is taken. Exercise 24 (Solution on p. 26.) a. What is the standard deviation? b. What is the parameter m? Exercise 25 What is the distribution for the length of time one battery lasts? Exercise 26 (Solution on p. 27.) What is the distribution for the mean length of time 64 batteries last? Exercise 27 What is the distribution for the total length of time 64 batteries last? Exercise 28 (Solution on p. 27.) Find the probability that the sample mean is between seven and 11. Exercise 29 Find the 80 th percentile for the total length of time 64 batteries last. Exercise 30 (Solution on p. 27.) Find the IQR for the mean amount of time 64 batteries last. Exercise 31 Find the middle 80% for the total amount of time 64 batteries last. Use the following information to answer the next eight exercises: A uniform distribution has a minimum of six and a maximum of ten. A sample of 50 is taken.
19 OpenStax-CNX module: m Exercise 32 (Solution on p. 27.) Find P(Σx > 420). Exercise 33 Find the 90 th percentile for the sums. Exercise 34 (Solution on p. 27.) Find the 15 th percentile for the sums. Exercise 35 Find the rst quartile for the sums. Exercise 36 (Solution on p. 27.) Find the third quartile for the sums. Exercise 37 Find the 80 th percentile for the sums. 5 Homework Exercise 38 The attention span of a two-year-old is exponentially distributed with a mean of about eight minutes. Suppose we randomly survey 60 two-year-olds. a. In words, X = b. X (, ) c. In words, X = d. X (, ) e. Before doing any calculations, which do you think will be higher? Explain why. i. The probability that an individual attention span is less than ten minutes. ii. The probability that the average attention span for the 60 children is less than ten minutes? f. Calculate the probabilities in part e. g. Explain why the distribution for X is not exponential. Exercise 39 (Solution on p. 27.) The closing stock prices of 35 U.S. semiconductor manufacturers are given as follows ; 30.25; ; 46.75; ; 18.25; 5; 0.125; ; 6.875; 28.25; 24.25; 21; 1.5; 30.25; 71; 43.5; 49.25; ; 31; 16.5; 9.5; 18.5; 18; 9; 10.5; ; 1.25; 18; 12.87; 7; ; 2.875; 60.25; a. In words, X = b. i. x = ii. s x = iii. n = c. Construct a histogram of the distribution of the averages. Start at x = Use bar widths of ten. d. In words, describe the distribution of stock prices. e. Randomly average ve stock prices together. (Use a random number generator.) Continue averaging ve pieces together until you have ten averages. List those ten averages. f. Use the ten averages from part e to calculate the following. i. x = ii. s x =
20 OpenStax-CNX module: m g. Construct a histogram of the distribution of the averages. Start at x = Use bar widths of ten. h. Does this histogram look like the graph in part c? i. In one or two complete sentences, explain why the graphs either look the same or look dierent? j. Based upon the theory of the central limit theorem, X (, ) Use the following information to answer the next three exercises: Richard's Furniture Company delivers furniture from 10 A.M. to 2 P.M. continuously and uniformly. We are interested in how long (in hours) past the 10 A.M. start time that individuals wait for their delivery. Exercise 40 X (, ) a. U(0,4) b. U(10,2) c. Eχp(2) d. N(2,1) Exercise 41 (Solution on p. 27.) The average wait time is: a. one hour. b. two hours. c. two and a half hours. d. four hours. Exercise 42 Suppose that it is now past noon on a delivery day. The probability that a person must wait at least one and a half more hours is: a. 1 4 b. 1 2 c. 3 4 d. 3 8 Use the following information to answer the next two exercises: The time to wait for a particular rural bus is distributed uniformly from zero to 75 minutes. One hundred riders are randomly sampled to learn how long they waited. Exercise 43 (Solution on p. 27.) The 90 th percentile sample average wait time (in minutes) for a sample of 100 riders is: a b c d Exercise 44 Would you be surprised, based upon numerical calculations, if the sample average wait time (in minutes) for 100 riders was less than 30 minutes? a. yes
21 OpenStax-CNX module: m b. no c. There is not enough information. Use the following to answer the next two exercises: The cost of unleaded gasoline in the Bay Area once followed an unknown distribution with a mean of $4.59 and a standard deviation of $0.10. Sixteen gas stations from the Bay Area are randomly chosen. We are interested in the average cost of gasoline for the 16 gas stations. Exercise 45 (Solution on p. 27.) What's the approximate probability that the average price for 16 gas stations is over $4.69? a. almost zero b c d. unknown Exercise 46 Find the probability that the average price for 30 gas stations is less than $4.55. a b c d e. 0 Exercise 47 (Solution on p. 27.) Suppose in a local Kindergarten through 12 th grade (K - 12) school district, 53 percent of the population favor a charter school for grades K through ve. A simple random sample of 300 is surveyed. Calculate following using the normal approximation to the binomial distribtion. a. Find the probability that less than 100 favor a charter school for grades K through 5. b. Find the probability that 170 or more favor a charter school for grades K through 5. c. Find the probability that no more than 140 favor a charter school for grades K through 5. d. Find the probability that there are fewer than 130 that favor a charter school for grades K through 5. e. Find the probability that exactly 150 favor a charter school for grades K through 5. If you have access to an appropriate calculator or computer software, try calculating these probabilities using the technology. Exercise 48 Four friends, Janice, Barbara, Kathy and Roberta, decided to carpool together to get to school. Each day the driver would be chosen by randomly selecting one of the four names. They carpool to school for 96 days. Use the normal approximation to the binomial to calculate the following probabilities. Round the standard deviation to four decimal places. a. Find the probability that Janice is the driver at most 20 days. b. Find the probability that Roberta is the driver more than 16 days. c. Find the probability that Barbara drives exactly 24 of those 96 days. Exercise 49 (Solution on p. 27.) X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let ΣX be the random variable of sums. For parts c through f, sketch the graph, shade the region, label and scale the horizontal axis for X, and nd the probability.
22 OpenStax-CNX module: m a. Sketch the distributions of X and X on the same graph. b. X (, ) c. P(x < 60) = d. Find the 30 th percentile for the mean. e. P(56 < x < 62) = f. P(18 < x < 58) = g. Σx (, ) h. Find the minimum value for the upper quartile for the sum. i. P(1,400 < Σx < 1,550) = Exercise 50 Suppose that the length of research papers is uniformly distributed from ten to 25 pages. We survey a class in which 55 research papers were turned in to a professor. The 55 research papers are considered a random collection of all papers. We are interested in the average length of the research papers. a. In words, X = b. X (, ) c. µ x = d. σ x = e. In words, X = f. X (, ) g. In words, ΣX = h. ΣX (, ) i. Without doing any calculations, do you think that it's likely that the professor will need to read a total of more than 1,050 pages? Why? j. Calculate the probability that the professor will need to read a total of more than 1,050 pages. k. Why is it so unlikely that the average length of the papers will be less than 12 pages? Exercise 51 (Solution on p. 27.) Salaries for teachers in a particular elementary school district are normally distributed with a mean of $44,000 and a standard deviation of $6,500. We randomly survey ten teachers from that district. a. Find the 90 th percentile for an individual teacher's salary. b. Find the 90 th percentile for the average teacher's salary. Exercise 52 The average length of a maternity stay in a U.S. hospital is said to be 2.4 days with a standard deviation of 0.9 days. We randomly survey 80 women who recently bore children in a U.S. hospital. a. In words, X = b. In words, X = c. X (, ) d. In words, ΣX = e. ΣX (, ) f. Is it likely that an individual stayed more than ve days in the hospital? Why or why not? g. Is it likely that the average stay for the 80 women was more than ve days? Why or why not? h. Which is more likely: i. An individual stayed more than ve days. ii. the average stay of 80 women was more than ve days.
23 OpenStax-CNX module: m i. If we were to sum up the women's stays, is it likely that, collectively they spent more than a year in the hospital? Why or why not? For each problem, wherever possible, provide graphs and use the calculator. Exercise 53 (Solution on p. 28.) NeverReady batteries has engineered a newer, longer lasting AAA battery. The company claims this battery has an average life span of 17 hours with a standard deviation of 0.8 hours. Your statistics class questions this claim. As a class, you randomly select 30 batteries and nd that the sample mean life span is 16.7 hours. If the process is working properly, what is the probability of getting a random sample of 30 batteries in which the sample mean lifetime is 16.7 hours or less? Is the company's claim reasonable? Exercise 54 Men have an average weight of 172 pounds with a standard deviation of 29 pounds. a. Find the probability that 20 randomly selected men will have a sum weight greater than 3600 lbs. b. If 20 men have a sum weight greater than 3500 lbs, then their total weight exceeds the safety limits for water taxis. Based on (a), is this a safety concern? Explain. Exercise 55 (Solution on p. 28.) M&M candies large candy bags have a claimed net weight of g. The standard deviation for the weight of the individual candies is g. The following table is from a stats experiment conducted by a statistics class.
24 OpenStax-CNX module: m Red Orange Yellow Brown Blue Green Table The bag contained 465 candies and he listed weights in the table came from randomly selected candies. Count the weights. a. Find the mean sample weight and the standard deviation of the sample weights of candies in the table. b. Find the sum of the sample weights in the table and the standard deviation of the sum the of the weights. c. If 465 M&Ms are randomly selected, nd the probability that their weights sum to at least d. Is the Mars Company's M&M labeling accurate?
25 OpenStax-CNX module: m Exercise 56 The Screw Right Company claims their 3 4 inch screws are within ±0.23 of the claimed mean diameter of inches with a standard deviation of inches. The following data were recorded Table 8 The screws were randomly selected from the local home repair store. a. Find the mean diameter and standard deviation for the sample b. Find the probability that 50 randomly selected screws will be within the stated tolerance levels. Is the company's diameter claim plausible? Exercise 57 (Solution on p. 28.) Your company has a contract to perform preventive maintenance on thousands of air-conditioners in a large city. Based on service records from previous years, the time that a technician spends servicing a unit averages one hour with a standard deviation of one hour. In the coming week, your company will service a simple random sample of 70 units in the city. You plan to budget an average of 1.1 hours per technician to complete the work. Will this be enough time? Exercise 58 A typical adult has an average IQ score of 105 with a standard deviation of 20. If 20 randomly selected adults are given an IQ tesst, what is the probability that the sample mean scores will be between 85 and 125 points? Exercise 59 (Solution on p. 28.) Certain coins have an average weight of grams with a standard deviation of g. If a vending machine is designed to accept coins whose weights range from g to g, what is the expected number of rejected coins when 280 randomly selected coins are inserted into the machine?
26 OpenStax-CNX module: m Solutions to Exercises in this Module to Exercise (p. 4): Solutions a b c d to Exercise (p. 7): Solutions a b c d. 3,441.6 Solution to Exercise (p. 7) a. P(x > 120) = normalcdf(120,99,114.8,13.1) = There is about a 3%, that the randomly selected woman will have systolics blood ( pressure greater ) than 120. b. P(x > 120) = normalcdf 120,114.8, = There is only a 0.6% chance that the average systolic blood pressure for the randomly selected group is greater than 120. c. The central limit theorem could not be used if the sample size were four and we did not know the original distribution was normal. The sample size would be too small. Solution to Exercise (p. 8) a. We know that µ x = µ = 69 and we have σ x = 2.8. The height of the doorway is found to be invnorm(0.95,69,2.8) = b. We know that µ x = µ = 69 and we have σ x = So, invnorm(0.95,69,0.28) = c. When designing the doorway heights, we need to incorporate as much variability as possible in order to accommodate as many passengers as possible. Therefore, we need to use the result based on part a. to Exercise (p. 10): Solutions Solution to Exercise (p. 17) a. U(24, 26), 25, b. N(25, ) c Solution to Exercise (p. 18) Solution to Exercise (p. 18) Solution to Exercise (p. 18) a. N(2,500, ) b. 0 Solution to Exercise (p. 18) 2, Solution to Exercise (p. 18) a. 10 b. 1 10
27 OpenStax-CNX module: m Solution ( to ) Exercise (p. 18) N 10, 10 8 Solution to Exercise (p. 18) Solution to Exercise (p. 18) 1.69 Solution to Exercise (p. 18) Solution to Exercise (p. 19) Solution to Exercise (p. 19) Solution to Exercise (p. 19) a. X = the closing stock prices for U.S. semiconductor manufacturers b. i. $20.71; ii. $17.31; iii. 35 c. d. Exponential distribution, X ( ) 1 Exp e. Answers will vary. f. i. $20.71; ii. $11.14 g. Answers will vary. h. Answers will vary. i. Answers ( will vary. ) j. N 20.71, Solution to Exercise (p. 20) b Solution to Exercise (p. 20) b Solution to Exercise (p. 21) a Solution to Exercise (p. 21) a. 0 b c d e Solution to Exercise (p. 21) a. Check student's ( ) solution. 9 b. X N 60, 25 c d e f g. N(1500, 45) h i Solution to Exercise (p. 22)
28 OpenStax-CNX module: m a. $52,330 b. $46,634 Solution to Exercise (p. 23) We have µ = 17, σ = 0.8, x = ( 16.7, and n = 30. To) calculate the probability, we use normalcdf(lower, σ upper, µ, n ) = normalcdf E 99,16.7,17, = If the process is working properly, then the probability that a sample of 30 batteries would have at most 16.7 lifetime hours is only 2%. Therefore, the class was justied to question the claim. Solution to Exercise (p. 23) a. For the sample, we have n = 100, x = 0.862, s = 0.05 b. Σx = 85.65, Σs = 5.18 c. normalcdf(396.9,e99,(465)(0.8565),(0.05)( 465)) 1 d. Since the probability of a sample of size 465 having at least a mean sum of is appproximately 1, we can conclude that Mars is correctly labeling their M&M packages. Solution to Exercise (p. 25) Use normalcdf ( ) 1 E 99,1.1,1, 70 = This means that there is an 80% chance that the service time will be less than 1.1 hours. It could be wise to schedule more time since there is an associated 20% chance that the maintenance time will be greater than 1.1 hours. Solution to Exercise (p.( 25) ) Since we have normalcdf 5.111,5.291,5.201, , we can conclude that practically all the coins are within the limits, therefore, there should be no rejected coins out of a well selected sample of size 280. Glossary Denition 1: Exponential Distribution a continuous random variable (RV) that appears when we are interested in the intervals of time between some random events, for example, the length of time between emergency arrivals at a hospital, notation: X Exp(m). The mean is µ = 1 m and the standard deviation is σ = 1 m. The probability density function is f (x) = me mx, x 0 and the cumulative distribution function is P(X x) = 1 e mx. Denition 2: Mean a number that measures the central tendency; a common name for mean is "average." The term "mean" is a shortened form of "arithmetic mean." By denition, the mean for a sample (denoted by x) is x =, and the mean for a population (denoted by µ) Sum of all values in the sample is Number of values in the sample Sum of all values in the population Number of values in the population. µ = Denition 3: Normal Distribution a continuous random variable (RV) with pdf f (x) = 1 σ 2π e (x µ2 2σ, where µ is the mean of the 2 distribution and σ is the standard deviation.; notation: X N(µ, σ). If µ = 0 and σ = 1, the RV is called the standard normal distribution. Denition 4: Uniform Distribution a continuous random variable (RV) that has equally likely outcomes over the domain, a < x < b; often referred as the Rectangular Distribution because the graph of the pdf has the form of a rectangle. Notation: X U(a, b). The mean is µ = a + b 2 and the standard deviation is
29 OpenStax-CNX module: m (b a) 2 σ = 12. The probability density function is f (x) = 1 b a for a < x < b or a x b. The cumulative distribution is P(X x) = x a b a.
Using the Central Limit
 Using the Central Limit Theorem By: OpenStaxCollege It is important for you to understand when to use the central limit theorem. If you are being asked to find the probability of the mean, use the clt
Using the Central Limit Theorem By: OpenStaxCollege It is important for you to understand when to use the central limit theorem. If you are being asked to find the probability of the mean, use the clt
7 THE CENTRAL LIMIT THEOREM
 CHAPTER 7 THE CENTRAL LIMIT THEOREM 373 7 THE CENTRAL LIMIT THEOREM Figure 7.1 If you want to figure out the distribution of the change people carry in their pockets, using the central limit theorem and
CHAPTER 7 THE CENTRAL LIMIT THEOREM 373 7 THE CENTRAL LIMIT THEOREM Figure 7.1 If you want to figure out the distribution of the change people carry in their pockets, using the central limit theorem and
Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the
 Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the mean, use the CLT for the mean. If you are being asked to
Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the mean, use the CLT for the mean. If you are being asked to
Central Limit Theorem: Homework
 Connexions module: m16952 1 Central Limit Theorem: Homework Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Connexions module: m16952 1 Central Limit Theorem: Homework Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
The Central Limit Theorem: Homework
 The Central Limit Theorem: Homework EXERCISE 1 X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let X be the random variable of sums.
The Central Limit Theorem: Homework EXERCISE 1 X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let X be the random variable of sums.
The Central Limit Theorem: Homework
 EERCISE 1 The Central Limit Theorem: Homework N(60, 9). Suppose that you form random samples of 25 from this distribution. Let be the random variable of averages. Let be the random variable of sums. For
EERCISE 1 The Central Limit Theorem: Homework N(60, 9). Suppose that you form random samples of 25 from this distribution. Let be the random variable of averages. Let be the random variable of sums. For
The Central Limit Theorem for Sums
 OpenStax-CNX module: m46997 1 The Central Limit Theorem for Sums OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0 Suppose X is a random
OpenStax-CNX module: m46997 1 The Central Limit Theorem for Sums OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0 Suppose X is a random
The Central Limit Theorem: Homework
 The Central Limit Theorem: Homework EXERCISE 1 X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let X be the random variable of sums.
The Central Limit Theorem: Homework EXERCISE 1 X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let X be the random variable of sums.
Continuous Random Variables: The Uniform Distribution *
 OpenStax-CNX module: m16819 1 Continuous Random Variables: The Uniform Distribution * Susan Dean Barbara Illowsky, Ph.D. This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution
OpenStax-CNX module: m16819 1 Continuous Random Variables: The Uniform Distribution * Susan Dean Barbara Illowsky, Ph.D. This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution
The Uniform Distribution
 Connexions module: m46972 The Uniform Distribution OpenStax College This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License 3.0 The uniform distribution
Connexions module: m46972 The Uniform Distribution OpenStax College This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License 3.0 The uniform distribution
CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES
 CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES DISCRETE RANDOM VARIABLE: Variable can take on only certain specified values. There are gaps between possible data values. Values may be counting numbers or
CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES DISCRETE RANDOM VARIABLE: Variable can take on only certain specified values. There are gaps between possible data values. Values may be counting numbers or
CH 5 Normal Probability Distributions Properties of the Normal Distribution
 Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Derived copy of Using the Normal Distribution *
 OpenStax-CNX module: m62375 1 Derived copy of Using the Normal Distribution * Cindy Sun Based on Using the Normal Distribution by OpenStax This work is produced by OpenStax-CNX and licensed under the Creative
OpenStax-CNX module: m62375 1 Derived copy of Using the Normal Distribution * Cindy Sun Based on Using the Normal Distribution by OpenStax This work is produced by OpenStax-CNX and licensed under the Creative
Normal Distribution: Introduction
 Connexions module: m16979 1 Normal Distribution: Introduction Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Connexions module: m16979 1 Normal Distribution: Introduction Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
The Central Limit Theorem for Sample Means (Averages)
 The Central Limit Theorem for Sample Means (Averages) By: OpenStaxCollege Suppose X is a random variable with a distribution that may be known or unknown (it can be any distribution). Using a subscript
The Central Limit Theorem for Sample Means (Averages) By: OpenStaxCollege Suppose X is a random variable with a distribution that may be known or unknown (it can be any distribution). Using a subscript
As you draw random samples of size n, as n increases, the sample means tend to be normally distributed.
 The Central Limit Theorem The central limit theorem (clt for short) is one of the most powerful and useful ideas in all of statistics. The clt says that if we collect samples of size n with a "large enough
The Central Limit Theorem The central limit theorem (clt for short) is one of the most powerful and useful ideas in all of statistics. The clt says that if we collect samples of size n with a "large enough
Chapter 7 Study Guide: The Central Limit Theorem
 Chapter 7 Study Guide: The Central Limit Theorem Introduction Why are we so concerned with means? Two reasons are that they give us a middle ground for comparison and they are easy to calculate. In this
Chapter 7 Study Guide: The Central Limit Theorem Introduction Why are we so concerned with means? Two reasons are that they give us a middle ground for comparison and they are easy to calculate. In this
Lecture Slides. Elementary Statistics Tenth Edition. by Mario F. Triola. and the Triola Statistics Series. Slide 1
 Lecture Slides Elementary Statistics Tenth Edition and the Triola Statistics Series by Mario F. Triola Slide 1 Chapter 6 Normal Probability Distributions 6-1 Overview 6-2 The Standard Normal Distribution
Lecture Slides Elementary Statistics Tenth Edition and the Triola Statistics Series by Mario F. Triola Slide 1 Chapter 6 Normal Probability Distributions 6-1 Overview 6-2 The Standard Normal Distribution
Chapter 4 and 5 Note Guide: Probability Distributions
 Chapter 4 and 5 Note Guide: Probability Distributions Probability Distributions for a Discrete Random Variable A discrete probability distribution function has two characteristics: Each probability is
Chapter 4 and 5 Note Guide: Probability Distributions Probability Distributions for a Discrete Random Variable A discrete probability distribution function has two characteristics: Each probability is
Statistics for Business and Economics: Random Variables:Continuous
 Statistics for Business and Economics: Random Variables:Continuous STT 315: Section 107 Acknowledgement: I d like to thank Dr. Ashoke Sinha for allowing me to use and edit the slides. Murray Bourne (interactive
Statistics for Business and Economics: Random Variables:Continuous STT 315: Section 107 Acknowledgement: I d like to thank Dr. Ashoke Sinha for allowing me to use and edit the slides. Murray Bourne (interactive
Section Introduction to Normal Distributions
 Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Example - Let X be the number of boys in a 4 child family. Find the probability distribution table:
 Chapter7 Probability Distributions and Statistics Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number of boys in
Chapter7 Probability Distributions and Statistics Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number of boys in
MidTerm 1) Find the following (round off to one decimal place):
 MidTerm 1) 68 49 21 55 57 61 70 42 59 50 66 99 Find the following (round off to one decimal place): Mean = 58:083, round off to 58.1 Median = 58 Range = max min = 99 21 = 78 St. Deviation = s = 8:535,
MidTerm 1) 68 49 21 55 57 61 70 42 59 50 66 99 Find the following (round off to one decimal place): Mean = 58:083, round off to 58.1 Median = 58 Range = max min = 99 21 = 78 St. Deviation = s = 8:535,
Part V - Chance Variability
 Part V - Chance Variability Dr. Joseph Brennan Math 148, BU Dr. Joseph Brennan (Math 148, BU) Part V - Chance Variability 1 / 78 Law of Averages In Chapter 13 we discussed the Kerrich coin-tossing experiment.
Part V - Chance Variability Dr. Joseph Brennan Math 148, BU Dr. Joseph Brennan (Math 148, BU) Part V - Chance Variability 1 / 78 Law of Averages In Chapter 13 we discussed the Kerrich coin-tossing experiment.
PROBABILITY DISTRIBUTIONS
 CHAPTER 3 PROBABILITY DISTRIBUTIONS Page Contents 3.1 Introduction to Probability Distributions 51 3.2 The Normal Distribution 56 3.3 The Binomial Distribution 60 3.4 The Poisson Distribution 64 Exercise
CHAPTER 3 PROBABILITY DISTRIBUTIONS Page Contents 3.1 Introduction to Probability Distributions 51 3.2 The Normal Distribution 56 3.3 The Binomial Distribution 60 3.4 The Poisson Distribution 64 Exercise
Collaborative Statistics Using Spreadsheets. Chapter 6
 Collaborative Statistics Using Spreadsheets This document is attributed to OpenStax-CNX Chapter 6 Open Assembly Edition Open Assembly editions of open textbooks are disaggregated versions designed to facilitate
Collaborative Statistics Using Spreadsheets This document is attributed to OpenStax-CNX Chapter 6 Open Assembly Edition Open Assembly editions of open textbooks are disaggregated versions designed to facilitate
The Uniform Distribution
 The Uniform Distribution EXAMPLE 1 The previous problem is an example of the uniform probability distribution. Illustrate the uniform distribution. The data that follows are 55 smiling times, in seconds,
The Uniform Distribution EXAMPLE 1 The previous problem is an example of the uniform probability distribution. Illustrate the uniform distribution. The data that follows are 55 smiling times, in seconds,
Lecture 9. Probability Distributions. Outline. Outline
 Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Math 227 Elementary Statistics. Bluman 5 th edition
 Math 227 Elementary Statistics Bluman 5 th edition CHAPTER 6 The Normal Distribution 2 Objectives Identify distributions as symmetrical or skewed. Identify the properties of the normal distribution. Find
Math 227 Elementary Statistics Bluman 5 th edition CHAPTER 6 The Normal Distribution 2 Objectives Identify distributions as symmetrical or skewed. Identify the properties of the normal distribution. Find
Lecture 9. Probability Distributions
 Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
ECON 214 Elements of Statistics for Economists 2016/2017
 ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
Continuous Probability Distributions
 8.1 Continuous Probability Distributions Distributions like the binomial probability distribution and the hypergeometric distribution deal with discrete data. The possible values of the random variable
8.1 Continuous Probability Distributions Distributions like the binomial probability distribution and the hypergeometric distribution deal with discrete data. The possible values of the random variable
Week 7. Texas A& M University. Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4
 Week 7 Oğuz Gezmiş Texas A& M University Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week7 1 / 19
Week 7 Oğuz Gezmiş Texas A& M University Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week7 1 / 19
Chapter 4 Random Variables & Probability. Chapter 4.5, 6, 8 Probability Distributions for Continuous Random Variables
 Chapter 4.5, 6, 8 Probability for Continuous Random Variables Discrete vs. continuous random variables Examples of continuous distributions o Uniform o Exponential o Normal Recall: A random variable =
Chapter 4.5, 6, 8 Probability for Continuous Random Variables Discrete vs. continuous random variables Examples of continuous distributions o Uniform o Exponential o Normal Recall: A random variable =
Chapter 5. Sampling Distributions
 Lecture notes, Lang Wu, UBC 1 Chapter 5. Sampling Distributions 5.1. Introduction In statistical inference, we attempt to estimate an unknown population characteristic, such as the population mean, µ,
Lecture notes, Lang Wu, UBC 1 Chapter 5. Sampling Distributions 5.1. Introduction In statistical inference, we attempt to estimate an unknown population characteristic, such as the population mean, µ,
Chapter 7: Sampling Distributions Chapter 7: Sampling Distributions
 Chapter 7: Sampling Distributions Objectives: Students will: Define a sampling distribution. Contrast bias and variability. Describe the sampling distribution of a proportion (shape, center, and spread).
Chapter 7: Sampling Distributions Objectives: Students will: Define a sampling distribution. Contrast bias and variability. Describe the sampling distribution of a proportion (shape, center, and spread).
Lecture 6: Chapter 6
 Lecture 6: Chapter 6 C C Moxley UAB Mathematics 3 October 16 6.1 Continuous Probability Distributions Last week, we discussed the binomial probability distribution, which was discrete. 6.1 Continuous Probability
Lecture 6: Chapter 6 C C Moxley UAB Mathematics 3 October 16 6.1 Continuous Probability Distributions Last week, we discussed the binomial probability distribution, which was discrete. 6.1 Continuous Probability
Example - Let X be the number of boys in a 4 child family. Find the probability distribution table:
 Chapter8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number
Chapter8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number
STAT Chapter 5: Continuous Distributions. Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s.
 STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
Midterm Test 1 (Sample) Student Name (PRINT):... Student Signature:... Use pencil, so that you can erase and rewrite if necessary.
 MA 180/418 Midterm Test 1 (Sample) Student Name (PRINT):............................................. Student Signature:................................................... Use pencil, so that you can erase
MA 180/418 Midterm Test 1 (Sample) Student Name (PRINT):............................................. Student Signature:................................................... Use pencil, so that you can erase
Example. Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables
 Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables You are dealt a hand of 5 cards. Find the probability distribution table for the number of hearts. Graph
Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables You are dealt a hand of 5 cards. Find the probability distribution table for the number of hearts. Graph
MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION
 MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION We have examined discrete random variables, those random variables for which we can list the possible values. We will now look at continuous random variables.
MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION We have examined discrete random variables, those random variables for which we can list the possible values. We will now look at continuous random variables.
2011 Pearson Education, Inc
 Statistics for Business and Economics Chapter 4 Random Variables & Probability Distributions Content 1. Two Types of Random Variables 2. Probability Distributions for Discrete Random Variables 3. The Binomial
Statistics for Business and Economics Chapter 4 Random Variables & Probability Distributions Content 1. Two Types of Random Variables 2. Probability Distributions for Discrete Random Variables 3. The Binomial
Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19)
 Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x
Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x
STAT Chapter 5: Continuous Distributions. Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s.
 STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
Chapter 8. Variables. Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc.
 Chapter 8 Random Variables Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc. 8.1 What is a Random Variable? Random Variable: assigns a number to each outcome of a random circumstance, or,
Chapter 8 Random Variables Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc. 8.1 What is a Random Variable? Random Variable: assigns a number to each outcome of a random circumstance, or,
1. Find the area under the standard normal distribution curve for each. (a) Between z = 0.19 and z = 1.23.
 Statistics Test 3 Name: KEY 1 Find the area under the standard normal distribution curve for each a Between = 019 and = 123 normalcdf 019, 123 = 04660 b To the left of = 156 normalcdf 100, 156 = 00594
Statistics Test 3 Name: KEY 1 Find the area under the standard normal distribution curve for each a Between = 019 and = 123 normalcdf 019, 123 = 04660 b To the left of = 156 normalcdf 100, 156 = 00594
Normal distribution. We say that a random variable X follows the normal distribution if the probability density function of X is given by
 Normal distribution The normal distribution is the most important distribution. It describes well the distribution of random variables that arise in practice, such as the heights or weights of people,
Normal distribution The normal distribution is the most important distribution. It describes well the distribution of random variables that arise in practice, such as the heights or weights of people,
The normal distribution is a theoretical model derived mathematically and not empirically.
 Sociology 541 The Normal Distribution Probability and An Introduction to Inferential Statistics Normal Approximation The normal distribution is a theoretical model derived mathematically and not empirically.
Sociology 541 The Normal Distribution Probability and An Introduction to Inferential Statistics Normal Approximation The normal distribution is a theoretical model derived mathematically and not empirically.
Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a
 Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a Announcements: There are some office hour changes for Nov 5, 8, 9 on website Week 5 quiz begins after class today and ends at
Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a Announcements: There are some office hour changes for Nov 5, 8, 9 on website Week 5 quiz begins after class today and ends at
EXERCISES FOR PRACTICE SESSION 2 OF STAT CAMP
 EXERCISES FOR PRACTICE SESSION 2 OF STAT CAMP Note 1: The exercises below that are referenced by chapter number are taken or modified from the following open-source online textbook that was adapted by
EXERCISES FOR PRACTICE SESSION 2 OF STAT CAMP Note 1: The exercises below that are referenced by chapter number are taken or modified from the following open-source online textbook that was adapted by
8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions 8-1
 8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions For Example: On August 8, 2011, the Dow dropped 634.8 points, sending shock waves through the financial community.
8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions For Example: On August 8, 2011, the Dow dropped 634.8 points, sending shock waves through the financial community.
FINAL REVIEW W/ANSWERS
 FINAL REVIEW W/ANSWERS ( 03/15/08 - Sharon Coates) Concepts to review before answering the questions: A population consists of the entire group of people or objects of interest to an investigator, while
FINAL REVIEW W/ANSWERS ( 03/15/08 - Sharon Coates) Concepts to review before answering the questions: A population consists of the entire group of people or objects of interest to an investigator, while
Probability. An intro for calculus students P= Figure 1: A normal integral
 Probability An intro for calculus students.8.6.4.2 P=.87 2 3 4 Figure : A normal integral Suppose we flip a coin 2 times; what is the probability that we get more than 2 heads? Suppose we roll a six-sided
Probability An intro for calculus students.8.6.4.2 P=.87 2 3 4 Figure : A normal integral Suppose we flip a coin 2 times; what is the probability that we get more than 2 heads? Suppose we roll a six-sided
ECON 214 Elements of Statistics for Economists
 ECON 214 Elements of Statistics for Economists Session 7 The Normal Distribution Part 1 Lecturer: Dr. Bernardin Senadza, Dept. of Economics Contact Information: bsenadza@ug.edu.gh College of Education
ECON 214 Elements of Statistics for Economists Session 7 The Normal Distribution Part 1 Lecturer: Dr. Bernardin Senadza, Dept. of Economics Contact Information: bsenadza@ug.edu.gh College of Education
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Chapter 6 Exam A Name The given values are discrete. Use the continuity correction and describe the region of the normal distribution that corresponds to the indicated probability. 1) The probability of
Chapter 6 Exam A Name The given values are discrete. Use the continuity correction and describe the region of the normal distribution that corresponds to the indicated probability. 1) The probability of
5.1 Personal Probability
 5. Probability Value Page 1 5.1 Personal Probability Although we think probability is something that is confined to math class, in the form of personal probability it is something we use to make decisions
5. Probability Value Page 1 5.1 Personal Probability Although we think probability is something that is confined to math class, in the form of personal probability it is something we use to make decisions
Commonly Used Distributions
 Chapter 4: Commonly Used Distributions 1 Introduction Statistical inference involves drawing a sample from a population and analyzing the sample data to learn about the population. We often have some knowledge
Chapter 4: Commonly Used Distributions 1 Introduction Statistical inference involves drawing a sample from a population and analyzing the sample data to learn about the population. We often have some knowledge
Density curves. (James Madison University) February 4, / 20
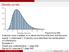 Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Uniform Probability Distribution. Continuous Random Variables &
 Continuous Random Variables & What is a Random Variable? It is a quantity whose values are real numbers and are determined by the number of desired outcomes of an experiment. Is there any special Random
Continuous Random Variables & What is a Random Variable? It is a quantity whose values are real numbers and are determined by the number of desired outcomes of an experiment. Is there any special Random
Chapter 4. Section 4.1 Objectives. Random Variables. Random Variables. Chapter 4: Probability Distributions
 Chapter 4: Probability s 4. Probability s 4. Binomial s Section 4. Objectives Distinguish between discrete random variables and continuous random variables Construct a discrete probability distribution
Chapter 4: Probability s 4. Probability s 4. Binomial s Section 4. Objectives Distinguish between discrete random variables and continuous random variables Construct a discrete probability distribution
Homework: Due Wed, Feb 20 th. Chapter 8, # 60a + 62a (count together as 1), 74, 82
 Announcements: Week 5 quiz begins at 4pm today and ends at 3pm on Wed If you take more than 20 minutes to complete your quiz, you will only receive partial credit. (It doesn t cut you off.) Today: Sections
Announcements: Week 5 quiz begins at 4pm today and ends at 3pm on Wed If you take more than 20 minutes to complete your quiz, you will only receive partial credit. (It doesn t cut you off.) Today: Sections
= 0.35 (or ˆp = We have 20 independent trials, each with probability of success (heads) equal to 0.5, so X has a B(20, 0.5) distribution.
 Chapter 5 Solutions 51 (a) n = 1500 (the sample size) (b) The Yes count seems like the most reasonable choice, but either count is defensible (c) X = 525 (or X = 975) (d) ˆp = 525 1500 = 035 (or ˆp = 975
Chapter 5 Solutions 51 (a) n = 1500 (the sample size) (b) The Yes count seems like the most reasonable choice, but either count is defensible (c) X = 525 (or X = 975) (d) ˆp = 525 1500 = 035 (or ˆp = 975
Central Limit Theorem
 Central Limit Theorem Lots of Samples 1 Homework Read Sec 6-5. Discussion Question pg 329 Do Ex 6-5 8-15 2 Objective Use the Central Limit Theorem to solve problems involving sample means 3 Sample Means
Central Limit Theorem Lots of Samples 1 Homework Read Sec 6-5. Discussion Question pg 329 Do Ex 6-5 8-15 2 Objective Use the Central Limit Theorem to solve problems involving sample means 3 Sample Means
work to get full credit.
 Chapter 18 Review Name Date Period Write complete answers, using complete sentences where necessary.show your work to get full credit. MULTIPLE CHOICE. Choose the one alternative that best completes the
Chapter 18 Review Name Date Period Write complete answers, using complete sentences where necessary.show your work to get full credit. MULTIPLE CHOICE. Choose the one alternative that best completes the
Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc.
 Chapter 8 Measures of Center Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc. Data that can only be integer
Chapter 8 Measures of Center Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc. Data that can only be integer
The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations.
 6.1 6.2 The Standard Normal Curve The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations. Basic Properties 1. The total area under the curve is.
6.1 6.2 The Standard Normal Curve The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations. Basic Properties 1. The total area under the curve is.
Central Limit Theorem (cont d) 7/28/2006
 Central Limit Theorem (cont d) 7/28/2006 Central Limit Theorem for Binomial Distributions Theorem. For the binomial distribution b(n, p, j) we have lim npq b(n, p, np + x npq ) = φ(x), n where φ(x) is
Central Limit Theorem (cont d) 7/28/2006 Central Limit Theorem for Binomial Distributions Theorem. For the binomial distribution b(n, p, j) we have lim npq b(n, p, np + x npq ) = φ(x), n where φ(x) is
Math 120 Introduction to Statistics Mr. Toner s Lecture Notes. Standardizing normal distributions The Standard Normal Curve
 6.1 6.2 The Standard Normal Curve Standardizing normal distributions The "bell-shaped" curve, or normal curve, is a probability distribution that describes many reallife situations. Basic Properties 1.
6.1 6.2 The Standard Normal Curve Standardizing normal distributions The "bell-shaped" curve, or normal curve, is a probability distribution that describes many reallife situations. Basic Properties 1.
Chapter 4. The Normal Distribution
 Chapter 4 The Normal Distribution 1 Chapter 4 Overview Introduction 4-1 Normal Distributions 4-2 Applications of the Normal Distribution 4-3 The Central Limit Theorem 4-4 The Normal Approximation to the
Chapter 4 The Normal Distribution 1 Chapter 4 Overview Introduction 4-1 Normal Distributions 4-2 Applications of the Normal Distribution 4-3 The Central Limit Theorem 4-4 The Normal Approximation to the
Normal Probability Distributions
 C H A P T E R Normal Probability Distributions 5 Section 5.2 Example 3 (pg. 248) Normal Probabilities Assume triglyceride levels of the population of the United States are normally distributed with a mean
C H A P T E R Normal Probability Distributions 5 Section 5.2 Example 3 (pg. 248) Normal Probabilities Assume triglyceride levels of the population of the United States are normally distributed with a mean
Statistics (This summary is for chapters 18, 29 and section H of chapter 19)
 Statistics (This summary is for chapters 18, 29 and section H of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x n =
Statistics (This summary is for chapters 18, 29 and section H of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x n =
STAT 3090 Test 2 - Version B Fall Student s Printed Name: PLEASE READ DIRECTIONS!!!!
 Student s Printed Name: Instructor: XID: Section #: Read each question very carefully. You are permitted to use a calculator on all portions of this exam. You are NOT allowed to use any textbook, notes,
Student s Printed Name: Instructor: XID: Section #: Read each question very carefully. You are permitted to use a calculator on all portions of this exam. You are NOT allowed to use any textbook, notes,
Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at
 Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. Let X represent the savings of a resident; X ~ N(3000,
Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. Let X represent the savings of a resident; X ~ N(3000,
In a binomial experiment of n trials, where p = probability of success and q = probability of failure. mean variance standard deviation
 Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
These Statistics NOTES Belong to:
 These Statistics NOTES Belong to: Topic Notes Questions Date 1 2 3 4 5 6 REVIEW DO EVERY QUESTION IN YOUR PROVINCIAL EXAM BINDER Important Calculator Functions to know for this chapter Normal Distributions
These Statistics NOTES Belong to: Topic Notes Questions Date 1 2 3 4 5 6 REVIEW DO EVERY QUESTION IN YOUR PROVINCIAL EXAM BINDER Important Calculator Functions to know for this chapter Normal Distributions
5-1 pg ,4,5, EOO,39,47,50,53, pg ,5,9,13,17,19,21,22,25,30,31,32, pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38
 5-1 pg. 242 3,4,5, 17-37 EOO,39,47,50,53,56 5-2 pg. 249 9,10,13,14,17,18 5-3 pg. 257 1,5,9,13,17,19,21,22,25,30,31,32,34 5-4 pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38 5-5 pg. 281 5-14,16,19,21,22,25,26,30
5-1 pg. 242 3,4,5, 17-37 EOO,39,47,50,53,56 5-2 pg. 249 9,10,13,14,17,18 5-3 pg. 257 1,5,9,13,17,19,21,22,25,30,31,32,34 5-4 pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38 5-5 pg. 281 5-14,16,19,21,22,25,26,30
Confidence Intervals and Sample Size
 Confidence Intervals and Sample Size Chapter 6 shows us how we can use the Central Limit Theorem (CLT) to 1. estimate a population parameter (such as the mean or proportion) using a sample, and. determine
Confidence Intervals and Sample Size Chapter 6 shows us how we can use the Central Limit Theorem (CLT) to 1. estimate a population parameter (such as the mean or proportion) using a sample, and. determine
Unit 2: Statistics Probability
 Applied Math 30 3-1: Distributions Probability Distribution: - a table or a graph that displays the theoretical probability for each outcome of an experiment. - P (any particular outcome) is between 0
Applied Math 30 3-1: Distributions Probability Distribution: - a table or a graph that displays the theoretical probability for each outcome of an experiment. - P (any particular outcome) is between 0
Math 160 Professor Busken Chapter 5 Worksheets
 Math 160 Professor Busken Chapter 5 Worksheets Name: 1. Find the expected value. Suppose you play a Pick 4 Lotto where you pay 50 to select a sequence of four digits, such as 2118. If you select the same
Math 160 Professor Busken Chapter 5 Worksheets Name: 1. Find the expected value. Suppose you play a Pick 4 Lotto where you pay 50 to select a sequence of four digits, such as 2118. If you select the same
Section Distributions of Random Variables
 Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
University of California, Los Angeles Department of Statistics. Normal distribution
 University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Normal distribution The normal distribution is the most important distribution. It describes
University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Normal distribution The normal distribution is the most important distribution. It describes
Section Distributions of Random Variables
 Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
CHAPTER 5 SAMPLING DISTRIBUTIONS
 CHAPTER 5 SAMPLING DISTRIBUTIONS Sampling Variability. We will visualize our data as a random sample from the population with unknown parameter μ. Our sample mean Ȳ is intended to estimate population mean
CHAPTER 5 SAMPLING DISTRIBUTIONS Sampling Variability. We will visualize our data as a random sample from the population with unknown parameter μ. Our sample mean Ȳ is intended to estimate population mean
BIOL The Normal Distribution and the Central Limit Theorem
 BIOL 300 - The Normal Distribution and the Central Limit Theorem In the first week of the course, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are
BIOL 300 - The Normal Distribution and the Central Limit Theorem In the first week of the course, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are
4.1 Probability Distributions
 Probability and Statistics Mrs. Leahy Chapter 4: Discrete Probability Distribution ALWAYS KEEP IN MIND: The Probability of an event is ALWAYS between: and!!!! 4.1 Probability Distributions Random Variables
Probability and Statistics Mrs. Leahy Chapter 4: Discrete Probability Distribution ALWAYS KEEP IN MIND: The Probability of an event is ALWAYS between: and!!!! 4.1 Probability Distributions Random Variables
Chapter 6. The Normal Probability Distributions
 Chapter 6 The Normal Probability Distributions 1 Chapter 6 Overview Introduction 6-1 Normal Probability Distributions 6-2 The Standard Normal Distribution 6-3 Applications of the Normal Distribution 6-5
Chapter 6 The Normal Probability Distributions 1 Chapter 6 Overview Introduction 6-1 Normal Probability Distributions 6-2 The Standard Normal Distribution 6-3 Applications of the Normal Distribution 6-5
The Binomial Probability Distribution
 The Binomial Probability Distribution MATH 130, Elements of Statistics I J. Robert Buchanan Department of Mathematics Fall 2017 Objectives After this lesson we will be able to: determine whether a probability
The Binomial Probability Distribution MATH 130, Elements of Statistics I J. Robert Buchanan Department of Mathematics Fall 2017 Objectives After this lesson we will be able to: determine whether a probability
No, because np = 100(0.02) = 2. The value of np must be greater than or equal to 5 to use the normal approximation.
 1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
Chapter 8. Binomial and Geometric Distributions
 Chapter 8 Binomial and Geometric Distributions Lesson 8-1, Part 1 Binomial Distribution What is a Binomial Distribution? Specific type of discrete probability distribution The outcomes belong to two categories
Chapter 8 Binomial and Geometric Distributions Lesson 8-1, Part 1 Binomial Distribution What is a Binomial Distribution? Specific type of discrete probability distribution The outcomes belong to two categories
Business Statistics 41000: Probability 4
 Business Statistics 41000: Probability 4 Drew D. Creal University of Chicago, Booth School of Business February 14 and 15, 2014 1 Class information Drew D. Creal Email: dcreal@chicagobooth.edu Office:
Business Statistics 41000: Probability 4 Drew D. Creal University of Chicago, Booth School of Business February 14 and 15, 2014 1 Class information Drew D. Creal Email: dcreal@chicagobooth.edu Office:
Binomial and Normal Distributions. Example: Determine whether the following experiments are binomial experiments. Explain.
 Binomial and Normal Distributions Objective 1: Determining if an Experiment is a Binomial Experiment For an experiment to be considered a binomial experiment, four things must hold: 1. The experiment is
Binomial and Normal Distributions Objective 1: Determining if an Experiment is a Binomial Experiment For an experiment to be considered a binomial experiment, four things must hold: 1. The experiment is
1 Sampling Distributions
 1 Sampling Distributions 1.1 Statistics and Sampling Distributions When a random sample is selected the numerical descriptive measures calculated from such a sample are called statistics. These statistics
1 Sampling Distributions 1.1 Statistics and Sampling Distributions When a random sample is selected the numerical descriptive measures calculated from such a sample are called statistics. These statistics
Chapter 4: Commonly Used Distributions. Statistics for Engineers and Scientists Fourth Edition William Navidi
 Chapter 4: Commonly Used Distributions Statistics for Engineers and Scientists Fourth Edition William Navidi 2014 by Education. This is proprietary material solely for authorized instructor use. Not authorized
Chapter 4: Commonly Used Distributions Statistics for Engineers and Scientists Fourth Edition William Navidi 2014 by Education. This is proprietary material solely for authorized instructor use. Not authorized
AMS7: WEEK 4. CLASS 3
 AMS7: WEEK 4. CLASS 3 Sampling distributions and estimators. Central Limit Theorem Normal Approximation to the Binomial Distribution Friday April 24th, 2015 Sampling distributions and estimators REMEMBER:
AMS7: WEEK 4. CLASS 3 Sampling distributions and estimators. Central Limit Theorem Normal Approximation to the Binomial Distribution Friday April 24th, 2015 Sampling distributions and estimators REMEMBER:
Chapter 7 1. Random Variables
 Chapter 7 1 Random Variables random variable numerical variable whose value depends on the outcome of a chance experiment - discrete if its possible values are isolated points on a number line - continuous
Chapter 7 1 Random Variables random variable numerical variable whose value depends on the outcome of a chance experiment - discrete if its possible values are isolated points on a number line - continuous
MLLunsford 1. Activity: Central Limit Theorem Theory and Computations
 MLLunsford 1 Activity: Central Limit Theorem Theory and Computations Concepts: The Central Limit Theorem; computations using the Central Limit Theorem. Prerequisites: The student should be familiar with
MLLunsford 1 Activity: Central Limit Theorem Theory and Computations Concepts: The Central Limit Theorem; computations using the Central Limit Theorem. Prerequisites: The student should be familiar with
A.REPRESENTATION OF DATA
 A.REPRESENTATION OF DATA (a) GRAPHS : PART I Q: Why do we need a graph paper? Ans: You need graph paper to draw: (i) Histogram (ii) Cumulative Frequency Curve (iii) Frequency Polygon (iv) Box-and-Whisker
A.REPRESENTATION OF DATA (a) GRAPHS : PART I Q: Why do we need a graph paper? Ans: You need graph paper to draw: (i) Histogram (ii) Cumulative Frequency Curve (iii) Frequency Polygon (iv) Box-and-Whisker
Statistical Methods in Practice STAT/MATH 3379
 Statistical Methods in Practice STAT/MATH 3379 Dr. A. B. W. Manage Associate Professor of Mathematics & Statistics Department of Mathematics & Statistics Sam Houston State University Overview 6.1 Discrete
Statistical Methods in Practice STAT/MATH 3379 Dr. A. B. W. Manage Associate Professor of Mathematics & Statistics Department of Mathematics & Statistics Sam Houston State University Overview 6.1 Discrete
Activity #17b: Central Limit Theorem #2. 1) Explain the Central Limit Theorem in your own words.
 Activity #17b: Central Limit Theorem #2 1) Explain the Central Limit Theorem in your own words. Importance of the CLT: You can standardize and use normal distribution tables to calculate probabilities
Activity #17b: Central Limit Theorem #2 1) Explain the Central Limit Theorem in your own words. Importance of the CLT: You can standardize and use normal distribution tables to calculate probabilities
