Derived copy of Using the Normal Distribution *
|
|
|
- Lenard Stafford
- 5 years ago
- Views:
Transcription
1 OpenStax-CNX module: m Derived copy of Using the Normal Distribution * Cindy Sun Based on Using the Normal Distribution by OpenStax This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 4.0 The shaded area in the following graph indicates the area to the left of x. This area is represented by the probability P(X < x). Normal tables, computers, and calculators can be used to provide or calculate the probability P(X < x). Figure 1 * Version 1.1: Aug 11, :50 pm
2 OpenStax-CNX module: m The area to the right is then P(X > x) = 1 P(X < x). Remember, P(X < x) = Area to the left of the vertical line through x. P(X > x) = 1 P(X < x) = Area to the right of the vertical line through x. P(X < x) is the same as P(X x) and P(X > x) is the same as P(X x) for continuous distributions. 1 Calculations of Probabilities Probabilities are calculated using technology. There are instructions given as necessary for the TI-83+ and TI-84 calculators. : To calculate the probability, use the probability tables provided in without the use of technology. The tables include instructions for how to use them. Example 1 If the area to the left is , then the area to the right is = : Exercise 1 ( on p. 21.) If the area to the left of x is 0.012, then what is the area to the right? Example 2 The nal exam scores in a statistics class were normally distributed with a mean of 63 and a standard deviation of ve. Problem 1 a. Find the probability that a randomly selected student scored more than 65 on the exam. a. Let X = a score on the nal exam. X N(63, 5), where µ = 63 and σ = 5 Draw a graph. Then, nd P(X > 65). P(X > 65) = For more details on how to construct such a probability graph, refer to Lab Worksheet 3.
3 OpenStax-CNX module: m Figure 2 The probability that any student selected at random scores more than 65 is : Go into 2nd DISTR. After pressing 2nd DISTR, press 2:normalcdf. The syntax for the instructions are as follows: normalcdf(lower value, upper value, mean, standard deviation) For this problem: normalcdf(65,1e99,63,5) = You get 1E99 (= ) by pressing 1, the EE key (a 2nd key) and then 99. Or, you can enter 10^99 instead. The number is way out in the right tail of the normal curve. We are calculating the area between 65 and In some instances, the lower number of the area might be 1E99 (= ). The number is way out in the left tail of the normal curve. : The TI probability program calculates a z-score and then the probability from the z-score. Before technology, the z-score was looked up in a standard normal probability table (because the math involved is too cumbersome) to nd the probability. In this example, a standard normal table with area to the left of the z-score was used. You calculate the z-score and look up the area to the left. The probability is the area to the right Z = 5 = 0.4 Area to the left is P(X > 65) = P(Z > 0.4) = 1-P(Z < 0.4) = = : Calculate the z-score: *Press 2nd Distr *Press 3:invNorm( *Enter the area to the left of z followed by )
4 OpenStax-CNX module: m *Press ENTER. For this Example, the steps are 2nd Distr 3:invNorm(.6554) ENTER The answer is which rounds to 0.4. Problem 2 b. Find the probability that a randomly selected student scored less than 85. b. Draw a graph. Then nd P(x < 85), and shade the graph. Using a computer or calculator, nd P(X < 85) = P(Z < 4.4)=1. normalcdf(0,85,63,5) = 1 (rounds to one) The probability that one student scores less than 85 is approximately one (or 100%). Problem 3 c. Find the 90 th percentile (that is, nd the score k that has 90% of the scores below k and 10% of the scores above k). c. Find the 90 th percentile. For each problem or part of a problem, draw a new graph. Draw the x-axis. Shade the area that corresponds to the 90 th percentile. Let k = the 90 th percentile. The variable k is located on the x-axis. P(x < k) is the area to the left of k. The 90 th percentile k separates the exam scores into those that are the same or lower than k and those that are the same or higher. Ninety percent of the test scores are the same or lower than k, and ten percent are the same or higher. The variable k is often called a critical value. k = 69.4
5 OpenStax-CNX module: m Figure 3 The 90 th percentile is This means that 90% of the test scores fall at or below 69.4 and 10% fall at or above. To get this answer by using the Standard Normal Table, rst nd the 90% percentile of the z score from the table, which is approximately 1.28 ( P(Z < 1.28)=0.8997, so we can say that 89.97% z scores are lower than 1.28), and therefore the corresponding x value is *5=69.4. To get this answer in Minitab, refer to Lab Worksheet 3. To get this answer on the calculator, follow this step: : invnorm in 2nd DISTR. invnorm(area to the left, mean, standard deviation) For this problem, invnorm(0.90,63,5) = 69.4 Problem 4 d. Find the 70 th percentile (that is, nd the score k such that 70% of scores are below k and 30% of the scores are above k). d. Find the 70 th percentile. Draw a new graph and label it appropriately. k = 65.6 The 70 th percentile is This means that 70% of the test scores fall at or below 65.5 and 30% fall at or above. The 70% percentile z score is 0.52, thus the corresponding x value is *5=65.6. invnorm(0.70,63,5) = 65.6
6 OpenStax-CNX module: m : Exercise 6 ( on p. 21.) The golf scores for a school team were normally distributed with a mean of 68 and a standard deviation of three. Find the probability that a randomly selected golfer scored less than 65. Example 3 A personal computer is used for oce work at home, research, communication, personal nances, education, entertainment, social networking, and a myriad of other things. Suppose that the average number of hours a household personal computer is used for entertainment is two hours per day. Assume the times for entertainment are normally distributed and the standard deviation for the times is half an hour. Problem 1 a. Find the probability that a household personal computer is used for entertainment between 1.8 and 2.75 hours per day. a. Let X = the amount of time (in hours) a household personal computer is used for entertainment. X N(2, 0.5) where µ = 2 and σ = 0.5. Find P(1.8 < x < 2.75). The probability for which you are looking is the area betweenx = 1.8 and x = P(1.8 < X < 2.75) = P(-0.4 < Z < 1.5) = P(Z < 1.5)-P(Z < -0.4)= = Figure 4 normalcdf(1.8,2.75,2,0.5) =
7 OpenStax-CNX module: m The probability that a household personal computer is used between 1.8 and 2.75 hours per day for entertainment is Problem 2 b. Find the maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment. b. To nd the maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment, nd the 25 th percentile,k, where P(x < k) = Figure 5 P(Z < -0.67)=0.25, the corresponding x value therefore is *0.5= Alternatively, invnorm(0.25,2,0.5) = 1.66 The maximum number of hours per day that the bottom quartile of households uses a personal computer for entertainment is 1.66 hours. : Exercise 9 ( on p. 21.) The golf scores for a school team were normally distributed with a mean of 68 and a standard deviation of three. Find the probability that a golfer scored between 66 and 70.
8 OpenStax-CNX module: m Example 4 There are approximately one billion smartphone users in the world today. In the United States the ages 13 to 55+ of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 36.9 years and 13.9 years, respectively. Problem 1 a. Determine the probability that a random smartphone user in the age range 13 to 55+ is between 23 and 64.7 years old. a. P(23 < X < 64.7)=P(-1 < Z < 2)=P(Z < 2)-P(Z < -1)= = Alternatively, normalcdf(23,64.7,36.9,13.9) = Problem 2 b. Determine the probability that a randomly selected smartphone user in the age range 13 to 55+ is at most 50.8 years old. b. P(X < 50.8)=P(Z < 1)= normalcdf(10 99,50.8,36.9,13.9) = Problem 3 c. Find the 80 th percentile of this distribution, and interpret it in a complete sentence. c. P(Z < 2.75)=0.84, the corresponding x value is *13.9= invnorm(0.80,36.9,13.9) = 48.6 The 80 th percentile is 48.6 years. 80% of the smartphone users in the age range are 48.6 years old or less. : Use the information in Example 4 to answer the following questions. Exercise 13 ( on p. 21.) a.find the 30 th percentile, and interpret it in a complete sentence. b.what is the probability that the age of a randomly selected smartphone user in the range 13 to 55+ is less than 27 years old. Example 5 There are approximately one billion smartphone users in the world today. In the United States the ages 13 to 55+ of smartphone users approximately follow a normal distribution with approximate mean and standard deviation of 36.9 years and 13.9 years respectively. Using this information,
9 OpenStax-CNX module: m answer the following questions (round answers to one decimal place). Problem Forty percent of the ages that range from 13 to 55+ are at least what age? Find k where P(x > k) = 0.40 ("At least" translates to "greater than or equal to.") 0.40 = the area to the right. Area to the left = = The area to the left of k = From the standard normal table, we see that P(Z < 0.25) = , which is the closest value to 0.6. Therefore, the corresponding x value is *13.9= Again, because is not the same as 0.60, the result may be slightly dierent from results obtained by computer software or calculators. invnorm(0.60,36.9,13.9) = k = Forty percent of the ages that range from 13 to 55+ are at least years. : Example 6 A citrus farmer who grows mandarin oranges nds that the diameters of mandarin oranges harvested on his farm follow a normal distribution with a mean diameter of 5.85 cm and a standard deviation of 0.24 cm. Problem 1 a. Find the probability that a randomly selected mandarin orange from this farm has a diameter larger than 6.0 cm. Sketch the graph. a. P(X > 6.0)= P(Z > 0.63)=1-P(Z < 0.63)= = Alternatively, normalcdf(6,10^99,5.85,0.24) =
10 OpenStax-CNX module: m Figure 6 Problem 2 b. The middle 20% of mandarin oranges from this farm have diameters between and. b. Suppose P(x1 < X < x2)=0.20, where x1 and x2 are symmetric around the center of This also translates to the following two statements: P(X < x1)=0.4, P(X < x2)=0.6, which are equivalent to P(Z < z1)=0.4 and P(Z < z2)=0.6, respectively. By using the standard normal table, we nd z1 as and z2 as These two z-scores are symmetric around the center of zero. We then use the Z formula and obtain x1 as *0.24=5.79 and x2 as *0.24=5.91. Obviously, these two values 5.79 and 5.91 are symmetric around the mean of = 0.80 The tails of the graph of the normal distribution each have an area of Find k1, the 40 th percentile, and k2, the 60 th percentile ( = 0.60). k1 = invnorm(0.40,5.85,0.24) = 5.79 cm k2 = invnorm(0.60,5.85,0.24) = 5.91 cm Problem 3 c. Find the 90 th percentile for the diameters of mandarin oranges, and interpret it in a complete sentence. c. P(X < x3)=p(z < z3)=0.9, z3 can be found from the standard normal table as 1.28, and therefore the x value is *0.24= The interpretation of is: Ninety percent of
11 OpenStax-CNX module: m the diameter of the mandarin oranges is at most cm. : 2 References Scratch-O Lottery Ticket Playing Tips. WinAtTheLottery.com, Available online at Naegele's rule. Wikipedia. Available online at (accessed May 14, 2013). 403: NUMMI. Chicago Public Media & Ira Glass, Available online at (accessed May 14, 2013). (accessed May 14, 2013). Smart Phone Users, By The Numbers. Visual.ly, Available online at (accessed May 14, 2013). Facebook Statistics. Statistics Brain. Available online at May 14, 2013). 3 Chapter Review The normal distribution, which is continuous, is the most important of all the probability distributions. Its graph is bell-shaped. This bell-shaped curve is used in almost all disciplines. Since it is a continuous distribution, the total area under the curve is one. The parameters of the normal are the mean µ and the standard deviation σ. A special normal distribution, called the standard normal distribution is the distribution of z-scores. Its mean is zero, and its standard deviation is one. 4 Formula Review Normal Distribution: X N(µ, σ) where µ is the mean and σ is the standard deviation. Standard Normal Distribution: Z N(0, 1). Calculator function for probability: normalcdf (lower x value of the area, upper x value of the area, mean, standard deviation) Calculator function for the k th percentile: k = invnorm (area to the left of k, mean, standard deviation) 5 Exercise 18 ( on p. 21.) How would you represent the area to the left of one in a probability statement?
12 OpenStax-CNX module: m Figure 7 Exercise 19 What is the area to the right of one? Figure 8 Exercise 20 ( on p. 21.) Is P(x < 1) equal to P(x 1)? Why? Exercise 21 How would you represent the area to the left of three in a probability statement? Figure 9
13 OpenStax-CNX module: m Exercise 22 ( on p. 21.) What is the area to the right of three? Figure 10 Exercise 23 If the area to the left of x in a normal distribution is 0.123, what is the area to the right of x? Exercise 24 ( on p. 21.) If the area to the right of x in a normal distribution is 0.543, what is the area to the left of x? Use the following information to answer the next four exercises: X N(54, 8) Exercise 25 Find the probability that x > 56. Exercise 26 ( on p. 21.) Find the probability that x < 30. Exercise 27 Find the 80 th percentile. Exercise 28 ( on p. 22.) Find the 60 th percentile. Exercise 29 X N(6, 2) Find the probability that x is between three and nine. Exercise 30 ( on p. 22.) X N(3, 4) Find the probability that x is between one and four. Exercise 31 X N(4, 5) Find the maximum of x in the bottom quartile. Exercise 32 ( on p. 22.) Use the following information to answer the next three exercise: The life of Sunshine CD players is normally distributed with a mean of 4.1 years and a standard deviation of 1.3 years. A CD player is guaranteed for three years. We are interested in the length of time a CD player lasts. Find the probability that a CD player will break down during the guarantee period.
14 OpenStax-CNX module: m a. Sketch the situation. Label and scale the axes. Shade the region corresponding to the probability. Figure 11 b. P(0 < x < ) = (Use zero for the minimum value of x.) Exercise 33 Find the probability that a CD player will last between 2.8 and six years. a. Sketch the situation. Label and scale the axes. Shade the region corresponding to the probability. Figure 12 b. P( < x < ) = Exercise 34 ( on p. 22.) Find the 70 th percentile of the distribution for the time a CD player lasts. a. Sketch the situation. Label and scale the axes. Shade the region corresponding to the lower 70%.
15 OpenStax-CNX module: m Figure 13 b. P(x < k) = Therefore, k = 6 Homework Use the following information to answer the next two exercises: The patient recovery time from a particular surgical procedure is normally distributed with a mean of 5.3 days and a standard deviation of 2.1 days. Exercise 35 What is the probability of spending more than two days in recovery? a b c d Exercise 36 ( on p. 22.) The 90 th percentile for recovery times is? a b c d Use the following information to answer the next three exercises: The length of time it takes to nd a parking space at 9 A.M. follows a normal distribution with a mean of ve minutes and a standard deviation of two minutes. Exercise 37 Based upon the given information and numerically justied, would you be surprised if it took less than one minute to nd a parking space? a. Yes b. No c. Unable to determine Exercise 38 ( on p. 22.) Find the probability that it takes at least eight minutes to nd a parking space.
16 OpenStax-CNX module: m a b c d Exercise 39 Seventy percent of the time, it takes more than how many minutes to nd a parking space? a b c d Exercise 40 ( on p. 22.) According to a study done by De Anza students, the height for Asian adult males is normally distributed with an average of 66 inches and a standard deviation of 2.5 inches. Suppose one Asian adult male is randomly chosen. Let X = height of the individual. a. X (, ) b. Find the probability that the person is between 65 and 69 inches. Include a sketch of the graph, and write a probability statement. c. Would you expect to meet many Asian adult males over 72 inches? Explain why or why not, and justify your answer numerically. d. The middle 40% of heights fall between what two values? Sketch the graph, and write the probability statement. Exercise 41 IQ is normally distributed with a mean of 100 and a standard deviation of 15. individual is randomly chosen. Let X = IQ of an individual. Suppose one a. X (, ) b. Find the probability that the person has an IQ greater than 120. Include a sketch of the graph, and write a probability statement. c. MENSA is an organization whose members have the top 2% of all IQs. Find the minimum IQ needed to qualify for the MENSA organization. Sketch the graph, and write the probability statement. d. The middle 50% of IQs fall between what two values? Sketch the graph and write the probability statement. Exercise 42 ( on p. 22.) The percent of fat calories that a person in America consumes each day is normally distributed with a mean of about 36 and a standard deviation of 10. Suppose that one individual is randomly chosen. Let X = percent of fat calories. a. X (, ) b. Find the probability that the percent of fat calories a person consumes is more than 40. Graph the situation. Shade in the area to be determined. c. Find the maximum number for the lower quarter of percent of fat calories. Sketch the graph and write the probability statement. Exercise 43 Suppose that the distance of y balls hit to the outeld (in baseball) is normally distributed with a mean of 250 feet and a standard deviation of 50 feet.
17 OpenStax-CNX module: m a. If X = distance in feet for a y ball, then X (, ) b. If one y ball is randomly chosen from this distribution, what is the probability that this ball traveled fewer than 220 feet? Sketch the graph. Scale the horizontal axis X. Shade the region corresponding to the probability. Find the probability. c. Find the 80 th percentile of the distribution of y balls. Sketch the graph, and write the probability statement. Exercise 44 ( on p. 22.) In China, four-year-olds average three hours a day unsupervised. Most of the unsupervised children live in rural areas, considered safe. Suppose that the standard deviation is 1.5 hours and the amount of time spent alone is normally distributed. We randomly select one Chinese four-year-old living in a rural area. We are interested in the amount of time the child spends alone per day. a. In words, dene the random variable X. b. X (, ) c. Find the probability that the child spends less than one hour per day unsupervised. Sketch the graph, and write the probability statement. d. What percent of the children spend over ten hours per day unsupervised? e. Seventy percent of the children spend at least how long per day unsupervised? Exercise 45 In the 1992 presidential election, Alaska's 40 election districts averaged 1,956.8 votes per district for President Clinton. The standard deviation was (There are only 40 election districts in Alaska.) The distribution of the votes per district for President Clinton was bell-shaped. Let X = number of votes for President Clinton for an election district. a. State the approximate distribution of X. b. Is 1,956.8 a population mean or a sample mean? How do you know? c. Find the probability that a randomly selected district had fewer than 1,600 votes for President Clinton. Sketch the graph and write the probability statement. d. Find the probability that a randomly selected district had between 1,800 and 2,000 votes for President Clinton. e. Find the third quartile for votes for President Clinton. Exercise 46 ( on p. 22.) Suppose that the duration of a particular type of criminal trial is known to be normally distributed with a mean of 21 days and a standard deviation of seven days. a. In words, dene the random variable X. b. X (, ) c. If one of the trials is randomly chosen, nd the probability that it lasted at least 24 days. Sketch the graph and write the probability statement. d. Sixty percent of all trials of this type are completed within how many days? Exercise 47 Terri Vogel, an amateur motorcycle racer, averages seconds per 2.5 mile lap (in a seven-lap race) with a standard deviation of 2.28 seconds. The distribution of her race times is normally distributed. We are interested in one of her randomly selected laps. a. In words, dene the random variable X. b. X (, ) c. Find the percent of her laps that are completed in less than 130 seconds.
18 OpenStax-CNX module: m d. The fastest 3% of her laps are under. e. The middle 80% of her laps are from seconds to seconds. Exercise 48 ( on p. 22.) Thuy Dau, Ngoc Bui, Sam Su, and Lan Voung conducted a survey as to how long customers at Lucky claimed to wait in the checkout line until their turn. Let X = time in line. Table 1 displays the ordered real data (in minutes): Table 1 a. Calculate the sample mean and the sample standard deviation. b. Construct a histogram. c. Draw a smooth curve through the midpoints of the tops of the bars. d. In words, describe the shape of your histogram and smooth curve. e. Let the sample mean approximate µ and the sample standard deviation approximate σ. The distribution of X can then be approximated by X (, ) f. Use the distribution in part e to calculate the probability that a person will wait fewer than 6.1 minutes. g. Determine the cumulative relative frequency for waiting less than 6.1 minutes. h. Why aren't the answers to part f and part g exactly the same? i. Why are the answers to part f and part g as close as they are? j. If only ten customers has been surveyed rather than 50, do you think the answers to part f and part g would have been closer together or farther apart? Explain your conclusion. Exercise 49 Suppose that Ricardo and Anita attend dierent colleges. Ricardo's GPA is the same as the average GPA at his school. Anita's GPA is 0.70 standard deviations above her school average. In complete sentences, explain why each of the following statements may be false. a. Ricardo's actual GPA is lower than Anita's actual GPA. b. Ricardo is not passing because his z-score is zero. c. Anita is in the 70 th percentile of students at her college. Exercise 50 ( on p. 23.) Table 2 shows a sample of the maximum capacity (maximum number of spectators) of sports stadiums. The table does not include horse-racing or motor-racing stadiums.
19 OpenStax-CNX module: m ,000 40,000 45,050 45,500 46,249 48,134 49,133 50,071 50,096 50,466 50,832 51,100 51,500 51,900 52,000 52,132 52,200 52,530 52,692 53,864 54,000 55,000 55,000 55,000 55,000 55,000 55,000 55,082 57,000 58,008 59,680 60,000 60,000 60,492 60,580 62,380 62,872 64,035 65,000 65,050 65,647 66,000 66,161 67,428 68,349 68,976 69,372 70,107 70,585 71,594 72,000 72,922 73,379 74,500 75,025 76,212 78,000 80,000 80,000 82,300 Table 2 a. Calculate the sample mean and the sample standard deviation for the maximum capacity of sports stadiums (the data). b. Construct a histogram. c. Draw a smooth curve through the midpoints of the tops of the bars of the histogram. d. In words, describe the shape of your histogram and smooth curve. e. Let the sample mean approximate µ and the sample standard deviation approximate σ. The distribution of X can then be approximated by X (, ). f. Use the distribution in part e to calculate the probability that the maximum capacity of sports stadiums is less than 67,000 spectators. g. Determine the cumulative relative frequency that the maximum capacity of sports stadiums is less than 67,000 spectators. Hint: Order the data and count the sports stadiums that have a maximum capacity less than 67,000. Divide by the total number of sports stadiums in the sample. h. Why aren't the answers to part f and part g exactly the same? Exercise 51 An expert witness for a paternity lawsuit testies that the length of a pregnancy is normally distributed with a mean of 280 days and a standard deviation of 13 days. An alleged father was out of the country from 240 to 306 days before the birth of the child, so the pregnancy would have been less than 240 days or more than 306 days long if he was the father. The birth was uncomplicated, and the child needed no medical intervention. What is the probability that he was NOT the father? What is the probability that he could be the father? Calculate the z-scores rst, and then use those to calculate the probability. Exercise 52 ( on p. 23.) A NUMMI assembly line, which has been operating since 1984, has built an average of 6,000 cars and trucks a week. Generally, 10% of the cars were defective coming o the assembly line. Suppose we draw a random sample of n = 100 cars. Let X represent the number of defective cars in the sample. What can we say about X in regard to the empirical rule (one standard deviation, two standard deviations and three standard deviations from the mean are being referred to)? Assume a normal distribution for the defective cars in the sample. Exercise 53 We ip a coin 100 times (n = 100) and note that it only comes up heads 20% (p = 0.20) of the time. The mean and standard deviation for the number of times the coin lands on heads is µ = 20 and σ = 4 (verify the mean and standard deviation). Solve the following:
20 OpenStax-CNX module: m a. There is about a 68% chance that the number of heads will be somewhere between and. b. There is about a chance that the number of heads will be somewhere between 12 and 28. c. There is about a chance that the number of heads will be somewhere between eight and 32. Exercise 54 ( on p. 23.) A $1 scratch o lotto ticket will be a winner one out of ve times. Out of a shipment of n = 190 lotto tickets, nd the probability for the lotto tickets that there are a. somewhere between 34 and 54 prizes. b. somewhere between 54 and 64 prizes. c. more than 64 prizes. Exercise 55 Facebook provides a variety of statistics on its Web site that detail the growth and popularity of the site. On average, 28 percent of 18 to 34 year olds check their Facebook proles before getting out of bed in the morning. Suppose this percentage follows a normal distribution with a standard deviation of ve percent. a. Find the probability that the percent of 18 to 34-year-olds who check Facebook before getting out of bed in the morning is at least 30. b. Find the 95 th percentile, and express it in a sentence.
21 OpenStax-CNX module: m s to Exercises in this Module to Exercise (p. 2) = to Exercise (p. 6) P(X < 65)=P(Z < -1)= normalcdf(10 99,65,68,3) = to Exercise (p. 7) P(66 < X < 70)=P(-0.67 < Z < 0.67)=1-2P(Z < -0.67)=1-2*0.2514= Alternatively, normalcdf(66,70,68,3) = Note that the dierence between these two answers is due to rounding o errors, that is, the Z scores in the Standard Normal Table only have two decimals. In this case, the answer by calculator is more precise. to Exercise (p. 8) Let X = a smart phone user whose age is 13 to 55+. X N(36.9, 13.9) a. To nd the 30 th percentile, nd k such that P(x < k) = By using the Standard Normal Table, we nd that P(Z < -0.52) = , where is the closest value to 0.3. Therefore, we compute the corresponding x value as *13.9= invnorm(0.30, 36.9, 13.9) = 29.6 years Thirty percent of smartphone users 13 to 55+ are at most 29.6 years and 70% are at least 29.6 years. b. Find P(x < 27) Figure 14 normalcdf(0,27,36.9,13.9) = (Note that normalcdf(10 99,27,36.9,13.9) = The two answers dier only by ) Again, please refer to Lab Worksheet 3 for instructions on how to construct the above probability graph. Alternatively, if you want to compute the probability by using the Standard Normal table, it follows that P(X < 27) = P(Z < -0.71) = Note that the z-score of has been rounded and therefore the resulting probability of is not very precise. to Exercise (p. 11) P(x < 1) to Exercise (p. 12) Yes, because they are the same in a continuous distribution: P(x = 1) = 0 to Exercise (p. 13) 1 P(x < 3) or P(x > 3) to Exercise (p. 13) = 0.457
22 OpenStax-CNX module: m to Exercise (p. 13) to Exercise (p. 13) to Exercise (p. 13) to Exercise (p. 13) a. Check student's solution. b. 3, to Exercise (p. 14) a. Check student's solution. b. 0.70, 4.78 years to Exercise (p. 15) c to Exercise (p. 15) d to Exercise (p. 16) a. X N(66, 2.5) b c. No, the probability that an Asian male is over 72 inches tall is to Exercise (p. 16) a. X N(36, 10) b. The probability that a person consumes more than 40% of their calories as fat is c. Approximately 25% of people consume less than 29.26% of their calories as fat. to Exercise (p. 17) a. X = number of hours that a Chinese four-year-old in a rural area is unsupervised during the day. b. X N(3, 1.5) c. The probability that the child spends less than one hour a day unsupervised is d. The probability that a child spends over ten hours a day unsupervised is less than e hours to Exercise (p. 17) a. X = the distribution of the number of days a particular type of criminal trial will take b. X N(21, 7) c. The probability that a randomly selected trial will last more than 24 days is d to Exercise (p. 18) a. mean = 5.51, s = 2.15 b. Check student's solution. c. Check student's solution. d. Check student's solution. e. X N(5.51, 2.15) f g. The cumulative frequency for less than 6.1 minutes is 0.64.
23 OpenStax-CNX module: m h. The answers to part f and part g are not exactly the same, because the normal distribution is only an approximation to the real one. i. The answers to part f and part g are close, because a normal distribution is an excellent approximation when the sample size is greater than 30. j. The approximation would have been less accurate, because the smaller sample size means that the data does not t normal curve as well. to Exercise (p. 18) 1. mean = 60,136 s = 10, Answers will vary. 3. Answers will vary. 4. Answers will vary. 5. X N(60136, 10468) The cumulative relative frequency is 43/60 = The answers for part f and part g are not the same, because the normal distribution is only an approximation. to Exercise (p. 19) n = 100; p = 0.1; q = 0.9 µ = np = (100)(0.10) = 10 σ = npq = (100)(0.1)(0.9) = 3 i. z = ±1: x 1 = µ + zσ = (3) = 13 and x2 = µ zσ = 10 1(3) = 7. 68% of the defective cars will fall between seven and 13. ii. z = ±2: x 1 = µ + zσ = (3) = 16 and x2 = µ zσ = 10 2(3) = % of the defective cars will fall between four and 16 iii. z = ±3: x 1 = µ + zσ = (3) = 19 and x2 = µ zσ = 10 3(3) = % of the defective cars will fall between one and 19. to Exercise (p. 20) n = 190; p = 1 5 = 0.2; q = 0.8 µ = np = (190)(0.2) = 38 σ = npq = (190)(0.2)(0.8) = a. For this problem: P(34 < x < 54) = normalcdf(34,54,48,5.5136) = b. For this problem: P(54 < x < 64) = normalcdf(54,64,48,5.5136) = c. For this problem: P(x > 64) = normalcdf(64,10 99,48,5.5136) = (approximately 0)
Normal Distribution: Introduction
 Connexions module: m16979 1 Normal Distribution: Introduction Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Connexions module: m16979 1 Normal Distribution: Introduction Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Collaborative Statistics Using Spreadsheets. Chapter 6
 Collaborative Statistics Using Spreadsheets This document is attributed to OpenStax-CNX Chapter 6 Open Assembly Edition Open Assembly editions of open textbooks are disaggregated versions designed to facilitate
Collaborative Statistics Using Spreadsheets This document is attributed to OpenStax-CNX Chapter 6 Open Assembly Edition Open Assembly editions of open textbooks are disaggregated versions designed to facilitate
Central Limit Theorem: Homework
 Connexions module: m16952 1 Central Limit Theorem: Homework Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Connexions module: m16952 1 Central Limit Theorem: Homework Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
The Central Limit Theorem: Homework
 The Central Limit Theorem: Homework EXERCISE 1 X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let X be the random variable of sums.
The Central Limit Theorem: Homework EXERCISE 1 X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let X be the random variable of sums.
The Central Limit Theorem: Homework
 The Central Limit Theorem: Homework EXERCISE 1 X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let X be the random variable of sums.
The Central Limit Theorem: Homework EXERCISE 1 X N(60, 9). Suppose that you form random samples of 25 from this distribution. Let X be the random variable of averages. Let X be the random variable of sums.
The Central Limit Theorem for Sample Means (Averages)
 The Central Limit Theorem for Sample Means (Averages) By: OpenStaxCollege Suppose X is a random variable with a distribution that may be known or unknown (it can be any distribution). Using a subscript
The Central Limit Theorem for Sample Means (Averages) By: OpenStaxCollege Suppose X is a random variable with a distribution that may be known or unknown (it can be any distribution). Using a subscript
The Central Limit Theorem: Homework
 EERCISE 1 The Central Limit Theorem: Homework N(60, 9). Suppose that you form random samples of 25 from this distribution. Let be the random variable of averages. Let be the random variable of sums. For
EERCISE 1 The Central Limit Theorem: Homework N(60, 9). Suppose that you form random samples of 25 from this distribution. Let be the random variable of averages. Let be the random variable of sums. For
The Central Limit Theorem for Sums
 OpenStax-CNX module: m46997 1 The Central Limit Theorem for Sums OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0 Suppose X is a random
OpenStax-CNX module: m46997 1 The Central Limit Theorem for Sums OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0 Suppose X is a random
As you draw random samples of size n, as n increases, the sample means tend to be normally distributed.
 The Central Limit Theorem The central limit theorem (clt for short) is one of the most powerful and useful ideas in all of statistics. The clt says that if we collect samples of size n with a "large enough
The Central Limit Theorem The central limit theorem (clt for short) is one of the most powerful and useful ideas in all of statistics. The clt says that if we collect samples of size n with a "large enough
CH 5 Normal Probability Distributions Properties of the Normal Distribution
 Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Chapter 6. The Normal Probability Distributions
 Chapter 6 The Normal Probability Distributions 1 Chapter 6 Overview Introduction 6-1 Normal Probability Distributions 6-2 The Standard Normal Distribution 6-3 Applications of the Normal Distribution 6-5
Chapter 6 The Normal Probability Distributions 1 Chapter 6 Overview Introduction 6-1 Normal Probability Distributions 6-2 The Standard Normal Distribution 6-3 Applications of the Normal Distribution 6-5
7 THE CENTRAL LIMIT THEOREM
 CHAPTER 7 THE CENTRAL LIMIT THEOREM 373 7 THE CENTRAL LIMIT THEOREM Figure 7.1 If you want to figure out the distribution of the change people carry in their pockets, using the central limit theorem and
CHAPTER 7 THE CENTRAL LIMIT THEOREM 373 7 THE CENTRAL LIMIT THEOREM Figure 7.1 If you want to figure out the distribution of the change people carry in their pockets, using the central limit theorem and
The Uniform Distribution
 Connexions module: m46972 The Uniform Distribution OpenStax College This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License 3.0 The uniform distribution
Connexions module: m46972 The Uniform Distribution OpenStax College This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License 3.0 The uniform distribution
Density curves. (James Madison University) February 4, / 20
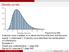 Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Using the Central Limit
 Using the Central Limit Theorem By: OpenStaxCollege It is important for you to understand when to use the central limit theorem. If you are being asked to find the probability of the mean, use the clt
Using the Central Limit Theorem By: OpenStaxCollege It is important for you to understand when to use the central limit theorem. If you are being asked to find the probability of the mean, use the clt
ECON 214 Elements of Statistics for Economists 2016/2017
 ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
Continuous Random Variables: The Uniform Distribution *
 OpenStax-CNX module: m16819 1 Continuous Random Variables: The Uniform Distribution * Susan Dean Barbara Illowsky, Ph.D. This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution
OpenStax-CNX module: m16819 1 Continuous Random Variables: The Uniform Distribution * Susan Dean Barbara Illowsky, Ph.D. This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution
Section Introduction to Normal Distributions
 Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Using the Central Limit Theorem
 OpenStax-CNX module: m46992 1 Using the Central Limit Theorem OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0 It is important for
OpenStax-CNX module: m46992 1 Using the Central Limit Theorem OpenStax College This work is produced by OpenStax-CNX and licensed under the Creative Commons Attribution License 3.0 It is important for
11.5: Normal Distributions
 11.5: Normal Distributions 11.5.1 Up to now, we ve dealt with discrete random variables, variables that take on only a finite (or countably infinite we didn t do these) number of values. A continuous random
11.5: Normal Distributions 11.5.1 Up to now, we ve dealt with discrete random variables, variables that take on only a finite (or countably infinite we didn t do these) number of values. A continuous random
No, because np = 100(0.02) = 2. The value of np must be greater than or equal to 5 to use the normal approximation.
 1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
Section 7.5 The Normal Distribution. Section 7.6 Application of the Normal Distribution
 Section 7.6 Application of the Normal Distribution A random variable that may take on infinitely many values is called a continuous random variable. A continuous probability distribution is defined by
Section 7.6 Application of the Normal Distribution A random variable that may take on infinitely many values is called a continuous random variable. A continuous probability distribution is defined by
Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19)
 Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x
Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x
Normal distribution. We say that a random variable X follows the normal distribution if the probability density function of X is given by
 Normal distribution The normal distribution is the most important distribution. It describes well the distribution of random variables that arise in practice, such as the heights or weights of people,
Normal distribution The normal distribution is the most important distribution. It describes well the distribution of random variables that arise in practice, such as the heights or weights of people,
Math 14, Homework 6.2 p. 337 # 3, 4, 9, 10, 15, 18, 19, 21, 22 Name
 Name 3. Population in U.S. Jails The average daily jail population in the United States is 706,242. If the distribution is normal and the standard deviation is 52,145, find the probability that on a randomly
Name 3. Population in U.S. Jails The average daily jail population in the United States is 706,242. If the distribution is normal and the standard deviation is 52,145, find the probability that on a randomly
Statistics (This summary is for chapters 18, 29 and section H of chapter 19)
 Statistics (This summary is for chapters 18, 29 and section H of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x n =
Statistics (This summary is for chapters 18, 29 and section H of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x n =
Lecture Slides. Elementary Statistics Tenth Edition. by Mario F. Triola. and the Triola Statistics Series. Slide 1
 Lecture Slides Elementary Statistics Tenth Edition and the Triola Statistics Series by Mario F. Triola Slide 1 Chapter 6 Normal Probability Distributions 6-1 Overview 6-2 The Standard Normal Distribution
Lecture Slides Elementary Statistics Tenth Edition and the Triola Statistics Series by Mario F. Triola Slide 1 Chapter 6 Normal Probability Distributions 6-1 Overview 6-2 The Standard Normal Distribution
Normal Probability Distributions
 C H A P T E R Normal Probability Distributions 5 Section 5.2 Example 3 (pg. 248) Normal Probabilities Assume triglyceride levels of the population of the United States are normally distributed with a mean
C H A P T E R Normal Probability Distributions 5 Section 5.2 Example 3 (pg. 248) Normal Probabilities Assume triglyceride levels of the population of the United States are normally distributed with a mean
These Statistics NOTES Belong to:
 These Statistics NOTES Belong to: Topic Notes Questions Date 1 2 3 4 5 6 REVIEW DO EVERY QUESTION IN YOUR PROVINCIAL EXAM BINDER Important Calculator Functions to know for this chapter Normal Distributions
These Statistics NOTES Belong to: Topic Notes Questions Date 1 2 3 4 5 6 REVIEW DO EVERY QUESTION IN YOUR PROVINCIAL EXAM BINDER Important Calculator Functions to know for this chapter Normal Distributions
Unit 2: Statistics Probability
 Applied Math 30 3-1: Distributions Probability Distribution: - a table or a graph that displays the theoretical probability for each outcome of an experiment. - P (any particular outcome) is between 0
Applied Math 30 3-1: Distributions Probability Distribution: - a table or a graph that displays the theoretical probability for each outcome of an experiment. - P (any particular outcome) is between 0
Example - Let X be the number of boys in a 4 child family. Find the probability distribution table:
 Chapter8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number
Chapter8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number
Chapter 4 and 5 Note Guide: Probability Distributions
 Chapter 4 and 5 Note Guide: Probability Distributions Probability Distributions for a Discrete Random Variable A discrete probability distribution function has two characteristics: Each probability is
Chapter 4 and 5 Note Guide: Probability Distributions Probability Distributions for a Discrete Random Variable A discrete probability distribution function has two characteristics: Each probability is
ECON 214 Elements of Statistics for Economists
 ECON 214 Elements of Statistics for Economists Session 7 The Normal Distribution Part 1 Lecturer: Dr. Bernardin Senadza, Dept. of Economics Contact Information: bsenadza@ug.edu.gh College of Education
ECON 214 Elements of Statistics for Economists Session 7 The Normal Distribution Part 1 Lecturer: Dr. Bernardin Senadza, Dept. of Economics Contact Information: bsenadza@ug.edu.gh College of Education
Math 14 Lecture Notes Ch The Normal Approximation to the Binomial Distribution. P (X ) = nc X p X q n X =
 6.4 The Normal Approximation to the Binomial Distribution Recall from section 6.4 that g A binomial experiment is a experiment that satisfies the following four requirements: 1. Each trial can have only
6.4 The Normal Approximation to the Binomial Distribution Recall from section 6.4 that g A binomial experiment is a experiment that satisfies the following four requirements: 1. Each trial can have only
Chapter 8. Variables. Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc.
 Chapter 8 Random Variables Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc. 8.1 What is a Random Variable? Random Variable: assigns a number to each outcome of a random circumstance, or,
Chapter 8 Random Variables Copyright 2004 Brooks/Cole, a division of Thomson Learning, Inc. 8.1 What is a Random Variable? Random Variable: assigns a number to each outcome of a random circumstance, or,
Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a
 Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a Announcements: There are some office hour changes for Nov 5, 8, 9 on website Week 5 quiz begins after class today and ends at
Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a Announcements: There are some office hour changes for Nov 5, 8, 9 on website Week 5 quiz begins after class today and ends at
2011 Pearson Education, Inc
 Statistics for Business and Economics Chapter 4 Random Variables & Probability Distributions Content 1. Two Types of Random Variables 2. Probability Distributions for Discrete Random Variables 3. The Binomial
Statistics for Business and Economics Chapter 4 Random Variables & Probability Distributions Content 1. Two Types of Random Variables 2. Probability Distributions for Discrete Random Variables 3. The Binomial
Chapter 4 Random Variables & Probability. Chapter 4.5, 6, 8 Probability Distributions for Continuous Random Variables
 Chapter 4.5, 6, 8 Probability for Continuous Random Variables Discrete vs. continuous random variables Examples of continuous distributions o Uniform o Exponential o Normal Recall: A random variable =
Chapter 4.5, 6, 8 Probability for Continuous Random Variables Discrete vs. continuous random variables Examples of continuous distributions o Uniform o Exponential o Normal Recall: A random variable =
Section Distributions of Random Variables
 Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
MAKING SENSE OF DATA Essentials series
 MAKING SENSE OF DATA Essentials series THE NORMAL DISTRIBUTION Copyright by City of Bradford MDC Prerequisites Descriptive statistics Charts and graphs The normal distribution Surveys and sampling Correlation
MAKING SENSE OF DATA Essentials series THE NORMAL DISTRIBUTION Copyright by City of Bradford MDC Prerequisites Descriptive statistics Charts and graphs The normal distribution Surveys and sampling Correlation
STAB22 section 1.3 and Chapter 1 exercises
 STAB22 section 1.3 and Chapter 1 exercises 1.101 Go up and down two times the standard deviation from the mean. So 95% of scores will be between 572 (2)(51) = 470 and 572 + (2)(51) = 674. 1.102 Same idea
STAB22 section 1.3 and Chapter 1 exercises 1.101 Go up and down two times the standard deviation from the mean. So 95% of scores will be between 572 (2)(51) = 470 and 572 + (2)(51) = 674. 1.102 Same idea
The Normal Probability Distribution
 102 The Normal Probability Distribution C H A P T E R 7 Section 7.2 4Example 1 (pg. 71) Finding Area Under a Normal Curve In this exercise, we will calculate the area to the left of 5 inches using a normal
102 The Normal Probability Distribution C H A P T E R 7 Section 7.2 4Example 1 (pg. 71) Finding Area Under a Normal Curve In this exercise, we will calculate the area to the left of 5 inches using a normal
Math 227 Elementary Statistics. Bluman 5 th edition
 Math 227 Elementary Statistics Bluman 5 th edition CHAPTER 6 The Normal Distribution 2 Objectives Identify distributions as symmetrical or skewed. Identify the properties of the normal distribution. Find
Math 227 Elementary Statistics Bluman 5 th edition CHAPTER 6 The Normal Distribution 2 Objectives Identify distributions as symmetrical or skewed. Identify the properties of the normal distribution. Find
Homework: Due Wed, Feb 20 th. Chapter 8, # 60a + 62a (count together as 1), 74, 82
 Announcements: Week 5 quiz begins at 4pm today and ends at 3pm on Wed If you take more than 20 minutes to complete your quiz, you will only receive partial credit. (It doesn t cut you off.) Today: Sections
Announcements: Week 5 quiz begins at 4pm today and ends at 3pm on Wed If you take more than 20 minutes to complete your quiz, you will only receive partial credit. (It doesn t cut you off.) Today: Sections
Binomial and Normal Distributions. Example: Determine whether the following experiments are binomial experiments. Explain.
 Binomial and Normal Distributions Objective 1: Determining if an Experiment is a Binomial Experiment For an experiment to be considered a binomial experiment, four things must hold: 1. The experiment is
Binomial and Normal Distributions Objective 1: Determining if an Experiment is a Binomial Experiment For an experiment to be considered a binomial experiment, four things must hold: 1. The experiment is
Example - Let X be the number of boys in a 4 child family. Find the probability distribution table:
 Chapter7 Probability Distributions and Statistics Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number of boys in
Chapter7 Probability Distributions and Statistics Distributions of Random Variables tthe value of the result of the probability experiment is a RANDOM VARIABLE. Example - Let X be the number of boys in
Statistics for Business and Economics: Random Variables:Continuous
 Statistics for Business and Economics: Random Variables:Continuous STT 315: Section 107 Acknowledgement: I d like to thank Dr. Ashoke Sinha for allowing me to use and edit the slides. Murray Bourne (interactive
Statistics for Business and Economics: Random Variables:Continuous STT 315: Section 107 Acknowledgement: I d like to thank Dr. Ashoke Sinha for allowing me to use and edit the slides. Murray Bourne (interactive
University of California, Los Angeles Department of Statistics. Normal distribution
 University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Normal distribution The normal distribution is the most important distribution. It describes
University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Normal distribution The normal distribution is the most important distribution. It describes
Lecture 9. Probability Distributions. Outline. Outline
 Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
. 13. The maximum error (margin of error) of the estimate for μ (based on known σ) is:
 Statistics Sample Exam 3 Solution Chapters 6 & 7: Normal Probability Distributions & Estimates 1. What percent of normally distributed data value lie within 2 standard deviations to either side of the
Statistics Sample Exam 3 Solution Chapters 6 & 7: Normal Probability Distributions & Estimates 1. What percent of normally distributed data value lie within 2 standard deviations to either side of the
STAT Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model
 STAT 203 - Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model In Chapter 5, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are good
STAT 203 - Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model In Chapter 5, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are good
5.1 Personal Probability
 5. Probability Value Page 1 5.1 Personal Probability Although we think probability is something that is confined to math class, in the form of personal probability it is something we use to make decisions
5. Probability Value Page 1 5.1 Personal Probability Although we think probability is something that is confined to math class, in the form of personal probability it is something we use to make decisions
The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations.
 6.1 6.2 The Standard Normal Curve The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations. Basic Properties 1. The total area under the curve is.
6.1 6.2 The Standard Normal Curve The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations. Basic Properties 1. The total area under the curve is.
Lecture 9. Probability Distributions
 Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
Introduction to Business Statistics QM 120 Chapter 6
 DEPARTMENT OF QUANTITATIVE METHODS & INFORMATION SYSTEMS Introduction to Business Statistics QM 120 Chapter 6 Spring 2008 Chapter 6: Continuous Probability Distribution 2 When a RV x is discrete, we can
DEPARTMENT OF QUANTITATIVE METHODS & INFORMATION SYSTEMS Introduction to Business Statistics QM 120 Chapter 6 Spring 2008 Chapter 6: Continuous Probability Distribution 2 When a RV x is discrete, we can
Math 120 Introduction to Statistics Mr. Toner s Lecture Notes. Standardizing normal distributions The Standard Normal Curve
 6.1 6.2 The Standard Normal Curve Standardizing normal distributions The "bell-shaped" curve, or normal curve, is a probability distribution that describes many reallife situations. Basic Properties 1.
6.1 6.2 The Standard Normal Curve Standardizing normal distributions The "bell-shaped" curve, or normal curve, is a probability distribution that describes many reallife situations. Basic Properties 1.
NORMAL RANDOM VARIABLES (Normal or gaussian distribution)
 NORMAL RANDOM VARIABLES (Normal or gaussian distribution) Many variables, as pregnancy lengths, foot sizes etc.. exhibit a normal distribution. The shape of the distribution is a symmetric bell shape.
NORMAL RANDOM VARIABLES (Normal or gaussian distribution) Many variables, as pregnancy lengths, foot sizes etc.. exhibit a normal distribution. The shape of the distribution is a symmetric bell shape.
6.1 Graphs of Normal Probability Distributions:
 6.1 Graphs of Normal Probability Distributions: Normal Distribution one of the most important examples of a continuous probability distribution, studied by Abraham de Moivre (1667 1754) and Carl Friedrich
6.1 Graphs of Normal Probability Distributions: Normal Distribution one of the most important examples of a continuous probability distribution, studied by Abraham de Moivre (1667 1754) and Carl Friedrich
MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION
 MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION We have examined discrete random variables, those random variables for which we can list the possible values. We will now look at continuous random variables.
MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION We have examined discrete random variables, those random variables for which we can list the possible values. We will now look at continuous random variables.
Statistics 511 Supplemental Materials
 Gaussian (or Normal) Random Variable In this section we introduce the Gaussian Random Variable, which is more commonly referred to as the Normal Random Variable. This is a random variable that has a bellshaped
Gaussian (or Normal) Random Variable In this section we introduce the Gaussian Random Variable, which is more commonly referred to as the Normal Random Variable. This is a random variable that has a bellshaped
NOTES: Chapter 4 Describing Data
 NOTES: Chapter 4 Describing Data Intro to Statistics COLYER Spring 2017 Student Name: Page 2 Section 4.1 ~ What is Average? Objective: In this section you will understand the difference between the three
NOTES: Chapter 4 Describing Data Intro to Statistics COLYER Spring 2017 Student Name: Page 2 Section 4.1 ~ What is Average? Objective: In this section you will understand the difference between the three
Example. Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables
 Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables You are dealt a hand of 5 cards. Find the probability distribution table for the number of hearts. Graph
Chapter 8 Probability Distributions and Statistics Section 8.1 Distributions of Random Variables You are dealt a hand of 5 cards. Find the probability distribution table for the number of hearts. Graph
Continuous Random Variables and the Normal Distribution
 Chapter 6 Continuous Random Variables and the Normal Distribution Continuous random variables are used to approximate probabilities where there are many possible outcomes or an infinite number of possible
Chapter 6 Continuous Random Variables and the Normal Distribution Continuous random variables are used to approximate probabilities where there are many possible outcomes or an infinite number of possible
Part V - Chance Variability
 Part V - Chance Variability Dr. Joseph Brennan Math 148, BU Dr. Joseph Brennan (Math 148, BU) Part V - Chance Variability 1 / 78 Law of Averages In Chapter 13 we discussed the Kerrich coin-tossing experiment.
Part V - Chance Variability Dr. Joseph Brennan Math 148, BU Dr. Joseph Brennan (Math 148, BU) Part V - Chance Variability 1 / 78 Law of Averages In Chapter 13 we discussed the Kerrich coin-tossing experiment.
Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc.
 Chapter 8 Measures of Center Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc. Data that can only be integer
Chapter 8 Measures of Center Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc. Data that can only be integer
CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES
 CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES DISCRETE RANDOM VARIABLE: Variable can take on only certain specified values. There are gaps between possible data values. Values may be counting numbers or
CHAPTERS 5 & 6: CONTINUOUS RANDOM VARIABLES DISCRETE RANDOM VARIABLE: Variable can take on only certain specified values. There are gaps between possible data values. Values may be counting numbers or
EXERCISES FOR PRACTICE SESSION 2 OF STAT CAMP
 EXERCISES FOR PRACTICE SESSION 2 OF STAT CAMP Note 1: The exercises below that are referenced by chapter number are taken or modified from the following open-source online textbook that was adapted by
EXERCISES FOR PRACTICE SESSION 2 OF STAT CAMP Note 1: The exercises below that are referenced by chapter number are taken or modified from the following open-source online textbook that was adapted by
5.4 Normal Approximation of the Binomial Distribution
 5.4 Normal Approximation of the Binomial Distribution Bernoulli Trials have 3 properties: 1. Only two outcomes - PASS or FAIL 2. n identical trials Review from yesterday. 3. Trials are independent - probability
5.4 Normal Approximation of the Binomial Distribution Bernoulli Trials have 3 properties: 1. Only two outcomes - PASS or FAIL 2. n identical trials Review from yesterday. 3. Trials are independent - probability
The Normal Probability Distribution
 1 The Normal Probability Distribution Key Definitions Probability Density Function: An equation used to compute probabilities for continuous random variables where the output value is greater than zero
1 The Normal Probability Distribution Key Definitions Probability Density Function: An equation used to compute probabilities for continuous random variables where the output value is greater than zero
Section Distributions of Random Variables
 Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Section 8.1 - Distributions of Random Variables Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Standard Normal Calculations
 Standard Normal Calculations Section 4.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 10-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Standard Normal Calculations Section 4.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 10-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
STATISTICAL DISTRIBUTIONS AND THE CALCULATOR
 STATISTICAL DISTRIBUTIONS AND THE CALCULATOR 1. Basic data sets a. Measures of Center - Mean ( ): average of all values. Characteristic: non-resistant is affected by skew and outliers. - Median: Either
STATISTICAL DISTRIBUTIONS AND THE CALCULATOR 1. Basic data sets a. Measures of Center - Mean ( ): average of all values. Characteristic: non-resistant is affected by skew and outliers. - Median: Either
Week 7. Texas A& M University. Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4
 Week 7 Oğuz Gezmiş Texas A& M University Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week7 1 / 19
Week 7 Oğuz Gezmiş Texas A& M University Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week7 1 / 19
A.REPRESENTATION OF DATA
 A.REPRESENTATION OF DATA (a) GRAPHS : PART I Q: Why do we need a graph paper? Ans: You need graph paper to draw: (i) Histogram (ii) Cumulative Frequency Curve (iii) Frequency Polygon (iv) Box-and-Whisker
A.REPRESENTATION OF DATA (a) GRAPHS : PART I Q: Why do we need a graph paper? Ans: You need graph paper to draw: (i) Histogram (ii) Cumulative Frequency Curve (iii) Frequency Polygon (iv) Box-and-Whisker
LECTURE 6 DISTRIBUTIONS
 LECTURE 6 DISTRIBUTIONS OVERVIEW Uniform Distribution Normal Distribution Random Variables Continuous Distributions MOST OF THE SLIDES ADOPTED FROM OPENINTRO STATS BOOK. NORMAL DISTRIBUTION Unimodal and
LECTURE 6 DISTRIBUTIONS OVERVIEW Uniform Distribution Normal Distribution Random Variables Continuous Distributions MOST OF THE SLIDES ADOPTED FROM OPENINTRO STATS BOOK. NORMAL DISTRIBUTION Unimodal and
Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the
 Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the mean, use the CLT for the mean. If you are being asked to
Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the mean, use the CLT for the mean. If you are being asked to
Chapter 6: Random Variables. Ch. 6-3: Binomial and Geometric Random Variables
 Chapter : Random Variables Ch. -3: Binomial and Geometric Random Variables X 0 2 3 4 5 7 8 9 0 0 P(X) 3???????? 4 4 When the same chance process is repeated several times, we are often interested in whether
Chapter : Random Variables Ch. -3: Binomial and Geometric Random Variables X 0 2 3 4 5 7 8 9 0 0 P(X) 3???????? 4 4 When the same chance process is repeated several times, we are often interested in whether
5.4 Normal Approximation of the Binomial Distribution Lesson MDM4U Jensen
 5.4 Normal Approximation of the Binomial Distribution Lesson MDM4U Jensen Review From Yesterday Bernoulli Trials have 3 properties: 1. 2. 3. Binomial Probability Distribution In a binomial experiment with
5.4 Normal Approximation of the Binomial Distribution Lesson MDM4U Jensen Review From Yesterday Bernoulli Trials have 3 properties: 1. 2. 3. Binomial Probability Distribution In a binomial experiment with
Shifting and rescaling data distributions
 Shifting and rescaling data distributions It is useful to consider the effect of systematic alterations of all the values in a data set. The simplest such systematic effect is a shift by a fixed constant.
Shifting and rescaling data distributions It is useful to consider the effect of systematic alterations of all the values in a data set. The simplest such systematic effect is a shift by a fixed constant.
Chapter 7 1. Random Variables
 Chapter 7 1 Random Variables random variable numerical variable whose value depends on the outcome of a chance experiment - discrete if its possible values are isolated points on a number line - continuous
Chapter 7 1 Random Variables random variable numerical variable whose value depends on the outcome of a chance experiment - discrete if its possible values are isolated points on a number line - continuous
22.2 Shape, Center, and Spread
 Name Class Date 22.2 Shape, Center, and Spread Essential Question: Which measures of center and spread are appropriate for a normal distribution, and which are appropriate for a skewed distribution? Eplore
Name Class Date 22.2 Shape, Center, and Spread Essential Question: Which measures of center and spread are appropriate for a normal distribution, and which are appropriate for a skewed distribution? Eplore
Statistics, Measures of Central Tendency I
 Statistics, Measures of Central Tendency I We are considering a random variable X with a probability distribution which has some parameters. We want to get an idea what these parameters are. We perfom
Statistics, Measures of Central Tendency I We are considering a random variable X with a probability distribution which has some parameters. We want to get an idea what these parameters are. We perfom
5-1 pg ,4,5, EOO,39,47,50,53, pg ,5,9,13,17,19,21,22,25,30,31,32, pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38
 5-1 pg. 242 3,4,5, 17-37 EOO,39,47,50,53,56 5-2 pg. 249 9,10,13,14,17,18 5-3 pg. 257 1,5,9,13,17,19,21,22,25,30,31,32,34 5-4 pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38 5-5 pg. 281 5-14,16,19,21,22,25,26,30
5-1 pg. 242 3,4,5, 17-37 EOO,39,47,50,53,56 5-2 pg. 249 9,10,13,14,17,18 5-3 pg. 257 1,5,9,13,17,19,21,22,25,30,31,32,34 5-4 pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38 5-5 pg. 281 5-14,16,19,21,22,25,26,30
Chapter 4 and Chapter 5 Test Review Worksheet
 Name: Date: Hour: Chapter 4 and Chapter 5 Test Review Worksheet You must shade all provided graphs, you must round all z-scores to 2 places after the decimal, you must round all probabilities to at least
Name: Date: Hour: Chapter 4 and Chapter 5 Test Review Worksheet You must shade all provided graphs, you must round all z-scores to 2 places after the decimal, you must round all probabilities to at least
Central Limit Theorem
 Central Limit Theorem Lots of Samples 1 Homework Read Sec 6-5. Discussion Question pg 329 Do Ex 6-5 8-15 2 Objective Use the Central Limit Theorem to solve problems involving sample means 3 Sample Means
Central Limit Theorem Lots of Samples 1 Homework Read Sec 6-5. Discussion Question pg 329 Do Ex 6-5 8-15 2 Objective Use the Central Limit Theorem to solve problems involving sample means 3 Sample Means
Unit2: Probabilityanddistributions. 3. Normal distribution
 Announcements Unit: Probabilityanddistributions 3 Normal distribution Sta 101 - Spring 015 Duke University, Department of Statistical Science February, 015 Peer evaluation 1 by Friday 11:59pm Office hours:
Announcements Unit: Probabilityanddistributions 3 Normal distribution Sta 101 - Spring 015 Duke University, Department of Statistical Science February, 015 Peer evaluation 1 by Friday 11:59pm Office hours:
Chapter Six Probability Distributions
 6.1 Probability Distributions Discrete Random Variable Chapter Six Probability Distributions x P(x) 2 0.08 4 0.13 6 0.25 8 0.31 10 0.16 12 0.01 Practice. Construct a probability distribution for the number
6.1 Probability Distributions Discrete Random Variable Chapter Six Probability Distributions x P(x) 2 0.08 4 0.13 6 0.25 8 0.31 10 0.16 12 0.01 Practice. Construct a probability distribution for the number
STAT Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model
 STAT 203 - Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model In Chapter 5, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are good
STAT 203 - Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model In Chapter 5, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are good
8.1 Binomial Distributions
 8.1 Binomial Distributions The Binomial Setting The 4 Conditions of a Binomial Setting: 1.Each observation falls into 1 of 2 categories ( success or fail ) 2 2.There is a fixed # n of observations. 3.All
8.1 Binomial Distributions The Binomial Setting The 4 Conditions of a Binomial Setting: 1.Each observation falls into 1 of 2 categories ( success or fail ) 2 2.There is a fixed # n of observations. 3.All
Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at
 Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. Let X represent the savings of a resident; X ~ N(3000,
Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. Let X represent the savings of a resident; X ~ N(3000,
The normal distribution is a theoretical model derived mathematically and not empirically.
 Sociology 541 The Normal Distribution Probability and An Introduction to Inferential Statistics Normal Approximation The normal distribution is a theoretical model derived mathematically and not empirically.
Sociology 541 The Normal Distribution Probability and An Introduction to Inferential Statistics Normal Approximation The normal distribution is a theoretical model derived mathematically and not empirically.
In a binomial experiment of n trials, where p = probability of success and q = probability of failure. mean variance standard deviation
 Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
Chapter Chapter 6. Modeling Random Events: The Normal and Binomial Models
 Chapter 6 107 Chapter 6 Modeling Random Events: The Normal and Binomial Models Chapter 6 108 Chapter 6 109 Table Number: Group Name: Group Members: Discrete Probability Distribution: Ichiro s Hit Parade
Chapter 6 107 Chapter 6 Modeling Random Events: The Normal and Binomial Models Chapter 6 108 Chapter 6 109 Table Number: Group Name: Group Members: Discrete Probability Distribution: Ichiro s Hit Parade
Consumer Guide Dealership Word of Mouth Internet
 8.1 Graphing Data In this chapter, we will study techniques for graphing data. We will see the importance of visually displaying large sets of data so that meaningful interpretations of the data can be
8.1 Graphing Data In this chapter, we will study techniques for graphing data. We will see the importance of visually displaying large sets of data so that meaningful interpretations of the data can be
Lecture 6: Normal distribution
 Lecture 6: Normal distribution Statistics 101 Mine Çetinkaya-Rundel February 2, 2012 Announcements Announcements HW 1 due now. Due: OQ 2 by Monday morning 8am. Statistics 101 (Mine Çetinkaya-Rundel) L6:
Lecture 6: Normal distribution Statistics 101 Mine Çetinkaya-Rundel February 2, 2012 Announcements Announcements HW 1 due now. Due: OQ 2 by Monday morning 8am. Statistics 101 (Mine Çetinkaya-Rundel) L6:
STT 315 Practice Problems Chapter 3.7 and 4
 STT 315 Practice Problems Chapter 3.7 and 4 Answer the question True or False. 1) The number of children in a family can be modelled using a continuous random variable. 2) For any continuous probability
STT 315 Practice Problems Chapter 3.7 and 4 Answer the question True or False. 1) The number of children in a family can be modelled using a continuous random variable. 2) For any continuous probability
Math Tech IIII, May 7
 Math Tech IIII, May 7 The Normal Probability Models Book Sections: 5.1, 5.2, & 5.3 Essential Questions: How can I use the normal distribution to compute probability? Standards: S.ID.4 Properties of the
Math Tech IIII, May 7 The Normal Probability Models Book Sections: 5.1, 5.2, & 5.3 Essential Questions: How can I use the normal distribution to compute probability? Standards: S.ID.4 Properties of the
Chapter 4. Section 4.1 Objectives. Random Variables. Random Variables. Chapter 4: Probability Distributions
 Chapter 4: Probability s 4. Probability s 4. Binomial s Section 4. Objectives Distinguish between discrete random variables and continuous random variables Construct a discrete probability distribution
Chapter 4: Probability s 4. Probability s 4. Binomial s Section 4. Objectives Distinguish between discrete random variables and continuous random variables Construct a discrete probability distribution
Normal Probability Distributions
 CHAPTER 5 Normal Probability Distributions 5.1 Introduction to Normal Distributions and the Standard Normal Distribution 5.2 Normal Distributions: Finding Probabilities 5.3 Normal Distributions: Finding
CHAPTER 5 Normal Probability Distributions 5.1 Introduction to Normal Distributions and the Standard Normal Distribution 5.2 Normal Distributions: Finding Probabilities 5.3 Normal Distributions: Finding
8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions 8-1
 8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions For Example: On August 8, 2011, the Dow dropped 634.8 points, sending shock waves through the financial community.
8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions For Example: On August 8, 2011, the Dow dropped 634.8 points, sending shock waves through the financial community.
