FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. modelu úrokových mier
|
|
|
- Cora Parks
- 5 years ago
- Views:
Transcription
1 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Bratislava 2013 Bc. Simona Chattová
2 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Diplomová práca Študijný program: Ekonomická a finančná matematika Študijný odbor: 1114 Aplikovaná matematika Školiace pracovisko: Katedra aplikovanej matematiky a štatistiky Školitel : RNDr. Beáta Stehlíková, PhD. Evidenčné číslo: 9bf58c65-a546-4e68-84aa-261f79294fc0 Bratislava 2013 Bc. Simona Chattová
3 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky ZADANIE ZÁVEREČNEJ PRÁCE Meno a priezvisko študenta: Študijný program: Študijný odbor: Typ záverečnej práce: Jazyk záverečnej práce: Bc. Simona Chattová ekonomická a finančná matematika (Jednoodborové štúdium, magisterský II. st., denná forma) aplikovaná matematika diplomová slovenský Názov: Cieľ: Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu Pri kalibrácii modelov úrokových mier sa dajú uvažovať dve kritériá: hodnota funkcie vierohodnosti a kvalita fitovania výnosových kriviek. V závislosti od toho, ktoré kritérium považujeme za dôležitejšie, môžeme ho optimalizovať v prvom kroku, a zostávajúce parametre určiť na základe druhého kritéria. Cieľom práce bude kalibrovať oboma spôsobmi (t. j. oboma výbermi prioritného kritéria) konvergenčný model Vašíčkovho typu - odvodiť potrebné účelové funkcie, navrhnúť spôsob ich optimalizácie a aplikovať ho na reálne dáta. Vedúci: Katedra: Vedúci katedry: Dátum zadania: RNDr. Mgr. Beáta Stehlíková, PhD. FMFI.KAMŠ - Katedra aplikovanej matematiky a štatistiky prof. RNDr. Daniel Ševčovič, CSc. Dátum schválenia: prof. RNDr. Daniel Ševčovič, CSc. garant študijného programu študent vedúci práce
4 Abstrakt Chattová, Simona: Kalibrácia konvergenčného modelu úrokových mier Vašíčkovho typu. [Diplomová práca] - Univerzita Komenského v Bratislave. Fakulta matematiky, fyziky a informatiky; Katedra aplikovanej matematiky a štatistiky. - Vedúci diplomovej práce: RNDr. Beáta Stehlíková, PhD., - Bratislava 2013 /60 s./ Táto diplomová práca sa zaoberá kalibráciou konvergenčného modelu Vašíčkovho typu s nulovou koreláciou. Ide o dvojfaktorový model úrokovej miery, ktorý popisuje dynamiku európskej úrokovej miery (úrokovej miery v rámci eurozóny), o ktorej predpokladáme, že ovplyvňuje vývoj domácej úrokovej miery, t.j. úrokovej miery krajiny, ktorá sa má onedlho stat členským štátom eurozóny. V práci navrhujeme metódu kalibrácie daného modelu, ktorá súčasne využíva časový rad hodnôt krátkodobej úrokovej miery aj výnosové krivky a teda berie do úvahy dve hodnotiace kritéria - hodnotu vierohodnostnej funkcie a kvalitu fitovania výnosových kriviek (t.j. váženú strednú kvadratickú chybu medzi teoretickými a trhovými výnosovými krivkami). Odvodíme príslušné účelové funkcie, určíme spôsob ich optimalizácie a aplikujeme navrhnutú metódu na reálne trhové dáta. Kl účové slová : dlhopisy časová štruktúra úrokových mier okamžitá úroková miera konvergenčný model Vašíčkovho typu kalibrácia
5 Abstract Chattová, Simona : Calibration of the convergence model of interest rates of Vasicek type. [Master s thesis] - Comenius University in Bratislava. Faculty of mathematics, physics and informatics; Department of applied mathematics and statistics. - Supervisor: RNDr. Beáta Stehlíková, PhD., - Bratislava /60 pp./ This work deals with the calibration of the convergence model of interest rates of Vasicek type with zero correlation. It is a two factor interest rate model that describes the dynamics of the european interest rate which is assumed to affect the development of the domestic interest rate(i.e. interest rate of a country entering the eurozone). The aim of this work is to provide new approach to estimation of the parameters in the given model - we propose a method, which uses time series of short-term interest rates and yield curves, and thus takes into account two criteria - likelihood function value and quality of yield curves fit (i.e. weighted mean square error between theoretical and market yield curves). We derive the cost functions, determine how to optimize them and apply the proposed method to real market data. Keywords : bonds term structureof interest rates short rate convergence model of Vasicek type calibration
6 Obsah Úvod 1 1 Teoretické základy modelovania úrokových mier Dlhopisy a časová štruktúra úrokových mier Okamžitá úroková miera Deriváty úrokovej miery Stochastické procesy a Itóova lema Klasifikácia modelov úrokových mier Jednofaktorové rovnovážne modely úrokových mier Ceny dlhopisov v jednofaktorových modeloch úrokových mier Ceny dlhopisov v jednofaktorovom Vašíčkovom modeli Pojem reálnej a rizikovo neutrálnej pravdepodobnostnej miery Dvojfaktorové rovnovážne modely úrokových mier Ceny dlhopisov v dvojfaktorových modeloch úrokových mier Ako odhadovat parametre modelov úrokových mier Metóda maximálnej vierohodnosti na odhad parametrov modelov úrokových mier Podmienené rozdelenie okamžitej úrokovej miery pre Vašíčkov model Metóda maximálnej vierohodnosti na odhad parametrov Vašíčkovho modelu Kalibrácia modelu založená na minimalizácii miery vzdialenosti reálnej a odhadovanej výnosovej krivky Konvergenčné modely úrokovej miery Konvergenčný model Vašíčkovho typu Konvergenčný model Vašíčkovho typu s nulovou koreláciou Odhad parametrov konvergenčného modelu Vašíčkovho typu s nulovou koreláciou Odhad parametrov procesu pre európsku úrokovú mieru Podmienené rozdelenie európskej úrokovej miery
7 5.1.2 Maximálne vierohodný odhad parametrov procesu pre európsku úrokovú mieru Odhad parametrov procesu pre európsku úrokovú mieru na základe minimalizácie miery vzdialenosti reálnej a odhadovanej výnosovej krivky Odhad trhovej ceny rizika v prípade jednofaktorového Vašíčkovho modelu Odhad parametrov procesu pre domácu úrokovú mieru Podmienené rozdelenie domácej úrokovej miery Maximálne vierohodný odhad parametrov procesu pre domácu úrokovú mieru Odhad parametrov procesu pre domácu úrokovú mieru na základe minimalizácie miery vzdialenosti reálnej a odhadovanej výnosovej krivky Odhad trhovej ceny rizika pre domácu úrokovú mieru v prípade konvergenčného modelu Vašíčkovho typu Kalibrácia vybraných modelov úrokových mier na reálnych dátach Výber dát Kalibrácia jednofaktorového Vašíčkovho modelu Kalibrácia konvergenčného modelu Vašíčkovho typu s nulovou koreláciou Záver 58 Literatúra 59
8 Úvod Za posledné dve desat ročia sa úrokové miery a oceňovanie derivátov od nich odvodených stali predmetom intenzívneho výskumu. V súčasnosti sa na finančných trhoch obchoduje s rôznymi derivátmi úrokových mier, a preto sú analyzované modely popisujúce vývoj úrokových mier rozhodujúce z viacerých dôvodov, vrátane určovania cien derivátov úrokových mier, ale aj kvantifikovania a riadenia finančného rizika. V tejto diplomovej práci sa budeme zaoberat kalibráciou konvergenčného modelu Vašíčkovho typu s nulovou koreláciou, ktorý patrí do triedy dvojfaktorových modelov okamžitej úrokovej miery. Daný model zachytáva vývoj európskej úrokovej miery, o ktorej sa predpokladá, že ovplyvňuje vývoj domácej úrokovej miery, t.j. úrokovej miery krajiny, ktorá sa v krátkom čase stane členským štátom eurozóny. Vývoj európskej úrokovej miery však nezávisí od vývoja domácej úrokovej miery. Ciel om práce je pre daný model navrhnút metódu kalibrácie, ktorá súčasne zohl adňuje dve kritéria - hodnotu funkcie vierohodnosti a kvalitu fitovania výnosových kriviek (t.j. váženú strednú kvadratickú chybu medzi teoretickými a trhovými výnosovými krivkami). V závislosti od toho, ktoré kritérium považujeme za dôležitejšie, optimalizujeme ho v prvom kroku a zostávajúce parametre určíme na základe druhého kritéria. Práca je rozdelená na 6 častí. Prvá kapitola predstavuje úvod do problematiky modelovania úrokových mier, vymedzuje pojmy dlhopisu, časovej štruktúry úrokovej miery a okamžitej úrokovej miery. Taktiež obsahuje prehl ad hlavných pojmov a nástrojov stochastického kalkulu, ktoré budeme v tejto práci používat. Základným predpokladom pri modelovaní úrokovej miery je totiž fakt, že jej vývoj je charakterizovaný stochastickým procesom. Druhá čast práce je venovaná klasifikácii modelov úrokových mier. Podrobnejšie sa v nej zaoberáme jednofaktorovými a dvojfaktorovými rovnovážnymi modelmi úrokových mier, ich formuláciou v reálnej a rizikovo neutrálnej pravdepodobnostnej miere a určením cien dlhopisov v týchto modeloch. Tretia kapitola dáva odpoved na otázku, akým spôsobom sa dajú odhadovat parametre modelov úrokových mier. Sú v nej analyzované dva prístupy v rámci kalibrácie jednofaktorového Vašíčkovho modelu a to odhad parametrov z časového radu krátkodobej úrokovej miery metódou maximálnej vierohodnosti a prístup zameraný na čo najlepšiu zhodu trhových a modelom implikovaných výnosových kriviek. V kapitole 4 charakterizujeme konvergenčné modely úrokových mier, pričom sa zameriame na konvergenčný model Vašíčkovho typu s nulovou aj nenulovou koreláciou 1
9 a popíšeme odvodenie riešenia parciálnej diferenciálnej rovnice pre ceny domácich dlhopisov implikované danými modelmi. Odhad parametrov konvergenčného modelu Vašíčkovho typu s nulovou koreláciou je náplňou piatej kapitoly, v ktorej sú odvodené odhady parametrov procesu pre európsku aj domácu úrokovú mieru s využitím dvoch prístupov podrobnejšie popísaných v kapitole 3. V záverečnej časti práce aplikujeme navrhnuté metódy kalibrácie jednofaktorového Vašíčkovho modelu a konvergenčného modelu Vašíčkovho typu s nulovou koreláciou na reálne trhové dáta a prezentujeme získané výsledky. 2
10 Kapitola 1 Teoretické základy modelovania úrokových mier V úvode tejto práce definujeme základné pojmy týkajúce sa modelovania úrokových mier a to pojem dlhopisu, časovej štruktúry úrokových mier a okamžitej úrokovej miery. Uvedieme aj základné pojmy a nástroje stochastického kalkulu. Podrobnejšie informácie nájde čitatel v [16]. 1.1 Dlhopisy a časová štruktúra úrokových mier Dlhopis je najjednoduchším derivátom úrokovej miery. Ide o cenný papier, s ktorým je spojené právo majitel a požadovat splácanie dlžnej sumy (nominálnej hodnoty) a vyplácanie výnosov z nej (kupónov) v presne stanovenom čase. Dlhopis teda pre jeho vypisovatel a predstavuje určitú formu pôžičky. Bezkupónový dlhopis s jednotkovou nominálnou hodnotou sa nazýva diskontný dlhopis. Pod dlhopisom budeme d alej rozumiet práve diskontný dlhopis. Označme P(t,T) cenu dlhopisu v čase t uzavretia kontraktu so splatnost ou v čase T. Nech výraz R(t,T) označuje spojitý úrok na obdobie od t do T. Potom pre cenu dlhopisu platí P(t,T) = e R(t,T)(T t). Ak teda poznáme ceny dlhopisov, môžeme určit krivku časovej štruktúry úrokovej miery využitím vzt ahu R(t,T) = ln[p(t,t)]. (1.1) T t Časová štruktúra úrokovej miery vyjadruje závislost úrokovej miery v čase t od doby splatnosti dlhopisu T. Taktiež môžeme časovú štruktúru úrokovej miery ekvivalentne definovat ako funkcionálnu závislost medzi výnosom dlhopisu a časom T t zostávajúcim do splatnosti daného dlhopisu. Preto sa krivka časovej štruktúry úrokovej miery označuje aj ako výnosová krivka, resp. krivka výnosov pre bezkupónové dlhopisy. 3
11 Tvar reálnej výnosovej krivky môže byt rôzny. Táto krivka je obvykle rastúca, ked že na dlhšie obdobie sa požičiava s vyšším úrokom. Pri očakávaní poklesu hodnôt úrokových mier je výnosová krivka klesajúca. Dlhopisy s dlhšou maturitou teda nemusia mat nutne vyššiu úrokovú mieru a výnosová krivka môže mat aj nemonotónny charakter. Obrázok 1.1 znázorňuje príklady časovej štruktúry úrokových sadzieb Euribor (Euro Interbank Offered Rate), Pribor (Prague Interbank Offered Rate), Bribor (Bratislava Interbank Offered Rate) a Libor (London Interbank Offered Rate) denominovaný v eurách (EuroLibor) Euribor Pribor výnos [%] výnos [%] doba splatnosti (v mesiacoch) doba splatnosti (v mesiacoch) Bribor EuroLibor výnos [%] výnos [%] doba splatnosti (v mesiacoch) doba splatnosti (v mesiacoch) Obr. 1.1: Príklady časovej štruktúry úrokovej miery Euribor 1 (Euro Interbank Offered Rate) je úroková sadzba, za ktorú si banky na medzibankovom trhu v rámci eurozóny požičiavajú peniaze. Táto medzibanková úverová sadzba sa určuje pre rôzne doby splatnosti a to 1, 2 alebo 3 týždne a 1 až 12 mesiacov. Je upravovaná na dennej báze a vypočíta sa ako aritmetický priemer odhadov úrokov referenčných bánk, za ktoré sú tieto banky ochotné platit za pôžičky od iných bánk, pričom štvrtina najvyšších a najnižších sadzieb sa vynecháva. Sadzba Euribor je kl účová pre stanovovanie úrokov v Európskej menovej únii. Napríklad úver s variabilnou úrokovou sadzbou môže byt kombináciou fixnej zložky a sadzby Euribor. 1 spracované podl a [25] 4
12 1.2 Okamžitá úroková miera Okamžitá (označovaná aj ako krátkodobá) úroková miera r(t) predstavuje začiatok krivky časovej štruktúry úrokovej miery a je definovaná vzt ahom r(t) = lim T t +R(t,T). Ide o bod reprezentujúci úrokovú mieru platnú na vel mi krátke obdobie. Nie je to však veličina, ktorá na trhu priamo existuje, preto ju musíme niečím nahradit. Časovo má k okamžitej úrokovej miere najbližšie sadzba EONIA (Euro Overnight Index Average), ktorá predstavuje jednodňovú medzibankovú úverovú sadzbu v rámci eurozóny. V praxi sa však short rate zvykne aproximovat týždennou, príp. mesačnou úrokovou mierou Eonia výnos [%] Obr. 1.2: Priebeh jednodňovej úrokovej sadzby EONIA za rok 2012 Modely krátkodobej úrokovej miery (tzv. short-rate modely) popisujú budúci vývoj úrokových mier na základe budúceho vývoja krátkodobej úrokovej miery. 1.3 Deriváty úrokovej miery Hodnoty derivátov úrokovej miery závisia od hodnoty úrokovej miery v určitom čase, príp. od hodnôt počas určitého časového intervalu. Existuje vel a obchodovaných finančných derivátov, ktorých hodnota závisí od vývoja úrokovej miery. Okrem už spomínaného dlhopisu sú to opcie na dlhopisy, swapy, deriváty typu cap a floor a mnohé iné. Deriváty úrokovej miery sa používajú na zaistenie voči fluktuáciám vo vývoji úrokovej miery a detailnejší popis ich vlastností a spôsobov oceňovania sa dá nájst v [16], [17]. 2 napr. autori práce [4] používajú ako proxy short rate výnosy štátnych pokladničných poukážok so splatnost ou 1 mesiac, zatial čo v práci [2] sú použité výnosy 3-mesačných štátnych pokladničných poukážok, v článku [1] je short rate aproximovaná eurodolárovou sadzbou s dobou splatnosti 1 týždeň 5
13 1.4 Stochastické procesy a Itóova lema Základným predpokladom pri modelovaní úrokovej miery je fakt, že dynamika úrokovej miery je charakterizovaná stochastickým procesom. Vývoj hodnôt úrokovej miery sa totiž nedá popísat deterministickou funkciou. V tejto časti práce uvedieme základy stochastického kalkulu, ktorý sa využíva pri oceňovaní derivátov úrokovej miery, pričom vychádzame z [16], [18]. Definícia Stochastický proces {X t,t 0} je t-parametrický systém náhodných premenných X t definovaných na pravdepodobnostnom priestore (Ω,F,P). Vo finančnej matematike sú modely krátkodobej úrokovej miery obvykle formulované v tvare stochastickej diferenciálnej rovnice. Ide o diferenciálnu rovnicu, v ktorej jeden alebo viacero členov je stochastickým procesom. Základným typom stochastického procesu je tzv. Wienerov proces, z ktorého sú odvodené mnohé d alšie. Definícia Wienerov proces {W t,t 0} je stochastický proces s nasledujúcimi vlastnost ami: s pravdepodobnost ou 1 sú trajektórie tohto procesu spojité a W(0) = 0, náhodná premenná W(t) má N(0,t) rozdelenie, a pre každé delenie t 0 = 0 < t 1 <... < t n sú prírastky W(t 1 ) W(t 0 ),W(t 2 ) W(t 1 ),...,W(t n ) W(t n 1 ) nezávislými náhodnými premennými. Na obrázku 1.3 je znázornených niekol ko realizácií Wienerovho procesu Obr. 1.3: Realizácie Wienerovho procesu Definícia Nech pre meratel nú funkciu f : a,b R platí b a f2 (y)dy <. Potom integrál b a n 1 f(y)dw(y) := lim f(y i )(w(y i+1 ) w(y i )), υ 0 i=0 6
14 kde υ = max(y i+1 y i ) je norma delenia a = y 0 < y 1 <... < y n = b intervalu a,b a {w(y),y 0} je Wienerov proces, sa nazýva Itóov integrál. Nasledujúca veta charakterizuje Itóov integrál pre meratel nú funkciu reálnej premennej ako náhodnú premennú s normálnym rozdelením. Veta 1.1. Nech f : a,b R je spojitá funkcia. Potom platí b a f(t)dw t N ( 0, b to znamená, že platia nasledujúce rovnosti ( b ) E f(t)dw t = 0, a ( [ b ] 2 ) E f(t)dw t = a a ) f 2 (t)dt, b a f 2 (t)dt. (1.2) Rovnost (1.2) popisuje vlastnost Itóovho integrálu, ktorá sa označuje ako tzv. Itóova izometria a v tejto práci sa použije na výpočet variancie stochastického procesu. Na určenie diferenciálu funkcie stochastického procesu sa používa Itóova lema, ktorá vyjadruje vzt ah medzi malou zmenou hodnoty funkcie náhodnej premennej a malou zmenou hodnoty samotnej náhodnej premennej. Veta 1.2. (Jednorozmerná Itóova lema). Nech funkcia x je riešením stochastickej diferenciálnej rovnice dx = µ(x,t)dt+σ(x,t)dw. Nech f C 2, f(x,t) : R 0, ) R. Potom pre diferenciál funkcie f platí ( f df = t +µ(x,t) f x + 1 ) 2 σ2 (x,t) 2 f dt+σ(x,t) f x 2 x dw. Itóova lema teda dáva odpoved na otázku, ako vyzerá stochastická diferenciálna rovnicapopisujúcavývojfunkcief(x,t)vprípade,žepremennáxjeriešeníminejzadanej stochastickej diferenciálnej rovnice. 7
15 Viacrozmerná verzia Itóovej lemy je sformulovaná v nasledujúcej vete. Veta 1.3. (Viacrozmerná Itóova lema). T Nech vektor premenných X = (X 1,X 2,...,X n ) spĺňa nasledujúcu sústavu stochastických diferenciálnych rovníc dx 1 = µ 1 (X,t)dt+σ 11 (X,t)dw σ 1m (X,t)dw m. dx n = µ n (X,t)dt+σ n1 (X,t)dw σ nm (X,t)dw m, kde w = (w 1,w 2,...,w m ) T je vektor Wienerových procesov, ktorých prírastky sú navzájom nezávislé, t.j. E(dw i dw j ) = 0 pre i j, E [ (dw i ) 2] = dt. Nech f C 2, f(x,t) : R n 0, ) R. Potom diferenciál funkcie f je daný vzt ahom df = f t dt+( Xf) T dx (dx)t ( 2 Xf ) dx, pričom X f resp. 2 X f predstavujú gradient resp. Hessovu maticu funkcie f vzhl adom na premenné X 1,X 2,...,X n a zároveň (dw i )(dw j ) = δ ij dt. Naviac členy rádu (dt) 2,(dw i )(dt) sú zanedbatel né v porovnaní s ostatnými členmi, ktoré vystupujú vo vzt ahu pre df. 8
16 Kapitola 2 Klasifikácia modelov úrokových mier V rámci modelovania úrokových mier existujú dva základné prístupy a teda rozlišujeme dva základné typy modelov: bezarbitrážne modely tieto modely sú založené na princípe vylúčenia arbitráže, a preto vychádzajú zo súčasnej krivky časovej štruktúry úrokovej miery, parametre v týchto modeloch sú teda funkciami času, rovnovážne modely tieto modely nepoužívajú aktuálnu výnosovú krivku ako vstupnú informáciu, ale aktuálne úrokové miery získame ako výstup modelu, v takomto prípade však dochádza k nekonzistencii medzi skutočnými (trhovými) a modelovanými úrokovými mierami v čase zostavovania modelu. Modely krátkodobých úrokových mier popisujú časovú štruktúru úrokových mier a sú obvykle formulované v tvare stochastickej diferenciálnej rovnice pre okamžitú úrokovú mieru, o ktorej predpokladáme, že je funkciou konečného počtu náhodných faktorov. Na základe počtu náhodných faktorov, pomocou ktorých modelujeme krátkodobú úrokovú mieru, rozlišujeme jednofaktorové a viacfaktorové modely. Vol ba modelu úrokovej miery závisí od toho, ktoré z vlastností úrokovej miery sú pre konkrétne ocenenie dôležité. Avšak v prípade príliš zložitých modelov vznikajú problémy s oceňovaním derivátov úrokových mier. V praxi je vhodné pracovat s modelom, ktorý spĺňa predovšetkým tieto vlastnosti jednoduchost a z nej vyplývajúca prijatel ná výpočtová náročnost, čo najlepšia zhoda s reálnymi dátami. Na druhej strane je vhodné požadovat, aby úroková miera nebola záporná ani nenadobúdala vel mi vel ké hodnoty, a teda disperzia by mala byt v súlade s očakávaniami možných hodnôt. Ďalej sa aj na základe historických časových radov dá očakávat, že úrokové miery sú z dlhodobého hl adiska prit ahované k nejakej dlhodobej priemernej úrovni, čo znamená, že príliš vysoké úrokové miery majú tendenciu klesat a naopak, 9
17 príliš nízke úrokové miery stúpajú. Vo všeobecnosti tiež platí, že volatility úrokových mier rozličných maturít sú rôzne. Úrokové miery platné na kratšie obdobia sa totiž zvyčajne vyznačujú výraznejšími fluktuáciami. Podrobnejšie informácie týkajúce sa rôznych modelov úrokových mier sa dajú nájst v knihách [3], [9], [13]. 2.1 Jednofaktorové rovnovážne modely úrokových mier Samotný názov jednofaktorové modely výchádza z toho, že v týchto modeloch je zahrnutý iba jeden náhodný faktor. Týmto faktorom je okamžitá úroková miera r, o ktorej predpokladáme, že sa riadi stochastickou diferenciálnou rovnicou v tvare dr = µ(r,t)dt+σ(r,t)dw, kde µ(r, t) predstavuje trend vo vývoji úrokovej miery, σ(r, t) vyjadruje volatilitu procesuadw jediferenciálwienerovhoprocesu.čímväčšiajehodnotastochastického člena σ(r, t)dw, tým väčšie sú náhodné fluktuácie úrokovej miery v okolí jej trendu. Pri úrokových mierach môžeme na príslušnom časovom horizonte identifikovat tendenciu ich návratu k tzv. dlhodobej rovnovážnej hodnote. Takáto vlastnost procesu sa označuje ako mean-reversion a je dôvodom obvyklej vol by driftovej funkcie µ(r,t) v tvare µ(r,t) = κ(θ r), kde κ a θ sú kladné konštanty. Stredná hodnota úrokovej miery je v takom prípade rýchlost ou κ prit ahovaná k limitnej hodnote θ. Je zrejmé, že platí de(r t ) = E(dr t ) = κ(θ E(r t ))dt, pričom riešenie danej diferenciálnej rovnice pre strednú hodnotu úrokovej miery vyzerá nasledovne E(r t ) = r 0 e κt +θ ( 1 e κt) a z toho vyplýva, že lim E(r t) = θ. t Od tvaru funkcie volatility σ(r, t) potom závisia d alšie vlastnosti modelov úrokových mier. Teraz popíšeme najdôležitejšie a najznámejšie jednofaktorové rovnovážne modely úrokovej miery, s ktorými sa čitatel môže oboznámit aj v [17]. Vašíčkov model publikovaný v[24] patrí k prvým navrhnutým modelom okamžitej úrokovej miery, ktorej vývoj je popísaný stochastickou diferenciálnou rovnicou dr = κ(θ r)dt+σdw. 10
18 Funkcia volatility tohto modelu je konštantná (deterministická) a teda nezávisí od aktuálnej hodnoty úrokovej miery. Ak je hodnota úrokovej miery blízka nule, tak z dôvodu konštantnej volatility môže úroková miera s nenulovou pravdepodobnost ou nadobudnút zápornú hodnotu. A práve predpoklad konštantnej volatility a z toho vyplývajúci fakt, že úroková miera sa môže dostat do záporných hodnôt, sú považované za pomerne vel ké nevýhody Vašíčkovho modelu. Poznamenajme, že pravdepodobnost s akou úroková miera nadobudne zápornú hodnotu, je funkciou času, aktuálnej hodnoty úrokovej miery a zvolených parametrov (pozri vzt ah (3.3), ktorý je odvodený v nasledujúcej kapitole, v ktorej sa zaoberáme aj pravdepodobnostným rozdelením úrokových mier) vývoj úrokovej miery limitná hodnota strednej hodnoty úrokovej miery Obr. 2.1: Simulácia vývoja úrokovej miery charakterizovanej Vašíčkovým modelom s parametrami κ = 3,θ = 1,σ = 0.05 Cox-Ingersoll-Ross model navrhnutý v [8] je d alším často používaným jednofaktorovým modelom, ktorý je reprezentovaný stochastickým procesom dr = κ(θ r)dt+σ rdw. Volatilita, ktorú predstavuje výraz σ r je úmerná odmocnine z r, čo implikuje, že jej hodnota sa s rastúcou úrokovou mierou zvyšuje (táto vlastnost sa označuje ako tzv. level effect). Pri nízkych úrokových mierach je teda hodnota volatility malá a ak by sa dosiahla nulová hodnota úrokovej miery, tak volatilita by bola tiež nulová. Ďalší vývoj by bol potom deterministický a určený driftom, ktorý je pre r = 0 kladný. Preto nie je možné, aby úroková miera nadobudla zápornú hodnotu, čo je výhodou tohto modelu v porovnaní s Vašíčkovým modelom. Zovšeobecnením uvedených dvoch modelov je tzv. Chan-Karolyi-Longstaff- Sanders model daný stochastickou diferenciálnou rovnicou dr = κ(θ r)dt+σr γ dw, ktorý bol navrhnutý v [4] za účelom porovnania modelov pre rôzne hodnoty parametra γ. Pre takýto proces vo všeobecnosti neexistuje explicitné riešenie parciálnej 11
19 2 1.8 vývoj úrokovej miery limitná hodnota strednej hodnoty úrokovej miery Obr. 2.2: Simulácia vývoja úrokovej miery charakterizovanej CIR modelom s parametrami κ = 2,θ = 1,σ = 0.05 diferenciálnej rovnice pre ceny dlhopisov (len pre špeciálnu vol bu parametra γ = 0 alebo γ = 1 2 ). V jednofaktorových modeloch úrokovej miery je teda výnosová krivka určená okamžitou úrokovou mierou a parametrami modelu. To znamená, že pre dané hodnoty parametrov modelu je výnosová krivka jednoznačne určená hodnotou okamžitej úrokovej miery Ceny dlhopisov v jednofaktorových modeloch úrokových mier Ako sme už spomenuli, bezkupónový dlhopis je najjednoduchším a základným derivátom úrokovej miery. Jeho oceňovaním sa zaoberáme z toho dôvodu, že ak poznáme ceny dlhopisov, tak na základe vzt ahu (1.1) vieme určit časovú štruktúru úrokovej miery. V tejto časti práce odvodíme parciálnu diferenciálnu rovnicu pre cenu P(r,t,T) bezkupónového dlhopisu, ktorá je funkciou maturity T, aktuálneho času t a hodnoty okamžitej úrokovej miery r v čase t, pričom využijeme rovnaký postup ako v [17]. Predpokladajme, že okamžitá úroková miera r sa riadi stochastickým procesom dr = µ(r,t)dt+σ(r,t)dw. Využitím Itóovej lemy 1.2 dostaneme nasledujúcu rovnicu pre diferenciál funkcie P ( ) P dp = t +µ P r + σ2 2 P dt+σ P 2 r 2 r dw = µ B (r,t)dt+σ B (r,t)dw, kde µ B (r,t) a σ B (r,t) označujú drift a volatilitu ceny dlhopisu. 12
20 Ďalej vytvoríme portfólio pozostávajúce z jedného dlhopisu s maturitou v čase T 1 a dlhopisov s maturitou v čase T 2. Hodnota Π takéhoto portfólia je Π = P(r,t,T 1 )+ P(r,t,T 2 ). Pre zmenu hodnoty daného portfólia potom platí dπ = dp(r,t,t 1 )+ dp(r,t,t 2 ) = [µ B (r,t,t 1 )+ µ B (r,t,t 2 )]dt+[σ B (r,t,t 1 )+ σ B (r,t,t 2 )]dw. (2.1) Chceme však, aby toto portfólio bolo bezrizikové. To znamená, že musíme eliminovat náhodnú čast rovnice (2.1) a to nasledovnou vol bou parametra = σ B(r,t,T 1 ) σ B (r,t,t 2 ). Vývoj hodnoty portfólia je napokon určený deterministickou rovnicou [ dπ = µ B (r,t,t 1 ) σ ] B(r,t,T 1 ) σ B (r,t,t 2 ) µ B(r,t,T 2 ) dt. (2.2) Z princípu vylúčenia arbitráže vyplýva, že výnos bezrizikového portfólia sa rovná hodnote bezrizikovej úrokovej miery. Inak povedané, zmena hodnoty portfólia sa musí rovnat výnosu portfólia v prípade jeho spojitého úročenia v banke pri úrokovej miere r, t.j. dπ = rπdt. Ako dôsledok tejto podmienky a rovnice (2.2) dostaneme µ B (r,t,t 1 ) σ [ B(r,t,T 1 ) σ B (r,t,t 2 ) µ B(r,t,T 2 ) = r P(r,t,T 1 ) σ ] B(r,t,T 1 ) σ B (r,t,t 2 ) P(r,t,T 2), čo implikuje rovnost µ B (r,t,t 1 ) rp(r,t,t 1 ) σ B (r,t,t 1 ) = µ B(r,t,T 2 ) P(r,t,T 2 ). (2.3) σ B (r,t,t 2 ) Všimnime si, že l avá strana rovnosti (2.3) je funkciou iba premennej T 1 a pravá strana funkciou iba T 2. Hodnoty T 1 a T 2 sme však na začiatku zvolili l ubovol né. Výrazy na jednotlivých stranách rovnosti teda nemôžu závisiet od času do splatnosti T, t.j. existuje taká funkcia λ(r, t), že platí λ(r,t) = µ B(r,t,T) rp(r,t,t). (2.4) σ B (r,t,t) Funkcia λ(r, t) sa nazýva trhová cena rizika (market price of risk) a vyjadruje očakávaný nárast výnosu dlhopisu na jednotku rizika. Po dosadení µ B a σ B do (2.4) dostaneme parciálnu diferenciálnu rovnicu pre cenu dlhopisu P(r, t, T) P t P +(µ λσ) r + 1 P 2 σ2 2 rp = 0 (2.5) r2 13
21 s koncovou podmienkou P(r,T,T) = 1 pre každé r > 0. Ceny dlhopisov s rôznymi splatnost ami určené ako riešenie parciálnej diferenciálnej rovnice (2.5) sú funkciou jediného faktora a to okamžitej úrokovej miery. Preto aj zmeny cien dlhopisov sú determinované iba zmenami v príslušnom faktore. Poznamenajme, že proces pre okamžitú úrokovú mieru sa dá sformulovat aj v tzv. rizikovo-neutrálnej pravdepodobnostnej miere a k tomu sa dá odvodit parciálna diferenciálna rovnica pre cenu dlhopisu bez trhovej ceny rizika s rizikovo-neutrálnymi parametrami. V takom prípade sa však tieto parametre nedajú odhadovat z historických dát o priebehu short rate, lebo tie pochádzajú z náhodného procesu v reálnej pravdepodobnostnej miere Ceny dlhopisov v jednofaktorovom Vašíčkovom modeli V tejto časti práce sa budeme bližšie zaoberat určením ceny dlhopisu v jednofaktorovom Vašíčkovom modeli a to z toho dôvodu, že túto cenu neskôr využijeme pri kalibrácii konvergenčného modelu Vašíčkovho typu, v rámci ktorého je vývoj európskej úrokovej miery popísaný práve jednofaktorovým Vašíčkovým modelom. Okamžitá úroková miera je vo Vašíčkovom modeli charakterizovaná stochastickou diferenciálnou rovnicou dr = κ(θ r)dt+σdw. Parciálna diferenciálna rovnica, ktorej riešením je cena bezkupónového dlhopisu, vyzerá nasledovne P τ P +[κ(θ r) λσ] r + 1 P 2 σ2 2 rp = 0 (2.6) r2 so zadanou začiatočnou podmienkou P(r,0) = 1 pre každé r > 0. Poznamenajme, že predpokladáme konštantnú trhovú cenu rizika λ(r, t) = λ. Teraz rovnakým spôsobom ako v [24] odvodíme explicitné riešenie danej parciálnej diferenciálnej rovnice, ktoré budeme hl adat v tvare P(r,τ) = A(τ)e B(τ)r. Je zrejmé, že zo začiatočnej podmienky P(r,0) = 1 pre každé r > 0 vyplýva A(0) = 1,B(0) = 0. Dosadením predpokladaného tvaru riešenia a jeho príslušných derivácií do rovnice (2.6) dostaneme nasledovnú identitu ) e (Ȧ A Br Ḃr [κ(θ r) λσ]abe Br σ2 AB 2 e Br rae Br = 0, ktorú upravíme tak, že združíme členy, ktoré obsahujú r a tie, ktoré neobsahujú r ( Ȧ+ 1 ) ) 2 σ2 AB 2 ABκθ+λσAB +ra (Ḃ +κb 1 = 0. (2.7) 14
22 Rovnost (2.7) musí byt splnená pre l ubovol né r, čo implikuje platnost nasledujúcich obyčajných diferenciálnych rovníc Ȧ+ 1 2 σ2 AB 2 ABκθ+λσAB = 0, Ḃ +κb 1 = 0. (2.8) Problém určenia funkcie P(r, τ) sme teda transformovali na úlohu nájst funkcie A(τ), B(τ) vyhovujúce systému obyčajných diferenciálnych rovníc (2.8). Na tomto mieste využijeme fakt, že obyčajná diferenciálna rovnica ẋ(t) = Gx+f(t), kdegjekonštanta,sozačiatočnoupodmienkoux(t 0 ) = x 0 mávovšeobecnostiriešenie v tvare x(t) = x 0 e G(t t 0) + t t 0 e G(t s) f(s)ds, (2.9) a preto riešenie diferenciálnej rovnice pre funkciu B spĺňajúce začiatočnú podmienku B(0) = 0 má tvar B(τ) = 1 e κτ κ Ked poznáme funkciu B, vieme dopočítat aj A a to integrovaním výrazu Ȧ A ( ) ( ] dlna A A a teda platí dτ = [ 1 lna(τ) = 2 σ2 dτ = (τ + e κτ κ. ) [ 1 dτ = lna(τ) = 2 σ2 B 2 B(κθ λσ) ( ) ] 1 e κτ 2 1 κ κ (1 e κτ )(κθ λσ) dτ λσκ σ2 )(θ 2κ 2 dτ, ) σ2 4κ 3 ( e 2κτ 2e κτ) +c. Využitím začiatočnej podmienky A(0) = 1 určíme hodnotu konštanty c: c = 1 λσκ σ2 (θ ) σ2 κ 2κ 2 4κ 3 a nakoniec dostaneme lna(τ) = (θ )( λσκ σ2 1 e κτ 2κ 2 κ τ ) σ2 ( ) 1 e κτ 2. 4κ 3 Riešením parciálnej diferenciálnej rovnice pre cenu dlhopisu ako derivátu okamžitej úrokovej miery, ktorej dynamika je charakterizovaná jednofaktorovým Vašíčkovým modelom, je teda funkcia P(r,τ) = A(τ)e B(τ)r, 15
23 kde )( λσκ σ2 1 A(τ) = exp [(θ 2κ 2 κ (1 e κτ ) τ ) σ2 ( ) ] 1 e κτ 2, 4κ 3 B(τ) = 1 e κτ κ. Na nasledujúcom obrázku sú okrem kriviek cien dlhopisov (vl avo) znázornené aj rôzne tvary výnosových kriviek (vpravo), ktoré je možné získat s využitím jednofaktorového Vašíčkovho modelu. A to rastúcu (zelená), klesajúcu (modrá) a výnosovú krivku, ktorá je najprv rastúca a potom má klesajúcu tendenciu (fialová) Obr. 2.3: Príklady cien dlhopisov (vl avo) a k nim prislúchajúcich výnosov (vpravo) v jednofaktorovom Vašíčkovom modeli s parametrami κ = 0.2,θ = 0.08,σ = 0.05,λ = Pojem reálnej a rizikovo neutrálnej pravdepodobnostnej miery Dynamiku okamžitej úrokovej miery charakterizovanú stochastickou diferenciálnou rovnicou môžeme analyzovat v rámci dvoch prístupov a to v reálnej alebo rizikovo neutrálnej pravdepodobnostnej miere. Formulácia modelu v reálnej miere nám umožňuje zachytit niektoré vlastnosti úrokovej miery, ako napr. mean reversion, zatial čo rizikovo neutrálna pravdepodobnostná miera reflektuje neexistenciu arbitráže na trhu a používa sa pri oceňovaní derivátov úrokovej miery. Vo všeobecnosti je rizikovo neutrálna pravdepodobnostná miera definovaná ako pravdepodobnostná miera, pri ktorej je súčasná hodnota finančného nástroja rovná očakávanej budúcej výplate vyplývajúcej z držania daného nástroja, diskontovanej do súčasnosti bezrizikovou úrokovou mierou. Vysvetlenie problematiky zmeny miery si vyžaduje definovat pojmy podmienenej strednej hodnoty a martingalu. V tejto časti práce popíšeme princíp zmeny miery iba okrajovo, detailnejšie vysvetlenie nájde čitatel v [16]. 16
24 V rámci zmeny miery ide z matematického hl adiska o prechod od vychýleného Wienerovho procesu v reálnej pravdepodobnostnej miere ku štandardnému Wienerovmu procesu v rizikovo neutrálnej miere. Dá sa ukázat, že ak formulujeme model v reálnej miere, tak musí existovat taká funkcia λ(r), ktorá vyjadruje nárast výnosu dlhopisu na jednotku rizika. Takáto funkcia sa potom nazýva trhová cena rizika a je spoločná pre všetky dlhopisy, nezávisí preto od maturity dlhopisu. Model úrokovej miery môže byt teda zadaný dvoma spôsobmi stochastickou diferenciálnou rovnicou v reálnej miere a trhovou cenou rizika, stochastickou diferenciálnou rovnicou v rizikovo neutrálnej miere. Funkcia volatility je však v oboch mierach rovnaká a pre funkciu vyjadrujúcu drift platí nasledujúci prevodný vzt ah [rizikovo neutrálny drift] = [reálny drift] [trhová cena rizika] [volatilita]. Jednofaktorový Vašíčkov model charakterizuje vývoj hodnôt short rate v reálnej miere v tvare stochastickej diferenciálnej rovnice čo zodpovedá zápisu dr = κ(θ r)dt+σdw, dr = (α+βr)dt+σdw, v rizikovo neutrálnej pravdepodobnostnej miere, pričom α = κθ λσ,β = κ. Všimnime si, že výraz κ(θ r) λσ je presne člen pri P v parciálnej diferenciálnej r rovnici (2.6) pre cenu dlhopisu v jednofaktorovom Vašíčkovom modeli. 2.3 Dvojfaktorové rovnovážne modely úrokových mier V jednofaktorových modeloch je časová štruktúra úrokových mier jednoznačne určená začiatkom výnosovej krivky. Dôvodom zavedenia d alšieho faktora do modelu je získanie väčších možností pre zachytenie vývoja analyzovanej úrokovej miery, ako aj širšieho spektra tvarov výnosových kriviek, ktoré model implikuje. V práci [12] nájde čitatel dôkaz toho, že v rámci jednofaktorového modelu úrokovej miery je možné získat práve 3 rôzne tvary výnosovej krivky, ktoré sú znázornené na obr Použitie jednofaktorového modelu teda nemôže implikovat napr. časovú štruktúru úrokovej miery znázornenú na obr. 4.2 v kapitole 4.1, v ktorej odvodíme ceny dlhopisov v dvojfaktorovom konvergenčnom modeli Vašíčkovho typu. 17
25 V dvojfaktorových modeloch je úroková miera vysvetl ovaná ako funkcia dvoch náhodných faktorov. Predpokladajme, že tieto náhodné faktory, označme ich x a y, vyhovujú stochastickým diferenciálnym rovniciam pričom dx = µ x (x,y)dt+σ x (x,y)dw 1, (2.10) dy = µ y (x,y)dt+σ y (x,y)dw 2, (2.11) cov(dw 1,dw 2 ) = E(dw 1 dw 2 ) = ρdt, t.j. predpokladáme konštantnú koreláciu ρ medzi prírastkami Wienerových procesov dw 1 a dw 2. Okamžitá úroková miera je teda funkciou náhodných faktorov x,y r = r(x,y). Uvedený model sa dá prepísat na tvar, v ktorom prírastky Wienerových procesov d w 1,d w 2 sú nezávislé dx = µ x (x,y)dt+σ x (x,y)d w 1, ] dy = µ y (x,y)dt+σ y (x,y)[( 1 ρ 2 )d w 2 +ρd w 1 a takýto tvar sa využíva pri simuláciách. V rámci dvojfaktorových modelov úrokovej miery existujú také, kde druhým faktorom je finančná premenná (napr. dlhodobá úroková miera, príp. rozdiel medzi dlhodobou a krátkodobou úrokovou mierou), alebo druhým faktorom môže byt niektorý z parametrov rovnice popisujúcej dynamiku krátkodobej úrokovej miery. Prehl ad základných dvojfaktorových rovnovážnych modelov úrokových mier je uvedený v [17]. Medzi najznámejšie dvojfaktorové modely patrí dvojfaktorový Vašíčkov model a dvojfaktorový CIR model. V týchto modeloch je okamžitá úroková miera súčtom dvoch nezávislých faktorov, ktorých dynamika je charakterizovaná stochastickou diferenciálnou rovnicou rovnakého typu ako okamžitá úroková miera v príslušnom jednofaktorovom modeli (pozri [17]). Dvojfaktorový Vašíčkov model má teda tvar dr 1 = κ 1 (θ 1 r 1 )dt+σ 1 dw 1, dr 2 = κ 2 (θ 2 r 2 )dt+σ 2 dw 2 a dvojfaktorový CIR model vyzerá nasledovne dr 1 = κ 1 (θ 1 r 1 )dt+σ 1 r1 dw 1, dr 2 = κ 2 (θ 2 r 2 )dt+σ 2 r2 dw 2. Konvergenčné modely úrokových mier tvoria podtriedu dvojfaktorových modelov a práve týmito modelmi sa v tejto práci budeme zaoberat podrobnejšie. Najjednoduchším konvergenčným modelom je konvergenčný model Vašíčkovho typu, ktorý bol navrhnutý v práci [7] a to v nasledovnom tvare cov(dw 1,dw 2 ) = ρdt, dr d = [a+b(r e r d )]dt+σ d dw d, dr e = c(d r e )dt+σ e dw e, 18
26 kde r d je domáca úroková miera, r e predstavuje úrokovú mieru v rámci eurozóny a ρ je koeficientom korelácie medzi prírastkami Wienerových procesov dw 1,dw 2. Daný konvergenčný model popisuje vývoj európskej úrokovej miery, o ktorej sa predpokladá, že ovplyvňuje vývoj domácej úrokovej miery. Fong - Vašíčkov model analyzovaný v [10] patrí medzi dvojfaktorové modely so stochastickou volatilitou. V tomto modeli je okamžitá úroková miera r charakterizovaná pomocou stochastickej diferenciálnej rovnice a volatilita y okamžitej úrokovej miery je riešením inej stochastickej diferenciálnej rovnice dr = κ 1 (θ 1 r)dt+ ydw 1, dy = κ 2 (θ 2 y)dt+v ydw Ceny dlhopisov v dvojfaktorových modeloch úrokových mier Na odvodenie ceny dlhopisu ako derivátu okamžitej úrokovej miery, ktorej dynamika je popísaná dvojfaktorovým modelom, sa využije podobný postup ako v prípade jednofaktorového modelu, pričom vychádzame z [17]. Uvažujme dvojfaktorový rovnovážny model úrokovej miery v tvare pričom r = r(x,y) dx = µ x (x,y)dt+σ x (x,y)dw 1, dy = µ y (x,y)dt+σ y (x,y)dw 2, cov(dw 1,dw 2 ) = ρdt, t.j. prírastky Wienerových procesov sú navzájom korelované s koeficientom korelácie ρ. Cena dlhopisu P so splatnost ou v čase T je preto funkciou aktuálneho času t a d alších dvoch premenných x a y, teda P = P(x,y,t). Aplikovaním viacrozmernej Itóovej lemy 1.3 na funkciu P(x, y, t) dostaneme predpis pre diferenciál tejto funkcie v tvare dp = µdt+σ 1 dw 1 +σ 2 dw 2, (2.12) kde µ = P t +µ p x x +µ y σ 1 = σ x P x, σ 2 = σ y P y. P y + σ2 x 2 P 2 x + σ2 y 2 P 2 2 y +ρσ 2 P xσ 2 y x y, Teraz zostavíme portfólio pozostávajúce z troch typov dlhopisov s rôznymi maturitami T 1,T 2,T 3. Hodnota takéhoto portfólia je Π = P(T 1 )V 1 +P(T 2 )V 2 +P(T 3 )V 3, 19
27 kde P(T i ) je cena dlhopisu so splatnost ou v čase T i a V i je počet dlhopisov v portfóliu so splatnost ou v čase T i pre i = 1,2,3. Využitím vzt ahu (2.12) dostaneme, že pre zmenu hodnoty daného portfólia platí dπ =V 1 dp(t 1 )+V 2 dp(t 2 )+V 3 dp(t 3 ) =[V 1 µ(t 1 )+V 2 µ(t 2 )+V 3 µ(t 3 )]dt+[v 1 σ 1 (T 1 )+V 2 σ 1 (T 2 )+V 3 σ 1 (T 3 )]dw 1 +[V 1 σ 2 (T 1 )+V 2 σ 2 (T 2 )+V 3 σ 2 (T 3 )]dw 2. Aby sme eliminovali náhodné zložky v predchádzajúcej rovnici, a teda aby hodnota portfólia bola deterministická, musia byt splnené nasledovné rovnosti V 1 σ 1 (T 1 )+V 2 σ 1 (T 2 )+V 3 σ 1 (T 3 ) = 0, (2.13) V 1 σ 2 (T 1 )+V 2 σ 2 (T 2 )+V 3 σ 2 (T 3 ) = 0. (2.14) Ďalej z dôvodu vylúčenia arbitráže sa miera návratnosti uvažovaného dlhopisového portfólia musí rovnat bezrizikovému výnosu, t.j. dπ = rπdt. Z toho vyplýva, že V 1 µ(t 1 )+V 2 µ(t 2 )+V 3 µ(t 3 ) = r[p(t 1 )V 1 +P(T 2 )V 2 +P(T 3 )V 3 ] a po úprave dostaneme V 1 [µ(t 1 ) rp(t 1 )]+V 2 [µ(t 2 ) rp(t 2 )]+V 3 [µ(t 3 ) rp(t 3 )] = 0. (2.15) Systém pozostávajúci z rovníc (2.13), (2.14), (2.15) môžeme zapísat v maticovom tvare σ 1 (T 1 ) σ 1 (T 2 ) σ 1 (T 3 ) V 1 0 σ 2 (T 1 ) σ 2 (T 2 ) σ 2 (T 3 ) V 2 = 0, µ(t 1 ) rp(t 1 ) µ(t 2 ) rp(t 2 ) µ(t 3 ) rp(t 3 ) V 3 0 pričom nás zaujíma nenulové riešenie tohto systému, ktoré existuje práve vtedy, ked riadky matice sú lineárne závislé. Rovnosti (2.13), (2.14) však musia byt lineárne nezávislé, lebo ak by bol druhý riadok nejakým násobkom prvého riadku matice, tak v modeli by bol iba jeden náhodný faktor a v konečnom dôsledku by sme dostali jednofaktorový model. To znamená, že tretí riadok musí byt lineárnou kombináciou prvých dvoch a teda existujú také λ 1,λ 2, že µ(t i ) rp(t i ) = λ 1 σ 1 (T i )+λ 2 σ 2 (T i ) pre i = 1,2,3. (2.16) Parametreλ 1,λ 2,ktorépredstavujútrhovécenyrizikaprislúchajúcefaktoromx,y, nemôžu byt funkciou doby splatnosti, ked že T 1,T 2,T 3 boli zvolené l ubovol ne a preto λ 1 = λ 1 (x,y,t), λ 2 = λ 2 (x,y,t). Dosadenímµ,σ 1,σ 2 z(2.12)dorovnice(2.16)dostanemenasledujúcuparciálnudiferenciálnu rovnicu pre cenu dlhopisu v dvojfaktorovom rovnovážnom modeli úrokovej miery P t +(µ x λ 1 σ x ) P x +(µ y λ 2 σ y ) P y P 2 σ2 x x P 2 2 σ2 y y +ρσ 2 P xσ 2 y rp = 0. x y 20
28 Kapitola 3 Ako odhadovat parametre modelov úrokových mier Kalibrácia modelov úrokových mier nepatrí medzi problémy s jednoznačným a priamočiarym riešením. Základným ciel om konkrétnej metódy kalibrácie modelu je určit hodnoty parametrov analyzovaného modelu tak, aby model čo najlepšie popisoval skutočný vývoj úrokovej miery. Parametre modelu môžeme odhadnút z časového radu krátkodobej úrokovej miery, ale aj prístupom, ktorý je zameraný na čo najlepšiu zhodu teoretických a skutočných výnosových kriviek. Tieto dva spôsoby sa dajú kombinovat ako napr. v článku [7], v ktorom autori všetky parametre okrem trhovej ceny rizika odhadli z časového radu short rate a výnosové krivky použili iba na odhad trhovej ceny rizika. Dá sa aplikovat aj opačný postup (pozri napr. [23]), kde sa najskôr optimalizuje účelová funkcia vyjadrujúca váženú strednú kvadratickú chybu medzi teoretickými a modelom implikovanými výnosovými krivkami a potom funkcia vierohodnosti. Táto čast práce je venovaná štúdiu daných dvoch prístupov v rámci kalibrácie jednofaktorového Vašíčkovho modelu a tvorí základ pre návrh novej metódy kalibrácie, ktorá súčasne využíva priebeh krátkodobej úrokovej miery aj výnosové krivky. Poznamenajme, že jednofaktorovým Vašíčkovým modelom sa na tomto mieste zaoberáme podrobnejšie, pretože ho neskôr využijeme v rámci konvergenčného modelu Vašíčkovho typu. 3.1 Metóda maximálnej vierohodnosti na odhad parametrov modelov úrokových mier Na odhad parametrov procesu, ktorý popisuje dynamiku úrokovej miery, môžeme v prípade, že poznáme rozdelenie hodnôt procesu, použit metódu maximálnej vierohodnosti. Je to pomerne často používaný prístup, ktorého ciel om je nájst také hodnoty parametrov, aby daná realizácia dát bola čo najpravdepodobnejšia. Podrobnejšie informácie týkajúce sa metódy maximálnej vierohodnosti nájde čitatel v [15]. Nech X 1,X 2,...,X n je náhodný výber z rozdelenia s hustotou f (x θ), t.j. X 1, X 2, 21
29 ..., X n sú nezávislé rovnako rozdelené náhodné premenné s hustotou f (x θ), a nech x 1,x 2,...,x n jerealizáciadanéhonáhodnéhovýberu.potomfunkcia vierohodnosti L ako funkcia parametra θ je definovaná nasledovne L(x θ) = L(x 1,x 2,...,x n θ) = n f(x i θ). Metóda maximálnej vierohodnosti spočíva v tom, že sa za odhad parametra θ zvolí taká hodnota θ, pre ktorú pri daných realizovaných hodnotách premenných funkcia vierohodnosti nadobúda svoje maximum. To znamená, že θ = argmax θ n f(x i θ). Obvykle namiesto funkcie vierohodnosti maximalizujeme jej prirodzený logaritmus, ktorý nazývame logaritmickou funkciou vierohodnosti. Použitím monotónnej transformácie sa totiž argument maxima nezmení, a preto θ = argmax θ n lnf(x i θ) Podmienené rozdelenie okamžitej úrokovej miery pre Vašíčkov model V tejto časti práce odvodíme podmienené rozdelenie okamžitej úrokovej miery, pričom budeme postupovat rovnakým spôsobom ako v [17]. Predpokladajme, že jednofaktorový Vašíčkov model je daný v tvare stochastickej diferenciálnej rovnice dr t = κ(θ r t )dt+σdw (3.1) a definujme proces y = e κt r. Pomocou Itóovej lemy určíme diferenciál d(e κt r) tohto nového procesu dy = d ( e κt r ) = (κe κt r +κ(θ r)e κt )dt+σe κt dw. Po úprave dostaneme nasledujúcu rovnost d ( e κt r ) = κθe κt dt+σe κt dw, ktorá sa integrovaním na intervale (t,t+ t) zmení na e κ(t+ t) r t+ t e κt r t = κθ t+ t t t+ t e κs ds+σ = θ ( e κ(t+ t) e κt) +σ t t+ t t e κs dw s e κs dw s. 22
30 Napokon dostávame explicitné vyjadrenie náhodnej premennej r t+ t pomocou stochastického integrálu t+ t r t+ t = e κ t r t +θ(1 e κ t )+σe κ(t+ t) e κs dw s, ktoré nám umožní určit podmienené rozdelenie náhodnej premennej r t+ t pri danej hodnote r t. Pre strednú hodnotu daného podmieneného rozdelenia teda platí E(r t+ t r t ) = e κ t r t +θ(1 e κ t ), ( ) t+ t ked že podl a tvrdenia 1.1 je E e κs dw t s = 0. Variancia rozdelenia premennej r t+ t sa dá vyjadrit nasledovne ( t+ t ) Var(r t+ t r t ) = σ 2 e 2κ(t+ t) Var e κs dw s t [ ( t+ t ) 2 ] = σ 2 e 2κ(t+ t) E e κs dw s, pričom využitím Itóovej izometrie (1.2) taktiež formulovanej v tvrdení 1.1 dostaneme Var(r t+ t r t ) = σ 2 e 2κ(t+ t) t+ t t t t (e κs ) 2 ds = σ2 2κ (1 e 2κ t ). Teda štatistický zápis podmieneného rozdelenia okamžitej úrokovej miery, ktorej vývoj je popísaný pomocou jednofaktorového Vašíčkovho modelu, má tvar ) r t+ t r t N (e κ t r t +θ(1 e κ t ), σ2 2κ (1 e 2κ t ). (3.2) Toto rozdelenie sa dá odvodit aj iným spôsobom (a to použitím tzv. Fokker - Planckovej rovnice), ktorý čitatel nájde v [17]. Teraz s využitím tvaru podmieneného rozdelenia úrokovej miery charakterizovanej jednofaktorovým Vašíčkovým modelom určíme pravdepodobnost, s akou sa úroková miera môže dostat do záporných hodnôt: P (r t+ t < 0 r t ) = P = Φ = Φ ( r t+ t E(r t+ t r t ) Var(rt+ t r t ( ) E(r t+ t r t ) Var(rt+ t r t ) e κ t r t +θ(e κ t 1) σ 2 2κ (1 e 2κ t ) ) < E(r t+ t r t ) Var(rt+ t r t ), (3.3) 23
31 kde Φ(.) je distribučná funkcia rozdelenia N (0, 1). Všimnime si, že analyzovaná pravdepodobnost je funkciou času, aktuálnej hodnoty úrokovej miery a zvolených parametrov. Napríklad pre odhady parametrov κ = 1.521, θ = , σ = z tabul ky 6.4, ktoré získame kalibráciou Vašíčkovho modelu na denných dátach sadzby Euribor za druhý kvartál roku 2011, a začiatočnú hodnotu úrokovej miery r t = je pravdepodobnost toho, že short rate o rok nadobudne zápornú hodnotu, rovná e 018, čo je prakticky nulová pravdepodobnost Metóda maximálnej vierohodnosti na odhad parametrov Vašíčkovho modelu Vzt ahy pre odhady parametrov κ, θ, σ Vašíčkovho modelu metódou maximálnej vierohodnosti sú bez dôkazu uvedené v [3]. Jedným z prínosov tejto práce je aj ich odvodenie, ktorým sa zaoberáme práve v tejto časti práce. Majme diskrétne pozorovania procesu (3.1), t.j. časový rad r 1,...,r n+1 hodnôt úrokovej miery, o ktorej predpokladáme, že jej dynamika je charakterizovaná pomocou jednofaktorového Vašíčkovho modelu. Nech t je časový interval medzi dvoma pozorovaniami. Zavedieme nové premenné η = e κ t,v 2 = σ2 2κ (1 e 2κ t ) a teda podl a (3.2) platí r t+ t r t N ( ηr t +θ(1 η),v 2). Využitím explicitného vyjadrenia hustoty normálneho rozdelenia v tomto prípade v tvare { } 1 f(r i+1 r i ) = exp [r i+1 ηr i θ(1 η)] 2 2πv 2 2v 2 vieme za predpokladu nezávislosti pozorovaní napísat hodnotu vierohodnostnej funkcie ako súčin hustôt náhodných premenných s normálnym rozdelením, t.j. L ( { } η,θ,v 2) n 1 = exp [r i+1 ηr i θ(1 η)] 2. 2πv 2 2v 2 Logaritmická vierohodnostná funkcia má potom tvar l ( η,θ,v 2) = lnl ( η,θ,v 2) = n 2 ln(2πv2 ) 1 2v 2 n [r i+1 ηr i θ(1 η)] 2. Ciel om je nájst hodnoty parametrov η,θ a v 2, ktoré budú predstavovat bod maxima pre funkciu l(η,θ,v 2 ). Takéto hodnoty sa spravidla (v prípade existencie parciálnych derivácií) získajú riešením tzv. vierohodnostných rovníc (t.j. parciálne derivácie položíme rovné nule) 24
32 l θ = (1 η) n [r v 2 i+1 ηr i θ(1 η)] = 0, (3.4) l η = 1 n {[r v 2 i+1 ηr i θ(1 η)](θ r i )} = 0, (3.5) l v 2 = n 2v v 4 n [r i+1 ηr i θ(1 η)] 2 = 0. (3.6) Pre odhady hodnôt parametrov θ a v 2 dostaneme nasledujúce výrazy [ n ] 1 θ = (r i+1 ηr i ), (3.7) n(1 η) v 2 = 1 n [ 2. r i+1 ηr i n θ(1 η)] (3.8) Ostáva už iba určit odhad parametra η, a to takým spôsobom, aby závisel len od pozorovaných hodnôt a aby sme tak mohli na základe odhadu ˆη explicitne určit odhad ˆθ a nakoniec využitím daných dvoch odhadov priamo určit odhad parametra v 2. Pre jednoduchost zavedieme nasledujúce označenie: s x = n r i, s y = n r i+1, s xy = n r i r i+1, s xx = n ri. 2 Potom rovnost (3.7) sa dá prepísat na tvar θ = s y ηs x n(1 η), pričomdosadenímtaktovyjadrenejhodnoty θdo(3.4)dostanemenasledujúcurovnicu n [( r i+1 ηr i (s )( )] y ηs x ) sy ηs x n n(1 η) r i = 0. Jednoduchými algebraickými úpravami danej rovnice napokon dostaneme vzt ah pre odhad parametra η v tvare η = s xs y ns xy s 2 x ns xx, a teda ( n ) 2 η = r i n n r 2 i 1( n n r i r i+1 n ) n r i r i+1. (3.9) 25
33 Odhady parametrov κ, θ, σ Vašíčkovho modelu (3.1) metódou maximálnej vierohodnosti sa teda dajú explicitne vyjadrit využitím nasledujúcich vzt ahov κ = 1 t ln η, [ n ] 1 θ = (r i+1 ηr i ), n(1 η) σ 2 = 2 κ (1 e 2 κ t ) v 2, kde η, v 2 spĺňajú (3.9), (3.8). 3.2 Kalibrácia modelu založená na minimalizácii miery vzdialenosti reálnej a odhadovanej výnosovej krivky Parametre modelu, ktorý charakterizuje vývoj úrokovej miery, sa dajú odhadnút aj na základe fitovania výnosových kriviek. Ciel om tohto prístupu je minimalizovat nejakú mieru vzdialenosti reálnej a odhadovanej výnosovej krivky. V článku [23] sa využíva minimalizácia váženého súčtu druhých mocnín rozdielov skutočných a modelom implikovaných výnosov a takýto spôsob použijeme aj v tejto práci. Budeme teda minimalizovat funkcionál F, ktorý vyzerá nasledovne F = 1 mn n m w ij [R(τ j,r i ) R ij ] 2, j=1 kder(τ j,r i ) = lnp(τ j,r i ) τ j jeteoretickývýnosvi-tydeňprej-tusplatnost implikovaný modelom a R ij predstavuje skutočný výnos v i-ty deň pre dobu splatnosti τ j. Môžeme si všimnút, že vstupnými dátami sú výnosové krivky z určitého časového obdobia, pričom váhy w ij vyjadrujú, aký vplyv majú jednotlivé odchýlky výnosových kriviek v rôznych časoch a pre rôzne maturity. Uvažujme teda stochastickú diferenciálnu rovnicu, ktorá definuje jednofaktorový Vašíčkov model v rizikovo neutrálnej pravdepodobnostnej miere dr = (α+βr)dt+σdw. (3.10) Z časti vieme, že cena dlhopisu v prípade Vašíčkovho modelu (3.10) má tvar kde P(r,τ) = A(τ)e B(τ)r, [( )( α A(τ) = exp β + σ2 1 2β 2 β (1 eβτ )+τ )+ σ2 ( ) ] 1 e βτ 2, 4κ 3 B(τ) = 1 eβτ β. 26
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky
 fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
fakulta matematiky, fyziky a informatiky univerzity komenského v bratislave Projekt z finančnej matematiky Bratislava 2008 Martin Takáč Fakulta Matematiky, Fyziky a Informatiky, Univerzita Komenského v
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky. Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová UNIVERZITA KOMENSKÉHO
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Rýchla asová ²kála volatility vo Fong-Va²í kovom modeli Diplomová práca Bratislava 2012 Bc. Radka Sele éniová UNIVERZITA KOMENSKÉHO
Odhady parametrov modelov
 Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
Odhady parametrov modelov časovej štruktúry úrokových mier Študentská vedecká konferencia Ivan Sutóris Univerzita Komenského v Bratislave Fakulta Matematiky, Fyziky a Informatiky Katedra Aplikovanej Matematiky
A THREE-FACTOR CONVERGENCE MODEL OF INTEREST RATES
 Proceedings of ALGORITMY 01 pp. 95 104 A THREE-FACTOR CONVERGENCE MODEL OF INTEREST RATES BEÁTA STEHLÍKOVÁ AND ZUZANA ZÍKOVÁ Abstract. A convergence model of interest rates explains the evolution of the
Proceedings of ALGORITMY 01 pp. 95 104 A THREE-FACTOR CONVERGENCE MODEL OF INTEREST RATES BEÁTA STEHLÍKOVÁ AND ZUZANA ZÍKOVÁ Abstract. A convergence model of interest rates explains the evolution of the
COMENIUS UNIVERSITY IN BRATISLAVA Faculty of Mathematics, Physics and Informatics Department of Applied Mathematics and Statistics
 COMENIUS UNIVERSITY IN BRATISLAVA Faculty of Mathematics, Physics and Informatics Department of Applied Mathematics and Statistics TWO-FACTOR CONVERGENCE MODEL OF COX-INGERSOLL-ROSS TYPE Master s Thesis
COMENIUS UNIVERSITY IN BRATISLAVA Faculty of Mathematics, Physics and Informatics Department of Applied Mathematics and Statistics TWO-FACTOR CONVERGENCE MODEL OF COX-INGERSOLL-ROSS TYPE Master s Thesis
Pokročilé metody kalibrace modelů
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Pokročilé metody kalibrace modelů úrokových sazeb Dominika Holotňáková Katedra pravděpodobnosti a matematické statistiky Vedoucí
Univerzita Karlova v Praze Matematicko-fyzikální fakulta DIPLOMOVÁ PRÁCE Pokročilé metody kalibrace modelů úrokových sazeb Dominika Holotňáková Katedra pravděpodobnosti a matematické statistiky Vedoucí
Averaged bond prices for Fong-Vasicek and the generalized Vasicek interest rates models
 MATHEMATICAL OPTIMIZATION Mathematical Methods In Economics And Industry 007 June 3 7, 007, Herl any, Slovak Republic Averaged bond prices for Fong-Vasicek and the generalized Vasicek interest rates models
MATHEMATICAL OPTIMIZATION Mathematical Methods In Economics And Industry 007 June 3 7, 007, Herl any, Slovak Republic Averaged bond prices for Fong-Vasicek and the generalized Vasicek interest rates models
Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií
 UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
UNIVERZITA KOMENSKÉHO FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY BRATISLAVA Martin Takáč Využitie aproximácie rozdelenia časovo spriemernenej hodnoty náhodnej premennej pri oceňovaní ázijských opcií Študentská
ON NON-EXISTENCE OF A ONE FACTOR INTEREST RATE MODEL FOR VOLATILITY AVERAGED GENERALIZED FONG VASICEK TERM STRUCTURES
 Proceedings of the Czech Japanese Seminar in Applied Mathematics 6 Czech Technical University in Prague, September 14-17, 6 pp. 1 8 ON NON-EXISTENCE OF A ONE FACTOR INTEREST RATE MODEL FOR VOLATILITY AVERAGED
Proceedings of the Czech Japanese Seminar in Applied Mathematics 6 Czech Technical University in Prague, September 14-17, 6 pp. 1 8 ON NON-EXISTENCE OF A ONE FACTOR INTEREST RATE MODEL FOR VOLATILITY AVERAGED
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio
 Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
Príloha č. 3: k Cenníku služieb JELLYFISH Finport Professional a Individuálne riadené portfólio Úrokové sadzby (úrokové sadzby pre kreditné úroky z hotovosti, debetné úroky z úverov poskytnutých brokerom
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY MODELOVANIE RIZIKOVO-NEUTRÁLNYCH PRAVDEPODOBNOSTÍ VÝVOJA CIEN FINANČNÝCH NÁSTROJOV DIPLOMOVÁ PRÁCA Bratislava, 23 Bc. Peter Štefko
Analytické aproximácie pri modelovaní cien opcií
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Analytické aproximácie pri modelovaní cien opcií Diplomová práca Bratislava 2014 Bc. Tomáš Karovič UNIVERZITA KOMENSKÉHO V BRATISLAVE
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie
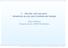 I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované stratégie Beáta Stehlíková Finančné deriváty, FMFI UK Bratislava I. Deriváty, call a put opcie, ohraničenia na ceny opcií, kombinované
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks
 Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
Riadenie úrokového rizika dlhopisových portfólií v komerčných bankách The Interest Risk Management of the Bond Portfolio in Commercial Banks Vladimír GVOZDJÁK Abstrakt Dlhopisy ako cenný papier predstavujú
CROSS SECTIONAL FORECASTS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CROSS SECTIONAL FORECASTS OF THE EQUITY PREMIUM Master's Thesis Katarína Beláková Bratislava 2013 COMENIUS UNIVERSITY IN
Financial Accelerator and Interest Rate in Selected Countries
 COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
COMENIUS UNIVERZITY, BRATISLAVA FACULTY OF MATHEMAICS, PHYSICS AND INFORMATICS Department of Applied Mathematics and Statistics Financial Accelerator and Interest Rate in Selected Countries Bc. Lenka Babjaková
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY. Zaistené stratégie. Bc. Tomáš Miklošovič.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY Zaistené stratégie Bc. Tomáš Miklošovič Diplomová práca Bratislava 200 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky,
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS A FIRM-FUNDAMENTALS BASED CORPORATE BOND INVESTMENT STRATEGY MASTER THESIS 2016 Bc. Michaela Floriánová COMENIUS UNIVERSITY
Attachment No. 1 Employees authorized for communication
 On behalf of Market Operator: Attachment No. 1 Employees authorized for communication Employees authorized for invoicing and payments: Head of billing Dana Vinická +421 917 931 470 dana.vinicka@okte.sk
On behalf of Market Operator: Attachment No. 1 Employees authorized for communication Employees authorized for invoicing and payments: Head of billing Dana Vinická +421 917 931 470 dana.vinicka@okte.sk
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Oceňovanie reálnych opcií pomocou stochastického dynamického programovania Diplomová práca Bratislava 2012 Bc. Jozef Mesároš
Globálne optimálne gama zaisťovanie s transakčnými nákladmi
 Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
Globálne optimálne gama zaisťovanie s transakčnými nákladmi DIPLOMOVÁ PRÁCA Zuzana Ceľuchová UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY KATEDRA APLIKOVANEJ MATEMATIKY A
UNIVERZITA KOMENSKÉHO V BRATISLAVE. Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ Veronika Kleinová
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky ZAISTENÉ A POISTENÉ STRATÉGIE 011 Veronika Kleinová UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky
25. Interest rates models. MA6622, Ernesto Mordecki, CityU, HK, References for this Lecture:
 25. Interest rates models MA6622, Ernesto Mordecki, CityU, HK, 2006. References for this Lecture: John C. Hull, Options, Futures & other Derivatives (Fourth Edition), Prentice Hall (2000) 1 Plan of Lecture
25. Interest rates models MA6622, Ernesto Mordecki, CityU, HK, 2006. References for this Lecture: John C. Hull, Options, Futures & other Derivatives (Fourth Edition), Prentice Hall (2000) 1 Plan of Lecture
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics
 Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Comenius University in Bratislava Faculty of Mathematics, Physics and Informatics Higher Order Finite Difference Schemes for Solving Path Dependent Options Master's Thesis Bratislava 2012 Bc. Michal Taká
Investigation of Dependency between Short Rate and Transition Rate on Pension Buy-outs. Arık, A. 1 Yolcu-Okur, Y. 2 Uğur Ö. 2
 Investigation of Dependency between Short Rate and Transition Rate on Pension Buy-outs Arık, A. 1 Yolcu-Okur, Y. 2 Uğur Ö. 2 1 Hacettepe University Department of Actuarial Sciences 06800, TURKEY 2 Middle
Investigation of Dependency between Short Rate and Transition Rate on Pension Buy-outs Arık, A. 1 Yolcu-Okur, Y. 2 Uğur Ö. 2 1 Hacettepe University Department of Actuarial Sciences 06800, TURKEY 2 Middle
Analytical and Numerical Approximative Methods for solving Multifactor Models for pricing of Financial Derivatives
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS DEPARTMENT OF APPLIED MATHEMATICS AND STATISTICS UNIVERSITY OF WUPPERTAL FACULTY OF MATHEMATICS AND NATURAL SCIENCES DEPARTMENT
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS DEPARTMENT OF APPLIED MATHEMATICS AND STATISTICS UNIVERSITY OF WUPPERTAL FACULTY OF MATHEMATICS AND NATURAL SCIENCES DEPARTMENT
Maticové algoritmy II systém lineárnych rovníc riešenie SLR pomocou Gaussovej eliminačnej metódy (GEM) determinanty výpočet determinantu pomocou GEM
 Maticové algoritmy II systém lineárnych rovníc riešenie SLR pomocou Gaussovej eliminačnej metódy (GEM) determinanty výpočet determinantu pomocou GEM Priesvitka 1 M. C. Escher: Relativity Priesvitka 2 Systém
Maticové algoritmy II systém lineárnych rovníc riešenie SLR pomocou Gaussovej eliminačnej metódy (GEM) determinanty výpočet determinantu pomocou GEM Priesvitka 1 M. C. Escher: Relativity Priesvitka 2 Systém
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ. Currency risk hedging in Flash Steel, a. s.
 VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ Zajištění proti kurzovému riziku ve společnosti Flash Steel, a. s. Currency risk hedging in Flash Steel, a. s. company
VYSOKÁ ŠKOLA BÁŇSKÁ TECHNICKÁ UNIVERZITA OSTRAVA EKONOMICKÁ FAKULTA KATEDRA FINANCÍ Zajištění proti kurzovému riziku ve společnosti Flash Steel, a. s. Currency risk hedging in Flash Steel, a. s. company
Konvergen né modely úrokových mier
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Konvergen né moely úrokových mier Diplomová práca Veúci iplomovej práce: RNDr. Beáta Stehlíková, PhD. Autor: Bc. Zuzana Zíková
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta Matematiky, Fyziky a Informatiky Konvergen né moely úrokových mier Diplomová práca Veúci iplomovej práce: RNDr. Beáta Stehlíková, PhD. Autor: Bc. Zuzana Zíková
Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš
 Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš Abstract Cieľ článku: Cieľom tohto článku je priblížiť zmeny hodnoty rizikovej prémie, identifikovať ktoré determinanty ju ovplyvňujú a ako
Vplyv finančnej krízy na hodnotu rizikovej prémie Pavel Kardoš Abstract Cieľ článku: Cieľom tohto článku je priblížiť zmeny hodnoty rizikovej prémie, identifikovať ktoré determinanty ju ovplyvňujú a ako
VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY
 VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY THE DEVELOPMENT OF THE AMOUNT OF LOANS GRANTED AND THEIR APPROPRIATE
VÝVOJ OBJEMU POSKYTNUTÝCH ÚVEROV A ICH DOHODNUTEJ PRIEMERNEJ ÚROKOVEJ SADZBY NA SLOVENSKU V KONTEXTE VÝVOJA ZÁKLADNEJ ÚROKOVEJ SADZBY THE DEVELOPMENT OF THE AMOUNT OF LOANS GRANTED AND THEIR APPROPRIATE
Calibration of Interest Rates
 WDS'12 Proceedings of Contributed Papers, Part I, 25 30, 2012. ISBN 978-80-7378-224-5 MATFYZPRESS Calibration of Interest Rates J. Černý Charles University, Faculty of Mathematics and Physics, Prague,
WDS'12 Proceedings of Contributed Papers, Part I, 25 30, 2012. ISBN 978-80-7378-224-5 MATFYZPRESS Calibration of Interest Rates J. Černý Charles University, Faculty of Mathematics and Physics, Prague,
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ UNIVERZITA KOMENSKÉHO V
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY VYUšITIE MEIXNEROVHO PROCESU PRI MODELOVANÍ FINANƒNÝCH TRHOV DIPLOMOVÁ PRÁCA 016 Bc. Ivana KRASULOVÁ UNIVERZITA KOMENSKÉHO V
Oceňovanie CMS Spread Range Accrual
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a štatistiky Oceňovanie CMS Spread Range Accrual Diplomová práca Matej Stračiak Vedúci práce:
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a štatistiky Oceňovanie CMS Spread Range Accrual Diplomová práca Matej Stračiak Vedúci práce:
Interest Rate Course Lecture 9. June
 Interest Rate Course Lecture 9 June 28 2010 Last days Want to find stochastic models consistent with observed i) yield curves and ii) dynamics of yield curve One factor models Two factor models Other approaches
Interest Rate Course Lecture 9 June 28 2010 Last days Want to find stochastic models consistent with observed i) yield curves and ii) dynamics of yield curve One factor models Two factor models Other approaches
Pouºitie metódy Monte Carlo vo nanciách
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky a ²tatistiky Pouºitie metódy Monte Carlo vo nanciách Diplomová práca tudijný odbor: 9.1.9 Aplikovaná
OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE
 NATIONAL AND REGIONAL ECONOMICS VIII OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE Ing. Radoslav BLAHOVEC Technická univerzita v Košiciach Ekonomická fakulta Katedra regionálnych vied a manažmentu Radoslav.Blahovec@tuke.sk
NATIONAL AND REGIONAL ECONOMICS VIII OPTIMALIZÁCIA KAPITÁLOVEJ SKLADBY INVESTÍCIE Ing. Radoslav BLAHOVEC Technická univerzita v Košiciach Ekonomická fakulta Katedra regionálnych vied a manažmentu Radoslav.Blahovec@tuke.sk
Applications to Fixed Income and Credit Markets
 Applications to Fixed Income and Credit Markets Jean-Pierre Fouque University of California Santa Barbara 28 Daiwa Lecture Series July 29 - August 1, 28 Kyoto University, Kyoto 1 Fixed Income Perturbations
Applications to Fixed Income and Credit Markets Jean-Pierre Fouque University of California Santa Barbara 28 Daiwa Lecture Series July 29 - August 1, 28 Kyoto University, Kyoto 1 Fixed Income Perturbations
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS
 COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
COMENIUS UNIVERSITY IN BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS CONSUMPTION SMOOTHING DURING THE FINANCIAL CRISIS MASTER S THESIS 2014 Bc. Tomáš Rizman COMENIUS UNIVERSITY IN BRATISLAVA
The stochastic calculus
 Gdansk A schedule of the lecture Stochastic differential equations Ito calculus, Ito process Ornstein - Uhlenbeck (OU) process Heston model Stopping time for OU process Stochastic differential equations
Gdansk A schedule of the lecture Stochastic differential equations Ito calculus, Ito process Ornstein - Uhlenbeck (OU) process Heston model Stopping time for OU process Stochastic differential equations
dt+ ρσ 2 1 ρ2 σ 2 κ i and that A is a rather lengthy expression that we may or may not need. (Brigo & Mercurio Lemma Thm , p. 135.
 A 2D Gaussian model (akin to Brigo & Mercurio Section 4.2) Suppose where ( κ1 0 dx(t) = 0 κ 2 r(t) = δ 0 +X 1 (t)+x 2 (t) )( X1 (t) X 2 (t) ) ( σ1 0 dt+ ρσ 2 1 ρ2 σ 2 )( dw Q 1 (t) dw Q 2 (t) ) In this
A 2D Gaussian model (akin to Brigo & Mercurio Section 4.2) Suppose where ( κ1 0 dx(t) = 0 κ 2 r(t) = δ 0 +X 1 (t)+x 2 (t) )( X1 (t) X 2 (t) ) ( σ1 0 dt+ ρσ 2 1 ρ2 σ 2 )( dw Q 1 (t) dw Q 2 (t) ) In this
25857 Interest Rate Modelling
 25857 Interest Rate Modelling UTS Business School University of Technology Sydney Chapter 23. Interest Rate Derivatives - One Factor Spot Rate Models May 22, 2014 1/116 Chapter 23. Interest Rate Derivatives
25857 Interest Rate Modelling UTS Business School University of Technology Sydney Chapter 23. Interest Rate Derivatives - One Factor Spot Rate Models May 22, 2014 1/116 Chapter 23. Interest Rate Derivatives
Linearity-Generating Processes, Unspanned Stochastic Volatility, and Interest-Rate Option Pricing
 Linearity-Generating Processes, Unspanned Stochastic Volatility, and Interest-Rate Option Pricing Liuren Wu, Baruch College Joint work with Peter Carr and Xavier Gabaix at New York University Board of
Linearity-Generating Processes, Unspanned Stochastic Volatility, and Interest-Rate Option Pricing Liuren Wu, Baruch College Joint work with Peter Carr and Xavier Gabaix at New York University Board of
HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY
 International Scientific Conference YOUNG SCIENTISTS 2011 HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY Marko LALIĆ Technická Univerzita v Košiciach, Ekonomická fakulta Katedra financií
International Scientific Conference YOUNG SCIENTISTS 2011 HEDGING PRIEMERU CENY S OPCIAMI V PODMIENKACH KONŠTANTNEJ VOLATILITY Marko LALIĆ Technická Univerzita v Košiciach, Ekonomická fakulta Katedra financií
Charles University in Prague Faculty of Social Sciences. Forecasting realized volatility: Do jumps in prices matter?
 Charles University in Prague Faculty of Social Sciences Institute of Economic Studies RIGOROSIS DIPLOMA THESIS ing realized volatility: Do jumps in prices matter? Author: Mgr. Štefan Lipták Supervisor:
Charles University in Prague Faculty of Social Sciences Institute of Economic Studies RIGOROSIS DIPLOMA THESIS ing realized volatility: Do jumps in prices matter? Author: Mgr. Štefan Lipták Supervisor:
(1) Consider a European call option and a European put option on a nondividend-paying stock. You are given:
 (1) Consider a European call option and a European put option on a nondividend-paying stock. You are given: (i) The current price of the stock is $60. (ii) The call option currently sells for $0.15 more
(1) Consider a European call option and a European put option on a nondividend-paying stock. You are given: (i) The current price of the stock is $60. (ii) The call option currently sells for $0.15 more
Structural Models of Credit Risk and Some Applications
 Structural Models of Credit Risk and Some Applications Albert Cohen Actuarial Science Program Department of Mathematics Department of Statistics and Probability albert@math.msu.edu August 29, 2018 Outline
Structural Models of Credit Risk and Some Applications Albert Cohen Actuarial Science Program Department of Mathematics Department of Statistics and Probability albert@math.msu.edu August 29, 2018 Outline
Application of CAPM for investment decisions in emerging countries
 Application of CAPM for investment decisions in emerging countries Peter Krištofík 1 Abstract The paper is focused on investment decisions of companies with a diversified shareholder base in emerging countries.
Application of CAPM for investment decisions in emerging countries Peter Krištofík 1 Abstract The paper is focused on investment decisions of companies with a diversified shareholder base in emerging countries.
dt + ρσ 2 1 ρ2 σ 2 B i (τ) = 1 e κ iτ κ i
 A 2D Gaussian model (akin to Brigo & Mercurio Section 4.2) Suppose where dx(t) = ( κ1 0 0 κ 2 ) ( X1 (t) X 2 (t) In this case we find (BLACKBOARD) that r(t) = δ 0 + X 1 (t) + X 2 (t) ) ( σ1 0 dt + ρσ 2
A 2D Gaussian model (akin to Brigo & Mercurio Section 4.2) Suppose where dx(t) = ( κ1 0 0 κ 2 ) ( X1 (t) X 2 (t) In this case we find (BLACKBOARD) that r(t) = δ 0 + X 1 (t) + X 2 (t) ) ( σ1 0 dt + ρσ 2
BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS
 BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS PRICING EMMS014S7 Tuesday, May 31 2011, 10:00am-13.15pm
BIRKBECK (University of London) MSc EXAMINATION FOR INTERNAL STUDENTS MSc FINANCIAL ENGINEERING DEPARTMENT OF ECONOMICS, MATHEMATICS AND STATIS- TICS PRICING EMMS014S7 Tuesday, May 31 2011, 10:00am-13.15pm
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA Martin Lauko
 Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA 2009 Martin Lauko Numerické a analytické aproximácie hranice predčasného uplatnenia americkej put opcie DIPLOMOVÁ
Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky DIPLOMOVÁ PRÁCA 2009 Martin Lauko Numerické a analytické aproximácie hranice predčasného uplatnenia americkej put opcie DIPLOMOVÁ
COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS
 COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS The risk sensitive dynamic accumulation model and optimal pension saving management DISSERTATION THESIS 2014 Mgr. Zuzana
COMENIUS UNIVERSITY, BRATISLAVA FACULTY OF MATHEMATICS, PHYSICS AND INFORMATICS The risk sensitive dynamic accumulation model and optimal pension saving management DISSERTATION THESIS 2014 Mgr. Zuzana
Univerzita Karlova v Praze Matematicko fyzikální fakulta
 Univerzita Karlova v Praze Matematicko fyzikální fakulta DIPLOMOVÁ PRÁCE Jana Garajová Modely úrokových měr ve spojitém čase Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Prof.
Univerzita Karlova v Praze Matematicko fyzikální fakulta DIPLOMOVÁ PRÁCE Jana Garajová Modely úrokových měr ve spojitém čase Katedra pravděpodobnosti a matematické statistiky Vedoucí diplomové práce: Prof.
APPROXIMATE FORMULAE FOR PRICING ZERO-COUPON BONDS AND THEIR ASYMPTOTIC ANALYSIS
 INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING Volume 1, Number 1, Pages 1 1 c 28 Institute for Scientific Computing and Information APPROXIMATE FORMULAE FOR PRICING ZERO-COUPON BONDS AND THEIR
INTERNATIONAL JOURNAL OF NUMERICAL ANALYSIS AND MODELING Volume 1, Number 1, Pages 1 1 c 28 Institute for Scientific Computing and Information APPROXIMATE FORMULAE FOR PRICING ZERO-COUPON BONDS AND THEIR
BAKALÁŘSKÁ PRÁCE. Eva Mináriková Analýza akciového trhu
 Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Eva Mináriková Analýza akciového trhu Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr. Jan
Univerzita Karlova v Praze Matematicko-fyzikální fakulta BAKALÁŘSKÁ PRÁCE Eva Mináriková Analýza akciového trhu Katedra pravděpodobnosti a matematické statistiky Vedoucí bakalářské práce: doc. RNDr. Jan
Problémy oceňovania Startupov v súčasnosti. The problems with valuation of startups at present
 Problémy oceňovania Startupov v súčasnosti. The problems with valuation of startups at present Ján Bukoven Abstrakt: V súčasnosti je ekonomický rast a konkurencieschopnosť rozvinutých krajín poháňaný hlavne
Problémy oceňovania Startupov v súčasnosti. The problems with valuation of startups at present Ján Bukoven Abstrakt: V súčasnosti je ekonomický rast a konkurencieschopnosť rozvinutých krajín poháňaný hlavne
Problematické stránky štandardných metód Value at Risk 1
 Problematické stránky štandardných metód Value at Risk 1 Martin ŠORF Abstrakt Príspevok sa venuje hodnoteniu štandardných metód merania Value at Risk z koncepčného hľadiska. Model historickej simulácie,
Problematické stránky štandardných metód Value at Risk 1 Martin ŠORF Abstrakt Príspevok sa venuje hodnoteniu štandardných metód merania Value at Risk z koncepčného hľadiska. Model historickej simulácie,
Import platobných príkazov vo formáte XML
 Import platobných príkazov vo formáte XML Internet banking podporuje import platobných príkazov vo formáte XML, ktorého štruktúra je definovaná normou ISO 20022. Táto norma definuje viacero typov správ
Import platobných príkazov vo formáte XML Internet banking podporuje import platobných príkazov vo formáte XML, ktorého štruktúra je definovaná normou ISO 20022. Táto norma definuje viacero typov správ
Multi-dimensional Term Structure Models
 Multi-dimensional Term Structure Models We will focus on the affine class. But first some motivation. A generic one-dimensional model for zero-coupon yields, y(t; τ), looks like this dy(t; τ) =... dt +
Multi-dimensional Term Structure Models We will focus on the affine class. But first some motivation. A generic one-dimensional model for zero-coupon yields, y(t; τ), looks like this dy(t; τ) =... dt +
Volatility Time Scales and. Perturbations
 Volatility Time Scales and Perturbations Jean-Pierre Fouque NC State University, soon UC Santa Barbara Collaborators: George Papanicolaou Stanford University Ronnie Sircar Princeton University Knut Solna
Volatility Time Scales and Perturbations Jean-Pierre Fouque NC State University, soon UC Santa Barbara Collaborators: George Papanicolaou Stanford University Ronnie Sircar Princeton University Knut Solna
Advances in Valuation Adjustments. Topquants Autumn 2015
 Advances in Valuation Adjustments Topquants Autumn 2015 Quantitative Advisory Services EY QAS team Modelling methodology design and model build Methodology and model validation Methodology and model optimisation
Advances in Valuation Adjustments Topquants Autumn 2015 Quantitative Advisory Services EY QAS team Modelling methodology design and model build Methodology and model validation Methodology and model optimisation
Výbor pre kontrolu rozpočtu PRACOVNÝ DOKUMENT
 Európsky parlament 2014-2019 Výbor pre kontrolu rozpočtu 18.1.2017 PRACOVNÝ DOKUMENT o osobitnej správe Dvora audítorov č. 26/2016 (absolutórium za rok 2015): Zvýšenie účinnosti krížového plnenia a dosiahnutie
Európsky parlament 2014-2019 Výbor pre kontrolu rozpočtu 18.1.2017 PRACOVNÝ DOKUMENT o osobitnej správe Dvora audítorov č. 26/2016 (absolutórium za rok 2015): Zvýšenie účinnosti krížového plnenia a dosiahnutie
VÝBER VHODNEJ METÓDY OCENENIA INVESTÍCIÍ 1.
 VÝBER VHODNEJ METÓDY OCENENIA INVESTÍCIÍ 1. Veronika Frnková ÚVOD V ekonomickej teórií možno nájsť rôzne metódy hodnotenia efektívnosti investícií, ktoré kopírujú požiadavky investorov na výstupnú informáciu
VÝBER VHODNEJ METÓDY OCENENIA INVESTÍCIÍ 1. Veronika Frnková ÚVOD V ekonomickej teórií možno nájsť rôzne metódy hodnotenia efektívnosti investícií, ktoré kopírujú požiadavky investorov na výstupnú informáciu
FDI development during the crisis from 2008 till now
 VŠB-TU Ostrava, Ekonomická fakulta, katedra Financí 8. -. září FDI development during the crisis from 8 till now Michal Fabuš, Miroslav Kohuťár Abstract Investments represent an important resource of country
VŠB-TU Ostrava, Ekonomická fakulta, katedra Financí 8. -. září FDI development during the crisis from 8 till now Michal Fabuš, Miroslav Kohuťár Abstract Investments represent an important resource of country
Lecture 5: Review of interest rate models
 Lecture 5: Review of interest rate models Xiaoguang Wang STAT 598W January 30th, 2014 (STAT 598W) Lecture 5 1 / 46 Outline 1 Bonds and Interest Rates 2 Short Rate Models 3 Forward Rate Models 4 LIBOR and
Lecture 5: Review of interest rate models Xiaoguang Wang STAT 598W January 30th, 2014 (STAT 598W) Lecture 5 1 / 46 Outline 1 Bonds and Interest Rates 2 Short Rate Models 3 Forward Rate Models 4 LIBOR and
UNIVERSITY OF CALGARY. Theoretical and Computational Analysis and Comparison of Stochastic Models of Energy. and Interest Rate Markets
 UNIVERSITY OF CALGARY Theoretical and Computational Analysis and Comparison of Stochastic Models of Energy and Interest Rate Markets by Tatiana Bukharina A THESIS SUBMITTED TO THE FACULTY OF GRADUATE STUDIES
UNIVERSITY OF CALGARY Theoretical and Computational Analysis and Comparison of Stochastic Models of Energy and Interest Rate Markets by Tatiana Bukharina A THESIS SUBMITTED TO THE FACULTY OF GRADUATE STUDIES
Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom
 Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom Príloha č. 1 k opatreniu Pozície štandardných derivátov sa konvertujú na ich ekvivalentnú pozíciu podkladového
Metódy konverzie pozícií štandardných derivátov pri výpočte celkového rizika záväzkovým prístupom Príloha č. 1 k opatreniu Pozície štandardných derivátov sa konvertujú na ich ekvivalentnú pozíciu podkladového
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY
 UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA
UNIVERZITA KOMENSKÉHO V BRATISLAVE FAKULTA MATEMATIKY, FYZIKY A INFORMATIKY ANALÝZA RIE ENÍ NELINEÁRNYCH ROVNÍC PRE OCEŒOVANIE FINANƒNÝCH DERIVÁTOV S PREMENLIVÝMI TRANSAKƒNÝMI NÁKLADMI DIPLOMOVÁ PRÁCA
Fakulta matematiky, fyziky a informatiky. Katedra aplikovanej matematiky a štatistiky EXOTICKÝCH OPCIÍ. Diplomová práca.
 UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
UNIVERZITA KOMENSKÉHO V BRATISLAVE Fakula maemaiky, fyziky a informaiky Kaedra aplikovanej maemaiky a šaisiky DELTA HEDGING EXOTICKÝCH OPCIÍ Diplomová práca Jakub HAVELKA 1114 Aplikovaná maemaika Ekonomická
Empirical Likelihood Estimation of Interest Rate Diffusion model
 Comenius University Bratislava Faculty of Mathematics, Physics and Informatics Department of Applied Mathematics and Statistics Economic and Financial Mathematics Empirical Likelihood Estimation of Interest
Comenius University Bratislava Faculty of Mathematics, Physics and Informatics Department of Applied Mathematics and Statistics Economic and Financial Mathematics Empirical Likelihood Estimation of Interest
θ(t ) = T f(0, T ) + σ2 T
 1 Derivatives Pricing and Financial Modelling Andrew Cairns: room M3.08 E-mail: A.Cairns@ma.hw.ac.uk Tutorial 10 1. (Ho-Lee) Let X(T ) = T 0 W t dt. (a) What is the distribution of X(T )? (b) Find E[exp(
1 Derivatives Pricing and Financial Modelling Andrew Cairns: room M3.08 E-mail: A.Cairns@ma.hw.ac.uk Tutorial 10 1. (Ho-Lee) Let X(T ) = T 0 W t dt. (a) What is the distribution of X(T )? (b) Find E[exp(
Pension Risk Management with Funding and Buyout Options
 Pension Risk Management with Funding and Buyout Options Samuel H. Cox, Yijia Lin and Tianxiang Shi Presented at Eleventh International Longevity Risk and Capital Markets Solutions Conference Lyon, France
Pension Risk Management with Funding and Buyout Options Samuel H. Cox, Yijia Lin and Tianxiang Shi Presented at Eleventh International Longevity Risk and Capital Markets Solutions Conference Lyon, France
Kapitola 14. Výmenné kurzy a devízový trh: meny ako aktíva
 Kapitola 14 Výmenné kurzy a devízový trh: meny ako aktíva Obsah Čo sú výmenné kurzy Výmenné kurzy a ceny tovarov Devízový trh Dopyt po mene a ostatných aktívach Model devízového trhu: vplyv úrokových sadzieb
Kapitola 14 Výmenné kurzy a devízový trh: meny ako aktíva Obsah Čo sú výmenné kurzy Výmenné kurzy a ceny tovarov Devízový trh Dopyt po mene a ostatných aktívach Model devízového trhu: vplyv úrokových sadzieb
Extended Libor Models and Their Calibration
 Extended Libor Models and Their Calibration Denis Belomestny Weierstraß Institute Berlin Vienna, 16 November 2007 Denis Belomestny (WIAS) Extended Libor Models and Their Calibration Vienna, 16 November
Extended Libor Models and Their Calibration Denis Belomestny Weierstraß Institute Berlin Vienna, 16 November 2007 Denis Belomestny (WIAS) Extended Libor Models and Their Calibration Vienna, 16 November
Chapter 3: Black-Scholes Equation and Its Numerical Evaluation
 Chapter 3: Black-Scholes Equation and Its Numerical Evaluation 3.1 Itô Integral 3.1.1 Convergence in the Mean and Stieltjes Integral Definition 3.1 (Convergence in the Mean) A sequence {X n } n ln of random
Chapter 3: Black-Scholes Equation and Its Numerical Evaluation 3.1 Itô Integral 3.1.1 Convergence in the Mean and Stieltjes Integral Definition 3.1 (Convergence in the Mean) A sequence {X n } n ln of random
Investment strategies and risk management for participating life insurance contracts
 1/20 Investment strategies and risk for participating life insurance contracts and Steven Haberman Cass Business School AFIR Colloquium Munich, September 2009 2/20 & Motivation Motivation New supervisory
1/20 Investment strategies and risk for participating life insurance contracts and Steven Haberman Cass Business School AFIR Colloquium Munich, September 2009 2/20 & Motivation Motivation New supervisory
Neistota pri oceňovaní technických rezerv poisťovní
 Neistota pri oceňovaní technických rezerv poisťovní Peter Marko 1 Abstrakt Technické rezervy sú dôležité z hľadiska schopnosti poisťovne plniť svoje záväzky vyplývajúce z poistných zmlúv v budúcnosti.
Neistota pri oceňovaní technických rezerv poisťovní Peter Marko 1 Abstrakt Technické rezervy sú dôležité z hľadiska schopnosti poisťovne plniť svoje záväzky vyplývajúce z poistných zmlúv v budúcnosti.
Lecture 18. More on option pricing. Lecture 18 1 / 21
 Lecture 18 More on option pricing Lecture 18 1 / 21 Introduction In this lecture we will see more applications of option pricing theory. Lecture 18 2 / 21 Greeks (1) The price f of a derivative depends
Lecture 18 More on option pricing Lecture 18 1 / 21 Introduction In this lecture we will see more applications of option pricing theory. Lecture 18 2 / 21 Greeks (1) The price f of a derivative depends
Interest rate models and Solvency II
 www.nr.no Outline Desired properties of interest rate models in a Solvency II setting. A review of three well-known interest rate models A real example from a Norwegian insurance company 2 Interest rate
www.nr.no Outline Desired properties of interest rate models in a Solvency II setting. A review of three well-known interest rate models A real example from a Norwegian insurance company 2 Interest rate
arxiv: v1 [q-fin.pr] 23 Feb 2014
![arxiv: v1 [q-fin.pr] 23 Feb 2014 arxiv: v1 [q-fin.pr] 23 Feb 2014](/thumbs/87/95850189.jpg) Time-dependent Heston model. G. S. Vasilev, Department of Physics, Sofia University, James Bourchier 5 blvd, 64 Sofia, Bulgaria CloudRisk Ltd (Dated: February 5, 04) This work presents an exact solution
Time-dependent Heston model. G. S. Vasilev, Department of Physics, Sofia University, James Bourchier 5 blvd, 64 Sofia, Bulgaria CloudRisk Ltd (Dated: February 5, 04) This work presents an exact solution
EX-POST VERIFICATION OF PREDICTION MODELS OF WAGE DISTRIBUTIONS
 EX-POST VERIFICATION OF PREDICTION MODELS OF WAGE DISTRIBUTIONS LUBOŠ MAREK, MICHAL VRABEC University of Economics, Prague, Faculty of Informatics and Statistics, Department of Statistics and Probability,
EX-POST VERIFICATION OF PREDICTION MODELS OF WAGE DISTRIBUTIONS LUBOŠ MAREK, MICHAL VRABEC University of Economics, Prague, Faculty of Informatics and Statistics, Department of Statistics and Probability,
ON THE FOUR-PARAMETER BOND PRICING MODEL. Man M. Chawla X-027, Regency Park II, DLF City Phase IV Gurgaon , Haryana, INDIA
 International Journal of Applied Mathematics Volume 29 No. 1 216, 53-68 ISSN: 1311-1728 printed version); ISSN: 1314-86 on-line version) doi: http://dx.doi.org/1.12732/ijam.v29i1.5 ON THE FOUR-PARAMETER
International Journal of Applied Mathematics Volume 29 No. 1 216, 53-68 ISSN: 1311-1728 printed version); ISSN: 1314-86 on-line version) doi: http://dx.doi.org/1.12732/ijam.v29i1.5 ON THE FOUR-PARAMETER
Counterparty Credit Risk Simulation
 Counterparty Credit Risk Simulation Alex Yang FinPricing http://www.finpricing.com Summary Counterparty Credit Risk Definition Counterparty Credit Risk Measures Monte Carlo Simulation Interest Rate Curve
Counterparty Credit Risk Simulation Alex Yang FinPricing http://www.finpricing.com Summary Counterparty Credit Risk Definition Counterparty Credit Risk Measures Monte Carlo Simulation Interest Rate Curve
CVaR Portfolio Models for Electricity Generating Capacities
 CVaR Portfolio Models for Electricity Generating Capacities Dizertačná práca Mgr. Jana Szolgayová Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky
CVaR Portfolio Models for Electricity Generating Capacities Dizertačná práca Mgr. Jana Szolgayová Univerzita Komenského v Bratislave Fakulta matematiky, fyziky a informatiky Katedra aplikovanej matematiky
Incorporating Managerial Cash-Flow Estimates and Risk Aversion to Value Real Options Projects. The Fields Institute for Mathematical Sciences
 Incorporating Managerial Cash-Flow Estimates and Risk Aversion to Value Real Options Projects The Fields Institute for Mathematical Sciences Sebastian Jaimungal sebastian.jaimungal@utoronto.ca Yuri Lawryshyn
Incorporating Managerial Cash-Flow Estimates and Risk Aversion to Value Real Options Projects The Fields Institute for Mathematical Sciences Sebastian Jaimungal sebastian.jaimungal@utoronto.ca Yuri Lawryshyn
The Lognormal Interest Rate Model and Eurodollar Futures
 GLOBAL RESEARCH ANALYTICS The Lognormal Interest Rate Model and Eurodollar Futures CITICORP SECURITIES,INC. 399 Park Avenue New York, NY 143 Keith Weintraub Director, Analytics 1-559-97 Michael Hogan Ex
GLOBAL RESEARCH ANALYTICS The Lognormal Interest Rate Model and Eurodollar Futures CITICORP SECURITIES,INC. 399 Park Avenue New York, NY 143 Keith Weintraub Director, Analytics 1-559-97 Michael Hogan Ex
MODELING VAR OF DAX INDEX USING GARCH MODEL 1
 Matej Štalmach MODELING VAR OF DAX INDEX USING GARCH MODEL 1 Introduction This paper aims to answer question how much money would somebody need if he wanted insurance against very unusual decrease of German
Matej Štalmach MODELING VAR OF DAX INDEX USING GARCH MODEL 1 Introduction This paper aims to answer question how much money would somebody need if he wanted insurance against very unusual decrease of German
Stochastic modelling of electricity markets Pricing Forwards and Swaps
 Stochastic modelling of electricity markets Pricing Forwards and Swaps Jhonny Gonzalez School of Mathematics The University of Manchester Magical books project August 23, 2012 Clip for this slide Pricing
Stochastic modelling of electricity markets Pricing Forwards and Swaps Jhonny Gonzalez School of Mathematics The University of Manchester Magical books project August 23, 2012 Clip for this slide Pricing
Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put opcií: Aplikácia na akcie SPDR Gold Shares
 Ing. Martina Rusnáková Katedra financií, Ekonomická fakulta echnická univerzita v Košiciach E-mail: martina.rusnakova@tuke.sk Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put
Ing. Martina Rusnáková Katedra financií, Ekonomická fakulta echnická univerzita v Košiciach E-mail: martina.rusnakova@tuke.sk Hedging proti poklesu ceny pomocou kúpy vanilla put opcií a kúpy down-in put
Parameter estimation in SDE:s
 Lund University Faculty of Engineering Statistics in Finance Centre for Mathematical Sciences, Mathematical Statistics HT 2011 Parameter estimation in SDE:s This computer exercise concerns some estimation
Lund University Faculty of Engineering Statistics in Finance Centre for Mathematical Sciences, Mathematical Statistics HT 2011 Parameter estimation in SDE:s This computer exercise concerns some estimation
Identifikácia trhových neefektívností na základe makroekonomických veličín
 Identifikácia trhových neefektívností na základe makroekonomických veličín Eduard BAUMÖHL Mária FARKAŠOVSKÁ Úvod Prvá komplexná publikácia zaoberajúca sa trhovými neefektívnosťami na akciovom trhu pochádza
Identifikácia trhových neefektívností na základe makroekonomických veličín Eduard BAUMÖHL Mária FARKAŠOVSKÁ Úvod Prvá komplexná publikácia zaoberajúca sa trhovými neefektívnosťami na akciovom trhu pochádza
25857 Interest Rate Modelling
 25857 UTS Business School University of Technology Sydney Chapter 20. Change of Numeraire May 15, 2014 1/36 Chapter 20. Change of Numeraire 1 The Radon-Nikodym Derivative 2 Option Pricing under Stochastic
25857 UTS Business School University of Technology Sydney Chapter 20. Change of Numeraire May 15, 2014 1/36 Chapter 20. Change of Numeraire 1 The Radon-Nikodym Derivative 2 Option Pricing under Stochastic
LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives
 Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Optimal Asset Allocation with Stochastic Interest Rates in Regime-switching Models
 Optimal Asset Allocation with Stochastic Interest Rates in Regime-switching Models Ruihua Liu Department of Mathematics University of Dayton, Ohio Joint Work With Cheng Ye and Dan Ren To appear in International
Optimal Asset Allocation with Stochastic Interest Rates in Regime-switching Models Ruihua Liu Department of Mathematics University of Dayton, Ohio Joint Work With Cheng Ye and Dan Ren To appear in International
Shape of the Yield Curve Under CIR Single Factor Model: A Note
 Shape of the Yield Curve Under CIR Single Factor Model: A Note Raymond Kan University of Chicago June, 1992 Abstract This note derives the shapes of the yield curve as a function of the current spot rate
Shape of the Yield Curve Under CIR Single Factor Model: A Note Raymond Kan University of Chicago June, 1992 Abstract This note derives the shapes of the yield curve as a function of the current spot rate
Calibration of Different Interest Rate Models for a Good Fit of Yield Curves
 Delft University of Technology Faculty of Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics Calibration of Different Interest Rate Models for a Good Fit of
Delft University of Technology Faculty of Electrical Engineering, Mathematics and Computer Science Delft Institute of Applied Mathematics Calibration of Different Interest Rate Models for a Good Fit of
( ) since this is the benefit of buying the asset at the strike price rather
 Review of some financial models for MAT 483 Parity and Other Option Relationships The basic parity relationship for European options with the same strike price and the same time to expiration is: C( KT
Review of some financial models for MAT 483 Parity and Other Option Relationships The basic parity relationship for European options with the same strike price and the same time to expiration is: C( KT
Ch 12. Interest Rate and Credit Models
 Ch. Interest Rate and Credit Models I. Equilibrium Interest Rate Models II. No-Arbitrage Interest Rate Models III. Forward Rate Models IV. Credit Risk Models This chapter introduces interest rate models
Ch. Interest Rate and Credit Models I. Equilibrium Interest Rate Models II. No-Arbitrage Interest Rate Models III. Forward Rate Models IV. Credit Risk Models This chapter introduces interest rate models
9 Oceňovanie derivátov
 9 Oceňovanie derivátov Finančné deriváty (financial derivatives) sú nástroje, ktorých hodnota je odvodená od ceny podkladového aktíva (underlying). Týmto môže byť komodita, akcia, dlhopis, menový kurz,
9 Oceňovanie derivátov Finančné deriváty (financial derivatives) sú nástroje, ktorých hodnota je odvodená od ceny podkladového aktíva (underlying). Týmto môže byť komodita, akcia, dlhopis, menový kurz,
Monte Carlo Simulations
 Monte Carlo Simulations Lecture 1 December 7, 2014 Outline Monte Carlo Methods Monte Carlo methods simulate the random behavior underlying the financial models Remember: When pricing you must simulate
Monte Carlo Simulations Lecture 1 December 7, 2014 Outline Monte Carlo Methods Monte Carlo methods simulate the random behavior underlying the financial models Remember: When pricing you must simulate
