Journal of Econometrics. A two-stage realized volatility approach to estimation of diffusion processes with discrete data
|
|
|
- Moris Preston
- 6 years ago
- Views:
Transcription
1 Journal of Econometrics 5 ( Contents lists available at ScienceDirect Journal of Econometrics journal homeage: A two-stage realized volatility aroach to estimation of diffusion rocesses with discrete data Peter C.B. Phillis a,b,c,d, Jun Yu e, a Cowles Foundation, Yale University, United States b Deartment of Economics, University of Auckl, New Zeal c Deartment of Economics, University of York, United ingdom d School of Economics, Singaore Management University, Singaore e School of Economics, Singaore Management University, 9 Stamford Road, Singaore 7893, Singaore a r t i c l e i n f o a b s t r a c t Article history: Available online 5 December 8 JEL classification: C3 C E43 G3 eywords: Maximum likelihood Girsanov theorem Discrete samling Continuous record Realized volatility his aer motivates introduces a two-stage method of estimating diffusion rocesses based on discretely samled observations. In the first stage we make use of the feasible central limit theory for realized volatility, as develoed in [Jacod, J., 994. Limit of rom measures associated with the increments of a Brownian semiartingal. Working aer, Laboratoire de Probabilities, Universite Pierre et Marie Curie, Paris] [Barndorff-Nielsen, O., Shehard, N.,. Econometric analysis of realized volatility its use in estimating stochastic volatility models. Journal of the Royal Statistical Society. Series B, 64, 53 8], to rovide a regression model for estimating the arameters in the diffusion function. In the second stage, the in-fill likelihood function is derived by means of the Girsanov theorem then used to estimate the arameters in the drift function. Consistency asymtotic distribution theory for these estimates are established in various contexts. he finite samle erformance of the roosed method is comared with that of the aroximate maximum likelihood method of [Aït-Sahalia, Y.,. Maximum likelihood estimation of discretely samled diffusion: A closed-form aroximation aroach. Econometrica. 7, 3 6]. 8 Elsevier B.V. All rights reserved.. Introduction For many years, continuous time models have enjoyed a great deal of success in finance (Merton, 99 as well as wide alications in economics (e.g., Dixit (993. Corresondingly, there has been growing interest in estimating continuous systems using econometric methods with discrete data. We thank two anonymous referees for their constructive comments. We also thank Yacine Aït-Sahalia, Yongmiao Hong, Chung-ming uan, Andy Lo, Neil Shehard, seminar articiants at the First Symosium on Econometric heory Alications in aiwan, the 6 North American Winter Meeting of Econometric Society, the First Finance Summer Cam at Singaore Management University for helful discussions. Phillis gratefully acknowledges visiting suort from the School of Economics at Singaore Management University, suort from a elly Fellowshi at the University of Auckl Business School from the NSF under Grant No. SES Yu gratefully acknowledges financial suort from the Ministry of Education AcRF ier fund under Grant No. 6B43-RS. Corresonding author. addresses: eter.hillis@yale.edu (P.C.B. Phillis, yujun@smu.edu.sg (J. Yu. Many models used in finance for modelling asset rices can be written in terms of a diffusion rocess as dx t = µ(x t ; θ dt + σ (X t ; θ db t, ( where B t is a stard Brownian motion, σ (X t ; θ is a known diffusion function, µ(x t ; θ is a known drift function, θ = (θ, θ is a vector of k + k unknown arameters. Note that we isolate the vector of arameters θ in the diffusion function from θ for reasons which will be clear below. he attractions of the Ito calculus make it easy to work with rocesses generated by diffusions like ( as a result these rocesses have been used widely in finance to model asset rices, including stock rices, interest rates, exchange rates. From an econometric stoint, the estimation roblem is to estimate θ from observed data, which are tyically recorded discretely at (,,..., n ( over a certain time interval [, ], where is the samling interval is the time san of the data. For examle, if X t is recorded as the annualized interest rate observed monthly (weekly or daily, we have = / (/5 or /5. yically, can be as large as 5 for US reasury Bills, but is generally much smaller for data from swa /$ see front matter 8 Elsevier B.V. All rights reserved. doi:.6/j.jeconom.8..6
2 4 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( markets. Also, due to time-of-day effects ossibly other market microstructure frictions, it is commonly believed that intra-day data do not comletely follow diffusion models such as (. As a result, daily lower frequencies are most frequently used to estimate continuous time models. However, Barndorff-Nielsen Shehard ( Bollerslev Zhou ( recently showed how to use information from intra-day data to estimate continuous time stochastic volatility models. A large class of estimation methods is based on the likelihood function derived from the transition robability density of discrete samling then resorts to long san asymtotic theory (i.e.. Excet for a few cases, the transition robability density does not have a closed form exression hence the exact maximum likelihood (ML method based on the likelihood function for the discretely samled data is not directly available. In the financial econometrics literature, interest in obtaining estimators which aroximate or aroach ML estimators has been growing, in view of the natural attractiveness of maximum likelihood its asymtotic roerties. Several alternative methods of this tye have been develoed in recent years. See Phillis Yu (in ressa for a survey of various alternative methods the discussion of their advantages drawbacks. he main urose of the resent aer is to roose an alternative method of estimating diffusion rocesses of the form given by model ( from discrete observations to establish asymtotic roerties by resorting to both the long san (i.e. in-fill asymtotics (i.e.. he estimation rocedure involves two stes. In the first ste, we roose to use a quadratic variation tye estimator of θ. In the second ste, an aroximate in-fill likelihood function is maximized to obtain a ML estimator of θ. his method has several advantages over the existing method. First, it is not deendent on finding an aroriate auxiliary model. Second, it does not require simulations or olynomial exansions hence is straightforward to imlement. hird, it decomoses the otimization roblem into two smaller scale otimization roblems, making the aroach comutationally more attractive. Finally, exerience with the rocedure both in simulations emirical alications indicates that the method works well in finite samles. he aer is organized as follows: Section reviews the literature on the ML estimation of diffusion rocesses motivates the aroach. Section 3 introduces the new method Section 4 derives the asymtotic roerties of the estimates. Section 5 resents some Monte Carlo evidence. Section 6 discusses the case of microstructure noises Section 6 concludes. Proofs are rovided in the Aendix.. Literature review motivation.. Literature review... ransition robability density based aroaches As exlained above, a large class of estimation methods is based on the likelihood function derived from the transition robability density of the discretely samled data. Suose (X i X (i, θ is the transition robability density. he Markov roerty of model ( imlies the following log-likelihood function for the discrete samle l D (θ = n log((x i X (i, θ. ( Under regularity conditions, the resulting estimator is consistent, asymtotically normally distributed asymtotically efficient (Billingsley, 96. Unfortunately, excet for a few cases, the transition density does not have a closed form exression hence the exact ML method based on the likelihood function of the discrete samle is not a ractical rocedure. In the financial econometrics literature, interest in finding estimators that aroach ML estimators in some quantifiable sense has been growing many alternative methods have been develoed in recent years. For examle, Lo (988 suggested calculating the transition robability density by solving a artial differential equation numerically. Nowman (997 suggested an aroach which assumes that the conditional volatility remains unchanged over the unit intervals so that he can aroximate the transition density using a Gaussian method. Yu Phillis ( used the stoing time technique to develo an exact Gaussian method. Pedersen (995 Brt Santa-Clara ( advocated an aroach which calculates the transition robability density using simulation with some auxiliary oints between each air of consecutive observations introduced. his method is also closely related to the Bayesian MCMC method roosed by Elerian et al. ( Eraker (. A drawback of these simulation-based aroaches is that the corresonding comutational cost will inevitably be high. As an imortant alternative to these numerical simulated ML methods, Aït-Sahalia ( roosed to aroximate the transition robability density of diffusions using analytical exansions via Hermite olynomials. Before obtaining the closed-form exansions, a Lamerti transform is erformed on the continuous time model so that the diffusion function becomes a constant. After that one then obtains a Hermite olynomial exansion of the transition density of the transformed variable around the normal distribution. Aït-Sahalia (999 imlemented the aroximate ML method documents its good erformance. As it is tyically tedious error rone to derive the Hermite exansion by h, Aït-Sahalia ( suggested using symbolic softwares, such as MAHEMAICA. Aart from these likelihood-based aroaches, numerous alternative methods are available. We simly refer readers to the book by Prakasa Rao (999a for a review of many alternative aroaches.... Aroaches based on realized volatility in-fill likelihood When the transition robability density does not have a closed form exression but X t is observed continuously over [, ], an alternative method can be used to estimate diffusion models. We now introduce motivate the aroach. When the diffusion term is known (i.e. σ (X t ; θ = σ (X t so does not deend on any unknown arameters, one can construct the exact continuous record log-likelihood via the Girsanov theorem (e.g., (Litser Shiryaev, as follows. l IF (θ = µ(x t ; θ σ (X t dx t µ (X t ; θ dt. σ (X t Lánska (979 established the consistency asymtotic normality of the continuous record ML estimator of θ when under a certain set of regularity conditions. he assumtions of a known diffusion function the availability of a continuous time record are not realistic in financial other alications. Motivated by the fact that the drift diffusion functions are of different orders (Bi Phillis, 3, 7, we argue that there can be advantages to estimating the diffusion arameters searately from the drift arameters. For examle, when σ (X t ; θ = θ, i.e., the diffusion function is an unknown constant, a two-stage aroach can be used to estimate the model. First, θ can be estimated directly by the realized volatility function, i.e., [X ] ˆθ =, (3
3 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( Fig.. Stardized realized volatility against the number of daily observations used to calculate the realized volatility. he daily data are simulated from the Vasicek model dx t =.6(.9 X t dt +.6dB t. Fig.. Stardized realized volatility against the number of daily observations used to calculate the realized volatility. he daily data are simulated from the Vasicek model dx t =.6(.9 X t dt +.db t. where [X ] imlies that (dx t = θ dt, hence = n (X i X (i. his is because model ( t, [X] = (dx t = θ dt = θ, where [X] is the quadratic variation of X, which can be consistently estimated by [X ] as. As a result, ˆθ should be a very good estimate of θ when is small, which is tyically the case for interest rate data. Indeed, in the secial case where the drift term is zero the diffusion term is an unknown constant, the exact discrete ( model (Phillis, 97 for the data is X i X (i = θ Bi B (i so the maximum likelihood estimator is trivially ˆθ (see also Aït-Sahalia et al. (5. Although this corresondence clearly does not aly to more general secifications, it seems likely that when is small the two estimators will be close to each other. Second, the following logarithmic continuous record likelihood function of model (, l IF (θ = µ(x t ; θ σ (X t ; ˆθ dx t µ (X t ; θ σ (X t ; ˆθ dt, may be aroximated by the in-fill likelihood function l AIF (θ = n µ(x (i ; θ (X i X (i ˆθ n µ (X (i ; θ, (4 ˆθ which is in turn maximized with resect to θ. Because θ is estimated by ML θ is close to an MLE, the two-stage rocedure may be interreted as a form of rofile ML estimation. his two-stage aroach is closely related to the method roosed by Florens-Zmirou (989, where a contrast function instead of the logarithmic in-fill likelihood function was used in the second ste. o better areciate the quality of aroximation of [X ] to [X], we simulate daily data from the Vasicek model dx t =.6(.9 X t dt +.6dB t, (5 Fig. 3. Stardized realized volatility against the number of weekly observations used to calculate the realized volatility. he weekly data are simulated from the Vasicek model dx t =.6(.9 X t dt +.6dB t. lot the stardized realized volatility, [X ] /, against the number of daily observations used to calculate [X ]. Quadratic variation theory imlies that as, [X ] / a.s. σ. It is clear from Fig. that although [X ] / is quite erratic initially but quickly settles down around σ. It seems that with only 3 35 observations one can get a good estimate of σ. We then increase the volatility rate from.6 to. decrease the samling frequency from daily to weekly. Results are lotted in Figs. 3, resectively. It clear that the conclusion about the raid convergence of [X ] / is quite robust to these changes. When the diffusion term is only known u to a scalar factor, that is when dx t = µ(x t ; θ dt + θ f (X t db t, (6 the above two-stage method is easily modified. First, θ estimated by ˆθ = n can be [X ]. (7 f (X (i
4 4 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( able Simulation results under the CIR model, dx t =.3(.9 X t dt +.6 X t db t, based on relications. Mean SD st for the average stard deviation across relications, resectively. Method κ =.3 µ =.9 σ =.6 Mean SD Mean SD Mean SD / MLE Yoshida Proosed / 5 MLE Yoshida Proosed /5 MLE Yoshida Proosed /5 MLE Yoshida Proosed /5 MLE Yoshida Proosed /5 MLE Yoshida Proosed Second, the following aroximate logarithmic in-fill likelihood function can then be maximized with resect to θ (denoting the resulting estimator by ˆθ l AIF (θ = n µ(x (i ; θ ˆθ f (X (i (X i X (i n µ (X (i ; θ ˆθ f (X (i. (8 his method is alicable to many oular interest rate models, including those roosed by Vasicek (977, Cox et al. (985 (CIR hereafter, Ahn Gao (999. It is also closely related to the method roosed by Yoshida (99. In articular, instead of using the estimator in (7, Yoshida (99 used the following estimator for θ : θ = n (X i X (i. (9 f (X (i Also,Yoshida (99 suggested using an iterative rocedure to construct a better estimate of θ (denoted by θ. Under the conditions of,,, Yoshida (99 derived limiting normal distributions for n ( θ θ (ˆθ θ. Since n / = /, the diffusion arameter enjoys a faster rate of convergence. Unfortunately, requiring the diffusion function to be either a constant onown u to a scalar function limits alicability the rocedures roosed by Florens-Zmirou (989 Yoshida (99 cannot be imlemented with more general diffusion rocesses. he restriction on the diffusion term regarding arameter deendence was somewhat relaxed in Hutton Nelson (986 who based estimation on the following first order condition of the logarithmic quasi-likelihood function: µ(x t ; θ/ θ dx σ t (X t ; θ µ (X t ; θ/ θ dt =. σ (X t ; θ Although their model seems to allow for a more flexible diffusion function, it requires that the drift term share the same set of arameters as the diffusion term. his assumtion is too restrictive for ractical alications. Moreover, although this onestage estimation aroach is easy to imlement, the estimation is mainly based on the drift function hence leads to inferior finite samle roerties, as we will show below in the context of a simle examle... Motivation Our two-stage method is in line with methods roosed by Florens-Zmirou (989 Yoshida (99. hat is, in the first stage, we estimate the arameters in the diffusion functions based on the realized volatility, a quantity which consistently estimates the quadratic variation under very mild conditions. In the second ste, by assuming the diffusion function to be known, we derive aroximate the logarithmic in-fill likelihood function. o motivate the two-ste aroach, we consider two simle examles.... Examle In the first examle, we consider estimating the following CIR model dx t = κ(µ X t dt + σ X t db t, ( using the exact ML method based on the transition robability density the two-stage method discussed in Section.. he natural estimator of σ based on realized volatility is [X ] ˆσ = n. ( X (i i= Moreover, since θ = (κ, µ, the logarithmic in-fill likelihood is, n κ(µ X (i (X i X (i ˆσ X (i i= n κ (µ X (i i= ˆσ X (i. ( CIR (985 showed that the distribution of X(t + conditional on X(t is non-central chi-squared, χ [cx(t, q +, λ(t], where c = κ/(σ ( e κ, λ(t = cr(te κ, q = κµ/σ, the second third arguments are the degrees of freedom non-centrality arameters, resectively. his transition robability density is used to calculate the likelihood function to obtain the exact ML estimates. able reorts some results obtained from a Monte Carlo study where we comare three estimation methods: exact ML, Yoshida s method which estimates σ by (9, the roosed method which estimates σ by (. We vary both the samling frequencies
5 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( able Simulation results under dx t =.dt +.db t based on relications. Mean variance are calculated across relications, resectively. rue value of α =. RV ML QML Mean Variance Mean Variance Mean Variance / / / time sans. Note that the arameters the samling frequencies are all set to emirically reasonable values. In all cases, the two two-stage methods are almost identical. his is not surrising as the two methods differ only in the first stage. Moreover, the two-stage methods erform comarably with the ML method. Even in the case where very coarsely samled data ( = / are available, the two-stage method works quite well. In most cases the two-stage methods erform slightly better than the ML method. In light of Phillis Yu (5, the observed bias in the estimates of κ are the result of the near unit root roblem. he observation that the two-stage method is not dominated by ML is quite remarkable, as the data generating rocess is based on the transition robability density on which ML itself is based. An interesting side result to emerge from this simulation is that the two-stage method is able to reduce the finite samle bias variance in κ in all cases, even though the reductions are small.... Examle he model in the second examle is taken from Hutton Nelson (986 dx t = αdt + αdb t. (3 Although this model is generally not well suited to interest rate data, the feature that the drift diffusion functions share the same arameter rovides a nice framework to investigate the relative erformance of the estimation method based on the diffusion only, against that based on the drift only that based on the drift diffusion jointly. he first method is based on the realized volatility hence only uses the diffusion term to estimate the model. It is easy to show that [X ] ˆα =. he second method is based on the transition robability density given by X i X (i N(X (i + α, α. Clearly this method uses information both in the drift diffusion functions. Denote the resulting estimate by ˆα. Note that this estimator is equivalent to the MLE of the discretized model via the Euler aroximation. he third method was roosed by Hutton Nelson (986. It uses mainly information in the drift function is based on maximization of the following logarithmic quasi-likelihood function α dx t α dt. As a result, the estimate has the following analytical exression: ˆα 3 = X. able reorts results obtained from a Monte Carlo study where we comare the three estimation methods with different samling frequencies. In all cases, the two-stage method ML erform much better than QML;, most remarkably, the two-stage method erforms better than ML ( hence the Euler method. Just as in examle, the fact that the simle two-stage method outerforms ML in finite samles is surrising. Moreover, the better erformance of the first second methods clearly reflects the order difference in the drift diffusion functions. 3. A two-stage method he estimation rocedure discussed in Section. is not directly alicable to general diffusions such as model, as it requires either a constant diffusion function or searability of the scalar arameter from the reminder of the diffusion function. As a result, we have to rovide a more general two-ste rocedure to estimate a diffusion rocess in the form of model (. In articular, in the first ste we roose to estimate the arameters in the diffusion function by using the feasible central limit theorem for realized volatility derived by Jacod (994 oularized by Barndorff- Nielsen Shehard (. Assume that X t is observed at a gird of discrete times t =,,..., M ( = ( M =,..., n (=,, (M +,..., where n = M with being a fixed ositive integer, is the time san of the data, is the samling frequency, M = O(n. his articular construction allows for the nonoverlaing sub-samles ((k M +,..., km, where k =,...,, so that each sub-samle has M observations over the interval ((k, k ]. For examle, if ten years of weekly observed interest rates are available we slit the data into ten blocks, then =, = /5, M = 5, =. he total number of observations is 5 the number of observations contained in each block is 5. he first limit in Box I follows by virtue of the definition of quadratic variation, while the second limit in Box I is the central limit theorem (CL which is due to Jacod (994 Barndorff-Nielsen Shehard (, the third limit in Box I involves a finite samle correction on the asymtotic theory (Barndorff-Nielsen Shehard, 5. It is shown in the latter reference that the third limit in Box I has a better finite samle erformance than that the second limit in Box I. Although in this aer we only use the realized volatility to estimate the quadratic variation, other realized ower variations, such as realized absolute variation, can be used in the same way. For the theoretical develoment of general realized ower variations, we refer readers to the articles by Barndorff-Nielsen Shehard (3 Barndorff-Nielsen et al. (6. Based on the CL i.e., the second limit in Box I, θ can be estimated in the first stage by running a (nonlinear least squares regression of the stardized realized volatility (X (k M +i X (k M +(i (4
6 44 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( As, n = M, so that M (X (k M +i X (k M +(i [X] k (X (k M +i X (k M +(i ([X] k log ( M [X] (k, (X (k M +i X (k M +(i log([x] k where = M (X (k M +i X (k M +(i 4 3 s k [X] (k d N(,, [X] (k + s k d N(,, r s k = max k, ( M M (X (k M +i X (k M +(i fo =,...,. Box I. where ˆθ = arg min θ Q (θ, Q (θ = { (X(k M +i X (k M +(i σ ( } X (k M +(i ; θ Box II. on the stardized diffusion function ([X] k [X] (k = ( σ (X (k t ; θ dt (5 σ ( X (k M +(i ; θ (6 fo =,...,. Denote the resulting estimator of θ by ˆθ. In fact, we can write ˆθ as the extremum estimator as in Box II. A similar regression in stardized log levels of realized volatility can be run using the third limit in Box I. his aroach rovides a more general estimation rocedure than those designed to estimate models with a constant diffusion or a scalar arameter in the diffusion function. Hence this aroach substantially generalizes the method offlorens-zmirou (989 the method of Yoshida (99 to a much wider class of diffusion rocesses. Indeed, when =, the least squares regression above is equivalent to minimizing the squared difference between the terms given by Eqs. (4 (5, which yields exactly the exression of the estimator (7 when the diffusion term is known u to the scalar factor. In the second stage, the aroximate log-likelihood function is maximized with resect to θ (denoting the resulting estimator by ˆθ l AIF (θ = n µ(x (i ; θ σ (X (i ; ˆθ (X i X (i n 4. Asymtotic results µ (X (i ; θ σ (X (i ; ˆθ. (7 he asymtotic theory of a slightly different two-stage estimator in the multivariate case was obtained in Yoshida (99 for models whose diffusion term is known u to a constant (matrix factor, where both infill long san asymtotics are emloyed both for the diffusion drift arameter estimators. In this section we first derive the asymtotic theory for the same class of (scalar models but only resort to long san asymtotics for the drift arameter asymtotic theory. We then investigate the asymtotic roerties of the estimators roosed in Section 3 for model ( whose diffusion function has a general form.
7 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( Scalar arameter in the diffusion function o highlight the differences between our aroach Yoshida (99, we first assume the data are generated according to the following stochastic differential equation: dx t = µ(x t ; θ dt + θ f (X tdb t. (8 Denote θ by τ θ by τ. Both µ( ; θ f ( are timehomogeneous, B-measurable functions on D = (l, u with l < u, where B is the σ -field generated by Borel sets on D. τ is estimated by ˆτ defined by Eq. (7; θ is estimated by ˆθ, the maximizer of Eq. (8. o rove consistency of ˆτ in a diffusion rocess with a constant diffusion term (i.e. f (X t =, Florens-Zmirou (989 assumed,,. he same set of assumtions were emloyed by Yoshida (99 to deal with the diffusion rocess for more general, but still known, f (X t. In this aer, using the theory of Jacod (994 Barndorff-Nielsen Shehard (, we show that the condition of an infinite time san of data (i.e. is not needed to develo the asymtotic theory for ˆτ, thereby extending the asymtotic results of Yoshida (99 in a significant way. We list the following conditions. Assumtion. Equation [X] t τ t f (X s ds = has a unique solution at τ > t >. Assumtion. inf x J f (x >, where J is a comact subset of the range of the rocess. Assumtion 3. t µ (X s ; θ ds < t <. Remark 4.. Assumtion is an identification condition Assumtion is a bounding ositivity condition on the volatility function. Assumtion 3 ensures weak convergence of the error rocess from the Euler aroximation to the diffusion rocess (Jacod Protter, 998. heorem 4. (Asymtotics of the Diffusion Parameter Estimate. Suose Assumtions hold, ˆτ τ as. If, in addition, Assumtion 3 holds, / (ˆτ τ d τ f (X s dw s f (X s ds where W t is a Brownian motion which is indeendent of X t. Remark 4.. With a different estimate for τ, we substantially imrove the results of Yoshida (99, who derived asymtotic roerties of the diffusion estimate assuming that, by only requiring in heorem 4. that. Our result is not surrising confirms the intuition that when the samling interval goes to zero, the samle ath within a finite time san, no matter how short, can erfectly reveal the quadratic variation of the rocess (see, for examle, Merton (98 at least over that time san. o establish the asymtotic roerties of the drift arameter estimate, we follow Yoshida (99 closely. In articular, we first list the following conditions. Assumtion 4. θ Θ where the arameter sace Θ R is a comact set with θ Int(Θ. Assumtion 5. Both µ( ; θ f ( functions are twice continuously differentiable. As a result, for any comact subset J of the range of the rocess, we have the following two conditions: (i (Lischitz condition here exists a constant L so that µ(x; θ µ(y; θ + θ f (x f (y L x y, for all x y in J. (ii (Growth condition here exists a constant L so that µ(x; θ + θ f (x L + x, for all x y in J. Assumtion 6. Define the scale measure of X t by ( x µ(y; θ s(x; θ = ex τ f (y dy, c where c is a generic constant. We assume the following conditions hold u c s(x; θdx = c l s(x; θdx =, u dx = A(θ <. s(x; θτ f (x l Assumtion 7. For arbitrary, su E( X t <. t Assumtion 8. Define the following function ( µ(x, θ Y(θ ; τ θ = µ(x, θ τ f (x µ(x, θ π θ (dx assume function Y( ; τ has the unique maximum at θ = θ, where π θ is defined in Remark 4.4. Assumtion 9. For fixed θ, the derivatives l µ(x; θ / x l l f (x/ x l (l =, exist they are continuous in x. For fixed x, l µ(x; θ / θ l exist. Moreover, l µ(x; θ / x l, l f (x/ x l, l µ(x; θ / θ l C( + x C, for l =,,. Assumtion. he matrix µ(x; θ Φ = θ (τ f (x µ(x; θ π θ (dx (9 θ is ositive definite. Remark 4.3. Under Assumtion 5, these exists a solution rocess for the stochastic differential equation the solution is unique. Remark 4.4. Under Assumtion 6, the rocess X t is ergodic with an invariant robability measure that has density π θ (x = A(θs(x; θτ f (x, for x (l, u with resect to Lebesque measure on (l, u, where A(θ s(x; θ are defined in Assumtion 6. We further assume that X π θ so that X t is a stationary rocess with X t π θ.
8 46 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( heorem 4. (Asymtotics of the Drift Parameter Estimates. Let ˆθ = argmax θ Θ log l AIF (θ with l AIF (θ given by Eq. (8. Suose Assumtions hold, ˆθ θ as. If, in addition,, / (ˆθ θ d N(, Φ, where Φ is given in Eq. ( General diffusions Now we consider the general case where Florens-Zmirou (989 Yoshida (99 are not alicable. Suose data are generated from the following stochastic differential equation dx t = µ(x t ; θ dt + σ (X t; θ db t, ( where θ Θ R θ Θ R. Both µ(, θ σ ( ; θ are time-homogeneous, B-measurable functions on D = (l, u with l < u, where B is the σ -field generated by Borel sets on D. θ is estimated by regressing (4 on (5, giving the extremum estimator in Box II; θ is estimated by ˆθ, defined by Eq. (7. As in the scalar factor arameter case, we show that an infinite time san (i.e. is not needed to develo the asymtotic theory for ˆθ. Some additional assumtions are required, given the nonlinear deendence of the diffusion σ (X t ; θ on θ. Also we have to modify some earlier Assumtions listed in Section 4.. Assumtion. he equation [X] t t σ (X s ; θ ds = t t has a unique solution at θ, t >. σ (X s ; θ ds σ (X s ; θ ds = ( Assumtion. inf x J σ (x; θ >, where J is a comact subset of the range of the rocess. Assumtion 4. θ Θ, θ Θ, where arameter saces Θ R k Θ R k are comact set with θ Int(Θ θ Int(Θ. Assumtion 5. Both µ( ; θ σ ( ; θ functions are twice continuously differentiable. As a result, for any comact subset J of the range of the rocess, we have the following two conditions: (i (Lischitz condition here exists a constant L so that µ(x; θ µ(y; θ + σ (x; θ σ (y; θ L x y, for all x y in J. (ii (Growth condition here exists a constant L so that µ(x; θ + σ (x; θ L + x, for all x y in J. Assumtion 6. Define the scale measure of X t by ( x µ(y; θ s(x; θ = ex σ (y; θ dy, c where c is a generic constant. We assume the following condition holds u c s(x; θdx = c l s(x; θdx =, u dx = A(θ <. s(x; θσ (x; θ l Assumtion 8. Define the following function θ Y(θ ; θ = µ(x, θ σ (x; θ ( µ(x, θ µ(x, θ assume Y( ; θ has the unique maximum at θ = θ. π θ (dx Assumtion 9. For fixed θ, the derivatives l µ(x; θ / x l l σ (x; θ / x l (l =, exist they are continuous in x. For fixed x, l µ(x; θ / θ l l σ (x; θ / θ l exist. Moreover, l µ(x; θ / x l, l σ (x; θ / x l, l µ(x; θ / θ l, l σ (x; θ / θ l C( + x C, for l =,,. Assumtion. he matrices µ(x; θ Φ = σ (x; θ θ µ(x; θ θ π θ (dx t σ ( ( X s ; θ σ Xs ; θ θ θ ds ( are ositive definite t σ 4 ( X s ; θ ds > for all t >. heorem 4.3. (Asymtotics of the Diffusion Parameter Estimate: Suose Assumtions hold. hen, ˆθ θ as σ (ˆθ / θ d (X s ;θ σ (X s ;θ (k θ θ ds σ ( 4 X (k s ; θ ds σ (X s ;θ (k θ σ ( X s ; θ dws σ (, 4 X (k s ; θ ds where W t is a Brownian motion which is indeendent of X t. heorem 4.4 (Asymtotics of the Drift Parameter Estimate. Let ˆθ = argmax log l AIF (θ with l AIF (θ given by Eq. (7. Suose Assumtions hold, then ˆθ θ as. If, in addition,, / (ˆθ θ d N(, Φ, where Φ is given in Eq. (. 5. Monte Carlo results o examine the erformance of the roosed rocedure, we estimate the following model for short-term interest rates due to Chan et al. (99, CLS hereafter, dx t = κ(µ X t dt + σ X γ t db t, (3 with κ =.6, µ =.9, σ =.6, γ =.5. We choose γ =.5 so that the true model becomes a CIR model which enables an exact data simulation. he arameters are estimated from years of daily data (5 observations. he exeriment is relicated times to get the means stard errors for each estimate. wo estimation methods are emloyed to estimate
9 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( able 3 Simulation results under the CLS model, dx t = κ(µ X t dt + σ X γ t db t, based on samles of 5 daily observations. rue values for κ, µ, σ, γ are.6,.9,.6,.5. Mean SD st for the average stard deviation across relications, resectively. AML wo-stage method = = = = 5 = Level Log Level Log Level Log Level Log Level Log γ Mean SD σ Mean SD κ Mean SD µ Mean SD the model: the aroximate ML method of Aït-Sahalia ( the roosed two-stage method. For the two-stage method, we imlement it based on both levels log levels, resectively. o use the two-stage methods, the number of subsamles has to be chosen. here is a trade-off between a large a small. On the one h, since determines the number of observations used for the nonlinear regression, a larger will generate more variation in [X] k [X] (k across subsamles hence rovide more accurate estimation of the arameters in the diffusion function. On the other h, if is too big, M will M be too small for (X (k M +i X (k M +(i to rovide a good aroximation to [X] k [X] (k, as Figs. 3 suggested. In the Monte Carlo study, we choose various values for, namely,,, 5. hese values corresond to 5, 5, 5, 5 5 for M, resectively. he simulation results are reorted in able 3. Several interesting results emerge from this table. First, the simulation results clearly indicate a trade-off between a large a small. When is, the variance is big for the two arameters in the diffusion function, indicating that the nonlinear least regression does not lead to accurate estimation to the diffusion arameters. he erformance of the rocedure imroves substantially when. However, when is large, a further increase in fails to imrove the finite samle erformance. For examle, for the two-stage method based on log-levels, the variances of the two diffusion arameters are slightly larger when = than those when = 5. Second, the estimation of arameters in the drift function does not seem to be deendent on the diffusion arameters in any critical way. his is because the information matrix for the diffusion arameters is orthogonal to that for the drift arameters in the CLS model. hirdly, when a reasonable value for is used, the quadratic variations are well estimated. Not surrisingly, therefore, our estimates are close to the aroximate ML method of Aït-Sahalia (. Finally, we note that the two-stage method based on log levels has better finite samle erformances than that based on levels, esecially when is large ( hence M is small, consistent with the finding in Barndorff-Nielsen Shehard (5. 6. Microstructure contamination Direct alication of the two-stage method roosed above requires that X t be observed. his assumtion may be too strong for ultra high frequency data because of the resence of various market microstructure effects which contaminate X t with noise, roducing bias inconsistency in realized volatility estimates. As a consequence, our two-stage rocedure has to be modified We thank a referee for ointing this out to us. in order to roduce consistent estimates of the arameters in the diffusion function. Suose the noise is orthogonal to X t indeendent identically distributed over the grid (,,..., n, i.e. Y i = X i + e i, (4 e i e j, i j e i X i, i, (5 with zero mean E (e i = ( finite variance E ei = σ, i. In the resence of market microstructure noise such as e i, we observed Y i instead of X i. While the ure noise assumtion (5 lacks realism, as discussed in Phillis Yu (6, it is commonly adoted in the literature as it simlifies identification econometric analysis see, for examle, Bi Russell (5, Hansen Lunde (6, Barndorff-Nielsen et al. (5 Zhang et al. (5. It is easy to show that as, the M realized volatility quantity (Y (k M +i Y (k M +(i diverges, making estimation in the first stage inconsistent. o rovide a consistent estimate of the quadratic variation differential [X] k [X] (k, one can use the realized kernel estimator of Barndorff-Nielsen et al. (5, the two-scale estimator of Zhang et al. (5, or the multi-scale estimator of Zhang (6. While these rocedures converge to the quadratic variation at slower rates than realized volatility in the absence of microstructure noise, they nonetheless rovide consistent nonarametric estimators of the required quantity can be emloyed to estimate the arameters in the diffusion function using the nonlinear regression, recisely as used above. Aït-Sahalia et al. (6 generalized the two-scale rocedure to cover time deendent noise this generalization can also be adoted in the first ste of our two-stage method in the same sirit. he asymtotic roerties of the resulting estimator may be extracted along lines similar to those used here, with consequential changes in the rate of convergence. he results are obviously of interest will rovide an aroach to continuous system estimation in the resence of noise. he details will be rovided in subsequent work. 7. Concluding remarks his aer rooses a two-stage method to estimate diffusion rocesses in a general form. In the first stage the realized volatility calculated from a sequence of slit samles is regressed on the corresonding quadratic variation in order to estimate all the arameters in the diffusion function. hen, conditional on the resulting consistent estimate of the diffusion, the infill likelihood function aroximation of the diffusion rocess can be readily constructed. he resulting discrete aroximation roduces estimates of all the arameters in the drift function. Monte Carlo simulations show that the finite samle erformance of the roosed method is very satisfactory as good
10 48 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( as conventional maximum likelihood even when the discrete likelihood can be obtained. One advantage of the roosed method is that a larger scale otimization roblem is decomosed into two smaller scale otimization roblems. Although, like other extreme estimators, our method tends to over estimate the mean reversion arameter, κ, the numerical attractability of our method makes it an ideal initial estimate for the jackknife method of Phillis Yu (5 or the simulation-based methods of Phillis Yu (in ress-b reduce the finite samle bias in κ. here exist alternative two-ste rocedures to estimate diffusion rocesses. For examle, in Bi Phillis (7, nonarametric estimates of the drift diffusion functions are matched with the arametric counterarts to rovide consistent estimation of arameters in the drift in the diffusion, resectively. One can certainly use our first ste estimate (i.e. via realized volatility in lace of the diffusion estimate (i.e. via kernel functions in the rocedure of Bi Phillis (7. he aroach can be readily extended to the multi-dimensional case. Both imlementation asymtotic theory only need trivial modifications. Since the method searates estimation of the drift diffusion functions, it may be a desirable method to use when the drift but not the diffusion involves certain market microstructure features. he two-ste aroach can be also adated to deal with the following diffusion model mixed with jums: dx t = µ(x t ; θ dt + σ (X t ; θ db t + f (X t ; θ 3 dz θ 3 t, where Z θ 3 t is a Lévy rocess with arameter θ 3. For this model realized volatility cannot be used to consistently estimate θ as it does not converge to σ (X t ; θ dt. However, emirical triower variation does converge to σ (X t ; θ dt. Barndorff-Nielsen Shehard et al. (6 obtained a central limit theorem for the triower variation rocess when a diffusion rocess is mixed with finite activity jums. Since the in-fill likelihood is readily available for jum-diffusion rocesses once the diffusion term is known, we can adot the following two-ste rocedure to estimate the model: first, use triower variation to estimate θ ; then, maximize the aroximated in-fill likelihood with resect to θ θ 3. he roerties of the resulting estimator will be reorted in future work. Aendix Proof of heorem 4.. It is known that all diffusion-tye rocesses are semi-martingales (Prakasa Rao, 999b. As a result, when, [X ] [X] = τ f (X s ds, where the convergence follows from the theory of quadratic variation for semi-martingales the equality follows from Assumtion. By Assumtion 3, we have ˆτ = n i= [X ] f (X (i [X] f (X s ds = τ. his roves the first art of heorem 4.. Since X t is a semi-martingale, by Ito s lemma for semimartinagles (Prakasa Rao, 999b we have X = [X] + X s dx s. Following heorem of Barndorff-Nielsen Shehard ( we have / ([X ] [X] d τ f (X s dw s, (6 where W t is a Brownian motion which is indeendent of X t. Hence, / (ˆτ τ = / = / f (X s ds By Assumtion 3, n i= f (X (i f (X s ds. n i= n i= [X ] f (X (i [X] f (X s ds f (X s ds [X ] [X]. (7 f (X (i By Slutsky s theorem, Eqs. (6 (7 imly that / (ˆτ τ d τ f (X s dw s. (8 f (X s ds his comletes the roof of heorem 4.. Proof of heorem 4.. Obviously, the roosed drift estimator is in the class of extremum estimators. Hence, one can rove consistency by checking sufficient conditions for extremum estimation roblems. It is convenient here to check the conditions given in Newey McFadden (994,., namely, comactness, continuity, uniform convergence, identifiability. Comactness of Θ, continuity of log l AIF (θ ; ˆτ the identification condition are assured by Assumtion, Assumtion 9 Assumtion 8, resectively. he uniform convergence of log l AIF (θ to Y(θ, τ follows from Proosition, Lemma Lemma in Yoshida (99. Hence the first art of the theorem is roved. o show asymtotic normality, we follow Yoshida (99 by obtaining the weak convergence of the likelihood ratio rom field, Z,n (τ, u = l AIF (θ + / u; ˆτ/l AIF (θ ; ˆτ. Under the listed conditions, Yoshida (99 showed that log Z,n (τ, u = u / i (i n i= µ(x; θ θ τ f (X (i τ f (xdw t u Φu + ρ,n (u, (9 where ρ,n (u Φ is defined in Eq. (9. From heorem 4., we have, η >, that there exists a a ositive number c such that P( / (ˆτ τ > c < η/. Let ˆτ = τ + / M we have, ɛ > P( log Z,n (ˆτ, u log Z,n (τ, u > ɛ = P( / (ˆτ τ > c + P( su M c log Z,n (ˆτ, u log Z,n (τ, u > ɛ < η. (3
11 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( where ˆθ = arg min θ Q (θ, Q (θ = { (X(k M +i X (k M +(i σ ( } X (k M +(i ; θ Box III. ( Q θ = 3/ θ 3/ = / g { i (X (k M +i X (k M +(i σ ( } X (k M +(i ; θ g i r k { (X(k M +i X (k M +(i σ ( X (k M +(i ; θ } Box IV. r k Combining Eqs. (9 (3 roves Proosition 4 of Yoshida (99. Similarly, we can obtain Proosition 5 6 of Yoshida (99 based on ˆτ. he week convergence of the likelihood rom field follows these roositions. In articular, / (ˆθ θ d N(, Φ. his comletes the roof of heorem 4.. Proof of heorem 4.3. he argument is briefly sketched here. We consider the case where the estimate ˆθ is obtained from the extremum estimation roblem suggested by the first equation in Box II. A similar argument can be emloyed in the case where stardized log levels of realized volatility are used in the regression based on the CL result suggested by the third limit in Box I. Observe that, as, Q (θ Q (θ { σ ( } X (k s ; θ k ds σ (X (k s ; θ ds = uniformly in θ, since σ ( 4 X (k s ; θ M (X (k M +i X (k M +(i [X] k [X] (k = (k σ ( X s ; θ ds, ds, M σ ( k X (k M +(i ; θ σ (X s ; θ ds, (3 (k uniformly in θ Θ in view of the comactness of Θ the smoothness of σ (X s ; θ. Next, r k = 3 M (X (k M +i X (k M +(i 4 σ ( 4 X s ; θ (k ds, (3 as in Barndorff-Nielsen Shehard (. hus, since Q (θ is minimized for θ = θ in view of (, we have ˆθ θ by a stard extremum estimator argument. Next, by a aylor series argument under the stated smoothness ositive definiteness assumtions, we have (ˆθ / θ = [ ( ] Q ( θ Q θ θ θ 3/ θ [ ( Q θ θ θ ] [ Q 3/ θ ( θ ], (33 where θ is on the line segment connecting ˆθ to θ thus satisfies θ θ. Setting g i = ( g X (k M +(i ; θ σ ( X (k M +(i ; θ =, θ we get the equation in Box IV, in view of heorem of Barndorff-Nielsen Shehard (, / M g i { (X(k M +i X (k M +(i σ ( X (k M +(i ; θ } d (k σ ( X s ; θ σ ( X s ; θ dws (34 θ where W s is a stard Brownian motion indeendent of X t. It follows from (3, (34 Box IV that Q 3/ θ ( θ Next we have ( Q θ θ θ d σ (X s ;θ (k θ σ ( X s ; θ dws σ (. (35 4 X (k s ; θ ds g i g i r k
12 5 P.C.B. Phillis, J. Yu / Journal of Econometrics 5 ( = = g i g i (k r k (k σ (X s ;θ θ σ (X s ;θ θ σ ( 4 X (k s ; θ ds σ (X s ;θ σ (X s ;θ θ θ σ ( 4 X (k s ; θ Combining (33, (35 (36 we obtain σ (ˆθ / θ d (X s ;θ (k σ ( 4 X (k s ; θ ds σ (X s ;θ (k θ σ ( X s ; θ dws σ (, 4 X (k s ; θ ds as stated. ds ds ds. (36 θ σ (X s ;θ θ ds Proof of heorem 4.4. he roof follows similar lines to the roof of heorem 4. is therefore omitted. References Ahn, D., Gao, B., 999. A arametric nonlinear model of term structure dynamics. Review of Financial Studies, Aït-Sahalia, Y., 999. ransition densities for interest rate other nonlinear diffusions. Journal of Finance 54, Aït-Sahalia, Y.,. Maximum likelihood estimation of discretely samled diffusion: A closed-form aroximation aroach. Econometrica 7, 3 6. Aït-Sahalia, Y., Mykl, P.A., Zhang, L., 5. How often to samle a continuoustime rocess in the resence of market microstructure noise. Review of Financial Studies 8, Aït-Sahalia, Y., Mykl, P.A., Zhang, L., 6. Ultra high-frequency volatility estimation with deendent microstructure noise. Working Paer, Princeton University. Bi, F.M., Russell, J., 5. Microstructure noise, realized volatility, otimal samling. Working aer, Graduate School of Business, University of Chicago. Bi, F.M., Phillis, P.C.B., 3. Fully nonarametric estimation of scalar diffusion models. Econometrica 7, Bi, F.M., Phillis, P.C.B., 7. A simle aroach to the arametric estimation of otentially nonstationary diffusions. Journal of Econometrics 37, Barndorff-Nielsen, O., Graversen, S.E., Jacod, J., Shehard, N., 6. Limit theorems for biower variation in financial econometrics. Econometric heory, Barndorff-Nielsen, O., Hansen, P., Lunde, A., Shehard, N., 5. Designing realized kernels to measure the ex-ost variation of equity rices in the resence of noise. Working aer, Nuffield College. Barndorff-Nielsen, O., Shehard, N.,. Econometric analysis of realized volatility its use in estimating stochastic volatility models. Journal of the Royal Statistical Society. Series B 64, Barndorff-Nielsen, O., Shehard, N., 3. Realized ower variation stochastic volatility. Bernoulli 9, Barndorff-Nielsen, O., Shehard, N., 5. How accurate is the asymtotic aroximation to the distribution of realized volatility? In: Andrews, D.W.., Powell, J., Ruud, P., Stock, J. (Eds., Identification Inference for Econometric Models. Cambridge University Press. Barndorff-Nielsen, O., Shehard, N., Winkel, M., 6. Limit theorems for multiower variation in the resence of jums in financial econometrics. Stochastic Processes Alications 6, Billingsley, P., 96. Statistical Inference for Markov Processes. University of Chicago Press, Chicago, US. Bollerslev,., Zhou, H.,. Estimating stochastic volatility diffusion using conditional moments of integrated volatility. Journal of Econometrics 9, Brt, M.W., Santa-Clara, P.,. Simulated likelihood estimation of diffusions with an alication to exchange rate dynamics in incomlete markets. Journal of Financial Economics 3, 6. Chan,.C., arolyi, G.A., Longstaff, F.A., Sers, A.B., 99. An emirical comarison of alternative models of short term interest rates. Journal of Finance 47, 9 7. Cox, J., Ingersoll, J., Ross, S., 985. A theory of the term structure of interest rates. Econometrica 53, Dixit, A., 993. he Art of Smooth Pasting. Harwood Academic Publishers, Readings, U. Elerian, O., Chib, S., Shehard, N.,. Likelihood inference for discretely observed non-linear diffusions. Econometrica 69, Eraker, B.,. MCMC analysis of diffusion models with alication to finance. Journal of Business Economic Statistics 9, Florens-Zmirou, D., 989. Aroximate discrete-time schemes for statistics of diffusion rocesses. Statistics, Hansen, P., Lunde, A., 6. Realized volatility market microstructure noise. Journal of Business Economic Statistics 4, 7 6. Hutton, J.E., Nelson, P., 986. Quasi-likelihood estimation for semimartingales. Stochastic Processes their Alications, Jacod, J., 994. Limit of rom measures associated with the increments of a Brownian semiartingal. Working aer, Laboratoire de Probabilities, Universite Pierre et Marie Curie, Paris. Jacod, J., Protter, P., 998. Asymtotic error distributions for the Euler method for stochastic differential equations. Annals of Probabilities 6, Lánska, V., 979. Minimum contrast estimation in diffusion rocesses. Journal of Alied Probability 6, Litser, R.S., Shiryaev, A.N.,. Statistics of Rom Processes. Sringer-Verlag, New York. Lo, Andrew W., 988. Maximum likelihood estimation of generalized Itô rocesses with discretely samled data. Econometric heory 4, Merton, R.C., 98. On estimating the exected return on the market: An exloratory investigation. Journal of Financial Economics 8, Merton, R.C., 99. Continuous-ime Finance. Blackwell, Oxford. Newey, W.., McFadden, D., 994. Large samle estimation hyothesis testing. In: Engle, R.F., McFadden, D. (Eds., Hbook of Econometrics, vol. 4. North- Holl, Amsterdam. Nowman,.B., 997. Gaussian estimation of single-factor continuous time models of the term structure of interest rates. Journal of Finance 5, Pedersen, A., 995. A new aroach to maximum likelihood estimation for stochastic differential equations based on discrete observation. Scinavian Journal of Statistics, Phillis, P.C.B., 97. he structural estimation of a stochastic differential equation system. Econometrica 4, 4. Phillis, P.C.B., Yu, J., 5. Jackknifing bond otion rices. Review of Financial Studies 8, Phillis, P.C.B., Yu, J., 6. Maximum likelihood Gaussian estimation of continuous time models in finance. Hbook of Financial ime Series (in ress-a. Phillis, P.C.B., Yu, J., 6. Realized variance market microstructure noise Comment. Journal of Business Economic Statistics 4, 8. Phillis, P.C.B., Yu, J., 8. Simulation-based estimation of contingent-claims rices. Review of Financial Studies (in ress-b. Prakasa Rao, B.L.S., 999a. Statistical Inference for Diffusion ye Processes. Arnold, London. Prakasa Rao, B.L.S., 999b. Semimartingales their Statistical Inference. Chaman Hall, Boca Raton, Florida. Vasicek, O., 977. An equilibrium characterization of the term structure. Journal of Financial Economics 5, Yoshida, N., 99. Estimation for diffusion rocesses from discrete observation. Journal of Multivariate Analysis 4, 4. Yu, J., Phillis, P.C.B.,. A Gaussion aroach for estimating continuous time models of short term interest rates. he Econometrics Journal 4, 5. Zhang, L., 6. Efficient estimation of stochastic volatility using noise observations: A multi-scale aroach. Bernoulli, Zhang, L., Mykl, P.A., Aït-Sahalia, Y., 5. A tale of two time scales: Determining integrated volatility with noisy high-frequency data. Journal of the American Statistical Association,
Supplemental Material: Buyer-Optimal Learning and Monopoly Pricing
 Sulemental Material: Buyer-Otimal Learning and Monooly Pricing Anne-Katrin Roesler and Balázs Szentes February 3, 207 The goal of this note is to characterize buyer-otimal outcomes with minimal learning
Sulemental Material: Buyer-Otimal Learning and Monooly Pricing Anne-Katrin Roesler and Balázs Szentes February 3, 207 The goal of this note is to characterize buyer-otimal outcomes with minimal learning
A Semi-parametric Test for Drift Speci cation in the Di usion Model
 A Semi-arametric est for Drift Seci cation in the Di usion Model Lin hu Indiana University Aril 3, 29 Abstract In this aer, we roose a misseci cation test for the drift coe cient in a semi-arametric di
A Semi-arametric est for Drift Seci cation in the Di usion Model Lin hu Indiana University Aril 3, 29 Abstract In this aer, we roose a misseci cation test for the drift coe cient in a semi-arametric di
Confidence Intervals for a Proportion Using Inverse Sampling when the Data is Subject to False-positive Misclassification
 Journal of Data Science 13(015), 63-636 Confidence Intervals for a Proortion Using Inverse Samling when the Data is Subject to False-ositive Misclassification Kent Riggs 1 1 Deartment of Mathematics and
Journal of Data Science 13(015), 63-636 Confidence Intervals for a Proortion Using Inverse Samling when the Data is Subject to False-ositive Misclassification Kent Riggs 1 1 Deartment of Mathematics and
Information and uncertainty in a queueing system
 Information and uncertainty in a queueing system Refael Hassin December 7, 7 Abstract This aer deals with the effect of information and uncertainty on rofits in an unobservable single server queueing system.
Information and uncertainty in a queueing system Refael Hassin December 7, 7 Abstract This aer deals with the effect of information and uncertainty on rofits in an unobservable single server queueing system.
Brownian Motion, the Gaussian Lévy Process
 Brownian Motion, the Gaussian Lévy Process Deconstructing Brownian Motion: My construction of Brownian motion is based on an idea of Lévy s; and in order to exlain Lévy s idea, I will begin with the following
Brownian Motion, the Gaussian Lévy Process Deconstructing Brownian Motion: My construction of Brownian motion is based on an idea of Lévy s; and in order to exlain Lévy s idea, I will begin with the following
Statistics and Probability Letters. Variance stabilizing transformations of Poisson, binomial and negative binomial distributions
 Statistics and Probability Letters 79 (9) 6 69 Contents lists available at ScienceDirect Statistics and Probability Letters journal homeage: www.elsevier.com/locate/staro Variance stabilizing transformations
Statistics and Probability Letters 79 (9) 6 69 Contents lists available at ScienceDirect Statistics and Probability Letters journal homeage: www.elsevier.com/locate/staro Variance stabilizing transformations
Worst-case evaluation complexity for unconstrained nonlinear optimization using high-order regularized models
 Worst-case evaluation comlexity for unconstrained nonlinear otimization using high-order regularized models E. G. Birgin, J. L. Gardenghi, J. M. Martínez, S. A. Santos and Ph. L. Toint 2 Aril 26 Abstract
Worst-case evaluation comlexity for unconstrained nonlinear otimization using high-order regularized models E. G. Birgin, J. L. Gardenghi, J. M. Martínez, S. A. Santos and Ph. L. Toint 2 Aril 26 Abstract
A NOTE ON SKEW-NORMAL DISTRIBUTION APPROXIMATION TO THE NEGATIVE BINOMAL DISTRIBUTION
 A NOTE ON SKEW-NORMAL DISTRIBUTION APPROXIMATION TO THE NEGATIVE BINOMAL DISTRIBUTION JYH-JIUAN LIN 1, CHING-HUI CHANG * AND ROSEMARY JOU 1 Deartment of Statistics Tamkang University 151 Ying-Chuan Road,
A NOTE ON SKEW-NORMAL DISTRIBUTION APPROXIMATION TO THE NEGATIVE BINOMAL DISTRIBUTION JYH-JIUAN LIN 1, CHING-HUI CHANG * AND ROSEMARY JOU 1 Deartment of Statistics Tamkang University 151 Ying-Chuan Road,
ON JARQUE-BERA TESTS FOR ASSESSING MULTIVARIATE NORMALITY
 Journal of Statistics: Advances in Theory and Alications Volume, umber, 009, Pages 07-0 O JARQUE-BERA TESTS FOR ASSESSIG MULTIVARIATE ORMALITY KAZUYUKI KOIZUMI, AOYA OKAMOTO and TAKASHI SEO Deartment of
Journal of Statistics: Advances in Theory and Alications Volume, umber, 009, Pages 07-0 O JARQUE-BERA TESTS FOR ASSESSIG MULTIVARIATE ORMALITY KAZUYUKI KOIZUMI, AOYA OKAMOTO and TAKASHI SEO Deartment of
SINGLE SAMPLING PLAN FOR VARIABLES UNDER MEASUREMENT ERROR FOR NON-NORMAL DISTRIBUTION
 ISSN -58 (Paer) ISSN 5-5 (Online) Vol., No.9, SINGLE SAMPLING PLAN FOR VARIABLES UNDER MEASUREMENT ERROR FOR NON-NORMAL DISTRIBUTION Dr. ketki kulkarni Jayee University of Engineering and Technology Guna
ISSN -58 (Paer) ISSN 5-5 (Online) Vol., No.9, SINGLE SAMPLING PLAN FOR VARIABLES UNDER MEASUREMENT ERROR FOR NON-NORMAL DISTRIBUTION Dr. ketki kulkarni Jayee University of Engineering and Technology Guna
Effects of Size and Allocation Method on Stock Portfolio Performance: A Simulation Study
 2011 3rd International Conference on Information and Financial Engineering IPEDR vol.12 (2011) (2011) IACSIT Press, Singaore Effects of Size and Allocation Method on Stock Portfolio Performance: A Simulation
2011 3rd International Conference on Information and Financial Engineering IPEDR vol.12 (2011) (2011) IACSIT Press, Singaore Effects of Size and Allocation Method on Stock Portfolio Performance: A Simulation
Limit Theorems for the Empirical Distribution Function of Scaled Increments of Itô Semimartingales at high frequencies
 Limit Theorems for the Empirical Distribution Function of Scaled Increments of Itô Semimartingales at high frequencies George Tauchen Duke University Viktor Todorov Northwestern University 2013 Motivation
Limit Theorems for the Empirical Distribution Function of Scaled Increments of Itô Semimartingales at high frequencies George Tauchen Duke University Viktor Todorov Northwestern University 2013 Motivation
Capital Budgeting: The Valuation of Unusual, Irregular, or Extraordinary Cash Flows
 Caital Budgeting: The Valuation of Unusual, Irregular, or Extraordinary Cash Flows ichael C. Ehrhardt Philli R. Daves Finance Deartment, SC 424 University of Tennessee Knoxville, TN 37996-0540 423-974-1717
Caital Budgeting: The Valuation of Unusual, Irregular, or Extraordinary Cash Flows ichael C. Ehrhardt Philli R. Daves Finance Deartment, SC 424 University of Tennessee Knoxville, TN 37996-0540 423-974-1717
A note on the existence of unique equivalent martingale measures in a Markovian setting
 Finance Stochast. 1, 251 257 1997 c Springer-Verlag 1997 A note on the existence of unique equivalent martingale measures in a Markovian setting Tina Hviid Rydberg University of Aarhus, Department of Theoretical
Finance Stochast. 1, 251 257 1997 c Springer-Verlag 1997 A note on the existence of unique equivalent martingale measures in a Markovian setting Tina Hviid Rydberg University of Aarhus, Department of Theoretical
Non-Inferiority Tests for the Ratio of Two Correlated Proportions
 Chater 161 Non-Inferiority Tests for the Ratio of Two Correlated Proortions Introduction This module comutes ower and samle size for non-inferiority tests of the ratio in which two dichotomous resonses
Chater 161 Non-Inferiority Tests for the Ratio of Two Correlated Proortions Introduction This module comutes ower and samle size for non-inferiority tests of the ratio in which two dichotomous resonses
INDEX NUMBERS. Introduction
 INDEX NUMBERS Introduction Index numbers are the indicators which reflect changes over a secified eriod of time in rices of different commodities industrial roduction (iii) sales (iv) imorts and exorts
INDEX NUMBERS Introduction Index numbers are the indicators which reflect changes over a secified eriod of time in rices of different commodities industrial roduction (iii) sales (iv) imorts and exorts
A Multi-Objective Approach to Portfolio Optimization
 RoseHulman Undergraduate Mathematics Journal Volume 8 Issue Article 2 A MultiObjective Aroach to Portfolio Otimization Yaoyao Clare Duan Boston College, sweetclare@gmail.com Follow this and additional
RoseHulman Undergraduate Mathematics Journal Volume 8 Issue Article 2 A MultiObjective Aroach to Portfolio Otimization Yaoyao Clare Duan Boston College, sweetclare@gmail.com Follow this and additional
Parameter estimation of diffusion models from discrete observations
 221 Parameter estimation of diffusion models from discrete observations Miljenko Huzak Abstract. A short review of diffusion parameter estimations methods from discrete observations is presented. The applicability
221 Parameter estimation of diffusion models from discrete observations Miljenko Huzak Abstract. A short review of diffusion parameter estimations methods from discrete observations is presented. The applicability
Central Limit Theorem for the Realized Volatility based on Tick Time Sampling. Masaaki Fukasawa. University of Tokyo
 Central Limit Theorem for the Realized Volatility based on Tick Time Sampling Masaaki Fukasawa University of Tokyo 1 An outline of this talk is as follows. What is the Realized Volatility (RV)? Known facts
Central Limit Theorem for the Realized Volatility based on Tick Time Sampling Masaaki Fukasawa University of Tokyo 1 An outline of this talk is as follows. What is the Realized Volatility (RV)? Known facts
Sharpe Ratios and Alphas in Continuous Time
 JOURNAL OF FINANCIAL AND QUANTITATIVE ANALYSIS VOL. 39, NO. 1, MARCH 2004 COPYRIGHT 2004, SCHOOL OF BUSINESS ADMINISTRATION, UNIVERSITY OF WASHINGTON, SEATTLE, WA 98195 Share Ratios and Alhas in Continuous
JOURNAL OF FINANCIAL AND QUANTITATIVE ANALYSIS VOL. 39, NO. 1, MARCH 2004 COPYRIGHT 2004, SCHOOL OF BUSINESS ADMINISTRATION, UNIVERSITY OF WASHINGTON, SEATTLE, WA 98195 Share Ratios and Alhas in Continuous
2/20/2013. of Manchester. The University COMP Building a yes / no classifier
 COMP4 Lecture 6 Building a yes / no classifier Buildinga feature-basedclassifier Whatis a classifier? What is an information feature? Building a classifier from one feature Probability densities and the
COMP4 Lecture 6 Building a yes / no classifier Buildinga feature-basedclassifier Whatis a classifier? What is an information feature? Building a classifier from one feature Probability densities and the
SUBORDINATION BY ORTHOGONAL MARTINGALES IN L p, 1 < p Introduction: Orthogonal martingales and the Beurling-Ahlfors transform
 SUBORDINATION BY ORTHOGONAL MARTINGALES IN L, 1 < PRABHU JANAKIRAMAN AND ALEXANDER VOLBERG 1. Introduction: Orthogonal martingales and the Beurling-Ahlfors transform We are given two martingales on the
SUBORDINATION BY ORTHOGONAL MARTINGALES IN L, 1 < PRABHU JANAKIRAMAN AND ALEXANDER VOLBERG 1. Introduction: Orthogonal martingales and the Beurling-Ahlfors transform We are given two martingales on the
Application of Monte-Carlo Tree Search to Traveling-Salesman Problem
 R4-14 SASIMI 2016 Proceedings Alication of Monte-Carlo Tree Search to Traveling-Salesman Problem Masato Shimomura Yasuhiro Takashima Faculty of Environmental Engineering University of Kitakyushu Kitakyushu,
R4-14 SASIMI 2016 Proceedings Alication of Monte-Carlo Tree Search to Traveling-Salesman Problem Masato Shimomura Yasuhiro Takashima Faculty of Environmental Engineering University of Kitakyushu Kitakyushu,
Sampling Procedure for Performance-Based Road Maintenance Evaluations
 Samling Procedure for Performance-Based Road Maintenance Evaluations Jesus M. de la Garza, Juan C. Piñero, and Mehmet E. Ozbek Maintaining the road infrastructure at a high level of condition with generally
Samling Procedure for Performance-Based Road Maintenance Evaluations Jesus M. de la Garza, Juan C. Piñero, and Mehmet E. Ozbek Maintaining the road infrastructure at a high level of condition with generally
A Comparative Study of Various Loss Functions in the Economic Tolerance Design
 A Comarative Study of Various Loss Functions in the Economic Tolerance Design Jeh-Nan Pan Deartment of Statistics National Chen-Kung University, Tainan, Taiwan 700, ROC Jianbiao Pan Deartment of Industrial
A Comarative Study of Various Loss Functions in the Economic Tolerance Design Jeh-Nan Pan Deartment of Statistics National Chen-Kung University, Tainan, Taiwan 700, ROC Jianbiao Pan Deartment of Industrial
AMH4 - ADVANCED OPTION PRICING. Contents
 AMH4 - ADVANCED OPTION PRICING ANDREW TULLOCH Contents 1. Theory of Option Pricing 2 2. Black-Scholes PDE Method 4 3. Martingale method 4 4. Monte Carlo methods 5 4.1. Method of antithetic variances 5
AMH4 - ADVANCED OPTION PRICING ANDREW TULLOCH Contents 1. Theory of Option Pricing 2 2. Black-Scholes PDE Method 4 3. Martingale method 4 4. Monte Carlo methods 5 4.1. Method of antithetic variances 5
Modeling and Estimating a Higher Systematic Co-Moment Asset Pricing Model in the Brazilian Stock Market. Autoria: Andre Luiz Carvalhal da Silva
 Modeling and Estimating a Higher Systematic Co-Moment Asset Pricing Model in the Brazilian Stock Market Autoria: Andre Luiz Carvalhal da Silva Abstract Many asset ricing models assume that only the second-order
Modeling and Estimating a Higher Systematic Co-Moment Asset Pricing Model in the Brazilian Stock Market Autoria: Andre Luiz Carvalhal da Silva Abstract Many asset ricing models assume that only the second-order
Buyer-Optimal Learning and Monopoly Pricing
 Buyer-Otimal Learning and Monooly Pricing Anne-Katrin Roesler and Balázs Szentes January 2, 217 Abstract This aer analyzes a bilateral trade model where the buyer s valuation for the object is uncertain
Buyer-Otimal Learning and Monooly Pricing Anne-Katrin Roesler and Balázs Szentes January 2, 217 Abstract This aer analyzes a bilateral trade model where the buyer s valuation for the object is uncertain
Midterm Exam: Tuesday 28 March in class Sample exam problems ( Homework 5 ) available tomorrow at the latest
 Plan Martingales 1. Basic Definitions 2. Examles 3. Overview of Results Reading: G&S Section 12.1-12.4 Next Time: More Martingales Midterm Exam: Tuesday 28 March in class Samle exam roblems ( Homework
Plan Martingales 1. Basic Definitions 2. Examles 3. Overview of Results Reading: G&S Section 12.1-12.4 Next Time: More Martingales Midterm Exam: Tuesday 28 March in class Samle exam roblems ( Homework
Asian Economic and Financial Review A MODEL FOR ESTIMATING THE DISTRIBUTION OF FUTURE POPULATION. Ben David Nissim.
 Asian Economic and Financial Review journal homeage: htt://www.aessweb.com/journals/5 A MODEL FOR ESTIMATING THE DISTRIBUTION OF FUTURE POPULATION Ben David Nissim Deartment of Economics and Management,
Asian Economic and Financial Review journal homeage: htt://www.aessweb.com/journals/5 A MODEL FOR ESTIMATING THE DISTRIBUTION OF FUTURE POPULATION Ben David Nissim Deartment of Economics and Management,
Quantitative Aggregate Effects of Asymmetric Information
 Quantitative Aggregate Effects of Asymmetric Information Pablo Kurlat February 2012 In this note I roose a calibration of the model in Kurlat (forthcoming) to try to assess the otential magnitude of the
Quantitative Aggregate Effects of Asymmetric Information Pablo Kurlat February 2012 In this note I roose a calibration of the model in Kurlat (forthcoming) to try to assess the otential magnitude of the
Math 416/516: Stochastic Simulation
 Math 416/516: Stochastic Simulation Haijun Li lih@math.wsu.edu Department of Mathematics Washington State University Week 13 Haijun Li Math 416/516: Stochastic Simulation Week 13 1 / 28 Outline 1 Simulation
Math 416/516: Stochastic Simulation Haijun Li lih@math.wsu.edu Department of Mathematics Washington State University Week 13 Haijun Li Math 416/516: Stochastic Simulation Week 13 1 / 28 Outline 1 Simulation
Testing for a Unit Root with Near-Integrated Volatility
 Testing for a Unit Root with Near-Integrated Volatility H. Peter Boswijk Department of Quantitative Economics, University of Amsterdam y January Abstract This paper considers tests for a unit root when
Testing for a Unit Root with Near-Integrated Volatility H. Peter Boswijk Department of Quantitative Economics, University of Amsterdam y January Abstract This paper considers tests for a unit root when
MODELLING 1-MONTH EURIBOR INTEREST RATE BY USING DIFFERENTIAL EQUATIONS WITH UNCERTAINTY
 Applied Mathematical and Computational Sciences Volume 7, Issue 3, 015, Pages 37-50 015 Mili Publications MODELLING 1-MONTH EURIBOR INTEREST RATE BY USING DIFFERENTIAL EQUATIONS WITH UNCERTAINTY J. C.
Applied Mathematical and Computational Sciences Volume 7, Issue 3, 015, Pages 37-50 015 Mili Publications MODELLING 1-MONTH EURIBOR INTEREST RATE BY USING DIFFERENTIAL EQUATIONS WITH UNCERTAINTY J. C.
Appendix Large Homogeneous Portfolio Approximation
 Aendix Large Homogeneous Portfolio Aroximation A.1 The Gaussian One-Factor Model and the LHP Aroximation In the Gaussian one-factor model, an obligor is assumed to default if the value of its creditworthiness
Aendix Large Homogeneous Portfolio Aroximation A.1 The Gaussian One-Factor Model and the LHP Aroximation In the Gaussian one-factor model, an obligor is assumed to default if the value of its creditworthiness
IEOR E4703: Monte-Carlo Simulation
 IEOR E4703: Monte-Carlo Simulation Simulating Stochastic Differential Equations Martin Haugh Department of Industrial Engineering and Operations Research Columbia University Email: martin.b.haugh@gmail.com
IEOR E4703: Monte-Carlo Simulation Simulating Stochastic Differential Equations Martin Haugh Department of Industrial Engineering and Operations Research Columbia University Email: martin.b.haugh@gmail.com
U. Carlos III de Madrid CEMFI. Meeting of the BIS Network on Banking and Asset Management Basel, 9 September 2014
 Search hfor Yield David Martinez-MieraMiera Rafael Reullo U. Carlos III de Madrid CEMFI Meeting of the BIS Network on Banking and Asset Management Basel, 9 Setember 2014 Motivation (i) Over the ast decade
Search hfor Yield David Martinez-MieraMiera Rafael Reullo U. Carlos III de Madrid CEMFI Meeting of the BIS Network on Banking and Asset Management Basel, 9 Setember 2014 Motivation (i) Over the ast decade
Absolute Return Volatility. JOHN COTTER* University College Dublin
 Absolute Return Volatility JOHN COTTER* University College Dublin Address for Correspondence: Dr. John Cotter, Director of the Centre for Financial Markets, Department of Banking and Finance, University
Absolute Return Volatility JOHN COTTER* University College Dublin Address for Correspondence: Dr. John Cotter, Director of the Centre for Financial Markets, Department of Banking and Finance, University
Risk Neutral Modelling Exercises
 Risk Neutral Modelling Exercises Geneviève Gauthier Exercise.. Assume that the rice evolution of a given asset satis es dx t = t X t dt + X t dw t where t = ( + sin (t)) and W = fw t : t g is a (; F; P)
Risk Neutral Modelling Exercises Geneviève Gauthier Exercise.. Assume that the rice evolution of a given asset satis es dx t = t X t dt + X t dw t where t = ( + sin (t)) and W = fw t : t g is a (; F; P)
508-B (Statistics Camp, Wash U, Summer 2016) Asymptotics. Author: Andrés Hincapié and Linyi Cao. This Version: August 9, 2016
 Asymtotics Author: Anrés Hincaié an Linyi Cao This Version: August 9, 2016 Asymtotics 3 In arametric moels, we usually assume that the oulation follows some istribution F (x θ) with unknown θ. Knowing
Asymtotics Author: Anrés Hincaié an Linyi Cao This Version: August 9, 2016 Asymtotics 3 In arametric moels, we usually assume that the oulation follows some istribution F (x θ) with unknown θ. Knowing
On the Power of Structural Violations in Priority Queues
 On the Power of Structural Violations in Priority Queues Amr Elmasry 1, Claus Jensen 2, Jyrki Katajainen 2, 1 Comuter Science Deartment, Alexandria University Alexandria, Egyt 2 Deartment of Comuting,
On the Power of Structural Violations in Priority Queues Amr Elmasry 1, Claus Jensen 2, Jyrki Katajainen 2, 1 Comuter Science Deartment, Alexandria University Alexandria, Egyt 2 Deartment of Comuting,
A GAUSSIAN APPROACH FOR CONTINUOUS TIME MODELS OF THE SHORT-TERM INTEREST RATE JUN YU AND PETER C. B. PHILLIPS COWLES FOUNDATION PAPER NO.
 A GAUSSIAN APPROACH FOR CONTINUOUS TIME MODELS OF THE SHORT-TERM INTEREST RATE BY JUN YU AND PETER C. B. PHILLIPS COWLES FOUNDATION PAPER NO. 1124 COWLES FOUNDATION FOR RESEARCH IN ECONOMICS YALE UNIVERSITY
A GAUSSIAN APPROACH FOR CONTINUOUS TIME MODELS OF THE SHORT-TERM INTEREST RATE BY JUN YU AND PETER C. B. PHILLIPS COWLES FOUNDATION PAPER NO. 1124 COWLES FOUNDATION FOR RESEARCH IN ECONOMICS YALE UNIVERSITY
LECTURE NOTES ON MICROECONOMICS
 LECTURE NOTES ON MCROECONOMCS ANALYZNG MARKETS WTH BASC CALCULUS William M. Boal Part : Consumers and demand Chater 5: Demand Section 5.: ndividual demand functions Determinants of choice. As noted in
LECTURE NOTES ON MCROECONOMCS ANALYZNG MARKETS WTH BASC CALCULUS William M. Boal Part : Consumers and demand Chater 5: Demand Section 5.: ndividual demand functions Determinants of choice. As noted in
Volatility. Roberto Renò. 2 March 2010 / Scuola Normale Superiore. Dipartimento di Economia Politica Università di Siena
 Dipartimento di Economia Politica Università di Siena 2 March 2010 / Scuola Normale Superiore What is? The definition of volatility may vary wildly around the idea of the standard deviation of price movements
Dipartimento di Economia Politica Università di Siena 2 March 2010 / Scuola Normale Superiore What is? The definition of volatility may vary wildly around the idea of the standard deviation of price movements
Revisiting the risk-return relation in the South African stock market
 Revisiting the risk-return relation in the South African stock market Author F. Darrat, Ali, Li, Bin, Wu, Leqin Published 0 Journal Title African Journal of Business Management Coyright Statement 0 Academic
Revisiting the risk-return relation in the South African stock market Author F. Darrat, Ali, Li, Bin, Wu, Leqin Published 0 Journal Title African Journal of Business Management Coyright Statement 0 Academic
Estimation of dynamic term structure models
 Estimation of dynamic term structure models Greg Duffee Haas School of Business, UC-Berkeley Joint with Richard Stanton, Haas School Presentation at IMA Workshop, May 2004 (full paper at http://faculty.haas.berkeley.edu/duffee)
Estimation of dynamic term structure models Greg Duffee Haas School of Business, UC-Berkeley Joint with Richard Stanton, Haas School Presentation at IMA Workshop, May 2004 (full paper at http://faculty.haas.berkeley.edu/duffee)
Optimally Thresholded Realized Power Variations for Lévy Jump Diffusion Models
 Optimally Thresholded Realized Power Variations for Lévy Jump Diffusion Models José E. Figueroa-López 1 1 Department of Statistics Purdue University University of Missouri-Kansas City Department of Mathematics
Optimally Thresholded Realized Power Variations for Lévy Jump Diffusion Models José E. Figueroa-López 1 1 Department of Statistics Purdue University University of Missouri-Kansas City Department of Mathematics
Causal Links between Foreign Direct Investment and Economic Growth in Egypt
 J I B F Research Science Press Causal Links between Foreign Direct Investment and Economic Growth in Egyt TAREK GHALWASH* Abstract: The main objective of this aer is to study the causal relationshi between
J I B F Research Science Press Causal Links between Foreign Direct Investment and Economic Growth in Egyt TAREK GHALWASH* Abstract: The main objective of this aer is to study the causal relationshi between
Stochastic Dynamical Systems and SDE s. An Informal Introduction
 Stochastic Dynamical Systems and SDE s An Informal Introduction Olav Kallenberg Graduate Student Seminar, April 18, 2012 1 / 33 2 / 33 Simple recursion: Deterministic system, discrete time x n+1 = f (x
Stochastic Dynamical Systems and SDE s An Informal Introduction Olav Kallenberg Graduate Student Seminar, April 18, 2012 1 / 33 2 / 33 Simple recursion: Deterministic system, discrete time x n+1 = f (x
Dr. Maddah ENMG 625 Financial Eng g II 10/16/06. Chapter 11 Models of Asset Dynamics (1)
 Dr Maddah ENMG 65 Financial Eng g II 0/6/06 Chater Models of Asset Dynamics () Overview Stock rice evolution over time is commonly modeled with one of two rocesses: The binomial lattice and geometric Brownian
Dr Maddah ENMG 65 Financial Eng g II 0/6/06 Chater Models of Asset Dynamics () Overview Stock rice evolution over time is commonly modeled with one of two rocesses: The binomial lattice and geometric Brownian
Model Estimation. Liuren Wu. Fall, Zicklin School of Business, Baruch College. Liuren Wu Model Estimation Option Pricing, Fall, / 16
 Model Estimation Liuren Wu Zicklin School of Business, Baruch College Fall, 2007 Liuren Wu Model Estimation Option Pricing, Fall, 2007 1 / 16 Outline 1 Statistical dynamics 2 Risk-neutral dynamics 3 Joint
Model Estimation Liuren Wu Zicklin School of Business, Baruch College Fall, 2007 Liuren Wu Model Estimation Option Pricing, Fall, 2007 1 / 16 Outline 1 Statistical dynamics 2 Risk-neutral dynamics 3 Joint
Solving dynamic portfolio choice problems by recursing on optimized portfolio weights or on the value function?
 DOI 0.007/s064-006-9073-z ORIGINAL PAPER Solving dynamic portfolio choice problems by recursing on optimized portfolio weights or on the value function? Jules H. van Binsbergen Michael W. Brandt Received:
DOI 0.007/s064-006-9073-z ORIGINAL PAPER Solving dynamic portfolio choice problems by recursing on optimized portfolio weights or on the value function? Jules H. van Binsbergen Michael W. Brandt Received:
A TRAJECTORIAL INTERPRETATION OF DOOB S MARTINGALE INEQUALITIES
 A RAJECORIAL INERPREAION OF DOOB S MARINGALE INEQUALIIES B. ACCIAIO, M. BEIGLBÖCK, F. PENKNER, W. SCHACHERMAYER, AND J. EMME Abstract. We resent a unified aroach to Doob s L maximal inequalities for 1
A RAJECORIAL INERPREAION OF DOOB S MARINGALE INEQUALIIES B. ACCIAIO, M. BEIGLBÖCK, F. PENKNER, W. SCHACHERMAYER, AND J. EMME Abstract. We resent a unified aroach to Doob s L maximal inequalities for 1
Pricing Dynamic Solvency Insurance and Investment Fund Protection
 Pricing Dynamic Solvency Insurance and Investment Fund Protection Hans U. Gerber and Gérard Pafumi Switzerland Abstract In the first part of the paper the surplus of a company is modelled by a Wiener process.
Pricing Dynamic Solvency Insurance and Investment Fund Protection Hans U. Gerber and Gérard Pafumi Switzerland Abstract In the first part of the paper the surplus of a company is modelled by a Wiener process.
Forward Vertical Integration: The Fixed-Proportion Case Revisited. Abstract
 Forward Vertical Integration: The Fixed-roortion Case Revisited Olivier Bonroy GAEL, INRA-ierre Mendès France University Bruno Larue CRÉA, Laval University Abstract Assuming a fixed-roortion downstream
Forward Vertical Integration: The Fixed-roortion Case Revisited Olivier Bonroy GAEL, INRA-ierre Mendès France University Bruno Larue CRÉA, Laval University Abstract Assuming a fixed-roortion downstream
Estimation of High-Frequency Volatility: An Autoregressive Conditional Duration Approach
 Estimation of High-Frequency Volatility: An Autoregressive Conditional Duration Approach Yiu-Kuen Tse School of Economics, Singapore Management University Thomas Tao Yang Department of Economics, Boston
Estimation of High-Frequency Volatility: An Autoregressive Conditional Duration Approach Yiu-Kuen Tse School of Economics, Singapore Management University Thomas Tao Yang Department of Economics, Boston
"Pricing Exotic Options using Strong Convergence Properties
 Fourth Oxford / Princeton Workshop on Financial Mathematics "Pricing Exotic Options using Strong Convergence Properties Klaus E. Schmitz Abe schmitz@maths.ox.ac.uk www.maths.ox.ac.uk/~schmitz Prof. Mike
Fourth Oxford / Princeton Workshop on Financial Mathematics "Pricing Exotic Options using Strong Convergence Properties Klaus E. Schmitz Abe schmitz@maths.ox.ac.uk www.maths.ox.ac.uk/~schmitz Prof. Mike
A COMPARISON AMONG PERFORMANCE MEASURES IN PORTFOLIO THEORY
 A COMPARISON AMONG PERFORMANCE MEASURES IN PORFOLIO HEORY Sergio Ortobelli * Almira Biglova ** Stoyan Stoyanov *** Svetlozar Rachev **** Frank Fabozzi * University of Bergamo Italy ** University of Karlsruhe
A COMPARISON AMONG PERFORMANCE MEASURES IN PORFOLIO HEORY Sergio Ortobelli * Almira Biglova ** Stoyan Stoyanov *** Svetlozar Rachev **** Frank Fabozzi * University of Bergamo Italy ** University of Karlsruhe
Maximize the Sharpe Ratio and Minimize a VaR 1
 Maximize the Share Ratio and Minimize a VaR 1 Robert B. Durand 2 Hedieh Jafarour 3,4 Claudia Klüelberg 5 Ross Maller 6 Aril 28, 2008 Abstract In addition to its role as the otimal ex ante combination of
Maximize the Share Ratio and Minimize a VaR 1 Robert B. Durand 2 Hedieh Jafarour 3,4 Claudia Klüelberg 5 Ross Maller 6 Aril 28, 2008 Abstract In addition to its role as the otimal ex ante combination of
STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL
 STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL YOUNGGEUN YOO Abstract. Ito s lemma is often used in Ito calculus to find the differentials of a stochastic process that depends on time. This paper will introduce
STOCHASTIC CALCULUS AND BLACK-SCHOLES MODEL YOUNGGEUN YOO Abstract. Ito s lemma is often used in Ito calculus to find the differentials of a stochastic process that depends on time. This paper will introduce
Weierstrass Institute for Applied Analysis and Stochastics Maximum likelihood estimation for jump diffusions
 Weierstrass Institute for Applied Analysis and Stochastics Maximum likelihood estimation for jump diffusions Hilmar Mai Mohrenstrasse 39 1117 Berlin Germany Tel. +49 3 2372 www.wias-berlin.de Haindorf
Weierstrass Institute for Applied Analysis and Stochastics Maximum likelihood estimation for jump diffusions Hilmar Mai Mohrenstrasse 39 1117 Berlin Germany Tel. +49 3 2372 www.wias-berlin.de Haindorf
A GENERALISED PRICE-SCORING MODEL FOR TENDER EVALUATION
 019-026 rice scoring 9/20/05 12:12 PM Page 19 A GENERALISED PRICE-SCORING MODEL FOR TENDER EVALUATION Thum Peng Chew BE (Hons), M Eng Sc, FIEM, P. Eng, MIEEE ABSTRACT This aer rooses a generalised rice-scoring
019-026 rice scoring 9/20/05 12:12 PM Page 19 A GENERALISED PRICE-SCORING MODEL FOR TENDER EVALUATION Thum Peng Chew BE (Hons), M Eng Sc, FIEM, P. Eng, MIEEE ABSTRACT This aer rooses a generalised rice-scoring
Optimum Thresholding for Semimartingales with Lévy Jumps under the mean-square error
 Optimum Thresholding for Semimartingales with Lévy Jumps under the mean-square error José E. Figueroa-López Department of Mathematics Washington University in St. Louis Spring Central Sectional Meeting
Optimum Thresholding for Semimartingales with Lévy Jumps under the mean-square error José E. Figueroa-López Department of Mathematics Washington University in St. Louis Spring Central Sectional Meeting
IEOR E4703: Monte-Carlo Simulation
 IEOR E4703: Monte-Carlo Simulation Other Miscellaneous Topics and Applications of Monte-Carlo Martin Haugh Department of Industrial Engineering and Operations Research Columbia University Email: martin.b.haugh@gmail.com
IEOR E4703: Monte-Carlo Simulation Other Miscellaneous Topics and Applications of Monte-Carlo Martin Haugh Department of Industrial Engineering and Operations Research Columbia University Email: martin.b.haugh@gmail.com
A random variable X is a function that assigns (real) numbers to the elements of the sample space S of a random experiment.
 RANDOM VARIABLES and PROBABILITY DISTRIBUTIONS A random variable X is a function that assigns (real) numbers to the elements of the samle sace S of a random exeriment. The value sace V of a random variable
RANDOM VARIABLES and PROBABILITY DISTRIBUTIONS A random variable X is a function that assigns (real) numbers to the elements of the samle sace S of a random exeriment. The value sace V of a random variable
Ultra High Frequency Volatility Estimation with Market Microstructure Noise. Yacine Aït-Sahalia. Per A. Mykland. Lan Zhang
 Ultra High Frequency Volatility Estimation with Market Microstructure Noise Yacine Aït-Sahalia Princeton University Per A. Mykland The University of Chicago Lan Zhang Carnegie-Mellon University 1. Introduction
Ultra High Frequency Volatility Estimation with Market Microstructure Noise Yacine Aït-Sahalia Princeton University Per A. Mykland The University of Chicago Lan Zhang Carnegie-Mellon University 1. Introduction
CS522 - Exotic and Path-Dependent Options
 CS522 - Exotic and Path-Deendent Otions Tibor Jánosi May 5, 2005 0. Other Otion Tyes We have studied extensively Euroean and American uts and calls. The class of otions is much larger, however. A digital
CS522 - Exotic and Path-Deendent Otions Tibor Jánosi May 5, 2005 0. Other Otion Tyes We have studied extensively Euroean and American uts and calls. The class of otions is much larger, however. A digital
Online Robustness Appendix to Are Household Surveys Like Tax Forms: Evidence from the Self Employed
 Online Robustness Aendix to Are Household Surveys Like Tax Forms: Evidence from the Self Emloyed October 01 Erik Hurst University of Chicago Geng Li Board of Governors of the Federal Reserve System Benjamin
Online Robustness Aendix to Are Household Surveys Like Tax Forms: Evidence from the Self Emloyed October 01 Erik Hurst University of Chicago Geng Li Board of Governors of the Federal Reserve System Benjamin
Evaluating an Alternative Risk Preference in Affine Term Structure Models
 Evaluating an Alternative Risk Preference in Affine Term Structure Models Jefferson Duarte University of Washington and IBMEC Dai and Singleton (2002) and Duffee (2002) show that there is a tension in
Evaluating an Alternative Risk Preference in Affine Term Structure Models Jefferson Duarte University of Washington and IBMEC Dai and Singleton (2002) and Duffee (2002) show that there is a tension in
Application of MCMC Algorithm in Interest Rate Modeling
 Application of MCMC Algorithm in Interest Rate Modeling Xiaoxia Feng and Dejun Xie Abstract Interest rate modeling is a challenging but important problem in financial econometrics. This work is concerned
Application of MCMC Algorithm in Interest Rate Modeling Xiaoxia Feng and Dejun Xie Abstract Interest rate modeling is a challenging but important problem in financial econometrics. This work is concerned
Comments on Hansen and Lunde
 Comments on Hansen and Lunde Eric Ghysels Arthur Sinko This Draft: September 5, 2005 Department of Finance, Kenan-Flagler School of Business and Department of Economics University of North Carolina, Gardner
Comments on Hansen and Lunde Eric Ghysels Arthur Sinko This Draft: September 5, 2005 Department of Finance, Kenan-Flagler School of Business and Department of Economics University of North Carolina, Gardner
TESTING THE CAPITAL ASSET PRICING MODEL AFTER CURRENCY REFORM: THE CASE OF ZIMBABWE STOCK EXCHANGE
 TESTING THE CAPITAL ASSET PRICING MODEL AFTER CURRENCY REFORM: THE CASE OF ZIMBABWE STOCK EXCHANGE Batsirai Winmore Mazviona 1 ABSTRACT The Caital Asset Pricing Model (CAPM) endeavors to exlain the relationshi
TESTING THE CAPITAL ASSET PRICING MODEL AFTER CURRENCY REFORM: THE CASE OF ZIMBABWE STOCK EXCHANGE Batsirai Winmore Mazviona 1 ABSTRACT The Caital Asset Pricing Model (CAPM) endeavors to exlain the relationshi
Price Gap and Welfare
 APPENDIX D Price Ga and Welfare Derivation of the Price-Ga Formula This aendix details the derivation of the rice-ga formula (see chaters 2 and 5) under two assumtions: (1) the simlest case, where there
APPENDIX D Price Ga and Welfare Derivation of the Price-Ga Formula This aendix details the derivation of the rice-ga formula (see chaters 2 and 5) under two assumtions: (1) the simlest case, where there
: now we have a family of utility functions for wealth increments z indexed by initial wealth w.
 Lotteries with Money Payoffs, continued Fix u, let w denote wealth, and set u ( z) u( z w) : now we have a family of utility functions for wealth increments z indexed by initial wealth w. (a) Recall from
Lotteries with Money Payoffs, continued Fix u, let w denote wealth, and set u ( z) u( z w) : now we have a family of utility functions for wealth increments z indexed by initial wealth w. (a) Recall from
We connect the mix-flexibility and dual-sourcing literatures by studying unreliable supply chains that produce
 MANUFACTURING & SERVICE OPERATIONS MANAGEMENT Vol. 7, No. 1, Winter 25,. 37 57 issn 1523-4614 eissn 1526-5498 5 71 37 informs doi 1.1287/msom.14.63 25 INFORMS On the Value of Mix Flexibility and Dual Sourcing
MANUFACTURING & SERVICE OPERATIONS MANAGEMENT Vol. 7, No. 1, Winter 25,. 37 57 issn 1523-4614 eissn 1526-5498 5 71 37 informs doi 1.1287/msom.14.63 25 INFORMS On the Value of Mix Flexibility and Dual Sourcing
Short-Time Asymptotic Methods in Financial Mathematics
 Short-Time Asymptotic Methods in Financial Mathematics José E. Figueroa-López Department of Mathematics Washington University in St. Louis Probability and Mathematical Finance Seminar Department of Mathematical
Short-Time Asymptotic Methods in Financial Mathematics José E. Figueroa-López Department of Mathematics Washington University in St. Louis Probability and Mathematical Finance Seminar Department of Mathematical
Monetary policy is a controversial
 Inflation Persistence: How Much Can We Exlain? PAU RABANAL AND JUAN F. RUBIO-RAMÍREZ Rabanal is an economist in the monetary and financial systems deartment at the International Monetary Fund in Washington,
Inflation Persistence: How Much Can We Exlain? PAU RABANAL AND JUAN F. RUBIO-RAMÍREZ Rabanal is an economist in the monetary and financial systems deartment at the International Monetary Fund in Washington,
Professor Huihua NIE, PhD School of Economics, Renmin University of China HOLD-UP, PROPERTY RIGHTS AND REPUTATION
 Professor uihua NIE, PhD School of Economics, Renmin University of China E-mail: niehuihua@gmail.com OD-UP, PROPERTY RIGTS AND REPUTATION Abstract: By introducing asymmetric information of investors abilities
Professor uihua NIE, PhD School of Economics, Renmin University of China E-mail: niehuihua@gmail.com OD-UP, PROPERTY RIGTS AND REPUTATION Abstract: By introducing asymmetric information of investors abilities
Worst-case evaluation complexity of regularization methods for smooth unconstrained optimization using Hölder continuous gradients
 Worst-case evaluation comlexity of regularization methods for smooth unconstrained otimization using Hölder continuous gradients C Cartis N I M Gould and Ph L Toint 26 June 205 Abstract The worst-case
Worst-case evaluation comlexity of regularization methods for smooth unconstrained otimization using Hölder continuous gradients C Cartis N I M Gould and Ph L Toint 26 June 205 Abstract The worst-case
1.1 Basic Financial Derivatives: Forward Contracts and Options
 Chapter 1 Preliminaries 1.1 Basic Financial Derivatives: Forward Contracts and Options A derivative is a financial instrument whose value depends on the values of other, more basic underlying variables
Chapter 1 Preliminaries 1.1 Basic Financial Derivatives: Forward Contracts and Options A derivative is a financial instrument whose value depends on the values of other, more basic underlying variables
DRAFT. 1 exercise in state (S, t), π(s, t) = 0 do not exercise in state (S, t) Review of the Risk Neutral Stock Dynamics
 Chapter 12 American Put Option Recall that the American option has strike K and maturity T and gives the holder the right to exercise at any time in [0, T ]. The American option is not straightforward
Chapter 12 American Put Option Recall that the American option has strike K and maturity T and gives the holder the right to exercise at any time in [0, T ]. The American option is not straightforward
Annex 4 - Poverty Predictors: Estimation and Algorithm for Computing Predicted Welfare Function
 Annex 4 - Poverty Predictors: Estimation and Algorithm for Comuting Predicted Welfare Function The Core Welfare Indicator Questionnaire (CWIQ) is an off-the-shelf survey ackage develoed by the World Bank
Annex 4 - Poverty Predictors: Estimation and Algorithm for Comuting Predicted Welfare Function The Core Welfare Indicator Questionnaire (CWIQ) is an off-the-shelf survey ackage develoed by the World Bank
A Stochastic Model of Optimal Debt Management and Bankruptcy
 A Stochastic Model of Otimal Debt Management and Bankrutcy Alberto Bressan (, Antonio Marigonda (, Khai T. Nguyen (, and Michele Palladino ( (* Deartment of Mathematics, Penn State University University
A Stochastic Model of Otimal Debt Management and Bankrutcy Alberto Bressan (, Antonio Marigonda (, Khai T. Nguyen (, and Michele Palladino ( (* Deartment of Mathematics, Penn State University University
Exact Sampling of Jump-Diffusion Processes
 1 Exact Sampling of Jump-Diffusion Processes and Dmitry Smelov Management Science & Engineering Stanford University Exact Sampling of Jump-Diffusion Processes 2 Jump-Diffusion Processes Ubiquitous in finance
1 Exact Sampling of Jump-Diffusion Processes and Dmitry Smelov Management Science & Engineering Stanford University Exact Sampling of Jump-Diffusion Processes 2 Jump-Diffusion Processes Ubiquitous in finance
Risk, Return, and Ross Recovery
 Risk, Return, and Ross Recovery Peter Carr and Jiming Yu Courant Institute, New York University September 13, 2012 Carr/Yu (NYU Courant) Risk, Return, and Ross Recovery September 13, 2012 1 / 30 P, Q,
Risk, Return, and Ross Recovery Peter Carr and Jiming Yu Courant Institute, New York University September 13, 2012 Carr/Yu (NYU Courant) Risk, Return, and Ross Recovery September 13, 2012 1 / 30 P, Q,
SOME APPLICATIONS OF OCCUPATION TIMES OF BROWNIAN MOTION WITH DRIFT IN MATHEMATICAL FINANCE
 c Applied Mathematics & Decision Sciences, 31, 63 73 1999 Reprints Available directly from the Editor. Printed in New Zealand. SOME APPLICAIONS OF OCCUPAION IMES OF BROWNIAN MOION WIH DRIF IN MAHEMAICAL
c Applied Mathematics & Decision Sciences, 31, 63 73 1999 Reprints Available directly from the Editor. Printed in New Zealand. SOME APPLICAIONS OF OCCUPAION IMES OF BROWNIAN MOION WIH DRIF IN MAHEMAICAL
Martingale Pricing Theory in Discrete-Time and Discrete-Space Models
 IEOR E4707: Foundations of Financial Engineering c 206 by Martin Haugh Martingale Pricing Theory in Discrete-Time and Discrete-Space Models These notes develop the theory of martingale pricing in a discrete-time,
IEOR E4707: Foundations of Financial Engineering c 206 by Martin Haugh Martingale Pricing Theory in Discrete-Time and Discrete-Space Models These notes develop the theory of martingale pricing in a discrete-time,
Chapter 1: Stochastic Processes
 Chater 1: Stochastic Processes 4 What are Stochastic Processes, and how do they fit in? STATS 210 Foundations of Statistics and Probability Tools for understanding randomness (random variables, distributions)
Chater 1: Stochastic Processes 4 What are Stochastic Processes, and how do they fit in? STATS 210 Foundations of Statistics and Probability Tools for understanding randomness (random variables, distributions)
No-arbitrage theorem for multi-factor uncertain stock model with floating interest rate
 Fuzzy Optim Decis Making 217 16:221 234 DOI 117/s17-16-9246-8 No-arbitrage theorem for multi-factor uncertain stock model with floating interest rate Xiaoyu Ji 1 Hua Ke 2 Published online: 17 May 216 Springer
Fuzzy Optim Decis Making 217 16:221 234 DOI 117/s17-16-9246-8 No-arbitrage theorem for multi-factor uncertain stock model with floating interest rate Xiaoyu Ji 1 Hua Ke 2 Published online: 17 May 216 Springer
The value of foresight
 Philip Ernst Department of Statistics, Rice University Support from NSF-DMS-1811936 (co-pi F. Viens) and ONR-N00014-18-1-2192 gratefully acknowledged. IMA Financial and Economic Applications June 11, 2018
Philip Ernst Department of Statistics, Rice University Support from NSF-DMS-1811936 (co-pi F. Viens) and ONR-N00014-18-1-2192 gratefully acknowledged. IMA Financial and Economic Applications June 11, 2018
Summary of the Chief Features of Alternative Asset Pricing Theories
 Summary o the Chie Features o Alternative Asset Pricing Theories CAP and its extensions The undamental equation o CAP ertains to the exected rate o return time eriod into the uture o any security r r β
Summary o the Chie Features o Alternative Asset Pricing Theories CAP and its extensions The undamental equation o CAP ertains to the exected rate o return time eriod into the uture o any security r r β
Semimartingales and their Statistical Inference
 Semimartingales and their Statistical Inference B.L.S. Prakasa Rao Indian Statistical Institute New Delhi, India CHAPMAN & HALL/CRC Boca Raten London New York Washington, D.C. Contents Preface xi 1 Semimartingales
Semimartingales and their Statistical Inference B.L.S. Prakasa Rao Indian Statistical Institute New Delhi, India CHAPMAN & HALL/CRC Boca Raten London New York Washington, D.C. Contents Preface xi 1 Semimartingales
LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives
 Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Weierstrass Institute for Applied Analysis and Stochastics LIBOR models, multi-curve extensions, and the pricing of callable structured derivatives John Schoenmakers 9th Summer School in Mathematical Finance
Parameter estimation in SDE:s
 Lund University Faculty of Engineering Statistics in Finance Centre for Mathematical Sciences, Mathematical Statistics HT 2011 Parameter estimation in SDE:s This computer exercise concerns some estimation
Lund University Faculty of Engineering Statistics in Finance Centre for Mathematical Sciences, Mathematical Statistics HT 2011 Parameter estimation in SDE:s This computer exercise concerns some estimation
Objectives. 3.3 Toward statistical inference
 Objectives 3.3 Toward statistical inference Poulation versus samle (CIS, Chater 6) Toward statistical inference Samling variability Further reading: htt://onlinestatbook.com/2/estimation/characteristics.html
Objectives 3.3 Toward statistical inference Poulation versus samle (CIS, Chater 6) Toward statistical inference Samling variability Further reading: htt://onlinestatbook.com/2/estimation/characteristics.html
Analysis on Mergers and Acquisitions (M&A) Game Theory of Petroleum Group Corporation
 DOI: 10.14355/ijams.2014.0301.03 Analysis on Mergers and Acquisitions (M&A) Game Theory of Petroleum Grou Cororation Minchang Xin 1, Yanbin Sun 2 1,2 Economic and Management Institute, Northeast Petroleum
DOI: 10.14355/ijams.2014.0301.03 Analysis on Mergers and Acquisitions (M&A) Game Theory of Petroleum Grou Cororation Minchang Xin 1, Yanbin Sun 2 1,2 Economic and Management Institute, Northeast Petroleum
The Impact of Flexibility And Capacity Allocation On The Performance of Primary Care Practices
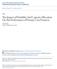 University of Massachusetts Amherst ScholarWorks@UMass Amherst Masters Theses 1911 - February 2014 2010 The Imact of Flexibility And Caacity Allocation On The Performance of Primary Care Practices Liang
University of Massachusetts Amherst ScholarWorks@UMass Amherst Masters Theses 1911 - February 2014 2010 The Imact of Flexibility And Caacity Allocation On The Performance of Primary Care Practices Liang
A Simple Approach to CAPM and Option Pricing. Riccardo Cesari and Carlo D Adda (University of Bologna)
 A imple Approach to CA and Option ricing Riccardo Cesari and Carlo D Adda (University of Bologna) rcesari@economia.unibo.it dadda@spbo.unibo.it eptember, 001 eywords: asset pricing, CA, option pricing.
A imple Approach to CA and Option ricing Riccardo Cesari and Carlo D Adda (University of Bologna) rcesari@economia.unibo.it dadda@spbo.unibo.it eptember, 001 eywords: asset pricing, CA, option pricing.
Journal of Banking & Finance
 Journal of Banking & Finance xxx (2010) xxx xxx Contents lists available at ScienceDirect Journal of Banking & Finance journal homeage: www.elsevier.com/locate/jbf How accurate is the square-root-of-time
Journal of Banking & Finance xxx (2010) xxx xxx Contents lists available at ScienceDirect Journal of Banking & Finance journal homeage: www.elsevier.com/locate/jbf How accurate is the square-root-of-time
Int. Statistical Inst.: Proc. 58th World Statistical Congress, 2011, Dublin (Session CPS001) p approach
 Int. Statistical Inst.: Proc. 58th World Statistical Congress, 2011, Dublin (Session CPS001) p.5901 What drives short rate dynamics? approach A functional gradient descent Audrino, Francesco University
Int. Statistical Inst.: Proc. 58th World Statistical Congress, 2011, Dublin (Session CPS001) p.5901 What drives short rate dynamics? approach A functional gradient descent Audrino, Francesco University
