4/8/13. Part 6. Trees (2) Outline. Balanced Search Trees. 2-3 Trees Trees Red-Black Trees AVL Trees. to maximum n. Tree A. Tree B.
|
|
|
- Miles McLaughlin
- 6 years ago
- Views:
Transcription
1 art 6. Trees (2) C 200 Algorithms and Data tructures 1 Outline 2-3 Trees Trees Red-Black Trees AV Trees 2 Balanced earch Trees Tree A Tree B to maximum n Tree D 3 1
2 Balanced earch Trees A search of a binary search tree can be as inefficient as a sequential search of a linked list. Balanced search trees address this problem Insert and delete items without deteriorating the tree s balance while maintaining a minimum-height search tree. A type of binary search tree where costs are guaranteed to be logarithmic search trees A tree in which each internal node (nonleaf) has either two or three children, and all leaves are at the same level. A 2-3 search tree is not a binary tree. 5 Rules for placing items A 2-node (with two children) must contain a single data item whose search key is greater than the left child s search key(s) and less than the right child s search key(s) A 3-node (with three children) must contain two data items whose search keys and satisfy the following relationships. is greater than the left child s search key(s) and less than the middle child s search key(s). is greater than the middle child s search key(s) and less than the right child s search key(s). A leaf may contain either one or two data items. 6 2
3 lacing items in a 2-node earch keys < earch keys > 7 lacing items in a 3-nodes earch keys < < earch keys < earch keys > 8 Traversing a 2-3 tree inorder (in tttree:twothreetree)!!if (tttree s root node r is a leaf){!!!!visit the data item(s)!!}!!else if (r has two data items){!!!!inorder(left subtree of tttree s root)!!!!visit the first data item!!!!inorder(middle subtree of tttree s root)!!!!visit the second data item!!!!inorder(right subtree of tttree s root)!!}!!else {// r has one data item!!!!inorder(left subtree of tttree s root)!!!!visit the data item!!!!inorder(right subtree of tttree s root)!!}! 9 3
4 earching a 2-3 tree (1/2) retrieveitem(in tttree:twothreetree,!!!!! in searchkey:keytype):treeitemtype!!if(searchkey is in tttree s root node r){!!!!treeitem = the data portion of r!!} else if (r is a leaf){!!!!treeitem = null;!!}!!// else search has the appropriate subtree!!else if (r has two data items){!!!!!if (searchkey < smaller search key of r){!!!!!treeitem = retrieveitem(r s left subtree, searchkey)!!!!}else if (searchkey < larger search key of r){!!!!!treeitem = retrieveitem(r s middle subtree, searchkey)!!!!}else {!!!!!treeitem = retrieveitem(r s right subtree, searchkey)!!!!}!!}! }! 10 earching a 2-3 tree (2/2)!// r has only one data item!!else {!!!! if (searchkey < r s searckkey){!!!!!treeitem = retrieveitem(r s left subtree, searchkey)!!!!}else {!!!!!treeitem = retrieveitem(r s right subtree, searchkey)!!!!}!!}! 11 Efficiency A binary search tree with n nodes cannot be shorter than A 2-3 tree with n nodes cannot be taller than A node in a 2-3 tree has at most two items. 12 4
5 Is searching a 2-3 tree is more efficient than a BT? After all, the nodes of a 2-3 tree can have three children horter than the shortest possible binary search tree! ore comparisons for each of the node. (twice the number of comparisons) Approximately equal to the number of comparisons in BT that is as balanced as possible. 13 Why Not Binary earch Tree? If you add new values to balanced BT, you can lose the balance of the tree Then WHY 2-3 trees? The 2-3 tree algorithm will keep the balance of the tree 15 5
6 The insertion algorithm ocate the leaf at which the search for I would terminate. Insert the new item into the leaf I Case 1. If the leaf I contains two items: you are done Case 2. If the leaf I contains three items: must split into n1 and n2. plit Case A: plit a leaf node plit Case B: plit an internal node plit Case C: plit a root node 16 plit Case A: plitting a left leaf node Overcrowded 17 plit Case A: plitting a right leaf node Overcrowded 18 6
7 plit Case B: plitting a left internal node Overcrowded n1 n2 a b a c d b c d e 19 plit Case B: plitting a right leaf node Overcrowded a n1 n2 b c c d d e e 20 plit Case C: plitting the root of a 2-3 tree a b c d 21 7
8 Growing the heights If every node on the path from the root of the tree to the leaf (into which the new item is inserted) contains two items. The recursive process of splitting a node and moving an item up to the node s parent will reach the root r plit r into r1 and r2 Create a new node r with a middle item The new node becomes a new root of the tree 22 Example: Inserting into a 2-3 tree You can insert items into the tree while maintaining its shape. Insert 39, 38, 37, 36, 35, 34, 33, Insert Case 1. node I contains two items Finished
9 Insert Case 2: eaf node became overcrowded plit Case A: ove up the middle one Finished Insert Case is added to a leaf node and the leaf node has two items Finished 26 Insert 36 (1/2) Case 2. eaf node became overcrowded plit case A: ove up the middle one Case 2. Internal node became overcrowded plit case B: Internal node: ove up the middle one 27 9
10 Insert 36 (1/2) Case 2: eaf node became overcrowded plit case A: ove up the middle one Case 2: Internal node became overcrowded plit case B: internal node: ove up the middle one Finished 28 Insert Case 1: 35 is added to a leaf node Finished Insert Case 2: eaf node became overcrowded plit Case A: ove up the middle one Finished
11 Insert Case 1: 33 is added to a leaf node Finished Insert Case 2: eaf node became overcrowded plit Case A: ove up the middle one Case 2: Internal node became overcrowded plit Case B: Internal Node: ove up the middle one Insert Case 2: eaf node became overcrowded plit Case A: ove up the middle one Case 2: Internal node became overcrowded plit Case B: Internal Node: ove up the middle one Case 2: Root node became overcrowded plit Case C: Root: ove up the middle one Finished 33 11
12 insertitem(1/2) insertitem(in tttree, in newitem)! First step: ocate the leafnode I!et skey be the search key of newitem.!!ocate the leaf leafnode in which skey belongs!!add newitem to leafnode!!if (leafnode now has three items){!!!!split(leafnode)!!}! Case 2:eafnode I has 3 items Case 1:eafnode I has 2 items split (inout n:treenode)!!if (n is the root){! plit Case C: split a root node!!!create a new node p!!}!!else{! plit Case A,B: split a leaf/internal node!!!et p be the parent of n!!}!!replace node n with two nodes, n1 and n2, so that p is their parent! Give n1 the item in n with the smallest search-key value!! Give n2 the item in n with the largest search-key value! 34 insertitem(2/2) plit Case B: split an internal node!if (n is not a leaf){!!!!!!n1 becomes the parent of n s two leftmost children!!!!!n2 becomes the parent of n s two right most children!!}!!ove the item in n that has the middle search-key value up to p!!if (p now has three items){!! split(p)! }! Recursive ethod 35 Deletion Algorithm ocate the node n Case 1. Is the node a leaf node? Case 2. Is the node an internal node? Find inorder successor and swap it Deletion will be in the leaf now. Fix case A. If an item will be left in the node: done Fix case B. A. If sibling has two items: redistributing values B. If no sibling has two items: merging a leaf DeleUon begins at a leaf 36 12
13 A. Redistributing Values: If sibling has two items B. erging a eaf : If no sibling has two items Redistributing values and children - - a b c d a b c d 39 13
14 erging internal nodes - - a b c a b c Deleting Root - - Height h Height h- 1 a b c a b c 41 Deleting
15 Deleting 70 : swap with inorder successor Case 2: 70 is NOT a leaf node 43 Deleting 70 : Delete from the leaf Fix Case B: No sibling has two items erge a leaf 44 Deleting 70:oving 80 down Finished Find smallest item in the parent node 45 15
16 Deleting 100-Delete value from leaf Fix Case B: ibling has two item Redistribute values 46 Deleting 100-Does it work? NO Deleting 100-Redistribute Finished
17 Deleting 80: swap with inorder successor Case 2: 80 is NOT a leaf node wap with inorder successor 49 Deleting 80: Delete value from leaf Fix Case 2: No sibling has two items erge a leaf Deleting 80: erge by moving 90 down Recursively called Fix Case 2: No sibling has two items erge an internal node (with children) 51 17
18 Deleting 80: erge down After Deleting 80 Finished High level algorithm (1/2) deleteitem(in tttree:twothreetree in searchkey)!!attempt to locate item theitem whose search key equals searchkey!!if (theitem is present){!!!!if (theitem is not in a leaf){! Find the node!!!! wap item the Item with its inorder successor, which!!!!will be in a leaf theeaf!!!}! Case 2: Is the node an Internal node?!!delete item theitem from leaf theeaf!!!if (theeaf now has no items){!!!!!fix(theeaf)! Recursive call!!!}!!!!return true!!}!!else{!!!!return false!!}! 54 18
19 High level algorithm (1/2) fix(in n:treenode)!!if (n is the root){!!!remove the root!!}else{!!!!et p be the parent of n!!!!if (some sibling of n has two items){! Fix Case A!!! Distribute items appropriately among n,!!!!!!the sibling, and p!!!!!if (n is internal){!!!!!!ove the appropriate child from sibling to n!! }!! }!!!!else {!!!!!Choose an adjacent sibling s of n! Fix Case B!!!!Bring the appropriate item down from p into s!!!!!if (n is internal) {!!!!!!ove n s child to s!!!!!}!!!!!remove node n!!!!!if (p is now empty){!!!!!!fix(p)!!!!!}!!!!}!!}! 55 Outline 2-3 Trees Trees Red-Black Trees AV Trees Trees 2-nodes, 3-nodes, and 4-nodes 4-nodes: nodes that have four children T is a tree of height h if T is empty T is of the form r r r T T R T T T R T T R T T R 57 19
20 Rules for lacing Data Items in the Nodes of a Tree A 2-node must contain a single data item whose search key satisfies the relationship in a 2-3 Tree A 3-node must contain two data items whose search keys satisfy the relationship in a 2-3 Tree A 4-node must contain three data items, whose search keys,, and satisfy the following relationship: 1. left child s search key(s) < < middle-left child s search key(s) 2. middle-left child s search key(s) < < middle-right child s search key(s) 3. middle-right child s search key(s) < < right child s search key(s) 58 A 4-node in a tree earch keys < < earch keys < earch keys > < earch keys < 59 earching and traversing a tree imple extension of the corresponding algorithms for a 2-3 tree Adding comparisons for the 4-node 60 20
21 Inserting into a tree Algorithm is similar to the insertion into a 2-3 tree. 2-3 tree: plit a node by moving one of its items up to its parent node tree: As soon as the search process encounters 4-nodes, it splits the 4-node. 61 Insert While determining the inseruon point, you encounter the 4- node plit by moving the middle value up Keep searching Add Insert
22 Insert Insert While determining the inseruon point, you encounter the 4- node plit by moving the middle value up Keep searching Add Insert
23 Insert While determining the inseruon point, you encounter the 4- node plit by moving the middle value 70 up Keep searching Add Insert plitting a 4-node root during insertion a b c d a b c d 69 23
24 plitting a 4-node whose parent is a 2- node during insertion a b c d e a b c d e 70 plitting a 4-node whose parent is a 3- node during insertion Q e f a b c d Q e a b c d f 71 ocate the node Deleting from tree Eliminates 1-key nodes ulling keys down the tree Goal: key can be removed from a leaf without leaving it empty wap with inorder successor Deletion should be always in the leaf node If the leaf is a 3-node or 4-node, remove item If you ensure that the item you delete does not occur in a 2-node, you can delete the item in one pass through the tree from root to leaf 72 24
25 Rotation for teal key from sibling Note: We cannot teal key from non- adjacent sibling 4/8/13 amgmi ee allickara 73 No adjacent sibling has more than one key teal key from parent - - How is this possible? 4/8/13 amgmi ee allickara 74 If the parent is root and siblings contain only one key 10 erge them as a new root 4/8/13 amgmi ee allickara 75 25
26 Remove /8/13 amgmi ee allickara 76 Running Time A tree with height h has between 2 h-1 and 4 h-1 leaves. If n is the total number of entries (including entries in internal nodes), then n >= 2 h - 1. By taking the logarithm of both sides, we find that h is in O (log n). The time spent visiting a node is typically longer than in a binary search tree because the nodes and the rotation and fusion operations arecomplicated but the time per node is still in O(1). The number of nodes visited is proportional to the height of the tree. Hence, the running times of the search(), insert(), and remove() operations are in O(h) and hence in O(log n), even in the worst case. 4/8/13 amgmi ee allickara and trees 2-3 and trees are easy-to-maintain in balance The reduction in height is offset by the increased number of comparisons that the search algorithm may require at each node. The tree needs only one pass through the tree for its insertion and deletion
27 Trees with ANY children nodes? Tree with many child nodes (e.g. 100 children) requires more comparisons at each node to determine which subtree to search. It is appropriate for external storage. oving from node to node is far more expensive than comparing the data values. 79 Outline 2-3 Trees Trees Red-Black Trees AV Trees 80 Red-Black Trees Represent a tree and retain the advantages of a tree without the storage overhead. Represent each 3-node and 4-node in a tree as an equivalent binary tree. Use red and black child references to distinguish between original 2-nodes, and 2-nodes that were generated from 3-nodes and 4-nodes. 2-nodes from original tree : black 2-nodes those result from splitting 3 and 4- nodes : red 81 27
28 i-clicker Question Ques%on : Is Red- Black tree a balanced Tree? A. Yes. B. No 4/8/13 amgmi ee allickara 82 Red-black representation of a 4-node a b c d a b c d Black reference Red reference 83 Red-black representation of a 3-node OR c a b c Black reference Red reference a a b b c 84 28
29 2-3-4 tree to a Red-black tree tree to a Red-black tree earching and traversing a red-black tree A red-black tree is a binary search tree earch and traverse it with binary search tree algorithms Ignore the color of the references 87 29
30 Inserting into a red-black tree plit each 4-node that you encounter Case 1: 4-node that is a root Case 2: 4-node whose parent is a 2-node Case 3: 4-node whose parent is a 3-node There is no 4-node whose parent is a 4-node. WHY? 88 Inserting Case 1: 4-node that is a root a b c d Black reference Red reference a b c d 89 Inserting Case 2: 4-node whose parent is a 2-node e e a b c d Black reference Red reference a b c d 90
31 Inserting Case 2: 4-node whose parent is a 2-node a a a b c d Black reference Red reference a b c d 91 Inserting Case 3: 4-node whose parent is a 3-node Example 1 Q f Q e e a b c d f a b c d Example 2 92 Inserting Case 3: Example 1 4-node whose parent is a 3-node Color Changes Q Q e f e f a b c d a b c d 93 31
32 Inserting Case 3: Example 2 4-node whose parent is a 3-node e Q f RotaUon and Color Changes WHY? a b c d e Q f a b c d 94 Inserting Case 3: 4-node whose parent is a 3-node a Example 3 Q Q Example 4 f f a b c d e b c d e 95 Inserting Case 3: Example 3 4-node whose parent is a 3-node RotaUon and Color Changes a Q Q f a f b c d e b c d e 96 32
33 Inserting Case 3: Example 4 4-node whose parent is a 3-node Q RotaUon and Color Changes f Q a f b c d e b c d e 97 Inserting Case 3: 4-node whose parent is a 3-node a b Example 5 Q a Example 6 Q b c d e f c d e f 98 Inserting Case 3: Example 5 4-node whose parent is a 3-node a b Q Color Changes a b Q c d e f c d e f 99 33
34 Deleting from a red-black tree This is similar to the deletion algorithm Frequently requires only color changes ore efficient than the corresponding operations on a tree 100 Outline 2-3 Trees Trees Red-Black Trees AV Trees 101 AV Tree Named after its inventors Adelson-Velskii and andis A balanced binary search tree Almost as efficient as a minimum-height binary search tree
35 AV Tree aintains a binary search tree with a height close to the minimum 1. Insert/Delete nodes following the algorithm of the BT. 2. onitor the shape. Determine whether any node in the tree has left and right subtrees whose heights differ by more than If it is not a balanced binary search tree, rotate the tree to rebalance the tree 103 Rotating Tree (1) ingle eft Rotation
36 Before and after a single left rotation that decreases the tree s height h h h + 1 h h h Rotation and Height? (1/2) Ader the rotaung, the height of the tree is reduced 107 Rotation and Height? (2/2) Ader the rotauon, the height of the tree is NOT reduced
37 h Rotations might not affect the tree s height h + 1 h + 1 h h + 1 h Double Rotation: Before Double Rotation: During
38 Double Rotation: After
CSCI 104 B-Trees (2-3, 2-3-4) and Red/Black Trees. Mark Redekopp David Kempe
 1 CSCI 104 B-Trees (2-3, 2-3-4) and Red/Black Trees Mark Redekopp David Kempe 2 An example of B-Trees 2-3 TREES 3 Definition 2-3 Tree is a tree where Non-leaf nodes have 1 value & 2 children or 2 values
1 CSCI 104 B-Trees (2-3, 2-3-4) and Red/Black Trees Mark Redekopp David Kempe 2 An example of B-Trees 2-3 TREES 3 Definition 2-3 Tree is a tree where Non-leaf nodes have 1 value & 2 children or 2 values
AVL Trees. The height of the left subtree can differ from the height of the right subtree by at most 1.
 AVL Trees In order to have a worst case running time for insert and delete operations to be O(log n), we must make it impossible for there to be a very long path in the binary search tree. The first balanced
AVL Trees In order to have a worst case running time for insert and delete operations to be O(log n), we must make it impossible for there to be a very long path in the binary search tree. The first balanced
Successor. CS 361, Lecture 19. Tree-Successor. Outline
 Successor CS 361, Lecture 19 Jared Saia University of New Mexico The successor of a node x is the node that comes after x in the sorted order determined by an in-order tree walk. If all keys are distinct,
Successor CS 361, Lecture 19 Jared Saia University of New Mexico The successor of a node x is the node that comes after x in the sorted order determined by an in-order tree walk. If all keys are distinct,
SET 1C Binary Trees. 2. (i) Define the height of a binary tree or subtree and also define a height balanced (AVL) tree. (2)
 SET 1C Binary Trees 1. Construct a binary tree whose preorder traversal is K L N M P R Q S T and inorder traversal is N L K P R M S Q T 2. (i) Define the height of a binary tree or subtree and also define
SET 1C Binary Trees 1. Construct a binary tree whose preorder traversal is K L N M P R Q S T and inorder traversal is N L K P R M S Q T 2. (i) Define the height of a binary tree or subtree and also define
COSC160: Data Structures Binary Trees. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Data Structures Binary Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Binary Trees I. Implementations I. Memory Management II. Binary Search Tree I. Operations Binary Trees A
COSC160: Data Structures Binary Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Binary Trees I. Implementations I. Memory Management II. Binary Search Tree I. Operations Binary Trees A
UNIT VI TREES. Marks - 14
 UNIT VI TREES Marks - 14 SYLLABUS 6.1 Non-linear data structures 6.2 Binary trees : Complete Binary Tree, Basic Terms: level number, degree, in-degree and out-degree, leaf node, directed edge, path, depth,
UNIT VI TREES Marks - 14 SYLLABUS 6.1 Non-linear data structures 6.2 Binary trees : Complete Binary Tree, Basic Terms: level number, degree, in-degree and out-degree, leaf node, directed edge, path, depth,
1 Solutions to Tute09
 s to Tute0 Questions 4. - 4. are straight forward. Q. 4.4 Show that in a binary tree of N nodes, there are N + NULL pointers. Every node has outgoing pointers. Therefore there are N pointers. Each node,
s to Tute0 Questions 4. - 4. are straight forward. Q. 4.4 Show that in a binary tree of N nodes, there are N + NULL pointers. Every node has outgoing pointers. Therefore there are N pointers. Each node,
Initializing A Max Heap. Initializing A Max Heap
 Initializing A Max Heap 3 4 5 6 7 8 70 8 input array = [-,,, 3, 4, 5, 6, 7, 8,, 0, ] Initializing A Max Heap 3 4 5 6 7 8 70 8 Start at rightmost array position that has a child. Index is n/. Initializing
Initializing A Max Heap 3 4 5 6 7 8 70 8 input array = [-,,, 3, 4, 5, 6, 7, 8,, 0, ] Initializing A Max Heap 3 4 5 6 7 8 70 8 Start at rightmost array position that has a child. Index is n/. Initializing
On the Optimality of a Family of Binary Trees Techical Report TR
 On the Optimality of a Family of Binary Trees Techical Report TR-011101-1 Dana Vrajitoru and William Knight Indiana University South Bend Department of Computer and Information Sciences Abstract In this
On the Optimality of a Family of Binary Trees Techical Report TR-011101-1 Dana Vrajitoru and William Knight Indiana University South Bend Department of Computer and Information Sciences Abstract In this
Ch 10 Trees. Introduction to Trees. Tree Representations. Binary Tree Nodes. Tree Traversals. Binary Search Trees
 Ch 10 Trees Introduction to Trees Tree Representations Binary Tree Nodes Tree Traversals Binary Search Trees 1 Binary Trees A binary tree is a finite set of elements called nodes. The set is either empty
Ch 10 Trees Introduction to Trees Tree Representations Binary Tree Nodes Tree Traversals Binary Search Trees 1 Binary Trees A binary tree is a finite set of elements called nodes. The set is either empty
> asympt( ln( n! ), n ); n 360n n
 8.4 Heap Sort (heapsort) We will now look at our first (n ln(n)) algorithm: heap sort. It will use a data structure that we have already seen: a binary heap. 8.4.1 Strategy and Run-time Analysis Given
8.4 Heap Sort (heapsort) We will now look at our first (n ln(n)) algorithm: heap sort. It will use a data structure that we have already seen: a binary heap. 8.4.1 Strategy and Run-time Analysis Given
2 all subsequent nodes. 252 all subsequent nodes. 401 all subsequent nodes. 398 all subsequent nodes. 330 all subsequent nodes
 ¼ À ÈÌ Ê ½¾ ÈÊÇ Ä ÅË ½µ ½¾º¾¹½ ¾µ ½¾º¾¹ µ ½¾º¾¹ µ ½¾º¾¹ µ ½¾º ¹ µ ½¾º ¹ µ ½¾º ¹¾ µ ½¾º ¹ µ ½¾¹¾ ½¼µ ½¾¹ ½ (1) CLR 12.2-1 Based on the structure of the binary tree, and the procedure of Tree-Search, any
¼ À ÈÌ Ê ½¾ ÈÊÇ Ä ÅË ½µ ½¾º¾¹½ ¾µ ½¾º¾¹ µ ½¾º¾¹ µ ½¾º¾¹ µ ½¾º ¹ µ ½¾º ¹ µ ½¾º ¹¾ µ ½¾º ¹ µ ½¾¹¾ ½¼µ ½¾¹ ½ (1) CLR 12.2-1 Based on the structure of the binary tree, and the procedure of Tree-Search, any
Priority Queues 9/10. Binary heaps Leftist heaps Binomial heaps Fibonacci heaps
 Priority Queues 9/10 Binary heaps Leftist heaps Binomial heaps Fibonacci heaps Priority queues are important in, among other things, operating systems (process control in multitasking systems), search
Priority Queues 9/10 Binary heaps Leftist heaps Binomial heaps Fibonacci heaps Priority queues are important in, among other things, operating systems (process control in multitasking systems), search
Chapter 16. Binary Search Trees (BSTs)
 Chapter 16 Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types of search trees designed
Chapter 16 Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types of search trees designed
Binary Tree Applications
 Binary Tree Applications Lecture 32 Section 19.2 Robb T. Koether Hampden-Sydney College Wed, Apr 17, 2013 Robb T. Koether (Hampden-Sydney College) Binary Tree Applications Wed, Apr 17, 2013 1 / 46 1 Expression
Binary Tree Applications Lecture 32 Section 19.2 Robb T. Koether Hampden-Sydney College Wed, Apr 17, 2013 Robb T. Koether (Hampden-Sydney College) Binary Tree Applications Wed, Apr 17, 2013 1 / 46 1 Expression
Practical session No. 5 Trees
 Practical session No. 5 Trees Tree Binary Tree k-tree Trees as Basic Data Structures ADT that stores elements hierarchically. Each node in the tree has a parent (except for the root), and zero or more
Practical session No. 5 Trees Tree Binary Tree k-tree Trees as Basic Data Structures ADT that stores elements hierarchically. Each node in the tree has a parent (except for the root), and zero or more
Homework #4. CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class
 Homework #4 CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class o Grades depend on neatness and clarity. o Write your answers with enough detail about your approach and concepts
Homework #4 CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class o Grades depend on neatness and clarity. o Write your answers with enough detail about your approach and concepts
Splay Trees Goodrich, Tamassia, Dickerson Splay Trees 1
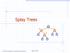 Spla Trees v 6 3 8 4 2004 Goodrich, Tamassia, Dickerson Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less
Spla Trees v 6 3 8 4 2004 Goodrich, Tamassia, Dickerson Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less
Practical session No. 5 Trees
 Practical session No. 5 Trees Tree Trees as Basic Data Structures ADT that stores elements hierarchically. With the exception of the root, each node in the tree has a parent and zero or more children nodes.
Practical session No. 5 Trees Tree Trees as Basic Data Structures ADT that stores elements hierarchically. With the exception of the root, each node in the tree has a parent and zero or more children nodes.
PRIORITY QUEUES. binary heaps d-ary heaps binomial heaps Fibonacci heaps. Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley
 PRIORITY QUEUES binary heaps d-ary heaps binomial heaps Fibonacci heaps Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated
PRIORITY QUEUES binary heaps d-ary heaps binomial heaps Fibonacci heaps Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated
Algorithms PRIORITY QUEUES. binary heaps d-ary heaps binomial heaps Fibonacci heaps. binary heaps d-ary heaps binomial heaps Fibonacci heaps
 Priority queue data type Lecture slides by Kevin Wayne Copyright 05 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos PRIORITY QUEUES binary heaps d-ary heaps binomial heaps Fibonacci
Priority queue data type Lecture slides by Kevin Wayne Copyright 05 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos PRIORITY QUEUES binary heaps d-ary heaps binomial heaps Fibonacci
Fundamental Algorithms - Surprise Test
 Technische Universität München Fakultät für Informatik Lehrstuhl für Effiziente Algorithmen Dmytro Chibisov Sandeep Sadanandan Winter Semester 007/08 Sheet Model Test January 16, 008 Fundamental Algorithms
Technische Universität München Fakultät für Informatik Lehrstuhl für Effiziente Algorithmen Dmytro Chibisov Sandeep Sadanandan Winter Semester 007/08 Sheet Model Test January 16, 008 Fundamental Algorithms
Design and Analysis of Algorithms 演算法設計與分析. Lecture 8 November 16, 2016 洪國寶
 Design and Analysis of Algorithms 演算法設計與分析 Lecture 8 November 6, 206 洪國寶 Outline Review Amortized analysis Advanced data structures Binary heaps Binomial heaps Fibonacci heaps Data structures for disjoint
Design and Analysis of Algorithms 演算法設計與分析 Lecture 8 November 6, 206 洪國寶 Outline Review Amortized analysis Advanced data structures Binary heaps Binomial heaps Fibonacci heaps Data structures for disjoint
Binary Search Tree and AVL Trees. Binary Search Tree. Binary Search Tree. Binary Search Tree. Techniques: How does the BST works?
 Binary Searc Tree and AVL Trees Binary Searc Tree A commonly-used data structure for storing and retrieving records in main memory PUC-Rio Eduardo S. Laber Binary Searc Tree Binary Searc Tree A commonly-used
Binary Searc Tree and AVL Trees Binary Searc Tree A commonly-used data structure for storing and retrieving records in main memory PUC-Rio Eduardo S. Laber Binary Searc Tree Binary Searc Tree A commonly-used
Binary and Binomial Heaps. Disclaimer: these slides were adapted from the ones by Kevin Wayne
 Binary and Binomial Heaps Disclaimer: these slides were adapted from the ones by Kevin Wayne Priority Queues Supports the following operations. Insert element x. Return min element. Return and delete minimum
Binary and Binomial Heaps Disclaimer: these slides were adapted from the ones by Kevin Wayne Priority Queues Supports the following operations. Insert element x. Return min element. Return and delete minimum
PARELLIZATION OF DIJKSTRA S ALGORITHM: COMPARISON OF VARIOUS PRIORITY QUEUES
 PARELLIZATION OF DIJKSTRA S ALGORITHM: COMPARISON OF VARIOUS PRIORITY QUEUES WIKTOR JAKUBIUK, KESHAV PURANMALKA 1. Introduction Dijkstra s algorithm solves the single-sourced shorest path problem on a
PARELLIZATION OF DIJKSTRA S ALGORITHM: COMPARISON OF VARIOUS PRIORITY QUEUES WIKTOR JAKUBIUK, KESHAV PURANMALKA 1. Introduction Dijkstra s algorithm solves the single-sourced shorest path problem on a
3/7/13. Binomial Tree. Binomial Tree. Binomial Tree. Binomial Tree. Number of nodes with respect to k? N(B o ) = 1 N(B k ) = 2 N(B k-1 ) = 2 k
 //1 Adapted from: Kevin Wayne B k B k B k : a binomial tree with the addition of a left child with another binomial tree Number of nodes with respect to k? N(B o ) = 1 N(B k ) = 2 N( ) = 2 k B 1 B 2 B
//1 Adapted from: Kevin Wayne B k B k B k : a binomial tree with the addition of a left child with another binomial tree Number of nodes with respect to k? N(B o ) = 1 N(B k ) = 2 N( ) = 2 k B 1 B 2 B
Design and Analysis of Algorithms. Lecture 9 November 20, 2013 洪國寶
 Design and Analysis of Algorithms 演算法設計與分析 Lecture 9 November 20, 2013 洪國寶 1 Outline Advanced data structures Binary heaps (review) Binomial heaps Fibonacci heaps Dt Data structures t for disjoint dijitsets
Design and Analysis of Algorithms 演算法設計與分析 Lecture 9 November 20, 2013 洪國寶 1 Outline Advanced data structures Binary heaps (review) Binomial heaps Fibonacci heaps Dt Data structures t for disjoint dijitsets
Design and Analysis of Algorithms 演算法設計與分析. Lecture 9 November 19, 2014 洪國寶
 Design and Analysis of Algorithms 演算法設計與分析 Lecture 9 November 19, 2014 洪國寶 1 Outline Advanced data structures Binary heaps(review) Binomial heaps Fibonacci heaps Data structures for disjoint sets 2 Mergeable
Design and Analysis of Algorithms 演算法設計與分析 Lecture 9 November 19, 2014 洪國寶 1 Outline Advanced data structures Binary heaps(review) Binomial heaps Fibonacci heaps Data structures for disjoint sets 2 Mergeable
1.6 Heap ordered trees
 1.6 Heap ordered trees A heap ordered tree is a tree satisfying the following condition. The key of a node is not greater than that of each child if any In a heap ordered tree, we can not implement find
1.6 Heap ordered trees A heap ordered tree is a tree satisfying the following condition. The key of a node is not greater than that of each child if any In a heap ordered tree, we can not implement find
CSE 21 Winter 2016 Homework 6 Due: Wednesday, May 11, 2016 at 11:59pm. Instructions
 CSE 1 Winter 016 Homework 6 Due: Wednesday, May 11, 016 at 11:59pm Instructions Homework should be done in groups of one to three people. You are free to change group members at any time throughout the
CSE 1 Winter 016 Homework 6 Due: Wednesday, May 11, 016 at 11:59pm Instructions Homework should be done in groups of one to three people. You are free to change group members at any time throughout the
Priority Queues. Fibonacci Heap
 ibonacci Heap hans to Sartaj Sahni for the original version of the slides Operation mae-heap insert find-min delete-min union decrease-ey delete Priority Queues Lined List Binary Binomial Heaps ibonacci
ibonacci Heap hans to Sartaj Sahni for the original version of the slides Operation mae-heap insert find-min delete-min union decrease-ey delete Priority Queues Lined List Binary Binomial Heaps ibonacci
Introduction to Greedy Algorithms: Huffman Codes
 Introduction to Greedy Algorithms: Huffman Codes Yufei Tao ITEE University of Queensland In computer science, one interesting method to design algorithms is to go greedy, namely, keep doing the thing that
Introduction to Greedy Algorithms: Huffman Codes Yufei Tao ITEE University of Queensland In computer science, one interesting method to design algorithms is to go greedy, namely, keep doing the thing that
Administration CSE 326: Data Structures
 Administration CSE : Data Structures Binomial Queues Neva Cherniavsky Summer Released today: Project, phase B Due today: Homework Released today: Homework I have office hours tomorrow // Binomial Queues
Administration CSE : Data Structures Binomial Queues Neva Cherniavsky Summer Released today: Project, phase B Due today: Homework Released today: Homework I have office hours tomorrow // Binomial Queues
Heaps. Heap/Priority queue. Binomial heaps: Advanced Algorithmics (4AP) Heaps Binary heap. Binomial heap. Jaak Vilo 2009 Spring
 .0.00 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Advanced Algorithmics (4AP) Heaps Jaak Vilo 00 Spring Binary heap http://en.wikipedia.org/wiki/binary_heap Binomial heap http://en.wikipedia.org/wiki/binomial_heap
.0.00 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Advanced Algorithmics (4AP) Heaps Jaak Vilo 00 Spring Binary heap http://en.wikipedia.org/wiki/binary_heap Binomial heap http://en.wikipedia.org/wiki/binomial_heap
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binomial Heaps CLRS 6.1, 6.2, 6.3 University of Manitoba Priority queues A priority queue is an abstract data type formed by a set S of
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binomial Heaps CLRS 6.1, 6.2, 6.3 University of Manitoba Priority queues A priority queue is an abstract data type formed by a set S of
Design and Analysis of Algorithms
 Design and Analysis of Algorithms Instructor: Sharma Thankachan Lecture 9: Binomial Heap Slides modified from Dr. Hon, with permission 1 About this lecture Binary heap supports various operations quickly:
Design and Analysis of Algorithms Instructor: Sharma Thankachan Lecture 9: Binomial Heap Slides modified from Dr. Hon, with permission 1 About this lecture Binary heap supports various operations quickly:
Supporting Information
 Supporting Information Novikoff et al. 0.073/pnas.0986309 SI Text The Recap Method. In The Recap Method in the paper, we described a schedule in terms of a depth-first traversal of a full binary tree,
Supporting Information Novikoff et al. 0.073/pnas.0986309 SI Text The Recap Method. In The Recap Method in the paper, we described a schedule in terms of a depth-first traversal of a full binary tree,
Heaps
 AdvancedAlgorithmics (4AP) Heaps Jaak Vilo 2009 Spring Jaak Vilo MTAT.03.190 Text Algorithms 1 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Binary heap http://en.wikipedia.org/wiki/binary_heap
AdvancedAlgorithmics (4AP) Heaps Jaak Vilo 2009 Spring Jaak Vilo MTAT.03.190 Text Algorithms 1 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Binary heap http://en.wikipedia.org/wiki/binary_heap
Heaps. c P. Flener/IT Dept/Uppsala Univ. AD1, FP, PK II Heaps 1
 Heaps (Version of 21 November 2005) A min-heap (resp. max-heap) is a data structure with fast extraction of the smallest (resp. largest) item (in O(lg n) time), as well as fast insertion (also in O(lg
Heaps (Version of 21 November 2005) A min-heap (resp. max-heap) is a data structure with fast extraction of the smallest (resp. largest) item (in O(lg n) time), as well as fast insertion (also in O(lg
Lecture 10/12 Data Structures (DAT037) Ramona Enache (with slides from Nick Smallbone and Nils Anders Danielsson)
 Lecture 10/12 Data Structures (DAT037) Ramona Enache (with slides from Nick Smallbone and Nils Anders Danielsson) Balanced BSTs: Problem The BST operahons take O(height of tree), so for unbalanced trees
Lecture 10/12 Data Structures (DAT037) Ramona Enache (with slides from Nick Smallbone and Nils Anders Danielsson) Balanced BSTs: Problem The BST operahons take O(height of tree), so for unbalanced trees
CSE 100: TREAPS AND RANDOMIZED SEARCH TREES
 CSE 100: TREAPS AND RANDOMIZED SEARCH TREES Midterm Review Practice Midterm covered during Sunday discussion Today Run time analysis of building the Huffman tree AVL rotations and treaps Huffman s algorithm
CSE 100: TREAPS AND RANDOMIZED SEARCH TREES Midterm Review Practice Midterm covered during Sunday discussion Today Run time analysis of building the Huffman tree AVL rotations and treaps Huffman s algorithm
Advanced Algorithmics (4AP) Heaps
 Advanced Algorithmics (4AP) Heaps Jaak Vilo 2009 Spring Jaak Vilo MTAT.03.190 Text Algorithms 1 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Binary heap http://en.wikipedia.org/wiki/binary
Advanced Algorithmics (4AP) Heaps Jaak Vilo 2009 Spring Jaak Vilo MTAT.03.190 Text Algorithms 1 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Binary heap http://en.wikipedia.org/wiki/binary
It is used when neither the TX nor RX knows anything about the statistics of the source sequence at the start of the transmission
 It is used when neither the TX nor RX knows anything about the statistics of the source sequence at the start of the transmission -The code can be described in terms of a binary tree -0 corresponds to
It is used when neither the TX nor RX knows anything about the statistics of the source sequence at the start of the transmission -The code can be described in terms of a binary tree -0 corresponds to
1 Binomial Tree. Structural Properties:
 Indian Institute of Information Technology Design and Manufacturing, Kancheepuram Chennai 600, India An Autonomous Institute under MHRD, Govt of India http://www.iiitdm.ac.in COM 0 Advanced Data Structures
Indian Institute of Information Technology Design and Manufacturing, Kancheepuram Chennai 600, India An Autonomous Institute under MHRD, Govt of India http://www.iiitdm.ac.in COM 0 Advanced Data Structures
Lesson 9: Heuristic Search and A* Search
 CAP 5602 Summer, 2011 Lesson 9: Heuristic Search and A* Search The topics 1. Heuristic Search 2. The A* Search 3. An example of the use of A* search. 1. Heuristic Search The idea of heuristics is to attach
CAP 5602 Summer, 2011 Lesson 9: Heuristic Search and A* Search The topics 1. Heuristic Search 2. The A* Search 3. An example of the use of A* search. 1. Heuristic Search The idea of heuristics is to attach
Meld(Q 1,Q 2 ) merge two sets
 Priority Queues MakeQueue Insert(Q,k,p) Delete(Q,k) DeleteMin(Q) Meld(Q 1,Q 2 ) Empty(Q) Size(Q) FindMin(Q) create new empty queue insert key k with priority p delete key k (given a pointer) delete key
Priority Queues MakeQueue Insert(Q,k,p) Delete(Q,k) DeleteMin(Q) Meld(Q 1,Q 2 ) Empty(Q) Size(Q) FindMin(Q) create new empty queue insert key k with priority p delete key k (given a pointer) delete key
BITTIGER #11. Oct
 BITTIGER #11 Oct 22 2016 PROBLEM LIST A. Five in a Row brute force, implementation B. Building Heap data structures, divide and conquer C. Guess Number with Lower or Higher Hints dynamic programming, mathematics
BITTIGER #11 Oct 22 2016 PROBLEM LIST A. Five in a Row brute force, implementation B. Building Heap data structures, divide and conquer C. Guess Number with Lower or Higher Hints dynamic programming, mathematics
Heap Building Bounds
 Heap Building Bounds Zhentao Li 1 and Bruce A. Reed 2 1 School of Computer Science, McGill University zhentao.li@mail.mcgill.ca 2 School of Computer Science, McGill University breed@cs.mcgill.ca Abstract.
Heap Building Bounds Zhentao Li 1 and Bruce A. Reed 2 1 School of Computer Science, McGill University zhentao.li@mail.mcgill.ca 2 School of Computer Science, McGill University breed@cs.mcgill.ca Abstract.
Fibonacci Heaps CLRS: Chapter 20 Last Revision: 21/09/04
 Fibonacci Heaps CLRS: Chapter 20 Last Revision: 21/09/04 1 Binary heap Binomial heap Fibonacci heap Procedure (worst-case) (worst-case) (amortized) Make-Heap Θ(1) Θ(1) Θ(1) Insert Θ(lg n) O(lg n) Θ(1)
Fibonacci Heaps CLRS: Chapter 20 Last Revision: 21/09/04 1 Binary heap Binomial heap Fibonacci heap Procedure (worst-case) (worst-case) (amortized) Make-Heap Θ(1) Θ(1) Θ(1) Insert Θ(lg n) O(lg n) Θ(1)
Data Structures, Algorithms, & Applications in C++ ( Chapter 9 )
 ) Priority Queues Two kinds of priority queues: Min priority queue. Max priority queue. Min Priority Queue Collection of elements. Each element has a priority or key. Supports following operations: isempty
) Priority Queues Two kinds of priority queues: Min priority queue. Max priority queue. Min Priority Queue Collection of elements. Each element has a priority or key. Supports following operations: isempty
On the Optimality of a Family of Binary Trees
 On the Optimality of a Family of Binary Trees Dana Vrajitoru Computer and Information Sciences Department Indiana University South Bend South Bend, IN 46645 Email: danav@cs.iusb.edu William Knight Computer
On the Optimality of a Family of Binary Trees Dana Vrajitoru Computer and Information Sciences Department Indiana University South Bend South Bend, IN 46645 Email: danav@cs.iusb.edu William Knight Computer
Splay Trees. Splay Trees - 1
 Splay Trees In balanced tree schemes, explicit rules are followed to ensure balance. In splay trees, there are no such rules. Search, insert, and delete operations are like in binary search trees, except
Splay Trees In balanced tree schemes, explicit rules are followed to ensure balance. In splay trees, there are no such rules. Search, insert, and delete operations are like in binary search trees, except
Outline for this Week
 Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, fexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, fexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
The Tree Data Model. Laura Kovács
 The Tree Data Model Laura Kovács Trees (Baumstrukturen) Definition Trees are sets of points, called nodes (Knoten) and lines, called edges (Kanten), connecting two distinct nodes, such that: n 2 n 3 n
The Tree Data Model Laura Kovács Trees (Baumstrukturen) Definition Trees are sets of points, called nodes (Knoten) and lines, called edges (Kanten), connecting two distinct nodes, such that: n 2 n 3 n
The potential function φ for the amortized analysis of an operation on Fibonacci heap at time (iteration) i is given by the following equation:
 Indian Institute of Information Technology Design and Manufacturing, Kancheepuram Chennai 600 127, India An Autonomous Institute under MHRD, Govt of India http://www.iiitdm.ac.in COM 01 Advanced Data Structures
Indian Institute of Information Technology Design and Manufacturing, Kancheepuram Chennai 600 127, India An Autonomous Institute under MHRD, Govt of India http://www.iiitdm.ac.in COM 01 Advanced Data Structures
Basic Data Structures. Figure 8.1 Lists, stacks, and queues. Terminology for Stacks. Terminology for Lists. Chapter 8: Data Abstractions
 Chapter 8: Data Abstractions Computer Science: An Overview Tenth Edition by J. Glenn Brookshear Chapter 8: Data Abstractions 8.1 Data Structure Fundamentals 8.2 Implementing Data Structures 8.3 A Short
Chapter 8: Data Abstractions Computer Science: An Overview Tenth Edition by J. Glenn Brookshear Chapter 8: Data Abstractions 8.1 Data Structure Fundamentals 8.2 Implementing Data Structures 8.3 A Short
Outline for this Week
 Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, flexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, flexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
1) S = {s}; 2) for each u V {s} do 3) dist[u] = cost(s, u); 4) Insert u into a 2-3 tree Q with dist[u] as the key; 5) for i = 1 to n 1 do 6) Identify
![1) S = {s}; 2) for each u V {s} do 3) dist[u] = cost(s, u); 4) Insert u into a 2-3 tree Q with dist[u] as the key; 5) for i = 1 to n 1 do 6) Identify 1) S = {s}; 2) for each u V {s} do 3) dist[u] = cost(s, u); 4) Insert u into a 2-3 tree Q with dist[u] as the key; 5) for i = 1 to n 1 do 6) Identify](/thumbs/77/75720566.jpg) CSE 3500 Algorithms and Complexity Fall 2016 Lecture 17: October 25, 2016 Dijkstra s Algorithm Dijkstra s algorithm for the SSSP problem generates the shortest paths in nondecreasing order of the shortest
CSE 3500 Algorithms and Complexity Fall 2016 Lecture 17: October 25, 2016 Dijkstra s Algorithm Dijkstra s algorithm for the SSSP problem generates the shortest paths in nondecreasing order of the shortest
Optimal Satisficing Tree Searches
 Optimal Satisficing Tree Searches Dan Geiger and Jeffrey A. Barnett Northrop Research and Technology Center One Research Park Palos Verdes, CA 90274 Abstract We provide an algorithm that finds optimal
Optimal Satisficing Tree Searches Dan Geiger and Jeffrey A. Barnett Northrop Research and Technology Center One Research Park Palos Verdes, CA 90274 Abstract We provide an algorithm that finds optimal
Introduction to Algorithms / Algorithms I Lecturer: Michael Dinitz Topic: Splay Trees Date: 9/27/16
 600.463 Introduction to lgoritms / lgoritms I Lecturer: Micael initz Topic: Splay Trees ate: 9/27/16 8.1 Introduction Today we re going to talk even more about binary searc trees. -trees, red-black trees,
600.463 Introduction to lgoritms / lgoritms I Lecturer: Micael initz Topic: Splay Trees ate: 9/27/16 8.1 Introduction Today we re going to talk even more about binary searc trees. -trees, red-black trees,
Information Theory and Coding Prof. S. N. Merchant Department of Electrical Engineering Indian Institute of Technology, Bombay
 Information Theory and Coding Prof. S. N. Merchant Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture - 15 Adaptive Huffman Coding Part I Huffman code are optimal for a
Information Theory and Coding Prof. S. N. Merchant Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture - 15 Adaptive Huffman Coding Part I Huffman code are optimal for a
CSE 417 Algorithms. Huffman Codes: An Optimal Data Compression Method
 CSE 417 Algorithms Huffman Codes: An Optimal Data Compression Method 1 Compression Example 100k file, 6 letter alphabet: a 45% b 13% c 12% d 16% e 9% f 5% File Size: ASCII, 8 bits/char: 800kbits 2 3 >
CSE 417 Algorithms Huffman Codes: An Optimal Data Compression Method 1 Compression Example 100k file, 6 letter alphabet: a 45% b 13% c 12% d 16% e 9% f 5% File Size: ASCII, 8 bits/char: 800kbits 2 3 >
Lecture 8 Feb 16, 2017
 CS 4: Advanced Algorithms Spring 017 Prof. Jelani Nelson Lecture 8 Feb 16, 017 Scribe: Tiffany 1 Overview In the last lecture we covered the properties of splay trees, including amortized O(log n) time
CS 4: Advanced Algorithms Spring 017 Prof. Jelani Nelson Lecture 8 Feb 16, 017 Scribe: Tiffany 1 Overview In the last lecture we covered the properties of splay trees, including amortized O(log n) time
Pattern Recognition Chapter 5: Decision Trees
 Pattern Recognition Chapter 5: Decision Trees Asst. Prof. Dr. Chumphol Bunkhumpornpat Department of Computer Science Faculty of Science Chiang Mai University Learning Objectives How decision trees are
Pattern Recognition Chapter 5: Decision Trees Asst. Prof. Dr. Chumphol Bunkhumpornpat Department of Computer Science Faculty of Science Chiang Mai University Learning Objectives How decision trees are
Data Structures. Binomial Heaps Fibonacci Heaps. Haim Kaplan & Uri Zwick December 2013
 Data Structures Binomial Heaps Fibonacci Heaps Haim Kaplan & Uri Zwick December 13 1 Heaps / Priority queues Binary Heaps Binomial Heaps Lazy Binomial Heaps Fibonacci Heaps Insert Find-min Delete-min Decrease-key
Data Structures Binomial Heaps Fibonacci Heaps Haim Kaplan & Uri Zwick December 13 1 Heaps / Priority queues Binary Heaps Binomial Heaps Lazy Binomial Heaps Fibonacci Heaps Insert Find-min Delete-min Decrease-key
Stanford University, CS 106X Homework Assignment 5: Priority Queue Binomial Heap Optional Extension
 Stanford University, CS 106X Homework Assignment 5: Priority Queue Binomial Heap Optional Extension Extension description by Jerry Cain. This document describes an optional extension to the assignment.
Stanford University, CS 106X Homework Assignment 5: Priority Queue Binomial Heap Optional Extension Extension description by Jerry Cain. This document describes an optional extension to the assignment.
9.7 Binomial Queues. This excerpt made available by permission of Robert Sedgewick, and of Pearson Education, Inc.
 406 9.7 CH lgorithms, 3rd dition, in Java, arts 1-4: Fundamentals, Data tructures, orting, and earching. obert edgewick, ddison-esley 2002. his excerpt made available by permission of obert edgewick, and
406 9.7 CH lgorithms, 3rd dition, in Java, arts 1-4: Fundamentals, Data tructures, orting, and earching. obert edgewick, ddison-esley 2002. his excerpt made available by permission of obert edgewick, and
F U N C T I O N A L P E A R L S Purely Functional 1-2 Brother Trees
 Under consideration for publication in J. Functional Programming 1 F U N C T I O N A L P E A R L S Purely Functional 1-2 Brother Trees RALF HINZE Computing Laboratory University of Oxford Wolfson Building,
Under consideration for publication in J. Functional Programming 1 F U N C T I O N A L P E A R L S Purely Functional 1-2 Brother Trees RALF HINZE Computing Laboratory University of Oxford Wolfson Building,
Lecture 5: Tuesday, January 27, Peterson s Algorithm satisfies the No Starvation property (Theorem 1)
 Com S 611 Spring Semester 2015 Advanced Topics on Distributed and Concurrent Algorithms Lecture 5: Tuesday, January 27, 2015 Instructor: Soma Chaudhuri Scribe: Nik Kinkel 1 Introduction This lecture covers
Com S 611 Spring Semester 2015 Advanced Topics on Distributed and Concurrent Algorithms Lecture 5: Tuesday, January 27, 2015 Instructor: Soma Chaudhuri Scribe: Nik Kinkel 1 Introduction This lecture covers
NOTES ON FIBONACCI TREES AND THEIR OPTIMALITY* YASUICHI HORIBE INTRODUCTION 1. FIBONACCI TREES
 0#0# NOTES ON FIBONACCI TREES AND THEIR OPTIMALITY* YASUICHI HORIBE Shizuoka University, Hamamatsu, 432, Japan (Submitted February 1982) INTRODUCTION Continuing a previous paper [3], some new observations
0#0# NOTES ON FIBONACCI TREES AND THEIR OPTIMALITY* YASUICHI HORIBE Shizuoka University, Hamamatsu, 432, Japan (Submitted February 1982) INTRODUCTION Continuing a previous paper [3], some new observations
Binomial Heaps. Bryan M. Franklin
 Binomial Heaps Bryan M. Franklin bmfrankl@mtu.edu 1 Tradeoffs Worst Case Operation Binary Heap Binomial Heap Make-Heap Θ(1) Θ(1) Insert Θ(lg n) O(lg n) Minimum Θ(1) O(lg n) Extract-Min Θ(lg n) Θ(lg n)
Binomial Heaps Bryan M. Franklin bmfrankl@mtu.edu 1 Tradeoffs Worst Case Operation Binary Heap Binomial Heap Make-Heap Θ(1) Θ(1) Insert Θ(lg n) O(lg n) Minimum Θ(1) O(lg n) Extract-Min Θ(lg n) Θ(lg n)
6.854J / J Advanced Algorithms Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
CS4311 Design and Analysis of Algorithms. Lecture 14: Amortized Analysis I
 CS43 Design and Analysis of Algorithms Lecture 4: Amortized Analysis I About this lecture Given a data structure, amortized analysis studies in a sequence of operations, the average time to perform an
CS43 Design and Analysis of Algorithms Lecture 4: Amortized Analysis I About this lecture Given a data structure, amortized analysis studies in a sequence of operations, the average time to perform an
The suffix binary search tree and suffix AVL tree
 Journal of Discrete Algorithms 1 (2003) 387 408 www.elsevier.com/locate/jda The suffix binary search tree and suffix AVL tree Robert W. Irving, Lorna Love Department of Computing Science, University of
Journal of Discrete Algorithms 1 (2003) 387 408 www.elsevier.com/locate/jda The suffix binary search tree and suffix AVL tree Robert W. Irving, Lorna Love Department of Computing Science, University of
Fibonacci Heaps Y Y o o u u c c an an s s u u b b m miitt P P ro ro b blle e m m S S et et 3 3 iin n t t h h e e b b o o x x u u p p fro fro n n tt..
 Fibonacci Heaps You You can can submit submit Problem Problem Set Set 3 in in the the box box up up front. front. Outline for Today Review from Last Time Quick refresher on binomial heaps and lazy binomial
Fibonacci Heaps You You can can submit submit Problem Problem Set Set 3 in in the the box box up up front. front. Outline for Today Review from Last Time Quick refresher on binomial heaps and lazy binomial
Priority queue. Advanced Algorithmics (6EAP) Binary heap. Heap/Priority queue. Binomial heaps: Merge two heaps.
 Priority queue Advanced Algorithmics (EAP) MTAT.03.38 Heaps Jaak Vilo 0 Spring Insert Q, x Retrieve x from Q s.t. x.value is min (or max) Sorted linked list: O(n) to insert x into right place O() access-
Priority queue Advanced Algorithmics (EAP) MTAT.03.38 Heaps Jaak Vilo 0 Spring Insert Q, x Retrieve x from Q s.t. x.value is min (or max) Sorted linked list: O(n) to insert x into right place O() access-
CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS
 CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS November 17, 2016. Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question.
CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS November 17, 2016. Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question.
MSU CSE Spring 2011 Exam 2-ANSWERS
 MSU CSE 260-001 Spring 2011 Exam 2-NSWERS Name: This is a closed book exam, with 9 problems on 5 pages totaling 100 points. Integer ivision/ Modulo rithmetic 1. We can add two numbers in base 2 by using
MSU CSE 260-001 Spring 2011 Exam 2-NSWERS Name: This is a closed book exam, with 9 problems on 5 pages totaling 100 points. Integer ivision/ Modulo rithmetic 1. We can add two numbers in base 2 by using
CS 106X Lecture 11: Sorting
 CS 106X Lecture 11: Sorting Friday, February 3, 2017 Programming Abstractions (Accelerated) Winter 2017 Stanford University Computer Science Department Lecturer: Chris Gregg reading: Programming Abstractions
CS 106X Lecture 11: Sorting Friday, February 3, 2017 Programming Abstractions (Accelerated) Winter 2017 Stanford University Computer Science Department Lecturer: Chris Gregg reading: Programming Abstractions
Conditional inference trees in dynamic microsimulation - modelling transition probabilities in the SMILE model
 4th General Conference of the International Microsimulation Association Canberra, Wednesday 11th to Friday 13th December 2013 Conditional inference trees in dynamic microsimulation - modelling transition
4th General Conference of the International Microsimulation Association Canberra, Wednesday 11th to Friday 13th December 2013 Conditional inference trees in dynamic microsimulation - modelling transition
CSCE 750, Fall 2009 Quizzes with Answers
 CSCE 750, Fall 009 Quizzes with Answers Stephen A. Fenner September 4, 011 1. Give an exact closed form for Simplify your answer as much as possible. k 3 k+1. We reduce the expression to a form we ve already
CSCE 750, Fall 009 Quizzes with Answers Stephen A. Fenner September 4, 011 1. Give an exact closed form for Simplify your answer as much as possible. k 3 k+1. We reduce the expression to a form we ve already
Priority Queues Based on Braun Trees
 Priority Queues Based on Braun Trees Tobias Nipkow September 19, 2015 Abstract This theory implements priority queues via Braun trees. Insertion and deletion take logarithmic time and preserve the balanced
Priority Queues Based on Braun Trees Tobias Nipkow September 19, 2015 Abstract This theory implements priority queues via Braun trees. Insertion and deletion take logarithmic time and preserve the balanced
Algorithmic Game Theory and Applications. Lecture 11: Games of Perfect Information
 Algorithmic Game Theory and Applications Lecture 11: Games of Perfect Information Kousha Etessami finite games of perfect information Recall, a perfect information (PI) game has only 1 node per information
Algorithmic Game Theory and Applications Lecture 11: Games of Perfect Information Kousha Etessami finite games of perfect information Recall, a perfect information (PI) game has only 1 node per information
Tree Diagram. Splitting Criterion. Splitting Criterion. Introduction. Building a Decision Tree. MS4424 Data Mining & Modelling Decision Tree
 Introduction MS4424 Data Mining & Modelling Decision Tree Lecturer : Dr Iris Yeung Room No : P7509 Tel No : 2788 8566 Email : msiris@cityu.edu.hk decision tree is a set of rules represented in a tree structure
Introduction MS4424 Data Mining & Modelling Decision Tree Lecturer : Dr Iris Yeung Room No : P7509 Tel No : 2788 8566 Email : msiris@cityu.edu.hk decision tree is a set of rules represented in a tree structure
CEC login. Student Details Name SOLUTIONS
 Student Details Name SOLUTIONS CEC login Instructions You have roughly 1 minute per point, so schedule your time accordingly. There is only one correct answer per question. Good luck! Question 1. Searching
Student Details Name SOLUTIONS CEC login Instructions You have roughly 1 minute per point, so schedule your time accordingly. There is only one correct answer per question. Good luck! Question 1. Searching
Decision Trees An Early Classifier
 An Early Classifier Jason Corso SUNY at Buffalo January 19, 2012 J. Corso (SUNY at Buffalo) Trees January 19, 2012 1 / 33 Introduction to Non-Metric Methods Introduction to Non-Metric Methods We cover
An Early Classifier Jason Corso SUNY at Buffalo January 19, 2012 J. Corso (SUNY at Buffalo) Trees January 19, 2012 1 / 33 Introduction to Non-Metric Methods Introduction to Non-Metric Methods We cover
Notes on Natural Logic
 Notes on Natural Logic Notes for PHIL370 Eric Pacuit November 16, 2012 1 Preliminaries: Trees A tree is a structure T = (T, E), where T is a nonempty set whose elements are called nodes and E is a relation
Notes on Natural Logic Notes for PHIL370 Eric Pacuit November 16, 2012 1 Preliminaries: Trees A tree is a structure T = (T, E), where T is a nonempty set whose elements are called nodes and E is a relation
Binary Decision Diagrams
 Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
A relation on 132-avoiding permutation patterns
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. VOL, 205, 285 302 A relation on 32-avoiding permutation patterns Natalie Aisbett School of Mathematics and Statistics, University of Sydney,
Discrete Mathematics and Theoretical Computer Science DMTCS vol. VOL, 205, 285 302 A relation on 32-avoiding permutation patterns Natalie Aisbett School of Mathematics and Statistics, University of Sydney,
Recitation 1. Solving Recurrences. 1.1 Announcements. Welcome to 15210!
 Recitation 1 Solving Recurrences 1.1 Announcements Welcome to 1510! The course website is http://www.cs.cmu.edu/ 1510/. It contains the syllabus, schedule, library documentation, staff contact information,
Recitation 1 Solving Recurrences 1.1 Announcements Welcome to 1510! The course website is http://www.cs.cmu.edu/ 1510/. It contains the syllabus, schedule, library documentation, staff contact information,
Outline. Objective. Previous Results Our Results Discussion Current Research. 1 Motivation. 2 Model. 3 Results
 On Threshold Esteban 1 Adam 2 Ravi 3 David 4 Sergei 1 1 Stanford University 2 Harvard University 3 Yahoo! Research 4 Carleton College The 8th ACM Conference on Electronic Commerce EC 07 Outline 1 2 3 Some
On Threshold Esteban 1 Adam 2 Ravi 3 David 4 Sergei 1 1 Stanford University 2 Harvard University 3 Yahoo! Research 4 Carleton College The 8th ACM Conference on Electronic Commerce EC 07 Outline 1 2 3 Some
Outline for Today. Quick refresher on binomial heaps and lazy binomial heaps. An important operation in many graph algorithms.
 Fibonacci Heaps Outline for Today Review from Last Time Quick refresher on binomial heaps and lazy binomial heaps. The Need for decrease-key An important operation in many graph algorithms. Fibonacci Heaps
Fibonacci Heaps Outline for Today Review from Last Time Quick refresher on binomial heaps and lazy binomial heaps. The Need for decrease-key An important operation in many graph algorithms. Fibonacci Heaps
c 2004 Society for Industrial and Applied Mathematics
 SIAM J. COMPUT. Vol. 33, No. 5, pp. 1011 1034 c 2004 Society for Industrial and Applied Mathematics EFFICIENT ALGORITHMS FOR OPTIMAL STREAM MERGING FOR MEDIA-ON-DEMAND AMOTZ BAR-NOY AND RICHARD E. LADNER
SIAM J. COMPUT. Vol. 33, No. 5, pp. 1011 1034 c 2004 Society for Industrial and Applied Mathematics EFFICIENT ALGORITHMS FOR OPTIMAL STREAM MERGING FOR MEDIA-ON-DEMAND AMOTZ BAR-NOY AND RICHARD E. LADNER
Binary Decision Diagrams
 Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
Structural Induction
 Structural Induction Jason Filippou CMSC250 @ UMCP 07-05-2016 Jason Filippou (CMSC250 @ UMCP) Structural Induction 07-05-2016 1 / 26 Outline 1 Recursively defined structures 2 Proofs Binary Trees Jason
Structural Induction Jason Filippou CMSC250 @ UMCP 07-05-2016 Jason Filippou (CMSC250 @ UMCP) Structural Induction 07-05-2016 1 / 26 Outline 1 Recursively defined structures 2 Proofs Binary Trees Jason
Data Structures and Algorithms February 10, 2007 Pennsylvania State University CSE 465 Professors Sofya Raskhodnikova & Adam Smith Handout 10
 Data Structures and Algorithms February 10, 2007 Pennsylvania State University CSE 465 Professors Sofya Raskhodnikova & Adam Smith Handout 10 Practice Exam 1 Do not open this exam booklet until you are
Data Structures and Algorithms February 10, 2007 Pennsylvania State University CSE 465 Professors Sofya Raskhodnikova & Adam Smith Handout 10 Practice Exam 1 Do not open this exam booklet until you are
CS188 Spring 2012 Section 4: Games
 CS188 Spring 2012 Section 4: Games 1 Minimax Search In this problem, we will explore adversarial search. Consider the zero-sum game tree shown below. Trapezoids that point up, such as at the root, represent
CS188 Spring 2012 Section 4: Games 1 Minimax Search In this problem, we will explore adversarial search. Consider the zero-sum game tree shown below. Trapezoids that point up, such as at the root, represent
CS360 Homework 14 Solution
 CS360 Homework 14 Solution Markov Decision Processes 1) Invent a simple Markov decision process (MDP) with the following properties: a) it has a goal state, b) its immediate action costs are all positive,
CS360 Homework 14 Solution Markov Decision Processes 1) Invent a simple Markov decision process (MDP) with the following properties: a) it has a goal state, b) its immediate action costs are all positive,
UNIT 2. Greedy Method GENERAL METHOD
 UNIT 2 GENERAL METHOD Greedy Method Greedy is the most straight forward design technique. Most of the problems have n inputs and require us to obtain a subset that satisfies some constraints. Any subset
UNIT 2 GENERAL METHOD Greedy Method Greedy is the most straight forward design technique. Most of the problems have n inputs and require us to obtain a subset that satisfies some constraints. Any subset
