Lecture 8 Feb 16, 2017
|
|
|
- Tamsin Moore
- 5 years ago
- Views:
Transcription
1 CS 4: Advanced Algorithms Spring 017 Prof. Jelani Nelson Lecture 8 Feb 16, 017 Scribe: Tiffany 1 Overview In the last lecture we covered the properties of splay trees, including amortized O(log n) time for operations, static finger, dynamic finger, and others. In this lecture we analyze splay trees, and begin discussion of online algorithms. Splay Tree Analysis.1 Notation Define a weight function on nodes w : {nodes} R 0. We will write our potential function in terms of w, and by taking different weight functions will allow us to prove different properties, such as amortized O(log n) operations and static optimality later on in this lecture. For now, think of w() = 1. Additionally, define s() := y subtree including and let the rank of a node be r() := lg(s()). It s not clear including a log here is well motivated, and indeed the original authors of the paper say as much. w(y) The potential function on a particular state S of the splay tree is φ(s) := T r() Additionally, let W = T w() be the size of the root.. Analysis of splay() taking O(log n) time Set w() = 1. Claim 1. The amortized cost of splay() is t splay 3 (r(root) r()) log(n) + 1 since the root has weight n. 1
2 z y D y A y A B C rotate(y) A B C D z rotate() B C z D Figure 1: Zig-zig step in splay operation (Case ) Claim. Suppose we are doing one of the cases of (1) zig, () zig-zig, or (3)zig-zag. Then amortized cost of performing each of these operations is Case (1): 3(r () r()) + 1 where r () is the rank of after the operation. Cases (), (3): 3(r () r()) Note that Claim implies Claim 1 because of a telescoping sum of the operations up the tree, so the final cost will be about 3(r(root) r()) where r() is the rank of the node that was located before splaying. Proof. We will just do the zig-zig case (case ), which as a reminder is when = y.left, y = z.left or the symmetric case. Other cases are similar. After the operation we know that r () = r(z). Using the definition of amortization, amortized cost = actual cost + Φ The actual cost is just rotations. We also know that since, y, z are the only ranks that change, then using r () = r(z) Φ = (r () + r (y) + r (z)) (r() + r(y) + r(z)) = r (y) + r (z) r() r(y) = r () + r (z) r() (1) where the last step follows due to r() r(y), r (y) r () due to the parental relationship between and y before and after the operation.
3 We try to bound r() + r (z): r() + r (z) ( ) = lg s()s (z) ( s() + s ) (z) lg ( s ) () lg = r () 1 by AM-GM where the last line follows since s() = w() + s(a) + s(b), s (z) = w(z) + s(c) + s(d), and s () = w() + w(y) + w(z) + s(a) + s(c) + s(d) s() + s (z). Therefore, we have that Subsituting into equation (1), we get r (z) r () r() Φ = r () + r (z) r() r () + r () r() r() = 3(r () r() and therefore as desired. t = + 3(r () r()) = 3(r () r()) So we can say splay and query take O(lg n), since query is simply walking down the tree and a splay. However, insert must be dealt with differently since we increased the potential function..3 Analysis of insert() The amortized cost of insert is Φ from inserting k levels down and O(splay) = O(log n). It suffices to bound Φ from the insert by O(log n) to achieve the desired amortized runtime. Suppose in order to insert, its parents above it in the BST are y 1 =.parent, y = y 1.parent,...y k = root. Then k Φ = r (y j ) r(y j ) as desired. j=1 = ( ) s(yj ) + 1 lg s(y j j ) ( ) s(y j ) + 1 = lg π j s(y j ) [ s(y ) lg s(y 1 ) s(y 3) s(y )... s(y ] k) + 1 s(y k ) ( ) s(yk ) + 1 = lg s(y 1 ) lg(s(y k ) + 1) = O(r(y k )) = O(lg n) w() = 1 s(y j ) + 1 s(y j+1 ) 3
4 .4 Static Optimality We want to be competitive with a BST built for the distribution of queries given, in the case that there are no inserts or deletes (there s a dynamic programming algorithm for constructing this). We claim that if a sequence of queries σ is long enough, splay trees achieve a constant within the optimal static BST, which is proven in the original splay tree paper by Tarjan and Sleator[]. Formally, given a query sequence σ and fied BST T, C splay (σ) O(n + C T (σ)) and once σ > n, this implies C OP T. Note that we can achieve n log n, which is better than n, though we won t prove it here. Proof. Suppose T puts node at the level l of the tree where l root = 0. Define w(x) = 1 3 l. Recall, (amortized costs) = (actual costs) + Φfinal Φ init (actual costs) = (amortized costs) + Φ init Φ final we will show that (amortized costs) = O(OP T ) and Φ init Φ final = O(n ), which is sufficient to prove the claim. Here, we rela the condition that Φ must be positive and zero on the initial data structure, since we account for the difference in potential eplicitly. Difference in potential: Note that Φ(S) = lg(s()), and we want to know how big of a magnitude this can get. Well, we know that 1 1 w() 1, so s() lg(s()) cn. So 3n 3n we know that lg(s()) cn for some constant c. Addditionally, we know since each s() 1, that lg(s()) O(n log n) Thus, the difference in potential is no more than O(n ). Amortized costs: Amortized cost of query() is O(amortized cost of splay()). It suffices to show that the amoritized cost of splay() is the same cost of accessing an item in the perfect BST T, which is l. ( ( )) W O(root) r()) = O lg s() where W = z w(z). We want this amoritized cost to be O(l ). We note that W C for some constant C, since W = z w(z) = z 1 n 3 = 1 lz 3 l (#nodes at level l) l=0 l l = O(1) 3 4
5 We know that W 1, so W = Θ(1). Therefore, ( ) W lg = Θ(1) lg(s()) s() ( ) 1 = Θ(1) lg = Θ(1 + l ) 3 l so we are done, sinc ethe cost is eactly a constant factor off of l, the cost in the optimal BST. 3 Online Algorithms Online algorithms are a class of algorithms in which one must make a sequence of irrevocable decisions without knowing the future. However, we want to be competitive the best sequence of decisions in hindsight. Definition 3. Let OP T be the optimal strategy given omniscience. We say that a strategys is r-competitive if for a sequence of events σ cost S (σ) r cost OP T (σ) + O(1) 3.1 Eamples Ski Rental Problem Suppose you are on a ski trip, and you let your friends dictate how long your group will continue skiing. Your friends will inform you each morning whether you will continue to ski that day, or leave the resort. You need skis, and there are two options: rent skis: $1 per day buy skis: $ B, one time payment at any time If you knew ahead of time how many days you wil stay at the resort n, your strategy would be to buy the skis on the first day if n > B and rent otherwise. What should your strategy be to minimize your regret? Strategy: You rent for B 1 days. If by the Bth day you did not leave, buy the skis. This is optimal for staying B 1 days, and the worst case is if you stay for eactly B days and leave the net day. Then you spent $B-1 dollars, but opt spent B, so you re always guaranteed to be within a factor of from the optimal. Indeed, the ski rental problem has competitve ratio r =, and no other online strategy can do better, which makes it the optimal. 5
6 3.1. Free Swag at the Career Fair You re standing in the middle of a hallway lined with n + 1 rooms at the career fair. Your friend tets you saying that there is some room in which a free laptops (!!!) are being given out by some company who really wants you to work for them. You want to get there as soon as possible, because if you get there too late, all the laptops may be claimed. Walking by a room takes constant time, and looking in as you walk past a room costs no time. What should be your strategy of eploring rooms? If you knew which room t had the swag in it, you would just walk to t, incurring t cost to get there. Suppose you re at room 0, and there are n rooms on either side of you, which we ll number 1,,...n on your right and n, n + 1,... 1 on your left. One strategy might be to go to rooms 1, 1,,, 4, 4,... until you find the room that you re looking for. This cost will be ( ) + ( ) + ( ) +... = 4( j ) 4 j+1 The worst case scenario arises when the jackpot room is t = j 1. Then we would pay 4 j+1 + j+1 + t = 13t. So this algorithm is 13-competitive. There eists a 9-competitive strategy where we traverse the rooms 1,, 4, 8,..., which we won t analyze here. 4 List Update Problem This mechanism was originally posed by Sleater and Tarjan[1], before which analysis of this kind was usually done assuming a known distribution of list accesses. There are n nodes in a linked list. We are given an access sequence σ where σ i [n], and we will call query on each of them. query(): start at head of the linked list cost(query()) = depth of in the linked list for free, we can move towards the front of the linked list for cost 1, we can swap two adjacent items that are not. Note that we can view paging as a list update problem with a different cost function, where { 0 if first k positions cost(query()) = 1 otherwise to simulate having k < n space in cache, and unbounded memory. 6
7 4.1 Different Heuristics Move to Front: move to the front of the list after querying (note, this is eactly the Least Recently Used cache eviction strategy in paging) Transpose: move one position closer to front Frequency count: Keeps items stored in decreasing order of access frequency References [1] Daniel Dominic Sleator, Robert Endre Tarjan. Amortized Efficiency of List Update and Paging Rules. Communications of the ACM, 8():0 08, [] Daniel Dominic Sleator, Robert Endre Tarjan. Self-adjusting binary search trees. J. ACM, 3(3):65686,
Lecture 9 Feb. 21, 2017
 CS 224: Advanced Algorithms Spring 2017 Lecture 9 Feb. 21, 2017 Prof. Jelani Nelson Scribe: Gavin McDowell 1 Overview Today: office hours 5-7, not 4-6. We re continuing with online algorithms. In this
CS 224: Advanced Algorithms Spring 2017 Lecture 9 Feb. 21, 2017 Prof. Jelani Nelson Scribe: Gavin McDowell 1 Overview Today: office hours 5-7, not 4-6. We re continuing with online algorithms. In this
Splay Trees. Splay Trees - 1
 Splay Trees In balanced tree schemes, explicit rules are followed to ensure balance. In splay trees, there are no such rules. Search, insert, and delete operations are like in binary search trees, except
Splay Trees In balanced tree schemes, explicit rules are followed to ensure balance. In splay trees, there are no such rules. Search, insert, and delete operations are like in binary search trees, except
6.854J / J Advanced Algorithms Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
15-451/651: Design & Analysis of Algorithms November 9 & 11, 2015 Lecture #19 & #20 last changed: November 10, 2015
 15-451/651: Design & Analysis of Algorithms November 9 & 11, 2015 Lecture #19 & #20 last changed: November 10, 2015 Last time we looked at algorithms for finding approximately-optimal solutions for NP-hard
15-451/651: Design & Analysis of Algorithms November 9 & 11, 2015 Lecture #19 & #20 last changed: November 10, 2015 Last time we looked at algorithms for finding approximately-optimal solutions for NP-hard
Introduction to Algorithms / Algorithms I Lecturer: Michael Dinitz Topic: Splay Trees Date: 9/27/16
 600.463 Introduction to lgoritms / lgoritms I Lecturer: Micael initz Topic: Splay Trees ate: 9/27/16 8.1 Introduction Today we re going to talk even more about binary searc trees. -trees, red-black trees,
600.463 Introduction to lgoritms / lgoritms I Lecturer: Micael initz Topic: Splay Trees ate: 9/27/16 8.1 Introduction Today we re going to talk even more about binary searc trees. -trees, red-black trees,
15-451/651: Design & Analysis of Algorithms October 23, 2018 Lecture #16: Online Algorithms last changed: October 22, 2018
 15-451/651: Design & Analysis of Algorithms October 23, 2018 Lecture #16: Online Algorithms last changed: October 22, 2018 Today we ll be looking at finding approximately-optimal solutions for problems
15-451/651: Design & Analysis of Algorithms October 23, 2018 Lecture #16: Online Algorithms last changed: October 22, 2018 Today we ll be looking at finding approximately-optimal solutions for problems
Homework #4. CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class
 Homework #4 CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class o Grades depend on neatness and clarity. o Write your answers with enough detail about your approach and concepts
Homework #4 CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class o Grades depend on neatness and clarity. o Write your answers with enough detail about your approach and concepts
Chapter 16. Binary Search Trees (BSTs)
 Chapter 16 Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types of search trees designed
Chapter 16 Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types of search trees designed
Successor. CS 361, Lecture 19. Tree-Successor. Outline
 Successor CS 361, Lecture 19 Jared Saia University of New Mexico The successor of a node x is the node that comes after x in the sorted order determined by an in-order tree walk. If all keys are distinct,
Successor CS 361, Lecture 19 Jared Saia University of New Mexico The successor of a node x is the node that comes after x in the sorted order determined by an in-order tree walk. If all keys are distinct,
Fibonacci Heaps Y Y o o u u c c an an s s u u b b m miitt P P ro ro b blle e m m S S et et 3 3 iin n t t h h e e b b o o x x u u p p fro fro n n tt..
 Fibonacci Heaps You You can can submit submit Problem Problem Set Set 3 in in the the box box up up front. front. Outline for Today Review from Last Time Quick refresher on binomial heaps and lazy binomial
Fibonacci Heaps You You can can submit submit Problem Problem Set Set 3 in in the the box box up up front. front. Outline for Today Review from Last Time Quick refresher on binomial heaps and lazy binomial
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binomial Heaps CLRS 6.1, 6.2, 6.3 University of Manitoba Priority queues A priority queue is an abstract data type formed by a set S of
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binomial Heaps CLRS 6.1, 6.2, 6.3 University of Manitoba Priority queues A priority queue is an abstract data type formed by a set S of
The potential function φ for the amortized analysis of an operation on Fibonacci heap at time (iteration) i is given by the following equation:
 Indian Institute of Information Technology Design and Manufacturing, Kancheepuram Chennai 600 127, India An Autonomous Institute under MHRD, Govt of India http://www.iiitdm.ac.in COM 01 Advanced Data Structures
Indian Institute of Information Technology Design and Manufacturing, Kancheepuram Chennai 600 127, India An Autonomous Institute under MHRD, Govt of India http://www.iiitdm.ac.in COM 01 Advanced Data Structures
CS4311 Design and Analysis of Algorithms. Lecture 14: Amortized Analysis I
 CS43 Design and Analysis of Algorithms Lecture 4: Amortized Analysis I About this lecture Given a data structure, amortized analysis studies in a sequence of operations, the average time to perform an
CS43 Design and Analysis of Algorithms Lecture 4: Amortized Analysis I About this lecture Given a data structure, amortized analysis studies in a sequence of operations, the average time to perform an
Splay Trees Goodrich, Tamassia, Dickerson Splay Trees 1
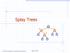 Spla Trees v 6 3 8 4 2004 Goodrich, Tamassia, Dickerson Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less
Spla Trees v 6 3 8 4 2004 Goodrich, Tamassia, Dickerson Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less
COSC160: Data Structures Binary Trees. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Data Structures Binary Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Binary Trees I. Implementations I. Memory Management II. Binary Search Tree I. Operations Binary Trees A
COSC160: Data Structures Binary Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Binary Trees I. Implementations I. Memory Management II. Binary Search Tree I. Operations Binary Trees A
Outline for Today. Quick refresher on binomial heaps and lazy binomial heaps. An important operation in many graph algorithms.
 Fibonacci Heaps Outline for Today Review from Last Time Quick refresher on binomial heaps and lazy binomial heaps. The Need for decrease-key An important operation in many graph algorithms. Fibonacci Heaps
Fibonacci Heaps Outline for Today Review from Last Time Quick refresher on binomial heaps and lazy binomial heaps. The Need for decrease-key An important operation in many graph algorithms. Fibonacci Heaps
Design and Analysis of Algorithms 演算法設計與分析. Lecture 8 November 16, 2016 洪國寶
 Design and Analysis of Algorithms 演算法設計與分析 Lecture 8 November 6, 206 洪國寶 Outline Review Amortized analysis Advanced data structures Binary heaps Binomial heaps Fibonacci heaps Data structures for disjoint
Design and Analysis of Algorithms 演算法設計與分析 Lecture 8 November 6, 206 洪國寶 Outline Review Amortized analysis Advanced data structures Binary heaps Binomial heaps Fibonacci heaps Data structures for disjoint
Heaps
 AdvancedAlgorithmics (4AP) Heaps Jaak Vilo 2009 Spring Jaak Vilo MTAT.03.190 Text Algorithms 1 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Binary heap http://en.wikipedia.org/wiki/binary_heap
AdvancedAlgorithmics (4AP) Heaps Jaak Vilo 2009 Spring Jaak Vilo MTAT.03.190 Text Algorithms 1 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Binary heap http://en.wikipedia.org/wiki/binary_heap
AVL Trees. The height of the left subtree can differ from the height of the right subtree by at most 1.
 AVL Trees In order to have a worst case running time for insert and delete operations to be O(log n), we must make it impossible for there to be a very long path in the binary search tree. The first balanced
AVL Trees In order to have a worst case running time for insert and delete operations to be O(log n), we must make it impossible for there to be a very long path in the binary search tree. The first balanced
1 Solutions to Tute09
 s to Tute0 Questions 4. - 4. are straight forward. Q. 4.4 Show that in a binary tree of N nodes, there are N + NULL pointers. Every node has outgoing pointers. Therefore there are N pointers. Each node,
s to Tute0 Questions 4. - 4. are straight forward. Q. 4.4 Show that in a binary tree of N nodes, there are N + NULL pointers. Every node has outgoing pointers. Therefore there are N pointers. Each node,
Sublinear Time Algorithms Oct 19, Lecture 1
 0368.416701 Sublinear Time Algorithms Oct 19, 2009 Lecturer: Ronitt Rubinfeld Lecture 1 Scribe: Daniel Shahaf 1 Sublinear-time algorithms: motivation Twenty years ago, there was practically no investigation
0368.416701 Sublinear Time Algorithms Oct 19, 2009 Lecturer: Ronitt Rubinfeld Lecture 1 Scribe: Daniel Shahaf 1 Sublinear-time algorithms: motivation Twenty years ago, there was practically no investigation
Fibonacci Heaps CLRS: Chapter 20 Last Revision: 21/09/04
 Fibonacci Heaps CLRS: Chapter 20 Last Revision: 21/09/04 1 Binary heap Binomial heap Fibonacci heap Procedure (worst-case) (worst-case) (amortized) Make-Heap Θ(1) Θ(1) Θ(1) Insert Θ(lg n) O(lg n) Θ(1)
Fibonacci Heaps CLRS: Chapter 20 Last Revision: 21/09/04 1 Binary heap Binomial heap Fibonacci heap Procedure (worst-case) (worst-case) (amortized) Make-Heap Θ(1) Θ(1) Θ(1) Insert Θ(lg n) O(lg n) Θ(1)
Optimal Satisficing Tree Searches
 Optimal Satisficing Tree Searches Dan Geiger and Jeffrey A. Barnett Northrop Research and Technology Center One Research Park Palos Verdes, CA 90274 Abstract We provide an algorithm that finds optimal
Optimal Satisficing Tree Searches Dan Geiger and Jeffrey A. Barnett Northrop Research and Technology Center One Research Park Palos Verdes, CA 90274 Abstract We provide an algorithm that finds optimal
3/7/13. Binomial Tree. Binomial Tree. Binomial Tree. Binomial Tree. Number of nodes with respect to k? N(B o ) = 1 N(B k ) = 2 N(B k-1 ) = 2 k
 //1 Adapted from: Kevin Wayne B k B k B k : a binomial tree with the addition of a left child with another binomial tree Number of nodes with respect to k? N(B o ) = 1 N(B k ) = 2 N( ) = 2 k B 1 B 2 B
//1 Adapted from: Kevin Wayne B k B k B k : a binomial tree with the addition of a left child with another binomial tree Number of nodes with respect to k? N(B o ) = 1 N(B k ) = 2 N( ) = 2 k B 1 B 2 B
Heaps. Heap/Priority queue. Binomial heaps: Advanced Algorithmics (4AP) Heaps Binary heap. Binomial heap. Jaak Vilo 2009 Spring
 .0.00 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Advanced Algorithmics (4AP) Heaps Jaak Vilo 00 Spring Binary heap http://en.wikipedia.org/wiki/binary_heap Binomial heap http://en.wikipedia.org/wiki/binomial_heap
.0.00 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Advanced Algorithmics (4AP) Heaps Jaak Vilo 00 Spring Binary heap http://en.wikipedia.org/wiki/binary_heap Binomial heap http://en.wikipedia.org/wiki/binomial_heap
Design and Analysis of Algorithms 演算法設計與分析. Lecture 9 November 19, 2014 洪國寶
 Design and Analysis of Algorithms 演算法設計與分析 Lecture 9 November 19, 2014 洪國寶 1 Outline Advanced data structures Binary heaps(review) Binomial heaps Fibonacci heaps Data structures for disjoint sets 2 Mergeable
Design and Analysis of Algorithms 演算法設計與分析 Lecture 9 November 19, 2014 洪國寶 1 Outline Advanced data structures Binary heaps(review) Binomial heaps Fibonacci heaps Data structures for disjoint sets 2 Mergeable
Advanced Algorithmics (4AP) Heaps
 Advanced Algorithmics (4AP) Heaps Jaak Vilo 2009 Spring Jaak Vilo MTAT.03.190 Text Algorithms 1 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Binary heap http://en.wikipedia.org/wiki/binary
Advanced Algorithmics (4AP) Heaps Jaak Vilo 2009 Spring Jaak Vilo MTAT.03.190 Text Algorithms 1 Heaps http://en.wikipedia.org/wiki/category:heaps_(structure) Binary heap http://en.wikipedia.org/wiki/binary
CSCI 104 B-Trees (2-3, 2-3-4) and Red/Black Trees. Mark Redekopp David Kempe
 1 CSCI 104 B-Trees (2-3, 2-3-4) and Red/Black Trees Mark Redekopp David Kempe 2 An example of B-Trees 2-3 TREES 3 Definition 2-3 Tree is a tree where Non-leaf nodes have 1 value & 2 children or 2 values
1 CSCI 104 B-Trees (2-3, 2-3-4) and Red/Black Trees Mark Redekopp David Kempe 2 An example of B-Trees 2-3 TREES 3 Definition 2-3 Tree is a tree where Non-leaf nodes have 1 value & 2 children or 2 values
> asympt( ln( n! ), n ); n 360n n
 8.4 Heap Sort (heapsort) We will now look at our first (n ln(n)) algorithm: heap sort. It will use a data structure that we have already seen: a binary heap. 8.4.1 Strategy and Run-time Analysis Given
8.4 Heap Sort (heapsort) We will now look at our first (n ln(n)) algorithm: heap sort. It will use a data structure that we have already seen: a binary heap. 8.4.1 Strategy and Run-time Analysis Given
Design and Analysis of Algorithms. Lecture 9 November 20, 2013 洪國寶
 Design and Analysis of Algorithms 演算法設計與分析 Lecture 9 November 20, 2013 洪國寶 1 Outline Advanced data structures Binary heaps (review) Binomial heaps Fibonacci heaps Dt Data structures t for disjoint dijitsets
Design and Analysis of Algorithms 演算法設計與分析 Lecture 9 November 20, 2013 洪國寶 1 Outline Advanced data structures Binary heaps (review) Binomial heaps Fibonacci heaps Dt Data structures t for disjoint dijitsets
Lecture 4: Divide and Conquer
 Lecture 4: Divide and Conquer Divide and Conquer Merge sort is an example of a divide-and-conquer algorithm Recall the three steps (at each level to solve a divideand-conquer problem recursively Divide
Lecture 4: Divide and Conquer Divide and Conquer Merge sort is an example of a divide-and-conquer algorithm Recall the three steps (at each level to solve a divideand-conquer problem recursively Divide
1 Online Problem Examples
 Comp 260: Advanced Algorithms Tufts University, Spring 2018 Prof. Lenore Cowen Scribe: Isaiah Mindich Lecture 9: Online Algorithms All of the algorithms we have studied so far operate on the assumption
Comp 260: Advanced Algorithms Tufts University, Spring 2018 Prof. Lenore Cowen Scribe: Isaiah Mindich Lecture 9: Online Algorithms All of the algorithms we have studied so far operate on the assumption
2. This algorithm does not solve the problem of finding a maximum cardinality set of non-overlapping intervals. Consider the following intervals:
 1. No solution. 2. This algorithm does not solve the problem of finding a maximum cardinality set of non-overlapping intervals. Consider the following intervals: E A B C D Obviously, the optimal solution
1. No solution. 2. This algorithm does not solve the problem of finding a maximum cardinality set of non-overlapping intervals. Consider the following intervals: E A B C D Obviously, the optimal solution
On the Optimality of a Family of Binary Trees Techical Report TR
 On the Optimality of a Family of Binary Trees Techical Report TR-011101-1 Dana Vrajitoru and William Knight Indiana University South Bend Department of Computer and Information Sciences Abstract In this
On the Optimality of a Family of Binary Trees Techical Report TR-011101-1 Dana Vrajitoru and William Knight Indiana University South Bend Department of Computer and Information Sciences Abstract In this
CMSC 441: Design & Analysis of Algorithms
 CMSC 441: Design & Analysis of Algorithms Hillol Kargupta http://www.cs.umbc.edu/~hillol/ hillol@cs.umbc.edu Today s Topics Amortized analysis April 19, 2011 CMSC 641 2 Amortized Analysis Aggregate Method
CMSC 441: Design & Analysis of Algorithms Hillol Kargupta http://www.cs.umbc.edu/~hillol/ hillol@cs.umbc.edu Today s Topics Amortized analysis April 19, 2011 CMSC 641 2 Amortized Analysis Aggregate Method
Binary Tree Applications
 Binary Tree Applications Lecture 32 Section 19.2 Robb T. Koether Hampden-Sydney College Wed, Apr 17, 2013 Robb T. Koether (Hampden-Sydney College) Binary Tree Applications Wed, Apr 17, 2013 1 / 46 1 Expression
Binary Tree Applications Lecture 32 Section 19.2 Robb T. Koether Hampden-Sydney College Wed, Apr 17, 2013 Robb T. Koether (Hampden-Sydney College) Binary Tree Applications Wed, Apr 17, 2013 1 / 46 1 Expression
Outline for this Week
 Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, fexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, fexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
PARELLIZATION OF DIJKSTRA S ALGORITHM: COMPARISON OF VARIOUS PRIORITY QUEUES
 PARELLIZATION OF DIJKSTRA S ALGORITHM: COMPARISON OF VARIOUS PRIORITY QUEUES WIKTOR JAKUBIUK, KESHAV PURANMALKA 1. Introduction Dijkstra s algorithm solves the single-sourced shorest path problem on a
PARELLIZATION OF DIJKSTRA S ALGORITHM: COMPARISON OF VARIOUS PRIORITY QUEUES WIKTOR JAKUBIUK, KESHAV PURANMALKA 1. Introduction Dijkstra s algorithm solves the single-sourced shorest path problem on a
SET 1C Binary Trees. 2. (i) Define the height of a binary tree or subtree and also define a height balanced (AVL) tree. (2)
 SET 1C Binary Trees 1. Construct a binary tree whose preorder traversal is K L N M P R Q S T and inorder traversal is N L K P R M S Q T 2. (i) Define the height of a binary tree or subtree and also define
SET 1C Binary Trees 1. Construct a binary tree whose preorder traversal is K L N M P R Q S T and inorder traversal is N L K P R M S Q T 2. (i) Define the height of a binary tree or subtree and also define
Introduction to Greedy Algorithms: Huffman Codes
 Introduction to Greedy Algorithms: Huffman Codes Yufei Tao ITEE University of Queensland In computer science, one interesting method to design algorithms is to go greedy, namely, keep doing the thing that
Introduction to Greedy Algorithms: Huffman Codes Yufei Tao ITEE University of Queensland In computer science, one interesting method to design algorithms is to go greedy, namely, keep doing the thing that
Unit 6: Amortized Analysis
 : Amortized Analysis Course contents: Aggregate method Accounting method Potential method Reading: Chapter 17 Y.-W. Chang 1 Amortized Analysis Why Amortized Analysis? Find a tight bound of a sequence of
: Amortized Analysis Course contents: Aggregate method Accounting method Potential method Reading: Chapter 17 Y.-W. Chang 1 Amortized Analysis Why Amortized Analysis? Find a tight bound of a sequence of
CS224W: Social and Information Network Analysis Jure Leskovec, Stanford University
 CS224W: Social and Information Network Analysis Jure Leskovec, Stanford University http://cs224w.stanford.edu 10/27/16 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis, http://cs224w.stanford.edu
CS224W: Social and Information Network Analysis Jure Leskovec, Stanford University http://cs224w.stanford.edu 10/27/16 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis, http://cs224w.stanford.edu
PRIORITY QUEUES. binary heaps d-ary heaps binomial heaps Fibonacci heaps. Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley
 PRIORITY QUEUES binary heaps d-ary heaps binomial heaps Fibonacci heaps Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated
PRIORITY QUEUES binary heaps d-ary heaps binomial heaps Fibonacci heaps Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos Last updated
Priority Queues 9/10. Binary heaps Leftist heaps Binomial heaps Fibonacci heaps
 Priority Queues 9/10 Binary heaps Leftist heaps Binomial heaps Fibonacci heaps Priority queues are important in, among other things, operating systems (process control in multitasking systems), search
Priority Queues 9/10 Binary heaps Leftist heaps Binomial heaps Fibonacci heaps Priority queues are important in, among other things, operating systems (process control in multitasking systems), search
Outline. Objective. Previous Results Our Results Discussion Current Research. 1 Motivation. 2 Model. 3 Results
 On Threshold Esteban 1 Adam 2 Ravi 3 David 4 Sergei 1 1 Stanford University 2 Harvard University 3 Yahoo! Research 4 Carleton College The 8th ACM Conference on Electronic Commerce EC 07 Outline 1 2 3 Some
On Threshold Esteban 1 Adam 2 Ravi 3 David 4 Sergei 1 1 Stanford University 2 Harvard University 3 Yahoo! Research 4 Carleton College The 8th ACM Conference on Electronic Commerce EC 07 Outline 1 2 3 Some
Administration CSE 326: Data Structures
 Administration CSE : Data Structures Binomial Queues Neva Cherniavsky Summer Released today: Project, phase B Due today: Homework Released today: Homework I have office hours tomorrow // Binomial Queues
Administration CSE : Data Structures Binomial Queues Neva Cherniavsky Summer Released today: Project, phase B Due today: Homework Released today: Homework I have office hours tomorrow // Binomial Queues
Outline for this Week
 Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, flexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, flexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
Algorithms PRIORITY QUEUES. binary heaps d-ary heaps binomial heaps Fibonacci heaps. binary heaps d-ary heaps binomial heaps Fibonacci heaps
 Priority queue data type Lecture slides by Kevin Wayne Copyright 05 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos PRIORITY QUEUES binary heaps d-ary heaps binomial heaps Fibonacci
Priority queue data type Lecture slides by Kevin Wayne Copyright 05 Pearson-Addison Wesley http://www.cs.princeton.edu/~wayne/kleinberg-tardos PRIORITY QUEUES binary heaps d-ary heaps binomial heaps Fibonacci
Price of Anarchy Smoothness Price of Stability. Price of Anarchy. Algorithmic Game Theory
 Smoothness Price of Stability Algorithmic Game Theory Smoothness Price of Stability Recall Recall for Nash equilibria: Strategic game Γ, social cost cost(s) for every state s of Γ Consider Σ PNE as the
Smoothness Price of Stability Algorithmic Game Theory Smoothness Price of Stability Recall Recall for Nash equilibria: Strategic game Γ, social cost cost(s) for every state s of Γ Consider Σ PNE as the
1 Binomial Tree. Structural Properties:
 Indian Institute of Information Technology Design and Manufacturing, Kancheepuram Chennai 600, India An Autonomous Institute under MHRD, Govt of India http://www.iiitdm.ac.in COM 0 Advanced Data Structures
Indian Institute of Information Technology Design and Manufacturing, Kancheepuram Chennai 600, India An Autonomous Institute under MHRD, Govt of India http://www.iiitdm.ac.in COM 0 Advanced Data Structures
Meld(Q 1,Q 2 ) merge two sets
 Priority Queues MakeQueue Insert(Q,k,p) Delete(Q,k) DeleteMin(Q) Meld(Q 1,Q 2 ) Empty(Q) Size(Q) FindMin(Q) create new empty queue insert key k with priority p delete key k (given a pointer) delete key
Priority Queues MakeQueue Insert(Q,k,p) Delete(Q,k) DeleteMin(Q) Meld(Q 1,Q 2 ) Empty(Q) Size(Q) FindMin(Q) create new empty queue insert key k with priority p delete key k (given a pointer) delete key
On the Optimality of a Family of Binary Trees
 On the Optimality of a Family of Binary Trees Dana Vrajitoru Computer and Information Sciences Department Indiana University South Bend South Bend, IN 46645 Email: danav@cs.iusb.edu William Knight Computer
On the Optimality of a Family of Binary Trees Dana Vrajitoru Computer and Information Sciences Department Indiana University South Bend South Bend, IN 46645 Email: danav@cs.iusb.edu William Knight Computer
CSE 100: TREAPS AND RANDOMIZED SEARCH TREES
 CSE 100: TREAPS AND RANDOMIZED SEARCH TREES Midterm Review Practice Midterm covered during Sunday discussion Today Run time analysis of building the Huffman tree AVL rotations and treaps Huffman s algorithm
CSE 100: TREAPS AND RANDOMIZED SEARCH TREES Midterm Review Practice Midterm covered during Sunday discussion Today Run time analysis of building the Huffman tree AVL rotations and treaps Huffman s algorithm
Lecture 5. 1 Online Learning. 1.1 Learning Setup (Perspective of Universe) CSCI699: Topics in Learning & Game Theory
 CSCI699: Topics in Learning & Game Theory Lecturer: Shaddin Dughmi Lecture 5 Scribes: Umang Gupta & Anastasia Voloshinov In this lecture, we will give a brief introduction to online learning and then go
CSCI699: Topics in Learning & Game Theory Lecturer: Shaddin Dughmi Lecture 5 Scribes: Umang Gupta & Anastasia Voloshinov In this lecture, we will give a brief introduction to online learning and then go
Recitation 1. Solving Recurrences. 1.1 Announcements. Welcome to 15210!
 Recitation 1 Solving Recurrences 1.1 Announcements Welcome to 1510! The course website is http://www.cs.cmu.edu/ 1510/. It contains the syllabus, schedule, library documentation, staff contact information,
Recitation 1 Solving Recurrences 1.1 Announcements Welcome to 1510! The course website is http://www.cs.cmu.edu/ 1510/. It contains the syllabus, schedule, library documentation, staff contact information,
About this lecture. Three Methods for the Same Purpose (1) Aggregate Method (2) Accounting Method (3) Potential Method.
 About this lecture Given a data structure, amortized analysis studies in a sequence of operations, the average time to perform an operation Introduce amortized cost of an operation Three Methods for the
About this lecture Given a data structure, amortized analysis studies in a sequence of operations, the average time to perform an operation Introduce amortized cost of an operation Three Methods for the
2 all subsequent nodes. 252 all subsequent nodes. 401 all subsequent nodes. 398 all subsequent nodes. 330 all subsequent nodes
 ¼ À ÈÌ Ê ½¾ ÈÊÇ Ä ÅË ½µ ½¾º¾¹½ ¾µ ½¾º¾¹ µ ½¾º¾¹ µ ½¾º¾¹ µ ½¾º ¹ µ ½¾º ¹ µ ½¾º ¹¾ µ ½¾º ¹ µ ½¾¹¾ ½¼µ ½¾¹ ½ (1) CLR 12.2-1 Based on the structure of the binary tree, and the procedure of Tree-Search, any
¼ À ÈÌ Ê ½¾ ÈÊÇ Ä ÅË ½µ ½¾º¾¹½ ¾µ ½¾º¾¹ µ ½¾º¾¹ µ ½¾º¾¹ µ ½¾º ¹ µ ½¾º ¹ µ ½¾º ¹¾ µ ½¾º ¹ µ ½¾¹¾ ½¼µ ½¾¹ ½ (1) CLR 12.2-1 Based on the structure of the binary tree, and the procedure of Tree-Search, any
Lecture 2: The Simple Story of 2-SAT
 0510-7410: Topics in Algorithms - Random Satisfiability March 04, 2014 Lecture 2: The Simple Story of 2-SAT Lecturer: Benny Applebaum Scribe(s): Mor Baruch 1 Lecture Outline In this talk we will show that
0510-7410: Topics in Algorithms - Random Satisfiability March 04, 2014 Lecture 2: The Simple Story of 2-SAT Lecturer: Benny Applebaum Scribe(s): Mor Baruch 1 Lecture Outline In this talk we will show that
Foundations of Artificial Intelligence
 Foundations of Artificial Intelligence 44. Monte-Carlo Tree Search: Introduction Thomas Keller Universität Basel May 27, 2016 Board Games: Overview chapter overview: 41. Introduction and State of the Art
Foundations of Artificial Intelligence 44. Monte-Carlo Tree Search: Introduction Thomas Keller Universität Basel May 27, 2016 Board Games: Overview chapter overview: 41. Introduction and State of the Art
Data Structures. Binomial Heaps Fibonacci Heaps. Haim Kaplan & Uri Zwick December 2013
 Data Structures Binomial Heaps Fibonacci Heaps Haim Kaplan & Uri Zwick December 13 1 Heaps / Priority queues Binary Heaps Binomial Heaps Lazy Binomial Heaps Fibonacci Heaps Insert Find-min Delete-min Decrease-key
Data Structures Binomial Heaps Fibonacci Heaps Haim Kaplan & Uri Zwick December 13 1 Heaps / Priority queues Binary Heaps Binomial Heaps Lazy Binomial Heaps Fibonacci Heaps Insert Find-min Delete-min Decrease-key
DRAFT. 1 exercise in state (S, t), π(s, t) = 0 do not exercise in state (S, t) Review of the Risk Neutral Stock Dynamics
 Chapter 12 American Put Option Recall that the American option has strike K and maturity T and gives the holder the right to exercise at any time in [0, T ]. The American option is not straightforward
Chapter 12 American Put Option Recall that the American option has strike K and maturity T and gives the holder the right to exercise at any time in [0, T ]. The American option is not straightforward
Max Registers, Counters and Monotone Circuits
 James Aspnes 1 Hagit Attiya 2 Keren Censor 2 1 Yale 2 Technion Counters Model Collects Our goal: build a cheap counter for an asynchronous shared-memory system. Two operations: increment and read. Read
James Aspnes 1 Hagit Attiya 2 Keren Censor 2 1 Yale 2 Technion Counters Model Collects Our goal: build a cheap counter for an asynchronous shared-memory system. Two operations: increment and read. Read
Binary Search Tree and AVL Trees. Binary Search Tree. Binary Search Tree. Binary Search Tree. Techniques: How does the BST works?
 Binary Searc Tree and AVL Trees Binary Searc Tree A commonly-used data structure for storing and retrieving records in main memory PUC-Rio Eduardo S. Laber Binary Searc Tree Binary Searc Tree A commonly-used
Binary Searc Tree and AVL Trees Binary Searc Tree A commonly-used data structure for storing and retrieving records in main memory PUC-Rio Eduardo S. Laber Binary Searc Tree Binary Searc Tree A commonly-used
COMP251: Amortized Analysis
 COMP251: Amortized Analysis Jérôme Waldispühl School of Computer Science McGill University Based on (Cormen et al., 2009) T n = 2 % T n 5 + n( What is the height of the recursion tree? log ( n log, n log
COMP251: Amortized Analysis Jérôme Waldispühl School of Computer Science McGill University Based on (Cormen et al., 2009) T n = 2 % T n 5 + n( What is the height of the recursion tree? log ( n log, n log
CS473-Algorithms I. Lecture 12. Amortized Analysis. Cevdet Aykanat - Bilkent University Computer Engineering Department
 CS473-Algorithms I Lecture 12 Amortized Analysis 1 Amortized Analysis Key point: The time required to perform a sequence of data structure operations is averaged over all operations performed Amortized
CS473-Algorithms I Lecture 12 Amortized Analysis 1 Amortized Analysis Key point: The time required to perform a sequence of data structure operations is averaged over all operations performed Amortized
1 Overview. 2 The Gradient Descent Algorithm. AM 221: Advanced Optimization Spring 2016
 AM 22: Advanced Optimization Spring 206 Prof. Yaron Singer Lecture 9 February 24th Overview In the previous lecture we reviewed results from multivariate calculus in preparation for our journey into convex
AM 22: Advanced Optimization Spring 206 Prof. Yaron Singer Lecture 9 February 24th Overview In the previous lecture we reviewed results from multivariate calculus in preparation for our journey into convex
Yao s Minimax Principle
 Complexity of algorithms The complexity of an algorithm is usually measured with respect to the size of the input, where size may for example refer to the length of a binary word describing the input,
Complexity of algorithms The complexity of an algorithm is usually measured with respect to the size of the input, where size may for example refer to the length of a binary word describing the input,
Lecture 5: Tuesday, January 27, Peterson s Algorithm satisfies the No Starvation property (Theorem 1)
 Com S 611 Spring Semester 2015 Advanced Topics on Distributed and Concurrent Algorithms Lecture 5: Tuesday, January 27, 2015 Instructor: Soma Chaudhuri Scribe: Nik Kinkel 1 Introduction This lecture covers
Com S 611 Spring Semester 2015 Advanced Topics on Distributed and Concurrent Algorithms Lecture 5: Tuesday, January 27, 2015 Instructor: Soma Chaudhuri Scribe: Nik Kinkel 1 Introduction This lecture covers
1) S = {s}; 2) for each u V {s} do 3) dist[u] = cost(s, u); 4) Insert u into a 2-3 tree Q with dist[u] as the key; 5) for i = 1 to n 1 do 6) Identify
![1) S = {s}; 2) for each u V {s} do 3) dist[u] = cost(s, u); 4) Insert u into a 2-3 tree Q with dist[u] as the key; 5) for i = 1 to n 1 do 6) Identify 1) S = {s}; 2) for each u V {s} do 3) dist[u] = cost(s, u); 4) Insert u into a 2-3 tree Q with dist[u] as the key; 5) for i = 1 to n 1 do 6) Identify](/thumbs/77/75720566.jpg) CSE 3500 Algorithms and Complexity Fall 2016 Lecture 17: October 25, 2016 Dijkstra s Algorithm Dijkstra s algorithm for the SSSP problem generates the shortest paths in nondecreasing order of the shortest
CSE 3500 Algorithms and Complexity Fall 2016 Lecture 17: October 25, 2016 Dijkstra s Algorithm Dijkstra s algorithm for the SSSP problem generates the shortest paths in nondecreasing order of the shortest
CS 573: Algorithmic Game Theory Lecture date: March 26th, 2008
 CS 573: Algorithmic Game Theory Lecture date: March 26th, 28 Instructor: Chandra Chekuri Scribe: Qi Li Contents Overview: Auctions in the Bayesian setting 1 1 Single item auction 1 1.1 Setting............................................
CS 573: Algorithmic Game Theory Lecture date: March 26th, 28 Instructor: Chandra Chekuri Scribe: Qi Li Contents Overview: Auctions in the Bayesian setting 1 1 Single item auction 1 1.1 Setting............................................
Chapter 5: Algorithms
 Chapter 5: Algorithms Computer Science: An Overview Tenth Edition by J. Glenn Brookshear Presentation files modified by Farn Wang Copyright 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Chapter 5: Algorithms Computer Science: An Overview Tenth Edition by J. Glenn Brookshear Presentation files modified by Farn Wang Copyright 2008 Pearson Education, Inc. Publishing as Pearson Addison-Wesley
Smoothed Analysis of Binary Search Trees
 Smoothed Analysis of Binary Search Trees Bodo Manthey and Rüdiger Reischuk Universität zu Lübeck, Institut für Theoretische Informatik Ratzeburger Allee 160, 23538 Lübeck, Germany manthey/reischuk@tcs.uni-luebeck.de
Smoothed Analysis of Binary Search Trees Bodo Manthey and Rüdiger Reischuk Universität zu Lübeck, Institut für Theoretische Informatik Ratzeburger Allee 160, 23538 Lübeck, Germany manthey/reischuk@tcs.uni-luebeck.de
Heap Building Bounds
 Heap Building Bounds Zhentao Li 1 and Bruce A. Reed 2 1 School of Computer Science, McGill University zhentao.li@mail.mcgill.ca 2 School of Computer Science, McGill University breed@cs.mcgill.ca Abstract.
Heap Building Bounds Zhentao Li 1 and Bruce A. Reed 2 1 School of Computer Science, McGill University zhentao.li@mail.mcgill.ca 2 School of Computer Science, McGill University breed@cs.mcgill.ca Abstract.
MBF1413 Quantitative Methods
 MBF1413 Quantitative Methods Prepared by Dr Khairul Anuar 4: Decision Analysis Part 1 www.notes638.wordpress.com 1. Problem Formulation a. Influence Diagrams b. Payoffs c. Decision Trees Content 2. Decision
MBF1413 Quantitative Methods Prepared by Dr Khairul Anuar 4: Decision Analysis Part 1 www.notes638.wordpress.com 1. Problem Formulation a. Influence Diagrams b. Payoffs c. Decision Trees Content 2. Decision
Binary and Binomial Heaps. Disclaimer: these slides were adapted from the ones by Kevin Wayne
 Binary and Binomial Heaps Disclaimer: these slides were adapted from the ones by Kevin Wayne Priority Queues Supports the following operations. Insert element x. Return min element. Return and delete minimum
Binary and Binomial Heaps Disclaimer: these slides were adapted from the ones by Kevin Wayne Priority Queues Supports the following operations. Insert element x. Return min element. Return and delete minimum
Online Appendix Optimal Time-Consistent Government Debt Maturity D. Debortoli, R. Nunes, P. Yared. A. Proofs
 Online Appendi Optimal Time-Consistent Government Debt Maturity D. Debortoli, R. Nunes, P. Yared A. Proofs Proof of Proposition 1 The necessity of these conditions is proved in the tet. To prove sufficiency,
Online Appendi Optimal Time-Consistent Government Debt Maturity D. Debortoli, R. Nunes, P. Yared A. Proofs Proof of Proposition 1 The necessity of these conditions is proved in the tet. To prove sufficiency,
Markov Decision Processes
 Markov Decision Processes Robert Platt Northeastern University Some images and slides are used from: 1. CS188 UC Berkeley 2. AIMA 3. Chris Amato Stochastic domains So far, we have studied search Can use
Markov Decision Processes Robert Platt Northeastern University Some images and slides are used from: 1. CS188 UC Berkeley 2. AIMA 3. Chris Amato Stochastic domains So far, we have studied search Can use
Online Algorithms SS 2013
 Faculty of Computer Science, Electrical Engineering and Mathematics Algorithms and Complexity research group Jun.-Prof. Dr. Alexander Skopalik Online Algorithms SS 2013 Summary of the lecture by Vanessa
Faculty of Computer Science, Electrical Engineering and Mathematics Algorithms and Complexity research group Jun.-Prof. Dr. Alexander Skopalik Online Algorithms SS 2013 Summary of the lecture by Vanessa
Lecture 7. Analysis of algorithms: Amortized Analysis. January Lecture 7
 Analysis of algorithms: Amortized Analysis January 2014 What is amortized analysis? Amortized analysis: set of techniques (Aggregate method, Accounting method, Potential method) for proving upper (worst-case)
Analysis of algorithms: Amortized Analysis January 2014 What is amortized analysis? Amortized analysis: set of techniques (Aggregate method, Accounting method, Potential method) for proving upper (worst-case)
Handout 4: Deterministic Systems and the Shortest Path Problem
 SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 4: Deterministic Systems and the Shortest Path Problem Instructor: Shiqian Ma January 27, 2014 Suggested Reading: Bertsekas
SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 4: Deterministic Systems and the Shortest Path Problem Instructor: Shiqian Ma January 27, 2014 Suggested Reading: Bertsekas
Priority queue. Advanced Algorithmics (6EAP) Binary heap. Heap/Priority queue. Binomial heaps: Merge two heaps.
 Priority queue Advanced Algorithmics (EAP) MTAT.03.38 Heaps Jaak Vilo 0 Spring Insert Q, x Retrieve x from Q s.t. x.value is min (or max) Sorted linked list: O(n) to insert x into right place O() access-
Priority queue Advanced Algorithmics (EAP) MTAT.03.38 Heaps Jaak Vilo 0 Spring Insert Q, x Retrieve x from Q s.t. x.value is min (or max) Sorted linked list: O(n) to insert x into right place O() access-
CSCE 750, Fall 2009 Quizzes with Answers
 CSCE 750, Fall 009 Quizzes with Answers Stephen A. Fenner September 4, 011 1. Give an exact closed form for Simplify your answer as much as possible. k 3 k+1. We reduce the expression to a form we ve already
CSCE 750, Fall 009 Quizzes with Answers Stephen A. Fenner September 4, 011 1. Give an exact closed form for Simplify your answer as much as possible. k 3 k+1. We reduce the expression to a form we ve already
CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS
 CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS November 17, 2016. Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question.
CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS November 17, 2016. Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question.
Initializing A Max Heap. Initializing A Max Heap
 Initializing A Max Heap 3 4 5 6 7 8 70 8 input array = [-,,, 3, 4, 5, 6, 7, 8,, 0, ] Initializing A Max Heap 3 4 5 6 7 8 70 8 Start at rightmost array position that has a child. Index is n/. Initializing
Initializing A Max Heap 3 4 5 6 7 8 70 8 input array = [-,,, 3, 4, 5, 6, 7, 8,, 0, ] Initializing A Max Heap 3 4 5 6 7 8 70 8 Start at rightmost array position that has a child. Index is n/. Initializing
Lecture Quantitative Finance Spring Term 2015
 and Lecture Quantitative Finance Spring Term 2015 Prof. Dr. Erich Walter Farkas Lecture 06: March 26, 2015 1 / 47 Remember and Previous chapters: introduction to the theory of options put-call parity fundamentals
and Lecture Quantitative Finance Spring Term 2015 Prof. Dr. Erich Walter Farkas Lecture 06: March 26, 2015 1 / 47 Remember and Previous chapters: introduction to the theory of options put-call parity fundamentals
Chapter 7 One-Dimensional Search Methods
 Chapter 7 One-Dimensional Search Methods An Introduction to Optimization Spring, 2014 1 Wei-Ta Chu Golden Section Search! Determine the minimizer of a function over a closed interval, say. The only assumption
Chapter 7 One-Dimensional Search Methods An Introduction to Optimization Spring, 2014 1 Wei-Ta Chu Golden Section Search! Determine the minimizer of a function over a closed interval, say. The only assumption
Algorithmic Game Theory and Applications. Lecture 11: Games of Perfect Information
 Algorithmic Game Theory and Applications Lecture 11: Games of Perfect Information Kousha Etessami finite games of perfect information Recall, a perfect information (PI) game has only 1 node per information
Algorithmic Game Theory and Applications Lecture 11: Games of Perfect Information Kousha Etessami finite games of perfect information Recall, a perfect information (PI) game has only 1 node per information
CS 343: Artificial Intelligence
 CS 343: Artificial Intelligence Markov Decision Processes II Prof. Scott Niekum The University of Texas at Austin [These slides based on those of Dan Klein and Pieter Abbeel for CS188 Intro to AI at UC
CS 343: Artificial Intelligence Markov Decision Processes II Prof. Scott Niekum The University of Texas at Austin [These slides based on those of Dan Klein and Pieter Abbeel for CS188 Intro to AI at UC
Information Theory and Coding Prof. S. N. Merchant Department of Electrical Engineering Indian Institute of Technology, Bombay
 Information Theory and Coding Prof. S. N. Merchant Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture - 15 Adaptive Huffman Coding Part I Huffman code are optimal for a
Information Theory and Coding Prof. S. N. Merchant Department of Electrical Engineering Indian Institute of Technology, Bombay Lecture - 15 Adaptive Huffman Coding Part I Huffman code are optimal for a
A relation on 132-avoiding permutation patterns
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. VOL, 205, 285 302 A relation on 32-avoiding permutation patterns Natalie Aisbett School of Mathematics and Statistics, University of Sydney,
Discrete Mathematics and Theoretical Computer Science DMTCS vol. VOL, 205, 285 302 A relation on 32-avoiding permutation patterns Natalie Aisbett School of Mathematics and Statistics, University of Sydney,
The suffix binary search tree and suffix AVL tree
 Journal of Discrete Algorithms 1 (2003) 387 408 www.elsevier.com/locate/jda The suffix binary search tree and suffix AVL tree Robert W. Irving, Lorna Love Department of Computing Science, University of
Journal of Discrete Algorithms 1 (2003) 387 408 www.elsevier.com/locate/jda The suffix binary search tree and suffix AVL tree Robert W. Irving, Lorna Love Department of Computing Science, University of
CS360 Homework 14 Solution
 CS360 Homework 14 Solution Markov Decision Processes 1) Invent a simple Markov decision process (MDP) with the following properties: a) it has a goal state, b) its immediate action costs are all positive,
CS360 Homework 14 Solution Markov Decision Processes 1) Invent a simple Markov decision process (MDP) with the following properties: a) it has a goal state, b) its immediate action costs are all positive,
Lecture 17. The model is parametrized by the time period, δt, and three fixed constant parameters, v, σ and the riskless rate r.
 Lecture 7 Overture to continuous models Before rigorously deriving the acclaimed Black-Scholes pricing formula for the value of a European option, we developed a substantial body of material, in continuous
Lecture 7 Overture to continuous models Before rigorously deriving the acclaimed Black-Scholes pricing formula for the value of a European option, we developed a substantial body of material, in continuous
Design and Analysis of Algorithms
 Design and Analysis of Algorithms Instructor: Sharma Thankachan Lecture 9: Binomial Heap Slides modified from Dr. Hon, with permission 1 About this lecture Binary heap supports various operations quickly:
Design and Analysis of Algorithms Instructor: Sharma Thankachan Lecture 9: Binomial Heap Slides modified from Dr. Hon, with permission 1 About this lecture Binary heap supports various operations quickly:
CS 188: Artificial Intelligence. Outline
 C 188: Artificial Intelligence Markov Decision Processes (MDPs) Pieter Abbeel UC Berkeley ome slides adapted from Dan Klein 1 Outline Markov Decision Processes (MDPs) Formalism Value iteration In essence
C 188: Artificial Intelligence Markov Decision Processes (MDPs) Pieter Abbeel UC Berkeley ome slides adapted from Dan Klein 1 Outline Markov Decision Processes (MDPs) Formalism Value iteration In essence
Problems and Solutions
 1 CHAPTER 1 Problems 1.1 Problems on Bonds Exercise 1.1 On 12/04/01, consider a fixed-coupon bond whose features are the following: face value: $1,000 coupon rate: 8% coupon frequency: semiannual maturity:
1 CHAPTER 1 Problems 1.1 Problems on Bonds Exercise 1.1 On 12/04/01, consider a fixed-coupon bond whose features are the following: face value: $1,000 coupon rate: 8% coupon frequency: semiannual maturity:
Fundamental Algorithms - Surprise Test
 Technische Universität München Fakultät für Informatik Lehrstuhl für Effiziente Algorithmen Dmytro Chibisov Sandeep Sadanandan Winter Semester 007/08 Sheet Model Test January 16, 008 Fundamental Algorithms
Technische Universität München Fakultät für Informatik Lehrstuhl für Effiziente Algorithmen Dmytro Chibisov Sandeep Sadanandan Winter Semester 007/08 Sheet Model Test January 16, 008 Fundamental Algorithms
Hedging. MATH 472 Financial Mathematics. J. Robert Buchanan
 Hedging MATH 472 Financial Mathematics J. Robert Buchanan 2018 Introduction Definition Hedging is the practice of making a portfolio of investments less sensitive to changes in market variables. There
Hedging MATH 472 Financial Mathematics J. Robert Buchanan 2018 Introduction Definition Hedging is the practice of making a portfolio of investments less sensitive to changes in market variables. There
An effective perfect-set theorem
 An effective perfect-set theorem David Belanger, joint with Keng Meng (Selwyn) Ng CTFM 2016 at Waseda University, Tokyo Institute for Mathematical Sciences National University of Singapore The perfect
An effective perfect-set theorem David Belanger, joint with Keng Meng (Selwyn) Ng CTFM 2016 at Waseda University, Tokyo Institute for Mathematical Sciences National University of Singapore The perfect
Binary Decision Diagrams
 Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
