Inference in Bayesian Networks
|
|
|
- Nelson May
- 6 years ago
- Views:
Transcription
1 Andrea Passerini Machine Learning
2 Inference in graphical models Description Assume we have evidence e on the state of a subset of variables E in the model (i.e. Bayesian Network) Inference amounts at computing the posterior probability of a subset X of the non-observed variables given the observations: p(x E = e) Note When we need to distinguish between variables and their values, we will indicate random variables with uppercase letters, and their values with lowercase ones.
3 Inference in graphical models Efficiency We can always compute the posterior probability as the ratio of two joint probabilities: p(x E = e) = p(x, E = e) p(e = e) The problem consists of estimating such joint probabilities when dealing with a large number of variables Directly working on the full joint probabilities requires time exponential in the number of variables For instance, if all N variables are discrete and take one of K possible values, a joint probability table has K N entries We would like to exploit the structure in graphical models to do inference more efficiently.
4 Inference in graphical models x 1 x 2 x N 1 x N Inference on a chain (1) p(x) = p(x 1 )p(x 2 X 1 )p(x 3 X 2 ) p(x N X N 1 ) The marginal probability of an arbitrary X n is: p(x n ) = p(x) X 1 X 2 X n 1 X n+1 X N Only the p(x N X N 1 ) is involved in the last summation which can be computed first, giving a function of X N 1 : µ β (X N 1 ) = X N p(x N X N 1 )
5 Inference in graphical models x 1 x 2 x N 1 x N Inference on a chain (2) the marginalization can be iterated as: µ β (X N 2 ) = X N 1 p(x N 1 X N 2 )µ β (X N 1 ) down to the desired variable X n, giving: µ β (X n ) = X n+1 p(x n+1 X n )µ β (X n+1 )
6 Inference in graphical models x 1 x 2 x N 1 x N Inference on a chain (3) The same procedure can be applied starting from the other end of the chain, giving: µ α (X 2 ) = X 1 p(x 1 )p(x 2 X 1 ) up to µ α (X n ) The marginal probability is now computed as the product of the contributions coming from both ends: p(x n ) = µ α (X n )µ β (X n )
7 Inference in graphical models µ α (x n 1 ) µ α (x n ) µ β (x n ) µ β (x n+1 ) x 1 x n 1 x n x n+1 x N Inference as message passing We can think of µ α (X n ) as a message passing from X n 1 to X n µ α (X n ) = X n 1 p(x n X n 1 )µ α (X n 1 ) We can think of µ β (X n ) as a message passing from X n+1 to X n µ β (X n ) = X n+1 p(x n+1 X n )µ β (X n+1 ) Each outgoing message is obtained multiplying the incoming message by the local probability, and summing over the node values
8 Inference in graphical models Full message passing Suppose we want to know marginal probabilities for a number of different variables X i : 1 We send a message from µ α (X 1 ) up to µ α (X N ) 2 We send a message from µ β (X N ) down to µ β (X 1 ) If all nodes store messages, we can compute any marginal probability as p(x i ) = µ α (X i )µ β (X i ) for any i having sent just a double number of messages wrt a single marginal computation
9 Inference in graphical models Adding evidence If some nodes X e are observed, we simply use their observed values instead of summing over all possible values when computing their messages Example p(x) = p(x 1 )p(x 2 X 1 )p(x 3 X 2 )p(x 4 X 3 ) The marginal probability of X 2 and observations X 1 = x e1 and X 3 = x e3 is: p(x 2, X 1 = x e1, X 3 = x e3 ) = p(x 1 = x e1 )p(x 2 X 1 = x e1 ) p(x 3 = x e3 X 2 ) X 4 p(x 4 X 3 = x e3 )
10 Inference Computing conditional probability given evidence When adding evidence, the message passing procedure computes the joint probability of the variable and the evidence, and it has to be normalized to obtain the conditional probability given the evidence: p(x n X e = x e ) = p(x n, X e = x e ) X n p(x n, X e = x e )
11 Inference Inference on trees (a) (b) (c) Efficient inference can be computed for the broaded family of tree-structured models: undirected trees (a) undirected graphs with a single path for each pair of nodes directed trees (b) directed graphs with a single node (the root) with no parents, and all other nodes with a single parent directed polytrees (c) directed graphs with multiple parents for node and multiple roots, but still a single (undirected) path between each pair of nodes
12 Factor graphs Description Efficient inference algorithms can be better explained using an alternative graphical representation called factor graph A factor graph is a graphical representation of a graphical model highlighting its factorization (i.e. conditional probabilities) The factor graph has one node for each node in the original graph The factor graph has one additional node (of a different type) for each factor A factor node has undirected links to each of the node variables in the factor
13 Factor graphs: examples x 1 x 2 x 1 x 2 f x 1 x 2 f c f a f b x 3 x 3 x 3 p(x3 x1,x2)p(x1)p(x2) f(x1,x2,x3)=p(x3 x1,x2)p(x1)p(x2) fc(x1,x2,x3)=p(x3 x1,x2) fa(x1)=p(x1) fb(x2)=p(x2)
14 Inference The sum-product algorithm The sum-product algorithm is an efficient algorithm for exact inference on tree-structured graphs It is a message passing algorithm as its simpler version for chains We will present it on factor graphs, assuming a tree-structured graph giving rise to a factor graph which is a tree The algorithm will be applicable to undirected models (i.e. Markov Networks) as well as directed ones (i.e. Bayesian Networks)
15 Inference Computing marginals We want to compute the marginal probability of X: p(x) = X\X p(x) Generalizing the message passing scheme seen for chains, this can be computed as the product of messages coming from all neighbouring factors f s : p(x) = µ fs X (X) f s ne(x) Fs(x, Xs) f s µ fs x(x) x
16 Inference x M µ xm f s (x M ) f s µ fs x(x) x Factor messages x m G m (x m, X sm ) Each factor message is the product of messages coming from nodes other than X, times the factor, summed over all possible values of the factor variables other than X (X 1,..., X M ): µ fs X (X) = X 1 X M f s (X, X 1,..., X M ) X m ne(f s)\x µ Xm f s (X m )
17 Inference f L x m f s f l F l (x m, X ml ) Node messages Each message from node X m to factor f s is the product of the factor messages to X m coming from factors other than f s : µ Xm fs (X m ) = µ fl X m (X m ) f l ne(x m)\f s
18 Inference Initialization Message passing start from leaves, either factors or nodes Messages from leaf factors are initialized to the factor itself (there will be no X m different from the destination on which to sum over) µ f x (x) = f(x) f x Messages from leaf nodes are initialized to 1 µ x f (x) = 1 x f
19 Inference Message passing scheme The node X whose marginal has to be computed is designed as root. Messages are sent from all leaves to their neighbours Each internal node sends its message towards the root as soon as it received messages from all other neighbours Once the root has collected all messages, the marginal can be computed as the product of them
20 Inference Full message passing scheme In order to be able to compute marginals for any node, messages need to pass in all directions: 1 Choose an arbitrary node as root 2 Collect messages for the root starting from leaves 3 Send messages from the root down to the leaves All messages passed in all directions using only twice the number of computations used for a single marginal
21 Inference example x 1 x 2 x 3 f a f b f c x 4 Consider the joint distribution as product of factors p(x) = f a (X 1, X 2 )f b (X 2, X 3 )f c (X 2, X 4 )
22 Inference example x 1 x 2 x 3 f a f b f c x 4 Choose X 3 as root
23 Inference example x 1 x 2 x 3 x 4 Send initial messages from leaves µ X1 f a (X 1 ) = 1 µ X4 f c (X 4 ) = 1
24 Inference example x 1 x 2 x 3 x 4 Send messages from factor nodes to X 2 µ fa X 2 (X 2 ) = X 1 f a (X 1, X 2 ) µ fc X 2 (X 2 ) = X 4 f c (X 2, X 4 )
25 Inference example x 1 x 2 x 3 x 4 Send message from X 2 to factor node f b µ X2 f b (X 2 ) = µ fa X 2 (X 2 )µ fc X 2 (X 2 )
26 Inference example x 1 x 2 x 3 x 4 Send message from f b to X 3 µ fb X 3 (X 3 ) = X 2 f b (X 2, X 3 )µ X2 f b (X 2 )
27 Inference example x 1 x 2 x 3 x 4 Send message from root X 3 µ X3 f b (X 3 ) = 1
28 Inference example x 1 x 2 x 3 x 4 Send message from f b to X 2 µ fb X 2 (X 2 ) = X 3 f b (X 2, X 3 )
29 Inference example x 1 x 2 x 3 x 4 Send messages from X 2 to factor nodes µ X2 f a (X 2 ) = µ fb X 2 (X 2 )µ fc X 2 (X 2 ) µ X2 f c (X 2 ) = µ fb X 2 (X 2 )µ fa X 2 (X 2 )
30 Inference example x 1 x 2 x 3 x 4 Send messages from factor nodes to leaves µ fa X 1 (X 1 ) = X 2 f a (X 1, X 2 )µ X2 f a (X 2 ) µ fc X 4 (X 4 ) = X 2 f c (X 2, X 4 )µ X2 f c (X 2 )
31 Inference example x 1 x 2 x 3 f a f b f c x 4 Compute for instance the marginal for X 2 p(x 2 ) = µ fa X2 (X 2 )µ fb X 2 (X 2 )µ fc X2 (X 2 ) = f a (X 1, X 2 ) f b (X 2, X 3 ) X1 X3 X4 f c (X 2, X 4 ) = X 1 f a (X 1, X 2 )f b (X 2, X 3 )f c (X 2, X 4 ) X 3 X 4 = p(x) X 1 X 3 X 4
32 Inference Adding evidence If some nodes X e are observed, we simply use their observed values instead of summing over all possible values when computing their messages After normalization, this gives the conditional probability given the evidence
33 Inference example A C D A P(A) C P(C D) D P(D) B P(B A,C)P(A)P(C D)P(D) P(B A,C) B Bayesian network Take a Bayesian network Build a factor graph representing it Compute the marginal for a variable (e.g. B)
34 Inference example A C D A P(A) C P(C D) D P(D) B P(B A,C)P(A)P(C D)P(D) P(B A,C) B Compute the marginal for B Leaf factor nodes send messages: µ fa A = P(A) µ fd D = P(D)
35 Inference example A C D A P(A) C P(C D) D P(D) B P(B A,C)P(A)P(C D)P(D) P(B A,C) B Compute the marginal for B A and D send messages: µ A fa,b,c (A) = µ fa A = P(A) µ D fc,d (D) = µ fd D = P(D)
36 Inference example A C D A P(A) C P(C D) D P(D) B P(B A,C)P(A)P(C D)P(D) P(B A,C) B Compute the marginal for B f C,D sends message: µ fc,d C(C) = D P(C D)µ fd D = D P(C D)P(D)
37 Inference example A C D A P(A) C P(C D) D P(D) B P(B A,C)P(A)P(C D)P(D) P(B A,C) B Compute the marginal for B C sends message: µ C fa,b,c (C) = µ fc,d C(C) = D P(C D)P(D)
38 Inference example A C D A P(A) C P(C D) D P(D) B P(B A,C)P(A)P(C D)P(D) P(B A,C) B Compute the marginal for B f A,B,C sends message: µ fa,b,c B(B) = P(B A, C)µ C fa,b,c (C)µ A fa,b,c (A) A C = P(B A, C)P(A) P(C D)P(D) A D C
39 Inference example A C D A P(A) C P(C D) D P(D) B P(B A,C)P(A)P(C D)P(D) P(B A,C) B Compute the marginal for B The desired marginal is obtained: P(B) = µ fa,b,c B(B) = P(B A, C)P(A) A C D = P(B A, C)P(A)P(C D)P(D) A C D = P(A, B, C, D) A D C P(C D)P(D)
40 Inference Finding the most probable configuration Note Given a joint probability distribution p(x) We wish to find the configuration for variables X having the highest probability: for which the probability is: X max = argmax p(x) X p(x max ) = max p(x) X We want the configuration which is jointly maximal for all variables We cannot simply compute p(x i ) for each i (using the sum-product algorithm) and maximize it
41 Inference The max-product algorithm p(x max ) = max X p(x) = max X 1 max p(x) X M As for the sum-product algorithm, we can exploit the distribution factorization to efficiently compute the maximum It suffices to replace sum with max in the sum-product algorithm Linear chain max p(x) = max max [p(x 1 )p(x 2 X 1 ) p(x N X N 1 )] X X 1 X N [ [ ]] = max p(x 1 )p(x 2 X 1 ) max p(x N X N 1 ) X 1 X N
42 Inference Message passing As for the sum-product algorithm, the max-product can be seen as message passing over the graph. The algorithm is thus easily applied to tree-structured graphs via their factor trees: µ f X (X) = max f (X, X 1,..., X M ) X 1,...X M µ X f (X) = µ fl X (X) f l ne(x)\f X m ne(f )\X µ Xm f (X m )
43 Inference Recoving maximal configuration Messages are passed from leaves to an arbitrarily chosen root X r The probability of maximal configuration is readily obtained as: p(x max ) = max X r f l ne(x r ) µ fl X r (X r ) The maximal configuration for the root is obtained as: Xr max = argmax µ fl X r (X r ) X r f l ne(x r ) We need to recover maximal configuration for the other variables
44 Inference Recoving maximal configuration When sending a message towards x, each factor node should store the configuration of the other variables which gave the maximum: φ f X (X) = argmax X 1,...,X M f (X, X 1,..., X M ) X m ne(f )\X µ Xm f (X m ) When the maximal configuration for the root node X r has been obtained, it can be used to retrieve the maximal configuration for the variables in neighbouring factors from: X1 max,..., XM max = φ f Xr (Xr max ) The procedure can be repeated back-tracking to the leaves, retrieving maximal values for all variables
45 Recoving maximal configuration Example for linear chain X max N = argmax X N µ fn 1,N X N (X N ) XN 1 max = φ f N 1,N X N (XN max ) XN 2 max = φ f N 2,N 1 X N 1 (XN 1 max ). X max 1 = φ f1,2 X 2 (X max 2 )
46 Recoving maximal configuration k = 1 k = 2 k = 3 n 2 n 1 n n + 1 Trellis for linear chain A trellis or lattice diagram shows the K possible states of each variable X n one per row For each state k of a variable X n, φ fn 1,n X n (X n ) defines a unique (maximal) previous state, linked by an edge in the diagram Once the maximal state for the last variable X N is chosen, the maximal states for other variables are recovering following the edges backward.
47 Inference Underflow issues The max-product algorithm relies on products (no summation) Products of many small probabilities can lead to underflow problems This can be addressed computing the logarithm of the probability instead The logarithm is monotonic, thus the proper maximal configuration is recovered: ( ) log max p(x) = max log p(x) X X The effect is replacing products with sums (of logs) in the max-product algorithm, giving the max-sum one
48 Inference Exact inference on general graphs The sum-product and max-product algorithms can be applied to tree-structured graphs Many applications require graphs with (undirected) loops An extension of this algorithms to generic graphs can be achieved with the junction tree algorithm The algorithm does not work on factor graphs, but on junction trees, tree-structured graphs with nodes containing clusters of variables of the original graph A message passing scheme analogous to the sum-product and max-product algorithms is run on the junction tree Problem The complexity on the algorithm is exponential on the maximal number of variables in a cluster, making it intractable for large complex graphs.
49 Inference Approximate inference In cases in which exact inference is intractable, we resort to approximate inference techniques A number of techniques for approximate inference exist: loopy belief propagation message passing on the original graph even if it contains loops variational methods deterministic approximations, assuming the posterior probability (given the evidence) factorizes in a particular way sampling methods approximate posterior is obtained sampling from the network
50 Inference Loopy belief propagation Apply sum-product algorithm even if it is not guaranteed to provide an exact solution We assume all nodes are in condition of sending messages (i.e. they already received a constant 1 message from all neighbours) A message passing schedule is chosen in order to decide which nodes start sending messages (e.g. flooding, all nodes send messages in all directions at each time step) Information flows many times around the graph (because of the loops), each message on a link replaces the previous one and is only based on the most recent messages received from the other neighbours The algorithm can eventually converge (no more changes in messages passing through any link) depending on the specific model over which it is applied
Exact Inference. Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4. x 3. f s. x 2. x 1
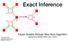 Exact Inference x 1 x 3 x 2 f s Geoffrey Roeder roeder@cs.toronto.edu 8 February 2018 Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4 Building Blocks UGMs, Cliques, Factor
Exact Inference x 1 x 3 x 2 f s Geoffrey Roeder roeder@cs.toronto.edu 8 February 2018 Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4 Building Blocks UGMs, Cliques, Factor
Sum-Product: Message Passing Belief Propagation
 Sum-Product: Message Passing Belief Propagation Probabilistic Graphical Models Sharif University of Technology Spring 2017 Soleymani All single-node marginals If we need the full set of marginals, repeating
Sum-Product: Message Passing Belief Propagation Probabilistic Graphical Models Sharif University of Technology Spring 2017 Soleymani All single-node marginals If we need the full set of marginals, repeating
Sum-Product: Message Passing Belief Propagation
 Sum-Product: Message Passing Belief Propagation 40-956 Advanced Topics in AI: Probabilistic Graphical Models Sharif University of Technology Soleymani Spring 2015 All single-node marginals If we need the
Sum-Product: Message Passing Belief Propagation 40-956 Advanced Topics in AI: Probabilistic Graphical Models Sharif University of Technology Soleymani Spring 2015 All single-node marginals If we need the
Factor Graphs, the Sum-Product Algorithm and TrueSkill TM
 Factor Graphs, the Sum-Product Algorithm and TrueSkill TM Kuhwan Jeong 1 1 Department of Statistics, Seoul National University, South Korea July, 2018 1 / 17 Introduction x i : a variable taking on values
Factor Graphs, the Sum-Product Algorithm and TrueSkill TM Kuhwan Jeong 1 1 Department of Statistics, Seoul National University, South Korea July, 2018 1 / 17 Introduction x i : a variable taking on values
UGM Crash Course: Conditional Inference and Cutset Conditioning
 UGM Crash Course: Conditional Inference and Cutset Conditioning Julie Nutini August 19 th, 2015 1 / 25 Conditional UGM 2 / 25 We know the value of one or more random variables i.e., we have observations,
UGM Crash Course: Conditional Inference and Cutset Conditioning Julie Nutini August 19 th, 2015 1 / 25 Conditional UGM 2 / 25 We know the value of one or more random variables i.e., we have observations,
Machine Learning in Computer Vision Markov Random Fields Part II
 Machine Learning in Computer Vision Markov Random Fields Part II Oren Freifeld Computer Science, Ben-Gurion University March 22, 2018 Mar 22, 2018 1 / 40 1 Some MRF Computations 2 Mar 22, 2018 2 / 40 Few
Machine Learning in Computer Vision Markov Random Fields Part II Oren Freifeld Computer Science, Ben-Gurion University March 22, 2018 Mar 22, 2018 1 / 40 1 Some MRF Computations 2 Mar 22, 2018 2 / 40 Few
Factor Graphs. Seungjin Choi
 Factor Graphs Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr 1 / 17 Tanner Graphs
Factor Graphs Seungjin Choi Department of Computer Science and Engineering Pohang University of Science and Technology 77 Cheongam-ro, Nam-gu, Pohang 37673, Korea seungjin@postech.ac.kr 1 / 17 Tanner Graphs
Machine Learning
 Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 13, 2011 Today: Graphical models Bayes Nets: Conditional independencies Inference Learning Readings:
Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 13, 2011 Today: Graphical models Bayes Nets: Conditional independencies Inference Learning Readings:
Exact Inference (9/30/13) 2 A brief review of Forward-Backward and EM for HMMs
 STA561: Probabilistic machine learning Exact Inference (9/30/13) Lecturer: Barbara Engelhardt Scribes: Jiawei Liang, He Jiang, Brittany Cohen 1 Validation for Clustering If we have two centroids, η 1 and
STA561: Probabilistic machine learning Exact Inference (9/30/13) Lecturer: Barbara Engelhardt Scribes: Jiawei Liang, He Jiang, Brittany Cohen 1 Validation for Clustering If we have two centroids, η 1 and
COMP90051 Statistical Machine Learning
 COMP90051 Statistical Machine Learning Semester 2, 2017 Lecturer: Trevor Cohn 22. PGM Probabilistic Inference Probabilistic inference on PGMs Computing marginal and conditional distributions from the joint
COMP90051 Statistical Machine Learning Semester 2, 2017 Lecturer: Trevor Cohn 22. PGM Probabilistic Inference Probabilistic inference on PGMs Computing marginal and conditional distributions from the joint
a 13 Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models The model
 Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models This is a lightly edited version of a chapter in a book being written by Jordan. Since this is
Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models This is a lightly edited version of a chapter in a book being written by Jordan. Since this is
Global Joint Distribution Factorizes into Local Marginal Distributions on Tree-Structured Graphs
 Teaching Note October 26, 2007 Global Joint Distribution Factorizes into Local Marginal Distributions on Tree-Structured Graphs Xinhua Zhang Xinhua.Zhang@anu.edu.au Research School of Information Sciences
Teaching Note October 26, 2007 Global Joint Distribution Factorizes into Local Marginal Distributions on Tree-Structured Graphs Xinhua Zhang Xinhua.Zhang@anu.edu.au Research School of Information Sciences
Machine Learning. Graphical Models. Marc Toussaint University of Stuttgart Summer 2015
 Machine Learning Graphical Models Marc Toussaint University of Stuttgart Summer 2015 Outline A. Introduction Motivation and definition of Bayes Nets Conditional independence in Bayes Nets Examples B. Inference
Machine Learning Graphical Models Marc Toussaint University of Stuttgart Summer 2015 Outline A. Introduction Motivation and definition of Bayes Nets Conditional independence in Bayes Nets Examples B. Inference
Probabilistic Graphical Models
 CS420, Machine Learning, Lecture 8 Probabilistic Graphical Models Weinan Zhang Shanghai Jiao Tong University http://wnzhang.net http://wnzhang.net/teaching/cs420/index.html Content of This Lecture Introduction
CS420, Machine Learning, Lecture 8 Probabilistic Graphical Models Weinan Zhang Shanghai Jiao Tong University http://wnzhang.net http://wnzhang.net/teaching/cs420/index.html Content of This Lecture Introduction
Computer Vision Group Prof. Daniel Cremers. 7. Sequential Data
 Group Prof. Daniel Cremers 7. Sequential Data Bayes Filter (Rep.) We can describe the overall process using a Dynamic Bayes Network: This incorporates the following Markov assumptions: (measurement) (state)!2
Group Prof. Daniel Cremers 7. Sequential Data Bayes Filter (Rep.) We can describe the overall process using a Dynamic Bayes Network: This incorporates the following Markov assumptions: (measurement) (state)!2
Final Examination CS540: Introduction to Artificial Intelligence
 Final Examination CS540: Introduction to Artificial Intelligence December 2008 LAST NAME: FIRST NAME: Problem Score Max Score 1 15 2 15 3 10 4 20 5 10 6 20 7 10 Total 100 Question 1. [15] Probabilistic
Final Examination CS540: Introduction to Artificial Intelligence December 2008 LAST NAME: FIRST NAME: Problem Score Max Score 1 15 2 15 3 10 4 20 5 10 6 20 7 10 Total 100 Question 1. [15] Probabilistic
BAYESIAN GAMES: GAMES OF INCOMPLETE INFORMATION
 BAYESIAN GAMES: GAMES OF INCOMPLETE INFORMATION MERYL SEAH Abstract. This paper is on Bayesian Games, which are games with incomplete information. We will start with a brief introduction into game theory,
BAYESIAN GAMES: GAMES OF INCOMPLETE INFORMATION MERYL SEAH Abstract. This paper is on Bayesian Games, which are games with incomplete information. We will start with a brief introduction into game theory,
A start of Variational Methods for ERGM Ranran Wang, UW
 A start of Variational Methods for ERGM Ranran Wang, UW MURI-UCI April 24, 2009 Outline A start of Variational Methods for ERGM [1] Introduction to ERGM Current methods of parameter estimation: MCMCMLE:
A start of Variational Methods for ERGM Ranran Wang, UW MURI-UCI April 24, 2009 Outline A start of Variational Methods for ERGM [1] Introduction to ERGM Current methods of parameter estimation: MCMCMLE:
EC316a: Advanced Scientific Computation, Fall Discrete time, continuous state dynamic models: solution methods
 EC316a: Advanced Scientific Computation, Fall 2003 Notes Section 4 Discrete time, continuous state dynamic models: solution methods We consider now solution methods for discrete time models in which decisions
EC316a: Advanced Scientific Computation, Fall 2003 Notes Section 4 Discrete time, continuous state dynamic models: solution methods We consider now solution methods for discrete time models in which decisions
On the Optimality of a Family of Binary Trees Techical Report TR
 On the Optimality of a Family of Binary Trees Techical Report TR-011101-1 Dana Vrajitoru and William Knight Indiana University South Bend Department of Computer and Information Sciences Abstract In this
On the Optimality of a Family of Binary Trees Techical Report TR-011101-1 Dana Vrajitoru and William Knight Indiana University South Bend Department of Computer and Information Sciences Abstract In this
Recall: Data Flow Analysis. Data Flow Analysis Recall: Data Flow Equations. Forward Data Flow, Again
 Data Flow Analysis 15-745 3/24/09 Recall: Data Flow Analysis A framework for proving facts about program Reasons about lots of little facts Little or no interaction between facts Works best on properties
Data Flow Analysis 15-745 3/24/09 Recall: Data Flow Analysis A framework for proving facts about program Reasons about lots of little facts Little or no interaction between facts Works best on properties
Markov Decision Processes: Making Decision in the Presence of Uncertainty. (some of) R&N R&N
 Markov Decision Processes: Making Decision in the Presence of Uncertainty (some of) R&N 16.1-16.6 R&N 17.1-17.4 Different Aspects of Machine Learning Supervised learning Classification - concept learning
Markov Decision Processes: Making Decision in the Presence of Uncertainty (some of) R&N 16.1-16.6 R&N 17.1-17.4 Different Aspects of Machine Learning Supervised learning Classification - concept learning
SIMULATION METHOD FOR SOLVING HYBRID INFLUENCE DIAGRAMS IN DECISION MAKING. Xi Chen Enlu Zhou
 Proceedings of the 2010 Winter Simulation Conference B. Johansson, S. Jain, J. Montoya-Torres, J. Hugan, and E. Yücesan, eds. SIMULATION METHOD FOR SOLVING HYBRID INFLUENCE DIAGRAMS IN DECISION MAKING
Proceedings of the 2010 Winter Simulation Conference B. Johansson, S. Jain, J. Montoya-Torres, J. Hugan, and E. Yücesan, eds. SIMULATION METHOD FOR SOLVING HYBRID INFLUENCE DIAGRAMS IN DECISION MAKING
Lecture 17: More on Markov Decision Processes. Reinforcement learning
 Lecture 17: More on Markov Decision Processes. Reinforcement learning Learning a model: maximum likelihood Learning a value function directly Monte Carlo Temporal-difference (TD) learning COMP-424, Lecture
Lecture 17: More on Markov Decision Processes. Reinforcement learning Learning a model: maximum likelihood Learning a value function directly Monte Carlo Temporal-difference (TD) learning COMP-424, Lecture
What is Greedy Approach? Control abstraction for Greedy Method. Three important activities
 0-0-07 What is Greedy Approach? Suppose that a problem can be solved by a sequence of decisions. The greedy method has that each decision is locally optimal. These locally optimal solutions will finally
0-0-07 What is Greedy Approach? Suppose that a problem can be solved by a sequence of decisions. The greedy method has that each decision is locally optimal. These locally optimal solutions will finally
15 : Approximate Inference: Monte Carlo Methods
 10-708: Probabilistic Graphical Models 10-708, Spring 2016 15 : Approximate Inference: Monte Carlo Methods Lecturer: Eric P. Xing Scribes: Binxuan Huang, Yotam Hechtlinger, Fuchen Liu 1 Introduction to
10-708: Probabilistic Graphical Models 10-708, Spring 2016 15 : Approximate Inference: Monte Carlo Methods Lecturer: Eric P. Xing Scribes: Binxuan Huang, Yotam Hechtlinger, Fuchen Liu 1 Introduction to
Making Decisions. CS 3793 Artificial Intelligence Making Decisions 1
 Making Decisions CS 3793 Artificial Intelligence Making Decisions 1 Planning under uncertainty should address: The world is nondeterministic. Actions are not certain to succeed. Many events are outside
Making Decisions CS 3793 Artificial Intelligence Making Decisions 1 Planning under uncertainty should address: The world is nondeterministic. Actions are not certain to succeed. Many events are outside
4 Reinforcement Learning Basic Algorithms
 Learning in Complex Systems Spring 2011 Lecture Notes Nahum Shimkin 4 Reinforcement Learning Basic Algorithms 4.1 Introduction RL methods essentially deal with the solution of (optimal) control problems
Learning in Complex Systems Spring 2011 Lecture Notes Nahum Shimkin 4 Reinforcement Learning Basic Algorithms 4.1 Introduction RL methods essentially deal with the solution of (optimal) control problems
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration
 Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
V. Lesser CS683 F2004
 The value of information Lecture 15: Uncertainty - 6 Example 1: You consider buying a program to manage your finances that costs $100. There is a prior probability of 0.7 that the program is suitable in
The value of information Lecture 15: Uncertainty - 6 Example 1: You consider buying a program to manage your finances that costs $100. There is a prior probability of 0.7 that the program is suitable in
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration
 Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
IEOR E4004: Introduction to OR: Deterministic Models
 IEOR E4004: Introduction to OR: Deterministic Models 1 Dynamic Programming Following is a summary of the problems we discussed in class. (We do not include the discussion on the container problem or the
IEOR E4004: Introduction to OR: Deterministic Models 1 Dynamic Programming Following is a summary of the problems we discussed in class. (We do not include the discussion on the container problem or the
CS 361: Probability & Statistics
 March 12, 2018 CS 361: Probability & Statistics Inference Binomial likelihood: Example Suppose we have a coin with an unknown probability of heads. We flip the coin 10 times and observe 2 heads. What can
March 12, 2018 CS 361: Probability & Statistics Inference Binomial likelihood: Example Suppose we have a coin with an unknown probability of heads. We flip the coin 10 times and observe 2 heads. What can
Notes on the EM Algorithm Michael Collins, September 24th 2005
 Notes on the EM Algorithm Michael Collins, September 24th 2005 1 Hidden Markov Models A hidden Markov model (N, Σ, Θ) consists of the following elements: N is a positive integer specifying the number of
Notes on the EM Algorithm Michael Collins, September 24th 2005 1 Hidden Markov Models A hidden Markov model (N, Σ, Θ) consists of the following elements: N is a positive integer specifying the number of
Complex Decisions. Sequential Decision Making
 Sequential Decision Making Outline Sequential decision problems Value iteration Policy iteration POMDPs (basic concepts) Slides partially based on the Book "Reinforcement Learning: an introduction" by
Sequential Decision Making Outline Sequential decision problems Value iteration Policy iteration POMDPs (basic concepts) Slides partially based on the Book "Reinforcement Learning: an introduction" by
CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS
 CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS November 17, 2016. Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question.
CMPSCI 311: Introduction to Algorithms Second Midterm Practice Exam SOLUTIONS November 17, 2016. Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question.
Final exam solutions
 EE365 Stochastic Control / MS&E251 Stochastic Decision Models Profs. S. Lall, S. Boyd June 5 6 or June 6 7, 2013 Final exam solutions This is a 24 hour take-home final. Please turn it in to one of the
EE365 Stochastic Control / MS&E251 Stochastic Decision Models Profs. S. Lall, S. Boyd June 5 6 or June 6 7, 2013 Final exam solutions This is a 24 hour take-home final. Please turn it in to one of the
CPSC 540: Machine Learning
 CPSC 540: Machine Learning Monte Carlo Methods Mark Schmidt University of British Columbia Winter 2019 Last Time: Markov Chains We can use Markov chains for density estimation, d p(x) = p(x 1 ) p(x }{{}
CPSC 540: Machine Learning Monte Carlo Methods Mark Schmidt University of British Columbia Winter 2019 Last Time: Markov Chains We can use Markov chains for density estimation, d p(x) = p(x 1 ) p(x }{{}
COSC 311: ALGORITHMS HW4: NETWORK FLOW
 COSC 311: ALGORITHMS HW4: NETWORK FLOW Solutions 1 Warmup 1) Finding max flows and min cuts. Here is a graph (the numbers in boxes represent the amount of flow along an edge, and the unadorned numbers
COSC 311: ALGORITHMS HW4: NETWORK FLOW Solutions 1 Warmup 1) Finding max flows and min cuts. Here is a graph (the numbers in boxes represent the amount of flow along an edge, and the unadorned numbers
CEC login. Student Details Name SOLUTIONS
 Student Details Name SOLUTIONS CEC login Instructions You have roughly 1 minute per point, so schedule your time accordingly. There is only one correct answer per question. Good luck! Question 1. Searching
Student Details Name SOLUTIONS CEC login Instructions You have roughly 1 minute per point, so schedule your time accordingly. There is only one correct answer per question. Good luck! Question 1. Searching
CS188 Spring 2012 Section 4: Games
 CS188 Spring 2012 Section 4: Games 1 Minimax Search In this problem, we will explore adversarial search. Consider the zero-sum game tree shown below. Trapezoids that point up, such as at the root, represent
CS188 Spring 2012 Section 4: Games 1 Minimax Search In this problem, we will explore adversarial search. Consider the zero-sum game tree shown below. Trapezoids that point up, such as at the root, represent
Q1. [?? pts] Search Traces
![Q1. [?? pts] Search Traces Q1. [?? pts] Search Traces](/thumbs/80/81482567.jpg) CS 188 Spring 2010 Introduction to Artificial Intelligence Midterm Exam Solutions Q1. [?? pts] Search Traces Each of the trees (G1 through G5) was generated by searching the graph (below, left) with a
CS 188 Spring 2010 Introduction to Artificial Intelligence Midterm Exam Solutions Q1. [?? pts] Search Traces Each of the trees (G1 through G5) was generated by searching the graph (below, left) with a
Gibbs Fields: Inference and Relation to Bayes Networks
 Statistical Techniques in Robotics (16-831, F10) Lecture#08 (Thursday September 16) Gibbs Fields: Inference and Relation to ayes Networks Lecturer: rew agnell Scribe:ebadeepta ey 1 1 Inference on Gibbs
Statistical Techniques in Robotics (16-831, F10) Lecture#08 (Thursday September 16) Gibbs Fields: Inference and Relation to ayes Networks Lecturer: rew agnell Scribe:ebadeepta ey 1 1 Inference on Gibbs
CSCE 750, Fall 2009 Quizzes with Answers
 CSCE 750, Fall 009 Quizzes with Answers Stephen A. Fenner September 4, 011 1. Give an exact closed form for Simplify your answer as much as possible. k 3 k+1. We reduce the expression to a form we ve already
CSCE 750, Fall 009 Quizzes with Answers Stephen A. Fenner September 4, 011 1. Give an exact closed form for Simplify your answer as much as possible. k 3 k+1. We reduce the expression to a form we ve already
Random Tree Method. Monte Carlo Methods in Financial Engineering
 Random Tree Method Monte Carlo Methods in Financial Engineering What is it for? solve full optimal stopping problem & estimate value of the American option simulate paths of underlying Markov chain produces
Random Tree Method Monte Carlo Methods in Financial Engineering What is it for? solve full optimal stopping problem & estimate value of the American option simulate paths of underlying Markov chain produces
Math 135: Answers to Practice Problems
 Math 35: Answers to Practice Problems Answers to problems from the textbook: Many of the problems from the textbook have answers in the back of the book. Here are the answers to the problems that don t
Math 35: Answers to Practice Problems Answers to problems from the textbook: Many of the problems from the textbook have answers in the back of the book. Here are the answers to the problems that don t
CPSC 540: Machine Learning
 CPSC 540: Machine Learning Monte Carlo Methods Mark Schmidt University of British Columbia Winter 2018 Last Time: Markov Chains We can use Markov chains for density estimation, p(x) = p(x 1 ) }{{} d p(x
CPSC 540: Machine Learning Monte Carlo Methods Mark Schmidt University of British Columbia Winter 2018 Last Time: Markov Chains We can use Markov chains for density estimation, p(x) = p(x 1 ) }{{} d p(x
CS221 / Spring 2018 / Sadigh. Lecture 7: MDPs I
 CS221 / Spring 2018 / Sadigh Lecture 7: MDPs I cs221.stanford.edu/q Question How would you get to Mountain View on Friday night in the least amount of time? bike drive Caltrain Uber/Lyft fly CS221 / Spring
CS221 / Spring 2018 / Sadigh Lecture 7: MDPs I cs221.stanford.edu/q Question How would you get to Mountain View on Friday night in the least amount of time? bike drive Caltrain Uber/Lyft fly CS221 / Spring
Lecture 7: MDPs I. Question. Course plan. So far: search problems. Uncertainty in the real world
 Lecture 7: MDPs I cs221.stanford.edu/q Question How would you get to Mountain View on Friday night in the least amount of time? bike drive Caltrain Uber/Lyft fly CS221 / Spring 2018 / Sadigh CS221 / Spring
Lecture 7: MDPs I cs221.stanford.edu/q Question How would you get to Mountain View on Friday night in the least amount of time? bike drive Caltrain Uber/Lyft fly CS221 / Spring 2018 / Sadigh CS221 / Spring
Adaptive Experiments for Policy Choice. March 8, 2019
 Adaptive Experiments for Policy Choice Maximilian Kasy Anja Sautmann March 8, 2019 Introduction The goal of many experiments is to inform policy choices: 1. Job search assistance for refugees: Treatments:
Adaptive Experiments for Policy Choice Maximilian Kasy Anja Sautmann March 8, 2019 Introduction The goal of many experiments is to inform policy choices: 1. Job search assistance for refugees: Treatments:
CS221 / Spring 2018 / Sadigh. Lecture 9: Games I
 CS221 / Spring 2018 / Sadigh Lecture 9: Games I Course plan Search problems Markov decision processes Adversarial games Constraint satisfaction problems Bayesian networks Reflex States Variables Logic
CS221 / Spring 2018 / Sadigh Lecture 9: Games I Course plan Search problems Markov decision processes Adversarial games Constraint satisfaction problems Bayesian networks Reflex States Variables Logic
Lecture outline W.B.Powell 1
 Lecture outline What is a policy? Policy function approximations (PFAs) Cost function approximations (CFAs) alue function approximations (FAs) Lookahead policies Finding good policies Optimizing continuous
Lecture outline What is a policy? Policy function approximations (PFAs) Cost function approximations (CFAs) alue function approximations (FAs) Lookahead policies Finding good policies Optimizing continuous
Sublinear Time Algorithms Oct 19, Lecture 1
 0368.416701 Sublinear Time Algorithms Oct 19, 2009 Lecturer: Ronitt Rubinfeld Lecture 1 Scribe: Daniel Shahaf 1 Sublinear-time algorithms: motivation Twenty years ago, there was practically no investigation
0368.416701 Sublinear Time Algorithms Oct 19, 2009 Lecturer: Ronitt Rubinfeld Lecture 1 Scribe: Daniel Shahaf 1 Sublinear-time algorithms: motivation Twenty years ago, there was practically no investigation
Principles of Program Analysis: Algorithms
 Principles of Program Analysis: Algorithms Transparencies based on Chapter 6 of the book: Flemming Nielson, Hanne Riis Nielson and Chris Hankin: Principles of Program Analysis. Springer Verlag 2005. c
Principles of Program Analysis: Algorithms Transparencies based on Chapter 6 of the book: Flemming Nielson, Hanne Riis Nielson and Chris Hankin: Principles of Program Analysis. Springer Verlag 2005. c
Is Greedy Coordinate Descent a Terrible Algorithm?
 Is Greedy Coordinate Descent a Terrible Algorithm? Julie Nutini, Mark Schmidt, Issam Laradji, Michael Friedlander, Hoyt Koepke University of British Columbia Optimization and Big Data, 2015 Context: Random
Is Greedy Coordinate Descent a Terrible Algorithm? Julie Nutini, Mark Schmidt, Issam Laradji, Michael Friedlander, Hoyt Koepke University of British Columbia Optimization and Big Data, 2015 Context: Random
The exam is closed book, closed calculator, and closed notes except your three crib sheets.
 CS 188 Spring 2016 Introduction to Artificial Intelligence Final V2 You have approximately 2 hours and 50 minutes. The exam is closed book, closed calculator, and closed notes except your three crib sheets.
CS 188 Spring 2016 Introduction to Artificial Intelligence Final V2 You have approximately 2 hours and 50 minutes. The exam is closed book, closed calculator, and closed notes except your three crib sheets.
Reinforcement Learning
 Reinforcement Learning MDP March May, 2013 MDP MDP: S, A, P, R, γ, µ State can be partially observable: Partially Observable MDPs () Actions can be temporally extended: Semi MDPs (SMDPs) and Hierarchical
Reinforcement Learning MDP March May, 2013 MDP MDP: S, A, P, R, γ, µ State can be partially observable: Partially Observable MDPs () Actions can be temporally extended: Semi MDPs (SMDPs) and Hierarchical
Markov Decision Processes
 Markov Decision Processes Ryan P. Adams COS 324 Elements of Machine Learning Princeton University We now turn to a new aspect of machine learning, in which agents take actions and become active in their
Markov Decision Processes Ryan P. Adams COS 324 Elements of Machine Learning Princeton University We now turn to a new aspect of machine learning, in which agents take actions and become active in their
Lecture 4: Divide and Conquer
 Lecture 4: Divide and Conquer Divide and Conquer Merge sort is an example of a divide-and-conquer algorithm Recall the three steps (at each level to solve a divideand-conquer problem recursively Divide
Lecture 4: Divide and Conquer Divide and Conquer Merge sort is an example of a divide-and-conquer algorithm Recall the three steps (at each level to solve a divideand-conquer problem recursively Divide
Binary Decision Diagrams
 Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
A potentially useful approach to model nonlinearities in time series is to assume different behavior (structural break) in different subsamples
 1.3 Regime switching models A potentially useful approach to model nonlinearities in time series is to assume different behavior (structural break) in different subsamples (or regimes). If the dates, the
1.3 Regime switching models A potentially useful approach to model nonlinearities in time series is to assume different behavior (structural break) in different subsamples (or regimes). If the dates, the
Likelihood Methods of Inference. Toss coin 6 times and get Heads twice.
 Methods of Inference Toss coin 6 times and get Heads twice. p is probability of getting H. Probability of getting exactly 2 heads is 15p 2 (1 p) 4 This function of p, is likelihood function. Definition:
Methods of Inference Toss coin 6 times and get Heads twice. p is probability of getting H. Probability of getting exactly 2 heads is 15p 2 (1 p) 4 This function of p, is likelihood function. Definition:
CS 174: Combinatorics and Discrete Probability Fall Homework 5. Due: Thursday, October 4, 2012 by 9:30am
 CS 74: Combinatorics and Discrete Probability Fall 0 Homework 5 Due: Thursday, October 4, 0 by 9:30am Instructions: You should upload your homework solutions on bspace. You are strongly encouraged to type
CS 74: Combinatorics and Discrete Probability Fall 0 Homework 5 Due: Thursday, October 4, 0 by 9:30am Instructions: You should upload your homework solutions on bspace. You are strongly encouraged to type
Binary Decision Diagrams
 Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
Binary Decision Diagrams Hao Zheng Department of Computer Science and Engineering University of South Florida Tampa, FL 33620 Email: zheng@cse.usf.edu Phone: (813)974-4757 Fax: (813)974-5456 Hao Zheng
Stat 260/CS Learning in Sequential Decision Problems. Peter Bartlett
 Stat 260/CS 294-102. Learning in Sequential Decision Problems. Peter Bartlett 1. Gittins Index: Discounted, Bayesian (hence Markov arms). Reduces to stopping problem for each arm. Interpretation as (scaled)
Stat 260/CS 294-102. Learning in Sequential Decision Problems. Peter Bartlett 1. Gittins Index: Discounted, Bayesian (hence Markov arms). Reduces to stopping problem for each arm. Interpretation as (scaled)
Uncertainty Analysis with UNICORN
 Uncertainty Analysis with UNICORN D.A.Ababei D.Kurowicka R.M.Cooke D.A.Ababei@ewi.tudelft.nl D.Kurowicka@ewi.tudelft.nl R.M.Cooke@ewi.tudelft.nl Delft Institute for Applied Mathematics Delft University
Uncertainty Analysis with UNICORN D.A.Ababei D.Kurowicka R.M.Cooke D.A.Ababei@ewi.tudelft.nl D.Kurowicka@ewi.tudelft.nl R.M.Cooke@ewi.tudelft.nl Delft Institute for Applied Mathematics Delft University
Log-linear Dynamics and Local Potential
 Log-linear Dynamics and Local Potential Daijiro Okada and Olivier Tercieux [This version: November 28, 2008] Abstract We show that local potential maximizer ([15]) with constant weights is stochastically
Log-linear Dynamics and Local Potential Daijiro Okada and Olivier Tercieux [This version: November 28, 2008] Abstract We show that local potential maximizer ([15]) with constant weights is stochastically
Laplace approximation
 NPFL108 Bayesian inference Approximate Inference Laplace approximation Filip Jurčíček Institute of Formal and Applied Linguistics Charles University in Prague Czech Republic Home page: http://ufal.mff.cuni.cz/~jurcicek
NPFL108 Bayesian inference Approximate Inference Laplace approximation Filip Jurčíček Institute of Formal and Applied Linguistics Charles University in Prague Czech Republic Home page: http://ufal.mff.cuni.cz/~jurcicek
1 Solutions to Tute09
 s to Tute0 Questions 4. - 4. are straight forward. Q. 4.4 Show that in a binary tree of N nodes, there are N + NULL pointers. Every node has outgoing pointers. Therefore there are N pointers. Each node,
s to Tute0 Questions 4. - 4. are straight forward. Q. 4.4 Show that in a binary tree of N nodes, there are N + NULL pointers. Every node has outgoing pointers. Therefore there are N pointers. Each node,
Reasoning with Uncertainty
 Reasoning with Uncertainty Markov Decision Models Manfred Huber 2015 1 Markov Decision Process Models Markov models represent the behavior of a random process, including its internal state and the externally
Reasoning with Uncertainty Markov Decision Models Manfred Huber 2015 1 Markov Decision Process Models Markov models represent the behavior of a random process, including its internal state and the externally
Lecture 9: Games I. Course plan. A simple game. Roadmap. Machine learning. Example: game 1
 Lecture 9: Games I Course plan Search problems Markov decision processes Adversarial games Constraint satisfaction problems Bayesian networks Reflex States Variables Logic Low-level intelligence Machine
Lecture 9: Games I Course plan Search problems Markov decision processes Adversarial games Constraint satisfaction problems Bayesian networks Reflex States Variables Logic Low-level intelligence Machine
Lecture 12: Introduction to reasoning under uncertainty. Actions and Consequences
 Lecture 12: Introduction to reasoning under uncertainty Preferences Utility functions Maximizing expected utility Value of information Bandit problems and the exploration-exploitation trade-off COMP-424,
Lecture 12: Introduction to reasoning under uncertainty Preferences Utility functions Maximizing expected utility Value of information Bandit problems and the exploration-exploitation trade-off COMP-424,
EE/AA 578 Univ. of Washington, Fall Homework 8
 EE/AA 578 Univ. of Washington, Fall 2016 Homework 8 1. Multi-label SVM. The basic Support Vector Machine (SVM) described in the lecture (and textbook) is used for classification of data with two labels.
EE/AA 578 Univ. of Washington, Fall 2016 Homework 8 1. Multi-label SVM. The basic Support Vector Machine (SVM) described in the lecture (and textbook) is used for classification of data with two labels.
Another Variant of 3sat. 3sat. 3sat Is NP-Complete. The Proof (concluded)
 3sat k-sat, where k Z +, is the special case of sat. The formula is in CNF and all clauses have exactly k literals (repetition of literals is allowed). For example, (x 1 x 2 x 3 ) (x 1 x 1 x 2 ) (x 1 x
3sat k-sat, where k Z +, is the special case of sat. The formula is in CNF and all clauses have exactly k literals (repetition of literals is allowed). For example, (x 1 x 2 x 3 ) (x 1 x 1 x 2 ) (x 1 x
Relational Regression Methods to Speed Up Monte-Carlo Planning
 Institute of Parallel and Distributed Systems University of Stuttgart Universitätsstraße 38 D 70569 Stuttgart Relational Regression Methods to Speed Up Monte-Carlo Planning Teresa Böpple Course of Study:
Institute of Parallel and Distributed Systems University of Stuttgart Universitätsstraße 38 D 70569 Stuttgart Relational Regression Methods to Speed Up Monte-Carlo Planning Teresa Böpple Course of Study:
Levin Reduction and Parsimonious Reductions
 Levin Reduction and Parsimonious Reductions The reduction R in Cook s theorem (p. 266) is such that Each satisfying truth assignment for circuit R(x) corresponds to an accepting computation path for M(x).
Levin Reduction and Parsimonious Reductions The reduction R in Cook s theorem (p. 266) is such that Each satisfying truth assignment for circuit R(x) corresponds to an accepting computation path for M(x).
ADVANCED MACROECONOMIC TECHNIQUES NOTE 6a
 316-406 ADVANCED MACROECONOMIC TECHNIQUES NOTE 6a Chris Edmond hcpedmond@unimelb.edu.aui Introduction to consumption-based asset pricing We will begin our brief look at asset pricing with a review of the
316-406 ADVANCED MACROECONOMIC TECHNIQUES NOTE 6a Chris Edmond hcpedmond@unimelb.edu.aui Introduction to consumption-based asset pricing We will begin our brief look at asset pricing with a review of the
Stochastic Games and Bayesian Games
 Stochastic Games and Bayesian Games CPSC 532L Lecture 10 Stochastic Games and Bayesian Games CPSC 532L Lecture 10, Slide 1 Lecture Overview 1 Recap 2 Stochastic Games 3 Bayesian Games Stochastic Games
Stochastic Games and Bayesian Games CPSC 532L Lecture 10 Stochastic Games and Bayesian Games CPSC 532L Lecture 10, Slide 1 Lecture Overview 1 Recap 2 Stochastic Games 3 Bayesian Games Stochastic Games
Equity correlations implied by index options: estimation and model uncertainty analysis
 1/18 : estimation and model analysis, EDHEC Business School (joint work with Rama COT) Modeling and managing financial risks Paris, 10 13 January 2011 2/18 Outline 1 2 of multi-asset models Solution to
1/18 : estimation and model analysis, EDHEC Business School (joint work with Rama COT) Modeling and managing financial risks Paris, 10 13 January 2011 2/18 Outline 1 2 of multi-asset models Solution to
Version A. Problem 1. Let X be the continuous random variable defined by the following pdf: 1 x/2 when 0 x 2, f(x) = 0 otherwise.
 Math 224 Q Exam 3A Fall 217 Tues Dec 12 Version A Problem 1. Let X be the continuous random variable defined by the following pdf: { 1 x/2 when x 2, f(x) otherwise. (a) Compute the mean µ E[X]. E[X] x
Math 224 Q Exam 3A Fall 217 Tues Dec 12 Version A Problem 1. Let X be the continuous random variable defined by the following pdf: { 1 x/2 when x 2, f(x) otherwise. (a) Compute the mean µ E[X]. E[X] x
Estimation after Model Selection
 Estimation after Model Selection Vanja M. Dukić Department of Health Studies University of Chicago E-Mail: vanja@uchicago.edu Edsel A. Peña* Department of Statistics University of South Carolina E-Mail:
Estimation after Model Selection Vanja M. Dukić Department of Health Studies University of Chicago E-Mail: vanja@uchicago.edu Edsel A. Peña* Department of Statistics University of South Carolina E-Mail:
Statistics for Managers Using Microsoft Excel 7 th Edition
 Statistics for Managers Using Microsoft Excel 7 th Edition Chapter 5 Discrete Probability Distributions Statistics for Managers Using Microsoft Excel 7e Copyright 014 Pearson Education, Inc. Chap 5-1 Learning
Statistics for Managers Using Microsoft Excel 7 th Edition Chapter 5 Discrete Probability Distributions Statistics for Managers Using Microsoft Excel 7e Copyright 014 Pearson Education, Inc. Chap 5-1 Learning
Numerical Methods in Option Pricing (Part III)
 Numerical Methods in Option Pricing (Part III) E. Explicit Finite Differences. Use of the Forward, Central, and Symmetric Central a. In order to obtain an explicit solution for the price of the derivative,
Numerical Methods in Option Pricing (Part III) E. Explicit Finite Differences. Use of the Forward, Central, and Symmetric Central a. In order to obtain an explicit solution for the price of the derivative,
Sequential Decision Making
 Sequential Decision Making Dynamic programming Christos Dimitrakakis Intelligent Autonomous Systems, IvI, University of Amsterdam, The Netherlands March 18, 2008 Introduction Some examples Dynamic programming
Sequential Decision Making Dynamic programming Christos Dimitrakakis Intelligent Autonomous Systems, IvI, University of Amsterdam, The Netherlands March 18, 2008 Introduction Some examples Dynamic programming
Crash-tolerant Consensus in Directed Graph Revisited
 Crash-tolerant Consensus in Directed Graph Revisited Ashish Choudhury Gayathri Garimella Arpita Patra Divya Ravi Pratik Sarkar Abstract Fault-tolerant distributed consensus is a fundamental problem in
Crash-tolerant Consensus in Directed Graph Revisited Ashish Choudhury Gayathri Garimella Arpita Patra Divya Ravi Pratik Sarkar Abstract Fault-tolerant distributed consensus is a fundamental problem in
Outline. 1 Introduction. 2 Algorithms. 3 Examples. Algorithm 1 General coordinate minimization framework. 1: Choose x 0 R n and set k 0.
 Outline Coordinate Minimization Daniel P. Robinson Department of Applied Mathematics and Statistics Johns Hopkins University November 27, 208 Introduction 2 Algorithms Cyclic order with exact minimization
Outline Coordinate Minimization Daniel P. Robinson Department of Applied Mathematics and Statistics Johns Hopkins University November 27, 208 Introduction 2 Algorithms Cyclic order with exact minimization
Counting Basics. Venn diagrams
 Counting Basics Sets Ways of specifying sets Union and intersection Universal set and complements Empty set and disjoint sets Venn diagrams Counting Inclusion-exclusion Multiplication principle Addition
Counting Basics Sets Ways of specifying sets Union and intersection Universal set and complements Empty set and disjoint sets Venn diagrams Counting Inclusion-exclusion Multiplication principle Addition
Mathematical Annex 5 Models with Rational Expectations
 George Alogoskoufis, Dynamic Macroeconomic Theory, 2015 Mathematical Annex 5 Models with Rational Expectations In this mathematical annex we examine the properties and alternative solution methods for
George Alogoskoufis, Dynamic Macroeconomic Theory, 2015 Mathematical Annex 5 Models with Rational Expectations In this mathematical annex we examine the properties and alternative solution methods for
Maximizing the Spread of Influence through a Social Network Problem/Motivation: Suppose we want to market a product or promote an idea or behavior in
 Maximizing the Spread of Influence through a Social Network Problem/Motivation: Suppose we want to market a product or promote an idea or behavior in a society. In order to do so, we can target individuals,
Maximizing the Spread of Influence through a Social Network Problem/Motivation: Suppose we want to market a product or promote an idea or behavior in a society. In order to do so, we can target individuals,
Essays on Some Combinatorial Optimization Problems with Interval Data
 Essays on Some Combinatorial Optimization Problems with Interval Data a thesis submitted to the department of industrial engineering and the institute of engineering and sciences of bilkent university
Essays on Some Combinatorial Optimization Problems with Interval Data a thesis submitted to the department of industrial engineering and the institute of engineering and sciences of bilkent university
Introduction to Decision Making. CS 486/686: Introduction to Artificial Intelligence
 Introduction to Decision Making CS 486/686: Introduction to Artificial Intelligence 1 Outline Utility Theory Decision Trees 2 Decision Making Under Uncertainty I give a robot a planning problem: I want
Introduction to Decision Making CS 486/686: Introduction to Artificial Intelligence 1 Outline Utility Theory Decision Trees 2 Decision Making Under Uncertainty I give a robot a planning problem: I want
Modelling, Estimation and Hedging of Longevity Risk
 IA BE Summer School 2016, K. Antonio, UvA 1 / 50 Modelling, Estimation and Hedging of Longevity Risk Katrien Antonio KU Leuven and University of Amsterdam IA BE Summer School 2016, Leuven Module II: Fitting
IA BE Summer School 2016, K. Antonio, UvA 1 / 50 Modelling, Estimation and Hedging of Longevity Risk Katrien Antonio KU Leuven and University of Amsterdam IA BE Summer School 2016, Leuven Module II: Fitting
CS340 Machine learning Bayesian model selection
 CS340 Machine learning Bayesian model selection Bayesian model selection Suppose we have several models, each with potentially different numbers of parameters. Example: M0 = constant, M1 = straight line,
CS340 Machine learning Bayesian model selection Bayesian model selection Suppose we have several models, each with potentially different numbers of parameters. Example: M0 = constant, M1 = straight line,
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50)
 Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 2 Random number generation January 18, 2018
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 2 Random number generation January 18, 2018
Stochastic Grid Bundling Method
 Stochastic Grid Bundling Method GPU Acceleration Delft University of Technology - Centrum Wiskunde & Informatica Álvaro Leitao Rodríguez and Cornelis W. Oosterlee London - December 17, 2015 A. Leitao &
Stochastic Grid Bundling Method GPU Acceleration Delft University of Technology - Centrum Wiskunde & Informatica Álvaro Leitao Rodríguez and Cornelis W. Oosterlee London - December 17, 2015 A. Leitao &
Introduction to Dynamic Programming
 Introduction to Dynamic Programming http://bicmr.pku.edu.cn/~wenzw/bigdata2018.html Acknowledgement: this slides is based on Prof. Mengdi Wang s and Prof. Dimitri Bertsekas lecture notes Outline 2/65 1
Introduction to Dynamic Programming http://bicmr.pku.edu.cn/~wenzw/bigdata2018.html Acknowledgement: this slides is based on Prof. Mengdi Wang s and Prof. Dimitri Bertsekas lecture notes Outline 2/65 1
CS 3331 Numerical Methods Lecture 2: Functions of One Variable. Cherung Lee
 CS 3331 Numerical Methods Lecture 2: Functions of One Variable Cherung Lee Outline Introduction Solving nonlinear equations: find x such that f(x ) = 0. Binary search methods: (Bisection, regula falsi)
CS 3331 Numerical Methods Lecture 2: Functions of One Variable Cherung Lee Outline Introduction Solving nonlinear equations: find x such that f(x ) = 0. Binary search methods: (Bisection, regula falsi)
Modelli Grafici Probabilistici (2): concetti generali
 Modelli Grafici Probabilistici (2): concetti generali Corso di Modelli di Computazione Affettiva Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it Giuseppe.Boccignone@unimi.it
Modelli Grafici Probabilistici (2): concetti generali Corso di Modelli di Computazione Affettiva Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it Giuseppe.Boccignone@unimi.it
Outline. Objective. Previous Results Our Results Discussion Current Research. 1 Motivation. 2 Model. 3 Results
 On Threshold Esteban 1 Adam 2 Ravi 3 David 4 Sergei 1 1 Stanford University 2 Harvard University 3 Yahoo! Research 4 Carleton College The 8th ACM Conference on Electronic Commerce EC 07 Outline 1 2 3 Some
On Threshold Esteban 1 Adam 2 Ravi 3 David 4 Sergei 1 1 Stanford University 2 Harvard University 3 Yahoo! Research 4 Carleton College The 8th ACM Conference on Electronic Commerce EC 07 Outline 1 2 3 Some
A Theory of Loss-leaders: Making Money by Pricing Below Cost
 A Theory of Loss-leaders: Making Money by Pricing Below Cost Maria-Florina Balcan Avrim Blum T-H. Hubert Chan MohammadTaghi Hajiaghayi ABSTRACT We consider the problem of assigning prices to goods of fixed
A Theory of Loss-leaders: Making Money by Pricing Below Cost Maria-Florina Balcan Avrim Blum T-H. Hubert Chan MohammadTaghi Hajiaghayi ABSTRACT We consider the problem of assigning prices to goods of fixed
