Gibbs Fields: Inference and Relation to Bayes Networks
|
|
|
- Rudolf Pierce
- 5 years ago
- Views:
Transcription
1 Statistical Techniques in Robotics (16-831, F10) Lecture#08 (Thursday September 16) Gibbs Fields: Inference and Relation to ayes Networks Lecturer: rew agnell Scribe:ebadeepta ey 1 1 Inference on Gibbs Fields Once we have learnt a Gibbs Field or a Markov Random Field (both of them are equivalent according to the Hammersly-lifford theorem) the main question is how to do inference on the learnt graphical model. There are two major types of queries that are useful in general. 1. Marginals 2. Most probable assignment given some observed nodes 1.1 Marginals P(X i observedx s) (1) The naive way of doing marginals is to sum over all possible combination of assignments to the unobserved variables. Assuming that we have a graph whose clique potentials are Gaussians we can write the marginal in the conventional way as: p( X observedx s) = (1/Z) exp( i j N i f(x i,x j )) (2) Here N i are the neighbors of the i th node. If the random variables in the node are binary and there are n such nodes and k of these nodes are observed then the number of elements is of the order of 2 n k. This is generally intractable as the number of nodes in a graph can easily be of the order of a few thousands or more. We will explore 2 methods of doing this: 1. Importance Sampling 2. Gibbs Sampling 1 Some content adapted from previous scribes: yron oots 1
2 1.1.1 Importance Sampling Generate samples from P(X) = i p(x i ) (3) while clamping nodes observed to the observed values. This means that we are not sampling the original distribution and hence we must weight each of the samples by the probability of the particular joint assignment. The marginal is then obtained from all the weighted samples by the ratio of the sum of the weights of the samples which satisfy the query divided to the total weight of all samples. p( X observedx s) = N c N (4) where N c = sum of weights of samples which satisfy the query and N is the total weight of all samples Gibbs Sampling The best way to explain Gibbs Sampling is to go over an example of how to do it and then try to get the intuition behind the procedure. Figure 1: Example lattice graph with a single node observed as 1. This kind of single layer graph is also called an Ising model. Refer to Fig It is a simple lattice structure also commonly called as the Ising model. Here the node in red has been observed to be the value 1. Given this observation we want to know what the values of the rest of the nodes in the graph. The pseudo-code for the Gibbs sampling algorithm is given in Algorithm.1. In line 1 you can randomly assign any value to all the unobserved nodes while fixing the observed nodes to the values observed. In lines 3 5 you move over the graph fixing the value of every i th node under consideration by sampling the conditional distribution for that particular node which is easy to do as the node under consideration is independent of the rest of the graph given its Markov blanket which in the case of Gibbs Fields are just its neighbors. This takes the form P(x i N(x i )) = 2
3 1 Z exp( i,j N f(x i,x j )) where N is the set of neighbors of x i. Please note that the updated value of x i is used as soon as it is computed while computing the value of its neighbor. This fact is noted in Algorithm.1 in line 4 where some of the nodes have t+1 in the index while others have t. Once you have gone over the whole graph once this completes the inner loop and you start over with the current updated state of the graph. All through the procedure the observed nodes remain fixed. Algorithm 1 Pseudo-code for the Gibbs sampling method on Gibbs Fields 1: X (0) :=< x 0 1,...,x0 k > 2: for t = 1 to T do 3: for i = 1 to K do 4: x (t+1) i 5: end for 6: end for = P(x i x (t+1) 1,...,x t+1 i 1,xt i+1,...,xt k ) Figure 2: For the node under consideration (yellow), its value is determined by the conditional distribution over all its neighboring nodes shown in the figure. Then this process is repeated over all the nodes in turn while keeping the observed nodes fixed to observed values. Intuition The Gibbs sampling procedure is an instance of the Metropolis-Hastings algorithm which is a type of Markov hain Monte arlo method. It is a Markov hain method since it is generating current samples depending only the last state of the entire graph. It is a Monte arlo method since the sampling is a probabilistic process. The idea is that by repeatedly sampling in the manner outlined the algorithm will converge to the actual distribution of the graph. The actual distribution of the graph can be thought of as the stationary distribution underlying the markov chain we are generating in our sampling procedure. The reader is directed to the read the first part of the excellent tutorial [1] for more intuition and the second part for all the related mathematical details. Gibbs Sampling Problems ritical Phenomena This is also sometimes referred to as ritical Slowing own. This happens when one node starts determining the value of another node really far away. This can start 3
4 happening when the sampling has gone through many iterations but there are regions of high probablity and low probability now in the graph. These regions may be very highly correlated and hence will cause the sampling to produce series of values which are similar. In general the stronger the connections between nodes the slower Gibbs sampling will run to converge in distribution. Another good reference which goes into great detail on the topic is [2]. 1.2 Most probable assignment given some observed nodes We will deal with this later. arg maxp( X observedx s) (5) X 2 Gibbs Fields and ayesian Networks You can go from ayesian Networks to Gibbs Fields but not vice versa. Even when you convert a ayesian Network to a Gibbs field you are going to lose information as will be illustrated in the example below. You can not necessarily convert a ayes net into a Gibbs field. For example, consider the ayes net in Figure 3. If you remove the arrows (Figure 4), then the graph is not equivalent. In particular observing node causes nodes A and to become independent. This is the opposite of what the original graph represented. Instead, we need to moralize the graph. Whenever there are two parents that are not connected (married), we connect them. Thus, Figure 5 shows the correct representation of the original ayes net. Note that during this conversion we actually lost information, namely that A and are marginally independent. A Figure 3: ayes Net 4
5 A Figure 4: INORRET A Figure 5: ORRET: Moralizing 2.1 Gibbs Sampling of ayesian Networks References [1] Philip Resnik and Eric Hardisty, Gibbs Sampling for the Uninitiated, UMIAS-TR , (2010). [2] Gilks, W.R. and Richardson, S. and Spiegelhalter,.J., Markov chain Monte arlo in practice, hapman & Hall/R, (1996). 5
Sum-Product: Message Passing Belief Propagation
 Sum-Product: Message Passing Belief Propagation Probabilistic Graphical Models Sharif University of Technology Spring 2017 Soleymani All single-node marginals If we need the full set of marginals, repeating
Sum-Product: Message Passing Belief Propagation Probabilistic Graphical Models Sharif University of Technology Spring 2017 Soleymani All single-node marginals If we need the full set of marginals, repeating
COS 513: Gibbs Sampling
 COS 513: Gibbs Sampling Matthew Salesi December 6, 2010 1 Overview Concluding the coverage of Markov chain Monte Carlo (MCMC) sampling methods, we look today at Gibbs sampling. Gibbs sampling is a simple
COS 513: Gibbs Sampling Matthew Salesi December 6, 2010 1 Overview Concluding the coverage of Markov chain Monte Carlo (MCMC) sampling methods, we look today at Gibbs sampling. Gibbs sampling is a simple
Machine Learning in Computer Vision Markov Random Fields Part II
 Machine Learning in Computer Vision Markov Random Fields Part II Oren Freifeld Computer Science, Ben-Gurion University March 22, 2018 Mar 22, 2018 1 / 40 1 Some MRF Computations 2 Mar 22, 2018 2 / 40 Few
Machine Learning in Computer Vision Markov Random Fields Part II Oren Freifeld Computer Science, Ben-Gurion University March 22, 2018 Mar 22, 2018 1 / 40 1 Some MRF Computations 2 Mar 22, 2018 2 / 40 Few
Sum-Product: Message Passing Belief Propagation
 Sum-Product: Message Passing Belief Propagation 40-956 Advanced Topics in AI: Probabilistic Graphical Models Sharif University of Technology Soleymani Spring 2015 All single-node marginals If we need the
Sum-Product: Message Passing Belief Propagation 40-956 Advanced Topics in AI: Probabilistic Graphical Models Sharif University of Technology Soleymani Spring 2015 All single-node marginals If we need the
Exact Inference. Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4. x 3. f s. x 2. x 1
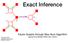 Exact Inference x 1 x 3 x 2 f s Geoffrey Roeder roeder@cs.toronto.edu 8 February 2018 Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4 Building Blocks UGMs, Cliques, Factor
Exact Inference x 1 x 3 x 2 f s Geoffrey Roeder roeder@cs.toronto.edu 8 February 2018 Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4 Building Blocks UGMs, Cliques, Factor
15 : Approximate Inference: Monte Carlo Methods
 10-708: Probabilistic Graphical Models 10-708, Spring 2016 15 : Approximate Inference: Monte Carlo Methods Lecturer: Eric P. Xing Scribes: Binxuan Huang, Yotam Hechtlinger, Fuchen Liu 1 Introduction to
10-708: Probabilistic Graphical Models 10-708, Spring 2016 15 : Approximate Inference: Monte Carlo Methods Lecturer: Eric P. Xing Scribes: Binxuan Huang, Yotam Hechtlinger, Fuchen Liu 1 Introduction to
COMP90051 Statistical Machine Learning
 COMP90051 Statistical Machine Learning Semester 2, 2017 Lecturer: Trevor Cohn 22. PGM Probabilistic Inference Probabilistic inference on PGMs Computing marginal and conditional distributions from the joint
COMP90051 Statistical Machine Learning Semester 2, 2017 Lecturer: Trevor Cohn 22. PGM Probabilistic Inference Probabilistic inference on PGMs Computing marginal and conditional distributions from the joint
THE NON - STOCK EXCHANGE DEALS OPTIMIZATION USING NETFLOW METHOD. V.B.Gorsky, V.P.Stepanov. Saving Bank of Russian Federation,
 THE NON - STOCK EXCHANGE DEALS OPTIMIZATION USING NETFLOW METHOD. V.B.Gorsky, V.P.Stepanov. Saving Bank of Russian Federation, e-mail: dwhome@sbrf.ru Abstract. We would like to present the solution of
THE NON - STOCK EXCHANGE DEALS OPTIMIZATION USING NETFLOW METHOD. V.B.Gorsky, V.P.Stepanov. Saving Bank of Russian Federation, e-mail: dwhome@sbrf.ru Abstract. We would like to present the solution of
Machine Learning
 Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 13, 2011 Today: Graphical models Bayes Nets: Conditional independencies Inference Learning Readings:
Machine Learning 10-601 Tom M. Mitchell Machine Learning Department Carnegie Mellon University October 13, 2011 Today: Graphical models Bayes Nets: Conditional independencies Inference Learning Readings:
Basic Framework. About this class. Rewards Over Time. [This lecture adapted from Sutton & Barto and Russell & Norvig]
![Basic Framework. About this class. Rewards Over Time. [This lecture adapted from Sutton & Barto and Russell & Norvig] Basic Framework. About this class. Rewards Over Time. [This lecture adapted from Sutton & Barto and Russell & Norvig]](/thumbs/82/85647934.jpg) Basic Framework [This lecture adapted from Sutton & Barto and Russell & Norvig] About this class Markov Decision Processes The Bellman Equation Dynamic Programming for finding value functions and optimal
Basic Framework [This lecture adapted from Sutton & Barto and Russell & Norvig] About this class Markov Decision Processes The Bellman Equation Dynamic Programming for finding value functions and optimal
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50)
 Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 5 Sequential Monte Carlo methods I January
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 5 Sequential Monte Carlo methods I January
Inference in Bayesian Networks
 Andrea Passerini passerini@disi.unitn.it Machine Learning Inference in graphical models Description Assume we have evidence e on the state of a subset of variables E in the model (i.e. Bayesian Network)
Andrea Passerini passerini@disi.unitn.it Machine Learning Inference in graphical models Description Assume we have evidence e on the state of a subset of variables E in the model (i.e. Bayesian Network)
Lecture 17: More on Markov Decision Processes. Reinforcement learning
 Lecture 17: More on Markov Decision Processes. Reinforcement learning Learning a model: maximum likelihood Learning a value function directly Monte Carlo Temporal-difference (TD) learning COMP-424, Lecture
Lecture 17: More on Markov Decision Processes. Reinforcement learning Learning a model: maximum likelihood Learning a value function directly Monte Carlo Temporal-difference (TD) learning COMP-424, Lecture
Sequential Decision Making
 Sequential Decision Making Dynamic programming Christos Dimitrakakis Intelligent Autonomous Systems, IvI, University of Amsterdam, The Netherlands March 18, 2008 Introduction Some examples Dynamic programming
Sequential Decision Making Dynamic programming Christos Dimitrakakis Intelligent Autonomous Systems, IvI, University of Amsterdam, The Netherlands March 18, 2008 Introduction Some examples Dynamic programming
CPSC 540: Machine Learning
 CPSC 540: Machine Learning Monte Carlo Methods Mark Schmidt University of British Columbia Winter 2018 Last Time: Markov Chains We can use Markov chains for density estimation, p(x) = p(x 1 ) }{{} d p(x
CPSC 540: Machine Learning Monte Carlo Methods Mark Schmidt University of British Columbia Winter 2018 Last Time: Markov Chains We can use Markov chains for density estimation, p(x) = p(x 1 ) }{{} d p(x
The exam is closed book, closed calculator, and closed notes except your one-page crib sheet.
 CS 188 Summer 2015 Introduction to Artificial Intelligence Midterm 2 You have approximately 80 minutes. The exam is closed book, closed calculator, and closed notes except your one-page crib sheet. Mark
CS 188 Summer 2015 Introduction to Artificial Intelligence Midterm 2 You have approximately 80 minutes. The exam is closed book, closed calculator, and closed notes except your one-page crib sheet. Mark
Sublinear Time Algorithms Oct 19, Lecture 1
 0368.416701 Sublinear Time Algorithms Oct 19, 2009 Lecturer: Ronitt Rubinfeld Lecture 1 Scribe: Daniel Shahaf 1 Sublinear-time algorithms: motivation Twenty years ago, there was practically no investigation
0368.416701 Sublinear Time Algorithms Oct 19, 2009 Lecturer: Ronitt Rubinfeld Lecture 1 Scribe: Daniel Shahaf 1 Sublinear-time algorithms: motivation Twenty years ago, there was practically no investigation
CPSC 540: Machine Learning
 CPSC 540: Machine Learning Monte Carlo Methods Mark Schmidt University of British Columbia Winter 2019 Last Time: Markov Chains We can use Markov chains for density estimation, d p(x) = p(x 1 ) p(x }{{}
CPSC 540: Machine Learning Monte Carlo Methods Mark Schmidt University of British Columbia Winter 2019 Last Time: Markov Chains We can use Markov chains for density estimation, d p(x) = p(x 1 ) p(x }{{}
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages
 Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Lecture 3 Tuesday, February 2, 2016 1 Inductive proofs, continued Last lecture we considered inductively defined sets, and
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Lecture 3 Tuesday, February 2, 2016 1 Inductive proofs, continued Last lecture we considered inductively defined sets, and
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50)
 Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 6 Sequential Monte Carlo methods II February
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 6 Sequential Monte Carlo methods II February
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages
 Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Lecture 3 Tuesday, January 30, 2018 1 Inductive sets Induction is an important concept in the theory of programming language.
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Lecture 3 Tuesday, January 30, 2018 1 Inductive sets Induction is an important concept in the theory of programming language.
A start of Variational Methods for ERGM Ranran Wang, UW
 A start of Variational Methods for ERGM Ranran Wang, UW MURI-UCI April 24, 2009 Outline A start of Variational Methods for ERGM [1] Introduction to ERGM Current methods of parameter estimation: MCMCMLE:
A start of Variational Methods for ERGM Ranran Wang, UW MURI-UCI April 24, 2009 Outline A start of Variational Methods for ERGM [1] Introduction to ERGM Current methods of parameter estimation: MCMCMLE:
Down-Up Metropolis-Hastings Algorithm for Multimodality
 Down-Up Metropolis-Hastings Algorithm for Multimodality Hyungsuk Tak Stat310 24 Nov 2015 Joint work with Xiao-Li Meng and David A. van Dyk Outline Motivation & idea Down-Up Metropolis-Hastings (DUMH) algorithm
Down-Up Metropolis-Hastings Algorithm for Multimodality Hyungsuk Tak Stat310 24 Nov 2015 Joint work with Xiao-Li Meng and David A. van Dyk Outline Motivation & idea Down-Up Metropolis-Hastings (DUMH) algorithm
Subject : Computer Science. Paper: Machine Learning. Module: Decision Theory and Bayesian Decision Theory. Module No: CS/ML/10.
 e-pg Pathshala Subject : Computer Science Paper: Machine Learning Module: Decision Theory and Bayesian Decision Theory Module No: CS/ML/0 Quadrant I e-text Welcome to the e-pg Pathshala Lecture Series
e-pg Pathshala Subject : Computer Science Paper: Machine Learning Module: Decision Theory and Bayesian Decision Theory Module No: CS/ML/0 Quadrant I e-text Welcome to the e-pg Pathshala Lecture Series
Single-Parameter Mechanisms
 Algorithmic Game Theory, Summer 25 Single-Parameter Mechanisms Lecture 9 (6 pages) Instructor: Xiaohui Bei In the previous lecture, we learned basic concepts about mechanism design. The goal in this area
Algorithmic Game Theory, Summer 25 Single-Parameter Mechanisms Lecture 9 (6 pages) Instructor: Xiaohui Bei In the previous lecture, we learned basic concepts about mechanism design. The goal in this area
Homework 1 posted, due Friday, September 30, 2 PM. Independence of random variables: We say that a collection of random variables
 Generating Functions Tuesday, September 20, 2011 2:00 PM Homework 1 posted, due Friday, September 30, 2 PM. Independence of random variables: We say that a collection of random variables Is independent
Generating Functions Tuesday, September 20, 2011 2:00 PM Homework 1 posted, due Friday, September 30, 2 PM. Independence of random variables: We say that a collection of random variables Is independent
The exam is closed book, closed calculator, and closed notes except your three crib sheets.
 CS 188 Spring 2016 Introduction to Artificial Intelligence Final V2 You have approximately 2 hours and 50 minutes. The exam is closed book, closed calculator, and closed notes except your three crib sheets.
CS 188 Spring 2016 Introduction to Artificial Intelligence Final V2 You have approximately 2 hours and 50 minutes. The exam is closed book, closed calculator, and closed notes except your three crib sheets.
Exact Inference (9/30/13) 2 A brief review of Forward-Backward and EM for HMMs
 STA561: Probabilistic machine learning Exact Inference (9/30/13) Lecturer: Barbara Engelhardt Scribes: Jiawei Liang, He Jiang, Brittany Cohen 1 Validation for Clustering If we have two centroids, η 1 and
STA561: Probabilistic machine learning Exact Inference (9/30/13) Lecturer: Barbara Engelhardt Scribes: Jiawei Liang, He Jiang, Brittany Cohen 1 Validation for Clustering If we have two centroids, η 1 and
CS 188: Artificial Intelligence
 CS 188: Artificial Intelligence Markov Decision Processes Dan Klein, Pieter Abbeel University of California, Berkeley Non-Deterministic Search 1 Example: Grid World A maze-like problem The agent lives
CS 188: Artificial Intelligence Markov Decision Processes Dan Klein, Pieter Abbeel University of California, Berkeley Non-Deterministic Search 1 Example: Grid World A maze-like problem The agent lives
Reinforcement Learning
 Reinforcement Learning Basic idea: Receive feedback in the form of rewards Agent s utility is defined by the reward function Must (learn to) act so as to maximize expected rewards Grid World The agent
Reinforcement Learning Basic idea: Receive feedback in the form of rewards Agent s utility is defined by the reward function Must (learn to) act so as to maximize expected rewards Grid World The agent
ELEMENTS OF MONTE CARLO SIMULATION
 APPENDIX B ELEMENTS OF MONTE CARLO SIMULATION B. GENERAL CONCEPT The basic idea of Monte Carlo simulation is to create a series of experimental samples using a random number sequence. According to the
APPENDIX B ELEMENTS OF MONTE CARLO SIMULATION B. GENERAL CONCEPT The basic idea of Monte Carlo simulation is to create a series of experimental samples using a random number sequence. According to the
Statistical Computing (36-350)
 Statistical Computing (36-350) Lecture 16: Simulation III: Monte Carlo Cosma Shalizi 21 October 2013 Agenda Monte Carlo Monte Carlo approximation of integrals and expectations The rejection method and
Statistical Computing (36-350) Lecture 16: Simulation III: Monte Carlo Cosma Shalizi 21 October 2013 Agenda Monte Carlo Monte Carlo approximation of integrals and expectations The rejection method and
Maximum Likelihood Estimation
 Maximum Likelihood Estimation EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #6 EPSY 905: Maximum Likelihood In This Lecture The basics of maximum likelihood estimation Ø The engine that
Maximum Likelihood Estimation EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #6 EPSY 905: Maximum Likelihood In This Lecture The basics of maximum likelihood estimation Ø The engine that
Strategies for Improving the Efficiency of Monte-Carlo Methods
 Strategies for Improving the Efficiency of Monte-Carlo Methods Paul J. Atzberger General comments or corrections should be sent to: paulatz@cims.nyu.edu Introduction The Monte-Carlo method is a useful
Strategies for Improving the Efficiency of Monte-Carlo Methods Paul J. Atzberger General comments or corrections should be sent to: paulatz@cims.nyu.edu Introduction The Monte-Carlo method is a useful
Adaptive Experiments for Policy Choice. March 8, 2019
 Adaptive Experiments for Policy Choice Maximilian Kasy Anja Sautmann March 8, 2019 Introduction The goal of many experiments is to inform policy choices: 1. Job search assistance for refugees: Treatments:
Adaptive Experiments for Policy Choice Maximilian Kasy Anja Sautmann March 8, 2019 Introduction The goal of many experiments is to inform policy choices: 1. Job search assistance for refugees: Treatments:
Probabilistic Graphical Models
 CS420, Machine Learning, Lecture 8 Probabilistic Graphical Models Weinan Zhang Shanghai Jiao Tong University http://wnzhang.net http://wnzhang.net/teaching/cs420/index.html Content of This Lecture Introduction
CS420, Machine Learning, Lecture 8 Probabilistic Graphical Models Weinan Zhang Shanghai Jiao Tong University http://wnzhang.net http://wnzhang.net/teaching/cs420/index.html Content of This Lecture Introduction
Machine Learning. Graphical Models. Marc Toussaint University of Stuttgart Summer 2015
 Machine Learning Graphical Models Marc Toussaint University of Stuttgart Summer 2015 Outline A. Introduction Motivation and definition of Bayes Nets Conditional independence in Bayes Nets Examples B. Inference
Machine Learning Graphical Models Marc Toussaint University of Stuttgart Summer 2015 Outline A. Introduction Motivation and definition of Bayes Nets Conditional independence in Bayes Nets Examples B. Inference
Optimization Prof. A. Goswami Department of Mathematics Indian Institute of Technology, Kharagpur. Lecture - 18 PERT
 Optimization Prof. A. Goswami Department of Mathematics Indian Institute of Technology, Kharagpur Lecture - 18 PERT (Refer Slide Time: 00:56) In the last class we completed the C P M critical path analysis
Optimization Prof. A. Goswami Department of Mathematics Indian Institute of Technology, Kharagpur Lecture - 18 PERT (Refer Slide Time: 00:56) In the last class we completed the C P M critical path analysis
Algorithmic Trading using Reinforcement Learning augmented with Hidden Markov Model
 Algorithmic Trading using Reinforcement Learning augmented with Hidden Markov Model Simerjot Kaur (sk3391) Stanford University Abstract This work presents a novel algorithmic trading system based on reinforcement
Algorithmic Trading using Reinforcement Learning augmented with Hidden Markov Model Simerjot Kaur (sk3391) Stanford University Abstract This work presents a novel algorithmic trading system based on reinforcement
Outline Introduction Game Representations Reductions Solution Concepts. Game Theory. Enrico Franchi. May 19, 2010
 May 19, 2010 1 Introduction Scope of Agent preferences Utility Functions 2 Game Representations Example: Game-1 Extended Form Strategic Form Equivalences 3 Reductions Best Response Domination 4 Solution
May 19, 2010 1 Introduction Scope of Agent preferences Utility Functions 2 Game Representations Example: Game-1 Extended Form Strategic Form Equivalences 3 Reductions Best Response Domination 4 Solution
Reinforcement Learning. Slides based on those used in Berkeley's AI class taught by Dan Klein
 Reinforcement Learning Slides based on those used in Berkeley's AI class taught by Dan Klein Reinforcement Learning Basic idea: Receive feedback in the form of rewards Agent s utility is defined by the
Reinforcement Learning Slides based on those used in Berkeley's AI class taught by Dan Klein Reinforcement Learning Basic idea: Receive feedback in the form of rewards Agent s utility is defined by the
Construction and behavior of Multinomial Markov random field models
 Graduate Theses and Dissertations Iowa State University Capstones, Theses and Dissertations 2010 Construction and behavior of Multinomial Markov random field models Kim Mueller Iowa State University Follow
Graduate Theses and Dissertations Iowa State University Capstones, Theses and Dissertations 2010 Construction and behavior of Multinomial Markov random field models Kim Mueller Iowa State University Follow
CS221 / Spring 2018 / Sadigh. Lecture 7: MDPs I
 CS221 / Spring 2018 / Sadigh Lecture 7: MDPs I cs221.stanford.edu/q Question How would you get to Mountain View on Friday night in the least amount of time? bike drive Caltrain Uber/Lyft fly CS221 / Spring
CS221 / Spring 2018 / Sadigh Lecture 7: MDPs I cs221.stanford.edu/q Question How would you get to Mountain View on Friday night in the least amount of time? bike drive Caltrain Uber/Lyft fly CS221 / Spring
Lecture 7: MDPs I. Question. Course plan. So far: search problems. Uncertainty in the real world
 Lecture 7: MDPs I cs221.stanford.edu/q Question How would you get to Mountain View on Friday night in the least amount of time? bike drive Caltrain Uber/Lyft fly CS221 / Spring 2018 / Sadigh CS221 / Spring
Lecture 7: MDPs I cs221.stanford.edu/q Question How would you get to Mountain View on Friday night in the least amount of time? bike drive Caltrain Uber/Lyft fly CS221 / Spring 2018 / Sadigh CS221 / Spring
We are not saying it s easy, we are just trying to make it simpler than before. An Online Platform for backtesting quantitative trading strategies.
 We are not saying it s easy, we are just trying to make it simpler than before. An Online Platform for backtesting quantitative trading strategies. Visit www.kuants.in to get your free access to Stock
We are not saying it s easy, we are just trying to make it simpler than before. An Online Platform for backtesting quantitative trading strategies. Visit www.kuants.in to get your free access to Stock
Markov Decision Processes
 Markov Decision Processes Ryan P. Adams COS 324 Elements of Machine Learning Princeton University We now turn to a new aspect of machine learning, in which agents take actions and become active in their
Markov Decision Processes Ryan P. Adams COS 324 Elements of Machine Learning Princeton University We now turn to a new aspect of machine learning, in which agents take actions and become active in their
THE UNIVERSITY OF TEXAS AT AUSTIN Department of Information, Risk, and Operations Management
 THE UNIVERSITY OF TEXAS AT AUSTIN Department of Information, Risk, and Operations Management BA 386T Tom Shively PROBABILITY CONCEPTS AND NORMAL DISTRIBUTIONS The fundamental idea underlying any statistical
THE UNIVERSITY OF TEXAS AT AUSTIN Department of Information, Risk, and Operations Management BA 386T Tom Shively PROBABILITY CONCEPTS AND NORMAL DISTRIBUTIONS The fundamental idea underlying any statistical
Outline for this Week
 Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, fexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
Binomial Heaps Outline for this Week Binomial Heaps (Today) A simple, fexible, and versatile priority queue. Lazy Binomial Heaps (Today) A powerful building block for designing advanced data structures.
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages
 Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Lecture 2 Thursday, January 30, 2014 1 Expressing Program Properties Now that we have defined our small-step operational
Harvard School of Engineering and Applied Sciences CS 152: Programming Languages Lecture 2 Thursday, January 30, 2014 1 Expressing Program Properties Now that we have defined our small-step operational
The mathematical definitions are given on screen.
 Text Lecture 3.3 Coherent measures of risk and back- testing Dear all, welcome back. In this class we will discuss one of the main drawbacks of Value- at- Risk, that is to say the fact that the VaR, as
Text Lecture 3.3 Coherent measures of risk and back- testing Dear all, welcome back. In this class we will discuss one of the main drawbacks of Value- at- Risk, that is to say the fact that the VaR, as
Business Statistics 41000: Probability 4
 Business Statistics 41000: Probability 4 Drew D. Creal University of Chicago, Booth School of Business February 14 and 15, 2014 1 Class information Drew D. Creal Email: dcreal@chicagobooth.edu Office:
Business Statistics 41000: Probability 4 Drew D. Creal University of Chicago, Booth School of Business February 14 and 15, 2014 1 Class information Drew D. Creal Email: dcreal@chicagobooth.edu Office:
Monte-Carlo Planning: Introduction and Bandit Basics. Alan Fern
 Monte-Carlo Planning: Introduction and Bandit Basics Alan Fern 1 Large Worlds We have considered basic model-based planning algorithms Model-based planning: assumes MDP model is available Methods we learned
Monte-Carlo Planning: Introduction and Bandit Basics Alan Fern 1 Large Worlds We have considered basic model-based planning algorithms Model-based planning: assumes MDP model is available Methods we learned
CS134: Networks Spring Random Variables and Independence. 1.2 Probability Distribution Function (PDF) Number of heads Probability 2 0.
 CS134: Networks Spring 2017 Prof. Yaron Singer Section 0 1 Probability 1.1 Random Variables and Independence A real-valued random variable is a variable that can take each of a set of possible values in
CS134: Networks Spring 2017 Prof. Yaron Singer Section 0 1 Probability 1.1 Random Variables and Independence A real-valued random variable is a variable that can take each of a set of possible values in
CHAPTER 5 STOCHASTIC SCHEDULING
 CHPTER STOCHSTIC SCHEDULING In some situations, estimating activity duration becomes a difficult task due to ambiguity inherited in and the risks associated with some work. In such cases, the duration
CHPTER STOCHSTIC SCHEDULING In some situations, estimating activity duration becomes a difficult task due to ambiguity inherited in and the risks associated with some work. In such cases, the duration
Making Decisions. CS 3793 Artificial Intelligence Making Decisions 1
 Making Decisions CS 3793 Artificial Intelligence Making Decisions 1 Planning under uncertainty should address: The world is nondeterministic. Actions are not certain to succeed. Many events are outside
Making Decisions CS 3793 Artificial Intelligence Making Decisions 1 Planning under uncertainty should address: The world is nondeterministic. Actions are not certain to succeed. Many events are outside
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration
 Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration
 Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Portfolio Analysis with Random Portfolios
 pjb25 Portfolio Analysis with Random Portfolios Patrick Burns http://www.burns-stat.com stat.com September 2006 filename 1 1 Slide 1 pjb25 This was presented in London on 5 September 2006 at an event sponsored
pjb25 Portfolio Analysis with Random Portfolios Patrick Burns http://www.burns-stat.com stat.com September 2006 filename 1 1 Slide 1 pjb25 This was presented in London on 5 September 2006 at an event sponsored
PROBABILITY. Wiley. With Applications and R ROBERT P. DOBROW. Department of Mathematics. Carleton College Northfield, MN
 PROBABILITY With Applications and R ROBERT P. DOBROW Department of Mathematics Carleton College Northfield, MN Wiley CONTENTS Preface Acknowledgments Introduction xi xiv xv 1 First Principles 1 1.1 Random
PROBABILITY With Applications and R ROBERT P. DOBROW Department of Mathematics Carleton College Northfield, MN Wiley CONTENTS Preface Acknowledgments Introduction xi xiv xv 1 First Principles 1 1.1 Random
Complex Decisions. Sequential Decision Making
 Sequential Decision Making Outline Sequential decision problems Value iteration Policy iteration POMDPs (basic concepts) Slides partially based on the Book "Reinforcement Learning: an introduction" by
Sequential Decision Making Outline Sequential decision problems Value iteration Policy iteration POMDPs (basic concepts) Slides partially based on the Book "Reinforcement Learning: an introduction" by
Binary Options Trading Strategies How to Become a Successful Trader?
 Binary Options Trading Strategies or How to Become a Successful Trader? Brought to You by: 1. Successful Binary Options Trading Strategy Successful binary options traders approach the market with three
Binary Options Trading Strategies or How to Become a Successful Trader? Brought to You by: 1. Successful Binary Options Trading Strategy Successful binary options traders approach the market with three
A Markov Chain Monte Carlo Approach to Estimate the Risks of Extremely Large Insurance Claims
 International Journal of Business and Economics, 007, Vol. 6, No. 3, 5-36 A Markov Chain Monte Carlo Approach to Estimate the Risks of Extremely Large Insurance Claims Wan-Kai Pang * Department of Applied
International Journal of Business and Economics, 007, Vol. 6, No. 3, 5-36 A Markov Chain Monte Carlo Approach to Estimate the Risks of Extremely Large Insurance Claims Wan-Kai Pang * Department of Applied
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 21 Successive Shortest Path Problem In this lecture, we continue our discussion
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 21 Successive Shortest Path Problem In this lecture, we continue our discussion
Overview. Transformation method Rejection method. Monte Carlo vs ordinary methods. 1 Random numbers. 2 Monte Carlo integration.
 Overview 1 Random numbers Transformation method Rejection method 2 Monte Carlo integration Monte Carlo vs ordinary methods 3 Summary Transformation method Suppose X has probability distribution p X (x),
Overview 1 Random numbers Transformation method Rejection method 2 Monte Carlo integration Monte Carlo vs ordinary methods 3 Summary Transformation method Suppose X has probability distribution p X (x),
4 Martingales in Discrete-Time
 4 Martingales in Discrete-Time Suppose that (Ω, F, P is a probability space. Definition 4.1. A sequence F = {F n, n = 0, 1,...} is called a filtration if each F n is a sub-σ-algebra of F, and F n F n+1
4 Martingales in Discrete-Time Suppose that (Ω, F, P is a probability space. Definition 4.1. A sequence F = {F n, n = 0, 1,...} is called a filtration if each F n is a sub-σ-algebra of F, and F n F n+1
On Implementation of the Markov Chain Monte Carlo Stochastic Approximation Algorithm
 On Implementation of the Markov Chain Monte Carlo Stochastic Approximation Algorithm Yihua Jiang, Peter Karcher and Yuedong Wang Abstract The Markov Chain Monte Carlo Stochastic Approximation Algorithm
On Implementation of the Markov Chain Monte Carlo Stochastic Approximation Algorithm Yihua Jiang, Peter Karcher and Yuedong Wang Abstract The Markov Chain Monte Carlo Stochastic Approximation Algorithm
CS 188: Artificial Intelligence
 CS 188: Artificial Intelligence Markov Decision Processes Dan Klein, Pieter Abbeel University of California, Berkeley Non Deterministic Search Example: Grid World A maze like problem The agent lives in
CS 188: Artificial Intelligence Markov Decision Processes Dan Klein, Pieter Abbeel University of California, Berkeley Non Deterministic Search Example: Grid World A maze like problem The agent lives in
Chapter 2 Uncertainty Analysis and Sampling Techniques
 Chapter 2 Uncertainty Analysis and Sampling Techniques The probabilistic or stochastic modeling (Fig. 2.) iterative loop in the stochastic optimization procedure (Fig..4 in Chap. ) involves:. Specifying
Chapter 2 Uncertainty Analysis and Sampling Techniques The probabilistic or stochastic modeling (Fig. 2.) iterative loop in the stochastic optimization procedure (Fig..4 in Chap. ) involves:. Specifying
UGM Crash Course: Conditional Inference and Cutset Conditioning
 UGM Crash Course: Conditional Inference and Cutset Conditioning Julie Nutini August 19 th, 2015 1 / 25 Conditional UGM 2 / 25 We know the value of one or more random variables i.e., we have observations,
UGM Crash Course: Conditional Inference and Cutset Conditioning Julie Nutini August 19 th, 2015 1 / 25 Conditional UGM 2 / 25 We know the value of one or more random variables i.e., we have observations,
Lecture 5. 1 Online Learning. 1.1 Learning Setup (Perspective of Universe) CSCI699: Topics in Learning & Game Theory
 CSCI699: Topics in Learning & Game Theory Lecturer: Shaddin Dughmi Lecture 5 Scribes: Umang Gupta & Anastasia Voloshinov In this lecture, we will give a brief introduction to online learning and then go
CSCI699: Topics in Learning & Game Theory Lecturer: Shaddin Dughmi Lecture 5 Scribes: Umang Gupta & Anastasia Voloshinov In this lecture, we will give a brief introduction to online learning and then go
Reasoning with Uncertainty
 Reasoning with Uncertainty Markov Decision Models Manfred Huber 2015 1 Markov Decision Process Models Markov models represent the behavior of a random process, including its internal state and the externally
Reasoning with Uncertainty Markov Decision Models Manfred Huber 2015 1 Markov Decision Process Models Markov models represent the behavior of a random process, including its internal state and the externally
2.1 Mathematical Basis: Risk-Neutral Pricing
 Chapter Monte-Carlo Simulation.1 Mathematical Basis: Risk-Neutral Pricing Suppose that F T is the payoff at T for a European-type derivative f. Then the price at times t before T is given by f t = e r(t
Chapter Monte-Carlo Simulation.1 Mathematical Basis: Risk-Neutral Pricing Suppose that F T is the payoff at T for a European-type derivative f. Then the price at times t before T is given by f t = e r(t
On Solving Integral Equations using. Markov Chain Monte Carlo Methods
 On Solving Integral quations using Markov Chain Monte Carlo Methods Arnaud Doucet Department of Statistics and Department of Computer Science, University of British Columbia, Vancouver, BC, Canada mail:
On Solving Integral quations using Markov Chain Monte Carlo Methods Arnaud Doucet Department of Statistics and Department of Computer Science, University of British Columbia, Vancouver, BC, Canada mail:
a 13 Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models The model
 Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models This is a lightly edited version of a chapter in a book being written by Jordan. Since this is
Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models This is a lightly edited version of a chapter in a book being written by Jordan. Since this is
Stochastic Optimal Control
 Stochastic Optimal Control Lecturer: Eilyan Bitar, Cornell ECE Scribe: Kevin Kircher, Cornell MAE These notes summarize some of the material from ECE 5555 (Stochastic Systems) at Cornell in the fall of
Stochastic Optimal Control Lecturer: Eilyan Bitar, Cornell ECE Scribe: Kevin Kircher, Cornell MAE These notes summarize some of the material from ECE 5555 (Stochastic Systems) at Cornell in the fall of
Lecture 6. 1 Polynomial-time algorithms for the global min-cut problem
 ORIE 633 Network Flows September 20, 2007 Lecturer: David P. Williamson Lecture 6 Scribe: Animashree Anandkumar 1 Polynomial-time algorithms for the global min-cut problem 1.1 The global min-cut problem
ORIE 633 Network Flows September 20, 2007 Lecturer: David P. Williamson Lecture 6 Scribe: Animashree Anandkumar 1 Polynomial-time algorithms for the global min-cut problem 1.1 The global min-cut problem
Option Pricing Using Bayesian Neural Networks
 Option Pricing Using Bayesian Neural Networks Michael Maio Pires, Tshilidzi Marwala School of Electrical and Information Engineering, University of the Witwatersrand, 2050, South Africa m.pires@ee.wits.ac.za,
Option Pricing Using Bayesian Neural Networks Michael Maio Pires, Tshilidzi Marwala School of Electrical and Information Engineering, University of the Witwatersrand, 2050, South Africa m.pires@ee.wits.ac.za,
Definition 4.1. In a stochastic process T is called a stopping time if you can tell when it happens.
 102 OPTIMAL STOPPING TIME 4. Optimal Stopping Time 4.1. Definitions. On the first day I explained the basic problem using one example in the book. On the second day I explained how the solution to the
102 OPTIMAL STOPPING TIME 4. Optimal Stopping Time 4.1. Definitions. On the first day I explained the basic problem using one example in the book. On the second day I explained how the solution to the
Artificial Neural Networks Lecture Notes
 Artificial Neural Networks Lecture Notes Part 10 About this file: This is the printer-friendly version of the file "lecture10.htm". In case the page is not properly displayed, use IE 5 or higher. Since
Artificial Neural Networks Lecture Notes Part 10 About this file: This is the printer-friendly version of the file "lecture10.htm". In case the page is not properly displayed, use IE 5 or higher. Since
CS360 Homework 14 Solution
 CS360 Homework 14 Solution Markov Decision Processes 1) Invent a simple Markov decision process (MDP) with the following properties: a) it has a goal state, b) its immediate action costs are all positive,
CS360 Homework 14 Solution Markov Decision Processes 1) Invent a simple Markov decision process (MDP) with the following properties: a) it has a goal state, b) its immediate action costs are all positive,
Week 2 Quantitative Analysis of Financial Markets Hypothesis Testing and Confidence Intervals
 Week 2 Quantitative Analysis of Financial Markets Hypothesis Testing and Confidence Intervals Christopher Ting http://www.mysmu.edu/faculty/christophert/ Christopher Ting : christopherting@smu.edu.sg :
Week 2 Quantitative Analysis of Financial Markets Hypothesis Testing and Confidence Intervals Christopher Ting http://www.mysmu.edu/faculty/christophert/ Christopher Ting : christopherting@smu.edu.sg :
Chapter 3. Dynamic discrete games and auctions: an introduction
 Chapter 3. Dynamic discrete games and auctions: an introduction Joan Llull Structural Micro. IDEA PhD Program I. Dynamic Discrete Games with Imperfect Information A. Motivating example: firm entry and
Chapter 3. Dynamic discrete games and auctions: an introduction Joan Llull Structural Micro. IDEA PhD Program I. Dynamic Discrete Games with Imperfect Information A. Motivating example: firm entry and
Web Extension: Continuous Distributions and Estimating Beta with a Calculator
 19878_02W_p001-008.qxd 3/10/06 9:51 AM Page 1 C H A P T E R 2 Web Extension: Continuous Distributions and Estimating Beta with a Calculator This extension explains continuous probability distributions
19878_02W_p001-008.qxd 3/10/06 9:51 AM Page 1 C H A P T E R 2 Web Extension: Continuous Distributions and Estimating Beta with a Calculator This extension explains continuous probability distributions
Global Joint Distribution Factorizes into Local Marginal Distributions on Tree-Structured Graphs
 Teaching Note October 26, 2007 Global Joint Distribution Factorizes into Local Marginal Distributions on Tree-Structured Graphs Xinhua Zhang Xinhua.Zhang@anu.edu.au Research School of Information Sciences
Teaching Note October 26, 2007 Global Joint Distribution Factorizes into Local Marginal Distributions on Tree-Structured Graphs Xinhua Zhang Xinhua.Zhang@anu.edu.au Research School of Information Sciences
Maximizing the Spread of Influence through a Social Network Problem/Motivation: Suppose we want to market a product or promote an idea or behavior in
 Maximizing the Spread of Influence through a Social Network Problem/Motivation: Suppose we want to market a product or promote an idea or behavior in a society. In order to do so, we can target individuals,
Maximizing the Spread of Influence through a Social Network Problem/Motivation: Suppose we want to market a product or promote an idea or behavior in a society. In order to do so, we can target individuals,
# generate data num.obs <- 100 y <- rnorm(num.obs,mean = theta.true, sd = sqrt(sigma.sq.true))
 Posterior Sampling from Normal Now we seek to create draws from the joint posterior distribution and the marginal posterior distributions and Note the marginal posterior distributions would be used to
Posterior Sampling from Normal Now we seek to create draws from the joint posterior distribution and the marginal posterior distributions and Note the marginal posterior distributions would be used to
Basic Data Analysis. Stephen Turnbull Business Administration and Public Policy Lecture 4: May 2, Abstract
 Basic Data Analysis Stephen Turnbull Business Administration and Public Policy Lecture 4: May 2, 2013 Abstract Introduct the normal distribution. Introduce basic notions of uncertainty, probability, events,
Basic Data Analysis Stephen Turnbull Business Administration and Public Policy Lecture 4: May 2, 2013 Abstract Introduct the normal distribution. Introduce basic notions of uncertainty, probability, events,
CS224W: Social and Information Network Analysis Jure Leskovec, Stanford University
 CS224W: Social and Information Network Analysis Jure Leskovec, Stanford University http://cs224w.stanford.edu 10/27/16 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis, http://cs224w.stanford.edu
CS224W: Social and Information Network Analysis Jure Leskovec, Stanford University http://cs224w.stanford.edu 10/27/16 Jure Leskovec, Stanford CS224W: Social and Information Network Analysis, http://cs224w.stanford.edu
II. Determinants of Asset Demand. Figure 1
 University of California, Merced EC 121-Money and Banking Chapter 5 Lecture otes Professor Jason Lee I. Introduction Figure 1 shows the interest rates for 3 month treasury bills. As evidenced by the figure,
University of California, Merced EC 121-Money and Banking Chapter 5 Lecture otes Professor Jason Lee I. Introduction Figure 1 shows the interest rates for 3 month treasury bills. As evidenced by the figure,
Market Volatility and Risk Proxies
 Market Volatility and Risk Proxies... an introduction to the concepts 019 Gary R. Evans. This slide set by Gary R. Evans is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International
Market Volatility and Risk Proxies... an introduction to the concepts 019 Gary R. Evans. This slide set by Gary R. Evans is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International
Theoretical Statistics. Lecture 4. Peter Bartlett
 1. Concentration inequalities. Theoretical Statistics. Lecture 4. Peter Bartlett 1 Outline of today s lecture We have been looking at deviation inequalities, i.e., bounds on tail probabilities likep(x
1. Concentration inequalities. Theoretical Statistics. Lecture 4. Peter Bartlett 1 Outline of today s lecture We have been looking at deviation inequalities, i.e., bounds on tail probabilities likep(x
Credit Card Default Predictive Modeling
 Credit Card Default Predictive Modeling Background: Predicting credit card payment default is critical for the successful business model of a credit card company. An accurate predictive model can help
Credit Card Default Predictive Modeling Background: Predicting credit card payment default is critical for the successful business model of a credit card company. An accurate predictive model can help
I. Time Series and Stochastic Processes
 I. Time Series and Stochastic Processes Purpose of this Module Introduce time series analysis as a method for understanding real-world dynamic phenomena Define different types of time series Explain the
I. Time Series and Stochastic Processes Purpose of this Module Introduce time series analysis as a method for understanding real-world dynamic phenomena Define different types of time series Explain the
Stock Market Prediction System
 Stock Market Prediction System W.N.N De Silva 1, H.M Samaranayaka 2, T.R Singhara 3, D.C.H Wijewardana 4. Sri Lanka Institute of Information Technology, Malabe, Sri Lanka. { 1 nathashanirmani55, 2 malmisamaranayaka,
Stock Market Prediction System W.N.N De Silva 1, H.M Samaranayaka 2, T.R Singhara 3, D.C.H Wijewardana 4. Sri Lanka Institute of Information Technology, Malabe, Sri Lanka. { 1 nathashanirmani55, 2 malmisamaranayaka,
Reinforcement Learning Analysis, Grid World Applications
 Reinforcement Learning Analysis, Grid World Applications Kunal Sharma GTID: ksharma74, CS 4641 Machine Learning Abstract This paper explores two Markov decision process problems with varying state sizes.
Reinforcement Learning Analysis, Grid World Applications Kunal Sharma GTID: ksharma74, CS 4641 Machine Learning Abstract This paper explores two Markov decision process problems with varying state sizes.
STOR Lecture 15. Jointly distributed Random Variables - III
 STOR 435.001 Lecture 15 Jointly distributed Random Variables - III Jan Hannig UNC Chapel Hill 1 / 17 Before we dive in Contents of this lecture 1. Conditional pmf/pdf: definition and simple properties.
STOR 435.001 Lecture 15 Jointly distributed Random Variables - III Jan Hannig UNC Chapel Hill 1 / 17 Before we dive in Contents of this lecture 1. Conditional pmf/pdf: definition and simple properties.
Chapter 5 Univariate time-series analysis. () Chapter 5 Univariate time-series analysis 1 / 29
 Chapter 5 Univariate time-series analysis () Chapter 5 Univariate time-series analysis 1 / 29 Time-Series Time-series is a sequence fx 1, x 2,..., x T g or fx t g, t = 1,..., T, where t is an index denoting
Chapter 5 Univariate time-series analysis () Chapter 5 Univariate time-series analysis 1 / 29 Time-Series Time-series is a sequence fx 1, x 2,..., x T g or fx t g, t = 1,..., T, where t is an index denoting
Markov Decision Processes
 Markov Decision Processes Robert Platt Northeastern University Some images and slides are used from: 1. CS188 UC Berkeley 2. AIMA 3. Chris Amato Stochastic domains So far, we have studied search Can use
Markov Decision Processes Robert Platt Northeastern University Some images and slides are used from: 1. CS188 UC Berkeley 2. AIMA 3. Chris Amato Stochastic domains So far, we have studied search Can use
FNCE 302, Investments H Guy Williams, 2008
 Sources http://finance.bi.no/~bernt/gcc_prog/recipes/recipes/node7.html It's all Greek to me, Chris McMahon Futures; Jun 2007; 36, 7 http://www.quantnotes.com Put Call Parity THIS IS THE CALL-PUT PARITY
Sources http://finance.bi.no/~bernt/gcc_prog/recipes/recipes/node7.html It's all Greek to me, Chris McMahon Futures; Jun 2007; 36, 7 http://www.quantnotes.com Put Call Parity THIS IS THE CALL-PUT PARITY
