Computer Vision Group Prof. Daniel Cremers. 7. Sequential Data
|
|
|
- Gerard Powers
- 5 years ago
- Views:
Transcription
1 Group Prof. Daniel Cremers 7. Sequential Data
2 Bayes Filter (Rep.) We can describe the overall process using a Dynamic Bayes Network: This incorporates the following Markov assumptions: (measurement) (state)!2 Group
3 Bayes Filter Without Actions Removing the action variables we obtain: Notation differs from Bishop! Discrete Variables This incorporates the following Markov assumptions: (measurement) (state)!3 Group
4 A Model for Sequential Data Observations in sequential data should not be modeled as independent variables such as: z 1 z 2 z 3 z 4 z 5 Examples: weather forecast, speech, handwritten text, etc. The observation at time t depends on the observation(s) of (an) earlier time step(s): z 1 z 2 z 3 z 4 z 5!4 Group
5 A Model for Sequential Data z 1 z 2 z 3 z 4 z 5 The joint distribution is therefore (d-sep): p(z 1...z n ) = p(z 1 ) ny i=2 p(z i z i 1 ) However: often data depends on several earlier observations (not just one) z 1 z 2 z 3 z 4 z 5!5 Group
6 A Model for Sequential Data z 1 z 2 z 3 z 4 z 5 p(z 1...z n ) = p(z 1 )p(z 2 z 1 ) ny p(z i z i 1, z i 2 ) Problem: number of stored parameters grows exponentially with the order of the Markov chain Question: can we model dependency of all previous observations with a limited number of parameters? i=3!6 Group
7 A Model for Sequential Data Idea: Introduce hidden (unobserved) variables: x 1 x 2 x 3 x 4 x 5 z 1 z 2 z 3 z 4 z 5!7 Group
8 A Model for Sequential Data Idea: Introduce hidden (unobserved) variables: x 1 x 2 x 3 x 4 x 5 z 1 z 2 z 3 z 4 z 5 Now we have: dsep(x n, {x 1,...,x n 2 }, x n 1 ), p(x n x 1,...,x n 2, x n 1 ) = p(x n x n 1 ) But: dsep(z n, {z 1,...,z n 2 }, z n 1 ), p(z n z 1,...,z n 2, z n 1 ), p(z n z n 1 ) And: number of parameters is nk(k-1) + const.!8 Group
9 Example Place recognition for mobile robots 3 different states: corridor, room, doorway Problem: misclassifications Idea: use information from previous time step!9 Group
10 General Formulation of an HMM 1.Discrete random variables Observation variables: {z n }, n = 1..N Discrete state variables (unobservable): {x n }, n = 1..N Number of states K: x n є{1 K} 2.Transition model p(x i x i-1 ) Model Parameters θ Markov assumption (x i only depends on x i-1 ) Represented as a K K transition matrix A Initial probability: p(x 0 ) repr. as π 1, π 2, π 3 3.Observation model p(z i x i ) with parameters φ Observation only depends on the current state Example: output of a local place classifier!10 Group
11 The Trellis Representation time k=1 A 11 A 11 k=2 k=3 A 33 A 33 n-2 n-1 n!11 Group
12 Application Example (1) Given an observation sequence z 1,z 2,z 3 Assume that the model parameters θ =(A, π, φ) are known What is the probability that the given observation sequence is actually observed under this model, i.e. the data likelihood p(z θ)? If we are given several different models, we can choose the one with highest probability Expressed as a supervised learning problem, this can be interpreted as the inference step (classification step)!12 Group
13 Application Example (2) Based on the data likelihood we can solve two different kinds of problems: Filtering: computes p(x n z 1:n ), i.e. state probability only based on previous observations Smoothing: computes p(x n z 1:N ), state probability based on all observations (including those from the future) 1 filtered 1 smoothed Filtering p(loaded) 0.5 Smoothing p(loaded) roll number roll number!13 Group
14 Application Example (3) Given an observation sequence z 1,z 2,z 3 Assume that the model parameters θ =(A, π, φ) are known What is the state sequence x 1,x 2,x 3 that explains best the given observation sequence? In the case of place recognition: which is the sequence of truly visited places that explains best the sequence of obtained place labels (classifications)?!14 Group
15 Application Example (4) Given an observation sequence z 1,z 2,z 3 What are the optimal model parameters θ =(A, π, φ)? This can be interpreted as the training step It is in general the most difficult problem!15 Group
16 Summary: 4 Operations on HMMs 1. Compute data likelihood p(z θ) from a known model Can be computed with the forward algorithm 2. Filtering or Smoothing of the state probability Filtering: forward algorithm Smoothing: forward-backward algorithm 3. Compute optimal state sequence with a known model Can be computed with the Viterbi-Algorithm 4. Learn model parameters for an observation sequence Can be computed using Expectation-Maximization (or Baum-Welch)!16 Group
17 The Forward Algorithm Goal: compute p(z θ) (we drop θ in the following) p(z 1,...,z n ) = p(z 1,...,z n, x n ) =: (x n ) x n x n!17 Group
18 The Forward Algorithm Goal: compute p(z θ) (we drop θ in the following) p(z 1,...,z n ) = We can calculate α recursively: p(z 1,...,z n, x n ) =: (x n ) x n x n (x n ) = p(z n x n ) x n 1 (x n 1 )p(x n x n 1 )!18 Group
19 The Forward Algorithm Goal: compute p(z θ) (we drop θ in the following) p(z 1,...,z n ) = We can calculate α recursively: p(z 1,...,z n, x n ) =: (x n ) x n x n (x n ) = p(z n x n ) x n 1 (x n 1 )p(x n x n 1 ) This is (almost) the same recursive formula as we had in the first lecture!!19 Group
20 The Forward Algorithm Goal: compute p(z θ) (we drop θ in the following) p(z 1,...,z n ) = We can calculate α recursively: p(z 1,...,z n, x n ) =: (x n ) x n x n (x n ) = p(z n x n ) x n 1 (x n 1 )p(x n x n 1 ) This is (almost) the same recursive formula as we had in the first lecture! Filtering: p(x n z 1,...,z n ) = p(z 1,...,z n, x n ) p(z 1,...,z n ) = (x n) P x n (x n )!20 Group
21 The Forward-Backward Algorithm As before we set We also define (x n ) = p(z 1,...,z n, x n ) (x n ) = p(z n+1,...,z N x n ) e.g. n = 5: x 1 x 2 x 3 x 4 x n x N 1 x N z 1 z 2 z 3 z 4 z n z N 1 z N!21 Group
22 The Forward-Backward Algorithm As before we set We also define (x n ) = p(z 1,...,z n, x n ) (x n ) = p(z n+1,...,z N x n ) This can be recursively computed (backwards): (x n 1 ) = p(z n,...,z N x n 1 ) = p(x n, z n,...,z N x n 1 ) x n = p(z n+1,...,z N x n, z n, x n 1 )p(x n, z n x n 1 ) x n = p(z n+1,...,z N x n )p(z n x n 1, x n )p(x n x n 1 ) x n = (x n )p(z n x n )p(x n x n 1 ) x n!22 Group
23 The Forward-Backward Algorithm As before we set We also define (x n ) = p(z 1,...,z n, x n ) (x n ) = p(z n+1,...,z N x n ) This can be recursively computed (backwards): (x n ) = x n+1 (x n+1 )p(z n+1 x n+1 )p(x n+1 x n ) This is also known as the message-passing algorithm ( sum-product )! forward messages αn (vector of length K) backward messages βn (vector of length K)!23 Group
24 Smoothing with Forward-Backward First we compute p(x n, z 1,...,z N ): p(x n, z 1,...,z N ) = p(z 1,...,z N x n )p(x n ) = p(z 1,...,z n x n )p(z n+1,...,z N x n )p(x n ) = p(z 1,...,z n, x n )p(z n+1,...,z N x n ) = (x n ) (x n )!24 Group
25 Smoothing with Forward-Backward First we compute p(x n, z 1,...,z N ): p(x n, z 1,...,z N ) = (x n ) (x n ) with that we can compute p(z 1,...,z N ): p(z 1,...,z N ) = p(x n, z 1,...,z N ) = (x n ) (x n ) x n x n!25 Group
26 Smoothing with Forward-Backward First we compute p(x n, z 1,...,z N ): p(x n, z 1,...,z N ) = (x n ) (x n ) with that we can compute p(z 1,...,z N ): p(z 1,...,z N ) = and finally: p(x n, z 1,...,z N ) = (x n ) (x n ) x n x n p(x n z 1,...,z N ) = p(x n, z 1,...,z N ) p(z 1,...,z N ) = (x n) (x n ) P x n (x n ) (x n )!26 Group
27 2. Computing the Most Likely States Goal: find a state sequence x 1,x 2,x 3 that maximizes the probability p(,z θ) Define (x n ) = max x 1,...,x n 1 p(x 1,...x n z 1,...z n ) This is the probability of state j by taking the most probable path. x n 1 x n x n+1 z n 1 z n z n+1!27 Group
28 2. Computing the Most Likely States Goal: find a state sequence x 1,x 2,x 3 that maximizes the probability p(,z θ) Define (x n ) = max x 1,...,x n 1 p(x 1,...x n z 1,...z n ) This can be computed recursively: (x n ) = max x n 1 (x n 1 )p(x n x n 1 )p(z n, x n ) we also have to compute the argmax: (x n ) = arg max x n 1 (x n 1 )p(x n x n 1 )p(z n, x n )!28 Group
29 Initialize: δ(x 0 ) = p(x 0 ) p(z 0 x 0 ) ψ(x 0 ) = 0 Compute recursively for n=1 N: δ(x n )= p(z n x n ) max [δ(x n-1 ) p(x n x n-1 )] ψ(x n )= argmax [δ(x n-1 ) p(x n x n-1 )] On termination: p(z, θ) = max δ(x N ) x N * = argmax δ(x N ) x N x n-1 Backtracking: x * n = ψ(x n+1 ) The Viterbi algorithm x N x n-1!29 Group
30 3. Learning the Model Parameters Given an observation sequence z 1,z 2,z 3 Find optimal model parameters θ= π,a,φ We need to maximize the likelihood p(z θ) Can not be solved in closed form Iterative algorithm Baum-Welch : a special case of the Expectation Maximization (EM) algorithm!30 Group
31 3. Learning the Model Parameters Idea: instead of maximizing we maximize the expected log likelihood: p(z 1,...,z N ) = p(z 1,...,z N, x 1,...,x N ) p(x 1,...,x N z 1,...,z N, ) log p(z 1,...,z N, x 1,...,x N ) it can be shown that this is a lower bound of the actual log-likelihood p(z θ) this is the general idea of the Expectation- Maximization (EM) algorithm!31 Group
32 The Baum-Welsh algorithm E-Step (assuming we know π,a,φ, i.e. θ old ) Define the posterior probability of being in state i at step k: Define γ(x n )= p(x n Z)!32 Group
33 The Baum-Welsh algorithm E-Step (assuming we know π,a,φ, i.e. θ old ) Define the posterior probability of being in state i at step k: Define γ(x n )= p(x n z1,,zn) It follows that γ(x n )= α(x n ) β(x n ) / p(z)!33 Group
34 The Baum-Welsh algorithm E-Step (assuming we know π,a,φ, i.e. θ old ) Define the posterior probability of being in state i at step k: Define γ(x n )= p(x n z1,,zn) It follows that γ(x n )= α(x n ) β(x n ) / p(z) Define ξ(x n-1,x n )= p(x n-1,x n Z) It follows that ξ(x n-1,x n )= α(x n-1 )p(z n x n )p(x n x n-1 )β(x n ) / p(z)!34 Group
35 The Baum-Welsh algorithm Note: γ(x n ) is a vector of length K; each entry γk(x n ) represents the probability that the state at time n is equal to k {1, K} Thus: The expected number of transitions from state k in the sequence is N i=1 k(x i )!35 Group
36 The Baum-Welsh algorithm Note: γ(x n ) is a vector of length K; each entry γk(x n ) represents the probability that the state at time n is equal to k {1, K} Thus: The expected number of transitions from state k in the sequence is N i=1 k(x i ) Similarly: The expected number of transitions from state j to state k in the sequence is N 1 i=1 j,k (x i, x i+1 )!36 Group
37 The Baum-Welsh algorithm With that we can compute new values for π,a,φ: k = k (x 1 ) A j,k = P N 1 i=1 j,k(x i, x i+1 ) P N i=1 j(x i ) ' j,k = P N i=1 j(x i ) k,xt P N i=1 j(x i ) here, we need forward and backward step! This is done until the likelihood does not increase anymore (convergence)!37 Group
38 The Baum-Welsh Algorithm - Summary Start with an initial estimate of θ=(π,a,φ) e.g. uniformly and k-means for φ Compute messages (E-Step) Compute new θ=(π,a,φ) (M-step) Iterate E and M until convergence In each iteration one full application of the forward-backward algorithm is performed Result gives a local optimum For other local optima, the algorithm needs to be started again with new initialization!38 Group
39 Summary HMMs are a way to model sequential data They assume discrete states Three possible operations can be performed with HMMs: Data likelihood, given a model and an observation Most likely state sequence, given a model and an observation Optimal Model parameters, given an observation Appropriate scaling solves numerical problems HMMs are widely used, e.g. in speech recognition!39 Group
Notes on the EM Algorithm Michael Collins, September 24th 2005
 Notes on the EM Algorithm Michael Collins, September 24th 2005 1 Hidden Markov Models A hidden Markov model (N, Σ, Θ) consists of the following elements: N is a positive integer specifying the number of
Notes on the EM Algorithm Michael Collins, September 24th 2005 1 Hidden Markov Models A hidden Markov model (N, Σ, Θ) consists of the following elements: N is a positive integer specifying the number of
Exact Inference (9/30/13) 2 A brief review of Forward-Backward and EM for HMMs
 STA561: Probabilistic machine learning Exact Inference (9/30/13) Lecturer: Barbara Engelhardt Scribes: Jiawei Liang, He Jiang, Brittany Cohen 1 Validation for Clustering If we have two centroids, η 1 and
STA561: Probabilistic machine learning Exact Inference (9/30/13) Lecturer: Barbara Engelhardt Scribes: Jiawei Liang, He Jiang, Brittany Cohen 1 Validation for Clustering If we have two centroids, η 1 and
Academic Research Review. Classifying Market Conditions Using Hidden Markov Model
 Academic Research Review Classifying Market Conditions Using Hidden Markov Model INTRODUCTION Best known for their applications in speech recognition, Hidden Markov Models (HMMs) are able to discern and
Academic Research Review Classifying Market Conditions Using Hidden Markov Model INTRODUCTION Best known for their applications in speech recognition, Hidden Markov Models (HMMs) are able to discern and
6.231 DYNAMIC PROGRAMMING LECTURE 3 LECTURE OUTLINE
 6.21 DYNAMIC PROGRAMMING LECTURE LECTURE OUTLINE Deterministic finite-state DP problems Backward shortest path algorithm Forward shortest path algorithm Shortest path examples Alternative shortest path
6.21 DYNAMIC PROGRAMMING LECTURE LECTURE OUTLINE Deterministic finite-state DP problems Backward shortest path algorithm Forward shortest path algorithm Shortest path examples Alternative shortest path
Algorithmic Trading using Reinforcement Learning augmented with Hidden Markov Model
 Algorithmic Trading using Reinforcement Learning augmented with Hidden Markov Model Simerjot Kaur (sk3391) Stanford University Abstract This work presents a novel algorithmic trading system based on reinforcement
Algorithmic Trading using Reinforcement Learning augmented with Hidden Markov Model Simerjot Kaur (sk3391) Stanford University Abstract This work presents a novel algorithmic trading system based on reinforcement
Lecture 17: More on Markov Decision Processes. Reinforcement learning
 Lecture 17: More on Markov Decision Processes. Reinforcement learning Learning a model: maximum likelihood Learning a value function directly Monte Carlo Temporal-difference (TD) learning COMP-424, Lecture
Lecture 17: More on Markov Decision Processes. Reinforcement learning Learning a model: maximum likelihood Learning a value function directly Monte Carlo Temporal-difference (TD) learning COMP-424, Lecture
The EM algorithm for HMMs
 The EM algorithm for HMMs Michael Collins February 22, 2012 Maximum-Likelihood Estimation for Fully Observed Data (Recap from earlier) We have fully observed data, x i,1... x i,m, s i,1... s i,m for i
The EM algorithm for HMMs Michael Collins February 22, 2012 Maximum-Likelihood Estimation for Fully Observed Data (Recap from earlier) We have fully observed data, x i,1... x i,m, s i,1... s i,m for i
Handout 4: Deterministic Systems and the Shortest Path Problem
 SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 4: Deterministic Systems and the Shortest Path Problem Instructor: Shiqian Ma January 27, 2014 Suggested Reading: Bertsekas
SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 4: Deterministic Systems and the Shortest Path Problem Instructor: Shiqian Ma January 27, 2014 Suggested Reading: Bertsekas
A potentially useful approach to model nonlinearities in time series is to assume different behavior (structural break) in different subsamples
 1.3 Regime switching models A potentially useful approach to model nonlinearities in time series is to assume different behavior (structural break) in different subsamples (or regimes). If the dates, the
1.3 Regime switching models A potentially useful approach to model nonlinearities in time series is to assume different behavior (structural break) in different subsamples (or regimes). If the dates, the
a 13 Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models The model
 Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models This is a lightly edited version of a chapter in a book being written by Jordan. Since this is
Notes on Hidden Markov Models Michael I. Jordan University of California at Berkeley Hidden Markov Models This is a lightly edited version of a chapter in a book being written by Jordan. Since this is
A Hidden Markov Model Approach to Information-Based Trading: Theory and Applications
 A Hidden Markov Model Approach to Information-Based Trading: Theory and Applications Online Supplementary Appendix Xiangkang Yin and Jing Zhao La Trobe University Corresponding author, Department of Finance,
A Hidden Markov Model Approach to Information-Based Trading: Theory and Applications Online Supplementary Appendix Xiangkang Yin and Jing Zhao La Trobe University Corresponding author, Department of Finance,
Hidden Markov Models. Selecting model parameters or training
 idden Markov Models Selecting model parameters or training idden Markov Models Motivation: The n'th observation in a chain of observations is influenced by a corresponding latent variable... Observations
idden Markov Models Selecting model parameters or training idden Markov Models Motivation: The n'th observation in a chain of observations is influenced by a corresponding latent variable... Observations
Hidden Markov Model for High Frequency Data
 Hidden Markov Model for High Frequency Data Department of Mathematics, Florida State University Joint Math Meeting, Baltimore, MD, January 15 What are HMMs? A Hidden Markov model (HMM) is a stochastic
Hidden Markov Model for High Frequency Data Department of Mathematics, Florida State University Joint Math Meeting, Baltimore, MD, January 15 What are HMMs? A Hidden Markov model (HMM) is a stochastic
Estimation of the Markov-switching GARCH model by a Monte Carlo EM algorithm
 Estimation of the Markov-switching GARCH model by a Monte Carlo EM algorithm Maciej Augustyniak Fields Institute February 3, 0 Stylized facts of financial data GARCH Regime-switching MS-GARCH Agenda Available
Estimation of the Markov-switching GARCH model by a Monte Carlo EM algorithm Maciej Augustyniak Fields Institute February 3, 0 Stylized facts of financial data GARCH Regime-switching MS-GARCH Agenda Available
Decision Theory: Value Iteration
 Decision Theory: Value Iteration CPSC 322 Decision Theory 4 Textbook 9.5 Decision Theory: Value Iteration CPSC 322 Decision Theory 4, Slide 1 Lecture Overview 1 Recap 2 Policies 3 Value Iteration Decision
Decision Theory: Value Iteration CPSC 322 Decision Theory 4 Textbook 9.5 Decision Theory: Value Iteration CPSC 322 Decision Theory 4, Slide 1 Lecture Overview 1 Recap 2 Policies 3 Value Iteration Decision
Markov Decision Processes: Making Decision in the Presence of Uncertainty. (some of) R&N R&N
 Markov Decision Processes: Making Decision in the Presence of Uncertainty (some of) R&N 16.1-16.6 R&N 17.1-17.4 Different Aspects of Machine Learning Supervised learning Classification - concept learning
Markov Decision Processes: Making Decision in the Presence of Uncertainty (some of) R&N 16.1-16.6 R&N 17.1-17.4 Different Aspects of Machine Learning Supervised learning Classification - concept learning
Unobserved Heterogeneity Revisited
 Unobserved Heterogeneity Revisited Robert A. Miller Dynamic Discrete Choice March 2018 Miller (Dynamic Discrete Choice) cemmap 7 March 2018 1 / 24 Distributional Assumptions about the Unobserved Variables
Unobserved Heterogeneity Revisited Robert A. Miller Dynamic Discrete Choice March 2018 Miller (Dynamic Discrete Choice) cemmap 7 March 2018 1 / 24 Distributional Assumptions about the Unobserved Variables
Sequential Decision Making
 Sequential Decision Making Dynamic programming Christos Dimitrakakis Intelligent Autonomous Systems, IvI, University of Amsterdam, The Netherlands March 18, 2008 Introduction Some examples Dynamic programming
Sequential Decision Making Dynamic programming Christos Dimitrakakis Intelligent Autonomous Systems, IvI, University of Amsterdam, The Netherlands March 18, 2008 Introduction Some examples Dynamic programming
6.231 DYNAMIC PROGRAMMING LECTURE 3 LECTURE OUTLINE
 6.21 DYNAMIC PROGRAMMING LECTURE LECTURE OUTLINE Deterministic finite-state DP problems Backward shortest path algorithm Forward shortest path algorithm Shortest path examples Alternative shortest path
6.21 DYNAMIC PROGRAMMING LECTURE LECTURE OUTLINE Deterministic finite-state DP problems Backward shortest path algorithm Forward shortest path algorithm Shortest path examples Alternative shortest path
Reasoning with Uncertainty
 Reasoning with Uncertainty Markov Decision Models Manfred Huber 2015 1 Markov Decision Process Models Markov models represent the behavior of a random process, including its internal state and the externally
Reasoning with Uncertainty Markov Decision Models Manfred Huber 2015 1 Markov Decision Process Models Markov models represent the behavior of a random process, including its internal state and the externally
Chapter 7: Estimation Sections
 Chapter 7: Estimation Sections 7.1 Statistical Inference Bayesian Methods: 7.2 Prior and Posterior Distributions 7.3 Conjugate Prior Distributions Frequentist Methods: 7.5 Maximum Likelihood Estimators
Chapter 7: Estimation Sections 7.1 Statistical Inference Bayesian Methods: 7.2 Prior and Posterior Distributions 7.3 Conjugate Prior Distributions Frequentist Methods: 7.5 Maximum Likelihood Estimators
Hidden Markov Models for Financial Market Predictions
 Hidden Markov Models for Financial Market Predictions Department of Mathematics and Statistics Youngstown State University Central Spring Sectional Meeting, Michigan State University, March 15 1 Introduction
Hidden Markov Models for Financial Market Predictions Department of Mathematics and Statistics Youngstown State University Central Spring Sectional Meeting, Michigan State University, March 15 1 Introduction
EE641 Digital Image Processing II: Purdue University VISE - October 29,
 EE64 Digital Image Processing II: Purdue University VISE - October 9, 004 The EM Algorithm. Suffient Statistics and Exponential Distributions Let p(y θ) be a family of density functions parameterized by
EE64 Digital Image Processing II: Purdue University VISE - October 9, 004 The EM Algorithm. Suffient Statistics and Exponential Distributions Let p(y θ) be a family of density functions parameterized by
Hidden Markov Models. Slides by Carl Kingsford. Based on Chapter 11 of Jones & Pevzner, An Introduction to Bioinformatics Algorithms
 Hidden Markov Models Slides by Carl Kingsford Based on Chapter 11 of Jones & Pevzner, An Introduction to Bioinformatics Algorithms Eukaryotic Genes & Exon Splicing Prokaryotic (bacterial) genes look like
Hidden Markov Models Slides by Carl Kingsford Based on Chapter 11 of Jones & Pevzner, An Introduction to Bioinformatics Algorithms Eukaryotic Genes & Exon Splicing Prokaryotic (bacterial) genes look like
Markov Decision Processes (MDPs) CS 486/686 Introduction to AI University of Waterloo
 Markov Decision Processes (MDPs) CS 486/686 Introduction to AI University of Waterloo Outline Sequential Decision Processes Markov chains Highlight Markov property Discounted rewards Value iteration Markov
Markov Decision Processes (MDPs) CS 486/686 Introduction to AI University of Waterloo Outline Sequential Decision Processes Markov chains Highlight Markov property Discounted rewards Value iteration Markov
Dynamic Portfolio Execution Detailed Proofs
 Dynamic Portfolio Execution Detailed Proofs Gerry Tsoukalas, Jiang Wang, Kay Giesecke March 16, 2014 1 Proofs Lemma 1 (Temporary Price Impact) A buy order of size x being executed against i s ask-side
Dynamic Portfolio Execution Detailed Proofs Gerry Tsoukalas, Jiang Wang, Kay Giesecke March 16, 2014 1 Proofs Lemma 1 (Temporary Price Impact) A buy order of size x being executed against i s ask-side
BCJR Algorithm. Veterbi Algorithm (revisted) Consider covolutional encoder with. And information sequences of length h = 5
 Chapter 2 BCJR Algorithm Ammar Abh-Hhdrohss Islamic University -Gaza ١ Veterbi Algorithm (revisted) Consider covolutional encoder with And information sequences of length h = 5 The trellis diagram has
Chapter 2 BCJR Algorithm Ammar Abh-Hhdrohss Islamic University -Gaza ١ Veterbi Algorithm (revisted) Consider covolutional encoder with And information sequences of length h = 5 The trellis diagram has
Pakes (1986): Patents as Options: Some Estimates of the Value of Holding European Patent Stocks
 Pakes (1986): Patents as Options: Some Estimates of the Value of Holding European Patent Stocks Spring 2009 Main question: How much are patents worth? Answering this question is important, because it helps
Pakes (1986): Patents as Options: Some Estimates of the Value of Holding European Patent Stocks Spring 2009 Main question: How much are patents worth? Answering this question is important, because it helps
Solution algorithm for Boz-Mendoza JME by Enrique G. Mendoza University of Pennsylvania, NBER & PIER
 Solution algorithm for Boz-Mendoza JME 2014 by Enrique G. Mendoza University of Pennsylvania, NBER & PIER Two-stage solution method At each date t of a sequence of T periods of observed realizations of
Solution algorithm for Boz-Mendoza JME 2014 by Enrique G. Mendoza University of Pennsylvania, NBER & PIER Two-stage solution method At each date t of a sequence of T periods of observed realizations of
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50)
 Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 5 Sequential Monte Carlo methods I January
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 5 Sequential Monte Carlo methods I January
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration
 Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Inference in Bayesian Networks
 Andrea Passerini passerini@disi.unitn.it Machine Learning Inference in graphical models Description Assume we have evidence e on the state of a subset of variables E in the model (i.e. Bayesian Network)
Andrea Passerini passerini@disi.unitn.it Machine Learning Inference in graphical models Description Assume we have evidence e on the state of a subset of variables E in the model (i.e. Bayesian Network)
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration
 Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Reinforcement Learning (1): Discrete MDP, Value Iteration, Policy Iteration Piyush Rai CS5350/6350: Machine Learning November 29, 2011 Reinforcement Learning Supervised Learning: Uses explicit supervision
Heterogeneous Hidden Markov Models
 Heterogeneous Hidden Markov Models José G. Dias 1, Jeroen K. Vermunt 2 and Sofia Ramos 3 1 Department of Quantitative methods, ISCTE Higher Institute of Social Sciences and Business Studies, Edifício ISCTE,
Heterogeneous Hidden Markov Models José G. Dias 1, Jeroen K. Vermunt 2 and Sofia Ramos 3 1 Department of Quantitative methods, ISCTE Higher Institute of Social Sciences and Business Studies, Edifício ISCTE,
TDT4171 Artificial Intelligence Methods
 TDT47 Artificial Intelligence Methods Lecture 7 Making Complex Decisions Norwegian University of Science and Technology Helge Langseth IT-VEST 0 helgel@idi.ntnu.no TDT47 Artificial Intelligence Methods
TDT47 Artificial Intelligence Methods Lecture 7 Making Complex Decisions Norwegian University of Science and Technology Helge Langseth IT-VEST 0 helgel@idi.ntnu.no TDT47 Artificial Intelligence Methods
Occasional Paper. Dynamic Methods for Analyzing Hedge-Fund Performance: A Note Using Texas Energy-Related Funds. Jiaqi Chen and Michael L.
 DALLASFED Occasional Paper Dynamic Methods for Analyzing Hedge-Fund Performance: A Note Using Texas Energy-Related Funds Jiaqi Chen and Michael L. Tindall Federal Reserve Bank of Dallas Financial Industry
DALLASFED Occasional Paper Dynamic Methods for Analyzing Hedge-Fund Performance: A Note Using Texas Energy-Related Funds Jiaqi Chen and Michael L. Tindall Federal Reserve Bank of Dallas Financial Industry
Bayesian course - problem set 3 (lecture 4)
 Bayesian course - problem set 3 (lecture 4) Ben Lambert November 14, 2016 1 Ticked off Imagine once again that you are investigating the occurrence of Lyme disease in the UK. This is a vector-borne disease
Bayesian course - problem set 3 (lecture 4) Ben Lambert November 14, 2016 1 Ticked off Imagine once again that you are investigating the occurrence of Lyme disease in the UK. This is a vector-borne disease
Making Complex Decisions
 Ch. 17 p.1/29 Making Complex Decisions Chapter 17 Ch. 17 p.2/29 Outline Sequential decision problems Value iteration algorithm Policy iteration algorithm Ch. 17 p.3/29 A simple environment 3 +1 p=0.8 2
Ch. 17 p.1/29 Making Complex Decisions Chapter 17 Ch. 17 p.2/29 Outline Sequential decision problems Value iteration algorithm Policy iteration algorithm Ch. 17 p.3/29 A simple environment 3 +1 p=0.8 2
Chapter 7: Estimation Sections
 1 / 40 Chapter 7: Estimation Sections 7.1 Statistical Inference Bayesian Methods: Chapter 7 7.2 Prior and Posterior Distributions 7.3 Conjugate Prior Distributions 7.4 Bayes Estimators Frequentist Methods:
1 / 40 Chapter 7: Estimation Sections 7.1 Statistical Inference Bayesian Methods: Chapter 7 7.2 Prior and Posterior Distributions 7.3 Conjugate Prior Distributions 7.4 Bayes Estimators Frequentist Methods:
Definition 4.1. In a stochastic process T is called a stopping time if you can tell when it happens.
 102 OPTIMAL STOPPING TIME 4. Optimal Stopping Time 4.1. Definitions. On the first day I explained the basic problem using one example in the book. On the second day I explained how the solution to the
102 OPTIMAL STOPPING TIME 4. Optimal Stopping Time 4.1. Definitions. On the first day I explained the basic problem using one example in the book. On the second day I explained how the solution to the
Lecture 22: Dynamic Filtering
 ECE 830 Fall 2011 Statistical Signal Processing instructor: R. Nowak Lecture 22: Dynamic Filtering 1 Dynamic Filtering In many applications we want to track a time-varying (dynamic) phenomenon. Example
ECE 830 Fall 2011 Statistical Signal Processing instructor: R. Nowak Lecture 22: Dynamic Filtering 1 Dynamic Filtering In many applications we want to track a time-varying (dynamic) phenomenon. Example
Multi-period Portfolio Choice and Bayesian Dynamic Models
 Multi-period Portfolio Choice and Bayesian Dynamic Models Petter Kolm and Gordon Ritter Courant Institute, NYU Paper appeared in Risk Magazine, Feb. 25 (2015) issue Working paper version: papers.ssrn.com/sol3/papers.cfm?abstract_id=2472768
Multi-period Portfolio Choice and Bayesian Dynamic Models Petter Kolm and Gordon Ritter Courant Institute, NYU Paper appeared in Risk Magazine, Feb. 25 (2015) issue Working paper version: papers.ssrn.com/sol3/papers.cfm?abstract_id=2472768
Final Examination CS540: Introduction to Artificial Intelligence
 Final Examination CS540: Introduction to Artificial Intelligence December 2008 LAST NAME: FIRST NAME: Problem Score Max Score 1 15 2 15 3 10 4 20 5 10 6 20 7 10 Total 100 Question 1. [15] Probabilistic
Final Examination CS540: Introduction to Artificial Intelligence December 2008 LAST NAME: FIRST NAME: Problem Score Max Score 1 15 2 15 3 10 4 20 5 10 6 20 7 10 Total 100 Question 1. [15] Probabilistic
Complex Decisions. Sequential Decision Making
 Sequential Decision Making Outline Sequential decision problems Value iteration Policy iteration POMDPs (basic concepts) Slides partially based on the Book "Reinforcement Learning: an introduction" by
Sequential Decision Making Outline Sequential decision problems Value iteration Policy iteration POMDPs (basic concepts) Slides partially based on the Book "Reinforcement Learning: an introduction" by
Lecture 7: Bayesian approach to MAB - Gittins index
 Advanced Topics in Machine Learning and Algorithmic Game Theory Lecture 7: Bayesian approach to MAB - Gittins index Lecturer: Yishay Mansour Scribe: Mariano Schain 7.1 Introduction In the Bayesian approach
Advanced Topics in Machine Learning and Algorithmic Game Theory Lecture 7: Bayesian approach to MAB - Gittins index Lecturer: Yishay Mansour Scribe: Mariano Schain 7.1 Introduction In the Bayesian approach
Lecture 12: MDP1. Victor R. Lesser. CMPSCI 683 Fall 2010
 Lecture 12: MDP1 Victor R. Lesser CMPSCI 683 Fall 2010 Biased Random GSAT - WalkSat Notice no random restart 2 Today s lecture Search where there is Uncertainty in Operator Outcome --Sequential Decision
Lecture 12: MDP1 Victor R. Lesser CMPSCI 683 Fall 2010 Biased Random GSAT - WalkSat Notice no random restart 2 Today s lecture Search where there is Uncertainty in Operator Outcome --Sequential Decision
Machine Learning in Computer Vision Markov Random Fields Part II
 Machine Learning in Computer Vision Markov Random Fields Part II Oren Freifeld Computer Science, Ben-Gurion University March 22, 2018 Mar 22, 2018 1 / 40 1 Some MRF Computations 2 Mar 22, 2018 2 / 40 Few
Machine Learning in Computer Vision Markov Random Fields Part II Oren Freifeld Computer Science, Ben-Gurion University March 22, 2018 Mar 22, 2018 1 / 40 1 Some MRF Computations 2 Mar 22, 2018 2 / 40 Few
Stat 260/CS Learning in Sequential Decision Problems. Peter Bartlett
 Stat 260/CS 294-102. Learning in Sequential Decision Problems. Peter Bartlett 1. Gittins Index: Discounted, Bayesian (hence Markov arms). Reduces to stopping problem for each arm. Interpretation as (scaled)
Stat 260/CS 294-102. Learning in Sequential Decision Problems. Peter Bartlett 1. Gittins Index: Discounted, Bayesian (hence Markov arms). Reduces to stopping problem for each arm. Interpretation as (scaled)
Dynamic Programming: An overview. 1 Preliminaries: The basic principle underlying dynamic programming
 Dynamic Programming: An overview These notes summarize some key properties of the Dynamic Programming principle to optimize a function or cost that depends on an interval or stages. This plays a key role
Dynamic Programming: An overview These notes summarize some key properties of the Dynamic Programming principle to optimize a function or cost that depends on an interval or stages. This plays a key role
COS402- Artificial Intelligence Fall Lecture 17: MDP: Value Iteration and Policy Iteration
 COS402- Artificial Intelligence Fall 2015 Lecture 17: MDP: Value Iteration and Policy Iteration Outline The Bellman equation and Bellman update Contraction Value iteration Policy iteration The Bellman
COS402- Artificial Intelligence Fall 2015 Lecture 17: MDP: Value Iteration and Policy Iteration Outline The Bellman equation and Bellman update Contraction Value iteration Policy iteration The Bellman
Top-down particle filtering for Bayesian decision trees
 Top-down particle filtering for Bayesian decision trees Balaji Lakshminarayanan 1, Daniel M. Roy 2 and Yee Whye Teh 3 1. Gatsby Unit, UCL, 2. University of Cambridge and 3. University of Oxford Outline
Top-down particle filtering for Bayesian decision trees Balaji Lakshminarayanan 1, Daniel M. Roy 2 and Yee Whye Teh 3 1. Gatsby Unit, UCL, 2. University of Cambridge and 3. University of Oxford Outline
Lecture outline W.B.Powell 1
 Lecture outline What is a policy? Policy function approximations (PFAs) Cost function approximations (CFAs) alue function approximations (FAs) Lookahead policies Finding good policies Optimizing continuous
Lecture outline What is a policy? Policy function approximations (PFAs) Cost function approximations (CFAs) alue function approximations (FAs) Lookahead policies Finding good policies Optimizing continuous
SEQUENTIAL DECISION PROBLEM WITH PARTIAL MAINTENANCE ON A PARTIALLY OBSERVABLE MARKOV PROCESS. Toru Nakai. Received February 22, 2010
 Scientiae Mathematicae Japonicae Online, e-21, 283 292 283 SEQUENTIAL DECISION PROBLEM WITH PARTIAL MAINTENANCE ON A PARTIALLY OBSERVABLE MARKOV PROCESS Toru Nakai Received February 22, 21 Abstract. In
Scientiae Mathematicae Japonicae Online, e-21, 283 292 283 SEQUENTIAL DECISION PROBLEM WITH PARTIAL MAINTENANCE ON A PARTIALLY OBSERVABLE MARKOV PROCESS Toru Nakai Received February 22, 21 Abstract. In
Regime Switching Volatility Calibration by the Baum-Welch Method
 Regime Switching Volatility Calibration by the Baum-Welch Method Abstract Regime switching volatility models provide a tractable method of modelling stochastic volatility. Currently the most popular method
Regime Switching Volatility Calibration by the Baum-Welch Method Abstract Regime switching volatility models provide a tractable method of modelling stochastic volatility. Currently the most popular method
Making Decisions. CS 3793 Artificial Intelligence Making Decisions 1
 Making Decisions CS 3793 Artificial Intelligence Making Decisions 1 Planning under uncertainty should address: The world is nondeterministic. Actions are not certain to succeed. Many events are outside
Making Decisions CS 3793 Artificial Intelligence Making Decisions 1 Planning under uncertainty should address: The world is nondeterministic. Actions are not certain to succeed. Many events are outside
Stochastic Dual Dynamic Programming Algorithm for Multistage Stochastic Programming
 Stochastic Dual Dynamic Programg Algorithm for Multistage Stochastic Programg Final presentation ISyE 8813 Fall 2011 Guido Lagos Wajdi Tekaya Georgia Institute of Technology November 30, 2011 Multistage
Stochastic Dual Dynamic Programg Algorithm for Multistage Stochastic Programg Final presentation ISyE 8813 Fall 2011 Guido Lagos Wajdi Tekaya Georgia Institute of Technology November 30, 2011 Multistage
ECS171: Machine Learning
 ECS171: Machine Learning Lecture 15: Tree-based Algorithms Cho-Jui Hsieh UC Davis March 7, 2018 Outline Decision Tree Random Forest Gradient Boosted Decision Tree (GBDT) Decision Tree Each node checks
ECS171: Machine Learning Lecture 15: Tree-based Algorithms Cho-Jui Hsieh UC Davis March 7, 2018 Outline Decision Tree Random Forest Gradient Boosted Decision Tree (GBDT) Decision Tree Each node checks
Optimal Stopping. Nick Hay (presentation follows Thomas Ferguson s Optimal Stopping and Applications) November 6, 2008
 (presentation follows Thomas Ferguson s and Applications) November 6, 2008 1 / 35 Contents: Introduction Problems Markov Models Monotone Stopping Problems Summary 2 / 35 The Secretary problem You have
(presentation follows Thomas Ferguson s and Applications) November 6, 2008 1 / 35 Contents: Introduction Problems Markov Models Monotone Stopping Problems Summary 2 / 35 The Secretary problem You have
Introduction to Sequential Monte Carlo Methods
 Introduction to Sequential Monte Carlo Methods Arnaud Doucet NCSU, October 2008 Arnaud Doucet () Introduction to SMC NCSU, October 2008 1 / 36 Preliminary Remarks Sequential Monte Carlo (SMC) are a set
Introduction to Sequential Monte Carlo Methods Arnaud Doucet NCSU, October 2008 Arnaud Doucet () Introduction to SMC NCSU, October 2008 1 / 36 Preliminary Remarks Sequential Monte Carlo (SMC) are a set
Adaptive Experiments for Policy Choice. March 8, 2019
 Adaptive Experiments for Policy Choice Maximilian Kasy Anja Sautmann March 8, 2019 Introduction The goal of many experiments is to inform policy choices: 1. Job search assistance for refugees: Treatments:
Adaptive Experiments for Policy Choice Maximilian Kasy Anja Sautmann March 8, 2019 Introduction The goal of many experiments is to inform policy choices: 1. Job search assistance for refugees: Treatments:
Analysis of the Bitcoin Exchange Using Particle MCMC Methods
 Analysis of the Bitcoin Exchange Using Particle MCMC Methods by Michael Johnson M.Sc., University of British Columbia, 2013 B.Sc., University of Winnipeg, 2011 Project Submitted in Partial Fulfillment
Analysis of the Bitcoin Exchange Using Particle MCMC Methods by Michael Johnson M.Sc., University of British Columbia, 2013 B.Sc., University of Winnipeg, 2011 Project Submitted in Partial Fulfillment
LINEAR DYNAMICAL SYSTEMS: A MACHINE LEARNING FRAMEWORK FOR FINANCIAL TIME SERIES ANALYSIS
 where R f(x)dx =. LINEAR DYNAMICAL SYSTEMS: A MACHINE LEARNING FRAMEWORK FOR FINANCIAL TIME SERIES ANALYSIS KEMBEY GBARAYOR JR Advisor: Professor Amy Greenwald Department of Computer Science, Brown University,
where R f(x)dx =. LINEAR DYNAMICAL SYSTEMS: A MACHINE LEARNING FRAMEWORK FOR FINANCIAL TIME SERIES ANALYSIS KEMBEY GBARAYOR JR Advisor: Professor Amy Greenwald Department of Computer Science, Brown University,
Reinforcement Learning. Monte Carlo and Temporal Difference Learning
 Reinforcement Learning Monte Carlo and Temporal Difference Learning Manfred Huber 2014 1 Monte Carlo Methods Dynamic Programming Requires complete knowledge of the MDP Spends equal time on each part of
Reinforcement Learning Monte Carlo and Temporal Difference Learning Manfred Huber 2014 1 Monte Carlo Methods Dynamic Programming Requires complete knowledge of the MDP Spends equal time on each part of
CSC 411: Lecture 08: Generative Models for Classification
 CSC 411: Lecture 08: Generative Models for Classification Richard Zemel, Raquel Urtasun and Sanja Fidler University of Toronto Zemel, Urtasun, Fidler (UofT) CSC 411: 08-Generative Models 1 / 23 Today Classification
CSC 411: Lecture 08: Generative Models for Classification Richard Zemel, Raquel Urtasun and Sanja Fidler University of Toronto Zemel, Urtasun, Fidler (UofT) CSC 411: 08-Generative Models 1 / 23 Today Classification
SUPPLEMENT TO EQUILIBRIA IN HEALTH EXCHANGES: ADVERSE SELECTION VERSUS RECLASSIFICATION RISK (Econometrica, Vol. 83, No. 4, July 2015, )
 Econometrica Supplementary Material SUPPLEMENT TO EQUILIBRIA IN HEALTH EXCHANGES: ADVERSE SELECTION VERSUS RECLASSIFICATION RISK (Econometrica, Vol. 83, No. 4, July 2015, 1261 1313) BY BEN HANDEL, IGAL
Econometrica Supplementary Material SUPPLEMENT TO EQUILIBRIA IN HEALTH EXCHANGES: ADVERSE SELECTION VERSUS RECLASSIFICATION RISK (Econometrica, Vol. 83, No. 4, July 2015, 1261 1313) BY BEN HANDEL, IGAL
BSc (Hons) Software Engineering BSc (Hons) Computer Science with Network Security
 BSc (Hons) Software Engineering BSc (Hons) Computer Science with Network Security Cohorts BCNS/ 06 / Full Time & BSE/ 06 / Full Time Resit Examinations for 2008-2009 / Semester 1 Examinations for 2008-2009
BSc (Hons) Software Engineering BSc (Hons) Computer Science with Network Security Cohorts BCNS/ 06 / Full Time & BSE/ 06 / Full Time Resit Examinations for 2008-2009 / Semester 1 Examinations for 2008-2009
6.825 Homework 3: Solutions
 6.825 Homework 3: Solutions 1 Easy EM You are given the network structure shown in Figure 1 and the data in the following table, with actual observed values for A, B, and C, and expected counts for D.
6.825 Homework 3: Solutions 1 Easy EM You are given the network structure shown in Figure 1 and the data in the following table, with actual observed values for A, B, and C, and expected counts for D.
SIMULATION METHOD FOR SOLVING HYBRID INFLUENCE DIAGRAMS IN DECISION MAKING. Xi Chen Enlu Zhou
 Proceedings of the 2010 Winter Simulation Conference B. Johansson, S. Jain, J. Montoya-Torres, J. Hugan, and E. Yücesan, eds. SIMULATION METHOD FOR SOLVING HYBRID INFLUENCE DIAGRAMS IN DECISION MAKING
Proceedings of the 2010 Winter Simulation Conference B. Johansson, S. Jain, J. Montoya-Torres, J. Hugan, and E. Yücesan, eds. SIMULATION METHOD FOR SOLVING HYBRID INFLUENCE DIAGRAMS IN DECISION MAKING
The exam is closed book, closed calculator, and closed notes except your three crib sheets.
 CS 188 Spring 2016 Introduction to Artificial Intelligence Final V2 You have approximately 2 hours and 50 minutes. The exam is closed book, closed calculator, and closed notes except your three crib sheets.
CS 188 Spring 2016 Introduction to Artificial Intelligence Final V2 You have approximately 2 hours and 50 minutes. The exam is closed book, closed calculator, and closed notes except your three crib sheets.
Dynamic Programming and Reinforcement Learning
 Dynamic Programming and Reinforcement Learning Daniel Russo Columbia Business School Decision Risk and Operations Division Fall, 2017 Daniel Russo (Columbia) Fall 2017 1 / 34 Supervised Machine Learning
Dynamic Programming and Reinforcement Learning Daniel Russo Columbia Business School Decision Risk and Operations Division Fall, 2017 Daniel Russo (Columbia) Fall 2017 1 / 34 Supervised Machine Learning
POMDPs: Partially Observable Markov Decision Processes Advanced AI
 POMDPs: Partially Observable Markov Decision Processes Advanced AI Wolfram Burgard Types of Planning Problems Classical Planning State observable Action Model Deterministic, accurate MDPs observable stochastic
POMDPs: Partially Observable Markov Decision Processes Advanced AI Wolfram Burgard Types of Planning Problems Classical Planning State observable Action Model Deterministic, accurate MDPs observable stochastic
An EM-Algorithm for Maximum-Likelihood Estimation of Mixed Frequency VARs
 An EM-Algorithm for Maximum-Likelihood Estimation of Mixed Frequency VARs Jürgen Antony, Pforzheim Business School and Torben Klarl, Augsburg University EEA 2016, Geneva Introduction frequent problem in
An EM-Algorithm for Maximum-Likelihood Estimation of Mixed Frequency VARs Jürgen Antony, Pforzheim Business School and Torben Klarl, Augsburg University EEA 2016, Geneva Introduction frequent problem in
Research Memo: Adding Nonfarm Employment to the Mixed-Frequency VAR Model
 Research Memo: Adding Nonfarm Employment to the Mixed-Frequency VAR Model Kenneth Beauchemin Federal Reserve Bank of Minneapolis January 2015 Abstract This memo describes a revision to the mixed-frequency
Research Memo: Adding Nonfarm Employment to the Mixed-Frequency VAR Model Kenneth Beauchemin Federal Reserve Bank of Minneapolis January 2015 Abstract This memo describes a revision to the mixed-frequency
Lecture 1: Lucas Model and Asset Pricing
 Lecture 1: Lucas Model and Asset Pricing Economics 714, Spring 2018 1 Asset Pricing 1.1 Lucas (1978) Asset Pricing Model We assume that there are a large number of identical agents, modeled as a representative
Lecture 1: Lucas Model and Asset Pricing Economics 714, Spring 2018 1 Asset Pricing 1.1 Lucas (1978) Asset Pricing Model We assume that there are a large number of identical agents, modeled as a representative
A start of Variational Methods for ERGM Ranran Wang, UW
 A start of Variational Methods for ERGM Ranran Wang, UW MURI-UCI April 24, 2009 Outline A start of Variational Methods for ERGM [1] Introduction to ERGM Current methods of parameter estimation: MCMCMLE:
A start of Variational Methods for ERGM Ranran Wang, UW MURI-UCI April 24, 2009 Outline A start of Variational Methods for ERGM [1] Introduction to ERGM Current methods of parameter estimation: MCMCMLE:
The exam is closed book, closed notes except a two-page crib sheet. Non-programmable calculators only.
 CS 188 Spring 2011 Introduction to Artificial Intelligence Final Exam INSTRUCTIONS You have 3 hours. The exam is closed book, closed notes except a two-page crib sheet. Non-programmable calculators only.
CS 188 Spring 2011 Introduction to Artificial Intelligence Final Exam INSTRUCTIONS You have 3 hours. The exam is closed book, closed notes except a two-page crib sheet. Non-programmable calculators only.
4 Reinforcement Learning Basic Algorithms
 Learning in Complex Systems Spring 2011 Lecture Notes Nahum Shimkin 4 Reinforcement Learning Basic Algorithms 4.1 Introduction RL methods essentially deal with the solution of (optimal) control problems
Learning in Complex Systems Spring 2011 Lecture Notes Nahum Shimkin 4 Reinforcement Learning Basic Algorithms 4.1 Introduction RL methods essentially deal with the solution of (optimal) control problems
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50)
 Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 6 Sequential Monte Carlo methods II February
Monte Carlo and Empirical Methods for Stochastic Inference (MASM11/FMSN50) Magnus Wiktorsson Centre for Mathematical Sciences Lund University, Sweden Lecture 6 Sequential Monte Carlo methods II February
Subject : Computer Science. Paper: Machine Learning. Module: Decision Theory and Bayesian Decision Theory. Module No: CS/ML/10.
 e-pg Pathshala Subject : Computer Science Paper: Machine Learning Module: Decision Theory and Bayesian Decision Theory Module No: CS/ML/0 Quadrant I e-text Welcome to the e-pg Pathshala Lecture Series
e-pg Pathshala Subject : Computer Science Paper: Machine Learning Module: Decision Theory and Bayesian Decision Theory Module No: CS/ML/0 Quadrant I e-text Welcome to the e-pg Pathshala Lecture Series
Final exam solutions
 EE365 Stochastic Control / MS&E251 Stochastic Decision Models Profs. S. Lall, S. Boyd June 5 6 or June 6 7, 2013 Final exam solutions This is a 24 hour take-home final. Please turn it in to one of the
EE365 Stochastic Control / MS&E251 Stochastic Decision Models Profs. S. Lall, S. Boyd June 5 6 or June 6 7, 2013 Final exam solutions This is a 24 hour take-home final. Please turn it in to one of the
Project exam for STK Computational statistics
 Project exam for STK4051 - Computational statistics Fall 2017 Part 1 (of 2) This is the first part of the exam project set for STK4051/9051, fall semester 2017. It is made available on the course website
Project exam for STK4051 - Computational statistics Fall 2017 Part 1 (of 2) This is the first part of the exam project set for STK4051/9051, fall semester 2017. It is made available on the course website
CS 188: Artificial Intelligence Fall 2011
 CS 188: Artificial Intelligence Fall 2011 Lecture 9: MDPs 9/22/2011 Dan Klein UC Berkeley Many slides over the course adapted from either Stuart Russell or Andrew Moore 2 Grid World The agent lives in
CS 188: Artificial Intelligence Fall 2011 Lecture 9: MDPs 9/22/2011 Dan Klein UC Berkeley Many slides over the course adapted from either Stuart Russell or Andrew Moore 2 Grid World The agent lives in
ADVANCED MACROECONOMIC TECHNIQUES NOTE 6a
 316-406 ADVANCED MACROECONOMIC TECHNIQUES NOTE 6a Chris Edmond hcpedmond@unimelb.edu.aui Introduction to consumption-based asset pricing We will begin our brief look at asset pricing with a review of the
316-406 ADVANCED MACROECONOMIC TECHNIQUES NOTE 6a Chris Edmond hcpedmond@unimelb.edu.aui Introduction to consumption-based asset pricing We will begin our brief look at asset pricing with a review of the
Non-Deterministic Search
 Non-Deterministic Search MDP s 1 Non-Deterministic Search How do you plan (search) when your actions might fail? In general case, how do you plan, when the actions have multiple possible outcomes? 2 Example:
Non-Deterministic Search MDP s 1 Non-Deterministic Search How do you plan (search) when your actions might fail? In general case, how do you plan, when the actions have multiple possible outcomes? 2 Example:
Introduction to Fall 2007 Artificial Intelligence Final Exam
 NAME: SID#: Login: Sec: 1 CS 188 Introduction to Fall 2007 Artificial Intelligence Final Exam You have 180 minutes. The exam is closed book, closed notes except a two-page crib sheet, basic calculators
NAME: SID#: Login: Sec: 1 CS 188 Introduction to Fall 2007 Artificial Intelligence Final Exam You have 180 minutes. The exam is closed book, closed notes except a two-page crib sheet, basic calculators
Overview: Representation Techniques
 1 Overview: Representation Techniques Week 6 Representations for classical planning problems deterministic environment; complete information Week 7 Logic programs for problem representations including
1 Overview: Representation Techniques Week 6 Representations for classical planning problems deterministic environment; complete information Week 7 Logic programs for problem representations including
EC316a: Advanced Scientific Computation, Fall Discrete time, continuous state dynamic models: solution methods
 EC316a: Advanced Scientific Computation, Fall 2003 Notes Section 4 Discrete time, continuous state dynamic models: solution methods We consider now solution methods for discrete time models in which decisions
EC316a: Advanced Scientific Computation, Fall 2003 Notes Section 4 Discrete time, continuous state dynamic models: solution methods We consider now solution methods for discrete time models in which decisions
Chapter 7: Estimation Sections
 1 / 31 : Estimation Sections 7.1 Statistical Inference Bayesian Methods: 7.2 Prior and Posterior Distributions 7.3 Conjugate Prior Distributions 7.4 Bayes Estimators Frequentist Methods: 7.5 Maximum Likelihood
1 / 31 : Estimation Sections 7.1 Statistical Inference Bayesian Methods: 7.2 Prior and Posterior Distributions 7.3 Conjugate Prior Distributions 7.4 Bayes Estimators Frequentist Methods: 7.5 Maximum Likelihood
CPS 270: Artificial Intelligence Markov decision processes, POMDPs
 CPS 270: Artificial Intelligence http://www.cs.duke.edu/courses/fall08/cps270/ Markov decision processes, POMDPs Instructor: Vincent Conitzer Warmup: a Markov process with rewards We derive some reward
CPS 270: Artificial Intelligence http://www.cs.duke.edu/courses/fall08/cps270/ Markov decision processes, POMDPs Instructor: Vincent Conitzer Warmup: a Markov process with rewards We derive some reward
IEOR E4004: Introduction to OR: Deterministic Models
 IEOR E4004: Introduction to OR: Deterministic Models 1 Dynamic Programming Following is a summary of the problems we discussed in class. (We do not include the discussion on the container problem or the
IEOR E4004: Introduction to OR: Deterministic Models 1 Dynamic Programming Following is a summary of the problems we discussed in class. (We do not include the discussion on the container problem or the
SYSM 6304: Risk and Decision Analysis Lecture 6: Pricing and Hedging Financial Derivatives
 SYSM 6304: Risk and Decision Analysis Lecture 6: Pricing and Hedging Financial Derivatives M. Vidyasagar Cecil & Ida Green Chair The University of Texas at Dallas Email: M.Vidyasagar@utdallas.edu October
SYSM 6304: Risk and Decision Analysis Lecture 6: Pricing and Hedging Financial Derivatives M. Vidyasagar Cecil & Ida Green Chair The University of Texas at Dallas Email: M.Vidyasagar@utdallas.edu October
Exact Inference. Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4. x 3. f s. x 2. x 1
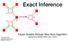 Exact Inference x 1 x 3 x 2 f s Geoffrey Roeder roeder@cs.toronto.edu 8 February 2018 Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4 Building Blocks UGMs, Cliques, Factor
Exact Inference x 1 x 3 x 2 f s Geoffrey Roeder roeder@cs.toronto.edu 8 February 2018 Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4 Building Blocks UGMs, Cliques, Factor
A simple wealth model
 Quantitative Macroeconomics Raül Santaeulàlia-Llopis, MOVE-UAB and Barcelona GSE Homework 5, due Thu Nov 1 I A simple wealth model Consider the sequential problem of a household that maximizes over streams
Quantitative Macroeconomics Raül Santaeulàlia-Llopis, MOVE-UAB and Barcelona GSE Homework 5, due Thu Nov 1 I A simple wealth model Consider the sequential problem of a household that maximizes over streams
CS 188: Artificial Intelligence
 CS 188: Artificial Intelligence Markov Decision Processes Dan Klein, Pieter Abbeel University of California, Berkeley Non Deterministic Search Example: Grid World A maze like problem The agent lives in
CS 188: Artificial Intelligence Markov Decision Processes Dan Klein, Pieter Abbeel University of California, Berkeley Non Deterministic Search Example: Grid World A maze like problem The agent lives in
Posterior Inference. , where should we start? Consider the following computational procedure: 1. draw samples. 2. convert. 3. compute properties
 Posterior Inference Example. Consider a binomial model where we have a posterior distribution for the probability term, θ. Suppose we want to make inferences about the log-odds γ = log ( θ 1 θ), where
Posterior Inference Example. Consider a binomial model where we have a posterior distribution for the probability term, θ. Suppose we want to make inferences about the log-odds γ = log ( θ 1 θ), where
EE266 Homework 5 Solutions
 EE, Spring 15-1 Professor S. Lall EE Homework 5 Solutions 1. A refined inventory model. In this problem we consider an inventory model that is more refined than the one you ve seen in the lectures. The
EE, Spring 15-1 Professor S. Lall EE Homework 5 Solutions 1. A refined inventory model. In this problem we consider an inventory model that is more refined than the one you ve seen in the lectures. The
Option Pricing Using Bayesian Neural Networks
 Option Pricing Using Bayesian Neural Networks Michael Maio Pires, Tshilidzi Marwala School of Electrical and Information Engineering, University of the Witwatersrand, 2050, South Africa m.pires@ee.wits.ac.za,
Option Pricing Using Bayesian Neural Networks Michael Maio Pires, Tshilidzi Marwala School of Electrical and Information Engineering, University of the Witwatersrand, 2050, South Africa m.pires@ee.wits.ac.za,
risks Hidden Markov Model for Stock Selection Risks 2015, 3, ; doi: /risks ISSN Article
 Risks 15, 3, 5-473; doi:10.3390/risks305 Article OPEN ACCESS risks ISSN 2227-9091 www.mdpi.com/journal/risks Hidden Markov Model for Stock Selection Nguyet Nguyen 1, * and Dung Nguyen 2 1 Faculty of Mathematics
Risks 15, 3, 5-473; doi:10.3390/risks305 Article OPEN ACCESS risks ISSN 2227-9091 www.mdpi.com/journal/risks Hidden Markov Model for Stock Selection Nguyet Nguyen 1, * and Dung Nguyen 2 1 Faculty of Mathematics
Probabilistic Robotics: Probabilistic Planning and MDPs
 Probabilistic Robotics: Probabilistic Planning and MDPs Slide credits: Wolfram Burgard, Dieter Fox, Cyrill Stachniss, Giorgio Grisetti, Maren Bennewitz, Christian Plagemann, Dirk Haehnel, Mike Montemerlo,
Probabilistic Robotics: Probabilistic Planning and MDPs Slide credits: Wolfram Burgard, Dieter Fox, Cyrill Stachniss, Giorgio Grisetti, Maren Bennewitz, Christian Plagemann, Dirk Haehnel, Mike Montemerlo,
Multi-armed bandits in dynamic pricing
 Multi-armed bandits in dynamic pricing Arnoud den Boer University of Twente, Centrum Wiskunde & Informatica Amsterdam Lancaster, January 11, 2016 Dynamic pricing A firm sells a product, with abundant inventory,
Multi-armed bandits in dynamic pricing Arnoud den Boer University of Twente, Centrum Wiskunde & Informatica Amsterdam Lancaster, January 11, 2016 Dynamic pricing A firm sells a product, with abundant inventory,
