Since his score is positive, he s above average. Since his score is not close to zero, his score is unusual.
|
|
|
- Patrick Arnold
- 5 years ago
- Views:
Transcription
1 Chapter 06: The Standard Deviation as a Ruler and the Normal Model This is the worst chapter title ever! This chapter is about the most important random variable distribution of them all the normal distribution. Measuring Position (again) Earlier (several chapters ago) we talked about quartiles as a method of measuring position. It turns out that there is another one: standardized scores. Let s define standardized scores in a very generic way for the moment, and then we ll see how they really get used a little later. Equation 1 - Standardized Scores datum mean standardized score= standard deviation Standardized scores measure the position of a datum relative to the mean, but in units of the standard deviation. Thus, these scores tell how many standard deviations above (or below) a datum is located. There are two things to know about standardized scores for now: the sign (positive or negative) tells whether a datum is above or below the mean, and the value (close to zero, or far from zero) tells how unusual the datum is (closer to zero means more typical). You can always use a standardized score to measure position but there are other things we can do with them that only work under certain conditions! Specifically, we can only attach probabilities to them when they are used with a normally distributed variable more on that after a few examples. Examples [1.] Zeke s parents are told that their son s IQ has a standardized score of 2.3. Explain what this means about Zeke s IQ relative to the others in his class. Since his score is positive, he s above average. Since his score is not close to zero, his score is unusual. [2.] In his PreCalculus class, Abe earned a final grade of 92. For his class as a whole, the mean final grade was 80 with a standard deviation of 7. Carol also just finished a PreCalculus class, where the class mean was 80 with a standard deviation of 3. Carol s final grade was 89. Which student performed better relative to their peers? Abe s standardized score is = and Carol s standardized score is = Both are above the mean, but Carol s score is farther from zero, so her score is more unusual she did better than Abe when compared to her peers. HOLLOMAN S AP STATISTICS BVD CHAPTER 06, PAGE 1 OF 6
2 The Normal Model The Idea There is one continuous random variable that is more important than the others that is the Normal Distribution. This is also referred to as a Gaussian Distribution, or sometimes as a bell curve. Unlike the discrete cases we studied where you can define the model in terms of a process the normal model really can really only be defined in terms of its graph. Figure 1 - A Normal Distribution Properties You need two numbers to describe a normal distribution the mean and the standard deviation. In the picture above, µ= 0 and σ = 1. The shape is perfectly symmetric about the mean. The standard deviation in a normal curve is actually not too hard to see. There is a special point on the curve (most people can pick out its general location with little difficulty) that helps to find the standard deviation. Figure 2 - The Inflection Point of a Normal Curve This special point is where the curve stops dropping more than sliding, and starts sliding more than dropping. It s called an inflection point but you don t need to remember that. What you do need to know is that the horizontal distance between this point and the mean is the value of the standard deviation. The domain of a normal distribution is all real numbers it continues infinitely in both directions. For this reason, most applications use models that are only approximately normal. In the discrete cases (binomial and geometric) I defined a probability mass function a function that produced probability values. The continuous variables require a slightly different approach. In the discrete case, the function value (analogous to the y-value on a graph like the HOLLOMAN S AP STATISTICS BVD CHAPTER 06, PAGE 2 OF 6
3 one above) is the probability. In the continuous case, the function value is not the probability rather, probability is found through area. You ve probably never found the area of a shape like the normal curve! That s OK we ve got ways to do that without getting too mathy. Here s the first The Empirical Rule First of all, know that the total area under a normal curve is 1 (since it represents all possible outcomes, the total probability is 1 and probability is now area). The area under a normal curve between µ σ and µ + σ is about 0.68; between µ 2σ and µ + 2σ is about 0.95; and between µ 3σ and µ + 3σ is about This is called the Empirical Rule, and can be used to approximate probabilities for normal distributions. Figure 3 - The Empirical Rule you may also want to use the facts that the distribution is symmetric, and that the total area is 1. It s also a really good idea to draw a picture of what you re trying to find! Examples [3.] The size of the frontal lobe of members of the Leptograpsus variegatus species (Australian crab) varies normally with mean 15.6mm and standard deviation 3.5mm. (a) What proportion of these crabs have frontal lobe measurements between 12.1mm and 19.1mm? (b) What proportion of these crabs have frontal lobe measurements greater than 22.6mm? (a) We are given µ= 15.6 and σ = 3.5. Notice that 12.1 = µ σ, and 19.1 = µ + σ. Thus, the proportion of crabs with frontal lobes between these measurements is about 0.68, or 68%. (b) 22.6= µ + 2σ 95% of these measurements are between 8.6 and 22.6; so 5% must be lower than 8.6 OR higher than Since the normal curve is symmetric about µ, the proportion above 22.6 must be about 2.5%. HOLLOMAN S AP STATISTICS BVD CHAPTER 06, PAGE 3 OF 6
4 [4.] PSAT Math scores for Sophomores who took the test in 2005 were approximately normally distributed with mean 44 and standard deviation 11. (a) What proportion of these scores were between 55 and 66? (b) What proportion of these scores were lower than 33? (c) Approximately what score would put a student in the top 2.5% of scores? (a) Note that 55 is at µ + σ and 66 is at µ + 2σ. I know that the proportion between µ σ and µ + σ is about 0.68 and that the proportion between µ 2σ and µ + 2σ is about If we subtract these, we get the proportion that are either between µ 2σ and µ σ or between µ + σ and µ + 2σ. Since we want only one of those, and since the distribution is symmetric, we can divide the difference by two to obtain the answer. Thus, the proportion is = (b) First note that 33 is at µ σ. I know that the proportion between µ σ and µ + σ is about 0.68, so the proportion that are either lower than µ σ or greater than µ + σ must be Since I only want one of those, and since we have symmetry, divide by two! The proportion is (c) This is a little different we know the area and we need to work that back to a value of the variable. A top area of gets doubled to make a top and bottom area of 0.05 and that makes a middle area of Great! I know that the proportion of scores between µ 2σ and µ + 2σ is about 0.95 so the upper score (the one marking the top 2.5%) must be at µ + 2σ. Thus, the score that puts you at the top 2.5% must be 44+ 2( 11) = 66. More Accurate Methods It is easy to see that this method has limited application we need something a bit more powerful. Did you notice that when we found that measurements were at µ + σ or µ 2σ that we were really finding standardized scores? No? Well, we were! If you are dealing with a normal distribution, then standardized scores are the gateway to more accurate probability. Let s get one bit of notation out of the way now that we are distinctly dealing with a particular distribution (the normal), let s adjust that formula for standardized scores: Equation 2 - Z-scores x µ z= σ Really, every standardized score is a z-score just remember that you can only turn a z-score into a probability if you know that the distribution is (at least approximately) normal. Normal Probability To find the area under any normal curve, first convert your measurements to z-scores. Once you ve converted any values of your original variable (x) into standard normal values (z), then it s time to use the Z Chart. The chart lists its z values (from about -3.4 to 3.4) to two decimal places. The units and tenths are found on the left margin of the page; the hundredths digit is HOLLOMAN S AP STATISTICS BVD CHAPTER 06, PAGE 4 OF 6
5 found along the top row. At the intersection of the row and column for your z, you will find the area under the normal curve to the left of that z. If you want the area to the right, or the area between two z values, you ll have to use two important properties of normal curves symmetry, and the total area under the curve is 1. or you could use the handy function in your calculator! Inverse Normal Calculations Of course, you don t always start with a variable and then find out how often it occurs. Sometimes, you know how often something occurs (or how often you want it to occur), and you need to find the value of the variable that ll make it happen. This is called an Inverse Normal Calculation. It works exactly backwards from a regular problem. In a regular problem, we take an x and make it a z; then we look that z up in the chart; then we read off the left-hand area. For an Inverse problem, we start by finding the left-hand area in the chart; then we read z, then we change z back into x. You should be able to (easily) do the algebra required to change z back to x. Here s a little graphic that I use to remember how to move between the various parts of a normal problem: Figure 4 - Normal Calculation Summary Examples [5.] Back to our crab example what proportion of crabs have frontal lobes larger than 18mm? First, the z-score: = Now use the chart or your calculator to find the right 3.5 hand area of [6.] The heights of 15 year old American males are approximately normally distributed with mean 170 cm and standard deviation 7.6 cm. What proportion of these young men have heights greater than 185 cm? Start with the z-score: = Now use your preferred tool to find the right hand 7.6 area: [7.] The maximum oxygen uptake of middle-aged American men is approximately normally distributed with mean 42.2 ml/kg/min and standard deviation 3.7 ml/kg/min. (a) What proportion of middle-aged men have maximum oxygen uptake levels lower than 35 ml/kg/min? HOLLOMAN S AP STATISTICS BVD CHAPTER 06, PAGE 5 OF 6
6 (b) Higher levels of maximum oxygen uptake are indicative of better health. What level would put a middle-aged man in the top 5% of healthy individuals? (a) z-score: = ; the proportion is (b) The z-score for the top 5% is ; that makes the variable value = ml/kg/min. ( )( ) [8.] Most measures of IQ are normally distributed, and scaled to have mean 100 and standard deviation 15. (a) What percentage of people will have IQs that are lower than 88? (b) The organization MENSA only accepts members who score in the top 2% of IQ tests. What range of scores would enable one to join MENSA? (c) People who score in the lowest 10% of IQ scores are often eligible for additional services in school. What range of IQ scores would enable a student to receive special services? (a) The z-score is = 0.8 and the proportion is (b) The z-score for the top 2% is ; that makes the IQ score = ( )( ) (c) The z-score for the lowest 10% is ; that makes the IQ score = ( )( ) The Normal Probability Plot There are times when you have some data and you want to check to see if the data are approximately normally distributed. There are ways to do that and the textbooks describes one of them at this point. I m going to wait and talk about this graph much later in the year (it isn t that important, really). HOLLOMAN S AP STATISTICS BVD CHAPTER 06, PAGE 6 OF 6
7.1 Graphs of Normal Probability Distributions
 7 Normal Distributions In Chapter 6, we looked at the distributions of discrete random variables in particular, the binomial. Now we turn out attention to continuous random variables in particular, the
7 Normal Distributions In Chapter 6, we looked at the distributions of discrete random variables in particular, the binomial. Now we turn out attention to continuous random variables in particular, the
The Normal Probability Distribution
 1 The Normal Probability Distribution Key Definitions Probability Density Function: An equation used to compute probabilities for continuous random variables where the output value is greater than zero
1 The Normal Probability Distribution Key Definitions Probability Density Function: An equation used to compute probabilities for continuous random variables where the output value is greater than zero
Both the quizzes and exams are closed book. However, For quizzes: Formulas will be provided with quiz papers if there is any need.
 Both the quizzes and exams are closed book. However, For quizzes: Formulas will be provided with quiz papers if there is any need. For exams (MD1, MD2, and Final): You may bring one 8.5 by 11 sheet of
Both the quizzes and exams are closed book. However, For quizzes: Formulas will be provided with quiz papers if there is any need. For exams (MD1, MD2, and Final): You may bring one 8.5 by 11 sheet of
When we look at a random variable, such as Y, one of the first things we want to know, is what is it s distribution?
 Distributions 1. What are distributions? When we look at a random variable, such as Y, one of the first things we want to know, is what is it s distribution? In other words, if we have a large number of
Distributions 1. What are distributions? When we look at a random variable, such as Y, one of the first things we want to know, is what is it s distribution? In other words, if we have a large number of
When we look at a random variable, such as Y, one of the first things we want to know, is what is it s distribution?
 Distributions 1. What are distributions? When we look at a random variable, such as Y, one of the first things we want to know, is what is it s distribution? In other words, if we have a large number of
Distributions 1. What are distributions? When we look at a random variable, such as Y, one of the first things we want to know, is what is it s distribution? In other words, if we have a large number of
The Normal Distribution
 Stat 6 Introduction to Business Statistics I Spring 009 Professor: Dr. Petrutza Caragea Section A Tuesdays and Thursdays 9:300:50 a.m. Chapter, Section.3 The Normal Distribution Density Curves So far we
Stat 6 Introduction to Business Statistics I Spring 009 Professor: Dr. Petrutza Caragea Section A Tuesdays and Thursdays 9:300:50 a.m. Chapter, Section.3 The Normal Distribution Density Curves So far we
The probability of having a very tall person in our sample. We look to see how this random variable is distributed.
 Distributions We're doing things a bit differently than in the text (it's very similar to BIOL 214/312 if you've had either of those courses). 1. What are distributions? When we look at a random variable,
Distributions We're doing things a bit differently than in the text (it's very similar to BIOL 214/312 if you've had either of those courses). 1. What are distributions? When we look at a random variable,
6.1 Graphs of Normal Probability Distributions:
 6.1 Graphs of Normal Probability Distributions: Normal Distribution one of the most important examples of a continuous probability distribution, studied by Abraham de Moivre (1667 1754) and Carl Friedrich
6.1 Graphs of Normal Probability Distributions: Normal Distribution one of the most important examples of a continuous probability distribution, studied by Abraham de Moivre (1667 1754) and Carl Friedrich
Chapter 6. y y. Standardizing with z-scores. Standardizing with z-scores (cont.)
 Starter Ch. 6: A z-score Analysis Starter Ch. 6 Your Statistics teacher has announced that the lower of your two tests will be dropped. You got a 90 on test 1 and an 85 on test 2. You re all set to drop
Starter Ch. 6: A z-score Analysis Starter Ch. 6 Your Statistics teacher has announced that the lower of your two tests will be dropped. You got a 90 on test 1 and an 85 on test 2. You re all set to drop
Chapter 6. The Normal Probability Distributions
 Chapter 6 The Normal Probability Distributions 1 Chapter 6 Overview Introduction 6-1 Normal Probability Distributions 6-2 The Standard Normal Distribution 6-3 Applications of the Normal Distribution 6-5
Chapter 6 The Normal Probability Distributions 1 Chapter 6 Overview Introduction 6-1 Normal Probability Distributions 6-2 The Standard Normal Distribution 6-3 Applications of the Normal Distribution 6-5
STAT:2010 Statistical Methods and Computing. Using density curves to describe the distribution of values of a quantitative
 STAT:10 Statistical Methods and Computing Normal Distributions Lecture 4 Feb. 6, 17 Kate Cowles 374 SH, 335-0727 kate-cowles@uiowa.edu 1 2 Using density curves to describe the distribution of values of
STAT:10 Statistical Methods and Computing Normal Distributions Lecture 4 Feb. 6, 17 Kate Cowles 374 SH, 335-0727 kate-cowles@uiowa.edu 1 2 Using density curves to describe the distribution of values of
ECON 214 Elements of Statistics for Economists
 ECON 214 Elements of Statistics for Economists Session 7 The Normal Distribution Part 1 Lecturer: Dr. Bernardin Senadza, Dept. of Economics Contact Information: bsenadza@ug.edu.gh College of Education
ECON 214 Elements of Statistics for Economists Session 7 The Normal Distribution Part 1 Lecturer: Dr. Bernardin Senadza, Dept. of Economics Contact Information: bsenadza@ug.edu.gh College of Education
Chapter 3. Lecture 3 Sections
 Chapter 3 Lecture 3 Sections 3.4 3.5 Measure of Position We would like to compare values from different data sets. We will introduce a z score or standard score. This measures how many standard deviation
Chapter 3 Lecture 3 Sections 3.4 3.5 Measure of Position We would like to compare values from different data sets. We will introduce a z score or standard score. This measures how many standard deviation
STAB22 section 1.3 and Chapter 1 exercises
 STAB22 section 1.3 and Chapter 1 exercises 1.101 Go up and down two times the standard deviation from the mean. So 95% of scores will be between 572 (2)(51) = 470 and 572 + (2)(51) = 674. 1.102 Same idea
STAB22 section 1.3 and Chapter 1 exercises 1.101 Go up and down two times the standard deviation from the mean. So 95% of scores will be between 572 (2)(51) = 470 and 572 + (2)(51) = 674. 1.102 Same idea
CH 5 Normal Probability Distributions Properties of the Normal Distribution
 Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
ECON 214 Elements of Statistics for Economists 2016/2017
 ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
STAT Chapter 5: Continuous Distributions. Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s.
 STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
Biostatistics and Design of Experiments Prof. Mukesh Doble Department of Biotechnology Indian Institute of Technology, Madras
 Biostatistics and Design of Experiments Prof. Mukesh Doble Department of Biotechnology Indian Institute of Technology, Madras Lecture - 05 Normal Distribution So far we have looked at discrete distributions
Biostatistics and Design of Experiments Prof. Mukesh Doble Department of Biotechnology Indian Institute of Technology, Madras Lecture - 05 Normal Distribution So far we have looked at discrete distributions
The normal distribution is a theoretical model derived mathematically and not empirically.
 Sociology 541 The Normal Distribution Probability and An Introduction to Inferential Statistics Normal Approximation The normal distribution is a theoretical model derived mathematically and not empirically.
Sociology 541 The Normal Distribution Probability and An Introduction to Inferential Statistics Normal Approximation The normal distribution is a theoretical model derived mathematically and not empirically.
Expected Value of a Random Variable
 Knowledge Article: Probability and Statistics Expected Value of a Random Variable Expected Value of a Discrete Random Variable You're familiar with a simple mean, or average, of a set. The mean value of
Knowledge Article: Probability and Statistics Expected Value of a Random Variable Expected Value of a Discrete Random Variable You're familiar with a simple mean, or average, of a set. The mean value of
8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions 8-1
 8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions For Example: On August 8, 2011, the Dow dropped 634.8 points, sending shock waves through the financial community.
8.2 The Standard Deviation as a Ruler Chapter 8 The Normal and Other Continuous Distributions For Example: On August 8, 2011, the Dow dropped 634.8 points, sending shock waves through the financial community.
1. Confidence Intervals (cont.)
 Math 1125-Introductory Statistics Lecture 23 11/1/06 1. Confidence Intervals (cont.) Let s review. We re in a situation, where we don t know µ, but we have a number from a normal population, either an
Math 1125-Introductory Statistics Lecture 23 11/1/06 1. Confidence Intervals (cont.) Let s review. We re in a situation, where we don t know µ, but we have a number from a normal population, either an
Lecture Slides. Elementary Statistics Tenth Edition. by Mario F. Triola. and the Triola Statistics Series. Slide 1
 Lecture Slides Elementary Statistics Tenth Edition and the Triola Statistics Series by Mario F. Triola Slide 1 Chapter 6 Normal Probability Distributions 6-1 Overview 6-2 The Standard Normal Distribution
Lecture Slides Elementary Statistics Tenth Edition and the Triola Statistics Series by Mario F. Triola Slide 1 Chapter 6 Normal Probability Distributions 6-1 Overview 6-2 The Standard Normal Distribution
Statistics 511 Supplemental Materials
 Gaussian (or Normal) Random Variable In this section we introduce the Gaussian Random Variable, which is more commonly referred to as the Normal Random Variable. This is a random variable that has a bellshaped
Gaussian (or Normal) Random Variable In this section we introduce the Gaussian Random Variable, which is more commonly referred to as the Normal Random Variable. This is a random variable that has a bellshaped
MA 1125 Lecture 05 - Measures of Spread. Wednesday, September 6, Objectives: Introduce variance, standard deviation, range.
 MA 115 Lecture 05 - Measures of Spread Wednesday, September 6, 017 Objectives: Introduce variance, standard deviation, range. 1. Measures of Spread In Lecture 04, we looked at several measures of central
MA 115 Lecture 05 - Measures of Spread Wednesday, September 6, 017 Objectives: Introduce variance, standard deviation, range. 1. Measures of Spread In Lecture 04, we looked at several measures of central
STAT Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model
 STAT 203 - Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model In Chapter 5, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are good
STAT 203 - Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model In Chapter 5, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are good
The Normal Distribution
 5.1 Introduction to Normal Distributions and the Standard Normal Distribution Section Learning objectives: 1. How to interpret graphs of normal probability distributions 2. How to find areas under the
5.1 Introduction to Normal Distributions and the Standard Normal Distribution Section Learning objectives: 1. How to interpret graphs of normal probability distributions 2. How to find areas under the
STAT 201 Chapter 6. Distribution
 STAT 201 Chapter 6 Distribution 1 Random Variable We know variable Random Variable: a numerical measurement of the outcome of a random phenomena Capital letter refer to the random variable Lower case letters
STAT 201 Chapter 6 Distribution 1 Random Variable We know variable Random Variable: a numerical measurement of the outcome of a random phenomena Capital letter refer to the random variable Lower case letters
5.1 Mean, Median, & Mode
 5.1 Mean, Median, & Mode definitions Mean: Median: Mode: Example 1 The Blue Jays score these amounts of runs in their last 9 games: 4, 7, 2, 4, 10, 5, 6, 7, 7 Find the mean, median, and mode: Example 2
5.1 Mean, Median, & Mode definitions Mean: Median: Mode: Example 1 The Blue Jays score these amounts of runs in their last 9 games: 4, 7, 2, 4, 10, 5, 6, 7, 7 Find the mean, median, and mode: Example 2
Normal Probability Distributions
 C H A P T E R Normal Probability Distributions 5 Section 5.2 Example 3 (pg. 248) Normal Probabilities Assume triglyceride levels of the population of the United States are normally distributed with a mean
C H A P T E R Normal Probability Distributions 5 Section 5.2 Example 3 (pg. 248) Normal Probabilities Assume triglyceride levels of the population of the United States are normally distributed with a mean
MAKING SENSE OF DATA Essentials series
 MAKING SENSE OF DATA Essentials series THE NORMAL DISTRIBUTION Copyright by City of Bradford MDC Prerequisites Descriptive statistics Charts and graphs The normal distribution Surveys and sampling Correlation
MAKING SENSE OF DATA Essentials series THE NORMAL DISTRIBUTION Copyright by City of Bradford MDC Prerequisites Descriptive statistics Charts and graphs The normal distribution Surveys and sampling Correlation
The Binomial Distribution
 The Binomial Distribution January 31, 2019 Contents The Binomial Distribution The Normal Approximation to the Binomial The Binomial Hypothesis Test Computing Binomial Probabilities in R 30 Problems The
The Binomial Distribution January 31, 2019 Contents The Binomial Distribution The Normal Approximation to the Binomial The Binomial Hypothesis Test Computing Binomial Probabilities in R 30 Problems The
STAT Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model
 STAT 203 - Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model In Chapter 5, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are good
STAT 203 - Chapter 6 The Standard Deviation (SD) as a Ruler and The Normal Model In Chapter 5, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are good
Section Introduction to Normal Distributions
 Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Applications of Data Dispersions
 1 Applications of Data Dispersions Key Definitions Standard Deviation: The standard deviation shows how far away each value is from the mean on average. Z-Scores: The distance between the mean and a given
1 Applications of Data Dispersions Key Definitions Standard Deviation: The standard deviation shows how far away each value is from the mean on average. Z-Scores: The distance between the mean and a given
THE UNIVERSITY OF TEXAS AT AUSTIN Department of Information, Risk, and Operations Management
 THE UNIVERSITY OF TEXAS AT AUSTIN Department of Information, Risk, and Operations Management BA 386T Tom Shively PROBABILITY CONCEPTS AND NORMAL DISTRIBUTIONS The fundamental idea underlying any statistical
THE UNIVERSITY OF TEXAS AT AUSTIN Department of Information, Risk, and Operations Management BA 386T Tom Shively PROBABILITY CONCEPTS AND NORMAL DISTRIBUTIONS The fundamental idea underlying any statistical
Department of Quantitative Methods & Information Systems. Business Statistics. Chapter 6 Normal Probability Distribution QMIS 120. Dr.
 Department of Quantitative Methods & Information Systems Business Statistics Chapter 6 Normal Probability Distribution QMIS 120 Dr. Mohammad Zainal Chapter Goals After completing this chapter, you should
Department of Quantitative Methods & Information Systems Business Statistics Chapter 6 Normal Probability Distribution QMIS 120 Dr. Mohammad Zainal Chapter Goals After completing this chapter, you should
Every data set has an average and a standard deviation, given by the following formulas,
 Discrete Data Sets A data set is any collection of data. For example, the set of test scores on the class s first test would comprise a data set. If we collect a sample from the population we are interested
Discrete Data Sets A data set is any collection of data. For example, the set of test scores on the class s first test would comprise a data set. If we collect a sample from the population we are interested
NORMAL RANDOM VARIABLES (Normal or gaussian distribution)
 NORMAL RANDOM VARIABLES (Normal or gaussian distribution) Many variables, as pregnancy lengths, foot sizes etc.. exhibit a normal distribution. The shape of the distribution is a symmetric bell shape.
NORMAL RANDOM VARIABLES (Normal or gaussian distribution) Many variables, as pregnancy lengths, foot sizes etc.. exhibit a normal distribution. The shape of the distribution is a symmetric bell shape.
CS 237: Probability in Computing
 CS 237: Probability in Computing Wayne Snyder Computer Science Department Boston University Lecture 12: Continuous Distributions Uniform Distribution Normal Distribution (motivation) Discrete vs Continuous
CS 237: Probability in Computing Wayne Snyder Computer Science Department Boston University Lecture 12: Continuous Distributions Uniform Distribution Normal Distribution (motivation) Discrete vs Continuous
STAT Chapter 5: Continuous Distributions. Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s.
 STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
The graph of a normal curve is symmetric with respect to the line x = µ, and has points of
 Stat 400, section 4.3 Normal Random Variables notes prepared by Tim Pilachowski Another often-useful probability density function is the normal density function, which graphs as the familiar bell-shaped
Stat 400, section 4.3 Normal Random Variables notes prepared by Tim Pilachowski Another often-useful probability density function is the normal density function, which graphs as the familiar bell-shaped
What s Normal? Chapter 8. Hitting the Curve. In This Chapter
 Chapter 8 What s Normal? In This Chapter Meet the normal distribution Standard deviations and the normal distribution Excel s normal distribution-related functions A main job of statisticians is to estimate
Chapter 8 What s Normal? In This Chapter Meet the normal distribution Standard deviations and the normal distribution Excel s normal distribution-related functions A main job of statisticians is to estimate
No, because np = 100(0.02) = 2. The value of np must be greater than or equal to 5 to use the normal approximation.
 1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
Measures of Variation. Section 2-5. Dotplots of Waiting Times. Waiting Times of Bank Customers at Different Banks in minutes. Bank of Providence
 Measures of Variation Section -5 1 Waiting Times of Bank Customers at Different Banks in minutes Jefferson Valley Bank 6.5 6.6 6.7 6.8 7.1 7.3 7.4 Bank of Providence 4. 5.4 5.8 6. 6.7 8.5 9.3 10.0 Mean
Measures of Variation Section -5 1 Waiting Times of Bank Customers at Different Banks in minutes Jefferson Valley Bank 6.5 6.6 6.7 6.8 7.1 7.3 7.4 Bank of Providence 4. 5.4 5.8 6. 6.7 8.5 9.3 10.0 Mean
Module Tag PSY_P2_M 7. PAPER No.2: QUANTITATIVE METHODS MODULE No.7: NORMAL DISTRIBUTION
 Subject Paper No and Title Module No and Title Paper No.2: QUANTITATIVE METHODS Module No.7: NORMAL DISTRIBUTION Module Tag PSY_P2_M 7 TABLE OF CONTENTS 1. Learning Outcomes 2. Introduction 3. Properties
Subject Paper No and Title Module No and Title Paper No.2: QUANTITATIVE METHODS Module No.7: NORMAL DISTRIBUTION Module Tag PSY_P2_M 7 TABLE OF CONTENTS 1. Learning Outcomes 2. Introduction 3. Properties
Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc.
 Chapter 8 Measures of Center Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc. Data that can only be integer
Chapter 8 Measures of Center Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc. Data that can only be integer
The Standard Deviation as a Ruler and the Normal Model. Copyright 2009 Pearson Education, Inc.
 The Standard Deviation as a Ruler and the Normal Mol Copyright 2009 Pearson Education, Inc. The trick in comparing very different-looking values is to use standard viations as our rulers. The standard
The Standard Deviation as a Ruler and the Normal Mol Copyright 2009 Pearson Education, Inc. The trick in comparing very different-looking values is to use standard viations as our rulers. The standard
Introduction to Statistics I
 Introduction to Statistics I Keio University, Faculty of Economics Continuous random variables Simon Clinet (Keio University) Intro to Stats November 1, 2018 1 / 18 Definition (Continuous random variable)
Introduction to Statistics I Keio University, Faculty of Economics Continuous random variables Simon Clinet (Keio University) Intro to Stats November 1, 2018 1 / 18 Definition (Continuous random variable)
Standard Normal Calculations
 Standard Normal Calculations Section 4.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 10-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Standard Normal Calculations Section 4.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 10-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
The Binomial Distribution
 The Binomial Distribution January 31, 2018 Contents The Binomial Distribution The Normal Approximation to the Binomial The Binomial Hypothesis Test Computing Binomial Probabilities in R 30 Problems The
The Binomial Distribution January 31, 2018 Contents The Binomial Distribution The Normal Approximation to the Binomial The Binomial Hypothesis Test Computing Binomial Probabilities in R 30 Problems The
Numerical Descriptive Measures. Measures of Center: Mean and Median
 Steve Sawin Statistics Numerical Descriptive Measures Having seen the shape of a distribution by looking at the histogram, the two most obvious questions to ask about the specific distribution is where
Steve Sawin Statistics Numerical Descriptive Measures Having seen the shape of a distribution by looking at the histogram, the two most obvious questions to ask about the specific distribution is where
Collaborative Statistics Using Spreadsheets. Chapter 6
 Collaborative Statistics Using Spreadsheets This document is attributed to OpenStax-CNX Chapter 6 Open Assembly Edition Open Assembly editions of open textbooks are disaggregated versions designed to facilitate
Collaborative Statistics Using Spreadsheets This document is attributed to OpenStax-CNX Chapter 6 Open Assembly Edition Open Assembly editions of open textbooks are disaggregated versions designed to facilitate
The Assumption(s) of Normality
 The Assumption(s) of Normality Copyright 2000, 2011, 2016, J. Toby Mordkoff This is very complicated, so I ll provide two versions. At a minimum, you should know the short one. It would be great if you
The Assumption(s) of Normality Copyright 2000, 2011, 2016, J. Toby Mordkoff This is very complicated, so I ll provide two versions. At a minimum, you should know the short one. It would be great if you
Chapter 4 Continuous Random Variables and Probability Distributions
 Chapter 4 Continuous Random Variables and Probability Distributions Part 2: More on Continuous Random Variables Section 4.5 Continuous Uniform Distribution Section 4.6 Normal Distribution 1 / 27 Continuous
Chapter 4 Continuous Random Variables and Probability Distributions Part 2: More on Continuous Random Variables Section 4.5 Continuous Uniform Distribution Section 4.6 Normal Distribution 1 / 27 Continuous
Determining Sample Size. Slide 1 ˆ ˆ. p q n E = z α / 2. (solve for n by algebra) n = E 2
 Determining Sample Size Slide 1 E = z α / 2 ˆ ˆ p q n (solve for n by algebra) n = ( zα α / 2) 2 p ˆ qˆ E 2 Sample Size for Estimating Proportion p When an estimate of ˆp is known: Slide 2 n = ˆ ˆ ( )
Determining Sample Size Slide 1 E = z α / 2 ˆ ˆ p q n (solve for n by algebra) n = ( zα α / 2) 2 p ˆ qˆ E 2 Sample Size for Estimating Proportion p When an estimate of ˆp is known: Slide 2 n = ˆ ˆ ( )
Section 7.5 The Normal Distribution. Section 7.6 Application of the Normal Distribution
 Section 7.6 Application of the Normal Distribution A random variable that may take on infinitely many values is called a continuous random variable. A continuous probability distribution is defined by
Section 7.6 Application of the Normal Distribution A random variable that may take on infinitely many values is called a continuous random variable. A continuous probability distribution is defined by
Section 5 3 The Mean and Standard Deviation of a Binomial Distribution!
 Section 5 3 The Mean and Standard Deviation of a Binomial Distribution! Previous sections required that you to find the Mean and Standard Deviation of a Binomial Distribution by using the values from a
Section 5 3 The Mean and Standard Deviation of a Binomial Distribution! Previous sections required that you to find the Mean and Standard Deviation of a Binomial Distribution by using the values from a
Unit 2: Statistics Probability
 Applied Math 30 3-1: Distributions Probability Distribution: - a table or a graph that displays the theoretical probability for each outcome of an experiment. - P (any particular outcome) is between 0
Applied Math 30 3-1: Distributions Probability Distribution: - a table or a graph that displays the theoretical probability for each outcome of an experiment. - P (any particular outcome) is between 0
Set up a normal distribution curve, to help estimate the percent of the band that, on average, practices a greater number of hours than Alexis.
 Section 5.5 Z-Scores Example 1 Alexis plays in her school jazz band. Band members practice an average of 16.5 h per week, with a standard deviation of 4.2 h. Alexis practices an average of 22 h per week.
Section 5.5 Z-Scores Example 1 Alexis plays in her school jazz band. Band members practice an average of 16.5 h per week, with a standard deviation of 4.2 h. Alexis practices an average of 22 h per week.
11.5: Normal Distributions
 11.5: Normal Distributions 11.5.1 Up to now, we ve dealt with discrete random variables, variables that take on only a finite (or countably infinite we didn t do these) number of values. A continuous random
11.5: Normal Distributions 11.5.1 Up to now, we ve dealt with discrete random variables, variables that take on only a finite (or countably infinite we didn t do these) number of values. A continuous random
5-1 pg ,4,5, EOO,39,47,50,53, pg ,5,9,13,17,19,21,22,25,30,31,32, pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38
 5-1 pg. 242 3,4,5, 17-37 EOO,39,47,50,53,56 5-2 pg. 249 9,10,13,14,17,18 5-3 pg. 257 1,5,9,13,17,19,21,22,25,30,31,32,34 5-4 pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38 5-5 pg. 281 5-14,16,19,21,22,25,26,30
5-1 pg. 242 3,4,5, 17-37 EOO,39,47,50,53,56 5-2 pg. 249 9,10,13,14,17,18 5-3 pg. 257 1,5,9,13,17,19,21,22,25,30,31,32,34 5-4 pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38 5-5 pg. 281 5-14,16,19,21,22,25,26,30
BIOL The Normal Distribution and the Central Limit Theorem
 BIOL 300 - The Normal Distribution and the Central Limit Theorem In the first week of the course, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are
BIOL 300 - The Normal Distribution and the Central Limit Theorem In the first week of the course, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are
MAS1403. Quantitative Methods for Business Management. Semester 1, Module leader: Dr. David Walshaw
 MAS1403 Quantitative Methods for Business Management Semester 1, 2018 2019 Module leader: Dr. David Walshaw Additional lecturers: Dr. James Waldren and Dr. Stuart Hall Announcements: Written assignment
MAS1403 Quantitative Methods for Business Management Semester 1, 2018 2019 Module leader: Dr. David Walshaw Additional lecturers: Dr. James Waldren and Dr. Stuart Hall Announcements: Written assignment
Linear Modeling Business 5 Supply and Demand
 Linear Modeling Business 5 Supply and Demand Supply and demand is a fundamental concept in business. Demand looks at the Quantity (Q) of a product that will be sold with respect to the Price (P) the product
Linear Modeling Business 5 Supply and Demand Supply and demand is a fundamental concept in business. Demand looks at the Quantity (Q) of a product that will be sold with respect to the Price (P) the product
Review. What is the probability of throwing two 6s in a row with a fair die? a) b) c) d) 0.333
 Review In most card games cards are dealt without replacement. What is the probability of being dealt an ace and then a 3? Choose the closest answer. a) 0.0045 b) 0.0059 c) 0.0060 d) 0.1553 Review What
Review In most card games cards are dealt without replacement. What is the probability of being dealt an ace and then a 3? Choose the closest answer. a) 0.0045 b) 0.0059 c) 0.0060 d) 0.1553 Review What
7. For the table that follows, answer the following questions: x y 1-1/4 2-1/2 3-3/4 4
 7. For the table that follows, answer the following questions: x y 1-1/4 2-1/2 3-3/4 4 - Would the correlation between x and y in the table above be positive or negative? The correlation is negative. -
7. For the table that follows, answer the following questions: x y 1-1/4 2-1/2 3-3/4 4 - Would the correlation between x and y in the table above be positive or negative? The correlation is negative. -
Chapter 5 Normal Probability Distributions
 Chapter 5 Normal Probability Distributions Section 5-1 Introduction to Normal Distributions and the Standard Normal Distribution A The normal distribution is the most important of the continuous probability
Chapter 5 Normal Probability Distributions Section 5-1 Introduction to Normal Distributions and the Standard Normal Distribution A The normal distribution is the most important of the continuous probability
Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at
 Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. Let X represent the savings of a resident; X ~ N(3000,
Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. Let X represent the savings of a resident; X ~ N(3000,
Quantitative Methods for Economics, Finance and Management (A86050 F86050)
 Quantitative Methods for Economics, Finance and Management (A86050 F86050) Matteo Manera matteo.manera@unimib.it Marzio Galeotti marzio.galeotti@unimi.it 1 This material is taken and adapted from Guy Judge
Quantitative Methods for Economics, Finance and Management (A86050 F86050) Matteo Manera matteo.manera@unimib.it Marzio Galeotti marzio.galeotti@unimi.it 1 This material is taken and adapted from Guy Judge
Chapter 7 Study Guide: The Central Limit Theorem
 Chapter 7 Study Guide: The Central Limit Theorem Introduction Why are we so concerned with means? Two reasons are that they give us a middle ground for comparison and they are easy to calculate. In this
Chapter 7 Study Guide: The Central Limit Theorem Introduction Why are we so concerned with means? Two reasons are that they give us a middle ground for comparison and they are easy to calculate. In this
2 DESCRIPTIVE STATISTICS
 Chapter 2 Descriptive Statistics 47 2 DESCRIPTIVE STATISTICS Figure 2.1 When you have large amounts of data, you will need to organize it in a way that makes sense. These ballots from an election are rolled
Chapter 2 Descriptive Statistics 47 2 DESCRIPTIVE STATISTICS Figure 2.1 When you have large amounts of data, you will need to organize it in a way that makes sense. These ballots from an election are rolled
In a moment, we will look at a simple example involving the function f(x) = 100 x
 Rates of Change Calculus is the study of the way that functions change. There are two types of rates of change: 1. Average rate of change. Instantaneous rate of change In a moment, we will look at a simple
Rates of Change Calculus is the study of the way that functions change. There are two types of rates of change: 1. Average rate of change. Instantaneous rate of change In a moment, we will look at a simple
Probability. An intro for calculus students P= Figure 1: A normal integral
 Probability An intro for calculus students.8.6.4.2 P=.87 2 3 4 Figure : A normal integral Suppose we flip a coin 2 times; what is the probability that we get more than 2 heads? Suppose we roll a six-sided
Probability An intro for calculus students.8.6.4.2 P=.87 2 3 4 Figure : A normal integral Suppose we flip a coin 2 times; what is the probability that we get more than 2 heads? Suppose we roll a six-sided
Lecture 8. The Binomial Distribution. Binomial Distribution. Binomial Distribution. Probability Distributions: Normal and Binomial
 Lecture 8 The Binomial Distribution Probability Distributions: Normal and Binomial 1 2 Binomial Distribution >A binomial experiment possesses the following properties. The experiment consists of a fixed
Lecture 8 The Binomial Distribution Probability Distributions: Normal and Binomial 1 2 Binomial Distribution >A binomial experiment possesses the following properties. The experiment consists of a fixed
Data Analysis and Statistical Methods Statistics 651
 Data Analysis and Statistical Methods Statistics 651 http://www.stat.tamu.edu/~suhasini/teaching.html Suhasini Subba Rao The binomial: mean and variance Recall that the number of successes out of n, denoted
Data Analysis and Statistical Methods Statistics 651 http://www.stat.tamu.edu/~suhasini/teaching.html Suhasini Subba Rao The binomial: mean and variance Recall that the number of successes out of n, denoted
3.1 Measures of Central Tendency
 3.1 Measures of Central Tendency n Summation Notation x i or x Sum observation on the variable that appears to the right of the summation symbol. Example 1 Suppose the variable x i is used to represent
3.1 Measures of Central Tendency n Summation Notation x i or x Sum observation on the variable that appears to the right of the summation symbol. Example 1 Suppose the variable x i is used to represent
Elementary Statistics
 Chapter 7 Estimation Goal: To become familiar with how to use Excel 2010 for Estimation of Means. There is one Stat Tool in Excel that is used with estimation of means, T.INV.2T. Open Excel and click on
Chapter 7 Estimation Goal: To become familiar with how to use Excel 2010 for Estimation of Means. There is one Stat Tool in Excel that is used with estimation of means, T.INV.2T. Open Excel and click on
Density curves. (James Madison University) February 4, / 20
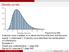 Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Prob and Stats, Nov 7
 Prob and Stats, Nov 7 The Standard Normal Distribution Book Sections: 7.1, 7.2 Essential Questions: What is the standard normal distribution, how is it related to all other normal distributions, and how
Prob and Stats, Nov 7 The Standard Normal Distribution Book Sections: 7.1, 7.2 Essential Questions: What is the standard normal distribution, how is it related to all other normal distributions, and how
Chapter Seven: Confidence Intervals and Sample Size
 Chapter Seven: Confidence Intervals and Sample Size A point estimate is: The best point estimate of the population mean µ is the sample mean X. Three Properties of a Good Estimator 1. Unbiased 2. Consistent
Chapter Seven: Confidence Intervals and Sample Size A point estimate is: The best point estimate of the population mean µ is the sample mean X. Three Properties of a Good Estimator 1. Unbiased 2. Consistent
A Derivation of the Normal Distribution. Robert S. Wilson PhD.
 A Derivation of the Normal Distribution Robert S. Wilson PhD. Data are said to be normally distributed if their frequency histogram is apporximated by a bell shaped curve. In practice, one can tell by
A Derivation of the Normal Distribution Robert S. Wilson PhD. Data are said to be normally distributed if their frequency histogram is apporximated by a bell shaped curve. In practice, one can tell by
3 3 Measures of Central Tendency and Dispersion from grouped data.notebook October 23, 2017
 Warm Up a. Determine the sample standard deviation weight. Express your answer rounded to three decimal places. b. Use the Empirical Rule to determine the percentage of M&Ms with weights between 0.803
Warm Up a. Determine the sample standard deviation weight. Express your answer rounded to three decimal places. b. Use the Empirical Rule to determine the percentage of M&Ms with weights between 0.803
Descriptive Statistics (Devore Chapter One)
 Descriptive Statistics (Devore Chapter One) 1016-345-01 Probability and Statistics for Engineers Winter 2010-2011 Contents 0 Perspective 1 1 Pictorial and Tabular Descriptions of Data 2 1.1 Stem-and-Leaf
Descriptive Statistics (Devore Chapter One) 1016-345-01 Probability and Statistics for Engineers Winter 2010-2011 Contents 0 Perspective 1 1 Pictorial and Tabular Descriptions of Data 2 1.1 Stem-and-Leaf
1 Describing Distributions with numbers
 1 Describing Distributions with numbers Only for quantitative variables!! 1.1 Describing the center of a data set The mean of a set of numerical observation is the familiar arithmetic average. To write
1 Describing Distributions with numbers Only for quantitative variables!! 1.1 Describing the center of a data set The mean of a set of numerical observation is the familiar arithmetic average. To write
Normal Model (Part 1)
 Normal Model (Part 1) Formulas New Vocabulary The Standard Deviation as a Ruler The trick in comparing very different-looking values is to use standard deviations as our rulers. The standard deviation
Normal Model (Part 1) Formulas New Vocabulary The Standard Deviation as a Ruler The trick in comparing very different-looking values is to use standard deviations as our rulers. The standard deviation
Math 227 Elementary Statistics. Bluman 5 th edition
 Math 227 Elementary Statistics Bluman 5 th edition CHAPTER 6 The Normal Distribution 2 Objectives Identify distributions as symmetrical or skewed. Identify the properties of the normal distribution. Find
Math 227 Elementary Statistics Bluman 5 th edition CHAPTER 6 The Normal Distribution 2 Objectives Identify distributions as symmetrical or skewed. Identify the properties of the normal distribution. Find
Lecture 9. Probability Distributions. Outline. Outline
 Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Confidence Intervals. σ unknown, small samples The t-statistic /22
 Confidence Intervals σ unknown, small samples The t-statistic 1 /22 Homework Read Sec 7-3. Discussion Question pg 365 Do Ex 7-3 1-4, 6, 9, 12, 14, 15, 17 2/22 Objective find the confidence interval for
Confidence Intervals σ unknown, small samples The t-statistic 1 /22 Homework Read Sec 7-3. Discussion Question pg 365 Do Ex 7-3 1-4, 6, 9, 12, 14, 15, 17 2/22 Objective find the confidence interval for
We use probability distributions to represent the distribution of a discrete random variable.
 Now we focus on discrete random variables. We will look at these in general, including calculating the mean and standard deviation. Then we will look more in depth at binomial random variables which are
Now we focus on discrete random variables. We will look at these in general, including calculating the mean and standard deviation. Then we will look more in depth at binomial random variables which are
Statistics 431 Spring 2007 P. Shaman. Preliminaries
 Statistics 4 Spring 007 P. Shaman The Binomial Distribution Preliminaries A binomial experiment is defined by the following conditions: A sequence of n trials is conducted, with each trial having two possible
Statistics 4 Spring 007 P. Shaman The Binomial Distribution Preliminaries A binomial experiment is defined by the following conditions: A sequence of n trials is conducted, with each trial having two possible
Categorical. A general name for non-numerical data; the data is separated into categories of some kind.
 Chapter 5 Categorical A general name for non-numerical data; the data is separated into categories of some kind. Nominal data Categorical data with no implied order. Eg. Eye colours, favourite TV show,
Chapter 5 Categorical A general name for non-numerical data; the data is separated into categories of some kind. Nominal data Categorical data with no implied order. Eg. Eye colours, favourite TV show,
Lecture 9. Probability Distributions
 Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
The Normal Model The famous bell curve
 Math 243 Sections 6.1-6.2 The Normal Model Here are some roughly symmetric, unimodal histograms The Normal Model The famous bell curve Example 1. Let s say the mean annual rainfall in Portland is 40 inches
Math 243 Sections 6.1-6.2 The Normal Model Here are some roughly symmetric, unimodal histograms The Normal Model The famous bell curve Example 1. Let s say the mean annual rainfall in Portland is 40 inches
Solutions for practice questions: Chapter 9, Statistics
 Solutions for practice questions: Chapter 9, Statistics If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. We know that µ is the mean of 30 values of y, 30 30 i= 1 2 ( y i
Solutions for practice questions: Chapter 9, Statistics If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. We know that µ is the mean of 30 values of y, 30 30 i= 1 2 ( y i
UNIT 4 NORMAL DISTRIBUTION: DEFINITION, CHARACTERISTICS AND PROPERTIES
 f UNIT 4 NORMAL DISTRIBUTION: DEFINITION, CHARACTERISTICS AND PROPERTIES Normal Distribution: Definition, Characteristics and Properties Structure 4.1 Introduction 4.2 Objectives 4.3 Definitions of Probability
f UNIT 4 NORMAL DISTRIBUTION: DEFINITION, CHARACTERISTICS AND PROPERTIES Normal Distribution: Definition, Characteristics and Properties Structure 4.1 Introduction 4.2 Objectives 4.3 Definitions of Probability
Continuous Probability Distributions
 Continuous Probability Distributions Chapter 7 Learning Objectives List the characteristics of the uniform distribution. Compute probabilities using the uniform distribution List the characteristics of
Continuous Probability Distributions Chapter 7 Learning Objectives List the characteristics of the uniform distribution. Compute probabilities using the uniform distribution List the characteristics of
But suppose we want to find a particular value for y, at which the probability is, say, 0.90? In other words, we want to figure out the following:
 More on distributions, and some miscellaneous topics 1. Reverse lookup and the normal distribution. Up until now, we wanted to find probabilities. For example, the probability a Swedish man has a brain
More on distributions, and some miscellaneous topics 1. Reverse lookup and the normal distribution. Up until now, we wanted to find probabilities. For example, the probability a Swedish man has a brain
Statistical Intervals (One sample) (Chs )
 7 Statistical Intervals (One sample) (Chs 8.1-8.3) Confidence Intervals The CLT tells us that as the sample size n increases, the sample mean X is close to normally distributed with expected value µ and
7 Statistical Intervals (One sample) (Chs 8.1-8.3) Confidence Intervals The CLT tells us that as the sample size n increases, the sample mean X is close to normally distributed with expected value µ and
In a binomial experiment of n trials, where p = probability of success and q = probability of failure. mean variance standard deviation
 Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
