AMS 7 Sampling Distributions, Central limit theorem, Confidence Intervals Lecture 4
|
|
|
- Nelson Tate
- 5 years ago
- Views:
Transcription
1 AMS 7 Sampling Distributions, Central limit theorem, Confidence Intervals Lecture 4 Department of Applied Mathematics and Statistics, University of California, Santa Cruz Summer / 26 Sampling Distributions!!!!!! If we sample cookies, what is the distribution of the # of chips in a cookie? Poisson This is the sampling distribution of the # of chips. What if we think about the average # of chips per cookie in a bag? Is this average the same for all bags? No, it is random, and its distribution is derived from the sampling distribution of an individual cookie. This is the sampling distribution of the mean 2 / 26
2 x 1 x 2 x 3 x M where x s are the mean number of chocolate chips in a cookie PER box, and M is the total number of boxes (number of trials. We are interested in what the distribution of the sample means looks like. X? 3 / 26 Formal definitions: The sampling distribution of the mean is the probability distribution of the sample means, x, with all samples having the same sample size n. The sampling distribution of the proportion is the probability distribution of the sample proportions, ˆp, with all samples having the same sample size n. 4 / 26
3 The Central Limit Theorem tells us that the sampling distribution of the mean will be approximately normal no matter what the distribution of the individual observations is. Formally... Central Limit Theorem If samples of size n are drawn from a population with mean µ and standard deviation σ, then the sampling distribution of the samples means, x, will be approximately normally distributed with mean µ x = µ and sd σ x = σ n. X? with mean µ and sd σ X N (µ x = µ, σ x = n σ where σ x is called the (population standard error (of the mean. 5 / 26 NOTE: If the population of individuals is normally distributed, then x is exactly normally distributed. Otherwise x is approximately normally distributed, with the approximation getting better as n increases. In general, n 30 is good. E.g. The population of the # of chocolate chips in a cookie follows a Poisson distribution, so the distribution of the mean # of chocolate chips in a box will be approximately normally distributed. E.g. The population of the length of sharks follows a normal distribution, so the distribution of the mean length of sharks is exactly normally distributed. Also note that as n, σ x 0. 6 / 26
4 Example: The weight of a cookie is normally distributed with mean µ = 11 grams and sd σ = 0.5 grams. What is the distribution of the mean weight of cookies in a sample of size 32? X N(11, ( 0.5 X N µ x = µ = 11, σ x = σ n = = So What is the probability that the average weight of a cookie in a bag of 32 will be at least 10.8? 7 / 26 P( X > 10.8 = P ( X µ x σ x > 10.8 µ x σ x = P ( Z > = P(Z > 2.27 = 1 P(Z < 2.27 = = whereas the probability of selecting a SINGLE cookie from the population with weight at least 10.8 would be... P(X > 10.8 = P ( X µ σ > 10.8 µ σ = P ( Z > = P(Z > 0.4 = 1 P(Z < 0.4 = = / 26
5 Now, suppose the manufacturer wants to label their packages so that 99% of the bags will have an average cookie weight at least that large. What mean cookie weight should they specify? P(Z < z = 0.01 z = 2.33 P(Zσ x + µ x < 2.33σ x + µ x = P( X < 2.33( = P( X < Therefore, 99% of the bags will have an average cookie weight at least whereas for the population of individual cookie weights, we can work out to see that 99% of the cookies will have a cookie weight of at least / 26. What if the manufacturer wants to claim that 95% of the bags will have an average weight in some interval? How do we find this interval? (assume symmetry We need to find z such that P( z < Z < z = 0.95 P(Z < z = = P(Z < 1.96 = (from z-table so, P( 1.96 < Z < 1.96 = 0.95 P( 1.96σ x + µ x < Zσ x + µ x < 1.96σ x + µ x = P( 1.96( < X < 1.96( = P(10.83 < X < = 0.95 So, 95% of the bags will have an average cookie weight between 10.83g and 11.17g. 10 / 26
6 (Some more Central Limit Theorem Examples Example: IQ scores are normally distributed with a mean of 100 points and a sd of 15 points. µ = 100 and σ = Find the probability that a randomly selected person will have a score below 97. P(X < 97 = P ( X < = P(Z < 0.2 = If a random sample of 100 people is taken, find the probability that the mean score of the sample is below 97. By the CLT X N(µ x = 100, σ x = : P( X < 97 = P ( X / 100 < / 100 = P(Z < 2 = / 26 Example: Suppose a batch of pepper seeds has a mean time to germination of 10.4 days with a sd of 2.13 days. What is the probability that a random sample of 49 seeds will have a mean germination time between 10 and 11 days? We need to find P(10 < X < P(10 < X ( < 11 = P / < X / < / 49 = P( 1.31 < Z < 1.97 = P(Z < 1.97 P(Z < 1.31 = = / 26
7 Normal Approximation to the Binomial Recall the Binomial distribution... Binomial Probability Distribution: If the following are met 1. Fixed number of trials, n 2. Trials are independent 3. Each trial has only two possible outcomes ( success, failure 4. The probability of success, p, is the same for each trial where the mean is given by µ = np and the sd is given by σ = np(1 p. 13 / 26 Although the binomial is a discrete distribution, and the normal is a continuous distribution, the normal distribution is a good approximation to the binomial distribution provided that, np 5 and n(1 p 5, i.e. there are (on average at least 5 successes and 5 failures Sort of like averaging over coin flips, so CLT applies. We approximate a binomial distribution with n and p, Bin(n, p, with a normal distribution having mean µ = np and sd σ = np(1 p: Bin(n, p N(µ = np, σ = np(1 p Note that because the binomial is discrete, but the normal is continuous, we typically use a continuity correction, moving the count by 1/2 such that the inequality still holds. 14 / 26
8 Example: A study found that 62% of the households in Alaska have a computer. If we take a random sample of 1000 Alaskan households, what is the probability that at least 640 have a computer? Basic idea: X = # households in the sample with a computer. X Bin(n = 1000, p = 0.62 µ = 1000(0.62 = 620, σ = 1000(0.62(0.38 = So, X N(µ = 620, σ = Detail: X is discrete, so you could never get X = or X = Continuity Correction: P(X 640 = P(X > P ( X > = P(Z > 1.27 = 1 P(Z < 1.27 = = / 26 How about a range? What is the probability of the number of households in the sample having a computer being between 615 and 625 non inclusive? P (615 < X < 625 = P (615.5 < X < = P ( < X < = P(Z < 0.29 P(Z < 0.29 = = / 26
9 Recall the example of finding an interval such that the mean cookie weight of the cookies in a randomly chosen bag of cookies has probability 0.95 of being in that interval. We want to find x 1 and x 2 such that P(x 1 < X < x 2 = Instead we can find z such that P( z < Z < z = / 26 From z-table we get P( 1.96 < Z < 1.96 = We use µ x and σ x to convert this interval into one in terms of mean weight of the cookies in a bag of 32 cookies. Z = X µ x σ x X = Zσ x + µ x P( 1.96σ x + µ x < Zσ x + µ x < 1.96σ x + µ x = P( 1.96( < X < 1.96( = P(10.83 < X < = / 26
10 What if we don t know the true population mean of a cookie, and want to learn it from the data (measurements of the sample? Inference: Our best guess (point estimate of the population mean µ is the sample mean x. How good do we think this guess is? It depends on the data: How much data? How were they collected? How much variability in the data? Example: Assume we know that the standard deviation of the weight of a cookie is 0.5g, but we don t know the mean weight of a cookie. We get a bag (sample of 32 cookies and find the average weight is 10.9g. How confident are we in this estimate? What would be an interval of plausible values? 19 / 26 Assuming cookie weights are approximately normally distributed (or using the CLT for the mean with n 30, that σ = 0.5 is known and that we have a simple random sample, starting with a standard normal, before we observe X we know P( 1.96 Z 1.96 = 0.95 ( x µ x P( 1.96 Z 1.96 = P ( σ x = P 1.96 x µ σ/ n 1.96 = P ( 1.96 n σ x µ 1.96 n σ = P (1.96 n σ µ x 1.96 n σ = P ( 1.96 n σ µ x 1.96 n σ = P ( x 1.96 n σ µ x n σ = 0.95 So, the random interval ( x 1.96 σ n, x σ n probability of containing the true population mean, µ!! has a 95% 95% of the intervals constructed this way will contain the true population mean µ! 20 / 26
11 An axiom (assumption of Frequentist Statistics is that unknown parameters have a fixed, right answer. So once we observe x, the interval is fixed, and the value of µ is fixed. So µ is either in the interval, or it isn t, but we don t know which. The interval we get when we use the observed x is a called a confidence interval. Example: For a sample bag of 32 cookies we have: x = 10.9g and σ = 0.5g. Find the 95% CI for the mean weight of all cookies. x 1.96 σ n = = x σ n = = So (10.73, is a 95% CI for µ. Technical Interpretation: We are 95% confident that µ is in this interval. 21 / 26 On average 95% of the intervals constructed this way will contain µ, but we don t know if this particular interval does contain it or not. Note that this is not a probability. The probability that µ is in this particular interval is 0 or 1, but we don t know which. CI is an interval estimate for µ. It provides a range of plausible values for µ. 22 / 26
12 More general form: (1 αci is x ± E, where E = z α/2 σ n = margin of error. z α/2 is the α 2 quantile of the standard normal distribution, i.e. P(Z z α/2 = α / 26 Example: Suppose a soda distributor is filling 20oz bottles and that from historical data, the sd of the contents of a bottle is known to be 0.03oz. Is the right amount of soda going into each bottle? Suppose a random sample of 34 bottles is found to have an average of 19.98oz. Find a 90% CI for the population mean contents. 1 α = 0.9 α = 0.1 α 2 = 0.05 = P(Z < (z-table So, z α/2 = and E = z α/2 σ n = = x ± E = ± = ( , So ( , is 90% CI for µ. Is it reasonable that 20oz are going to each bottle? 24 / 26
13 How do we determine the sample size needed for a desired margin of error?... example continued: Suppose we want to be able to estimate soda contents with a margin of error of = E = z α/2 σ n = n n = = n = ( = We need to round up, so that the margin of error is no larger than specified, so n = In general, n = ( zα/2 σ E 2 Note: the sample size increases rapidly as the margin of error reduces. 25 / 26 Key Concepts!!!!! Sampling Distribution of the mean Sampling Distribution of the proportion Central Limit Theorem Normal Approximation to the Binomial Confidence Interval 26 / 26
. 13. The maximum error (margin of error) of the estimate for μ (based on known σ) is:
 Statistics Sample Exam 3 Solution Chapters 6 & 7: Normal Probability Distributions & Estimates 1. What percent of normally distributed data value lie within 2 standard deviations to either side of the
Statistics Sample Exam 3 Solution Chapters 6 & 7: Normal Probability Distributions & Estimates 1. What percent of normally distributed data value lie within 2 standard deviations to either side of the
Elementary Statistics Lecture 5
 Elementary Statistics Lecture 5 Sampling Distributions Chong Ma Department of Statistics University of South Carolina Chong Ma (Statistics, USC) STAT 201 Elementary Statistics 1 / 24 Outline 1 Introduction
Elementary Statistics Lecture 5 Sampling Distributions Chong Ma Department of Statistics University of South Carolina Chong Ma (Statistics, USC) STAT 201 Elementary Statistics 1 / 24 Outline 1 Introduction
ECO220Y Continuous Probability Distributions: Normal Readings: Chapter 9, section 9.10
 ECO220Y Continuous Probability Distributions: Normal Readings: Chapter 9, section 9.10 Fall 2011 Lecture 8 Part 2 (Fall 2011) Probability Distributions Lecture 8 Part 2 1 / 23 Normal Density Function f
ECO220Y Continuous Probability Distributions: Normal Readings: Chapter 9, section 9.10 Fall 2011 Lecture 8 Part 2 (Fall 2011) Probability Distributions Lecture 8 Part 2 1 / 23 Normal Density Function f
Class 12. Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science. Marquette University MATH 1700
 Class 12 Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science Copyright 2017 by D.B. Rowe 1 Agenda: Recap Chapter 6.1-6.2 Lecture Chapter 6.3-6.5 Problem Solving Session. 2
Class 12 Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science Copyright 2017 by D.B. Rowe 1 Agenda: Recap Chapter 6.1-6.2 Lecture Chapter 6.3-6.5 Problem Solving Session. 2
Confidence Intervals Introduction
 Confidence Intervals Introduction A point estimate provides no information about the precision and reliability of estimation. For example, the sample mean X is a point estimate of the population mean μ
Confidence Intervals Introduction A point estimate provides no information about the precision and reliability of estimation. For example, the sample mean X is a point estimate of the population mean μ
Normal distribution. We say that a random variable X follows the normal distribution if the probability density function of X is given by
 Normal distribution The normal distribution is the most important distribution. It describes well the distribution of random variables that arise in practice, such as the heights or weights of people,
Normal distribution The normal distribution is the most important distribution. It describes well the distribution of random variables that arise in practice, such as the heights or weights of people,
Chapter 5. Sampling Distributions
 Lecture notes, Lang Wu, UBC 1 Chapter 5. Sampling Distributions 5.1. Introduction In statistical inference, we attempt to estimate an unknown population characteristic, such as the population mean, µ,
Lecture notes, Lang Wu, UBC 1 Chapter 5. Sampling Distributions 5.1. Introduction In statistical inference, we attempt to estimate an unknown population characteristic, such as the population mean, µ,
Probability Theory and Simulation Methods. April 9th, Lecture 20: Special distributions
 April 9th, 2018 Lecture 20: Special distributions Week 1 Chapter 1: Axioms of probability Week 2 Chapter 3: Conditional probability and independence Week 4 Chapters 4, 6: Random variables Week 9 Chapter
April 9th, 2018 Lecture 20: Special distributions Week 1 Chapter 1: Axioms of probability Week 2 Chapter 3: Conditional probability and independence Week 4 Chapters 4, 6: Random variables Week 9 Chapter
Chapter 9: Sampling Distributions
 Chapter 9: Sampling Distributions 9. Introduction This chapter connects the material in Chapters 4 through 8 (numerical descriptive statistics, sampling, and probability distributions, in particular) with
Chapter 9: Sampling Distributions 9. Introduction This chapter connects the material in Chapters 4 through 8 (numerical descriptive statistics, sampling, and probability distributions, in particular) with
STAT Chapter 7: Central Limit Theorem
 STAT 251 - Chapter 7: Central Limit Theorem In this chapter we will introduce the most important theorem in statistics; the central limit theorem. What have we seen so far? First, we saw that for an i.i.d
STAT 251 - Chapter 7: Central Limit Theorem In this chapter we will introduce the most important theorem in statistics; the central limit theorem. What have we seen so far? First, we saw that for an i.i.d
Chapter 9. Sampling Distributions. A sampling distribution is created by, as the name suggests, sampling.
 Chapter 9 Sampling Distributions 9.1 Sampling Distributions A sampling distribution is created by, as the name suggests, sampling. The method we will employ on the rules of probability and the laws of
Chapter 9 Sampling Distributions 9.1 Sampling Distributions A sampling distribution is created by, as the name suggests, sampling. The method we will employ on the rules of probability and the laws of
Class 16. Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science. Marquette University MATH 1700
 Class 16 Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science Copyright 013 by D.B. Rowe 1 Agenda: Recap Chapter 7. - 7.3 Lecture Chapter 8.1-8. Review Chapter 6. Problem Solving
Class 16 Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science Copyright 013 by D.B. Rowe 1 Agenda: Recap Chapter 7. - 7.3 Lecture Chapter 8.1-8. Review Chapter 6. Problem Solving
SAMPLING DISTRIBUTIONS. Chapter 7
 SAMPLING DISTRIBUTIONS Chapter 7 7.1 How Likely Are the Possible Values of a Statistic? The Sampling Distribution Statistic and Parameter Statistic numerical summary of sample data: p-hat or xbar Parameter
SAMPLING DISTRIBUTIONS Chapter 7 7.1 How Likely Are the Possible Values of a Statistic? The Sampling Distribution Statistic and Parameter Statistic numerical summary of sample data: p-hat or xbar Parameter
2011 Pearson Education, Inc
 Statistics for Business and Economics Chapter 4 Random Variables & Probability Distributions Content 1. Two Types of Random Variables 2. Probability Distributions for Discrete Random Variables 3. The Binomial
Statistics for Business and Economics Chapter 4 Random Variables & Probability Distributions Content 1. Two Types of Random Variables 2. Probability Distributions for Discrete Random Variables 3. The Binomial
Distribution of the Sample Mean
 Distribution of the Sample Mean MATH 130, Elements of Statistics I J. Robert Buchanan Department of Mathematics Fall 2018 Experiment (1 of 3) Suppose we have the following population : 4 8 1 2 3 4 9 1
Distribution of the Sample Mean MATH 130, Elements of Statistics I J. Robert Buchanan Department of Mathematics Fall 2018 Experiment (1 of 3) Suppose we have the following population : 4 8 1 2 3 4 9 1
Activity #17b: Central Limit Theorem #2. 1) Explain the Central Limit Theorem in your own words.
 Activity #17b: Central Limit Theorem #2 1) Explain the Central Limit Theorem in your own words. Importance of the CLT: You can standardize and use normal distribution tables to calculate probabilities
Activity #17b: Central Limit Theorem #2 1) Explain the Central Limit Theorem in your own words. Importance of the CLT: You can standardize and use normal distribution tables to calculate probabilities
University of California, Los Angeles Department of Statistics. Normal distribution
 University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Normal distribution The normal distribution is the most important distribution. It describes
University of California, Los Angeles Department of Statistics Statistics 110A Instructor: Nicolas Christou Normal distribution The normal distribution is the most important distribution. It describes
ECON 214 Elements of Statistics for Economists 2016/2017
 ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
Statistics Class 15 3/21/2012
 Statistics Class 15 3/21/2012 Quiz 1. Cans of regular Pepsi are labeled to indicate that they contain 12 oz. Data Set 17 in Appendix B lists measured amounts for a sample of Pepsi cans. The same statistics
Statistics Class 15 3/21/2012 Quiz 1. Cans of regular Pepsi are labeled to indicate that they contain 12 oz. Data Set 17 in Appendix B lists measured amounts for a sample of Pepsi cans. The same statistics
A random variable (r. v.) is a variable whose value is a numerical outcome of a random phenomenon.
 Chapter 14: random variables p394 A random variable (r. v.) is a variable whose value is a numerical outcome of a random phenomenon. Consider the experiment of tossing a coin. Define a random variable
Chapter 14: random variables p394 A random variable (r. v.) is a variable whose value is a numerical outcome of a random phenomenon. Consider the experiment of tossing a coin. Define a random variable
Statistics 13 Elementary Statistics
 Statistics 13 Elementary Statistics Summer Session I 2012 Lecture Notes 5: Estimation with Confidence intervals 1 Our goal is to estimate the value of an unknown population parameter, such as a population
Statistics 13 Elementary Statistics Summer Session I 2012 Lecture Notes 5: Estimation with Confidence intervals 1 Our goal is to estimate the value of an unknown population parameter, such as a population
The Central Limit Theorem. Sec. 8.2: The Random Variable. it s Distribution. it s Distribution
 The Central Limit Theorem Sec. 8.1: The Random Variable it s Distribution Sec. 8.2: The Random Variable it s Distribution X p and and How Should You Think of a Random Variable? Imagine a bag with numbers
The Central Limit Theorem Sec. 8.1: The Random Variable it s Distribution Sec. 8.2: The Random Variable it s Distribution X p and and How Should You Think of a Random Variable? Imagine a bag with numbers
Midterm Exam III Review
 Midterm Exam III Review Dr. Joseph Brennan Math 148, BU Dr. Joseph Brennan (Math 148, BU) Midterm Exam III Review 1 / 25 Permutations and Combinations ORDER In order to count the number of possible ways
Midterm Exam III Review Dr. Joseph Brennan Math 148, BU Dr. Joseph Brennan (Math 148, BU) Midterm Exam III Review 1 / 25 Permutations and Combinations ORDER In order to count the number of possible ways
5.3 Interval Estimation
 5.3 Interval Estimation Ulrich Hoensch Wednesday, March 13, 2013 Confidence Intervals Definition Let θ be an (unknown) population parameter. A confidence interval with confidence level C is an interval
5.3 Interval Estimation Ulrich Hoensch Wednesday, March 13, 2013 Confidence Intervals Definition Let θ be an (unknown) population parameter. A confidence interval with confidence level C is an interval
STAT 241/251 - Chapter 7: Central Limit Theorem
 STAT 241/251 - Chapter 7: Central Limit Theorem In this chapter we will introduce the most important theorem in statistics; the central limit theorem. What have we seen so far? First, we saw that for an
STAT 241/251 - Chapter 7: Central Limit Theorem In this chapter we will introduce the most important theorem in statistics; the central limit theorem. What have we seen so far? First, we saw that for an
STA 320 Fall Thursday, Dec 5. Sampling Distribution. STA Fall
 STA 320 Fall 2013 Thursday, Dec 5 Sampling Distribution STA 320 - Fall 2013-1 Review We cannot tell what will happen in any given individual sample (just as we can not predict a single coin flip in advance).
STA 320 Fall 2013 Thursday, Dec 5 Sampling Distribution STA 320 - Fall 2013-1 Review We cannot tell what will happen in any given individual sample (just as we can not predict a single coin flip in advance).
Statistics and Probability
 Statistics and Probability Continuous RVs (Normal); Confidence Intervals Outline Continuous random variables Normal distribution CLT Point estimation Confidence intervals http://www.isrec.isb-sib.ch/~darlene/geneve/
Statistics and Probability Continuous RVs (Normal); Confidence Intervals Outline Continuous random variables Normal distribution CLT Point estimation Confidence intervals http://www.isrec.isb-sib.ch/~darlene/geneve/
Chapter 8 Statistical Intervals for a Single Sample
 Chapter 8 Statistical Intervals for a Single Sample Part 1: Confidence intervals (CI) for population mean µ Section 8-1: CI for µ when σ 2 known & drawing from normal distribution Section 8-1.2: Sample
Chapter 8 Statistical Intervals for a Single Sample Part 1: Confidence intervals (CI) for population mean µ Section 8-1: CI for µ when σ 2 known & drawing from normal distribution Section 8-1.2: Sample
STAT Chapter 7: Confidence Intervals
 STAT 515 -- Chapter 7: Confidence Intervals With a point estimate, we used a single number to estimate a parameter. We can also use a set of numbers to serve as reasonable estimates for the parameter.
STAT 515 -- Chapter 7: Confidence Intervals With a point estimate, we used a single number to estimate a parameter. We can also use a set of numbers to serve as reasonable estimates for the parameter.
Chapter 7 presents the beginning of inferential statistics. The two major activities of inferential statistics are
 Chapter 7 presents the beginning of inferential statistics. Concept: Inferential Statistics The two major activities of inferential statistics are 1 to use sample data to estimate values of population
Chapter 7 presents the beginning of inferential statistics. Concept: Inferential Statistics The two major activities of inferential statistics are 1 to use sample data to estimate values of population
CH 5 Normal Probability Distributions Properties of the Normal Distribution
 Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Version A. Problem 1. Let X be the continuous random variable defined by the following pdf: 1 x/2 when 0 x 2, f(x) = 0 otherwise.
 Math 224 Q Exam 3A Fall 217 Tues Dec 12 Version A Problem 1. Let X be the continuous random variable defined by the following pdf: { 1 x/2 when x 2, f(x) otherwise. (a) Compute the mean µ E[X]. E[X] x
Math 224 Q Exam 3A Fall 217 Tues Dec 12 Version A Problem 1. Let X be the continuous random variable defined by the following pdf: { 1 x/2 when x 2, f(x) otherwise. (a) Compute the mean µ E[X]. E[X] x
Section Introduction to Normal Distributions
 Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Lecture 8 - Sampling Distributions and the CLT
 Lecture 8 - Sampling Distributions and the CLT Statistics 102 Kenneth K. Lopiano September 18, 2013 1 Basics Improvements 2 Variability of Estimates Activity Sampling distributions - via simulation Sampling
Lecture 8 - Sampling Distributions and the CLT Statistics 102 Kenneth K. Lopiano September 18, 2013 1 Basics Improvements 2 Variability of Estimates Activity Sampling distributions - via simulation Sampling
Sampling and sampling distribution
 Sampling and sampling distribution September 12, 2017 STAT 101 Class 5 Slide 1 Outline of Topics 1 Sampling 2 Sampling distribution of a mean 3 Sampling distribution of a proportion STAT 101 Class 5 Slide
Sampling and sampling distribution September 12, 2017 STAT 101 Class 5 Slide 1 Outline of Topics 1 Sampling 2 Sampling distribution of a mean 3 Sampling distribution of a proportion STAT 101 Class 5 Slide
Estimation Y 3. Confidence intervals I, Feb 11,
 Estimation Example: Cholesterol levels of heart-attack patients Data: Observational study at a Pennsylvania medical center blood cholesterol levels patients treated for heart attacks measurements 2, 4,
Estimation Example: Cholesterol levels of heart-attack patients Data: Observational study at a Pennsylvania medical center blood cholesterol levels patients treated for heart attacks measurements 2, 4,
Class 13. Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science. Marquette University MATH 1700
 Class 13 Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science Copyright 017 by D.B. Rowe 1 Agenda: Recap Chapter 6.3 6.5 Lecture Chapter 7.1 7. Review Chapter 5 for Eam 3.
Class 13 Daniel B. Rowe, Ph.D. Department of Mathematics, Statistics, and Computer Science Copyright 017 by D.B. Rowe 1 Agenda: Recap Chapter 6.3 6.5 Lecture Chapter 7.1 7. Review Chapter 5 for Eam 3.
Data Analysis and Statistical Methods Statistics 651
 Review of previous lecture: Why confidence intervals? Data Analysis and Statistical Methods Statistics 651 http://www.stat.tamu.edu/~suhasini/teaching.html Suhasini Subba Rao Suppose you want to know the
Review of previous lecture: Why confidence intervals? Data Analysis and Statistical Methods Statistics 651 http://www.stat.tamu.edu/~suhasini/teaching.html Suhasini Subba Rao Suppose you want to know the
Lecture 9. Probability Distributions. Outline. Outline
 Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Determining Sample Size. Slide 1 ˆ ˆ. p q n E = z α / 2. (solve for n by algebra) n = E 2
 Determining Sample Size Slide 1 E = z α / 2 ˆ ˆ p q n (solve for n by algebra) n = ( zα α / 2) 2 p ˆ qˆ E 2 Sample Size for Estimating Proportion p When an estimate of ˆp is known: Slide 2 n = ˆ ˆ ( )
Determining Sample Size Slide 1 E = z α / 2 ˆ ˆ p q n (solve for n by algebra) n = ( zα α / 2) 2 p ˆ qˆ E 2 Sample Size for Estimating Proportion p When an estimate of ˆp is known: Slide 2 n = ˆ ˆ ( )
Chapter 5. Statistical inference for Parametric Models
 Chapter 5. Statistical inference for Parametric Models Outline Overview Parameter estimation Method of moments How good are method of moments estimates? Interval estimation Statistical Inference for Parametric
Chapter 5. Statistical inference for Parametric Models Outline Overview Parameter estimation Method of moments How good are method of moments estimates? Interval estimation Statistical Inference for Parametric
STAT Chapter 5: Continuous Distributions. Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s.
 STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
Lecture 9. Probability Distributions
 Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
STA258H5. Al Nosedal and Alison Weir. Winter Al Nosedal and Alison Weir STA258H5 Winter / 41
 STA258H5 Al Nosedal and Alison Weir Winter 2017 Al Nosedal and Alison Weir STA258H5 Winter 2017 1 / 41 NORMAL APPROXIMATION TO THE BINOMIAL DISTRIBUTION. Al Nosedal and Alison Weir STA258H5 Winter 2017
STA258H5 Al Nosedal and Alison Weir Winter 2017 Al Nosedal and Alison Weir STA258H5 Winter 2017 1 / 41 NORMAL APPROXIMATION TO THE BINOMIAL DISTRIBUTION. Al Nosedal and Alison Weir STA258H5 Winter 2017
The Binomial Probability Distribution
 The Binomial Probability Distribution MATH 130, Elements of Statistics I J. Robert Buchanan Department of Mathematics Fall 2017 Objectives After this lesson we will be able to: determine whether a probability
The Binomial Probability Distribution MATH 130, Elements of Statistics I J. Robert Buchanan Department of Mathematics Fall 2017 Objectives After this lesson we will be able to: determine whether a probability
CHAPTER 5 SAMPLING DISTRIBUTIONS
 CHAPTER 5 SAMPLING DISTRIBUTIONS Sampling Variability. We will visualize our data as a random sample from the population with unknown parameter μ. Our sample mean Ȳ is intended to estimate population mean
CHAPTER 5 SAMPLING DISTRIBUTIONS Sampling Variability. We will visualize our data as a random sample from the population with unknown parameter μ. Our sample mean Ȳ is intended to estimate population mean
BIO5312 Biostatistics Lecture 5: Estimations
 BIO5312 Biostatistics Lecture 5: Estimations Yujin Chung September 27th, 2016 Fall 2016 Yujin Chung Lec5: Estimations Fall 2016 1/34 Recap Yujin Chung Lec5: Estimations Fall 2016 2/34 Today s lecture and
BIO5312 Biostatistics Lecture 5: Estimations Yujin Chung September 27th, 2016 Fall 2016 Yujin Chung Lec5: Estimations Fall 2016 1/34 Recap Yujin Chung Lec5: Estimations Fall 2016 2/34 Today s lecture and
The Binomial Distribution
 The Binomial Distribution Properties of a Binomial Experiment 1. It consists of a fixed number of observations called trials. 2. Each trial can result in one of only two mutually exclusive outcomes labeled
The Binomial Distribution Properties of a Binomial Experiment 1. It consists of a fixed number of observations called trials. 2. Each trial can result in one of only two mutually exclusive outcomes labeled
ECO220Y Estimation: Confidence Interval Estimator for Sample Proportions Readings: Chapter 11 (skip 11.5)
 ECO220Y Estimation: Confidence Interval Estimator for Sample Proportions Readings: Chapter 11 (skip 11.5) Fall 2011 Lecture 10 (Fall 2011) Estimation Lecture 10 1 / 23 Review: Sampling Distributions Sample
ECO220Y Estimation: Confidence Interval Estimator for Sample Proportions Readings: Chapter 11 (skip 11.5) Fall 2011 Lecture 10 (Fall 2011) Estimation Lecture 10 1 / 23 Review: Sampling Distributions Sample
Part V - Chance Variability
 Part V - Chance Variability Dr. Joseph Brennan Math 148, BU Dr. Joseph Brennan (Math 148, BU) Part V - Chance Variability 1 / 78 Law of Averages In Chapter 13 we discussed the Kerrich coin-tossing experiment.
Part V - Chance Variability Dr. Joseph Brennan Math 148, BU Dr. Joseph Brennan (Math 148, BU) Part V - Chance Variability 1 / 78 Law of Averages In Chapter 13 we discussed the Kerrich coin-tossing experiment.
Density curves. (James Madison University) February 4, / 20
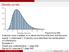 Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Chapter 14 : Statistical Inference 1. Note : Here the 4-th and 5-th editions of the text have different chapters, but the material is the same.
 Chapter 14 : Statistical Inference 1 Chapter 14 : Introduction to Statistical Inference Note : Here the 4-th and 5-th editions of the text have different chapters, but the material is the same. Data x
Chapter 14 : Statistical Inference 1 Chapter 14 : Introduction to Statistical Inference Note : Here the 4-th and 5-th editions of the text have different chapters, but the material is the same. Data x
BIOL The Normal Distribution and the Central Limit Theorem
 BIOL 300 - The Normal Distribution and the Central Limit Theorem In the first week of the course, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are
BIOL 300 - The Normal Distribution and the Central Limit Theorem In the first week of the course, we introduced a few measures of center and spread, and discussed how the mean and standard deviation are
Consider the following examples: ex: let X = tossing a coin three times and counting the number of heads
 Overview Both chapters and 6 deal with a similar concept probability distributions. The difference is that chapter concerns itself with discrete probability distribution while chapter 6 covers continuous
Overview Both chapters and 6 deal with a similar concept probability distributions. The difference is that chapter concerns itself with discrete probability distribution while chapter 6 covers continuous
1 Small Sample CI for a Population Mean µ
 Lecture 7: Small Sample Confidence Intervals Based on a Normal Population Distribution Readings: Sections 7.4-7.5 1 Small Sample CI for a Population Mean µ The large sample CI x ± z α/2 s n was constructed
Lecture 7: Small Sample Confidence Intervals Based on a Normal Population Distribution Readings: Sections 7.4-7.5 1 Small Sample CI for a Population Mean µ The large sample CI x ± z α/2 s n was constructed
MATH 3200 Exam 3 Dr. Syring
 . Suppose n eligible voters are polled (randomly sampled) from a population of size N. The poll asks voters whether they support or do not support increasing local taxes to fund public parks. Let M be
. Suppose n eligible voters are polled (randomly sampled) from a population of size N. The poll asks voters whether they support or do not support increasing local taxes to fund public parks. Let M be
The Normal Approximation to the Binomial
 Lecture 16 The Normal Approximation to the Binomial We can calculate l binomial i probabilities bbilii using The binomial formula The cumulative binomial tables When n is large, and p is not too close
Lecture 16 The Normal Approximation to the Binomial We can calculate l binomial i probabilities bbilii using The binomial formula The cumulative binomial tables When n is large, and p is not too close
MLLunsford 1. Activity: Central Limit Theorem Theory and Computations
 MLLunsford 1 Activity: Central Limit Theorem Theory and Computations Concepts: The Central Limit Theorem; computations using the Central Limit Theorem. Prerequisites: The student should be familiar with
MLLunsford 1 Activity: Central Limit Theorem Theory and Computations Concepts: The Central Limit Theorem; computations using the Central Limit Theorem. Prerequisites: The student should be familiar with
Standard Normal, Inverse Normal and Sampling Distributions
 Standard Normal, Inverse Normal and Sampling Distributions Section 5.5 & 6.6 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy
Standard Normal, Inverse Normal and Sampling Distributions Section 5.5 & 6.6 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 9-3339 Cathy
AP Statistics Ch 8 The Binomial and Geometric Distributions
 Ch 8.1 The Binomial Distributions The Binomial Setting A situation where these four conditions are satisfied is called a binomial setting. 1. Each observation falls into one of just two categories, which
Ch 8.1 The Binomial Distributions The Binomial Setting A situation where these four conditions are satisfied is called a binomial setting. 1. Each observation falls into one of just two categories, which
1 Sampling Distributions
 1 Sampling Distributions 1.1 Statistics and Sampling Distributions When a random sample is selected the numerical descriptive measures calculated from such a sample are called statistics. These statistics
1 Sampling Distributions 1.1 Statistics and Sampling Distributions When a random sample is selected the numerical descriptive measures calculated from such a sample are called statistics. These statistics
NORMAL RANDOM VARIABLES (Normal or gaussian distribution)
 NORMAL RANDOM VARIABLES (Normal or gaussian distribution) Many variables, as pregnancy lengths, foot sizes etc.. exhibit a normal distribution. The shape of the distribution is a symmetric bell shape.
NORMAL RANDOM VARIABLES (Normal or gaussian distribution) Many variables, as pregnancy lengths, foot sizes etc.. exhibit a normal distribution. The shape of the distribution is a symmetric bell shape.
Chapter 7. Confidence Intervals and Sample Sizes. Definition. Definition. Definition. Definition. Confidence Interval : CI. Point Estimate.
 Chapter 7 Confidence Intervals and Sample Sizes 7. Estimating a Proportion p 7.3 Estimating a Mean µ (σ known) 7.4 Estimating a Mean µ (σ unknown) 7.5 Estimating a Standard Deviation σ In a recent poll,
Chapter 7 Confidence Intervals and Sample Sizes 7. Estimating a Proportion p 7.3 Estimating a Mean µ (σ known) 7.4 Estimating a Mean µ (σ unknown) 7.5 Estimating a Standard Deviation σ In a recent poll,
Chapter 6.1 Confidence Intervals. Stat 226 Introduction to Business Statistics I. Chapter 6, Section 6.1
 Stat 226 Introduction to Business Statistics I Spring 2009 Professor: Dr. Petrutza Caragea Section A Tuesdays and Thursdays 9:30-10:50 a.m. Chapter 6, Section 6.1 Confidence Intervals Confidence Intervals
Stat 226 Introduction to Business Statistics I Spring 2009 Professor: Dr. Petrutza Caragea Section A Tuesdays and Thursdays 9:30-10:50 a.m. Chapter 6, Section 6.1 Confidence Intervals Confidence Intervals
The Bernoulli distribution
 This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License. Your use of this material constitutes acceptance of that license and the conditions of use of materials on this
AMS7: WEEK 4. CLASS 3
 AMS7: WEEK 4. CLASS 3 Sampling distributions and estimators. Central Limit Theorem Normal Approximation to the Binomial Distribution Friday April 24th, 2015 Sampling distributions and estimators REMEMBER:
AMS7: WEEK 4. CLASS 3 Sampling distributions and estimators. Central Limit Theorem Normal Approximation to the Binomial Distribution Friday April 24th, 2015 Sampling distributions and estimators REMEMBER:
4.2 Bernoulli Trials and Binomial Distributions
 Arkansas Tech University MATH 3513: Applied Statistics I Dr. Marcel B. Finan 4.2 Bernoulli Trials and Binomial Distributions A Bernoulli trial 1 is an experiment with exactly two outcomes: Success and
Arkansas Tech University MATH 3513: Applied Statistics I Dr. Marcel B. Finan 4.2 Bernoulli Trials and Binomial Distributions A Bernoulli trial 1 is an experiment with exactly two outcomes: Success and
As you draw random samples of size n, as n increases, the sample means tend to be normally distributed.
 The Central Limit Theorem The central limit theorem (clt for short) is one of the most powerful and useful ideas in all of statistics. The clt says that if we collect samples of size n with a "large enough
The Central Limit Theorem The central limit theorem (clt for short) is one of the most powerful and useful ideas in all of statistics. The clt says that if we collect samples of size n with a "large enough
Central Limit Theorem (cont d) 7/28/2006
 Central Limit Theorem (cont d) 7/28/2006 Central Limit Theorem for Binomial Distributions Theorem. For the binomial distribution b(n, p, j) we have lim npq b(n, p, np + x npq ) = φ(x), n where φ(x) is
Central Limit Theorem (cont d) 7/28/2006 Central Limit Theorem for Binomial Distributions Theorem. For the binomial distribution b(n, p, j) we have lim npq b(n, p, np + x npq ) = φ(x), n where φ(x) is
MAS1403. Quantitative Methods for Business Management. Semester 1, Module leader: Dr. David Walshaw
 MAS1403 Quantitative Methods for Business Management Semester 1, 2018 2019 Module leader: Dr. David Walshaw Additional lecturers: Dr. James Waldren and Dr. Stuart Hall Announcements: Written assignment
MAS1403 Quantitative Methods for Business Management Semester 1, 2018 2019 Module leader: Dr. David Walshaw Additional lecturers: Dr. James Waldren and Dr. Stuart Hall Announcements: Written assignment
Statistics 251: Statistical Methods Sampling Distributions Module
 Statistics 251: Statistical Methods Sampling Distributions Module 7 2018 Three Types of Distributions data distribution the distribution of a variable in a sample population distribution the probability
Statistics 251: Statistical Methods Sampling Distributions Module 7 2018 Three Types of Distributions data distribution the distribution of a variable in a sample population distribution the probability
HOMEWORK: Due Mon 11/8, Chapter 9: #15, 25, 37, 44
 This week: Chapter 9 (will do 9.6 to 9.8 later, with Chap. 11) Understanding Sampling Distributions: Statistics as Random Variables ANNOUNCEMENTS: Shandong Min will give the lecture on Friday. See website
This week: Chapter 9 (will do 9.6 to 9.8 later, with Chap. 11) Understanding Sampling Distributions: Statistics as Random Variables ANNOUNCEMENTS: Shandong Min will give the lecture on Friday. See website
Section Random Variables and Histograms
 Section 3.1 - Random Variables and Histograms Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
Section 3.1 - Random Variables and Histograms Definition: A random variable is a rule that assigns a number to each outcome of an experiment. Example 1: Suppose we toss a coin three times. Then we could
CHAPTER 8. Confidence Interval Estimation Point and Interval Estimates
 CHAPTER 8. Confidence Interval Estimation Point and Interval Estimates A point estimate is a single number, a confidence interval provides additional information about the variability of the estimate Lower
CHAPTER 8. Confidence Interval Estimation Point and Interval Estimates A point estimate is a single number, a confidence interval provides additional information about the variability of the estimate Lower
Review: Population, sample, and sampling distributions
 Review: Population, sample, and sampling distributions A population with mean µ and standard deviation σ For instance, µ = 0, σ = 1 0 1 Sample 1, N=30 Sample 2, N=30 Sample 100000000000 InterquartileRange
Review: Population, sample, and sampling distributions A population with mean µ and standard deviation σ For instance, µ = 0, σ = 1 0 1 Sample 1, N=30 Sample 2, N=30 Sample 100000000000 InterquartileRange
Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the
 Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the mean, use the CLT for the mean. If you are being asked to
Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the mean, use the CLT for the mean. If you are being asked to
Lecture 3. Sampling distributions. Counts, Proportions, and sample mean.
 Lecture 3 Sampling distributions. Counts, Proportions, and sample mean. Statistical Inference: Uses data and summary statistics (mean, variances, proportions, slopes) to draw conclusions about a population
Lecture 3 Sampling distributions. Counts, Proportions, and sample mean. Statistical Inference: Uses data and summary statistics (mean, variances, proportions, slopes) to draw conclusions about a population
5.4 Normal Approximation of the Binomial Distribution
 5.4 Normal Approximation of the Binomial Distribution Bernoulli Trials have 3 properties: 1. Only two outcomes - PASS or FAIL 2. n identical trials Review from yesterday. 3. Trials are independent - probability
5.4 Normal Approximation of the Binomial Distribution Bernoulli Trials have 3 properties: 1. Only two outcomes - PASS or FAIL 2. n identical trials Review from yesterday. 3. Trials are independent - probability
Confidence Intervals and Sample Size
 Confidence Intervals and Sample Size Chapter 6 shows us how we can use the Central Limit Theorem (CLT) to 1. estimate a population parameter (such as the mean or proportion) using a sample, and. determine
Confidence Intervals and Sample Size Chapter 6 shows us how we can use the Central Limit Theorem (CLT) to 1. estimate a population parameter (such as the mean or proportion) using a sample, and. determine
11.5: Normal Distributions
 11.5: Normal Distributions 11.5.1 Up to now, we ve dealt with discrete random variables, variables that take on only a finite (or countably infinite we didn t do these) number of values. A continuous random
11.5: Normal Distributions 11.5.1 Up to now, we ve dealt with discrete random variables, variables that take on only a finite (or countably infinite we didn t do these) number of values. A continuous random
Chapter 7.2: Large-Sample Confidence Intervals for a Population Mean and Proportion. Instructor: Elvan Ceyhan
 1 Chapter 7.2: Large-Sample Confidence Intervals for a Population Mean and Proportion Instructor: Elvan Ceyhan Outline of this chapter: Large-Sample Interval for µ Confidence Intervals for Population Proportion
1 Chapter 7.2: Large-Sample Confidence Intervals for a Population Mean and Proportion Instructor: Elvan Ceyhan Outline of this chapter: Large-Sample Interval for µ Confidence Intervals for Population Proportion
MidTerm 1) Find the following (round off to one decimal place):
 MidTerm 1) 68 49 21 55 57 61 70 42 59 50 66 99 Find the following (round off to one decimal place): Mean = 58:083, round off to 58.1 Median = 58 Range = max min = 99 21 = 78 St. Deviation = s = 8:535,
MidTerm 1) 68 49 21 55 57 61 70 42 59 50 66 99 Find the following (round off to one decimal place): Mean = 58:083, round off to 58.1 Median = 58 Range = max min = 99 21 = 78 St. Deviation = s = 8:535,
Chapter Six Probability Distributions
 6.1 Probability Distributions Discrete Random Variable Chapter Six Probability Distributions x P(x) 2 0.08 4 0.13 6 0.25 8 0.31 10 0.16 12 0.01 Practice. Construct a probability distribution for the number
6.1 Probability Distributions Discrete Random Variable Chapter Six Probability Distributions x P(x) 2 0.08 4 0.13 6 0.25 8 0.31 10 0.16 12 0.01 Practice. Construct a probability distribution for the number
Commonly Used Distributions
 Chapter 4: Commonly Used Distributions 1 Introduction Statistical inference involves drawing a sample from a population and analyzing the sample data to learn about the population. We often have some knowledge
Chapter 4: Commonly Used Distributions 1 Introduction Statistical inference involves drawing a sample from a population and analyzing the sample data to learn about the population. We often have some knowledge
In a binomial experiment of n trials, where p = probability of success and q = probability of failure. mean variance standard deviation
 Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
MA 1125 Lecture 12 - Mean and Standard Deviation for the Binomial Distribution. Objectives: Mean and standard deviation for the binomial distribution.
 MA 5 Lecture - Mean and Standard Deviation for the Binomial Distribution Friday, September 9, 07 Objectives: Mean and standard deviation for the binomial distribution.. Mean and Standard Deviation of the
MA 5 Lecture - Mean and Standard Deviation for the Binomial Distribution Friday, September 9, 07 Objectives: Mean and standard deviation for the binomial distribution.. Mean and Standard Deviation of the
Sampling. Marc H. Mehlman University of New Haven. Marc Mehlman (University of New Haven) Sampling 1 / 20.
 Sampling Marc H. Mehlman marcmehlman@yahoo.com University of New Haven (University of New Haven) Sampling 1 / 20 Table of Contents 1 Sampling Distributions 2 Central Limit Theorem 3 Binomial Distribution
Sampling Marc H. Mehlman marcmehlman@yahoo.com University of New Haven (University of New Haven) Sampling 1 / 20 Table of Contents 1 Sampling Distributions 2 Central Limit Theorem 3 Binomial Distribution
MA 1125 Lecture 18 - Normal Approximations to Binomial Distributions. Objectives: Compute probabilities for a binomial as a normal distribution.
 MA 25 Lecture 8 - Normal Approximations to Binomial Distributions Friday, October 3, 207 Objectives: Compute probabilities for a binomial as a normal distribution.. Normal Approximations to the Binomial
MA 25 Lecture 8 - Normal Approximations to Binomial Distributions Friday, October 3, 207 Objectives: Compute probabilities for a binomial as a normal distribution.. Normal Approximations to the Binomial
chapter 13: Binomial Distribution Exercises (binomial)13.6, 13.12, 13.22, 13.43
 chapter 13: Binomial Distribution ch13-links binom-tossing-4-coins binom-coin-example ch13 image Exercises (binomial)13.6, 13.12, 13.22, 13.43 CHAPTER 13: Binomial Distributions The Basic Practice of Statistics
chapter 13: Binomial Distribution ch13-links binom-tossing-4-coins binom-coin-example ch13 image Exercises (binomial)13.6, 13.12, 13.22, 13.43 CHAPTER 13: Binomial Distributions The Basic Practice of Statistics
1. Variability in estimates and CLT
 Unit3: Foundationsforinference 1. Variability in estimates and CLT Sta 101 - Fall 2015 Duke University, Department of Statistical Science Dr. Çetinkaya-Rundel Slides posted at http://bit.ly/sta101_f15
Unit3: Foundationsforinference 1. Variability in estimates and CLT Sta 101 - Fall 2015 Duke University, Department of Statistical Science Dr. Çetinkaya-Rundel Slides posted at http://bit.ly/sta101_f15
Data Analysis and Statistical Methods Statistics 651
 Data Analysis and Statistical Methods Statistics 651 http://wwwstattamuedu/~suhasini/teachinghtml Suhasini Subba Rao Review of previous lecture The main idea in the previous lecture is that the sample
Data Analysis and Statistical Methods Statistics 651 http://wwwstattamuedu/~suhasini/teachinghtml Suhasini Subba Rao Review of previous lecture The main idea in the previous lecture is that the sample
Problem Set 07 Discrete Random Variables
 Name Problem Set 07 Discrete Random Variables MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the mean of the random variable. 1) The random
Name Problem Set 07 Discrete Random Variables MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the mean of the random variable. 1) The random
Binomal and Geometric Distributions
 Binomal and Geometric Distributions Sections 3.2 & 3.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 7-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
Binomal and Geometric Distributions Sections 3.2 & 3.3 Cathy Poliak, Ph.D. cathy@math.uh.edu Office in Fleming 11c Department of Mathematics University of Houston Lecture 7-2311 Cathy Poliak, Ph.D. cathy@math.uh.edu
χ 2 distributions and confidence intervals for population variance
 χ 2 distributions and confidence intervals for population variance Let Z be a standard Normal random variable, i.e., Z N(0, 1). Define Y = Z 2. Y is a non-negative random variable. Its distribution is
χ 2 distributions and confidence intervals for population variance Let Z be a standard Normal random variable, i.e., Z N(0, 1). Define Y = Z 2. Y is a non-negative random variable. Its distribution is
LECTURE 6 DISTRIBUTIONS
 LECTURE 6 DISTRIBUTIONS OVERVIEW Uniform Distribution Normal Distribution Random Variables Continuous Distributions MOST OF THE SLIDES ADOPTED FROM OPENINTRO STATS BOOK. NORMAL DISTRIBUTION Unimodal and
LECTURE 6 DISTRIBUTIONS OVERVIEW Uniform Distribution Normal Distribution Random Variables Continuous Distributions MOST OF THE SLIDES ADOPTED FROM OPENINTRO STATS BOOK. NORMAL DISTRIBUTION Unimodal and
Homework Assignments
 Homework Assignments Week 1 (p. 57) #4.1, 4., 4.3 Week (pp 58 6) #4.5, 4.6, 4.8(a), 4.13, 4.0, 4.6(b), 4.8, 4.31, 4.34 Week 3 (pp 15 19) #1.9, 1.1, 1.13, 1.15, 1.18 (pp 9 31) #.,.6,.9 Week 4 (pp 36 37)
Homework Assignments Week 1 (p. 57) #4.1, 4., 4.3 Week (pp 58 6) #4.5, 4.6, 4.8(a), 4.13, 4.0, 4.6(b), 4.8, 4.31, 4.34 Week 3 (pp 15 19) #1.9, 1.1, 1.13, 1.15, 1.18 (pp 9 31) #.,.6,.9 Week 4 (pp 36 37)
LESSON 7 INTERVAL ESTIMATION SAMIE L.S. LY
 LESSON 7 INTERVAL ESTIMATION SAMIE L.S. LY 1 THIS WEEK S PLAN Part I: Theory + Practice ( Interval Estimation ) Part II: Theory + Practice ( Interval Estimation ) z-based Confidence Intervals for a Population
LESSON 7 INTERVAL ESTIMATION SAMIE L.S. LY 1 THIS WEEK S PLAN Part I: Theory + Practice ( Interval Estimation ) Part II: Theory + Practice ( Interval Estimation ) z-based Confidence Intervals for a Population
Math : Spring 2008
 Math 1070-2: Spring 2008 Lecture 7 Davar Khoshnevisan Department of Mathematics University of Utah http://www.math.utah.edu/ davar February 27, 2008 An example A WHO study of health: In Canada, the systolic
Math 1070-2: Spring 2008 Lecture 7 Davar Khoshnevisan Department of Mathematics University of Utah http://www.math.utah.edu/ davar February 27, 2008 An example A WHO study of health: In Canada, the systolic
The binomial distribution p314
 The binomial distribution p314 Example: A biased coin (P(H) = p = 0.6) ) is tossed 5 times. Let X be the number of H s. Fine P(X = 2). This X is a binomial r. v. The binomial setting p314 1. There are
The binomial distribution p314 Example: A biased coin (P(H) = p = 0.6) ) is tossed 5 times. Let X be the number of H s. Fine P(X = 2). This X is a binomial r. v. The binomial setting p314 1. There are
Math 14 Lecture Notes Ch The Normal Approximation to the Binomial Distribution. P (X ) = nc X p X q n X =
 6.4 The Normal Approximation to the Binomial Distribution Recall from section 6.4 that g A binomial experiment is a experiment that satisfies the following four requirements: 1. Each trial can have only
6.4 The Normal Approximation to the Binomial Distribution Recall from section 6.4 that g A binomial experiment is a experiment that satisfies the following four requirements: 1. Each trial can have only
