The Normal Probability Distribution
|
|
|
- Olivia Norris
- 5 years ago
- Views:
Transcription
1 102 The Normal Probability Distribution C H A P T E R 7 Section 7.2 4Example 1 (pg. 71) Finding Area Under a Normal Curve In this exercise, we will calculate the area to the left of 5 inches using a normal distribution with μ = 8.72 and σ =.17. The TI-84 has two methods for calculating this area. Method 1: Normalcdf(lowerbound, upperbound, μ,σ ) computes the area between a lowerbound and an upperbound. In this example, you are computing the area from negative infinity to 5. Negative infinity is specified by (-) 1 2 nd [EE] 9 9 (Note: EE is found above the comma, ). Try entering 1 EE 99 into your calculator. Now, to find P(X < 5) we will calculate the area to the left of 5. Press 2 nd [DISTR] and select 2:normalcdf( and type in -1E99, 5, 8.72,.17 ) and press ENTER. (Note: For this example, μ = 8.72 and σ =.17)
2 Section Method 2: This method calculates the area and also displays a graph of the probability distribution.to find P(X < 5) and include a graph, you must first set up the WINDOW so that the graph will be displayed properly. You will need to set Xmin equal to ( μ - σ ) and Xmax equal to ( μ + σ ). Press WINDOW and set Xmin equal to ( μ - σ ) by typing in *.17. Press ENTER and set Xmax equal to ( μ + σ ) by typing in *.17. Set Xscl equal to σ, which is.17. Setting the Y-range is a little more difficult to do. We will start by setting Ymax. A good rule - of - thumb is to set Ymax equal to.5 /σ. For this example, set Ymax =.5/.17 by scrolling down to Ymax and typing.5/.17. Use the up arrow to highlight Ymin. A good value for Ymin is (-) Ymax / 4 so type in (-).158 / 4. Press 2 nd [DRAW] and select 1:ClrDraw and press ENTER ENTER. Press 2 nd [STATPLOT] and TURN OFF all PLOTS. Make sure that there is nothing stored in the Y-registers. Press Y= and check the Y-registers. If any of them contain a function, move the cursor to that Y-register and press CLEAR. Press 2 nd [DISTR], highlight DRAW and select 1:ShadeNorm( and type in -1E99, 5, 8.72,.17 ) and press ENTER. Conclusion: The proportion of -year-old females who are less than 5 inches tall is
3 104 Note: When using the TI-84 (or any other technology tool), the answers you obtain may vary slightly from the answers that you would obtain using the standard normal table. Consequently, your answers may not be exactly the same as the answers found in your textbook. The differences are simply due to rounding. If we want to find the proportion of -year-old females whose height is greater than 5 inches, we will calculate the area to the right of 5. Method 1: Use Normalcdf(lowerbound, upperbound, μ,σ ). In this example, you are computing the area from 5 positive infinity. Positive infinity is specified by 1 2 nd [EE] 9 9 (Note: EE is found above the comma, ). Now, to find P(X > 5) we will calculate the area to the right of 5. Press 2 nd [DISTR] and select 2:normalcdf( and type in 5, 1E99, 8.72,.17 ) and press ENTER. (Note: For this example, μ = 8.72 and σ =.17) Method 2: To find P(X >5) and include a graph, you must first set up the WINDOW so that the graph will be displayed properly. You will need to set Xmin equal to ( μ - σ ) and Xmax equal to ( μ + σ ). Press WINDOW and set Xmin equal to ( μ - σ ) by typing in *.17. Press ENTER and set Xmax equal to ( μ + σ ) by typing in *.17. Set Xscl equal to σ, which is.17. Setting the Y-range is a little more difficult to do. We will start by setting Ymax. A good rule - of - thumb is to set Ymax equal to.5 /σ. For this example, set Ymax =.5/.17 by scrolling down to Ymax and typing.5/.17. Use the up arrow to highlight Ymin. A good value for Ymin is (-) Ymax / 4 so type in (-).158 / 4. Press 2 nd [DRAW] and select 1:ClrDraw and press ENTER ENTER. Press 2 nd [STATPLOT] and TURN OFF all PLOTS. Make sure that there is nothing stored in the Y-registers. Press Y= and check the Y-registers. If any of them contain a function, move the cursor to that Y-register and press CLEAR.
4 Section Press 2 nd [DISTR], highlight DRAW and select 1:ShadeNorm( and type in 5, 1E99, 8.72,.17 ) and press ENTER.
5 106 4Example 2 (pg. 72) Finding the Probability of a Normal Random Variable In this exercise, we will calculate the area between 5 and 40 using a normal distribution with μ = 8.72 and σ =.17. Method 1:To find P(5 X 40) press 2 nd [DISTR], select 2:normalcdf( and type in 5, 40, 8.72,.17 ) and press ENTER. Method 2: To find the probability and include a graph, you must first set up the WINDOW so that the graph will be displayed properly. You will need to set Xmin equal to ( μ - σ ) and Xmax equal to ( μ + σ ). Press WINDOW and set Xmin equal to ( μ - σ ) by typing in *.17. Press ENTER and set Xmax equal to ( μ + σ ) by typing in *.17. Set Xscl equal to σ, which is.17. Setting the Y-range is a little more difficult to do. A good rule - of - thumb is to set Ymax equal to.5 /σ. For this example, set Ymax =.5/.17. Use the up arrow to highlight Ymin. A good value for Ymin is (-) Ymax / 4 so type in (-).158 / 4. Press 2 nd [DRAW] and select 1:ClrDraw and press ENTER ENTER. Press 2 nd [STATPLOT] and TURN OFF all PLOTS. Make sure that there is nothing stored in the Y-registers. Press Y= and check the Y-registers. If any of them contain a function, move the cursor to that Y-register and press CLEAR. Press 2 nd [DISTR], highlight DRAW and select 1:ShadeNorm( and type in 5, 40, 8.72,.17 ) and press ENTER.
6 Section Conclusion: The probability that a randomly selected three-year-old female is between 5 and 40 inches tall is.565 or 5.65%.
7 108 Example (pg. 74) Finding the Value of a Normal Random Variable This is an inverse normal problem and the command invnorm( area, μ,σ ) is used. In this type of problem, a percentage of the area under the normal curve is given and you are asked to find the corresponding X-value. The area value that you ENTER into the TI-84 must always be area to the left of an X-value. In this example, the percentage given is the bottom 20 %, (the 20 th percentile). This area (bottom 20%) is an area to the left, so that is the value of the area that we enter into the invnorm command. The area value must be entered in decimal form. Press 2 nd [DISTR] and select :invnorm( and type in.20, 8.72,.17 ) and press ENTER. Conclusion: The height that separates the bottom 20% of three-year-old females from the top 80% is 6.05 inches.
8 Section Example 4 (pg.75) Finding the Value of a Normal Random Variable This is an inverse normal problem and the command invnorm( area, μ,σ ) is used. In this problem the middle area is That leaves an area of 0.10 to be equally divided between the left and right tail areas. Each of these areas are, therefore, equal to The score that marks the lower edge of the middle 90% corresponds to a left area of To find the X-value corresponding to a left area of 0.05, press 2 nd [DISTR] and select :invnorm( and type in.05, 516, 116 ) and press ENTER. The score that separates the middle 90% from the top 5% is actually the score that separates the bottom 95% (the middle 90% plus the 5% in the left tail) from the top 5%. To find the X-value corresponding to a left area of 0.95, press 2 nd [DISTR] and select :invnorm( and type in.95, 516, 116 ) and press ENTER. The middle 90% of the distribution lies between the scores 25 and 707.
9 110 4Example 5 (pg. 77) Finding the value Z α This is an inverse normal problem and the command invnorm( area, μ,σ ) is used. In this type of problem, an area under the normal curve is given and you are asked to find the corresponding Z-score. In this example, the area given is the area to the right of a Z-score. The area is (The area value that you enter into the TI-84 must always be area to the left of a Z-score.). To find the Z-score corresponding to right area of 0.10, subtract 0.10 from 1 to obtain the area to the left of the Z-score. Press 2 nd [DISTR] and select :invnorm( and type in.90, 0, 1 ) and press ENTER. The Z-score that has an area to the right equal to 0.10 is Z = 1.28.
10 Section Section 7. 4Example 2 (pg. 84) A Normal Probability Plot Press STAT and select 1:Edit and press ENTER. Clear all data from L1. ENTER the data from Table 4 on pg. 8 into L1. To set up the normal probability plot, first make sure that there is nothing stored in the Y-registers. Press Y=tand check the Y-registers. If any of them contain a function, move the cursor to that Y-register and press CLEAR. Press 2 nd [STAT PLOT]. Press ENTER to select Plot 1. Highlight On and press ENTER. Set Type to the normal probability plot which is the third selection in the second row. Press ENTER. Set Data List to L1 and Data Axis to X. Next, there are three different types of Marks that you can select for the graph. The first choice, a small square, is the best one to use. Press ZOOM and select 9:ZoomStat and ENTER. The calculator draws the normal probability plot with a horizontal line at the X- axis. This plot is fairly linear, indicating that the data generally follows a normal distribution.
11 112 Section 7.4 4Example 1 (pg.90) Normal Approximation to the Binomial In this binomial experiment, the random variable, X, is the number of individuals with blood type O-negative; the probability, p, that an individual has type O- negative blood is 0.07 and the sample size, n, is 500. We will approximate the probability that fewer than 0 individuals in the sample have type O-negative blood, that is, P(X < 0) using the normal approximation to the binomial. In order to use the normal approximation to the binomial, the first step is to verify that n*p*(1-p) 10. In this example, 500 *.07 *.9 = 2.55, so the requirement is satisfied. Next, calculate the mean and standard deviation of this binomial random variable. The mean, μ, equals n*p = 500 *.07 = 5. The standard deviation, σ, equals n* p*(1 p) = 500*.07*.9 = To approximate P(X < 0) with a normal probability, we calculate P(X 29.5). (Note: This adjustment from 0 to 29.5 is called a continuity correction). Press 2 nd [DISTR], select 2:normalcdf( and type in type in -1E99, 29.5, 5, 5.71 ) and press ENTER. You can compare this probability ( ) that you obtained through a normal approximation to the actual probability obtained from the binomial distribution. Press 2 nd [DISTR], select B:binomcdf( and type in press ENTER. 500,.07, 29 ) and
12 Section The actual P(X < 0) is
13 114 4Example 2 (pg. 91) Normal Approximation to the Binomial In this binomial experiment, the random variable, X, is the number of adult Americans who favor the death penalty for individuals convicted of murder; the probability, p, that an adult American favors the death penalty 0.65 and the sample size, n, is We will approximate the probability that no more than 60 individuals in the sample favor the death penalty, that is, P(X 60) using the normal approximation to the binomial. In order to use the normal approximation to the binomial, the first step is to verify that n*p*(1-p) 10. In this example, 1000 *.65 *.5 = 227.5, so the requirement is satisfied. First, calculate the mean and standard deviation of this binomial random variable. The mean, μ, equals n*p = 1000 *.65 = 650. The standard deviation, σ, equals n * p * (1 p) = 1000 *.65 *.5 = To approximate P(X 60) with a normal probability we calculate P(X 60.5) (Note: This adjustment from 60 to 60.5 is called a continuity correction). Press 2 nd [DISTR], select 2:normalcdf( and type in -1E99, 60.5, 650, ) and press ENTER. The approximate P(X 60) is This result of.0985 indicates that there is approximately a 10% chance that a random sample will contain no more than 60 individuals who favor the death penalty if, in fact, the true proportion of adults who favor the death penalty is 65%. Since the sample result that Erica obtained is not very unusual, she concludes that her survey does not contradict Gallup s findings.
14 TI-89 Instructions 115 TI-89 Instructions: These instructions are designed to give you an overview of the normal probability distribution functions on the TI-89. The TI-89 has two methods for finding areas under the normal curve and displaying the probabilities. Method 1: The area under the normal curve is calculated and a graph of the curve is displayed. To use this method, begin by turning off all other graphs. First check the y-registers by pressing and Y= and clearing all the y-functions. In the Stats/List Editor, press F2 and select 1:Plot Setup. Press F to clear all plots. Press ESC to return to the Editor. Press F5 and select 1:Shade and select 1:Shade Normal. Fill in the entry boxes in the Shade Normal screen (lower bound, upper bound, µ and σ.) Press ENTER. Method 2: The probability is calculated without a display of the normal curve. In the Stats/List Editor, press F5 and select 4:Normal Cdf. Fill in the entry boxes in the Normal Cdf screen (lower bound, upper bound, µ and σ.) Press ENTER. To calculate an x-value that corresponds to a given left-sided area under the normal curve, press F5 and select 2:Inverse and select 1:Inverse Normal. Fill in the entry boxes (left-sided area, µ and σ). Press ENTER.
15 116 TI-Nspire Instructions: These instructions are designed to give you an overview of the normal probability distribution functions on the TI-Nspire handhelds. Press c and select 6:New Document. (Note: If you currently have a document open, the next screen will ask if you want to save the document. Press e to select No. Press.) Select 1:Add Calculator. To access the probability functions (i.e., binomial, normal, poisson, geometric, etc.), press b, select 5:Probability and select 5:Distributions. A menu of probability distributions will be displayed in a list on the left side of the screen. To calculate a probability for the Normal Distribution, select 2:Normal Cdf and enter lower bound, upper bound, µ and σ. Press. To calculate an x-value that corresponds to a given left-sided area under the normal curve, select :Inverse Normal. Fill in the entry boxes (left-sided area, µ and σ). Press.
Normal Probability Distributions
 C H A P T E R Normal Probability Distributions 5 Section 5.2 Example 3 (pg. 248) Normal Probabilities Assume triglyceride levels of the population of the United States are normally distributed with a mean
C H A P T E R Normal Probability Distributions 5 Section 5.2 Example 3 (pg. 248) Normal Probabilities Assume triglyceride levels of the population of the United States are normally distributed with a mean
Continuous Random Variables and the Normal Distribution
 Chapter 6 Continuous Random Variables and the Normal Distribution Continuous random variables are used to approximate probabilities where there are many possible outcomes or an infinite number of possible
Chapter 6 Continuous Random Variables and the Normal Distribution Continuous random variables are used to approximate probabilities where there are many possible outcomes or an infinite number of possible
3. Continuous Probability Distributions
 3.1 Continuous probability distributions 3. Continuous Probability Distributions K The normal probability distribution A continuous random variable X is said to have a normal distribution if it has a probability
3.1 Continuous probability distributions 3. Continuous Probability Distributions K The normal probability distribution A continuous random variable X is said to have a normal distribution if it has a probability
Using the TI-83 Statistical Features
 Entering data (working with lists) Consider the following small data sets: Using the TI-83 Statistical Features Data Set 1: {1, 2, 3, 4, 5} Data Set 2: {2, 3, 4, 4, 6} Press STAT to access the statistics
Entering data (working with lists) Consider the following small data sets: Using the TI-83 Statistical Features Data Set 1: {1, 2, 3, 4, 5} Data Set 2: {2, 3, 4, 4, 6} Press STAT to access the statistics
Statistics TI-83 Usage Handout
 Statistics TI-83 Usage Handout This handout includes instructions for performing several different functions on a TI-83 calculator for use in Statistics. The Contents table below lists the topics covered
Statistics TI-83 Usage Handout This handout includes instructions for performing several different functions on a TI-83 calculator for use in Statistics. The Contents table below lists the topics covered
Manual for the TI-83, TI-84, and TI-89 Calculators
 Manual for the TI-83, TI-84, and TI-89 Calculators to accompany Mendenhall/Beaver/Beaver s Introduction to Probability and Statistics, 13 th edition James B. Davis Contents Chapter 1 Introduction...4 Chapter
Manual for the TI-83, TI-84, and TI-89 Calculators to accompany Mendenhall/Beaver/Beaver s Introduction to Probability and Statistics, 13 th edition James B. Davis Contents Chapter 1 Introduction...4 Chapter
STATISTICAL DISTRIBUTIONS AND THE CALCULATOR
 STATISTICAL DISTRIBUTIONS AND THE CALCULATOR 1. Basic data sets a. Measures of Center - Mean ( ): average of all values. Characteristic: non-resistant is affected by skew and outliers. - Median: Either
STATISTICAL DISTRIBUTIONS AND THE CALCULATOR 1. Basic data sets a. Measures of Center - Mean ( ): average of all values. Characteristic: non-resistant is affected by skew and outliers. - Median: Either
Unit 2: Statistics Probability
 Applied Math 30 3-1: Distributions Probability Distribution: - a table or a graph that displays the theoretical probability for each outcome of an experiment. - P (any particular outcome) is between 0
Applied Math 30 3-1: Distributions Probability Distribution: - a table or a graph that displays the theoretical probability for each outcome of an experiment. - P (any particular outcome) is between 0
Binomial and Normal Distributions. Example: Determine whether the following experiments are binomial experiments. Explain.
 Binomial and Normal Distributions Objective 1: Determining if an Experiment is a Binomial Experiment For an experiment to be considered a binomial experiment, four things must hold: 1. The experiment is
Binomial and Normal Distributions Objective 1: Determining if an Experiment is a Binomial Experiment For an experiment to be considered a binomial experiment, four things must hold: 1. The experiment is
Graphing Calculator Appendix
 Appendix GC GC-1 This appendix contains some keystroke suggestions for many graphing calculator operations that are featured in this text. The keystrokes are for the TI-83/ TI-83 Plus calculators. The
Appendix GC GC-1 This appendix contains some keystroke suggestions for many graphing calculator operations that are featured in this text. The keystrokes are for the TI-83/ TI-83 Plus calculators. The
Chapter 6: Continuous Probability Distributions
 Chapter 6: Continuous Probability Distributions Chapter 5 dealt with probability distributions arising from discrete random variables. Mostly that chapter focused on the binomial experiment. There are
Chapter 6: Continuous Probability Distributions Chapter 5 dealt with probability distributions arising from discrete random variables. Mostly that chapter focused on the binomial experiment. There are
Chapter 8 Probability Models
 Chapter 8 Probability Models We ve already used the calculator to find probabilities based on normal models. There are many more models which are useful. This chapter explores three such models. Many types
Chapter 8 Probability Models We ve already used the calculator to find probabilities based on normal models. There are many more models which are useful. This chapter explores three such models. Many types
Statistics (This summary is for chapters 18, 29 and section H of chapter 19)
 Statistics (This summary is for chapters 18, 29 and section H of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x n =
Statistics (This summary is for chapters 18, 29 and section H of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x n =
Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19)
 Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x
Statistics (This summary is for chapters 17, 28, 29 and section G of chapter 19) Mean, Median, Mode Mode: most common value Median: middle value (when the values are in order) Mean = total how many = x
No, because np = 100(0.02) = 2. The value of np must be greater than or equal to 5 to use the normal approximation.
 1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
1) If n 100 and p 0.02 in a binomial experiment, does this satisfy the rule for a normal approximation? Why or why not? No, because np 100(0.02) 2. The value of np must be greater than or equal to 5 to
Week 7. Texas A& M University. Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4
 Week 7 Oğuz Gezmiş Texas A& M University Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week7 1 / 19
Week 7 Oğuz Gezmiş Texas A& M University Department of Mathematics Texas A& M University, College Station Section 3.2, 3.3 and 3.4 Oğuz Gezmiş (TAMU) Topics in Contemporary Mathematics II Week7 1 / 19
. 13. The maximum error (margin of error) of the estimate for μ (based on known σ) is:
 Statistics Sample Exam 3 Solution Chapters 6 & 7: Normal Probability Distributions & Estimates 1. What percent of normally distributed data value lie within 2 standard deviations to either side of the
Statistics Sample Exam 3 Solution Chapters 6 & 7: Normal Probability Distributions & Estimates 1. What percent of normally distributed data value lie within 2 standard deviations to either side of the
The instructions on this page also work for the TI-83 Plus and the TI-83 Plus Silver Edition.
 The instructions on this page also work for the TI-83 Plus and the TI-83 Plus Silver Edition. The position of the graphically represented keys can be found by moving your mouse on top of the graphic. Turn
The instructions on this page also work for the TI-83 Plus and the TI-83 Plus Silver Edition. The position of the graphically represented keys can be found by moving your mouse on top of the graphic. Turn
Overview. Definitions. Definitions. Graphs. Chapter 5 Probability Distributions. probability distributions
 Chapter 5 Probability Distributions 5-1 Overview 5-2 Random Variables 5-3 Binomial Probability Distributions 5-4 Mean, Variance, and Standard Deviation for the Binomial Distribution 5-5 The Poisson Distribution
Chapter 5 Probability Distributions 5-1 Overview 5-2 Random Variables 5-3 Binomial Probability Distributions 5-4 Mean, Variance, and Standard Deviation for the Binomial Distribution 5-5 The Poisson Distribution
The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations.
 6.1 6.2 The Standard Normal Curve The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations. Basic Properties 1. The total area under the curve is.
6.1 6.2 The Standard Normal Curve The "bell-shaped" curve, or normal curve, is a probability distribution that describes many real-life situations. Basic Properties 1. The total area under the curve is.
Math 120 Introduction to Statistics Mr. Toner s Lecture Notes. Standardizing normal distributions The Standard Normal Curve
 6.1 6.2 The Standard Normal Curve Standardizing normal distributions The "bell-shaped" curve, or normal curve, is a probability distribution that describes many reallife situations. Basic Properties 1.
6.1 6.2 The Standard Normal Curve Standardizing normal distributions The "bell-shaped" curve, or normal curve, is a probability distribution that describes many reallife situations. Basic Properties 1.
Use the data you collected and plot the points to create scattergrams or scatter plots.
 Key terms: bivariate data, scatterplot (also called scattergram), correlation (positive, negative, or none as well as strong or weak), regression equation, interpolation, extrapolation, and correlation
Key terms: bivariate data, scatterplot (also called scattergram), correlation (positive, negative, or none as well as strong or weak), regression equation, interpolation, extrapolation, and correlation
Chapter 7 1. Random Variables
 Chapter 7 1 Random Variables random variable numerical variable whose value depends on the outcome of a chance experiment - discrete if its possible values are isolated points on a number line - continuous
Chapter 7 1 Random Variables random variable numerical variable whose value depends on the outcome of a chance experiment - discrete if its possible values are isolated points on a number line - continuous
Confidence Intervals and Sample Size
 Confidence Intervals and Sample Size Chapter 6 shows us how we can use the Central Limit Theorem (CLT) to 1. estimate a population parameter (such as the mean or proportion) using a sample, and. determine
Confidence Intervals and Sample Size Chapter 6 shows us how we can use the Central Limit Theorem (CLT) to 1. estimate a population parameter (such as the mean or proportion) using a sample, and. determine
5.4 Normal Approximation of the Binomial Distribution Lesson MDM4U Jensen
 5.4 Normal Approximation of the Binomial Distribution Lesson MDM4U Jensen Review From Yesterday Bernoulli Trials have 3 properties: 1. 2. 3. Binomial Probability Distribution In a binomial experiment with
5.4 Normal Approximation of the Binomial Distribution Lesson MDM4U Jensen Review From Yesterday Bernoulli Trials have 3 properties: 1. 2. 3. Binomial Probability Distribution In a binomial experiment with
5.4 Normal Approximation of the Binomial Distribution
 5.4 Normal Approximation of the Binomial Distribution Bernoulli Trials have 3 properties: 1. Only two outcomes - PASS or FAIL 2. n identical trials Review from yesterday. 3. Trials are independent - probability
5.4 Normal Approximation of the Binomial Distribution Bernoulli Trials have 3 properties: 1. Only two outcomes - PASS or FAIL 2. n identical trials Review from yesterday. 3. Trials are independent - probability
Lecture Slides. Elementary Statistics Tenth Edition. by Mario F. Triola. and the Triola Statistics Series. Slide 1
 Lecture Slides Elementary Statistics Tenth Edition and the Triola Statistics Series by Mario F. Triola Slide 1 Chapter 6 Normal Probability Distributions 6-1 Overview 6-2 The Standard Normal Distribution
Lecture Slides Elementary Statistics Tenth Edition and the Triola Statistics Series by Mario F. Triola Slide 1 Chapter 6 Normal Probability Distributions 6-1 Overview 6-2 The Standard Normal Distribution
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Chapter 6 Exam A Name The given values are discrete. Use the continuity correction and describe the region of the normal distribution that corresponds to the indicated probability. 1) The probability of
Chapter 6 Exam A Name The given values are discrete. Use the continuity correction and describe the region of the normal distribution that corresponds to the indicated probability. 1) The probability of
Statistics for Business and Economics: Random Variables:Continuous
 Statistics for Business and Economics: Random Variables:Continuous STT 315: Section 107 Acknowledgement: I d like to thank Dr. Ashoke Sinha for allowing me to use and edit the slides. Murray Bourne (interactive
Statistics for Business and Economics: Random Variables:Continuous STT 315: Section 107 Acknowledgement: I d like to thank Dr. Ashoke Sinha for allowing me to use and edit the slides. Murray Bourne (interactive
Chapter 5 Normal Probability Distributions
 Chapter 5 Normal Probability Distributions Section 5-1 Introduction to Normal Distributions and the Standard Normal Distribution A The normal distribution is the most important of the continuous probability
Chapter 5 Normal Probability Distributions Section 5-1 Introduction to Normal Distributions and the Standard Normal Distribution A The normal distribution is the most important of the continuous probability
Shifting and rescaling data distributions
 Shifting and rescaling data distributions It is useful to consider the effect of systematic alterations of all the values in a data set. The simplest such systematic effect is a shift by a fixed constant.
Shifting and rescaling data distributions It is useful to consider the effect of systematic alterations of all the values in a data set. The simplest such systematic effect is a shift by a fixed constant.
Discrete Random Variables and Their Probability Distributions
 Chapter 5 Discrete Random Variables and Their Probability Distributions Mean and Standard Deviation of a Discrete Random Variable Computing the mean and standard deviation of a discrete random variable
Chapter 5 Discrete Random Variables and Their Probability Distributions Mean and Standard Deviation of a Discrete Random Variable Computing the mean and standard deviation of a discrete random variable
7 THE CENTRAL LIMIT THEOREM
 CHAPTER 7 THE CENTRAL LIMIT THEOREM 373 7 THE CENTRAL LIMIT THEOREM Figure 7.1 If you want to figure out the distribution of the change people carry in their pockets, using the central limit theorem and
CHAPTER 7 THE CENTRAL LIMIT THEOREM 373 7 THE CENTRAL LIMIT THEOREM Figure 7.1 If you want to figure out the distribution of the change people carry in their pockets, using the central limit theorem and
Chapter 4 and Chapter 5 Test Review Worksheet
 Name: Date: Hour: Chapter 4 and Chapter 5 Test Review Worksheet You must shade all provided graphs, you must round all z-scores to 2 places after the decimal, you must round all probabilities to at least
Name: Date: Hour: Chapter 4 and Chapter 5 Test Review Worksheet You must shade all provided graphs, you must round all z-scores to 2 places after the decimal, you must round all probabilities to at least
Section 15.0: The Normal Distribution
 Section 15.0: The Normal Distribution The Normal distribution is the most widely recognized of all probability distributions. It is a continuous distribution, which means its graph has no gaps. The shape
Section 15.0: The Normal Distribution The Normal distribution is the most widely recognized of all probability distributions. It is a continuous distribution, which means its graph has no gaps. The shape
CH 5 Normal Probability Distributions Properties of the Normal Distribution
 Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Properties of the Normal Distribution Example A friend that is always late. Let X represent the amount of minutes that pass from the moment you are suppose to meet your friend until the moment your friend
Graphing a Binomial Probability Distribution Histogram
 Chapter 6 8A: Using a Normal Distribution to Approximate a Binomial Probability Distribution Graphing a Binomial Probability Distribution Histogram Lower and Upper Class Boundaries are used to graph the
Chapter 6 8A: Using a Normal Distribution to Approximate a Binomial Probability Distribution Graphing a Binomial Probability Distribution Histogram Lower and Upper Class Boundaries are used to graph the
Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at
 Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. Let X represent the savings of a resident; X ~ N(3000,
Solutions for practice questions: Chapter 15, Probability Distributions If you find any errors, please let me know at mailto:msfrisbie@pfrisbie.com. 1. Let X represent the savings of a resident; X ~ N(3000,
As you draw random samples of size n, as n increases, the sample means tend to be normally distributed.
 The Central Limit Theorem The central limit theorem (clt for short) is one of the most powerful and useful ideas in all of statistics. The clt says that if we collect samples of size n with a "large enough
The Central Limit Theorem The central limit theorem (clt for short) is one of the most powerful and useful ideas in all of statistics. The clt says that if we collect samples of size n with a "large enough
Density curves. (James Madison University) February 4, / 20
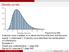 Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Density curves Figure 6.2 p 230. A density curve is always on or above the horizontal axis, and has area exactly 1 underneath it. A density curve describes the overall pattern of a distribution. Example
Lecture 35 Section Wed, Mar 26, 2008
 on Lecture 35 Section 10.2 Hampden-Sydney College Wed, Mar 26, 2008 Outline on 1 2 3 4 5 on 6 7 on We will familiarize ourselves with the t distribution. Then we will see how to use it to test a hypothesis
on Lecture 35 Section 10.2 Hampden-Sydney College Wed, Mar 26, 2008 Outline on 1 2 3 4 5 on 6 7 on We will familiarize ourselves with the t distribution. Then we will see how to use it to test a hypothesis
3500. What types of numbers do not make sense for x? What types of numbers do not make sense for y? Graph y = 250 x+
 Name Date TI-84+ GC 19 Choosing an Appropriate Window for Applications Objective: Choose appropriate window for applications Example 1: A small company makes a toy. The price of one toy x (in dollars)
Name Date TI-84+ GC 19 Choosing an Appropriate Window for Applications Objective: Choose appropriate window for applications Example 1: A small company makes a toy. The price of one toy x (in dollars)
5-1 pg ,4,5, EOO,39,47,50,53, pg ,5,9,13,17,19,21,22,25,30,31,32, pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38
 5-1 pg. 242 3,4,5, 17-37 EOO,39,47,50,53,56 5-2 pg. 249 9,10,13,14,17,18 5-3 pg. 257 1,5,9,13,17,19,21,22,25,30,31,32,34 5-4 pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38 5-5 pg. 281 5-14,16,19,21,22,25,26,30
5-1 pg. 242 3,4,5, 17-37 EOO,39,47,50,53,56 5-2 pg. 249 9,10,13,14,17,18 5-3 pg. 257 1,5,9,13,17,19,21,22,25,30,31,32,34 5-4 pg.269 1,29,13,16,17,19,20,25,26,28,31,33,38 5-5 pg. 281 5-14,16,19,21,22,25,26,30
Discrete Probability Distributions
 Page 1 of 6 Discrete Probability Distributions In order to study inferential statistics, we need to combine the concepts from descriptive statistics and probability. This combination makes up the basics
Page 1 of 6 Discrete Probability Distributions In order to study inferential statistics, we need to combine the concepts from descriptive statistics and probability. This combination makes up the basics
Section 3.5a Applying the Normal Distribution MDM4U Jensen
 Section 3.5a Applying the Normal Distribution MDM4U Jensen Part 1: Normal Distribution Video While watching the video, answer the following questions 1. What is another name for the Empirical rule? The
Section 3.5a Applying the Normal Distribution MDM4U Jensen Part 1: Normal Distribution Video While watching the video, answer the following questions 1. What is another name for the Empirical rule? The
Chapter 6 Confidence Intervals
 Chapter 6 Confidence Intervals Section 6-1 Confidence Intervals for the Mean (Large Samples) VOCABULARY: Point Estimate A value for a parameter. The most point estimate of the population parameter is the
Chapter 6 Confidence Intervals Section 6-1 Confidence Intervals for the Mean (Large Samples) VOCABULARY: Point Estimate A value for a parameter. The most point estimate of the population parameter is the
5.1 Sampling Distributions for Counts and Proportions. Ulrich Hoensch MAT210 Rocky Mountain College Billings, MT 59102
 5.1 Sampling Distributions for Counts and Proportions Ulrich Hoensch MAT210 Rocky Mountain College Billings, MT 59102 Sampling and Population Distributions Example: Count of People with Bachelor s Degrees
5.1 Sampling Distributions for Counts and Proportions Ulrich Hoensch MAT210 Rocky Mountain College Billings, MT 59102 Sampling and Population Distributions Example: Count of People with Bachelor s Degrees
Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc.
 Chapter 8 Measures of Center Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc. Data that can only be integer
Chapter 8 Measures of Center Data that can be any numerical value are called continuous. These are usually things that are measured, such as height, length, time, speed, etc. Data that can only be integer
Math Tech IIII, Mar 13
 Math Tech IIII, Mar 13 The Binomial Distribution III Book Sections: 4.2 Essential Questions: What do I need to know about the binomial distribution? Standards: DA-5.6 What Makes a Binomial Experiment?
Math Tech IIII, Mar 13 The Binomial Distribution III Book Sections: 4.2 Essential Questions: What do I need to know about the binomial distribution? Standards: DA-5.6 What Makes a Binomial Experiment?
Analyzing Accumulated Change: More Applications of Integrals & 7.1 Differences of Accumulated Changes
 Chapter 7 Analyzing Accumulated Change: More Applications of Integrals & 7.1 Differences of Accumulated Changes This chapter helps you effectively use your calculatorõs numerical integrator with various
Chapter 7 Analyzing Accumulated Change: More Applications of Integrals & 7.1 Differences of Accumulated Changes This chapter helps you effectively use your calculatorõs numerical integrator with various
Section 3.4 The Normal Distribution
 Section 3.4 The Normal Distribution Properties of the Normal Distribution Curve 1. We denote the normal random variable with X = x. 2. The curve has a peak at x = µ. 3. The curve is symmetric about the
Section 3.4 The Normal Distribution Properties of the Normal Distribution Curve 1. We denote the normal random variable with X = x. 2. The curve has a peak at x = µ. 3. The curve is symmetric about the
PROBABILITY DISTRIBUTIONS. Chapter 6
 PROBABILITY DISTRIBUTIONS Chapter 6 6.1 Summarize Possible Outcomes and their Probabilities Random Variable Random variable is numerical outcome of random phenomenon www.physics.umd.edu 3 Random Variable
PROBABILITY DISTRIBUTIONS Chapter 6 6.1 Summarize Possible Outcomes and their Probabilities Random Variable Random variable is numerical outcome of random phenomenon www.physics.umd.edu 3 Random Variable
Ti 83/84. Descriptive Statistics for a List of Numbers
 Ti 83/84 Descriptive Statistics for a List of Numbers Quiz scores in a (fictitious) class were 10.5, 13.5, 8, 12, 11.3, 9, 9.5, 5, 15, 2.5, 10.5, 7, 11.5, 10, and 10.5. It s hard to get much of a sense
Ti 83/84 Descriptive Statistics for a List of Numbers Quiz scores in a (fictitious) class were 10.5, 13.5, 8, 12, 11.3, 9, 9.5, 5, 15, 2.5, 10.5, 7, 11.5, 10, and 10.5. It s hard to get much of a sense
Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a
 Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a Announcements: There are some office hour changes for Nov 5, 8, 9 on website Week 5 quiz begins after class today and ends at
Homework: Due Wed, Nov 3 rd Chapter 8, # 48a, 55c and 56 (count as 1), 67a Announcements: There are some office hour changes for Nov 5, 8, 9 on website Week 5 quiz begins after class today and ends at
Section 7.5 The Normal Distribution. Section 7.6 Application of the Normal Distribution
 Section 7.6 Application of the Normal Distribution A random variable that may take on infinitely many values is called a continuous random variable. A continuous probability distribution is defined by
Section 7.6 Application of the Normal Distribution A random variable that may take on infinitely many values is called a continuous random variable. A continuous probability distribution is defined by
Section Introduction to Normal Distributions
 Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
Section 6.1-6.2 Introduction to Normal Distributions 2012 Pearson Education, Inc. All rights reserved. 1 of 105 Section 6.1-6.2 Objectives Interpret graphs of normal probability distributions Find areas
PROBABILITY AND STATISTICS CHAPTER 4 NOTES DISCRETE PROBABILITY DISTRIBUTIONS
 PROBABILITY AND STATISTICS CHAPTER 4 NOTES DISCRETE PROBABILITY DISTRIBUTIONS I. INTRODUCTION TO RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS A. Random Variables 1. A random variable x represents a value
PROBABILITY AND STATISTICS CHAPTER 4 NOTES DISCRETE PROBABILITY DISTRIBUTIONS I. INTRODUCTION TO RANDOM VARIABLES AND PROBABILITY DISTRIBUTIONS A. Random Variables 1. A random variable x represents a value
Examples: Random Variables. Discrete and Continuous Random Variables. Probability Distributions
 Random Variables Examples: Random variable a variable (typically represented by x) that takes a numerical value by chance. Number of boys in a randomly selected family with three children. Possible values:
Random Variables Examples: Random variable a variable (typically represented by x) that takes a numerical value by chance. Number of boys in a randomly selected family with three children. Possible values:
Midterm Test 1 (Sample) Student Name (PRINT):... Student Signature:... Use pencil, so that you can erase and rewrite if necessary.
 MA 180/418 Midterm Test 1 (Sample) Student Name (PRINT):............................................. Student Signature:................................................... Use pencil, so that you can erase
MA 180/418 Midterm Test 1 (Sample) Student Name (PRINT):............................................. Student Signature:................................................... Use pencil, so that you can erase
BARUCH COLLEGE MATH 2205 SPRING MANUAL FOR THE UNIFORM FINAL EXAMINATION Joseph Collison, Warren Gordon, Walter Wang, April Allen Materowski
 BARUCH COLLEGE MATH 05 SPRING 006 MANUAL FOR THE UNIFORM FINAL EXAMINATION Joseph Collison, Warren Gordon, Walter Wang, April Allen Materowski The final examination for Math 05 will consist of two parts.
BARUCH COLLEGE MATH 05 SPRING 006 MANUAL FOR THE UNIFORM FINAL EXAMINATION Joseph Collison, Warren Gordon, Walter Wang, April Allen Materowski The final examination for Math 05 will consist of two parts.
MidTerm 1) Find the following (round off to one decimal place):
 MidTerm 1) 68 49 21 55 57 61 70 42 59 50 66 99 Find the following (round off to one decimal place): Mean = 58:083, round off to 58.1 Median = 58 Range = max min = 99 21 = 78 St. Deviation = s = 8:535,
MidTerm 1) 68 49 21 55 57 61 70 42 59 50 66 99 Find the following (round off to one decimal place): Mean = 58:083, round off to 58.1 Median = 58 Range = max min = 99 21 = 78 St. Deviation = s = 8:535,
GETTING STARTED. To OPEN MINITAB: Click Start>Programs>Minitab14>Minitab14 or Click Minitab 14 on your Desktop
 Minitab 14 1 GETTING STARTED To OPEN MINITAB: Click Start>Programs>Minitab14>Minitab14 or Click Minitab 14 on your Desktop The Minitab session will come up like this 2 To SAVE FILE 1. Click File>Save Project
Minitab 14 1 GETTING STARTED To OPEN MINITAB: Click Start>Programs>Minitab14>Minitab14 or Click Minitab 14 on your Desktop The Minitab session will come up like this 2 To SAVE FILE 1. Click File>Save Project
The Normal Probability Distribution
 1 The Normal Probability Distribution Key Definitions Probability Density Function: An equation used to compute probabilities for continuous random variables where the output value is greater than zero
1 The Normal Probability Distribution Key Definitions Probability Density Function: An equation used to compute probabilities for continuous random variables where the output value is greater than zero
(i.e. the rate of change of y with respect to x)
 Section 1.3 - Linear Functions and Math Models Example 1: Questions we d like to answer: 1. What is the slope of the line? 2. What is the equation of the line? 3. What is the y-intercept? 4. What is the
Section 1.3 - Linear Functions and Math Models Example 1: Questions we d like to answer: 1. What is the slope of the line? 2. What is the equation of the line? 3. What is the y-intercept? 4. What is the
Elementary Statistics Blue Book. The Normal Curve
 Elementary Statistics Blue Book How to work smarter not harder The Normal Curve 68.2% 95.4% 99.7 % -4-3 -2-1 0 1 2 3 4 Z Scores John G. Blom May 2011 01 02 TI 30XA Key Strokes 03 07 TI 83/84 Key Strokes
Elementary Statistics Blue Book How to work smarter not harder The Normal Curve 68.2% 95.4% 99.7 % -4-3 -2-1 0 1 2 3 4 Z Scores John G. Blom May 2011 01 02 TI 30XA Key Strokes 03 07 TI 83/84 Key Strokes
Math Tech IIII, Mar 6
 Math Tech IIII, Mar 6 The Binomial Distribution II Book Sections: 4.2 Essential Questions: How can I compute the probability of any event? What do I need to know about the binomial distribution? Standards:
Math Tech IIII, Mar 6 The Binomial Distribution II Book Sections: 4.2 Essential Questions: How can I compute the probability of any event? What do I need to know about the binomial distribution? Standards:
FINITE MATH LECTURE NOTES. c Janice Epstein 1998, 1999, 2000 All rights reserved.
 FINITE MATH LECTURE NOTES c Janice Epstein 1998, 1999, 2000 All rights reserved. August 27, 2001 Chapter 1 Straight Lines and Linear Functions In this chapter we will learn about lines - how to draw them
FINITE MATH LECTURE NOTES c Janice Epstein 1998, 1999, 2000 All rights reserved. August 27, 2001 Chapter 1 Straight Lines and Linear Functions In this chapter we will learn about lines - how to draw them
Chapter 8. Binomial and Geometric Distributions
 Chapter 8 Binomial and Geometric Distributions Lesson 8-1, Part 1 Binomial Distribution What is a Binomial Distribution? Specific type of discrete probability distribution The outcomes belong to two categories
Chapter 8 Binomial and Geometric Distributions Lesson 8-1, Part 1 Binomial Distribution What is a Binomial Distribution? Specific type of discrete probability distribution The outcomes belong to two categories
Derived copy of Using the Normal Distribution *
 OpenStax-CNX module: m62375 1 Derived copy of Using the Normal Distribution * Cindy Sun Based on Using the Normal Distribution by OpenStax This work is produced by OpenStax-CNX and licensed under the Creative
OpenStax-CNX module: m62375 1 Derived copy of Using the Normal Distribution * Cindy Sun Based on Using the Normal Distribution by OpenStax This work is produced by OpenStax-CNX and licensed under the Creative
MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION
 MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION We have examined discrete random variables, those random variables for which we can list the possible values. We will now look at continuous random variables.
MATH 104 CHAPTER 5 page 1 NORMAL DISTRIBUTION We have examined discrete random variables, those random variables for which we can list the possible values. We will now look at continuous random variables.
These Statistics NOTES Belong to:
 These Statistics NOTES Belong to: Topic Notes Questions Date 1 2 3 4 5 6 REVIEW DO EVERY QUESTION IN YOUR PROVINCIAL EXAM BINDER Important Calculator Functions to know for this chapter Normal Distributions
These Statistics NOTES Belong to: Topic Notes Questions Date 1 2 3 4 5 6 REVIEW DO EVERY QUESTION IN YOUR PROVINCIAL EXAM BINDER Important Calculator Functions to know for this chapter Normal Distributions
Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the
 Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the mean, use the CLT for the mean. If you are being asked to
Using the Central Limit Theorem It is important for you to understand when to use the CLT. If you are being asked to find the probability of the mean, use the CLT for the mean. If you are being asked to
In a binomial experiment of n trials, where p = probability of success and q = probability of failure. mean variance standard deviation
 Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
Name In a binomial experiment of n trials, where p = probability of success and q = probability of failure mean variance standard deviation µ = n p σ = n p q σ = n p q Notation X ~ B(n, p) The probability
The Central Limit Theorem for Sample Means (Averages)
 The Central Limit Theorem for Sample Means (Averages) By: OpenStaxCollege Suppose X is a random variable with a distribution that may be known or unknown (it can be any distribution). Using a subscript
The Central Limit Theorem for Sample Means (Averages) By: OpenStaxCollege Suppose X is a random variable with a distribution that may be known or unknown (it can be any distribution). Using a subscript
1Find probabilities by. 2Solve real-world. Now. Then. Why?
 Distributions Then You found probabilities with permutations and combinations. (Lesson 12-4) Now 1Find probabilities by using random variables. 2Solve real-world problems using distributions. Why? A gaming
Distributions Then You found probabilities with permutations and combinations. (Lesson 12-4) Now 1Find probabilities by using random variables. 2Solve real-world problems using distributions. Why? A gaming
Chapter 14 - Random Variables
 Chapter 14 - Random Variables October 29, 2014 There are many scenarios where probabilities are used to determine risk factors. Examples include Insurance, Casino, Lottery, Business, Medical, and other
Chapter 14 - Random Variables October 29, 2014 There are many scenarios where probabilities are used to determine risk factors. Examples include Insurance, Casino, Lottery, Business, Medical, and other
Chapter 6: Random Variables. Ch. 6-3: Binomial and Geometric Random Variables
 Chapter : Random Variables Ch. -3: Binomial and Geometric Random Variables X 0 2 3 4 5 7 8 9 0 0 P(X) 3???????? 4 4 When the same chance process is repeated several times, we are often interested in whether
Chapter : Random Variables Ch. -3: Binomial and Geometric Random Variables X 0 2 3 4 5 7 8 9 0 0 P(X) 3???????? 4 4 When the same chance process is repeated several times, we are often interested in whether
Sampling Distributions
 Section 8.1 119 Sampling Distributions Section 8.1 C H A P T E R 8 4Example 2 (pg. 378) Sampling Distribution of the Sample Mean The heights of 3-year-old girls are normally distributed with μ=38.72 and
Section 8.1 119 Sampling Distributions Section 8.1 C H A P T E R 8 4Example 2 (pg. 378) Sampling Distribution of the Sample Mean The heights of 3-year-old girls are normally distributed with μ=38.72 and
Normal Distribution: Introduction
 Connexions module: m16979 1 Normal Distribution: Introduction Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Connexions module: m16979 1 Normal Distribution: Introduction Susan Dean Barbara Illowsky, Ph.D. This work is produced by The Connexions Project and licensed under the Creative Commons Attribution License
Chapter 4 Probability Distributions
 Slide 1 Chapter 4 Probability Distributions Slide 2 4-1 Overview 4-2 Random Variables 4-3 Binomial Probability Distributions 4-4 Mean, Variance, and Standard Deviation for the Binomial Distribution 4-5
Slide 1 Chapter 4 Probability Distributions Slide 2 4-1 Overview 4-2 Random Variables 4-3 Binomial Probability Distributions 4-4 Mean, Variance, and Standard Deviation for the Binomial Distribution 4-5
ECON 214 Elements of Statistics for Economists 2016/2017
 ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
ECON 214 Elements of Statistics for Economists 2016/2017 Topic The Normal Distribution Lecturer: Dr. Bernardin Senadza, Dept. of Economics bsenadza@ug.edu.gh College of Education School of Continuing and
CHAPTER 7 INTRODUCTION TO SAMPLING DISTRIBUTIONS
 CHAPTER 7 INTRODUCTION TO SAMPLING DISTRIBUTIONS Note: This section uses session window commands instead of menu choices CENTRAL LIMIT THEOREM (SECTION 7.2 OF UNDERSTANDABLE STATISTICS) The Central Limit
CHAPTER 7 INTRODUCTION TO SAMPLING DISTRIBUTIONS Note: This section uses session window commands instead of menu choices CENTRAL LIMIT THEOREM (SECTION 7.2 OF UNDERSTANDABLE STATISTICS) The Central Limit
CH 6 Review Normal Probability Distributions College Statistics
 CH 6 Review Normal Probability Distributions College Statistics Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Using the following uniform density
CH 6 Review Normal Probability Distributions College Statistics Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Using the following uniform density
The Normal Distribution. (Ch 4.3)
 5 The Normal Distribution (Ch 4.3) The Normal Distribution The normal distribution is probably the most important distribution in all of probability and statistics. Many populations have distributions
5 The Normal Distribution (Ch 4.3) The Normal Distribution The normal distribution is probably the most important distribution in all of probability and statistics. Many populations have distributions
TI-83 Plus Workshop. Al Maturo,
 Solving Equations with one variable. Enter the equation into: Y 1 = x x 6 Y = x + 5x + 3 Y 3 = x 3 5x + 1 TI-83 Plus Workshop Al Maturo, AMATURO@las.ch We shall refer to this in print as f(x). We shall
Solving Equations with one variable. Enter the equation into: Y 1 = x x 6 Y = x + 5x + 3 Y 3 = x 3 5x + 1 TI-83 Plus Workshop Al Maturo, AMATURO@las.ch We shall refer to this in print as f(x). We shall
STAT Chapter 5: Continuous Distributions. Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s.
 STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
STAT 515 -- Chapter 5: Continuous Distributions Probability distributions are used a bit differently for continuous r.v. s than for discrete r.v. s. Continuous distributions typically are represented by
Lecture 9. Probability Distributions. Outline. Outline
 Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
Outline Lecture 9 Probability Distributions 6-1 Introduction 6- Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7- Properties of the Normal Distribution
ECON 214 Elements of Statistics for Economists
 ECON 214 Elements of Statistics for Economists Session 7 The Normal Distribution Part 1 Lecturer: Dr. Bernardin Senadza, Dept. of Economics Contact Information: bsenadza@ug.edu.gh College of Education
ECON 214 Elements of Statistics for Economists Session 7 The Normal Distribution Part 1 Lecturer: Dr. Bernardin Senadza, Dept. of Economics Contact Information: bsenadza@ug.edu.gh College of Education
Chapter 4 Random Variables & Probability. Chapter 4.5, 6, 8 Probability Distributions for Continuous Random Variables
 Chapter 4.5, 6, 8 Probability for Continuous Random Variables Discrete vs. continuous random variables Examples of continuous distributions o Uniform o Exponential o Normal Recall: A random variable =
Chapter 4.5, 6, 8 Probability for Continuous Random Variables Discrete vs. continuous random variables Examples of continuous distributions o Uniform o Exponential o Normal Recall: A random variable =
Lecture 9. Probability Distributions
 Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
Lecture 9 Probability Distributions Outline 6-1 Introduction 6-2 Probability Distributions 6-3 Mean, Variance, and Expectation 6-4 The Binomial Distribution Outline 7-2 Properties of the Normal Distribution
AP Statistics Quiz A Chapter 17
 AP Statistics Quiz A Chapter 17 Name The American Red Cross says that about 11% of the U.S. population has Type B blood. A blood drive is being held at your school. 1. How many blood donors should the
AP Statistics Quiz A Chapter 17 Name The American Red Cross says that about 11% of the U.S. population has Type B blood. A blood drive is being held at your school. 1. How many blood donors should the
The Normal Distribution
 Stat 6 Introduction to Business Statistics I Spring 009 Professor: Dr. Petrutza Caragea Section A Tuesdays and Thursdays 9:300:50 a.m. Chapter, Section.3 The Normal Distribution Density Curves So far we
Stat 6 Introduction to Business Statistics I Spring 009 Professor: Dr. Petrutza Caragea Section A Tuesdays and Thursdays 9:300:50 a.m. Chapter, Section.3 The Normal Distribution Density Curves So far we
Math 166: Topics in Contemporary Mathematics II
 Math 166: Topics in Contemporary Mathematics II Ruomeng Lan Texas A&M University October 15, 2014 Ruomeng Lan (TAMU) Math 166 October 15, 2014 1 / 12 Mean, Median and Mode Definition: 1. The average or
Math 166: Topics in Contemporary Mathematics II Ruomeng Lan Texas A&M University October 15, 2014 Ruomeng Lan (TAMU) Math 166 October 15, 2014 1 / 12 Mean, Median and Mode Definition: 1. The average or
Overview. Definitions. Definitions. Graphs. Chapter 4 Probability Distributions. probability distributions
 Chapter 4 Probability Distributions 4-1 Overview 4-2 Random Variables 4-3 Binomial Probability Distributions 4-4 Mean, Variance, and Standard Deviation for the Binomial Distribution 4-5 The Poisson Distribution
Chapter 4 Probability Distributions 4-1 Overview 4-2 Random Variables 4-3 Binomial Probability Distributions 4-4 Mean, Variance, and Standard Deviation for the Binomial Distribution 4-5 The Poisson Distribution
Binomial Probabilities The actual probability that P ( X k ) the formula n P X k p p. = for any k in the range {0, 1, 2,, n} is given by. n n!
 Introduction We are often more interested in experiments in which there are two outcomes of interest (success/failure, make/miss, yes/no, etc.). In this chapter we study two types of probability distributions
Introduction We are often more interested in experiments in which there are two outcomes of interest (success/failure, make/miss, yes/no, etc.). In this chapter we study two types of probability distributions
Homework: Due Wed, Feb 20 th. Chapter 8, # 60a + 62a (count together as 1), 74, 82
 Announcements: Week 5 quiz begins at 4pm today and ends at 3pm on Wed If you take more than 20 minutes to complete your quiz, you will only receive partial credit. (It doesn t cut you off.) Today: Sections
Announcements: Week 5 quiz begins at 4pm today and ends at 3pm on Wed If you take more than 20 minutes to complete your quiz, you will only receive partial credit. (It doesn t cut you off.) Today: Sections
22.2 Shape, Center, and Spread
 Name Class Date 22.2 Shape, Center, and Spread Essential Question: Which measures of center and spread are appropriate for a normal distribution, and which are appropriate for a skewed distribution? Eplore
Name Class Date 22.2 Shape, Center, and Spread Essential Question: Which measures of center and spread are appropriate for a normal distribution, and which are appropriate for a skewed distribution? Eplore
Using the Central Limit
 Using the Central Limit Theorem By: OpenStaxCollege It is important for you to understand when to use the central limit theorem. If you are being asked to find the probability of the mean, use the clt
Using the Central Limit Theorem By: OpenStaxCollege It is important for you to understand when to use the central limit theorem. If you are being asked to find the probability of the mean, use the clt
Stat 101 Exam 1 - Embers Important Formulas and Concepts 1
 1 Chapter 1 1.1 Definitions Stat 101 Exam 1 - Embers Important Formulas and Concepts 1 1. Data Any collection of numbers, characters, images, or other items that provide information about something. 2.
1 Chapter 1 1.1 Definitions Stat 101 Exam 1 - Embers Important Formulas and Concepts 1 1. Data Any collection of numbers, characters, images, or other items that provide information about something. 2.
Math Tech IIII, May 7
 Math Tech IIII, May 7 The Normal Probability Models Book Sections: 5.1, 5.2, & 5.3 Essential Questions: How can I use the normal distribution to compute probability? Standards: S.ID.4 Properties of the
Math Tech IIII, May 7 The Normal Probability Models Book Sections: 5.1, 5.2, & 5.3 Essential Questions: How can I use the normal distribution to compute probability? Standards: S.ID.4 Properties of the
