A Fast Algorithm for Computing Binomial Coefficients Modulo Powers of Two
|
|
|
- Candice Whitehead
- 5 years ago
- Views:
Transcription
1 A Fast Algorithm for Computing Binomial Coefficients Modulo Powers of Two Mugurel Ionut Andreica To cite this version: Mugurel Ionut Andreica. A Fast Algorithm for Computing Binomial Coefficients Modulo Powers of Two. The Scientific World Journal, Hindawi Publishing Corporation, 3, 3, <.55/3/75358>. <hal-9477> HAL Id: hal Submitted on 3 Nov 3 HAL is a multi-disciplinary open access archive for the deposit and dissemination of scientific research documents, whether they are published or not. The documents may come from teaching and research institutions in France or abroad, or from public or private research centers. L archive ouverte pluridisciplinaire HAL, est destinée au dépôt et à la diffusion de documents scientifiques de niveau recherche, publiés ou non, émanant des établissements d enseignement et de recherche français ou étrangers, des laboratoires publics ou privés.
2 A Fast Algorithm for Computing Binomial Coefficients Modulo Powers of Two Mugurel Ionuţ ANDREICA Computer Science Department, Politehnica University of Bucharest, Bucharest, Romania Key words: binomial coefficients;modulo; powers of two; power sums; elementary symmetric polynomials; algorithm Abstract: I present a new algorithm for computing binomial coefficients modulo N. The proposed method has an O(N 3 Multiplication(N+N 4 preprocessing time, after which a binomial coefficient with P N - can be computed modulo N in O(N log(n Multiplication(N time. Multiplication(N denotes the time complexity of multiplying two N-bit numbers, which can range from O(N to O(N log(n log(log(n or better. Thus, the overall time complexity for evaluating M binomial coefficients modulo N, with P N -, is O((N 3 +M N log(n Multiplication(N+N 4. After preprocessing we can actually compute binomial coefficients modulo any R with R N. For larger values of P and variations of Lucas theorem must be used first in order to reduce the computation to the evaluation of multiple (O(log(P binomial coefficients P, (or restricted types of factorials P! modulo N, with P N -.. INTRODUCTION In this paper I present a novel efficient algorithm for computing binomial coefficients modulo N (N. The definition of the binomial coefficient is the usual one: P!!( P! = ( We will mainly consider the case where P N - and, after fully handling this case, we will discuss how to compute modulo N for P N. The presented algorithm consists of a preprocessing stage which taes O(N 3 Multiplication(N+N 4 time, where Multiplication(N is the time complexity for multiplying two N-bit numbers. Multiplication(N can range from O(N (the naive multiplication algorithm to O(N log(n log(log(n or slightly better [9, 7]. After the preprocessing stage, a binomial coefficient (with P N - can be computed modulo N in O(N log(n Multiplication(N time. Of course, the presented algorithm can evaluate a binomial coefficient modulo any with N (after computing it modulo N we only need to eep the least significant bits out of the computed N bits. The rest of this paper is structured as follows. In Sections -6 I present the steps of the preprocessing stage. In Sections 7-9 I present the algorithm which computes the binomial coefficients modulo N, considering that the preprocessing stage was completed. In Section I discuss related wor and in Section I conclude and discuss future wor. I will summarize below the contents of each section describing the preprocessing steps and the algorithm itself. The preprocessing stage consists of 5 steps. The first step consists of computing all the small binomial coefficients. The term small refers to the values of P and. A binomial coefficient is defined to be small if P N. This step is presented in Section. There are O(N small binomial coefficients and we can compute all of them with only O(N additions of pairs of N-bit numbers. The second preprocessing step (presented in Section 3 consists of computing a set of large binomial coefficients. All the binomial coefficients of the form P -X,, with X, N, are defined to be large. There are O(N 3 such binomial coefficients and all of them can be computed in O(N Multiplication(N+N 4 overall time. This step requires the largest amount of memory (among all the preprocessing steps in order to store the O(N 3 large binomial coefficients. In Section 4 I present the third step of the preprocessing stage, which consists of computing power sums of consecutive numbers (where the number of such numbers is a power of. There are O(N powers sums which can all be computed in O(N log(n Multiplication(N time. The 4 th preprocesing step (presented in Section 5 consists of computing the sums of the products of the elements of all the subsets of a given size of a set consisting of the first P ( P N positive integer numbers. In order to achieve this goal inclusion-exclusion-based equations from the theory of elementary symmetric functions and polynomials are used. There are only O(N values being computed, but it taes O(N 3 Multiplication(N time to compute them. This step is the performance bottlenec step in the preprocessing stage. Finally, in Section 6 I present the last step of the preprocessing stage: computing the sums of the products of the elements of all the odd-element subsets of a given size of a set consisting of the first P ( P N positive integer numbers. Lie in the previous case there are O(N values which need to be computed during this step. In Section 7 I will show how to efficiently find the largest odd divisior (modulo N of P! (for P N -. In Section 8 I will present the actual algorithm for computing binomial coefficients modulo N (for P N - and in Section 9 I will discuss extensions to the case P N. Note that by precomputing all the mentioned values we are capable of achieving a running time of O(N log(n Multiplication(N for computing a single binomial coefficient (with P N -. When computing M binomial coefficients we achieve a running time of O(M N log(n Multiplication(N. Since computing a binomial coefficient requires the values from the preprocessing stage, the time complexity would increase significantly if we had to compute all those values for each binomial coefficient (instead of computing them only once and then reusing them for each binomial coefficient.
3 . COMPUTING SMALL BINOMIAL COEFFICIENTS: FOR P N The first step of the preprocessing algorithm consists of computing the binomial coefficients S = mod N for small values of P and ( P N. This can be achieved easily with O(N N-bit additions (O(N 3 time overall, as an addition taes O(N time. We have: S= ( and S>P= (3 For P we use the well-nown formula: S = SP-,- + SP-, (mod N (4 3. COMPUTING LARGE BINOMIAL COEFFICIENTS: P -X, FOR X, N The second step of the preprocessing algorithm consists of computing large binomial coefficients P -X, modulo N for X, N; we denote these values by LX,. Obviously, if P <X or > P -X then LX,=. Otherwise, let Xmax(P = min{ P, N} (5 For X Xmax(P, from the definition of the binomial coefficients, we have that LX,= (6 and LX,>=LX,- ( P -X-+/ (7 Since all the computations are performed modulo N, we need to perform multiplications by -. But only has a multiplicative inverse (modulo N if it is odd. Thus, we will have to compute two different values: LC (X, = the largest odd divisor of P -X,; Exp (X, = the exponent of in the prime factor decomposition of P -X,. We start with LC (X,= and Exp (X,=. For > we will compute: A = the largest odd divisior of P -X-+ B = the exponent of in the prime factor decomposition of P -X-+ C = the largest odd divisior of D = the exponent of in the prime factor decomposition of Finding A and B can be performed in O(N time by examining the bits of P -X-+. With these values computed we will have: LC (X,> = LC (X,- A C - Exp (X,> = Exp (X, + B - D We will assume that the multiplicative inverses of all the odd numbers C from to N were precomputed. The inverse of an odd number C (modulo N, for N 3 is equal to N C = C (8 For N the inverse of an odd number is the odd number itself. Eq. (8 provides a way of computing the inverse of an odd number C< N using O(N N-bit multiplications. Note that more efficient alternatives exist - e.g. in [] an algorithm with O(N N-bit additions, left bit-shifts and right bit-shifts for computing the inverse is presented (which would tae only O(N time overall, instead of O(N Multiplication(N. However, the algorithm obtained from eq. (8 will never be the bottlenec in any step of the presented algorithm, so there will be no problem using it. After computing the values LC (X, and Exp (X, we have: X, LX, = LC (X, (mod N (9 We will assume that we previously precomputed all the numbers for N. This way we have a method for computing all the values LX,. Let s perform a time complexity analysis. For each of the O(N 3 tuples (X, we spend O(N+Multiplication(N time. Precomputing the inverses of small numbers ( N taes O(N Multiplication(N time (it taes O(N Multiplication(N time to apply eq. (8. Precomputing the powers of two taes only O(N time (we simply shift one bit to the left to obtain +. A more efficient method is to apply the previously defined algorithm only for X=Xmax(P. Then, for X<Xmax(P and min{n, P -X} we have: LX, = LX+,- + LX+, (mod N ( With this method we spend O(N+Multiplication(N time only for O(N tuples (the tuples (X,. For the remaining O(N 3 tuples we perform a simple addition (which taes O(N time. Thus, the overall time complexity is O(N Multiplication(N+N 4. Exp 4. COMPUTING POWER SUMS OF CONSECUTIVE NUMBERS In this section we will efficiently compute power sums of consecutive numbers starting from and ending at a power of two. We define ( P PSUM( = ( P = (mod N, ( = where P N and N. We will start with the easy cases: PSUM(,= (independent of the value of and PSUM(= P (mod N. For P and we can write PSUM( = PSUM(P-, + ( P- + + ( P ( P- + P- (mod N ( Let s consider the terms ( P- +i ( i P-. Using Newton s binomial theorem, we can write this term as, ( = i Thus, PSUM( can be written as PSUM(P-, + = i= = =, (, (, ( i= i i = = PSUM ( P, (3 (4 Note that all the terms with > N / (P- are zero modulo N (because (P- is a multiple of N. Thus, we only need to evaluate O(min{,N/(P-} such terms: N min{, } = PSUM ( = PSUM ( P, + S, ( PSUM ( P, (5 Assuming that we previously computed all the values Si, ( i, N, then this part taes O(N log(n
4 Multiplication(N time (because, for each value of, the algorithm performs at most O(+N/ + N/ N/(N- =O(N log(n multiplications for all the values of P. 5. COMPUTING SUMS OF SUBSET PRODUCTS In this section we will compute the values SSP( = the sum of all the products of the elements of the -elementsubsets of the numbers,,..., P (modulo N for P N and min{ P,N}. To be more precise, SSP( = v(... v( (mod N (6 v ( < v( <... < v( We have SSP(= and SSP(=PSUM( (i.e. the sum of all the numbers,,..., P. For N we will use formulas based on the inclusionexclusion principle derived from the theory of power sum and elementary symmetric polynomials [6]: SSP( = ( PSUM ( (7 = The problem that we face now is that - (mod N exists only when is odd. This implies that we will not be able to compute all the values SSP( (for a fixed value of P with the same precision. Let s define Precision(=the maximum value U N such that the last U bits of SSP( are correct (i.e. we were able to compute SSP( modulo U, but not modulo V for V>U, unless we perform computations modulo N for N >N. Obviously, Precision(=Precision(=N. Let s consider the case. We will have Precision( Precision(-: the precision either stays the same or decreases as increases. At first we evaluate the sum Sum( = ( PSUM (. (8 = This sum is correctly computed modulo Precision(-. Then we compute: A=the largest odd divisor of B=the exponent of in the prime factor decomposition of We set Precision(=Precision(--B. We then multiply Sum( by A -, obtaining Sum (. Finally, we can compute SSP( as Sum ( divided by B. It should be mentioned that A - is computed as the multiplicative inverse of A modulo Precision(- instead of modulo N. We should now prove that Precision(>N- for. This is obviously true for =. In general, Precision( is equal to N minus the exponent of in!. Since the exponent of in! is equal to log =, (9 it is obvious that this value cannot exceed -. Thus, Precision( N-(->N-. This proof is very important. Although we cannot compute all the SSP( values with the same precision, we will see that this precision will be sufficient in order to obtain exact and correct results when computing binomial coefficients modulo N. This is because in all the equations where SSP( is involved, it will be multiplied by. Let s perform the time complexity analysis now. For each pair ( we need to perform N multiplications of N-bit numbers. It would seem that we also need to compute - for each pair ( (which would require another N multiplications of N-bit numbers for raising to the P appropriate power. Although this would not affect the theoretical time complexity, we should notice that Precision( depends only on the numbers,...,, and does not depend on P at all (we only need to have P. Thus, we only need to compute - once for the first value of P for which we will compute SSP( (and then we will cache - and use it later when it is needed. Overall, the time complexity is dominated by the N 3 multiplications which need to be performed, obtaining an O(N 3 Multiplication(N time complexity. This step of the preprocessing stage is the bottlenec, having the largest time complexity (it is the step which dominates the computations of the preprocessing stage. 6. COMPUTING SUMS OF ODD-ELEMENT SUBSET PRODUCTS In this section we will compute the values SOSP( = the sum of all the products of the elements of the odd R- element-subsets of the numbers,,..., P, where R= P- - (for P N and min{ P-,N}. To be more precise, SOSP( = u(... u( R (mod N ( P u ( < u( <... < u( R < u(i is odd, i R P- R= This time we are interested in subsets with large sizes, i.e. sizes ranging from P- -N to P- (and, thus, having N. For = we are interested in computing the product = ( (mod N ( By using Newton s binomial theorem we can rewrite eq. ( as: = SSP ( P, ( (mod N ( We notice that for N each term of the sum is zero modulo N. Moreover, notice that SSP(P-, is multiplied by. Since the precision of SSP(P-, is larger than N-, the result of this multiplication is exact modulo N. Thus, by iterating through all the values of from to min{ P-,N-} we have an algorithm which requires O(N multiplications of N-bit numbers for computing SOSP(. For > we will need to use a different approach. Let s choose a subset of odd numbers from to P- of size P- -: u(,..., u( P- -. The product of all the elements in the subset is equal to u(... u( P- - = ( v(-... ( v( P- - - (we wrote u(i= v(i- for i P- -. By using Newton s binomial theorem we can rewrite this product as: = ( P, (3 where we denoted by SSP v(,..., v( ( P, v(,..., v( the sum of products of the elements of the subsets of size of the set {v(,..., v( P- -}. In order to compute SOSP( we will need to sum eq. (3 over all the odd-element subsets u(,..., u( P- - (or, equivalently, over all the subsets v(,..., v( P- - of the set {,,..., P- }. Again, we should notice that all the terms of the sum from eq. (3 are zero modulo N for N. Let s consider a subset w(,..., w( of the set {,..., P- } (with N. This subset is part of P- -, P- -- subsets v(,..., v( P- - (where each element is chosen from the set
5 {,..., P- }. With this observation we can rewrite eq. (3 as: min{ N, } = (, P, (4 Since P- -, P- --= P- -, and we already computed these values as LP-,,, we can finally rewrite eq. (4 as: min{ N, } = ( LC ( P,, P, (5 We can now use eq. (5 directly in order to obtain an algorithm performing O(N multiplications of N-bit numbers for computing SOSP(. Of course, as before, all computations are performed modulo N. The time complexity in this case is simple to analyze: there are O(N 3 multiplications performed, so the complexity is O(N 3 Multiplication(N. This part can be improved because, as we will see in Section 7, for a given value of P we will only need the values SOSP( such that N/(P+. Thus, overall, we actually need to compute the values SOSP( for only O(N log(n pairs ( instead of O(N such pairs. In this case the time complexity drops down to O(N log(n Multiplication(N. 7. COMPUTING THE LARGEST ODD DIVISOR OF P! MODULO N In this section we will compute the largest odd divisor of P! (modulo N. We will denote this number by F (P. Let s consider the binary decomposition of i.e. P = ( (K (6 where (>...>(K (we will assume P and, thus, K. We will first evaluate FODD(P = the product of all the odd numbers less than or equal to P! (modulo N. For each bit (i of P we will compute a value FFODD(i. FFODD( will be equal to the product (modulo N of all the odd numbers from the interval [, ( ]. FFODD(i> will be equal to the product (modulo N of all the odd numbers from the interval [ ( (i- +, ( (i- + (i ]. Thus, we will have FODD(P = FFODD( FFODD(K. (7 FFODD( is easy to compute. If (= then FFODD(=; otherwise it is equal to SOSP((,. Let s consider now the case i>. Let X(i be equal to ( (i-. If (i= then FFODD(i=(X(i+ mod N. Otherwise we can write FFODD(i as ( i ( X ( i + (mod N (8 = By using Newton s binomial theorem we can rewrite eq. (8 as ( i ( i SSP ( ( i, ( X ( i (9 = We must notice that we only need to consider values of up to min{ (i-,n-}, because for N the corresponding term of the sum is zero modulo N. We should also notice that SSP((i-, is multiplied by. Since its precision is larger than N-, the multiplication of SSP((i-, and is exact modulo N. Then we iterate with in descending order. For the initial value of we compute XP(i=(X(i- ; for the other values we only multiply XP(i by (X(i- - in order to obtain XP(i as (X(i-. We now have an algorithm performing O(N multiplications of N-bit numbers for computing FFODD(i. Overall, we have an algorithm performing O(N multiplications of N-bit numbers for computing FODD(P (O(N multiplications for each of the O(N bits of P. However, we can do better, by rewriting eq. (8 in a different way. ( i X ( i SOSP( ( i, (3 = Note that X(i is even. In fact, it is a multiple of (i-, meaning that it is at least a multiple of (i+. For >(N/((i+ each term of the sum will be zero modulo N. Thus, we only need to consider at most N/((i++ terms (from = to =N/((i+. We will start with XP(i= when = and then, for each subsequent value of, we will multiply XP(i by X(i in order to have XP(i=X(i at each iteration. Overall we only need to consider O(N log(n terms for computing FODD(P (O(N + N/((+ + N/(( N/((K+; for each such term an N-bit multiplication needs to be performed. Now that we have a method of efficiently computing FODD(P, we can write F (P> as: F (P> = FODD(P + F (P/ (3 F ( P is equal to. Since P is of the order of magnitude of N and FODD(P can be evaluated with O(N log(n N-bit multiplications, computing F (P will require O(N log(n N-bit multiplications, obtaining an O(N log(n Multiplication(N time complexity. 8. COMPUTING THE BINOMIAL COEFFICIENT ( P N - MOD N Let s consider the binomial coefficient with P N -. In order to evaluate it modulo N we will first need to compute F (P, F ( and F (P-. Then, we will need to find the largest exponent exp(x such that exp(x is a divisor of X!, for X= and P-. We can use eq. (9 for this. Then, the answer will be exp(p-exp(-exp(p- F (P F ( - F (P- - (mod N (3 As discussed earlier, the multiplicative inverse of an odd number C modulo N can be computed by using eq. (8, using O(N N-bit multiplications. Computing exp(x, where X N - can be performed in O(N time (O(N bit shifts to the right and O(N N-bit number additions. Thus, the time complexity for computing the binomial coefficient modulo N is dominated by the computation of F (P, F ( and F (P-. 9. EXTENSIONS FOR COMPUTING MODULO N FOR P N In order to compute a binomial coefficient modulo N for P N (and P we need to mae use of some variations of Lucas theorem [5]. If P=P N +P and = N + then, according to [5], we have: = P N/, N/ P, (mod N (33 Thus, in order to compute modulo N we will need to evaluate O(log(P binomial coefficients P, where,p N -. After the O(N 3 Multiplication(N preprocessing stage, evaluating modulo N will tae only O(N log(n log(p Multiplication(N+log (P time (the log (P factor appears when P N because we need to perform O(log(P divisions, each of which taing O(log(P time because they can be implemented by shifting bits to the
6 right, in order to obtain the O(log(P binomial coefficients or factorials which are needed in order to compute modulo N. Other methods for reducing the computation of modulo N (for P N to the computation of multiple (O(log(P factorials P! (of a restricted type with P N - were presented in [].. RELATED WORK The problem of computing binomial coefficients modulo various numbers has been widely studied in the scientific literature. In [8] properties of binomial coefficients modulo prime numbers are discussed, including Lucas theorem, which provides a simple way of computing modulo R, where R is a prime number. The computation of is reduced to the computation of multiple (O(log(P binomial coefficients P, modulo R, with P R-. In [4] the authors studied periodicity properties of the binomial coefficients modulo both prime and composite numbers. Congruence properties of binomial coefficients modulo prime powers were presented in [5] and congruence properties of products of binomial coefficients modulo composite numbers were studied in [3]. The general method of computing binomial coefficients modulo a composite number M is to evaluate them modulo the (maximal prime powers which are divisors of M and then use the Chinese Remained Theorem [6] in order to obtain the result modulo M (as observed in [3], but in [3] a more direct study of these values is performed (i.e. the Chinese Remainder Theorem is not used. Properties of the residues of binomial coefficients and their products modulo prime powers were studied in [3]. An algorithm for computing binomial coefficients modulo prime powers (for any prime was presented in []. The algorithm taes O(log (P + v 4 log(p log(u + v 4 u log 3 (u time for computing modulo u v, where u is a prime number (this time complexity was stated in [], but a sufficiently detailed complexity analysis was not provided. When u= and v=n this reduces to O(log (P + N 4 log(p + N 4. If we consider Multiplication(N=O(N our algorithm taes O(N 5 time for preprocessing and O(N 4 log(n log(p+log (P in order to compute in the general case. These time complexities are slightly worse than the ones obtained in []. However, when considering Multiplication(N=O(N log(n log(log(n [9, 7] we obtain an O(N 4 log(n log(log(n time complexity for the preprocessing stage and an O(N 3 log (N log(log(n log(p+log (P time complexity for actually computing the binomial coefficient modulo N. In this case our time complexities are slightly better than the ones presented in [] (when log(p>log(n log(log(n. However, it is not clear which time complexity for the multiplication of two N- bit numbers was considered in []. [7] uses sums of binomial coefficients modulo when obtaining results related to the Garsia entropy. Binomial coefficients also occur in other equations regarding information theory formulas (e.g. [, 8]. Binomial coefficients also have applications in many other areas (e.g., statistics [], binomial distribution [4], Chebyshev polynomials [], etc... CONCLUSIONS AND FUTURE WORK In this paper I presented a novel efficient algorithm for computing binomial coefficients modulo N. The algorithm consists of a preprocessing stage, after which any number of binomial coefficients can be computed modulo N (or modulo any number with N. The time complexity of the presented algorithm is comparable with that of state-of-the-art algorithms for computing binomial coefficients modulo prime powers []. In fact, the time complexity of the algorithm presented in this paper is slightly better than that of the algorithm presented in [], but since a sufficiently detailed analysis of the time complexity in [] is not provided by the authors, it is not clear if the algorithm from [] cannot be improved any further. In any case, because the algorithm presented in this paper consists of a preprocessing stage, a slightly worse preprocessing time complexity (in some cases could be balanced by computing multiple binomial coefficients (when the preprocessing stage, which is the bottlenec, is run only once. When computing a small number of binomial coefficients (e.g. ust one, the bottlenec of the algorithm (in the preprocessing stage consists of the computation of sums of products of elements of subsets having sizes to N (described in Section 5. That step requires N 3 multiplications of N-bit numbers, while all the other steps need fewer multiplications (and one of the steps requires N 3 additions of N-bit numbers. If the values SSP( defined in Section 5 could be computed faster, the algorithm presented in this paper could be considerably improved. As future wor I intend to study the problem of computing the SSP( values in a more efficient manner.. REFERENCES [] M. E. Andreica, Forecasts of Employment in the Romanian Industry based on Simulations and Panel Data Models, Metalurgia International, vol. 8 (3, pp. 4-45, 3. [] P. Barry, On the Connection Coefficients of the Chebyshev-Boubaer Polynomials, The Scientific World Journal, Volume 3, Article ID 65786, pages, 3. [3] T. X. Cai, A. Granville, On the Residues of Binomial Coefficients and Their Products Modulo Prime Powers, Acta Mathematica Sinica, vol. 8 (, pp ,. [4] E. von Collani, K. Drager, Binomial Distribution Handboo for Scientists and Engineers, Birhӓuser,. [5] K. Davis, W. Webb, A Binomial Coefficient Congruence Modulo Prime Powers, Journal of Number Theory, vol. 43 (, pp. -3, 993. [6] C. Ding, D. Pei, A. Salomaa, Chinese Remainder Theorem: Applications in Computing, Coding, Cryptography, World Scientific Publishing, 996. [7] M. Edson, Calculating the Numbers of Representations and the Garsia Entropy in Linear Numeration Systems, Monatshefte für Mathemati, vol. 69 (, pp. 6-85, 3. [8] N. Fine, Binomial Coefficients Modulo a Prime, The American Mathematical Monthly, vol. 54, pp , 947. [9] M. Fürer, Faster Integer Multiplication, SIAM Journal on Computing, vol. 39 (3, pp , 9. [] A. Granville, Arithmetic Properties of Binomial Coefficients I: Binomial Coefficients Modulo Prime Powers, Canadian Mathematical Society Conference Proceedings, pp , 997. [] R. M. Gray, Entropy and Information Theory, nd Edition, Springer-Verlag,. [] P. Kornerup, D. W. Matula, Finite Precision Number Systems and Arithmetic, Cambridge University Press,.
7 [3] A. D. Loveless, A Congruence for Products of Binomial Coefficients Modulo a Composite, INTEGERS: Electronic Journal of Combinatorial Number Theory, vol. 7 (, 7. [4] C.-J. Lu, S.-C. Tsai, The Periodic Property of Binomial Coefficients Modulo M and Its Applications, Proceedings of the th SIAM Conference on Discrete Mathematics,. [5] R. Mestrovic, Variations of Lucas Theorem Modulo Prime Powers, arxiv:3.5 [math.nt],. [6] T. K. Moon, Error Correction Coding: Mathematical Methods and Algorithms, John Wiley & Sons, 5. [7] A. Schonhage, V. Strassen, Schnelle Multipliation großer Zahlen, Computing, vol. 7, pp. 8-9, 97. [8] N. Tapus, P. G. Popescu, New Entropy Upper Bound, Applied Mathematics Letters, vol. 5 (, pp ,.
Photovoltaic deployment: from subsidies to a market-driven growth: A panel econometrics approach
 Photovoltaic deployment: from subsidies to a market-driven growth: A panel econometrics approach Anna Créti, Léonide Michael Sinsin To cite this version: Anna Créti, Léonide Michael Sinsin. Photovoltaic
Photovoltaic deployment: from subsidies to a market-driven growth: A panel econometrics approach Anna Créti, Léonide Michael Sinsin To cite this version: Anna Créti, Léonide Michael Sinsin. Photovoltaic
Equilibrium payoffs in finite games
 Equilibrium payoffs in finite games Ehud Lehrer, Eilon Solan, Yannick Viossat To cite this version: Ehud Lehrer, Eilon Solan, Yannick Viossat. Equilibrium payoffs in finite games. Journal of Mathematical
Equilibrium payoffs in finite games Ehud Lehrer, Eilon Solan, Yannick Viossat To cite this version: Ehud Lehrer, Eilon Solan, Yannick Viossat. Equilibrium payoffs in finite games. Journal of Mathematical
Parameter sensitivity of CIR process
 Parameter sensitivity of CIR process Sidi Mohamed Ould Aly To cite this version: Sidi Mohamed Ould Aly. Parameter sensitivity of CIR process. Electronic Communications in Probability, Institute of Mathematical
Parameter sensitivity of CIR process Sidi Mohamed Ould Aly To cite this version: Sidi Mohamed Ould Aly. Parameter sensitivity of CIR process. Electronic Communications in Probability, Institute of Mathematical
Money in the Production Function : A New Keynesian DSGE Perspective
 Money in the Production Function : A New Keynesian DSGE Perspective Jonathan Benchimol To cite this version: Jonathan Benchimol. Money in the Production Function : A New Keynesian DSGE Perspective. ESSEC
Money in the Production Function : A New Keynesian DSGE Perspective Jonathan Benchimol To cite this version: Jonathan Benchimol. Money in the Production Function : A New Keynesian DSGE Perspective. ESSEC
The National Minimum Wage in France
 The National Minimum Wage in France Timothy Whitton To cite this version: Timothy Whitton. The National Minimum Wage in France. Low pay review, 1989, pp.21-22. HAL Id: hal-01017386 https://hal-clermont-univ.archives-ouvertes.fr/hal-01017386
The National Minimum Wage in France Timothy Whitton To cite this version: Timothy Whitton. The National Minimum Wage in France. Low pay review, 1989, pp.21-22. HAL Id: hal-01017386 https://hal-clermont-univ.archives-ouvertes.fr/hal-01017386
Ricardian equivalence and the intertemporal Keynesian multiplier
 Ricardian equivalence and the intertemporal Keynesian multiplier Jean-Pascal Bénassy To cite this version: Jean-Pascal Bénassy. Ricardian equivalence and the intertemporal Keynesian multiplier. PSE Working
Ricardian equivalence and the intertemporal Keynesian multiplier Jean-Pascal Bénassy To cite this version: Jean-Pascal Bénassy. Ricardian equivalence and the intertemporal Keynesian multiplier. PSE Working
About the reinterpretation of the Ghosh model as a price model
 About the reinterpretation of the Ghosh model as a price model Louis De Mesnard To cite this version: Louis De Mesnard. About the reinterpretation of the Ghosh model as a price model. [Research Report]
About the reinterpretation of the Ghosh model as a price model Louis De Mesnard To cite this version: Louis De Mesnard. About the reinterpretation of the Ghosh model as a price model. [Research Report]
Equivalence in the internal and external public debt burden
 Equivalence in the internal and external public debt burden Philippe Darreau, François Pigalle To cite this version: Philippe Darreau, François Pigalle. Equivalence in the internal and external public
Equivalence in the internal and external public debt burden Philippe Darreau, François Pigalle To cite this version: Philippe Darreau, François Pigalle. Equivalence in the internal and external public
Networks Performance and Contractual Design: Empirical Evidence from Franchising
 Networks Performance and Contractual Design: Empirical Evidence from Franchising Magali Chaudey, Muriel Fadairo To cite this version: Magali Chaudey, Muriel Fadairo. Networks Performance and Contractual
Networks Performance and Contractual Design: Empirical Evidence from Franchising Magali Chaudey, Muriel Fadairo To cite this version: Magali Chaudey, Muriel Fadairo. Networks Performance and Contractual
A note on health insurance under ex post moral hazard
 A note on health insurance under ex post moral hazard Pierre Picard To cite this version: Pierre Picard. A note on health insurance under ex post moral hazard. 2016. HAL Id: hal-01353597
A note on health insurance under ex post moral hazard Pierre Picard To cite this version: Pierre Picard. A note on health insurance under ex post moral hazard. 2016. HAL Id: hal-01353597
Strategic complementarity of information acquisition in a financial market with discrete demand shocks
 Strategic complementarity of information acquisition in a financial market with discrete demand shocks Christophe Chamley To cite this version: Christophe Chamley. Strategic complementarity of information
Strategic complementarity of information acquisition in a financial market with discrete demand shocks Christophe Chamley To cite this version: Christophe Chamley. Strategic complementarity of information
Control-theoretic framework for a quasi-newton local volatility surface inversion
 Control-theoretic framework for a quasi-newton local volatility surface inversion Gabriel Turinici To cite this version: Gabriel Turinici. Control-theoretic framework for a quasi-newton local volatility
Control-theoretic framework for a quasi-newton local volatility surface inversion Gabriel Turinici To cite this version: Gabriel Turinici. Control-theoretic framework for a quasi-newton local volatility
Inequalities in Life Expectancy and the Global Welfare Convergence
 Inequalities in Life Expectancy and the Global Welfare Convergence Hippolyte D Albis, Florian Bonnet To cite this version: Hippolyte D Albis, Florian Bonnet. Inequalities in Life Expectancy and the Global
Inequalities in Life Expectancy and the Global Welfare Convergence Hippolyte D Albis, Florian Bonnet To cite this version: Hippolyte D Albis, Florian Bonnet. Inequalities in Life Expectancy and the Global
Motivations and Performance of Public to Private operations : an international study
 Motivations and Performance of Public to Private operations : an international study Aurelie Sannajust To cite this version: Aurelie Sannajust. Motivations and Performance of Public to Private operations
Motivations and Performance of Public to Private operations : an international study Aurelie Sannajust To cite this version: Aurelie Sannajust. Motivations and Performance of Public to Private operations
The Hierarchical Agglomerative Clustering with Gower index: a methodology for automatic design of OLAP cube in ecological data processing context
 The Hierarchical Agglomerative Clustering with Gower index: a methodology for automatic design of OLAP cube in ecological data processing context Lucile Sautot, Bruno Faivre, Ludovic Journaux, Paul Molin
The Hierarchical Agglomerative Clustering with Gower index: a methodology for automatic design of OLAP cube in ecological data processing context Lucile Sautot, Bruno Faivre, Ludovic Journaux, Paul Molin
IS-LM and the multiplier: A dynamic general equilibrium model
 IS-LM and the multiplier: A dynamic general equilibrium model Jean-Pascal Bénassy To cite this version: Jean-Pascal Bénassy. IS-LM and the multiplier: A dynamic general equilibrium model. PSE Working Papers
IS-LM and the multiplier: A dynamic general equilibrium model Jean-Pascal Bénassy To cite this version: Jean-Pascal Bénassy. IS-LM and the multiplier: A dynamic general equilibrium model. PSE Working Papers
Rôle de la protéine Gas6 et des cellules précurseurs dans la stéatohépatite et la fibrose hépatique
 Rôle de la protéine Gas6 et des cellules précurseurs dans la stéatohépatite et la fibrose hépatique Agnès Fourcot To cite this version: Agnès Fourcot. Rôle de la protéine Gas6 et des cellules précurseurs
Rôle de la protéine Gas6 et des cellules précurseurs dans la stéatohépatite et la fibrose hépatique Agnès Fourcot To cite this version: Agnès Fourcot. Rôle de la protéine Gas6 et des cellules précurseurs
The German unemployment since the Hartz reforms: Permanent or transitory fall?
 The German unemployment since the Hartz reforms: Permanent or transitory fall? Gaëtan Stephan, Julien Lecumberry To cite this version: Gaëtan Stephan, Julien Lecumberry. The German unemployment since the
The German unemployment since the Hartz reforms: Permanent or transitory fall? Gaëtan Stephan, Julien Lecumberry To cite this version: Gaëtan Stephan, Julien Lecumberry. The German unemployment since the
BDHI: a French national database on historical floods
 BDHI: a French national database on historical floods M. Lang, D. Coeur, A. Audouard, M. Villanova Oliver, J.P. Pene To cite this version: M. Lang, D. Coeur, A. Audouard, M. Villanova Oliver, J.P. Pene.
BDHI: a French national database on historical floods M. Lang, D. Coeur, A. Audouard, M. Villanova Oliver, J.P. Pene To cite this version: M. Lang, D. Coeur, A. Audouard, M. Villanova Oliver, J.P. Pene.
Characterization of bijective discretized rotations by Gaussian integers
 Characterization of bijective discretized rotations by Gaussian integers Tristan Roussillon, David Coeurjolly To cite this version: Tristan Roussillon, David Coeurjolly. Characterization of bijective discretized
Characterization of bijective discretized rotations by Gaussian integers Tristan Roussillon, David Coeurjolly To cite this version: Tristan Roussillon, David Coeurjolly. Characterization of bijective discretized
ELEMENTS OF MONTE CARLO SIMULATION
 APPENDIX B ELEMENTS OF MONTE CARLO SIMULATION B. GENERAL CONCEPT The basic idea of Monte Carlo simulation is to create a series of experimental samples using a random number sequence. According to the
APPENDIX B ELEMENTS OF MONTE CARLO SIMULATION B. GENERAL CONCEPT The basic idea of Monte Carlo simulation is to create a series of experimental samples using a random number sequence. According to the
Yield to maturity modelling and a Monte Carlo Technique for pricing Derivatives on Constant Maturity Treasury (CMT) and Derivatives on forward Bonds
 Yield to maturity modelling and a Monte Carlo echnique for pricing Derivatives on Constant Maturity reasury (CM) and Derivatives on forward Bonds Didier Kouokap Youmbi o cite this version: Didier Kouokap
Yield to maturity modelling and a Monte Carlo echnique for pricing Derivatives on Constant Maturity reasury (CM) and Derivatives on forward Bonds Didier Kouokap Youmbi o cite this version: Didier Kouokap
Solution Week 60 (11/3/03) Cereal box prizes
 Solution Wee 60 /3/03 Cereal box prizes First Solution: Assume that you have collected c of the colors, and let B c be the number of boxes it taes to get the next color. The average value of B c, which
Solution Wee 60 /3/03 Cereal box prizes First Solution: Assume that you have collected c of the colors, and let B c be the number of boxes it taes to get the next color. The average value of B c, which
Modèles DSGE Nouveaux Keynésiens, Monnaie et Aversion au Risque.
 Modèles DSGE Nouveaux Keynésiens, Monnaie et Aversion au Risque. Jonathan Benchimol To cite this version: Jonathan Benchimol. Modèles DSGE Nouveaux Keynésiens, Monnaie et Aversion au Risque.. Economies
Modèles DSGE Nouveaux Keynésiens, Monnaie et Aversion au Risque. Jonathan Benchimol To cite this version: Jonathan Benchimol. Modèles DSGE Nouveaux Keynésiens, Monnaie et Aversion au Risque.. Economies
A revisit of the Borch rule for the Principal-Agent Risk-Sharing problem
 A revisit of the Borch rule for the Principal-Agent Risk-Sharing problem Jessica Martin, Anthony Réveillac To cite this version: Jessica Martin, Anthony Réveillac. A revisit of the Borch rule for the Principal-Agent
A revisit of the Borch rule for the Principal-Agent Risk-Sharing problem Jessica Martin, Anthony Réveillac To cite this version: Jessica Martin, Anthony Réveillac. A revisit of the Borch rule for the Principal-Agent
The Sustainability and Outreach of Microfinance Institutions
 The Sustainability and Outreach of Microfinance Institutions Jaehun Sim, Vittaldas Prabhu To cite this version: Jaehun Sim, Vittaldas Prabhu. The Sustainability and Outreach of Microfinance Institutions.
The Sustainability and Outreach of Microfinance Institutions Jaehun Sim, Vittaldas Prabhu To cite this version: Jaehun Sim, Vittaldas Prabhu. The Sustainability and Outreach of Microfinance Institutions.
Properties of IRR Equation with Regard to Ambiguity of Calculating of Rate of Return and a Maximum Number of Solutions
 Properties of IRR Equation with Regard to Ambiguity of Calculating of Rate of Return and a Maximum Number of Solutions IRR equation is widely used in financial mathematics for different purposes, such
Properties of IRR Equation with Regard to Ambiguity of Calculating of Rate of Return and a Maximum Number of Solutions IRR equation is widely used in financial mathematics for different purposes, such
Two dimensional Hotelling model : analytical results and numerical simulations
 Two dimensional Hotelling model : analytical results and numerical simulations Hernán Larralde, Pablo Jensen, Margaret Edwards To cite this version: Hernán Larralde, Pablo Jensen, Margaret Edwards. Two
Two dimensional Hotelling model : analytical results and numerical simulations Hernán Larralde, Pablo Jensen, Margaret Edwards To cite this version: Hernán Larralde, Pablo Jensen, Margaret Edwards. Two
Richardson Extrapolation Techniques for the Pricing of American-style Options
 Richardson Extrapolation Techniques for the Pricing of American-style Options June 1, 2005 Abstract Richardson Extrapolation Techniques for the Pricing of American-style Options In this paper we re-examine
Richardson Extrapolation Techniques for the Pricing of American-style Options June 1, 2005 Abstract Richardson Extrapolation Techniques for the Pricing of American-style Options In this paper we re-examine
Dynamics of the exchange rate in Tunisia
 Dynamics of the exchange rate in Tunisia Ammar Samout, Nejia Nekâa To cite this version: Ammar Samout, Nejia Nekâa. Dynamics of the exchange rate in Tunisia. International Journal of Academic Research
Dynamics of the exchange rate in Tunisia Ammar Samout, Nejia Nekâa To cite this version: Ammar Samout, Nejia Nekâa. Dynamics of the exchange rate in Tunisia. International Journal of Academic Research
French German flood risk geohistory in the Rhine Graben
 French German flood risk geohistory in the Rhine Graben Brice Martin, Iso Himmelsbach, Rüdiger Glaser, Lauriane With, Ouarda Guerrouah, Marie - Claire Vitoux, Axel Drescher, Romain Ansel, Karin Dietrich
French German flood risk geohistory in the Rhine Graben Brice Martin, Iso Himmelsbach, Rüdiger Glaser, Lauriane With, Ouarda Guerrouah, Marie - Claire Vitoux, Axel Drescher, Romain Ansel, Karin Dietrich
Essays on Some Combinatorial Optimization Problems with Interval Data
 Essays on Some Combinatorial Optimization Problems with Interval Data a thesis submitted to the department of industrial engineering and the institute of engineering and sciences of bilkent university
Essays on Some Combinatorial Optimization Problems with Interval Data a thesis submitted to the department of industrial engineering and the institute of engineering and sciences of bilkent university
Mathematics Notes for Class 12 chapter 1. Relations and Functions
 1 P a g e Mathematics Notes for Class 12 chapter 1. Relations and Functions Relation If A and B are two non-empty sets, then a relation R from A to B is a subset of A x B. If R A x B and (a, b) R, then
1 P a g e Mathematics Notes for Class 12 chapter 1. Relations and Functions Relation If A and B are two non-empty sets, then a relation R from A to B is a subset of A x B. If R A x B and (a, b) R, then
On equation. Boris Bartolomé. January 25 th, Göttingen Universität & Institut de Mathémathiques de Bordeaux
 Göttingen Universität & Institut de Mathémathiques de Bordeaux Boris.Bartolome@mathematik.uni-goettingen.de Boris.Bartolome@math.u-bordeaux1.fr January 25 th, 2016 January 25 th, 2016 1 / 19 Overview 1
Göttingen Universität & Institut de Mathémathiques de Bordeaux Boris.Bartolome@mathematik.uni-goettingen.de Boris.Bartolome@math.u-bordeaux1.fr January 25 th, 2016 January 25 th, 2016 1 / 19 Overview 1
The Quantity Theory of Money Revisited: The Improved Short-Term Predictive Power of of Household Money Holdings with Regard to prices
 The Quantity Theory of Money Revisited: The Improved Short-Term Predictive Power of of Household Money Holdings with Regard to prices Jean-Charles Bricongne To cite this version: Jean-Charles Bricongne.
The Quantity Theory of Money Revisited: The Improved Short-Term Predictive Power of of Household Money Holdings with Regard to prices Jean-Charles Bricongne To cite this version: Jean-Charles Bricongne.
The binomial interpolated lattice method fro step double barrier options
 The binomial interpolated lattice method fro step double barrier options Elisa Appolloni, Gaudenzi Marcellino, Antonino Zanette To cite this version: Elisa Appolloni, Gaudenzi Marcellino, Antonino Zanette.
The binomial interpolated lattice method fro step double barrier options Elisa Appolloni, Gaudenzi Marcellino, Antonino Zanette To cite this version: Elisa Appolloni, Gaudenzi Marcellino, Antonino Zanette.
Computational Independence
 Computational Independence Björn Fay mail@bfay.de December 20, 2014 Abstract We will introduce different notions of independence, especially computational independence (or more precise independence by
Computational Independence Björn Fay mail@bfay.de December 20, 2014 Abstract We will introduce different notions of independence, especially computational independence (or more precise independence by
Rôle de la régulation génique dans l adaptation : approche par analyse comparative du transcriptome de drosophile
 Rôle de la régulation génique dans l adaptation : approche par analyse comparative du transcriptome de drosophile François Wurmser To cite this version: François Wurmser. Rôle de la régulation génique
Rôle de la régulation génique dans l adaptation : approche par analyse comparative du transcriptome de drosophile François Wurmser To cite this version: François Wurmser. Rôle de la régulation génique
A lower bound on seller revenue in single buyer monopoly auctions
 A lower bound on seller revenue in single buyer monopoly auctions Omer Tamuz October 7, 213 Abstract We consider a monopoly seller who optimally auctions a single object to a single potential buyer, with
A lower bound on seller revenue in single buyer monopoly auctions Omer Tamuz October 7, 213 Abstract We consider a monopoly seller who optimally auctions a single object to a single potential buyer, with
A Centrality-based RSU Deployment Approach for Vehicular Ad Hoc Networks
 A Centrality-based RSU Deployment Approach for Vehicular Ad Hoc etwors Zhenyu Wang, Jun Zheng, Yuying Wu, athalie Mitton To cite this version: Zhenyu Wang, Jun Zheng, Yuying Wu, athalie Mitton. A Centrality-based
A Centrality-based RSU Deployment Approach for Vehicular Ad Hoc etwors Zhenyu Wang, Jun Zheng, Yuying Wu, athalie Mitton To cite this version: Zhenyu Wang, Jun Zheng, Yuying Wu, athalie Mitton. A Centrality-based
Algebra homework 8 Homomorphisms, isomorphisms
 MATH-UA.343.005 T.A. Louis Guigo Algebra homework 8 Homomorphisms, isomorphisms For every n 1 we denote by S n the n-th symmetric group. Exercise 1. Consider the following permutations: ( ) ( 1 2 3 4 5
MATH-UA.343.005 T.A. Louis Guigo Algebra homework 8 Homomorphisms, isomorphisms For every n 1 we denote by S n the n-th symmetric group. Exercise 1. Consider the following permutations: ( ) ( 1 2 3 4 5
Asymptotic Notation. Instructor: Laszlo Babai June 14, 2002
 Asymptotic Notation Instructor: Laszlo Babai June 14, 2002 1 Preliminaries Notation: exp(x) = e x. Throughout this course we shall use the following shorthand in quantifier notation. ( a) is read as for
Asymptotic Notation Instructor: Laszlo Babai June 14, 2002 1 Preliminaries Notation: exp(x) = e x. Throughout this course we shall use the following shorthand in quantifier notation. ( a) is read as for
Realizability of n-vertex Graphs with Prescribed Vertex Connectivity, Edge Connectivity, Minimum Degree, and Maximum Degree
 Realizability of n-vertex Graphs with Prescribed Vertex Connectivity, Edge Connectivity, Minimum Degree, and Maximum Degree Lewis Sears IV Washington and Lee University 1 Introduction The study of graph
Realizability of n-vertex Graphs with Prescribed Vertex Connectivity, Edge Connectivity, Minimum Degree, and Maximum Degree Lewis Sears IV Washington and Lee University 1 Introduction The study of graph
Wage bargaining with non-stationary preferences under strike decision
 Wage bargaining with non-stationary preferences under strike decision Ahmet Ozkardas, Agnieszka Rusinowska To cite this version: Ahmet Ozkardas, Agnieszka Rusinowska. Wage bargaining with non-stationary
Wage bargaining with non-stationary preferences under strike decision Ahmet Ozkardas, Agnieszka Rusinowska To cite this version: Ahmet Ozkardas, Agnieszka Rusinowska. Wage bargaining with non-stationary
MATH 116: Material Covered in Class and Quiz/Exam Information
 MATH 116: Material Covered in Class and Quiz/Exam Information August 23 rd. Syllabus. Divisibility and linear combinations. Example 1: Proof of Theorem 2.4 parts (a), (c), and (g). Example 2: Exercise
MATH 116: Material Covered in Class and Quiz/Exam Information August 23 rd. Syllabus. Divisibility and linear combinations. Example 1: Proof of Theorem 2.4 parts (a), (c), and (g). Example 2: Exercise
Neural Network Prediction of Stock Price Trend Based on RS with Entropy Discretization
 2017 International Conference on Materials, Energy, Civil Engineering and Computer (MATECC 2017) Neural Network Prediction of Stock Price Trend Based on RS with Entropy Discretization Huang Haiqing1,a,
2017 International Conference on Materials, Energy, Civil Engineering and Computer (MATECC 2017) Neural Network Prediction of Stock Price Trend Based on RS with Entropy Discretization Huang Haiqing1,a,
Maximum Contiguous Subsequences
 Chapter 8 Maximum Contiguous Subsequences In this chapter, we consider a well-know problem and apply the algorithm-design techniques that we have learned thus far to this problem. While applying these
Chapter 8 Maximum Contiguous Subsequences In this chapter, we consider a well-know problem and apply the algorithm-design techniques that we have learned thus far to this problem. While applying these
EFFICIENT MONTE CARLO ALGORITHM FOR PRICING BARRIER OPTIONS
 Commun. Korean Math. Soc. 23 (2008), No. 2, pp. 285 294 EFFICIENT MONTE CARLO ALGORITHM FOR PRICING BARRIER OPTIONS Kyoung-Sook Moon Reprinted from the Communications of the Korean Mathematical Society
Commun. Korean Math. Soc. 23 (2008), No. 2, pp. 285 294 EFFICIENT MONTE CARLO ALGORITHM FOR PRICING BARRIER OPTIONS Kyoung-Sook Moon Reprinted from the Communications of the Korean Mathematical Society
Math 167: Mathematical Game Theory Instructor: Alpár R. Mészáros
 Math 167: Mathematical Game Theory Instructor: Alpár R. Mészáros Midterm #1, February 3, 2017 Name (use a pen): Student ID (use a pen): Signature (use a pen): Rules: Duration of the exam: 50 minutes. By
Math 167: Mathematical Game Theory Instructor: Alpár R. Mészáros Midterm #1, February 3, 2017 Name (use a pen): Student ID (use a pen): Signature (use a pen): Rules: Duration of the exam: 50 minutes. By
6-3 Dividing Polynomials
 Polynomials can be divided using long division just like you learned with numbers. Divide) 24 6 5 6 24-8 4-0 4 Remainder 24 6 = 5 4 6 Example : Using Long Division to Divide a Polynomial Divide using
Polynomials can be divided using long division just like you learned with numbers. Divide) 24 6 5 6 24-8 4-0 4 Remainder 24 6 = 5 4 6 Example : Using Long Division to Divide a Polynomial Divide using
MAC Learning Objectives. Learning Objectives (Cont.)
 MAC 1140 Module 12 Introduction to Sequences, Counting, The Binomial Theorem, and Mathematical Induction Learning Objectives Upon completing this module, you should be able to 1. represent sequences. 2.
MAC 1140 Module 12 Introduction to Sequences, Counting, The Binomial Theorem, and Mathematical Induction Learning Objectives Upon completing this module, you should be able to 1. represent sequences. 2.
Why ruin theory should be of interest for insurance practitioners and risk managers nowadays
 Why ruin theory should be of interest for insurance practitioners and risk managers nowadays Stéphane Loisel, Hans-U. Gerber To cite this version: Stéphane Loisel, Hans-U. Gerber. Why ruin theory should
Why ruin theory should be of interest for insurance practitioners and risk managers nowadays Stéphane Loisel, Hans-U. Gerber To cite this version: Stéphane Loisel, Hans-U. Gerber. Why ruin theory should
Drug launch timing and international reference pricing
 Drug launch timing and international reference pricing Nicolas Houy, Izabela Jelovac To cite this version: Nicolas Houy, Izabela Jelovac. Drug launch timing and international reference pricing. Working
Drug launch timing and international reference pricing Nicolas Houy, Izabela Jelovac To cite this version: Nicolas Houy, Izabela Jelovac. Drug launch timing and international reference pricing. Working
CONSTRUCTION OF CODES BY LATTICE VALUED FUZZY SETS. 1. Introduction. Novi Sad J. Math. Vol. 35, No. 2, 2005,
 Novi Sad J. Math. Vol. 35, No. 2, 2005, 155-160 CONSTRUCTION OF CODES BY LATTICE VALUED FUZZY SETS Mališa Žižović 1, Vera Lazarević 2 Abstract. To every finite lattice L, one can associate a binary blockcode,
Novi Sad J. Math. Vol. 35, No. 2, 2005, 155-160 CONSTRUCTION OF CODES BY LATTICE VALUED FUZZY SETS Mališa Žižović 1, Vera Lazarević 2 Abstract. To every finite lattice L, one can associate a binary blockcode,
Do Professional Economists Forecasts Reflect Okun s Law? Some Evidence for the G7 Countries
 Do Professional Economists Forecasts Reflect Okun s Law? Some Evidence for the G Countries Georg Stadtmann, Jan-Christoph Ruelke Christian Pierdzioch To cite this version: Georg Stadtmann, Jan-Christoph
Do Professional Economists Forecasts Reflect Okun s Law? Some Evidence for the G Countries Georg Stadtmann, Jan-Christoph Ruelke Christian Pierdzioch To cite this version: Georg Stadtmann, Jan-Christoph
Inefficient Lock-in with Sophisticated and Myopic Players
 Inefficient Lock-in with Sophisticated and Myopic Players Aidas Masiliunas To cite this version: Aidas Masiliunas. Inefficient Lock-in with Sophisticated and Myopic Players. 2016. HAL
Inefficient Lock-in with Sophisticated and Myopic Players Aidas Masiliunas To cite this version: Aidas Masiliunas. Inefficient Lock-in with Sophisticated and Myopic Players. 2016. HAL
Chapter 1 Additional Questions
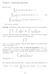 Chapter Additional Questions 8) Prove that n=3 n= n= converges if, and only if, σ >. nσ nlogn) σ converges if, and only if, σ >. 3) nlognloglogn) σ converges if, and only if, σ >. Can you see a pattern?
Chapter Additional Questions 8) Prove that n=3 n= n= converges if, and only if, σ >. nσ nlogn) σ converges if, and only if, σ >. 3) nlognloglogn) σ converges if, and only if, σ >. Can you see a pattern?
On the Number of Permutations Avoiding a Given Pattern
 On the Number of Permutations Avoiding a Given Pattern Noga Alon Ehud Friedgut February 22, 2002 Abstract Let σ S k and τ S n be permutations. We say τ contains σ if there exist 1 x 1 < x 2
On the Number of Permutations Avoiding a Given Pattern Noga Alon Ehud Friedgut February 22, 2002 Abstract Let σ S k and τ S n be permutations. We say τ contains σ if there exist 1 x 1 < x 2
A distributed Laplace transform algorithm for European options
 A distributed Laplace transform algorithm for European options 1 1 A. J. Davies, M. E. Honnor, C.-H. Lai, A. K. Parrott & S. Rout 1 Department of Physics, Astronomy and Mathematics, University of Hertfordshire,
A distributed Laplace transform algorithm for European options 1 1 A. J. Davies, M. E. Honnor, C.-H. Lai, A. K. Parrott & S. Rout 1 Department of Physics, Astronomy and Mathematics, University of Hertfordshire,
COMBINATORIAL CONVOLUTION SUMS DERIVED FROM DIVISOR FUNCTIONS AND FAULHABER SUMS
 GLASNIK MATEMATIČKI Vol. 49(69(014, 351 367 COMBINATORIAL CONVOLUTION SUMS DERIVED FROM DIVISOR FUNCTIONS AND FAULHABER SUMS Bumkyu Cho, Daeyeoul Kim and Ho Park Dongguk University-Seoul, National Institute
GLASNIK MATEMATIČKI Vol. 49(69(014, 351 367 COMBINATORIAL CONVOLUTION SUMS DERIVED FROM DIVISOR FUNCTIONS AND FAULHABER SUMS Bumkyu Cho, Daeyeoul Kim and Ho Park Dongguk University-Seoul, National Institute
Lecture 4: Divide and Conquer
 Lecture 4: Divide and Conquer Divide and Conquer Merge sort is an example of a divide-and-conquer algorithm Recall the three steps (at each level to solve a divideand-conquer problem recursively Divide
Lecture 4: Divide and Conquer Divide and Conquer Merge sort is an example of a divide-and-conquer algorithm Recall the three steps (at each level to solve a divideand-conquer problem recursively Divide
Creating a winner s curse via jump bids
 Creating a winner s curse via jump bids David Ettinger, Fabio Michelucci To cite this version: David Ettinger, Fabio Michelucci. Creating a winner s curse via jump bids. Review of Economic Design, Springer
Creating a winner s curse via jump bids David Ettinger, Fabio Michelucci To cite this version: David Ettinger, Fabio Michelucci. Creating a winner s curse via jump bids. Review of Economic Design, Springer
Yao s Minimax Principle
 Complexity of algorithms The complexity of an algorithm is usually measured with respect to the size of the input, where size may for example refer to the length of a binary word describing the input,
Complexity of algorithms The complexity of an algorithm is usually measured with respect to the size of the input, where size may for example refer to the length of a binary word describing the input,
5.6 Special Products of Polynomials
 5.6 Special Products of Polynomials Learning Objectives Find the square of a binomial Find the product of binomials using sum and difference formula Solve problems using special products of polynomials
5.6 Special Products of Polynomials Learning Objectives Find the square of a binomial Find the product of binomials using sum and difference formula Solve problems using special products of polynomials
Interpolation. 1 What is interpolation? 2 Why are we interested in this?
 Interpolation 1 What is interpolation? For a certain function f (x we know only the values y 1 = f (x 1,,y n = f (x n For a point x different from x 1,,x n we would then like to approximate f ( x using
Interpolation 1 What is interpolation? For a certain function f (x we know only the values y 1 = f (x 1,,y n = f (x n For a point x different from x 1,,x n we would then like to approximate f ( x using
An Adjusted Trinomial Lattice for Pricing Arithmetic Average Based Asian Option
 American Journal of Applied Mathematics 2018; 6(2): 28-33 http://www.sciencepublishinggroup.com/j/ajam doi: 10.11648/j.ajam.20180602.11 ISSN: 2330-0043 (Print); ISSN: 2330-006X (Online) An Adjusted Trinomial
American Journal of Applied Mathematics 2018; 6(2): 28-33 http://www.sciencepublishinggroup.com/j/ajam doi: 10.11648/j.ajam.20180602.11 ISSN: 2330-0043 (Print); ISSN: 2330-006X (Online) An Adjusted Trinomial
The ruin probabilities of a multidimensional perturbed risk model
 MATHEMATICAL COMMUNICATIONS 231 Math. Commun. 18(2013, 231 239 The ruin probabilities of a multidimensional perturbed risk model Tatjana Slijepčević-Manger 1, 1 Faculty of Civil Engineering, University
MATHEMATICAL COMMUNICATIONS 231 Math. Commun. 18(2013, 231 239 The ruin probabilities of a multidimensional perturbed risk model Tatjana Slijepčević-Manger 1, 1 Faculty of Civil Engineering, University
An Algorithm for Distributing Coalitional Value Calculations among Cooperating Agents
 An Algorithm for Distributing Coalitional Value Calculations among Cooperating Agents Talal Rahwan and Nicholas R. Jennings School of Electronics and Computer Science, University of Southampton, Southampton
An Algorithm for Distributing Coalitional Value Calculations among Cooperating Agents Talal Rahwan and Nicholas R. Jennings School of Electronics and Computer Science, University of Southampton, Southampton
The Riskiness of Risk Models
 The Riskiness of Risk Models Christophe Boucher, Bertrand Maillet To cite this version: Christophe Boucher, Bertrand Maillet. The Riskiness of Risk Models. Documents de travail du Centre d Economie de
The Riskiness of Risk Models Christophe Boucher, Bertrand Maillet To cite this version: Christophe Boucher, Bertrand Maillet. The Riskiness of Risk Models. Documents de travail du Centre d Economie de
On some key research issues in Enterprise Risk Management related to economic capital and diversification effect at group level
 On some key research issues in Enterprise Risk Management related to economic capital and diversification effect at group level Wayne Fisher, Stéphane Loisel, Shaun Wang To cite this version: Wayne Fisher,
On some key research issues in Enterprise Risk Management related to economic capital and diversification effect at group level Wayne Fisher, Stéphane Loisel, Shaun Wang To cite this version: Wayne Fisher,
Online Mechanism Design for VMs Allocation in Private Cloud
 Online Mechanism Design for VMs Allocation in Private Cloud Xiaohong Wu, Yonggen Gu, Guoqiang Li, Jie Tao, Jingyu Chen, Xiaolong Ma To cite this version: Xiaohong Wu, Yonggen Gu, Guoqiang Li, Jie Tao,
Online Mechanism Design for VMs Allocation in Private Cloud Xiaohong Wu, Yonggen Gu, Guoqiang Li, Jie Tao, Jingyu Chen, Xiaolong Ma To cite this version: Xiaohong Wu, Yonggen Gu, Guoqiang Li, Jie Tao,
A Result on the Distribution of Quadratic Residues with Applications to Elliptic Curve Cryptography
 A Result on the Distribution of Quadratic Residues with Applications to Elliptic Curve Cryptography Muralidhara V.N. and Sandeep Sen {murali, ssen}@cse.iitd.ernet.in Department of Computer Science and
A Result on the Distribution of Quadratic Residues with Applications to Elliptic Curve Cryptography Muralidhara V.N. and Sandeep Sen {murali, ssen}@cse.iitd.ernet.in Department of Computer Science and
The Complexity of Simple and Optimal Deterministic Mechanisms for an Additive Buyer. Xi Chen, George Matikas, Dimitris Paparas, Mihalis Yannakakis
 The Complexity of Simple and Optimal Deterministic Mechanisms for an Additive Buyer Xi Chen, George Matikas, Dimitris Paparas, Mihalis Yannakakis Seller has n items for sale The Set-up Seller has n items
The Complexity of Simple and Optimal Deterministic Mechanisms for an Additive Buyer Xi Chen, George Matikas, Dimitris Paparas, Mihalis Yannakakis Seller has n items for sale The Set-up Seller has n items
A Property Equivalent to n-permutability for Infinite Groups
 Journal of Algebra 221, 570 578 (1999) Article ID jabr.1999.7996, available online at http://www.idealibrary.com on A Property Equivalent to n-permutability for Infinite Groups Alireza Abdollahi* and Aliakbar
Journal of Algebra 221, 570 578 (1999) Article ID jabr.1999.7996, available online at http://www.idealibrary.com on A Property Equivalent to n-permutability for Infinite Groups Alireza Abdollahi* and Aliakbar
GENERATION OF STANDARD NORMAL RANDOM NUMBERS. Naveen Kumar Boiroju and M. Krishna Reddy
 GENERATION OF STANDARD NORMAL RANDOM NUMBERS Naveen Kumar Boiroju and M. Krishna Reddy Department of Statistics, Osmania University, Hyderabad- 500 007, INDIA Email: nanibyrozu@gmail.com, reddymk54@gmail.com
GENERATION OF STANDARD NORMAL RANDOM NUMBERS Naveen Kumar Boiroju and M. Krishna Reddy Department of Statistics, Osmania University, Hyderabad- 500 007, INDIA Email: nanibyrozu@gmail.com, reddymk54@gmail.com
DISRUPTION MANAGEMENT FOR SUPPLY CHAIN COORDINATION WITH EXPONENTIAL DEMAND FUNCTION
 Acta Mathematica Scientia 2006,26B(4):655 669 www.wipm.ac.cn/publish/ ISRUPTION MANAGEMENT FOR SUPPLY CHAIN COORINATION WITH EXPONENTIAL EMAN FUNCTION Huang Chongchao ( ) School of Mathematics and Statistics,
Acta Mathematica Scientia 2006,26B(4):655 669 www.wipm.ac.cn/publish/ ISRUPTION MANAGEMENT FOR SUPPLY CHAIN COORINATION WITH EXPONENTIAL EMAN FUNCTION Huang Chongchao ( ) School of Mathematics and Statistics,
3.1 Properties of Binomial Coefficients
 3 Properties of Binomial Coefficients 31 Properties of Binomial Coefficients Here is the famous recursive formula for binomial coefficients Lemma 31 For 1 < n, 1 1 ( n 1 ) This equation can be proven by
3 Properties of Binomial Coefficients 31 Properties of Binomial Coefficients Here is the famous recursive formula for binomial coefficients Lemma 31 For 1 < n, 1 1 ( n 1 ) This equation can be proven by
Inequalities between retirees and workers: an empirical model to capture the effect of taxation
 Inequalities between and : an empirical model to capture the effect of taxation Bérangère Legendre To cite this version: Bérangère Legendre. Inequalities between and : an empirical model to capture the
Inequalities between and : an empirical model to capture the effect of taxation Bérangère Legendre To cite this version: Bérangère Legendre. Inequalities between and : an empirical model to capture the
The extreme downside risk of the S P 500 stock index
 The extreme downside risk of the S P 500 stock index Sofiane Aboura To cite this version: Sofiane Aboura. The extreme downside risk of the S P 500 stock index. Journal of Financial Transformation, 2009,
The extreme downside risk of the S P 500 stock index Sofiane Aboura To cite this version: Sofiane Aboura. The extreme downside risk of the S P 500 stock index. Journal of Financial Transformation, 2009,
ESTIMATION OF MODIFIED MEASURE OF SKEWNESS. Elsayed Ali Habib *
 Electronic Journal of Applied Statistical Analysis EJASA, Electron. J. App. Stat. Anal. (2011), Vol. 4, Issue 1, 56 70 e-issn 2070-5948, DOI 10.1285/i20705948v4n1p56 2008 Università del Salento http://siba-ese.unile.it/index.php/ejasa/index
Electronic Journal of Applied Statistical Analysis EJASA, Electron. J. App. Stat. Anal. (2011), Vol. 4, Issue 1, 56 70 e-issn 2070-5948, DOI 10.1285/i20705948v4n1p56 2008 Università del Salento http://siba-ese.unile.it/index.php/ejasa/index
Factors of 10 = = 2 5 Possible pairs of factors:
 Factoring Trinomials Worksheet #1 1. b 2 + 8b + 7 Signs inside the two binomials are identical and positive. Factors of b 2 = b b Factors of 7 = 1 7 b 2 + 8b + 7 = (b + 1)(b + 7) 2. n 2 11n + 10 Signs
Factoring Trinomials Worksheet #1 1. b 2 + 8b + 7 Signs inside the two binomials are identical and positive. Factors of b 2 = b b Factors of 7 = 1 7 b 2 + 8b + 7 = (b + 1)(b + 7) 2. n 2 11n + 10 Signs
Reduced complexity in M/Ph/c/N queues
 Reduced complexity in M/Ph/c/N queues Alexandre Brandwajn, Thomas Begin To cite this version: Alexandre Brandwajn, Thomas Begin. Reduced complexity in M/Ph/c/N queues. [Research Report] RR-8303, INRIA.
Reduced complexity in M/Ph/c/N queues Alexandre Brandwajn, Thomas Begin To cite this version: Alexandre Brandwajn, Thomas Begin. Reduced complexity in M/Ph/c/N queues. [Research Report] RR-8303, INRIA.
Single Price Mechanisms for Revenue Maximization in Unlimited Supply Combinatorial Auctions
 Single Price Mechanisms for Revenue Maximization in Unlimited Supply Combinatorial Auctions Maria-Florina Balcan Avrim Blum Yishay Mansour February 2007 CMU-CS-07-111 School of Computer Science Carnegie
Single Price Mechanisms for Revenue Maximization in Unlimited Supply Combinatorial Auctions Maria-Florina Balcan Avrim Blum Yishay Mansour February 2007 CMU-CS-07-111 School of Computer Science Carnegie
The communication complexity of the private value single item bisection auction
 The communication complexity of the private value single item bisection auction Elena Grigorieva P.Jean-Jacques Herings Rudolf Müller Dries Vermeulen June 1, 004 Abstract In this paper we present a new
The communication complexity of the private value single item bisection auction Elena Grigorieva P.Jean-Jacques Herings Rudolf Müller Dries Vermeulen June 1, 004 Abstract In this paper we present a new
Confidence Intervals for the Median and Other Percentiles
 Confidence Intervals for the Median and Other Percentiles Authored by: Sarah Burke, Ph.D. 12 December 2016 Revised 22 October 2018 The goal of the STAT COE is to assist in developing rigorous, defensible
Confidence Intervals for the Median and Other Percentiles Authored by: Sarah Burke, Ph.D. 12 December 2016 Revised 22 October 2018 The goal of the STAT COE is to assist in developing rigorous, defensible
Optimal Tax Base with Administrative fixed Costs
 Optimal Tax Base with Administrative fixed osts Stéphane Gauthier To cite this version: Stéphane Gauthier. Optimal Tax Base with Administrative fixed osts. Documents de travail du entre d Economie de la
Optimal Tax Base with Administrative fixed osts Stéphane Gauthier To cite this version: Stéphane Gauthier. Optimal Tax Base with Administrative fixed osts. Documents de travail du entre d Economie de la
Carbon Prices during the EU ETS Phase II: Dynamics and Volume Analysis
 Carbon Prices during the EU ETS Phase II: Dynamics and Volume Analysis Julien Chevallier To cite this version: Julien Chevallier. Carbon Prices during the EU ETS Phase II: Dynamics and Volume Analysis.
Carbon Prices during the EU ETS Phase II: Dynamics and Volume Analysis Julien Chevallier To cite this version: Julien Chevallier. Carbon Prices during the EU ETS Phase II: Dynamics and Volume Analysis.
Administering Systemic Risk vs. Administering Justice: What Can We Do Now that We Have Agreed to Pay Differences?
 Administering Systemic Risk vs. Administering Justice: What Can We Do Now that We Have Agreed to Pay Differences? Pierre-Charles Pradier To cite this version: Pierre-Charles Pradier. Administering Systemic
Administering Systemic Risk vs. Administering Justice: What Can We Do Now that We Have Agreed to Pay Differences? Pierre-Charles Pradier To cite this version: Pierre-Charles Pradier. Administering Systemic
TWO-PERIODIC TERNARY RECURRENCES AND THEIR BINET-FORMULA 1. INTRODUCTION
 TWO-PERIODIC TERNARY RECURRENCES AND THEIR BINET-FORMULA M. ALP, N. IRMAK and L. SZALAY Abstract. The properties of k-periodic binary recurrences have been discussed by several authors. In this paper,
TWO-PERIODIC TERNARY RECURRENCES AND THEIR BINET-FORMULA M. ALP, N. IRMAK and L. SZALAY Abstract. The properties of k-periodic binary recurrences have been discussed by several authors. In this paper,
Towards New Technical Indicators for Trading Systems and Risk Management
 Towards New Technical Indicators for Trading Systems and Risk Management Michel Fliess, Cédric Join To cite this version: Michel Fliess, Cédric Join. Towards New Technical Indicators for Trading Systems
Towards New Technical Indicators for Trading Systems and Risk Management Michel Fliess, Cédric Join To cite this version: Michel Fliess, Cédric Join. Towards New Technical Indicators for Trading Systems
Optimal Production-Inventory Policy under Energy Buy-Back Program
 The inth International Symposium on Operations Research and Its Applications (ISORA 10) Chengdu-Jiuzhaigou, China, August 19 23, 2010 Copyright 2010 ORSC & APORC, pp. 526 532 Optimal Production-Inventory
The inth International Symposium on Operations Research and Its Applications (ISORA 10) Chengdu-Jiuzhaigou, China, August 19 23, 2010 Copyright 2010 ORSC & APORC, pp. 526 532 Optimal Production-Inventory
November 2006 LSE-CDAM
 NUMERICAL APPROACHES TO THE PRINCESS AND MONSTER GAME ON THE INTERVAL STEVE ALPERN, ROBBERT FOKKINK, ROY LINDELAUF, AND GEERT JAN OLSDER November 2006 LSE-CDAM-2006-18 London School of Economics, Houghton
NUMERICAL APPROACHES TO THE PRINCESS AND MONSTER GAME ON THE INTERVAL STEVE ALPERN, ROBBERT FOKKINK, ROY LINDELAUF, AND GEERT JAN OLSDER November 2006 LSE-CDAM-2006-18 London School of Economics, Houghton
On integer-valued means and the symmetric maximum
 On integer-valued means and the symmetric maximum Miguel Couceiro, Michel Grabisch To cite this version: Miguel Couceiro, Michel Grabisch. On integer-valued means and the symmetric maximum. Aequationes
On integer-valued means and the symmetric maximum Miguel Couceiro, Michel Grabisch To cite this version: Miguel Couceiro, Michel Grabisch. On integer-valued means and the symmetric maximum. Aequationes
A note on the number of (k, l)-sum-free sets
 A note on the number of (k, l)-sum-free sets Tomasz Schoen Mathematisches Seminar Universität zu Kiel Ludewig-Meyn-Str. 4, 4098 Kiel, Germany tos@numerik.uni-kiel.de and Department of Discrete Mathematics
A note on the number of (k, l)-sum-free sets Tomasz Schoen Mathematisches Seminar Universität zu Kiel Ludewig-Meyn-Str. 4, 4098 Kiel, Germany tos@numerik.uni-kiel.de and Department of Discrete Mathematics
The efficiency of fair division
 The efficiency of fair division Ioannis Caragiannis, Christos Kaklamanis, Panagiotis Kanellopoulos, and Maria Kyropoulou Research Academic Computer Technology Institute and Department of Computer Engineering
The efficiency of fair division Ioannis Caragiannis, Christos Kaklamanis, Panagiotis Kanellopoulos, and Maria Kyropoulou Research Academic Computer Technology Institute and Department of Computer Engineering
A First Course in Probability
 A First Course in Probability Seventh Edition Sheldon Ross University of Southern California PEARSON Prentice Hall Upper Saddle River, New Jersey 07458 Preface 1 Combinatorial Analysis 1 1.1 Introduction
A First Course in Probability Seventh Edition Sheldon Ross University of Southern California PEARSON Prentice Hall Upper Saddle River, New Jersey 07458 Preface 1 Combinatorial Analysis 1 1.1 Introduction
Asymptotic refinements of bootstrap tests in a linear regression model ; A CHM bootstrap using the first four moments of the residuals
 Asymptotic refinements of bootstrap tests in a linear regression model ; A CHM bootstrap using the first four moments of the residuals Pierre-Eric Treyens To cite this version: Pierre-Eric Treyens. Asymptotic
Asymptotic refinements of bootstrap tests in a linear regression model ; A CHM bootstrap using the first four moments of the residuals Pierre-Eric Treyens To cite this version: Pierre-Eric Treyens. Asymptotic
Competitive Algorithms for Online Leasing Problem in Probabilistic Environments
 Competitive Algorithms for Online Leasing Problem in Probabilistic Environments Yinfeng Xu,2 and Weijun Xu 2 School of Management, Xi an Jiaotong University, Xi an, Shaan xi, 70049, P.R. China xuweijun75@63.com
Competitive Algorithms for Online Leasing Problem in Probabilistic Environments Yinfeng Xu,2 and Weijun Xu 2 School of Management, Xi an Jiaotong University, Xi an, Shaan xi, 70049, P.R. China xuweijun75@63.com
European Debt Crisis: How a Public debt Restructuring Can Solve a Private Debt issue
 European Debt Crisis: How a Public debt Restructuring Can Solve a Private Debt issue David Cayla To cite this version: David Cayla. European Debt Crisis: How a Public debt Restructuring Can Solve a Private
European Debt Crisis: How a Public debt Restructuring Can Solve a Private Debt issue David Cayla To cite this version: David Cayla. European Debt Crisis: How a Public debt Restructuring Can Solve a Private
Power-Law Networks in the Stock Market: Stability and Dynamics
 Power-Law Networks in the Stock Market: Stability and Dynamics VLADIMIR BOGINSKI, SERGIY BUTENKO, PANOS M. PARDALOS Department of Industrial and Systems Engineering University of Florida 303 Weil Hall,
Power-Law Networks in the Stock Market: Stability and Dynamics VLADIMIR BOGINSKI, SERGIY BUTENKO, PANOS M. PARDALOS Department of Industrial and Systems Engineering University of Florida 303 Weil Hall,
