More Advanced Single Machine Models. University at Buffalo IE661 Scheduling Theory 1
|
|
|
- Gerard Kelly
- 5 years ago
- Views:
Transcription
1 More Advanced Single Machine Models University at Buffalo IE661 Scheduling Theory 1
2 Total Earliness And Tardiness Non-regular performance measures Ej + Tj Early jobs (Set j 1 ) and Late jobs (Set j 2 ) are scheduled according to LPT and SPT. Minimizing Total Earliness And Tardiness with a loose due date. Assume: 1. d j =d. 2. p 1 p 2 p 3. p n Step 1: Assign job 1 to set j 1. set k=2 Step 2: Assign job k to set j 1 and job k+1 to set j 2 or vice versa. Step 3: If k+2 n 1, set k=k+2 and go to step 2. If k+2 = n, assign job n to either j 1 or j 2 and STOP. If k+2 = n + 1, all jobs have been assigned ; STOP. Flexible in assigning jobs to sets j 1 and j 2.. Assignment is such that the total processing times of set j 1 is minimized. University at Buffalo IE661 Scheduling Theory 2
3 Total Earliness And Tardiness (Cont.) Assume: 1. d j =d. 2. p 1 p 2 p 3. p n Minimizing Total Earliness And Tardiness with a tight due date. Step 1: Set τ 1 =d and τ 2 = p j - d Set k=1 Step 2: If τ 1 > τ 2, assign job k to the first unfilled position in the sequence and set τ 1= τ 1 -p k. If τ 1 < τ 2, assign job k to the last unfilled position in the sequence and set τ 2= τ 2 -p k. Step 3: If k < n, set k = k+1 and go to step 2. If k = n, STOP. University at Buffalo IE661 Scheduling Theory 3
4 Example: Jobs p j τ τ Sequence 1XXXXX 1XXXX2 13XXX2 13XX42 13X University at Buffalo IE661 Scheduling Theory 4
5 Total Earliness And Tardiness (Cont.) If we consider w Ej + w Tj,where the weights are not necessary the same for the two performance measures but the due dates are same, the earlier algorithms can be generalized easily for solving this problem. Now if we consider w j Ej + w j Tj and d j =d, then the weighted LPT and weighted SPT rules have to be used for sequencing. Now if we consider w j Ej + w j Tj and d j d, the problem is NP hard. Due to different due dates it might not be optimal to process the jobs without interruption. Idle times in between consecutive jobs might be necessary. Given a predetermined ordering of the jobs, the timings of the processing of the jobs and the idle times can be computed in polynomial times. University at Buffalo IE661 Scheduling Theory 5
6 Lemma 1: If d j+1 d j p j+1, then there is no idle time between jobs j and j+1. Three cases: 1. J is early. 2. J is completed exactly at its due date. 3. J is late. Lemma 2: In each cluster in a schedule, the early jobs proceed the tardy job. Moreover, if the jobs j and j+1 are in the same cluster and are both early, then E j E j+1. If the jobs are both late,then T j T j+1. For a cluster; d j+1 d j p j+1. Subtracting t+p j from both sides, we get d j+1 -d j -t -p j p j+1 -t -p j. Solving we get, d j -C j d j+1 -C j+1 University at Buffalo IE661 Scheduling Theory 6
7 The job sequence 1,2,3.n can be decomposed into m clusters with each cluster representing a subsequence. We compute the optimal shift for each cluster. For a cluster with jobs k,k+1,..,l; let (j) = w l + w l l = k to j A block is a sequence of clusters that are processed without interruption. Let E(r) = E jr = d jr C jr where j r is the last job in cluster σ r that is early. Hence E(r) = min j (d jr C jr ) ; where k j j r. Now let (r) = j r = max (j) ; where k j j r. If none of the jobs in the cluster is early, then E(r) = and (r) = - w l. If E(r) 1 for the last early job in every cluster of the block, a shift of the entire block by one unit time to the right decreases the total cost by (r) (the summation is over the block). University at Buffalo IE661 Scheduling Theory 7
8 Optimizing timings given a predetermined sequence Algorithm: Step1: Identify the clusters and compute (r) and E(r) for each cluster. Step2 : Find the smallest s s.t. (r) 0. Set the original C k for each job of the first s cluster. If s = m, then STOP; other wise go to step 3. If no such s exists, then go to step 4. Step3: Remove the first s clusters from the list. Go to step 2 to consider the reduced sets of cluster. Step 4: Find minimum (E(1) E(m)). Increase all C k by minimum (E(1) E(m)). Eliminate all early jobs that are no longer early. Update E(r) and (r). Go to step 2. University at Buffalo IE661 Scheduling Theory 8
9 Optimizing Timings Given A Predetermined Sequence Jobs pj dj w j w j University at Buffalo IE661 Scheduling Theory 9
10 σ 1 = 1,2 ; σ 2 = 3,4,5 ; σ 3 = 6,7 Completion times will be 3,5,12,15.. E(r) = Min(d j c j) and (r) = max j Cluster E(r) (r) Cluster 2 3 E(r) 1 Infinity (r) The optimal completion times are: 3,5,14,17,23,25,33 University at Buffalo IE661 Scheduling Theory 10
11 Primary and Secondary Objectives α β γ 1 (Opt.), γ 2. Lemma: For the single machine problem with n jobs subject to the constraint that all due dates have to be met, there exists a schedule that minimizes C j in which job k is scheduled last, if and only if 1. d k p j 2. p k p L, for all L such that d L p j Minimizing total completion times with deadlines (backward algorithm). Algorithm: Step 1: Set k = n, τ = p j, j c = {1,2,...,n} Step 2: Find k* in j c s.t. d k* τ and p k* p L, for all jobs L in j c s.t. d L τ Put job k* in position k of the sequence. Step 3: Decrease k by 1 ; decrease τ by p k*. Delete job k* from j c. Step 4: If k 1 go to Step 2, otherwise STOP. University at Buffalo IE661 Scheduling Theory 11
12 Pareto-optimal schedule: is the one in which it is not possible to decrease the value of one objective without increasing the value of the other. 1 β θ 1 γ + 1 θ 2 γ ; where θ 2 1, θ 2 are the weights of the two objectives. C j L max EDD L max (SPT/EDD) L max Trade-off between total completion time and maximum lateness University at Buffalo IE661 Scheduling Theory 12
13 SEQUENCE-DEPENDENT SETUP PROBLEMS University at Buffalo IE661 Scheduling Theory 13
14 Sequence-Dependent Setup Problems 1. An algorithm which gives an optimal schedule with the minimum makespan with sequence-dependent setup times 1 S jk C max University at Buffalo IE661 Scheduling Theory 14
15 Single machine: r j =0, no sequence dependent setup times 1 S jk C max NP hard C max = j p j Set-up times have a special structure and hence an efficient solution procedure is possible. Consider a structure where two parameters associated with job j : a j and b j 1. At the completion of the job the machine state is b j 2. To start the job the machine must be in state a j s jk = a k - b j is the total setup time necessary to bring the machine from state bj to ak state. Machine speed. Travelling Salesman Problem with n+1 cities j 0, j 1,, j n. The additional city Co has parameters ao & bo. University at Buffalo IE661 Scheduling Theory 15
16 k = φ(j) is the relation that maps each element of {0, 1, 2,.,n} onto a unique element of {0, 1, 2,..,n}.Traveling salesman is leaving city j for city k. {0, 1, 2, 3} {2, 3, 1, 0} 0 2 φ(0) = 2 φ(1) = φ(2) = 1 φ(3) = {0, 1, 2, 3} {2, 1, 3, 0} b k a φ(j) b j b 2 b 1 a φ(k) a φ(2) a φ(1) cost of going from 1 to φ(1) is a φ(1) - b 1 University at Buffalo IE661 Scheduling Theory 16
17 Swap I(j,k) applied to a permutation φ produces another permutation φ by affecting only the assignments of j and k and leaving the others unchanged. φ (k) = φ(j) φ (j) = φ(k) φ (l) = φ(l), l j, k University at Buffalo IE661 Scheduling Theory 17
18 a φ(k) b k b j a φ(j) change in cost due to swap I(j, k) Lemma. If the swap causes two arrows that did nor cross earlier { [ bj, bk ] n {[a φ,bφ ]. to cross, then the cost of the tour C φ I(j,k) increases and vice versa. Cφ I(j,k) = [ b j,b k ] [a φ(j), b φ(k) ]. Here, [ a,b ] = 2 (b-a) if b a 2 (a-b) if b < a University at Buffalo IE661 Scheduling Theory 18
19 Lemma. An optimal permutation mapping φ * is obtained if : bj bk implies that a φ (j) a φ (k). This is an optimal permutation mapping and not necessary a feasible tour. φ * might consist p distinct sub tours. A swap on i & j, belonging to different sub-tours, will cause them to cross each other and thus coalesce into one and increase the cost. Hence we select the cheapest arc that connects two of the p sub-tours and so on. University at Buffalo IE661 Scheduling Theory 19
20 Lemma. The collection of arcs that connect the undirected graph with the least cost contain only arcs that connect city j to city j+1. Consider k > j+1. Cφ I(j,k) = [ b j,b k ] [a φ(j),b φ(k) ] i [ b i,b i+1 ] [a φ*(i),b φ*(i+1) ] for i= j,., k-1 Hence the cost of swapping two nonadjacent arrows is at least equal to the cost of swapping all arrows between them. Here no arrows are allowed to cross. But in order to connect two sub-tours this condition might not be valid. University at Buffalo IE661 Scheduling Theory 20
21 b 3 =6 a 3 = 8 C φ I(1,2) = [ 1,4 ] [ 2,3 ] = 2(3-2) = 2 C φ I(2,3) = [4,6 ] [ 3,8 ] = 2(6-4) = 4 b 2 = 4 a 2 = 3 b 1 = 1 a 1 = 2 a 3 = 8 b 3 =6 a 3 = 8 b 3 =6 b 2 = 4 a 2 = 3 b 2 = 4 a 2 = 3 a 1 = 2 b 1 = 1 a 1 = 2 I(1,2) then I(2,3) Cφ I(1,2) = [1,4 ] [ 2,3 ] = 2(3-2) = 2 Cφ I(2,3) = [4,6 ] [ 2,8 ] = 2(6-4) = 4 b 1 = 1 I(2,3) then I(1,2) Cφ I(2,3) = [4,6 ] [ 3,8 ] = 2(6-4) = 4 Cφ I(1,2) = [1,4 ] [ 2,8 ] = 2(4-2) = 4 Here cost increased. University at Buffalo IE661 Scheduling Theory 21
22 A node is of Type 1 if b j a φ(j) (arrow points up) A node is of Type 2 if b j > a φ(j) (arrow points down) A swap is of Type 1 if lower node is of Type 1 A swap is of Type 2 if lower node is of Type 2 If swaps I(j, j+1) of Type 1 are performed in decreasing order of the node indices, followed by swaps of Type 2 in increasing order of the node indices then a single tour is obtained without changing any C φ* I(j, j+1) involved in the swaps University at Buffalo IE661 Scheduling Theory 22
23 Algorithm + Example 7 jobs b j a j Step 1. Arrange the b j in order of size and renumber the jobs so that b 1 b 2... b n Arrange the a j in order of size. The permutation mapping φ* is defined by φ* (j) = k, k being such that a k is the jth smallest of the a. University at Buffalo IE661 Scheduling Theory 23
24 a 4 =45 b 7 =40 a 6 =34 b 6 =31 b 5 =26 b 4 =19 b 3 =15 b 2 =3 b 1 =1 a 5 =22 a 7 =18 a 3 =16 a 1 =7 a 2 =4 jobs b j a j a φ* (j) φ*(j) University at Buffalo IE661 Scheduling Theory 24
25 Step 2. Form an undirected graph with n nodes and undirected arcs connecting the jth and φ*(j) nodes, j=1, n. If the current graph has only one component then STOP ; otherwise go to Step University at Buffalo IE661 Scheduling Theory 25
26 Step 3. Compute the swap costs C φ * I(j, j+1) for j=1,,n C φ* I(j, j+1) = 2 max ( min (b j+1, a φ*(j+1) ) - max (b j, a φ*(j) ) ), 0 ) C φ* I(1, 2) = 2 max ( (3-4), 0 ) = 0 C φ* I(2, 3) = 2 max ( (15-7), 0 ) = 16 C φ* I(3, 4) = 2 max ( (18-16), 0 ) = 4 C φ* I(4, 5) = 2 max ( (22-19), 0 ) = 6 C φ* I(5, 6) = 2 max ( (31-26), 0 ) = 10 C φ* I(6, 7) = 2 max ( (40-34), 0 ) = 12 University at Buffalo IE661 Scheduling Theory 26
27 Step 4. Select the smallest value C φ* I(j, j+1) such that j is in one component and j+1 in another. In case of a tie for smallest, choose any. Insert the undirected arc R j, j+1 into the graph. Repeat this step until all the components in the undirected graph are connected University at Buffalo IE661 Scheduling Theory 27
28 Step 5. Divide the arcs added in Step 4 into two groups. Those R j, j+1 for which b j a φ(j) go in group 1, those for which b j > a φ(j) go in group 2. arcs b j a φ*(j) group R 2, 3 b 2 =3 a 1 =7 1 R 3, 4 b 3 =15 a 3 =16 1 R 4, 5 b 4 =19 a 7 =18 2 R 5, 6 b 5 =26 a 5 =22 2 Step 6. Find the largest index j 1 such that R j1, j1 +1 is in group 1. Find the second largest index, and so on, up to j l assuming there are l elements in the group. Find the smallest index k 1 such that R k1, k1 +1 is in group 2. Find the second smallest index, and so on, up to k m assuming there are m elements in the group. j 1 = 3, j 2 = 2, k 1 = 4, k 2 = 5 University at Buffalo IE661 Scheduling Theory 28
29 Step 7. The optimal tour φ** is constructed by applying the following sequence of swaps on the permutation φ*: φ** = φ* I(j 1,j 1 +1) I(j 2,j 2 +1) I(j l,j l +1) I(k 1,k 1 +1) I(k 2, k 2 +1) I(k m,k m +1) φ** = φ* I(3,4) I(2,3) I(4,5) I(5,6) Type 1 Type 2 University at Buffalo IE661 Scheduling Theory 29
30 a 4 =45 a 4 =45 b 7 =40 a 6 =34 b 7 =40 a 6 =34 b 6 =31 b 6 =31 b 5 =26 b 4 =19 b 3 =15 a 5 =22 a 7 =18 a 3 =16 a 1 =7 b 5 =26 b 4 =19 b 3 =15 a 5 =22 a 7 =18 a 3 =16 a 1 =7 b 2 =3 b 1 =1 a 2 =4 b 2 =3 b 1 =1 a 2 =4 φ* I(3,4) φ* I(3,4) I(2,3) University at Buffalo IE661 Scheduling Theory 30
31 a 4 =45 a 4 =45 b 7 =40 a 6 =34 b 7 =40 a 6 =34 b 6 =31 b 6 =31 b 5 =26 b 4 =19 b 3 =15 a 5 =22 a 7 =18 a 3 =16 a 1 =7 b 5 =26 b 4 =19 b 3 =15 a 5 =22 a 7 =18 a 3 =16 a 1 =7 b 2 =3 b 1 =1 a 2 =4 b 2 =3 b 1 =1 a 2 =4 φ* I(3,4) I(2,3) I(4,5) φ** = φ* I(3,4) I(2,3) I(4,5) I(5,6) University at Buffalo IE661 Scheduling Theory 31
32 a 4 =45 b 7 =40 a 6 =34 b 6 =31 b 5 =26 b 4 =19 b 3 =15 b 2 =3 b 1 =1 a 5 =22 a 7 =18 a 3 =16 a 1 =7 a 2 =4 φ** = φ* I(3,4) I(2,3) I(4,5) I(5,6) The optimal tour is: The cost of the tour is: = 57 University at Buffalo IE661 Scheduling Theory 32
For every job, the start time on machine j+1 is greater than or equal to the completion time on machine j.
 Flow Shop Scheduling - makespan A flow shop is one where all the jobs visit all the machine for processing in the given order. If we consider a flow shop with n jobs and two machines (M1 and M2), all the
Flow Shop Scheduling - makespan A flow shop is one where all the jobs visit all the machine for processing in the given order. If we consider a flow shop with n jobs and two machines (M1 and M2), all the
IEOR E4004: Introduction to OR: Deterministic Models
 IEOR E4004: Introduction to OR: Deterministic Models 1 Dynamic Programming Following is a summary of the problems we discussed in class. (We do not include the discussion on the container problem or the
IEOR E4004: Introduction to OR: Deterministic Models 1 Dynamic Programming Following is a summary of the problems we discussed in class. (We do not include the discussion on the container problem or the
Single Machine Inserted Idle Time Scheduling with Release Times and Due Dates
 Single Machine Inserted Idle Time Scheduling with Release Times and Due Dates Natalia Grigoreva Department of Mathematics and Mechanics, St.Petersburg State University, Russia n.s.grig@gmail.com Abstract.
Single Machine Inserted Idle Time Scheduling with Release Times and Due Dates Natalia Grigoreva Department of Mathematics and Mechanics, St.Petersburg State University, Russia n.s.grig@gmail.com Abstract.
6 -AL- ONE MACHINE SEQUENCING TO MINIMIZE MEAN FLOW TIME WITH MINIMUM NUMBER TARDY. Hamilton Emmons \,«* Technical Memorandum No. 2.
 li. 1. 6 -AL- ONE MACHINE SEQUENCING TO MINIMIZE MEAN FLOW TIME WITH MINIMUM NUMBER TARDY f \,«* Hamilton Emmons Technical Memorandum No. 2 May, 1973 1 il 1 Abstract The problem of sequencing n jobs on
li. 1. 6 -AL- ONE MACHINE SEQUENCING TO MINIMIZE MEAN FLOW TIME WITH MINIMUM NUMBER TARDY f \,«* Hamilton Emmons Technical Memorandum No. 2 May, 1973 1 il 1 Abstract The problem of sequencing n jobs on
Handout 4: Deterministic Systems and the Shortest Path Problem
 SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 4: Deterministic Systems and the Shortest Path Problem Instructor: Shiqian Ma January 27, 2014 Suggested Reading: Bertsekas
SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 4: Deterministic Systems and the Shortest Path Problem Instructor: Shiqian Ma January 27, 2014 Suggested Reading: Bertsekas
Homework #4. CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class
 Homework #4 CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class o Grades depend on neatness and clarity. o Write your answers with enough detail about your approach and concepts
Homework #4 CMSC351 - Spring 2013 PRINT Name : Due: Thu Apr 16 th at the start of class o Grades depend on neatness and clarity. o Write your answers with enough detail about your approach and concepts
Essays on Some Combinatorial Optimization Problems with Interval Data
 Essays on Some Combinatorial Optimization Problems with Interval Data a thesis submitted to the department of industrial engineering and the institute of engineering and sciences of bilkent university
Essays on Some Combinatorial Optimization Problems with Interval Data a thesis submitted to the department of industrial engineering and the institute of engineering and sciences of bilkent university
Optimization Methods. Lecture 16: Dynamic Programming
 15.093 Optimization Methods Lecture 16: Dynamic Programming 1 Outline 1. The knapsack problem Slide 1. The traveling salesman problem 3. The general DP framework 4. Bellman equation 5. Optimal inventory
15.093 Optimization Methods Lecture 16: Dynamic Programming 1 Outline 1. The knapsack problem Slide 1. The traveling salesman problem 3. The general DP framework 4. Bellman equation 5. Optimal inventory
CS599: Algorithm Design in Strategic Settings Fall 2012 Lecture 6: Prior-Free Single-Parameter Mechanism Design (Continued)
 CS599: Algorithm Design in Strategic Settings Fall 2012 Lecture 6: Prior-Free Single-Parameter Mechanism Design (Continued) Instructor: Shaddin Dughmi Administrivia Homework 1 due today. Homework 2 out
CS599: Algorithm Design in Strategic Settings Fall 2012 Lecture 6: Prior-Free Single-Parameter Mechanism Design (Continued) Instructor: Shaddin Dughmi Administrivia Homework 1 due today. Homework 2 out
6.231 DYNAMIC PROGRAMMING LECTURE 3 LECTURE OUTLINE
 6.21 DYNAMIC PROGRAMMING LECTURE LECTURE OUTLINE Deterministic finite-state DP problems Backward shortest path algorithm Forward shortest path algorithm Shortest path examples Alternative shortest path
6.21 DYNAMIC PROGRAMMING LECTURE LECTURE OUTLINE Deterministic finite-state DP problems Backward shortest path algorithm Forward shortest path algorithm Shortest path examples Alternative shortest path
Outline. 1 Introduction. 2 Algorithms. 3 Examples. Algorithm 1 General coordinate minimization framework. 1: Choose x 0 R n and set k 0.
 Outline Coordinate Minimization Daniel P. Robinson Department of Applied Mathematics and Statistics Johns Hopkins University November 27, 208 Introduction 2 Algorithms Cyclic order with exact minimization
Outline Coordinate Minimization Daniel P. Robinson Department of Applied Mathematics and Statistics Johns Hopkins University November 27, 208 Introduction 2 Algorithms Cyclic order with exact minimization
Levin Reduction and Parsimonious Reductions
 Levin Reduction and Parsimonious Reductions The reduction R in Cook s theorem (p. 266) is such that Each satisfying truth assignment for circuit R(x) corresponds to an accepting computation path for M(x).
Levin Reduction and Parsimonious Reductions The reduction R in Cook s theorem (p. 266) is such that Each satisfying truth assignment for circuit R(x) corresponds to an accepting computation path for M(x).
UNIT 2. Greedy Method GENERAL METHOD
 UNIT 2 GENERAL METHOD Greedy Method Greedy is the most straight forward design technique. Most of the problems have n inputs and require us to obtain a subset that satisfies some constraints. Any subset
UNIT 2 GENERAL METHOD Greedy Method Greedy is the most straight forward design technique. Most of the problems have n inputs and require us to obtain a subset that satisfies some constraints. Any subset
6.231 DYNAMIC PROGRAMMING LECTURE 3 LECTURE OUTLINE
 6.21 DYNAMIC PROGRAMMING LECTURE LECTURE OUTLINE Deterministic finite-state DP problems Backward shortest path algorithm Forward shortest path algorithm Shortest path examples Alternative shortest path
6.21 DYNAMIC PROGRAMMING LECTURE LECTURE OUTLINE Deterministic finite-state DP problems Backward shortest path algorithm Forward shortest path algorithm Shortest path examples Alternative shortest path
Finding optimal arbitrage opportunities using a quantum annealer
 Finding optimal arbitrage opportunities using a quantum annealer White Paper Finding optimal arbitrage opportunities using a quantum annealer Gili Rosenberg Abstract We present two formulations for finding
Finding optimal arbitrage opportunities using a quantum annealer White Paper Finding optimal arbitrage opportunities using a quantum annealer Gili Rosenberg Abstract We present two formulations for finding
THE TRAVELING SALESMAN PROBLEM FOR MOVING POINTS ON A LINE
 THE TRAVELING SALESMAN PROBLEM FOR MOVING POINTS ON A LINE GÜNTER ROTE Abstract. A salesperson wants to visit each of n objects that move on a line at given constant speeds in the shortest possible time,
THE TRAVELING SALESMAN PROBLEM FOR MOVING POINTS ON A LINE GÜNTER ROTE Abstract. A salesperson wants to visit each of n objects that move on a line at given constant speeds in the shortest possible time,
Advanced Operations Research Prof. G. Srinivasan Dept of Management Studies Indian Institute of Technology, Madras
 Advanced Operations Research Prof. G. Srinivasan Dept of Management Studies Indian Institute of Technology, Madras Lecture 23 Minimum Cost Flow Problem In this lecture, we will discuss the minimum cost
Advanced Operations Research Prof. G. Srinivasan Dept of Management Studies Indian Institute of Technology, Madras Lecture 23 Minimum Cost Flow Problem In this lecture, we will discuss the minimum cost
Stochastic Optimization Methods in Scheduling. Rolf H. Möhring Technische Universität Berlin Combinatorial Optimization and Graph Algorithms
 Stochastic Optimization Methods in Scheduling Rolf H. Möhring Technische Universität Berlin Combinatorial Optimization and Graph Algorithms More expensive and longer... Eurotunnel Unexpected loss of 400,000,000
Stochastic Optimization Methods in Scheduling Rolf H. Möhring Technische Universität Berlin Combinatorial Optimization and Graph Algorithms More expensive and longer... Eurotunnel Unexpected loss of 400,000,000
Another Variant of 3sat. 3sat. 3sat Is NP-Complete. The Proof (concluded)
 3sat k-sat, where k Z +, is the special case of sat. The formula is in CNF and all clauses have exactly k literals (repetition of literals is allowed). For example, (x 1 x 2 x 3 ) (x 1 x 1 x 2 ) (x 1 x
3sat k-sat, where k Z +, is the special case of sat. The formula is in CNF and all clauses have exactly k literals (repetition of literals is allowed). For example, (x 1 x 2 x 3 ) (x 1 x 1 x 2 ) (x 1 x
Optimal Integer Delay Budget Assignment on Directed Acyclic Graphs
 Optimal Integer Delay Budget Assignment on Directed Acyclic Graphs E. Bozorgzadeh S. Ghiasi A. Takahashi M. Sarrafzadeh Computer Science Department University of California, Los Angeles (UCLA) Los Angeles,
Optimal Integer Delay Budget Assignment on Directed Acyclic Graphs E. Bozorgzadeh S. Ghiasi A. Takahashi M. Sarrafzadeh Computer Science Department University of California, Los Angeles (UCLA) Los Angeles,
monotone circuit value
 monotone circuit value A monotone boolean circuit s output cannot change from true to false when one input changes from false to true. Monotone boolean circuits are hence less expressive than general circuits.
monotone circuit value A monotone boolean circuit s output cannot change from true to false when one input changes from false to true. Monotone boolean circuits are hence less expressive than general circuits.
Another Variant of 3sat
 Another Variant of 3sat Proposition 32 3sat is NP-complete for expressions in which each variable is restricted to appear at most three times, and each literal at most twice. (3sat here requires only that
Another Variant of 3sat Proposition 32 3sat is NP-complete for expressions in which each variable is restricted to appear at most three times, and each literal at most twice. (3sat here requires only that
CSE202: Algorithm Design and Analysis. Ragesh Jaiswal, CSE, UCSD
 Fractional knapsack Problem Fractional knapsack: You are a thief and you have a sack of size W. There are n divisible items. Each item i has a volume W (i) and a total value V (i). Design an algorithm
Fractional knapsack Problem Fractional knapsack: You are a thief and you have a sack of size W. There are n divisible items. Each item i has a volume W (i) and a total value V (i). Design an algorithm
Integer Solution to a Graph-based Linear Programming Problem
 Integer Solution to a Graph-based Linear Programming Problem E. Bozorgzadeh S. Ghiasi A. Takahashi M. Sarrafzadeh Computer Science Department University of California, Los Angeles (UCLA) Los Angeles, CA
Integer Solution to a Graph-based Linear Programming Problem E. Bozorgzadeh S. Ghiasi A. Takahashi M. Sarrafzadeh Computer Science Department University of California, Los Angeles (UCLA) Los Angeles, CA
6.231 DYNAMIC PROGRAMMING LECTURE 8 LECTURE OUTLINE
 6.231 DYNAMIC PROGRAMMING LECTURE 8 LECTURE OUTLINE Suboptimal control Cost approximation methods: Classification Certainty equivalent control: An example Limited lookahead policies Performance bounds
6.231 DYNAMIC PROGRAMMING LECTURE 8 LECTURE OUTLINE Suboptimal control Cost approximation methods: Classification Certainty equivalent control: An example Limited lookahead policies Performance bounds
Master Thesis Mathematics
 Radboud Universiteit Nijmegen Master Thesis Mathematics Scheduling with job dependent machine speed Author: Veerle Timmermans Supervisor: Tjark Vredeveld Wieb Bosma May 21, 2014 Abstract The power consumption
Radboud Universiteit Nijmegen Master Thesis Mathematics Scheduling with job dependent machine speed Author: Veerle Timmermans Supervisor: Tjark Vredeveld Wieb Bosma May 21, 2014 Abstract The power consumption
Methods and Models of Loss Reserving Based on Run Off Triangles: A Unifying Survey
 Methods and Models of Loss Reserving Based on Run Off Triangles: A Unifying Survey By Klaus D Schmidt Lehrstuhl für Versicherungsmathematik Technische Universität Dresden Abstract The present paper provides
Methods and Models of Loss Reserving Based on Run Off Triangles: A Unifying Survey By Klaus D Schmidt Lehrstuhl für Versicherungsmathematik Technische Universität Dresden Abstract The present paper provides
Pakes (1986): Patents as Options: Some Estimates of the Value of Holding European Patent Stocks
 Pakes (1986): Patents as Options: Some Estimates of the Value of Holding European Patent Stocks Spring 2009 Main question: How much are patents worth? Answering this question is important, because it helps
Pakes (1986): Patents as Options: Some Estimates of the Value of Holding European Patent Stocks Spring 2009 Main question: How much are patents worth? Answering this question is important, because it helps
Lecture 6. 1 Polynomial-time algorithms for the global min-cut problem
 ORIE 633 Network Flows September 20, 2007 Lecturer: David P. Williamson Lecture 6 Scribe: Animashree Anandkumar 1 Polynomial-time algorithms for the global min-cut problem 1.1 The global min-cut problem
ORIE 633 Network Flows September 20, 2007 Lecturer: David P. Williamson Lecture 6 Scribe: Animashree Anandkumar 1 Polynomial-time algorithms for the global min-cut problem 1.1 The global min-cut problem
A Learning Theory of Ranking Aggregation
 A Learning Theory of Ranking Aggregation France/Japan Machine Learning Workshop Anna Korba, Stephan Clémençon, Eric Sibony November 14, 2017 Télécom ParisTech Outline 1. The Ranking Aggregation Problem
A Learning Theory of Ranking Aggregation France/Japan Machine Learning Workshop Anna Korba, Stephan Clémençon, Eric Sibony November 14, 2017 Télécom ParisTech Outline 1. The Ranking Aggregation Problem
Lie Algebras and Representation Theory Homework 7
 Lie Algebras and Representation Theory Homework 7 Debbie Matthews 2015-05-19 Problem 10.5 If σ W can be written as a product of t simple reflections, prove that t has the same parity as l(σ). Let = {α
Lie Algebras and Representation Theory Homework 7 Debbie Matthews 2015-05-19 Problem 10.5 If σ W can be written as a product of t simple reflections, prove that t has the same parity as l(σ). Let = {α
Corrections to the Second Edition of Modeling and Analysis of Stochastic Systems
 Corrections to the Second Edition of Modeling and Analysis of Stochastic Systems Vidyadhar Kulkarni November, 200 Send additional corrections to the author at his email address vkulkarn@email.unc.edu.
Corrections to the Second Edition of Modeling and Analysis of Stochastic Systems Vidyadhar Kulkarni November, 200 Send additional corrections to the author at his email address vkulkarn@email.unc.edu.
Exact Inference (9/30/13) 2 A brief review of Forward-Backward and EM for HMMs
 STA561: Probabilistic machine learning Exact Inference (9/30/13) Lecturer: Barbara Engelhardt Scribes: Jiawei Liang, He Jiang, Brittany Cohen 1 Validation for Clustering If we have two centroids, η 1 and
STA561: Probabilistic machine learning Exact Inference (9/30/13) Lecturer: Barbara Engelhardt Scribes: Jiawei Liang, He Jiang, Brittany Cohen 1 Validation for Clustering If we have two centroids, η 1 and
A relation on 132-avoiding permutation patterns
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. VOL, 205, 285 302 A relation on 32-avoiding permutation patterns Natalie Aisbett School of Mathematics and Statistics, University of Sydney,
Discrete Mathematics and Theoretical Computer Science DMTCS vol. VOL, 205, 285 302 A relation on 32-avoiding permutation patterns Natalie Aisbett School of Mathematics and Statistics, University of Sydney,
UGM Crash Course: Conditional Inference and Cutset Conditioning
 UGM Crash Course: Conditional Inference and Cutset Conditioning Julie Nutini August 19 th, 2015 1 / 25 Conditional UGM 2 / 25 We know the value of one or more random variables i.e., we have observations,
UGM Crash Course: Conditional Inference and Cutset Conditioning Julie Nutini August 19 th, 2015 1 / 25 Conditional UGM 2 / 25 We know the value of one or more random variables i.e., we have observations,
CEC login. Student Details Name SOLUTIONS
 Student Details Name SOLUTIONS CEC login Instructions You have roughly 1 minute per point, so schedule your time accordingly. There is only one correct answer per question. Good luck! Question 1. Searching
Student Details Name SOLUTIONS CEC login Instructions You have roughly 1 minute per point, so schedule your time accordingly. There is only one correct answer per question. Good luck! Question 1. Searching
Introduction to Greedy Algorithms: Huffman Codes
 Introduction to Greedy Algorithms: Huffman Codes Yufei Tao ITEE University of Queensland In computer science, one interesting method to design algorithms is to go greedy, namely, keep doing the thing that
Introduction to Greedy Algorithms: Huffman Codes Yufei Tao ITEE University of Queensland In computer science, one interesting method to design algorithms is to go greedy, namely, keep doing the thing that
6.231 DYNAMIC PROGRAMMING LECTURE 10 LECTURE OUTLINE
 6.231 DYNAMIC PROGRAMMING LECTURE 10 LECTURE OUTLINE Rollout algorithms Cost improvement property Discrete deterministic problems Approximations of rollout algorithms Discretization of continuous time
6.231 DYNAMIC PROGRAMMING LECTURE 10 LECTURE OUTLINE Rollout algorithms Cost improvement property Discrete deterministic problems Approximations of rollout algorithms Discretization of continuous time
6.896 Topics in Algorithmic Game Theory February 10, Lecture 3
 6.896 Topics in Algorithmic Game Theory February 0, 200 Lecture 3 Lecturer: Constantinos Daskalakis Scribe: Pablo Azar, Anthony Kim In the previous lecture we saw that there always exists a Nash equilibrium
6.896 Topics in Algorithmic Game Theory February 0, 200 Lecture 3 Lecturer: Constantinos Daskalakis Scribe: Pablo Azar, Anthony Kim In the previous lecture we saw that there always exists a Nash equilibrium
Dynamic Programming cont. We repeat: The Dynamic Programming Template has three parts.
 Page 1 Dynamic Programming cont. We repeat: The Dynamic Programming Template has three parts. Subproblems Sometimes this is enough if the algorithm and its complexity is obvious. Recursion Algorithm Must
Page 1 Dynamic Programming cont. We repeat: The Dynamic Programming Template has three parts. Subproblems Sometimes this is enough if the algorithm and its complexity is obvious. Recursion Algorithm Must
Options Pricing Using Combinatoric Methods Postnikov Final Paper
 Options Pricing Using Combinatoric Methods 18.04 Postnikov Final Paper Annika Kim May 7, 018 Contents 1 Introduction The Lattice Model.1 Overview................................ Limitations of the Lattice
Options Pricing Using Combinatoric Methods 18.04 Postnikov Final Paper Annika Kim May 7, 018 Contents 1 Introduction The Lattice Model.1 Overview................................ Limitations of the Lattice
Chapter 7: Portfolio Theory
 Chapter 7: Portfolio Theory 1. Introduction 2. Portfolio Basics 3. The Feasible Set 4. Portfolio Selection Rules 5. The Efficient Frontier 6. Indifference Curves 7. The Two-Asset Portfolio 8. Unrestriceted
Chapter 7: Portfolio Theory 1. Introduction 2. Portfolio Basics 3. The Feasible Set 4. Portfolio Selection Rules 5. The Efficient Frontier 6. Indifference Curves 7. The Two-Asset Portfolio 8. Unrestriceted
1 Appendix A: Definition of equilibrium
 Online Appendix to Partnerships versus Corporations: Moral Hazard, Sorting and Ownership Structure Ayca Kaya and Galina Vereshchagina Appendix A formally defines an equilibrium in our model, Appendix B
Online Appendix to Partnerships versus Corporations: Moral Hazard, Sorting and Ownership Structure Ayca Kaya and Galina Vereshchagina Appendix A formally defines an equilibrium in our model, Appendix B
Fiscal Devaluations in a Model with Capital
 Fiscal Devaluations in a Model with Capital Emmanuel Farhi Harvard University Gita Gopinath Harvard University Oleg Itskhoki Princeton University First Draft: June 3 2011 This Draft: September 25 2014
Fiscal Devaluations in a Model with Capital Emmanuel Farhi Harvard University Gita Gopinath Harvard University Oleg Itskhoki Princeton University First Draft: June 3 2011 This Draft: September 25 2014
Quadrant marked mesh patterns in 123-avoiding permutations
 Quadrant marked mesh patterns in 23-avoiding permutations Dun Qiu Department of Mathematics University of California, San Diego La Jolla, CA 92093-02. USA duqiu@math.ucsd.edu Jeffrey Remmel Department
Quadrant marked mesh patterns in 23-avoiding permutations Dun Qiu Department of Mathematics University of California, San Diego La Jolla, CA 92093-02. USA duqiu@math.ucsd.edu Jeffrey Remmel Department
Notes on the EM Algorithm Michael Collins, September 24th 2005
 Notes on the EM Algorithm Michael Collins, September 24th 2005 1 Hidden Markov Models A hidden Markov model (N, Σ, Θ) consists of the following elements: N is a positive integer specifying the number of
Notes on the EM Algorithm Michael Collins, September 24th 2005 1 Hidden Markov Models A hidden Markov model (N, Σ, Θ) consists of the following elements: N is a positive integer specifying the number of
Adjusting scheduling model with release and due dates in production planning
 PRODUCTION & MANUFACTURING RESEARCH ARTICLE Adjusting scheduling model with release and due dates in production planning Elisa Chinos and Nodari Vakhania Cogent Engineering (2017), 4: 1321175 Page 1 of
PRODUCTION & MANUFACTURING RESEARCH ARTICLE Adjusting scheduling model with release and due dates in production planning Elisa Chinos and Nodari Vakhania Cogent Engineering (2017), 4: 1321175 Page 1 of
3.4 Copula approach for modeling default dependency. Two aspects of modeling the default times of several obligors
 3.4 Copula approach for modeling default dependency Two aspects of modeling the default times of several obligors 1. Default dynamics of a single obligor. 2. Model the dependence structure of defaults
3.4 Copula approach for modeling default dependency Two aspects of modeling the default times of several obligors 1. Default dynamics of a single obligor. 2. Model the dependence structure of defaults
The Stackelberg Minimum Spanning Tree Game
 The Stackelberg Minimum Spanning Tree Game J. Cardinal, E. Demaine, S. Fiorini, G. Joret, S. Langerman, I. Newman, O. Weimann, The Stackelberg Minimum Spanning Tree Game, WADS 07 Stackelberg Game 2 players:
The Stackelberg Minimum Spanning Tree Game J. Cardinal, E. Demaine, S. Fiorini, G. Joret, S. Langerman, I. Newman, O. Weimann, The Stackelberg Minimum Spanning Tree Game, WADS 07 Stackelberg Game 2 players:
Activity Predecessors Durations (days) a - 3 b a 4 c a 5 d a 4 e b 2 f d 9 g c, e 6 h f, g 2
 CHAPTER 11 INDUSTRIAL ENGINEERING YEAR 2012 ONE MARK MCQ 11.1 Which one of the following is NOT a decision taken during the aggregate production planning stage? (A) Scheduling of machines (B) Amount of
CHAPTER 11 INDUSTRIAL ENGINEERING YEAR 2012 ONE MARK MCQ 11.1 Which one of the following is NOT a decision taken during the aggregate production planning stage? (A) Scheduling of machines (B) Amount of
On Packing Densities of Set Partitions
 On Packing Densities of Set Partitions Adam M.Goyt 1 Department of Mathematics Minnesota State University Moorhead Moorhead, MN 56563, USA goytadam@mnstate.edu Lara K. Pudwell Department of Mathematics
On Packing Densities of Set Partitions Adam M.Goyt 1 Department of Mathematics Minnesota State University Moorhead Moorhead, MN 56563, USA goytadam@mnstate.edu Lara K. Pudwell Department of Mathematics
6.231 DYNAMIC PROGRAMMING LECTURE 5 LECTURE OUTLINE
 6.231 DYNAMIC PROGRAMMING LECTURE 5 LECTURE OUTLINE Stopping problems Scheduling problems Minimax Control 1 PURE STOPPING PROBLEMS Two possible controls: Stop (incur a one-time stopping cost, and move
6.231 DYNAMIC PROGRAMMING LECTURE 5 LECTURE OUTLINE Stopping problems Scheduling problems Minimax Control 1 PURE STOPPING PROBLEMS Two possible controls: Stop (incur a one-time stopping cost, and move
Collinear Triple Hypergraphs and the Finite Plane Kakeya Problem
 Collinear Triple Hypergraphs and the Finite Plane Kakeya Problem Joshua Cooper August 14, 006 Abstract We show that the problem of counting collinear points in a permutation (previously considered by the
Collinear Triple Hypergraphs and the Finite Plane Kakeya Problem Joshua Cooper August 14, 006 Abstract We show that the problem of counting collinear points in a permutation (previously considered by the
Lecture 7: Bayesian approach to MAB - Gittins index
 Advanced Topics in Machine Learning and Algorithmic Game Theory Lecture 7: Bayesian approach to MAB - Gittins index Lecturer: Yishay Mansour Scribe: Mariano Schain 7.1 Introduction In the Bayesian approach
Advanced Topics in Machine Learning and Algorithmic Game Theory Lecture 7: Bayesian approach to MAB - Gittins index Lecturer: Yishay Mansour Scribe: Mariano Schain 7.1 Introduction In the Bayesian approach
Homework solutions, Chapter 8
 Homework solutions, Chapter 8 NOTE: We might think of 8.1 as being a section devoted to setting up the networks and 8.2 as solving them, but only 8.2 has a homework section. Section 8.2 2. Use Dijkstra
Homework solutions, Chapter 8 NOTE: We might think of 8.1 as being a section devoted to setting up the networks and 8.2 as solving them, but only 8.2 has a homework section. Section 8.2 2. Use Dijkstra
Orthogonality to the value group is the same as generic stability in C-minimal expansions of ACVF
 Orthogonality to the value group is the same as generic stability in C-minimal expansions of ACVF Will Johnson February 18, 2014 1 Introduction Let T be some C-minimal expansion of ACVF. Let U be the monster
Orthogonality to the value group is the same as generic stability in C-minimal expansions of ACVF Will Johnson February 18, 2014 1 Introduction Let T be some C-minimal expansion of ACVF. Let U be the monster
Strong Subgraph k-connectivity of Digraphs
 Strong Subgraph k-connectivity of Digraphs Yuefang Sun joint work with Gregory Gutin, Anders Yeo, Xiaoyan Zhang yuefangsun2013@163.com Department of Mathematics Shaoxing University, China July 2018, Zhuhai
Strong Subgraph k-connectivity of Digraphs Yuefang Sun joint work with Gregory Gutin, Anders Yeo, Xiaoyan Zhang yuefangsun2013@163.com Department of Mathematics Shaoxing University, China July 2018, Zhuhai
Exact Inference. Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4. x 3. f s. x 2. x 1
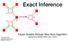 Exact Inference x 1 x 3 x 2 f s Geoffrey Roeder roeder@cs.toronto.edu 8 February 2018 Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4 Building Blocks UGMs, Cliques, Factor
Exact Inference x 1 x 3 x 2 f s Geoffrey Roeder roeder@cs.toronto.edu 8 February 2018 Factor Graphs through Max-Sum Algorithm Figures from Bishop PRML Sec. 8.3/8.4 Building Blocks UGMs, Cliques, Factor
COSC 311: ALGORITHMS HW4: NETWORK FLOW
 COSC 311: ALGORITHMS HW4: NETWORK FLOW Solutions 1 Warmup 1) Finding max flows and min cuts. Here is a graph (the numbers in boxes represent the amount of flow along an edge, and the unadorned numbers
COSC 311: ALGORITHMS HW4: NETWORK FLOW Solutions 1 Warmup 1) Finding max flows and min cuts. Here is a graph (the numbers in boxes represent the amount of flow along an edge, and the unadorned numbers
Integer Programming Models
 Integer Programming Models Fabio Furini December 10, 2014 Integer Programming Models 1 Outline 1 Combinatorial Auctions 2 The Lockbox Problem 3 Constructing an Index Fund Integer Programming Models 2 Integer
Integer Programming Models Fabio Furini December 10, 2014 Integer Programming Models 1 Outline 1 Combinatorial Auctions 2 The Lockbox Problem 3 Constructing an Index Fund Integer Programming Models 2 Integer
Algorithmic Game Theory (a primer) Depth Qualifying Exam for Ashish Rastogi (Ph.D. candidate)
 Algorithmic Game Theory (a primer) Depth Qualifying Exam for Ashish Rastogi (Ph.D. candidate) 1 Game Theory Theory of strategic behavior among rational players. Typical game has several players. Each player
Algorithmic Game Theory (a primer) Depth Qualifying Exam for Ashish Rastogi (Ph.D. candidate) 1 Game Theory Theory of strategic behavior among rational players. Typical game has several players. Each player
Deterministic Sampling Algorithms for Network Design
 Algorithmica 2011 60: 110 151 DOI 10.1007/s00453-009-9344-x Deterministic Sampling Algorithms for Network Design Anke van Zuylen Received: 17 November 2008 / Accepted: 13 July 2009 / Published online:
Algorithmica 2011 60: 110 151 DOI 10.1007/s00453-009-9344-x Deterministic Sampling Algorithms for Network Design Anke van Zuylen Received: 17 November 2008 / Accepted: 13 July 2009 / Published online:
Outline Introduction Game Representations Reductions Solution Concepts. Game Theory. Enrico Franchi. May 19, 2010
 May 19, 2010 1 Introduction Scope of Agent preferences Utility Functions 2 Game Representations Example: Game-1 Extended Form Strategic Form Equivalences 3 Reductions Best Response Domination 4 Solution
May 19, 2010 1 Introduction Scope of Agent preferences Utility Functions 2 Game Representations Example: Game-1 Extended Form Strategic Form Equivalences 3 Reductions Best Response Domination 4 Solution
The Correlation Smile Recovery
 Fortis Bank Equity & Credit Derivatives Quantitative Research The Correlation Smile Recovery E. Vandenbrande, A. Vandendorpe, Y. Nesterov, P. Van Dooren draft version : March 2, 2009 1 Introduction Pricing
Fortis Bank Equity & Credit Derivatives Quantitative Research The Correlation Smile Recovery E. Vandenbrande, A. Vandendorpe, Y. Nesterov, P. Van Dooren draft version : March 2, 2009 1 Introduction Pricing
Babu Banarasi Das National Institute of Technology and Management
 Babu Banarasi Das National Institute of Technology and Management Department of Computer Applications Question Bank Masters of Computer Applications (MCA) NEW Syllabus (Affiliated to U. P. Technical University,
Babu Banarasi Das National Institute of Technology and Management Department of Computer Applications Question Bank Masters of Computer Applications (MCA) NEW Syllabus (Affiliated to U. P. Technical University,
Part 1: q Theory and Irreversible Investment
 Part 1: q Theory and Irreversible Investment Goal: Endogenize firm characteristics and risk. Value/growth Size Leverage New issues,... This lecture: q theory of investment Irreversible investment and real
Part 1: q Theory and Irreversible Investment Goal: Endogenize firm characteristics and risk. Value/growth Size Leverage New issues,... This lecture: q theory of investment Irreversible investment and real
Lecture 3: Return vs Risk: Mean-Variance Analysis
 Lecture 3: Return vs Risk: Mean-Variance Analysis 3.1 Basics We will discuss an important trade-off between return (or reward) as measured by expected return or mean of the return and risk as measured
Lecture 3: Return vs Risk: Mean-Variance Analysis 3.1 Basics We will discuss an important trade-off between return (or reward) as measured by expected return or mean of the return and risk as measured
Technical Report Doc ID: TR April-2009 (Last revised: 02-June-2009)
 Technical Report Doc ID: TR-1-2009. 14-April-2009 (Last revised: 02-June-2009) The homogeneous selfdual model algorithm for linear optimization. Author: Erling D. Andersen In this white paper we present
Technical Report Doc ID: TR-1-2009. 14-April-2009 (Last revised: 02-June-2009) The homogeneous selfdual model algorithm for linear optimization. Author: Erling D. Andersen In this white paper we present
Comprehensive Exam. August 19, 2013
 Comprehensive Exam August 19, 2013 You have a total of 180 minutes to complete the exam. If a question seems ambiguous, state why, sharpen it up and answer the sharpened-up question. Good luck! 1 1 Menu
Comprehensive Exam August 19, 2013 You have a total of 180 minutes to complete the exam. If a question seems ambiguous, state why, sharpen it up and answer the sharpened-up question. Good luck! 1 1 Menu
Analysis of equilibrium prices and quantities within network-structured markets applying the Lagrange function method
 19th International Congress on odelling and Simulation, Perth, Australia, 12 16 December 2011 http://mssanz.org.au/modsim2011 Analysis of equilibrium prices and quantities within network-structured markets
19th International Congress on odelling and Simulation, Perth, Australia, 12 16 December 2011 http://mssanz.org.au/modsim2011 Analysis of equilibrium prices and quantities within network-structured markets
Term Structure Lattice Models
 IEOR E4706: Foundations of Financial Engineering c 2016 by Martin Haugh Term Structure Lattice Models These lecture notes introduce fixed income derivative securities and the modeling philosophy used to
IEOR E4706: Foundations of Financial Engineering c 2016 by Martin Haugh Term Structure Lattice Models These lecture notes introduce fixed income derivative securities and the modeling philosophy used to
HIGH ORDER DISCONTINUOUS GALERKIN METHODS FOR 1D PARABOLIC EQUATIONS. Ahmet İzmirlioğlu. BS, University of Pittsburgh, 2004
 HIGH ORDER DISCONTINUOUS GALERKIN METHODS FOR D PARABOLIC EQUATIONS by Ahmet İzmirlioğlu BS, University of Pittsburgh, 24 Submitted to the Graduate Faculty of Art and Sciences in partial fulfillment of
HIGH ORDER DISCONTINUOUS GALERKIN METHODS FOR D PARABOLIC EQUATIONS by Ahmet İzmirlioğlu BS, University of Pittsburgh, 24 Submitted to the Graduate Faculty of Art and Sciences in partial fulfillment of
CS134: Networks Spring Random Variables and Independence. 1.2 Probability Distribution Function (PDF) Number of heads Probability 2 0.
 CS134: Networks Spring 2017 Prof. Yaron Singer Section 0 1 Probability 1.1 Random Variables and Independence A real-valued random variable is a variable that can take each of a set of possible values in
CS134: Networks Spring 2017 Prof. Yaron Singer Section 0 1 Probability 1.1 Random Variables and Independence A real-valued random variable is a variable that can take each of a set of possible values in
Optimally Thresholded Realized Power Variations for Lévy Jump Diffusion Models
 Optimally Thresholded Realized Power Variations for Lévy Jump Diffusion Models José E. Figueroa-López 1 1 Department of Statistics Purdue University University of Missouri-Kansas City Department of Mathematics
Optimally Thresholded Realized Power Variations for Lévy Jump Diffusion Models José E. Figueroa-López 1 1 Department of Statistics Purdue University University of Missouri-Kansas City Department of Mathematics
An Efficient Algorithm for Dynamic Pricing using a Graphical Representation
 An Efficient Algorithm for Dynamic Pricing using a Graphical Representation Maxime C. Cohen Google Research, New York, NY 10011, maxccohen@google.com Swati Gupta Massachusetts Institute of Technology,
An Efficient Algorithm for Dynamic Pricing using a Graphical Representation Maxime C. Cohen Google Research, New York, NY 10011, maxccohen@google.com Swati Gupta Massachusetts Institute of Technology,
Cook s Theorem: the First NP-Complete Problem
 Cook s Theorem: the First NP-Complete Problem Theorem 37 (Cook (1971)) sat is NP-complete. sat NP (p. 113). circuit sat reduces to sat (p. 284). Now we only need to show that all languages in NP can be
Cook s Theorem: the First NP-Complete Problem Theorem 37 (Cook (1971)) sat is NP-complete. sat NP (p. 113). circuit sat reduces to sat (p. 284). Now we only need to show that all languages in NP can be
Value of Flexibility in Managing R&D Projects Revisited
 Value of Flexibility in Managing R&D Projects Revisited Leonardo P. Santiago & Pirooz Vakili November 2004 Abstract In this paper we consider the question of whether an increase in uncertainty increases
Value of Flexibility in Managing R&D Projects Revisited Leonardo P. Santiago & Pirooz Vakili November 2004 Abstract In this paper we consider the question of whether an increase in uncertainty increases
MACROECONOMICS. Prelim Exam
 MACROECONOMICS Prelim Exam Austin, June 1, 2012 Instructions This is a closed book exam. If you get stuck in one section move to the next one. Do not waste time on sections that you find hard to solve.
MACROECONOMICS Prelim Exam Austin, June 1, 2012 Instructions This is a closed book exam. If you get stuck in one section move to the next one. Do not waste time on sections that you find hard to solve.
Optimal Satisficing Tree Searches
 Optimal Satisficing Tree Searches Dan Geiger and Jeffrey A. Barnett Northrop Research and Technology Center One Research Park Palos Verdes, CA 90274 Abstract We provide an algorithm that finds optimal
Optimal Satisficing Tree Searches Dan Geiger and Jeffrey A. Barnett Northrop Research and Technology Center One Research Park Palos Verdes, CA 90274 Abstract We provide an algorithm that finds optimal
Lecture 4: Return vs Risk: Mean-Variance Analysis
 Lecture 4: Return vs Risk: Mean-Variance Analysis 4.1 Basics Given a cool of many different stocks, you want to decide, for each stock in the pool, whether you include it in your portfolio and (if yes)
Lecture 4: Return vs Risk: Mean-Variance Analysis 4.1 Basics Given a cool of many different stocks, you want to decide, for each stock in the pool, whether you include it in your portfolio and (if yes)
A convenient analytical and visual technique of PERT and CPM prove extremely valuable in assisting the managers in managing the projects.
 Introduction Any project involves planning, scheduling and controlling a number of interrelated activities with use of limited resources, namely, men, machines, materials, money and time. The projects
Introduction Any project involves planning, scheduling and controlling a number of interrelated activities with use of limited resources, namely, men, machines, materials, money and time. The projects
Optimal Stopping. Nick Hay (presentation follows Thomas Ferguson s Optimal Stopping and Applications) November 6, 2008
 (presentation follows Thomas Ferguson s and Applications) November 6, 2008 1 / 35 Contents: Introduction Problems Markov Models Monotone Stopping Problems Summary 2 / 35 The Secretary problem You have
(presentation follows Thomas Ferguson s and Applications) November 6, 2008 1 / 35 Contents: Introduction Problems Markov Models Monotone Stopping Problems Summary 2 / 35 The Secretary problem You have
2. This algorithm does not solve the problem of finding a maximum cardinality set of non-overlapping intervals. Consider the following intervals:
 1. No solution. 2. This algorithm does not solve the problem of finding a maximum cardinality set of non-overlapping intervals. Consider the following intervals: E A B C D Obviously, the optimal solution
1. No solution. 2. This algorithm does not solve the problem of finding a maximum cardinality set of non-overlapping intervals. Consider the following intervals: E A B C D Obviously, the optimal solution
Lecture 5: Iterative Combinatorial Auctions
 COMS 6998-3: Algorithmic Game Theory October 6, 2008 Lecture 5: Iterative Combinatorial Auctions Lecturer: Sébastien Lahaie Scribe: Sébastien Lahaie In this lecture we examine a procedure that generalizes
COMS 6998-3: Algorithmic Game Theory October 6, 2008 Lecture 5: Iterative Combinatorial Auctions Lecturer: Sébastien Lahaie Scribe: Sébastien Lahaie In this lecture we examine a procedure that generalizes
Mengdi Wang. July 3rd, Laboratory for Information and Decision Systems, M.I.T.
 Practice July 3rd, 2012 Laboratory for Information and Decision Systems, M.I.T. 1 2 Infinite-Horizon DP Minimize over policies the objective cost function J π (x 0 ) = lim N E w k,k=0,1,... DP π = {µ 0,µ
Practice July 3rd, 2012 Laboratory for Information and Decision Systems, M.I.T. 1 2 Infinite-Horizon DP Minimize over policies the objective cost function J π (x 0 ) = lim N E w k,k=0,1,... DP π = {µ 0,µ
Production Management Winter 2002 Odette School of Business University of Windsor. Midterm Exam 2 Solution Tuesday, March 26, 7:00 9:00 pm
 Name (print, please) ID Production Management 7-604 Winter 00 Odette School of Business University of Windsor Midterm Exam Solution Tuesday, March 6, 7:00 9:00 pm Instructor: Mohammed Fazle Baki Aids Permitted:
Name (print, please) ID Production Management 7-604 Winter 00 Odette School of Business University of Windsor Midterm Exam Solution Tuesday, March 6, 7:00 9:00 pm Instructor: Mohammed Fazle Baki Aids Permitted:
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras
 Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 21 Successive Shortest Path Problem In this lecture, we continue our discussion
Advanced Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture 21 Successive Shortest Path Problem In this lecture, we continue our discussion
Dynamic Programming: An overview. 1 Preliminaries: The basic principle underlying dynamic programming
 Dynamic Programming: An overview These notes summarize some key properties of the Dynamic Programming principle to optimize a function or cost that depends on an interval or stages. This plays a key role
Dynamic Programming: An overview These notes summarize some key properties of the Dynamic Programming principle to optimize a function or cost that depends on an interval or stages. This plays a key role
Financial Optimization ISE 347/447. Lecture 15. Dr. Ted Ralphs
 Financial Optimization ISE 347/447 Lecture 15 Dr. Ted Ralphs ISE 347/447 Lecture 15 1 Reading for This Lecture C&T Chapter 12 ISE 347/447 Lecture 15 2 Stock Market Indices A stock market index is a statistic
Financial Optimization ISE 347/447 Lecture 15 Dr. Ted Ralphs ISE 347/447 Lecture 15 1 Reading for This Lecture C&T Chapter 12 ISE 347/447 Lecture 15 2 Stock Market Indices A stock market index is a statistic
Lecture 10: The knapsack problem
 Optimization Methods in Finance (EPFL, Fall 2010) Lecture 10: The knapsack problem 24.11.2010 Lecturer: Prof. Friedrich Eisenbrand Scribe: Anu Harjula The knapsack problem The Knapsack problem is a problem
Optimization Methods in Finance (EPFL, Fall 2010) Lecture 10: The knapsack problem 24.11.2010 Lecturer: Prof. Friedrich Eisenbrand Scribe: Anu Harjula The knapsack problem The Knapsack problem is a problem
June 11, Dynamic Programming( Weighted Interval Scheduling)
 Dynamic Programming( Weighted Interval Scheduling) June 11, 2014 Problem Statement: 1 We have a resource and many people request to use the resource for periods of time (an interval of time) 2 Each interval
Dynamic Programming( Weighted Interval Scheduling) June 11, 2014 Problem Statement: 1 We have a resource and many people request to use the resource for periods of time (an interval of time) 2 Each interval
Outsourcing versus technology transfer: Hotelling meets Stackelberg
 Outsourcing versus technology transfer: Hotelling meets Stackelberg Andrea Pierce Debapriya Sen May 23, 2011 Abstract We consider a Hotelling duopoly with two firms A and B in the final good market. Both
Outsourcing versus technology transfer: Hotelling meets Stackelberg Andrea Pierce Debapriya Sen May 23, 2011 Abstract We consider a Hotelling duopoly with two firms A and B in the final good market. Both
Cost Sharing in a Job Scheduling Problem
 Cost Sharing in a Job Scheduling Problem Debasis Mishra Bharath Rangarajan April 19, 2005 Abstract A set of jobs need to be served by a server which can serve only one job at a time. Jobs have processing
Cost Sharing in a Job Scheduling Problem Debasis Mishra Bharath Rangarajan April 19, 2005 Abstract A set of jobs need to be served by a server which can serve only one job at a time. Jobs have processing
Ramsey s Growth Model (Solution Ex. 2.1 (f) and (g))
 Problem Set 2: Ramsey s Growth Model (Solution Ex. 2.1 (f) and (g)) Exercise 2.1: An infinite horizon problem with perfect foresight In this exercise we will study at a discrete-time version of Ramsey
Problem Set 2: Ramsey s Growth Model (Solution Ex. 2.1 (f) and (g)) Exercise 2.1: An infinite horizon problem with perfect foresight In this exercise we will study at a discrete-time version of Ramsey
The exam is closed book, closed calculator, and closed notes except your one-page crib sheet.
 CS 188 Spring 2015 Introduction to Artificial Intelligence Midterm 1 You have approximately 2 hours and 50 minutes. The exam is closed book, closed calculator, and closed notes except your one-page crib
CS 188 Spring 2015 Introduction to Artificial Intelligence Midterm 1 You have approximately 2 hours and 50 minutes. The exam is closed book, closed calculator, and closed notes except your one-page crib
On-line Supplement for Constraint Aggregation in Column Generation Models for Resource-Constrained Covering Problems
 Submitted to INFORMS Journal on Computing manuscript (Please, provide the mansucript number!) Authors are encouraged to submit new papers to INFORMS journals by means of a style file template, which includes
Submitted to INFORMS Journal on Computing manuscript (Please, provide the mansucript number!) Authors are encouraged to submit new papers to INFORMS journals by means of a style file template, which includes
Competitive Market Model
 57 Chapter 5 Competitive Market Model The competitive market model serves as the basis for the two different multi-user allocation methods presented in this thesis. This market model prices resources based
57 Chapter 5 Competitive Market Model The competitive market model serves as the basis for the two different multi-user allocation methods presented in this thesis. This market model prices resources based
Failure and Rescue in an Interbank Network
 Failure and Rescue in an Interbank Network Luitgard A. M. Veraart London School of Economics and Political Science October 202 Joint work with L.C.G Rogers (University of Cambridge) Paris 202 Luitgard
Failure and Rescue in an Interbank Network Luitgard A. M. Veraart London School of Economics and Political Science October 202 Joint work with L.C.G Rogers (University of Cambridge) Paris 202 Luitgard
A 2 period dynamic general equilibrium model
 A 2 period dynamic general equilibrium model Suppose that there are H households who live two periods They are endowed with E 1 units of labor in period 1 and E 2 units of labor in period 2, which they
A 2 period dynamic general equilibrium model Suppose that there are H households who live two periods They are endowed with E 1 units of labor in period 1 and E 2 units of labor in period 2, which they
Handout 8: Introduction to Stochastic Dynamic Programming. 2 Examples of Stochastic Dynamic Programming Problems
 SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 8: Introduction to Stochastic Dynamic Programming Instructor: Shiqian Ma March 10, 2014 Suggested Reading: Chapter 1 of Bertsekas,
SEEM 3470: Dynamic Optimization and Applications 2013 14 Second Term Handout 8: Introduction to Stochastic Dynamic Programming Instructor: Shiqian Ma March 10, 2014 Suggested Reading: Chapter 1 of Bertsekas,
