Addiction - Multinomial Model
|
|
|
- Rodney Silvester Greene
- 5 years ago
- Views:
Transcription
1 Addiction - Multinomial Model February 8, 2012 First the addiction data are loaded and attached. > library(catdata) > data(addiction) > attach(addiction) For the multinomial logit model the function multinom from the nnet package is used. > library(nnet) The response ill has to be used as factor. > ill <- as.factor(ill) > addiction$ill<-as.factor(addiction$ill) The first model is a model with the covariates gender, university and a linear effect of age > multinom0 <- multinom(ill ~ gender + age + university, data=addiction) # weights: 15 (8 variable) initial value iter 10 value final value converged > summary(multinom0) multinom(formula = ill ~ gender + age + university, data = addiction) (Intercept) gender age university Std. Errors: (Intercept) gender age university Residual Deviance: AIC:
2 Another possibility to fit multinomial response models is given by the function vglm from the package VGAM. > library(vgam) > multivgam0<-vglm(ill ~ gender + age + university, multinomial(reflevel=1), + data=addiction) > summary(multivgam0) vglm(formula = ill ~ gender + age + university, family = multinomial(reflevel = 1), data = addiction) Pearson Residuals: Min 1Q Median 3Q Max log(mu[,2]/mu[,1]) log(mu[,3]/mu[,1]) Value Std. Error t value (Intercept): (Intercept): gender: gender: age: age: university: university: Number of linear predictors: 2 Names of linear predictors: log(mu[,2]/mu[,1]), log(mu[,3]/mu[,1]) Dispersion Parameter for multinomial family: 1 Residual Deviance: on 1356 degrees of freedom Log-likelihood: on 1356 degrees of freedom Number of Iterations: 4 Both models yield the same parameter estimates. The second model includes an additional quadratic effect of age. > addiction$age2 <- addiction$age^2 > multinom1 <- update(multinom0,. ~. + age2) # weights: 18 (10 variable) initial value iter 10 value final value converged 2
3 > summary(multinom1) multinom(formula = ill ~ gender + age + university + age2, data = addiction) (Intercept) gender age university age Std. Errors: (Intercept) gender age university age Residual Deviance: AIC: > multivgam1<-vglm(ill ~ gender + age + university + age2, multinomial(reflevel=1), + data=addiction) > summary(multivgam1) vglm(formula = ill ~ gender + age + university + age2, family = multinomial(reflevel = 1), data = addiction) Pearson Residuals: Min 1Q Median 3Q Max log(mu[,2]/mu[,1]) log(mu[,3]/mu[,1]) Value Std. Error t value (Intercept): (Intercept): gender: gender: age: age: university: university: age2: age2: Number of linear predictors: 2 Names of linear predictors: log(mu[,2]/mu[,1]), log(mu[,3]/mu[,1]) Dispersion Parameter for multinomial family: 1 Residual Deviance: on 1354 degrees of freedom 3
4 Log-likelihood: on 1354 degrees of freedom Number of Iterations: 4 It should be noted that the standard errors for the models generated by nnet and VGAM differ when age is included quadratically. The parameter estimates are equal again. Now the necessity of the quadratic term is tested by using the function anova. > anova(multinom0,multinom1) Likelihood ratio tests of Multinomial Models Response: ill Model Resid. df Resid. Dev Test Df LR stat. 1 gender + age + university gender + age + university + age vs Pr(Chi) e-08 > multinom1$dev - multinom0$dev [1] Now we plot the probabilities for the responses against age. First a sequence within the range of age has to be created. > minage <- min(na.omit(age)) > maxage <- max(na.omit(age)) > ageindex <- seq(minage, maxage, 0.1) > n <- length(ageindex) Now the vectors for the other covariates and the data sets for men and women are built. > ageindex2 <- ageindex^2 > gender1 <- rep(1, n) > gender0 <- rep(0, n) > university1 <- rep(1, n) > datamale <- as.data.frame(cbind(gender=gender0,age=ageindex,university= + university1,age2=ageindex2)) > datafemale <- as.data.frame(cbind(gender=gender1,age=ageindex,university= + university1,age2=ageindex2)) Now for the built data sets the probabilities based on model multinom1 are computed. > probsmale <- predict(multinom1, datamale, type="probs") > probsfemale <- predict(multinom1, datafemale, type="probs") 4
5 Now the probabilities can be plotted. > par(cex=1.4, lwd=2) > plot(ageindex, probsmale[,1], type="l", lty=1, ylim=c(0,1), main= + "men with university degree", ylab="probabilities") > lines(ageindex, probsmale[,2], lty="dotted") > lines(ageindex, probsmale[,3], lty="dashed") > legend("topright", legend=c("weak-willed", "diseased", "both"), lty=c("solid", + "dotted", "dashed")) men with university degree probabilities Weak willed diseased both ageindex > par(cex=1.4, lwd=2) > plot(ageindex, probsfemale[,1], type="l", lty=1, ylim=c(0,1), main= + "women with university degree", ylab="probabilities") > lines(ageindex, probsfemale[,2], lty="dotted") > lines(ageindex, probsfemale[,3], lty="dashed") > legend("topright", legend=c("weak-willed", "diseased", "both"), + lty=c("solid", "dotted", "dashed")) 5
6 women with university degree probabilities Weak willed diseased both ageindex 6
Case Study: Applying Generalized Linear Models
Case Study: Applying Generalized Linear Models Dr. Kempthorne May 12, 2016 Contents 1 Generalized Linear Models of Semi-Quantal Biological Assay Data 2 1.1 Coal miners Pneumoconiosis Data.................
Ordinal and categorical variables
Ordinal and categorical variables Ben Bolker October 29, 2018 Licensed under the Creative Commons attribution-noncommercial license (http: //creativecommons.org/licenses/by-nc/3.0/). Please share & remix
Negative Binomial Model for Count Data Log-linear Models for Contingency Tables - Introduction
Negative Binomial Model for Count Data Log-linear Models for Contingency Tables - Introduction Statistics 149 Spring 2006 Copyright 2006 by Mark E. Irwin Negative Binomial Family Example: Absenteeism from
############################ ### toxo.r ### ############################
############################ ### toxo.r ### ############################ toxo < read.table(file="n:\\courses\\stat8620\\fall 08\\toxo.dat",header=T) #toxo < read.table(file="c:\\documents and Settings\\dhall\\My
Ordinal Multinomial Logistic Regression. Thom M. Suhy Southern Methodist University May14th, 2013
Ordinal Multinomial Logistic Thom M. Suhy Southern Methodist University May14th, 2013 GLM Generalized Linear Model (GLM) Framework for statistical analysis (Gelman and Hill, 2007, p. 135) Linear Continuous
ORDERED MULTINOMIAL LOGISTIC REGRESSION ANALYSIS. Pooja Shivraj Southern Methodist University
ORDERED MULTINOMIAL LOGISTIC REGRESSION ANALYSIS Pooja Shivraj Southern Methodist University KINDS OF REGRESSION ANALYSES Linear Regression Logistic Regression Dichotomous dependent variable (yes/no, died/
Multiple Regression and Logistic Regression II. Dajiang 525 Apr
Multiple Regression and Logistic Regression II Dajiang Liu @PHS 525 Apr-19-2016 Materials from Last Time Multiple regression model: Include multiple predictors in the model = + + + + How to interpret the
Logistic Regression. Logistic Regression Theory
Logistic Regression Dr. J. Kyle Roberts Southern Methodist University Simmons School of Education and Human Development Department of Teaching and Learning Logistic Regression The linear probability model.
Logistic Regression with R: Example One
Logistic Regression with R: Example One math = read.table("http://www.utstat.toronto.edu/~brunner/appliedf12/data/mathcat.data") math[1:5,] hsgpa hsengl hscalc course passed outcome 1 78.0 80 Yes Mainstrm
Generalized Linear Models
Generalized Linear Models Scott Creel Wednesday, September 10, 2014 This exercise extends the prior material on using the lm() function to fit an OLS regression and test hypotheses about effects on a parameter.
Categorical Outcomes. Statistical Modelling in Stata: Categorical Outcomes. R by C Table: Example. Nominal Outcomes. Mark Lunt.
Categorical Outcomes Statistical Modelling in Stata: Categorical Outcomes Mark Lunt Arthritis Research UK Epidemiology Unit University of Manchester Nominal Ordinal 28/11/2017 R by C Table: Example Categorical,
> budworm$samplogit < log((budworm$y+0.5)/(budworm$m budworm$y+0.5))
budworm < read.table(file="n:\\courses\\stat8620\\fall 08\\budworm.dat",header=T) #budworm < read.table(file="c:\\documents and Settings\\dhall\\My Documents\\Dan's Work Stuff\\courses\\STAT8620\\Fall
Using R to Create Synthetic Discrete Response Regression Models
Arizona State University From the SelectedWorks of Joseph M Hilbe July 3, 2011 Using R to Create Synthetic Discrete Response Regression Models Joseph Hilbe, Arizona State University Available at: https://works.bepress.com/joseph_hilbe/3/
Logit Analysis. Using vttown.dta. Albert Satorra, UPF
Logit Analysis Using vttown.dta Logit Regression Odds ratio The most common way of interpreting a logit is to convert it to an odds ratio using the exp() function. One can convert back using the ln()
Statistics 175 Applied Statistics Generalized Linear Models Jianqing Fan
Statistics 175 Applied Statistics Generalized Linear Models Jianqing Fan Example 1 (Kyhposis data): (The data set kyphosis consists of measurements on 81 children following corrective spinal surgery. Variable
Stat 401XV Exam 3 Spring 2017
Stat 40XV Exam Spring 07 I have neither given nor received unauthorized assistance on this exam. Name Signed Date Name Printed ATTENTION! Incorrect numerical answers unaccompanied by supporting reasoning
Let us assume that we are measuring the yield of a crop plant on 5 different plots at 4 different observation times.
Mixed-effects models An introduction by Christoph Scherber Up to now, we have been dealing with linear models of the form where ß0 and ß1 are parameters of fixed value. Example: Let us assume that we are
Step 1: Load the appropriate R package. Step 2: Fit a separate mixed model for each independence claim in the basis set.
Step 1: Load the appropriate R package. You will need two libraries: nlme and lme4. Step 2: Fit a separate mixed model for each independence claim in the basis set. For instance, in Table 2 the first basis
Introduction to General and Generalized Linear Models
Introduction to General and Generalized Linear Models Generalized Linear Models - IIIb Henrik Madsen March 18, 2012 Henrik Madsen () Chapman & Hall March 18, 2012 1 / 32 Examples Overdispersion and Offset!
AIC = Log likelihood = BIC =
- log: /mnt/ide1/home/sschulh1/apc/apc_examplelog log type: text opened on: 21 Jul 2006, 18:08:20 *replicate table 5 and cols 7-9 of table 3 in Yang, Fu and Land (2004) *Stata can maximize GLM objective
Chapter 8 Exercises 1. Data Analysis & Graphics Using R Solutions to Exercises (May 1, 2010)
Chapter 8 Exercises 1 Data Analysis & Graphics Using R Solutions to Exercises (May 1, 2010) Preliminaries > library(daag) Exercise 1 The following table shows numbers of occasions when inhibition (i.e.,
Logistic Regression II
Logistic Regression II Michael Friendly Psych 6136 November 9, 2017 age*sex effect plot 0 10 20 30 40 50 1.00 sex Female sex : Female sex : Male Male 0.75 0.999 Survived 0.50 0.25 survived 0.990 0.950
MODEL SELECTION CRITERIA IN R:
1. R 2 statistics We may use MODEL SELECTION CRITERIA IN R R 2 = SS R SS T = 1 SS Res SS T or R 2 Adj = 1 SS Res/(n p) SS T /(n 1) = 1 ( ) n 1 (1 R 2 ). n p where p is the total number of parameters. R
GGraph. Males Only. Premium. Experience. GGraph. Gender. 1 0: R 2 Linear = : R 2 Linear = Page 1
GGraph 9 Gender : R Linear =.43 : R Linear =.769 8 7 6 5 4 3 5 5 Males Only GGraph Page R Linear =.43 R Loess 9 8 7 6 5 4 5 5 Explore Case Processing Summary Cases Valid Missing Total N Percent N Percent
Random Effects ANOVA
Random Effects ANOVA Grant B. Morgan Baylor University This post contains code for conducting a random effects ANOVA. Make sure the following packages are installed: foreign, lme4, lsr, lattice. library(foreign)
Building and Checking Survival Models
Building and Checking Survival Models David M. Rocke May 23, 2017 David M. Rocke Building and Checking Survival Models May 23, 2017 1 / 53 hodg Lymphoma Data Set from KMsurv This data set consists of information
Stat 328, Summer 2005
Stat 328, Summer 2005 Exam #2, 6/18/05 Name (print) UnivID I have neither given nor received any unauthorized aid in completing this exam. Signed Answer each question completely showing your work where
Generalized Linear Models
Generalized Linear Models Ordinal Logistic Regression Dr. Tackett 11.27.2018 1 / 26 Announcements HW 8 due Thursday, 11/29 Lab 10 due Sunday, 12/2 Exam II, Thursday 12/6 2 / 26 Packages library(knitr)
WesVar uses repeated replication variance estimation methods exclusively and as a result does not offer the Taylor Series Linearization approach.
CHAPTER 9 ANALYSIS EXAMPLES REPLICATION WesVar 4.3 GENERAL NOTES ABOUT ANALYSIS EXAMPLES REPLICATION These examples are intended to provide guidance on how to use the commands/procedures for analysis of
Lecture Note: Analysis of Financial Time Series Spring 2017, Ruey S. Tsay
Lecture Note: Analysis of Financial Time Series Spring 2017, Ruey S. Tsay Seasonal Time Series: TS with periodic patterns and useful in predicting quarterly earnings pricing weather-related derivatives
boxcox() returns the values of α and their loglikelihoods,
Solutions to Selected Computer Lab Problems and Exercises in Chapter 11 of Statistics and Data Analysis for Financial Engineering, 2nd ed. by David Ruppert and David S. Matteson c 2016 David Ruppert and
Lecture Note: Analysis of Financial Time Series Spring 2008, Ruey S. Tsay. Seasonal Time Series: TS with periodic patterns and useful in
Lecture Note: Analysis of Financial Time Series Spring 2008, Ruey S. Tsay Seasonal Time Series: TS with periodic patterns and useful in predicting quarterly earnings pricing weather-related derivatives
Didacticiel - Études de cas. In this tutorial, we show how to implement a multinomial logistic regression with TANAGRA.
Subject In this tutorial, we show how to implement a multinomial logistic regression with TANAGRA. Logistic regression is a technique for maing predictions when the dependent variable is a dichotomy, and
Model fit assessment via marginal model plots
The Stata Journal (2010) 10, Number 2, pp. 215 225 Model fit assessment via marginal model plots Charles Lindsey Texas A & M University Department of Statistics College Station, TX lindseyc@stat.tamu.edu
> attach(grocery) > boxplot(sales~discount, ylab="sales",xlab="discount")
Example of More than 2 Categories, and Analysis of Covariance Example > attach(grocery) > boxplot(sales~discount, ylab="sales",xlab="discount") Sales 160 200 240 > tapply(sales,discount,mean) 10.00% 15.00%
Generalized Multilevel Regression Example for a Binary Outcome
Psy 510/610 Multilevel Regression, Spring 2017 1 HLM Generalized Multilevel Regression Example for a Binary Outcome Specifications for this Bernoulli HLM2 run Problem Title: no title The data source for
Study 2: data analysis. Example analysis using R
Study 2: data analysis Example analysis using R Steps for data analysis Install software on your computer or locate computer with software (e.g., R, systat, SPSS) Prepare data for analysis Subjects (rows)
1 Stat 8053, Fall 2011: GLMMs
Stat 805, Fall 0: GLMMs The data come from a 988 fertility survey in Bangladesh. Data were collected on 94 women grouped into 60 districts. The response of interest is whether or not the woman is using
Bradley-Terry Models. Stat 557 Heike Hofmann
Bradley-Terry Models Stat 557 Heike Hofmann Outline Definition: Bradley-Terry Fitting the model Extension: Order Effects Extension: Ordinal & Nominal Response Repeated Measures Bradley-Terry Model (1952)
Module 9: Single-level and Multilevel Models for Ordinal Responses. Stata Practical 1
Module 9: Single-level and Multilevel Models for Ordinal Responses Pre-requisites Modules 5, 6 and 7 Stata Practical 1 George Leckie, Tim Morris & Fiona Steele Centre for Multilevel Modelling If you find
Lecture 21: Logit Models for Multinomial Responses Continued
Lecture 21: Logit Models for Multinomial Responses Continued Dipankar Bandyopadhyay, Ph.D. BMTRY 711: Analysis of Categorical Data Spring 2011 Division of Biostatistics and Epidemiology Medical University
Morten Frydenberg Wednesday, 12 May 2004
" $% " * +, " --. / ",, 2 ", $, % $ 4 %78 % / "92:8/- 788;?5"= "8= < < @ "A57 57 "χ 2 = -value=. 5 OR =, OR = = = + OR B " B Linear ang Logistic Regression: Note. = + OR 2 women - % β β = + woman
Review questions for Multinomial Logit/Probit, Tobit, Heckit, Quantile Regressions
1. I estimated a multinomial logit model of employment behavior using data from the 2006 Current Population Survey. The three possible outcomes for a person are employed (outcome=1), unemployed (outcome=2)
Multiple regression - a brief introduction
Multiple regression - a brief introduction Multiple regression is an extension to regular (simple) regression. Instead of one X, we now have several. Suppose, for example, that you are trying to predict
Logit Models for Binary Data
Chapter 3 Logit Models for Binary Data We now turn our attention to regression models for dichotomous data, including logistic regression and probit analysis These models are appropriate when the response
The SAS System 11:03 Monday, November 11,
The SAS System 11:3 Monday, November 11, 213 1 The CONTENTS Procedure Data Set Name BIO.AUTO_PREMIUMS Observations 5 Member Type DATA Variables 3 Engine V9 Indexes Created Monday, November 11, 213 11:4:19
BEcon Program, Faculty of Economics, Chulalongkorn University Page 1/7
Mid-term Exam (November 25, 2005, 0900-1200hr) Instructions: a) Textbooks, lecture notes and calculators are allowed. b) Each must work alone. Cheating will not be tolerated. c) Attempt all the tests.
Predicting Charitable Contributions
Predicting Charitable Contributions By Lauren Meyer Executive Summary Charitable contributions depend on many factors from financial security to personal characteristics. This report will focus on demographic
Empirical Asset Pricing for Tactical Asset Allocation
Introduction Process Model Conclusion Department of Finance The University of Connecticut School of Business stephen.r.rush@gmail.com May 10, 2012 Background Portfolio Managers Want to justify fees with
Appendix. Table A.1 (Part A) The Author(s) 2015 G. Chakrabarti and C. Sen, Green Investing, SpringerBriefs in Finance, DOI /
Appendix Table A.1 (Part A) Dependent variable: probability of crisis (own) Method: ML binary probit (quadratic hill climbing) Included observations: 47 after adjustments Convergence achieved after 6 iterations
Intro to GLM Day 2: GLM and Maximum Likelihood
Intro to GLM Day 2: GLM and Maximum Likelihood Federico Vegetti Central European University ECPR Summer School in Methods and Techniques 1 / 32 Generalized Linear Modeling 3 steps of GLM 1. Specify the
sociology SO5032 Quantitative Research Methods Brendan Halpin, Sociology, University of Limerick Spring 2018 SO5032 Quantitative Research Methods
1 SO5032 Quantitative Research Methods Brendan Halpin, Sociology, University of Limerick Spring 2018 Lecture 10: Multinomial regression baseline category extension of binary What if we have multiple possible
Lapse Modeling for the Post-Level Period
Lapse Modeling for the Post-Level Period A Practical Application of Predictive Modeling JANUARY 2015 SPONSORED BY Committee on Finance Research PREPARED BY Richard Xu, FSA, Ph.D. Dihui Lai, Ph.D. Minyu
Lecture 1: Empirical Properties of Returns
Lecture 1: Empirical Properties of Returns Econ 589 Eric Zivot Spring 2011 Updated: March 29, 2011 Daily CC Returns on MSFT -0.3 r(t) -0.2-0.1 0.1 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996
FAV i R This paper is produced mechanically as part of FAViR. See for more information.
The POT package By Avraham Adler FAV i R This paper is produced mechanically as part of FAViR. See http://www.favir.net for more information. Abstract This paper is intended to briefly demonstrate the
Non-linearities in Simple Regression
Non-linearities in Simple Regression 1. Eample: Monthly Earnings and Years of Education In this tutorial, we will focus on an eample that eplores the relationship between total monthly earnings and years
Maximum Likelihood Estimation
Maximum Likelihood Estimation EPSY 905: Fundamentals of Multivariate Modeling Online Lecture #6 EPSY 905: Maximum Likelihood In This Lecture The basics of maximum likelihood estimation Ø The engine that
Credit Risk Modelling
Credit Risk Modelling Tiziano Bellini Università di Bologna December 13, 2013 Tiziano Bellini (Università di Bologna) Credit Risk Modelling December 13, 2013 1 / 55 Outline Framework Credit Risk Modelling
Creation of Synthetic Discrete Response Regression Models
Arizona State University From the SelectedWorks of Joseph M Hilbe 2010 Creation of Synthetic Discrete Response Regression Models Joseph Hilbe, Arizona State University Available at: https://works.bepress.com/joseph_hilbe/2/
To be two or not be two, that is a LOGISTIC question
MWSUG 2016 - Paper AA18 To be two or not be two, that is a LOGISTIC question Robert G. Downer, Grand Valley State University, Allendale, MI ABSTRACT A binary response is very common in logistic regression
STK Lecture 7 finalizing clam size modelling and starting on pricing
STK 4540 Lecture 7 finalizing clam size modelling and starting on pricing Overview Important issues Models treated Curriculum Duration (in lectures) What is driving the result of a nonlife insurance company?
proc genmod; model malform/total = alcohol / dist=bin link=identity obstats; title 'Table 2.7'; title2 'Identity Link';
BIOS 6244 Analysis of Categorical Data Assignment 5 s 1. Consider Exercise 4.4, p. 98. (i) Write the SAS code, including the DATA step, to fit the linear probability model and the logit model to the data
Girma Tefera*, Legesse Negash and Solomon Buke. Department of Statistics, College of Natural Science, Jimma University. Ethiopia.
Vol. 5(2), pp. 15-21, July, 2014 DOI: 10.5897/IJSTER2013.0227 Article Number: C81977845738 ISSN 2141-6559 Copyright 2014 Author(s) retain the copyright of this article http://www.academicjournals.org/ijster
Two Way ANOVA in R Solutions
Two Way ANOVA in R Solutions Solutions to exercises found here # Exercise 1 # #Read in the moth experiment data setwd("h:/datasets") moth.experiment = read.csv("moth trap experiment.csv", header = TRUE)
STA 4504/5503 Sample questions for exam True-False questions.
STA 4504/5503 Sample questions for exam 2 1. True-False questions. (a) For General Social Survey data on Y = political ideology (categories liberal, moderate, conservative), X 1 = gender (1 = female, 0
Regression Review and Robust Regression. Slides prepared by Elizabeth Newton (MIT)
Regression Review and Robust Regression Slides prepared by Elizabeth Newton (MIT) S-Plus Oil City Data Frame Monthly Excess Returns of Oil City Petroleum, Inc. Stocks and the Market SUMMARY: The oilcity
book 2014/5/6 15:21 page 261 #285
book 2014/5/6 15:21 page 261 #285 Chapter 10 Simulation Simulations provide a powerful way to answer questions and explore properties of statistical estimators and procedures. In this chapter, we will
GLM III - The Matrix Reloaded
GLM III - The Matrix Reloaded Duncan Anderson, Serhat Guven 12 March 2013 2012 Towers Watson. All rights reserved. Agenda "Quadrant Saddles" The Tweedie Distribution "Emergent Interactions" Dispersion
is the bandwidth and controls the level of smoothing of the estimator, n is the sample size and
Paper PH100 Relationship between Total charges and Reimbursements in Outpatient Visits Using SAS GLIMMIX Chakib Battioui, University of Louisville, Louisville, KY ABSTRACT The purpose of this paper is
MCMC Package Example
MCMC Package Example Charles J. Geyer April 4, 2005 This is an example of using the mcmc package in R. The problem comes from a take-home question on a (take-home) PhD qualifying exam (School of Statistics,
Modelling the potential human capital on the labor market using logistic regression in R
Modelling the potential human capital on the labor market using logistic regression in R Ana-Maria Ciuhu (dobre.anamaria@hotmail.com) Institute of National Economy, Romanian Academy; National Institute
a. Explain why the coefficients change in the observed direction when switching from OLS to Tobit estimation.
1. Using data from IRS Form 5500 filings by U.S. pension plans, I estimated a model of contributions to pension plans as ln(1 + c i ) = α 0 + U i α 1 + PD i α 2 + e i Where the subscript i indicates the
Sean Howard Econometrics Final Project Paper. An Analysis of the Determinants and Factors of Physical Education Attendance in the Fourth Quarter
Sean Howard Econometrics Final Project Paper An Analysis of the Determinants and Factors of Physical Education Attendance in the Fourth Quarter Introduction This project attempted to gain a more complete
Final Exam Suggested Solutions
University of Washington Fall 003 Department of Economics Eric Zivot Economics 483 Final Exam Suggested Solutions This is a closed book and closed note exam. However, you are allowed one page of handwritten
Mixed models in R using the lme4 package Part 3: Inference based on profiled deviance
Mixed models in R using the lme4 package Part 3: Inference based on profiled deviance Douglas Bates Department of Statistics University of Wisconsin - Madison Madison January 11, 2011
CREDIT RISK MODELING IN R. Logistic regression: introduction
CREDIT RISK MODELING IN R Logistic regression: introduction Final data structure > str(training_set) 'data.frame': 19394 obs. of 8 variables: $ loan_status : Factor w/ 2 levels "0","1": 1 1 1 1 1 1 1 1
Log-linear Modeling Under Generalized Inverse Sampling Scheme
Log-linear Modeling Under Generalized Inverse Sampling Scheme Soumi Lahiri (1) and Sunil Dhar (2) (1) Department of Mathematical Sciences New Jersey Institute of Technology University Heights, Newark,
Projects for Bayesian Computation with R
Projects for Bayesian Computation with R Laura Vana & Kurt Hornik Winter Semeter 2018/2019 1 S&P Rating Data On the homepage of this course you can find a time series for Standard & Poors default data
Analysis of Variance in Matrix form
Analysis of Variance in Matrix form The ANOVA table sums of squares, SSTO, SSR and SSE can all be expressed in matrix form as follows. week 9 Multiple Regression A multiple regression model is a model
6 Multiple Regression
More than one X variable. 6 Multiple Regression Why? Might be interested in more than one marginal effect Omitted Variable Bias (OVB) 6.1 and 6.2 House prices and OVB Should I build a fireplace? The following
Internet Appendix to The Booms and Busts of Beta Arbitrage
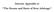Internet Appendix to The Booms and Busts of Beta Arbitrage Table A1: Event Time CoBAR This table reports some basic statistics of CoBAR, the excess comovement among low beta stocks over the period 1970
Longitudinal Logistic Regression: Breastfeeding of Nepalese Children
Longitudinal Logistic Regression: Breastfeeding of Nepalese Children Scientific Question Determine whether the breastfeeding of Nepalese children varies with child age and/or sex of child. Data: Nepal
σ e, which will be large when prediction errors are Linear regression model
Linear regression model we assume that two quantitative variables, x and y, are linearly related; that is, the population of (x, y) pairs are related by an ideal population regression line y = α + βx +
Regression and Simulation
Regression and Simulation This is an introductory R session, so it may go slowly if you have never used R before. Do not be discouraged. A great way to learn a new language like this is to plunge right
Lecture Note of Bus 41202, Spring 2010: Analysis of Multiple Series with Applications. x 1t x 2t. holdings (OIH) and energy select section SPDR (XLE).
Lecture Note of Bus 41202, Spring 2010: Analysis of Multiple Series with Applications Focus on two series (i.e., bivariate case) Time series: Data: x 1, x 2,, x T. X t = Some examples: (a) U.S. quarterly
SEX DISCRIMINATION PROBLEM
SEX DISCRIMINATION PROBLEM 5. Displaying Relationships between Variables In this section we will use scatterplots to examine the relationship between the dependent variable (starting salary) and each of
Determination of the Optimal Stratum Boundaries in the Monthly Retail Trade Survey in the Croatian Bureau of Statistics
Determination of the Optimal Stratum Boundaries in the Monthly Retail Trade Survey in the Croatian Bureau of Statistics Ivana JURINA (jurinai@dzs.hr) Croatian Bureau of Statistics Lidija GLIGOROVA (gligoroval@dzs.hr)
LAMPIRAN. Null Hypothesis: LO has a unit root Exogenous: Constant Lag Length: 1 (Automatic based on SIC, MAXLAG=13)
74 LAMPIRAN Lampiran 1 Analisis ARIMA 1.1. Uji Stasioneritas Variabel 1. Data Harga Minyak Riil Level Null Hypothesis: LO has a unit root Lag Length: 1 (Automatic based on SIC, MAXLAG=13) Augmented Dickey-Fuller
Labor Supply and Taxation in Europe
Labor Supply and Taxation in Europe Fabrizio Colonna - Banca d Italia Stefania Marcassa - Paris School of Economics November 16, 2010 Motivation Observe differences in Female Labor Force Participation
Regression Model Assumptions Solutions
Regression Model Assumptions Solutions Below are the solutions to these exercises on model diagnostics using residual plots. # Exercise 1 # data("cars") head(cars) speed dist 1 4 2 2 4 10 3 7 4 4 7 22
Example 1 of econometric analysis: the Market Model
Example 1 of econometric analysis: the Market Model IGIDR, Bombay 14 November, 2008 The Market Model Investors want an equation predicting the return from investing in alternative securities. Return is
Window Width Selection for L 2 Adjusted Quantile Regression
Window Width Selection for L 2 Adjusted Quantile Regression Yoonsuh Jung, The Ohio State University Steven N. MacEachern, The Ohio State University Yoonkyung Lee, The Ohio State University Technical Report
11. Logistic modeling of proportions
11. Logistic modeling of proportions Retrieve the data File on main menu Open worksheet C:\talks\strirling\employ.ws = Note Postcode is neighbourhood in Glasgow Cell is element of the table for each postcode
Sociology Exam 3 Answer Key - DRAFT May 8, 2007
Sociology 63993 Exam 3 Answer Key - DRAFT May 8, 2007 I. True-False. (20 points) Indicate whether the following statements are true or false. If false, briefly explain why. 1. The odds of an event occurring
Subject CS1 Actuarial Statistics 1 Core Principles. Syllabus. for the 2019 exams. 1 June 2018
` Subject CS1 Actuarial Statistics 1 Core Principles Syllabus for the 2019 exams 1 June 2018 Copyright in this Core Reading is the property of the Institute and Faculty of Actuaries who are the sole distributors.
Americans AV Preferences: Dynamic Ride-Sharing, Privacy & Long-Distance Mode Choices. Dr. Kara Kockelman & Krishna Murthy Gurumurthy
Americans AV Preferences: Dynamic Ride-Sharing, Privacy & Long-Distance Mode Choices Dr. Kara Kockelman & Krishna Murthy Gurumurthy Survey Stats. 2,588 Americans answered 70-questions. 1,258 responses
Duration Models: Parametric Models
Duration Models: Parametric Models Brad 1 1 Department of Political Science University of California, Davis January 28, 2011 Parametric Models Some Motivation for Parametrics Consider the hazard rate:
Statistical Models of Stocks and Bonds. Zachary D Easterling: Department of Economics. The University of Akron
Statistical Models of Stocks and Bonds Zachary D Easterling: Department of Economics The University of Akron Abstract One of the key ideas in monetary economics is that the prices of investments tend to
Session 178 TS, Stats for Health Actuaries. Moderator: Ian G. Duncan, FSA, FCA, FCIA, FIA, MAAA. Presenter: Joan C. Barrett, FSA, MAAA
Session 178 TS, Stats for Health Actuaries Moderator: Ian G. Duncan, FSA, FCA, FCIA, FIA, MAAA Presenter: Joan C. Barrett, FSA, MAAA Session 178 Statistics for Health Actuaries October 14, 2015 Presented
Table 4. Probit model of union membership. Probit coefficients are presented below. Data from March 2008 Current Population Survey.
1. Using a probit model and data from the 2008 March Current Population Survey, I estimated a probit model of the determinants of pension coverage. Three specifications were estimated. The first included