THE current Internet is used by a widely heterogeneous
|
|
|
- Nathaniel Short
- 6 years ago
- Views:
Transcription
1 1712 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 50, NO. 11, NOVEMBER 2005 Efficiency Loss in a Network Resource Allocation Game: The Case of Elastic Supply Ramesh Johari, Member, IEEE, Shie Mannor, Member, IEEE, and John N. Tsitsiklis, Fellow, IEEE Abstract We consider a resource allocation problem where individual users wish to send data across a network to maximize their utility, and a cost is incurred at each link that depends on the total rate sent through the link. It is known that as long as users do not anticipate the effect of their actions on prices, a simple proportional pricing mechanism can maximize the sum of users utilities minus the cost (called aggregate surplus). Continuing previous efforts to quanty the effects of selfish behavior in network pricing mechanisms, we consider the possibility that users anticipate the effect of their actions on link prices. Under the assumption that the links marginal cost functions are convex, we establish existence of a Nash equilibrium. We show that the aggregate surplus at a Nash equilibrium is no worse than a factor of times the optimal aggregate surplus; thus, the efficiency loss when users are selfish is no more than approximately 34%. Index Terms Congestion pricing, network resource allocation. THE current Internet is used by a widely heterogeneous population of users; not only are dferent types of traffic sharing the same network, but dferent end users place dferent values on their perceived network performance. This has led to a surge of interest in congestion pricing, where the network is treated as a market, and prices are set to mediate demand and supply of network resources; see, e.g., [1] and [2]. We investigate a specic price mechanism considered by Kelly et al. in [3] (motivated by the proposal made in [4]). For simplicity, let us first consider the special case of a single link; in this case the mechanism works as follows. Each user submits a bid, or total willingness-to-pay, to the link manager. This represents the total amount the user expects to pay. The link manager then chooses a total rate and price such that the product of price and rate is equal to the sum of the bids, and the price is equal to marginal cost; note, in particular, that the supply of the link is elastic, i.e., it is not fixed in advance. Finally, each user receives a fraction of the allocated rate in Manuscript received June 14, 2004; revised June 24, Recommended by Associate Editor R. S. Srikant. This work was supported in part by the National Science Foundation under a Graduate Research Fellowship and Grant ECS , and by the Defense Advanced Research Projects Agency under the Next Generation Internet Initiative. A preliminary version of this paper appeared in the Proceedings of the 43rd IEEE Conference on Decision and Control, Bahamas, December R. Johari is with the Department of Management Science and Engineering, Stanford University, Stanford, CA USA ( ramesh.johari@stanford.edu). S. Mannor is with the Department of Electrical and Computer Engineering, McGill University, Montreal, QC H3A 2A7, Canada ( shie@ece.mcgill.ca). J. N. Tsitsiklis is with the Department of Electrical Engineering and Computer Science, the Massachusetts Institute of Technology, Cambridge, MA USA ( jnt@mit.edu). Digital Object Identier /TAC proportion to their bid. It is shown in [3] that users do not anticipate the effect of their bid on the price, such a scheme maximizes the sum of users utilities minus the cost of the total allocated rate, known as the aggregate surplus (see [5, Ch. 10]). The pricing mechanism of [3] takes as input the bids of the users, and produces as output the price of the link, and the resulting rate allocation to the users. Kelly et al. [3] continue on to discuss distributed algorithms for implementation of this market-clearing process: given the bids of the users, the authors present two algorithms which converge to the market-clearing price and rate allocation. Indeed, much of the interest in this market mechanism stems from its desirable properties as a decentralized system, including both stability and scalability. For details, we refer the reader to [6] [9]. One important interpretation of the price given to users in the algorithms of [3] is that it can provide early notication of congestion. Building on the explicit congestion notication (ECN) proposal [10], this interpretation suggests that the network might charge users proactively, in hopes of avoiding congestion later. From an implementation standpoint, such a sht implies that rather than a hard capacity constraint (i.e., a link is overloaded when the rate through it exceeds the capacity of the link), the link has an elastic capacity (i.e., the link gradually begins to signal a buildup of congestion before the link s true capacity is actually met). Many proposals have been made for active queue management (AQM) to achieve good performance with ECN; see, e.g., [11] [14]. This issue is of secondary importance to our discussion, as we do not concern ourselves with the specic interpretation of the cost function at the link. (An insightful discussion of the relationship between active queue management and the cost function of the link may be found in [15].) In this paper, we investigate the robustness of the market mechanism of [3] when users attempt to manipulate the market. Formally, we consider a model where users anticipate the effects of their actions on the link prices. This makes the model a game, and we ask two fundamental questions. First, does a Nash equilibrium exist for this game? And second, how inefficient is such an equilibrium relative to the maximal aggregate surplus? We show that Nash equilibria exist, and that the efficiency loss is no more than a factor of the maximal aggregate surplus (approximately 34%) when users are price anticipating. Such an investigation forms part of a broader body of work on quantying efficiency loss in environments where participants are selfish. Results have been obtained for routing [16] [18], traffic networks [19], [20] and network design problems [21], [22]. Our work is most closely related to that of [23], where the /$ IEEE
2 JOHARI et al.: EFFICIENCY LOSS IN A NETWORK RESOURCE ALLOCATION GAME 1713 same market mechanism as in this paper was considered for the case where the supply of a link is fixed, or inelastic; this was the mechanism first presented in [4]. Johari and Tsitsiklis show the efficiency loss when users are price anticipating is no worse than 25% [23]. The outline of the remainder of the paper is as follows. We consider a single link in isolation; extensions to general networks are discussed in [24]. In Section I, we describe the market mechanism for a single link, and recapitulate the results of Kelly et al. [3]. In Section II, we describe a game where users are price anticipating, and establish the existence of a Nash equilibrium. We also establish necessary and sufficient conditions for a strategy vector to be a Nash equilibrium. These conditions are used in Section III to prove the main result of the paper for a single link: That when users are price anticipating, the efficiency loss that is, the loss in aggregate surplus relative to the maximum is no more than 34%. In Section IV, we compare the settings of inelastic and elastic supply. In particular, we consider a limit of cost functions which approach a hard capacity constraint. We show that these cost functions are monomials and we let the exponent tend to infinity, then the efficiency loss approaches 25%, which is consistent with the result of [23]. Some conclusions are offered in Section V. I. BACKGROUND Suppose users share a single communication link. Let denote the rate allocated to user. We assume that user receives a utility equal to the allocated rate is. In addition, we let denote the total rate allocated at the link, and let denote the cost incurred at the link when the total allocated rate is. We will assume that both and are measured in the same monetary units. A natural interpretation is that is the monetary value to user of a rate allocation, and is a monetary cost for congestion at the link when the total allocated rate is. We make the following assumptions regarding and. Assumption 1: For each, over the domain the utility function is concave, strictly increasing, and continuously dferentiable, and the right directional derivative at 0, denoted,isfinite. Assumption 2: There exists a continuous, convex, strictly increasing function over with, such that for : Thus, is strictly convex and strictly increasing. Concavity in Assumption 1 corresponds to elastic traffic, as defined by Shenker [25]; such traffic includes file transfers such as FTP connections and peer-to-peer connections. Note that Assumption 2 does not require the price function to be dferentiable. Indeed, assuming smoothness of would simply some of the technical arguments in the paper. However, we later require the use of nondferentiable price functions in our proof of Theorem 8. Given complete knowledge and centralized control of the system, a natural problem for the network manager to try to solve is the following [4]: SYSTEM maximize (1) subject to (2) Since the objective function (1) is continuous, and increases at most linearly while increases superlinearly, an optimal solution exists for (1), (2); since the feasible region is convex and is strictly convex, the functions are strictly concave, then the optimal solution is unique. We refer to the objective function (1) as the aggregate surplus; this is the net monetary benefit to the economy consisting of the users and the single link [5]. For convenience, we define a function surplus which gives the aggregate surplus at an allocation surplus (3) Due to the decentralized nature of the system, the resource manager may not have an exact specication of the utility functions [4]. As a result, we consider the following pricing scheme for rate allocation. Each user makes a payment (also called a bid) of to the resource manager. Given the vector, the resource manager chooses a rate allocation. We assume the manager treats all users alike in other words, the network manager does not price dferentiate. Thus the network manager sets a single price ; we assume that for all, and otherwise. All users are then charged the same price, leading to Associated with this choice of price is an aggregate rate function,defined by We will assume that is measured in the same monetary units as both and. In this case, given a price, user acts to maximize the following payoff function over : The first term represents the utility to user of receiving a rate allocation equal to ; the second term is the payment made to the manager. Observe that since utility is measured in monetary units, the payoff is quasilinear in money, a typical assumption in modeling market mechanisms [5]. Notice that as formulated before, the payoff function assumes that user acts as a price taker; that is, user does not anticipate the effect of his choice of on the price and, hence, (4) (5)
3 1714 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 50, NO. 11, NOVEMBER 2005 on his resulting rate allocation. Informally, we expect that in such a situation the aggregate surplus will be maximized the network manager sets a price equal to marginal cost, i.e., the price function satisfies According to the following proposition a joint solution to (4) and (6) can always be found; the proof is straightforward, and details may be found in [24]. This proposition is then used to show that when users optimize (5) and the price is set to satisfy (6), aggregate surplus is maximized. Proposition 1: Suppose Assumption 2 holds. Given any vector of bids, there exists a unique pair satisfying (4) and (6), and in this case is the unique solution to: Furthermore, has the following properties: 1) ;2) is continuous for ;3) is a strictly increasing and strictly concave function of ; and 4) as. Observe that we can view (7) as a market-clearing process. Given the total revenue from the users, the link manager chooses an aggregate rate so that the revenue is exactly equal to the aggregate charge. Due to Assumption 2, this market-clearing aggregate rate is uniquely determined. Kelly et al. present two algorithms in [3] which amount to dynamic processes of market-clearing; as a result, a key motivation for the mechanism we study in this paper is that it represents the equilibrium behavior of the algorithms in [3]. Kelly et al. show in [3] that when users are nonanticipating, and the network sets the price according to (4) and (6), the resulting allocation solves SYSTEM. This is formalized in the following theorem, adapted from [3]. Theorem 2 (Kelly et al., [3]): Suppose Assumptions 1 and 2 hold. For any, let be the unique solution to (4) and (6). Then there exists a vector such that, and (8) For any such vector, the vector solves. If the functions are strictly concave, such a vector is unique. Theorem 2 shows that with an appropriate choice of price function (as determined by (4) and (6)), and under the assumption that the users behave as price takers, there exists a bid vector where all users have optimally chosen their bids, with respect to the given price ; and the aggregate surplus is maximized at this equilibrium. However, when the price taking assumption is violated, the model changes into a game and the guarantee of Theorem 2 is no longer valid. We investigate this game in the following section. (6) (7) II. SINGLE LINK GAME We now consider an alternative model where the users of a single link are price anticipating, rather than price taking, and play a game to acquire a share of the link. Throughout the remainder of this section and the next, we will assume that the link manager sets the price according to the unique choice prescribed by Proposition 1, as follows. Assumption 3: For any, the aggregate rate is the solution to (7):. Furthermore, for each, is given by Note that we have and and, hence, is always well defined. We adopt the notation to denote the vector of all bids by users other than, i.e.,.given, each user chooses to maximize (9) (10) over nonnegative. The payoff function is similar to the payoff function, except that the user now anticipates that the network will set the price according to Assumption 3, as captured by the allocated rate.anash equilibrium of the game defined by is a vector such that for all for all (11) In the next section, we show that a Nash equilibrium always exists, and give necessary and sufficient conditions for a vector to be a Nash equilibrium. In Section II-B, we outline a class of price functions for which the Nash equilibrium is unique. A. Existence of Nash Equilibrium In this section, we establish that a Nash equilibrium exists for the game defined by. We start by establishing certain properties of in the following proposition. Proposition 3: Suppose that Assumptions 1 3 hold. Then: 1) is a continuous function of ; and 2) for any, is strictly increasing and concave in, and as. Proof: We first show 1): that is a continuous function of. Recall from Proposition 1 that is a continuous function of, and. Now at any vector such that,wehave,so ; thus continuity of at follows by continuity of and. Suppose instead that, and consider a sequence such that as. Then, as, from parts 1) and 2) of Proposition 1; since for all, we must have as,as required.
4 JOHARI et al.: EFFICIENCY LOSS IN A NETWORK RESOURCE ALLOCATION GAME 1715 We now show 2): that is concave and strictly increasing in, with as. From Assumption 3, we can rewrite the definition of as (12) From this expression and Proposition 1, it follows that is strictly increasing in. To show as, we only need that as, a fact that was shown in Proposition 1. It remains to be shown that for fixed, is a concave function of. Since we have already shown that is continuous, we may assume without loss of generality that. We will only consider the case where is twice dferentiable; the extension to general uses a simple limiting argument, and details can be found in [24]. When is twice dferentiable, it follows from (7) that is twice dferentiable in. Since, we can dferentiate (12) twice to find vector to be a Nash equilibrium. Since the payoff of user is concave, these necessary conditions will in fact be sufficient for to be a Nash equilibrium. We begin with some concepts from convex analysis [27], [28]. An extended real-valued function is a function ; such a function is called proper for all, and for at least one. We say that a scalar is a subgradient of an extended real-valued function at for all,wehave. The subdferential of at, denoted, is the set of all subgradients of at. Finally, given an extended real-valued function, we denote the right directional derivative of at by and left directional derivative of at by ( they exist). If is convex, then, provided the directional derivatives exist. For the remainder of this paper, we view any price function as an extended real-valued convex function, by defining for. Our first step is a lemma identying the directional derivatives of as a function of ; for notational convenience, we introduce the following definitions of and, for : (14) From Proposition 1, is a strictly concave function of ; thus the last term in the sum above is nonpositive. To show that is concave in, therefore, it suffices to show that the sum of the first two terms is negative, i.e., Note that under Assumption 2, we have for. Lemma 5: Suppose Assumptions 1 3 hold. Then, for all with, is directionally dferentiable with respect to. These directional derivatives are given by (13) By dferentiating both sides of (7), we find that (15) From (7), we have Substituting these relations, and noting that since is strictly increasing, we conclude that (13) holds, as required. Thus is concave in, as long as is twice dferentiable. The previous proposition establishes concavity and continuity of ; this guarantees existence of a Nash equilibrium, as the following proposition shows. The proof is an application of Rosen s existence theorem [26]; details may be found in [24]. Proposition 4: Suppose that Assumptions 1 3 hold. Then there exists a Nash equilibrium for the game defined by. In the remainder of this section, we establish necessary and sufficient conditions for a vector to be a Nash equilibrium. Because the price function may not be dferentiable, we will use subgradients to describe necessary local conditions for a (16) Furthermore,, and then. Proof: Existence of the directional derivatives is obtained because is a concave function of (from Proposition 3). Fix a vector of bids, such that. Since is an increasing concave function of, and the convex function is directionally dferentiable at (see [28, Th. 23.1]), we can apply the chain rule to compute the right directional derivative of (7) with respect to Thus, as long as, exists, and is given by
5 1716 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 50, NO. 11, NOVEMBER 2005 We conclude from (9) that the right directional derivative of with respect to is given by We may substitute using Lemma 5 to find that equilibrium, then is a Nash Simplying, this reduces to (15). Note that since and,wehave. A similar analysis follows for the left directional derivative. For notational convenience, we make the following definitions for : (17) Under Assumption 2, we have for. The next proposition is the central result of this section: It provides simple local conditions that are necessary and sufficient for a vector to be a Nash equilibrium. Proposition 6: Suppose that Assumptions 1 3 hold. Then, is a Nash equilibrium of the game defined by, and only, and with,, the following two conditions hold for all : (18) (19) Conversely, and satisfy (18), (19), and, then the vector is a Nash equilibrium with and. Proof: We first show that is a Nash equilibrium, then we must have. Suppose not; then for all. Fix a user ; for,wehave, which approaches infinity as. Thus,, and thus we have In particular, an infinitesimal increase of strictly increases the payoff of user,so cannot be a Nash equilibrium. Thus, is a Nash equilibrium, then. Now, let be a Nash equilibrium. We established in Lemma 5 that is directionally dferentiable in for each, as long as. Thus, from (11), is a Nash equilibrium, then the following two conditions must hold: Since the condition is identical to the condition, this establishes the conditions in the proposition. Conversely, and the preceding two conditions hold, then we may reverse the argument: since the payoff function of user is a concave function of for each (from Proposition 3), (18), (19) are sufficient for to be a Nash equilibrium. Finally, suppose that and satisfy (18), (19), with. Then let. We then have (since ); and, so that. Since,wehave, so that. Thus, is a Nash equilibrium, as required. Note that the preceding proposition identies a Nash equilibrium entirely in terms of the allocation made; and conversely, we find a pair which satisfies (18), (19) with and, then there exists a Nash equilibrium which yields that allocation. In particular, the set of allocations which can arise at Nash equilibria coincides with those vectors such that, and (18), (19) are satisfied. B. Nondecreasing Elasticity Price Functions: Uniqueness of Nash Equilibrium In this section, we demonstrate that for a certain class of dferentiable price functions, there exists a unique Nash equilibrium of the game defined by. We consider price functions which satisfy the following additional assumption. Assumption 4: The price function is dferentiable, and exhibits nondecreasing elasticity: For, there holds To gain some intuition for the concept of nondecreasing elasticity, consider a price function satisfying Assumption 2. The quantity is known as the elasticity of a price function [5]. Note that the elasticity of is the derivative of with respect to. From this viewpoint, we see that nondecreasing elasticity is equivalent to the requirement that is a convex function in. (Note that this is not equivalent to the requirement that is a convex function of.) Nondecreasing elasticity can also be interpreted by considering the price function as the inverse of the supply function ; the supply function gives the amount of rate the provider is willing to supply at a given price [5]. In this case, nondecreasing elasticity of the price function is equivalent to nonincreasing elasticity of the supply function. Nondecreasing elasticity captures a wide range of price functions; we give two common examples that follow. Example 1 (The M/M/1 Queue): Consider the cost function, where and are constants;
6 JOHARI et al.: EFFICIENCY LOSS IN A NETWORK RESOURCE ALLOCATION GAME 1717 then the cost is proportional to the steady-state queue size in an M/M/1 queue with service rate and arrival rate. (Note that we must view as an extended real-valued function, with for ; this does not affect any of the analysis of this paper.) It is straightforward to check that, as long as,wehave which is a strictly increasing function of. Thus, satisfies Assumption 4. Example 2 (M/M/1 Overflow Probability): Consider the function, where,, and is an integer. Then, the price is set proportional to the probability that an M/M/1 queue exceeds a buffer level, when the service rate is and the arrival rate is. In this case we have, so that satisfies Assumption 4. We now prove the key property of dferentiable nondecreasing elasticity price functions in the current development: For such functions, there exists a unique Nash equilibrium of the game defined by. Proposition 7: Suppose Assumptions 1 3 hold. If in addition is dferentiable and exhibits nondecreasing elasticity (Assumption 4 holds), then there exists a unique Nash equilibrium for the game defined by. Proof: We use the expressions (18), (19) to show that the Nash equilibrium is unique under Assumption 4. Observe that in this case, from (17), we may define for, and conclude that is a Nash equilibrium and only and the following optimality conditions hold: (20) (21) Suppose we have two Nash equilibria,, with ; then, and. Note that is nonincreasing as increases; and is nondecreasing as increases (from Assumption 4) and, therefore,. Furthermore,, then from (20) we have ; thus,so as well [from (21)]. Now note that the right-hand side of (20) is strictly larger at than at ; thus the left hand side must be strictly larger at than at as well. This is only possible for each user, since we have shown in the preceding paragraph that ; is nonincreasing as increases; and. Since,wehave which is a contradiction. Thus, at the two Nash equilibria, we must have, so we can let,, and. Then, all Nash equilibria satisfy (22) (23) However, now we observe that the left hand side of (22) is strictly decreasing in, sogiven, there exists at most one solution to (22). Since, this implies the Nash equilibrium must be unique. We observe that uniqueness of the Nash equilibrium implies an additional desirable property in the case of symmetric users. If two users share the same utility function, and the price function is dferentiable, we conclude from Proposition 7 that at the unique Nash equilibrium, these users submit exactly the same bid (and, hence, receive exactly the same rate allocation). We also note that in general, Nash equilibria need not be unique. As an example, consider a case with two users, where, for. Let the price function be for, and for. Then, it is straightforward to very that any pair such that for, and, satisfies (18), (19) with ; thus, by Proposition 6, there exist Nash equilibria that correspond to each of these. Note, however, that the price function is not dferentiable; it is not clear whether, in general, dferentiability of suffices to guarantee a unique Nash equilibrium. III. EFFICIENCY LOSS: THE SINGLE LINK CASE We let denote an optimal solution to SYSTEM, defined in (1), (2), and let denote any Nash equilibrium of the game defined by. We now investigate the efficiency loss of this system; that is, how much aggregate surplus is lost because the users attempt to game the system? To answer this question, we must compare the aggregate surplus obtained when the users fully evaluate the effect of their actions on the price, and the aggregate surplus obtained by choosing an allocation which maximizes aggregate surplus. The following theorem is the main result of this paper: It states that the efficiency loss is no more than approximately 34%, and that this bound is essentially tight. Theorem 8: Suppose that Assumptions 1 3 hold. Suppose also that for all. Let be any solution to, and let be any Nash equilibrium of the game defined by. Then, we have the following bound: surplus surplus (24) where surplus is defined in (3). In other words, there is no more than approximately a 34% efficiency loss when users are price anticipating. Furthermore, this bound is tight: For every, there exists a choice of, a choice of (linear) utility functions,, and a (piecewise linear) price function such that a Nash equilibrium and a solution to SYSTEM exist with surplus surplus (25)
7 1718 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 50, NO. 11, NOVEMBER 2005 Proof: The proof of (24) consists of a sequence of steps. 1) We show that the worst case ratio occurs when the utility function of each user is linear. 2) We restrict attention to games where the total allocated Nash equilibrium rate is. 3) We compute the worst case choice of linear utility functions, for a fixed price function and total Nash equilibrium rate. 4) We prove that it suffices to consider a special class of piecewise linear price functions. 5) Combining steps 1) 3), we compute the worst case efficiency loss by minimizing the ratio of Nash equilibrium aggregate surplus to maximal aggregate surplus, over the worst case choice of games with linear utility functions [from step 2)] and our restricted class of piecewise linear price functions [from step 3)]. Step 1: Show that we may assume without loss of generality that is linear for each user, i.e., without loss of generality we may assume, where and for. The proof of this claim is similar to the proof of [23, Lemma 4]. Let denote any solution to, and let denote a Nash equilibrium, for an arbitrary collection of utility functions satisfying the assumptions of the theorem. We let denote the allocation vector at the Nash equilibrium. For each user, wedefine a new utility function, where ; we know that by Assumption 1. Then, observe that we replace the utility functions with the linear utility functions, the vector remains a Nash equilibrium; this follows from the necessary and sufficient conditions of Proposition 6. We first show that. To see this, note from (19) that for all such that. Thus, for such a user,so, by convexity (Assumption 2). Next, we note that. This follows since is strictly increasing and nonnegative, while ; thus is sufficiently small for all, we will have, which implies (since is a solution to SYSTEM). Using concavity, we have for each that.defining and expanding the definition of surplus,wehave surplus surplus (Note that all denominators are positive, since we have shown that.) Since we assumed, wehave by concavity; and since, we have the inequality Now, observe that the right hand side of the previous expression is the ratio of the Nash equilibrium aggregate surplus to the maximal aggregate surplus, when the utility functions are ; since this ratio is no larger than the same ratio for the original utility functions, we can restrict attention to games where the utility function of each user is linear. Finally, by replacing by, and the cost function by, we may assume without loss of generality that. Thus, by relabeling the users necessary, we assume for the remainder of the proof that for all, where and for. Before continuing, we observe that under these conditions, we have the following relation: To see this, note that at any fixed value of, the left hand side is maximized by allocating the entire rate to user 1. Thus, the ratio of Nash equilibrium aggregate surplus to maximal aggregate surplus becomes (26) Note that the denominator is positive, since ; and further, the optimal solution in the denominator occurs at the unique value of such that. Step 2: Show that we may restrict attention to games where the total allocated rate at the Nash equilibrium is. Fix a cost function satisfying Assumption 2. Let be a Nash equilibrium, and let be the resulting allocation. Let be the total allocated rate at the Nash equilibrium; note that by Proposition 6. We now define a new price function according to, and a new cost function ; note that. Then, it is straightforward to check that satisfies Assumption 2. We will use hats to denote the corresponding functions when the price function is :,,,, etc. Define. Then we claim that is a Nash equilibrium when the price function is. First observe that ; thus. Furthermore,. Finally, note that
8 JOHARI et al.: EFFICIENCY LOSS IN A NETWORK RESOURCE ALLOCATION GAME 1719 from which we conclude that, and similarly. Recall that is a Nash equilibrium for the price function ; thus, we combine the preceding conclusions and apply Proposition 6, we have that is a Nash equilibrium when the price function is, with total allocated rate and allocation. To complete the proof of this step, we note the following chain of equalities: where we make the substitution. But now note that the right hand side is the ratio of Nash equilibrium aggregate surplus to maximal aggregate surplus for a game where the total allocated rate at the Nash equilibrium is equal to 1. Consequently, in computing the worst case efficiency loss, we may restrict our attention to games where the Nash equilibrium allocated rate is equal to 1. Step 3: For a fixed price function, determine the instance of linear utility functions that minimizes Nash equilibrium aggregate surplus, for a fixed Nash equilibrium allocated rate. Note that fixing the price function fixes the optimal aggregate surplus; thus minimizing the aggregate surplus at Nash equilibrium also yields the worst case efficiency loss. We will optimize over the set of all games where users have linear utility functions [satisfying the conditions of step 1)], and where the total Nash equilibrium rate is. We use the necessary and sufficient conditions of Proposition 6. Note that by fixing the price function and the total rate, the Nash equilibrium price is fixed,, and and are fixed as well [from the definition (17)]; for notational convenience, we abbreviate,,, and for the duration of this step. Since, for a fixed value of the game with linear utility functions that minimizes aggregate surplus is given by solving the following optimization problem (with unknowns ): minimize (27) subject to (28) (29) (30) (31) (32) (Note that we have applied Proposition 6: we solve the preceding problem and find an allocation and coefficients, then there exists a Nash equilibrium with.) The objective function is the aggregate surplus given a Nash equilibrium allocation. Conditions (28) and (29) are equivalent to the Nash equilibrium conditions established in Proposition 6. The constraint (30) ensures that the total allocation made is equal to 1, and the constraint (31) follows from Step 1. The constraint (32) ensures the rate allocated to each user is nonnegative. We solve this problem through a sequence of reductions. We first show we may assume without loss of generality that the constraint (29) holds with equality for all users. The resulting problem is symmetric in the users ; we next show that a feasible solution exists and only and is sufficiently large, and we conclude using a convexity argument that at an optimal solution. Finally, we show the worst-case occurs in the limit where, and calculate the resulting Nash equilibrium aggregate surplus. We first show that it suffices to optimize over all such that (29) holds with equality for. Note that is a feasible solution to (27) (32), then from (29) (32), and the fact that, we conclude that.now, for some, but the corresponding constraint in (29) does not hold with equality, we can reduce until the constraint in (29) does hold with equality; by this process, we obtain a smaller value for the objective function (27). On the other hand, for some, we can set ; since, this preserves feasibility, but does not impact the term in the objective function (27). Therefore, we can restrict attention to feasible solutions for which Having done so, observe that the constraint (31) that may be written as (33) Finally, the constraint (31) that becomes redundant, as it is guaranteed by the fact that [from (30)], (by definition), and (33). We now use the preceding observations to simply the optimization problem (27) (32) as follows: minimize (34) subject to (35) (36) (37) (38) The objective function (34) equals (27) upon substitution for for, from (33). We know that when [from (28) and (29)]; thus the constraint (35) is equivalent to the constraints (28) and (29) for user 1 with. The constraint (28) for is redundant and eliminated, since (29)
9 1720 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 50, NO. 11, NOVEMBER 2005 holds with equality for. The constraint (36) is equivalent to the allocation constraint (30); and the constraint (37) ensures, as required in (31). We first note that for a feasible solution to (34) (38) to exist, we must have. We have already shown that we must have a feasible solution exists. Furthermore, from (35) we observe that the smallest feasible value of is. We require from (36) and (38), so we must have, which yields the restriction that. Thus, there only exist Nash equilibria with total rate 1 and price : (39) We will assume for the remainder of this step that (39) is satisfied. We note that is a feasible solution to (34) (38) with users, then letting, the vector is a feasible solution to (34) (38) with users, and with the same objective function value (34) as. Thus, the minimal objective function value cannot increase as increases, so the worst case efficiency loss occurs in the limit where. We now solve (34) (38) for a fixed feasible value of. From the constraints (36), (37), we observe that a feasible solution to (34) (38) exists and only the following condition holds in addition to (39): In this case, the following symmetric solution is feasible: (40) (41) Furthermore, since the objective function is strictly convex and symmetric in the variables, and the feasible region is convex, the symmetric solution (41) must be optimal. If we substitute the optimal solution (41) into the objective function (34) and take the limit as, then the constraint (40) is vacuously satisfied, and the objective function becomes. Since we have shown that, the worst case occurs at the smallest feasible value of ; from (35), this value is (42) The resulting worst case Nash equilibrium aggregate surplus is To complete the proof of the theorem, we will consider the ratio of this Nash equilibrium aggregate surplus to the maximal aggregate surplus; we denote this ratio by as a function of the price function (43) Note that henceforth, the scalar used throughout step 3) will be denoted, and we return to denoting the price function by. Thus, as defined in (43) is a function of the entire price function. For completeness, we summarize in the following lemma an intermediate tightness result which will be necessary to prove the tightness of the bound in the theorem. Lemma 9: Suppose that assumptions 2) and 3) are satisfied. Then, there exists and a choice of linear utility functions, where, with total Nash equilibrium rate 1, and only (39) is satisfied, i.e., (44) In this case, given, there exists and a collection of users where user has utility function, such that is a Nash equilibrium allocation with, and (45) Proof of Lemma: The proof follows from step 3). We have shown that there exists a Nash equilibrium with total rate 1, then (44) must be satisfied. Conversely, (44) is satisfied, we proceed as follows: Define according to (42); choose large enough that (40) is satisfied; define according to (41); and then define according to (33) with. Then, it follows that is a feasible solution to (27) (32), which (by Proposition 6) guarantees there exists a Nash equilibrium whose total allocated rate equals 1. The bound in (45) then follows by the proof of step 3). The remainder of the proof amounts to minimizing the worst case ratio of Nash equilibrium aggregate surplus to maximal aggregate surplus, over all valid choices of. A valid choice of is any price function such that at least one choice of linear utility functions satisfying the conditions of step 1) leads to a Nash equilibrium with total allocated rate 1. By Lemma 9, all such functions are characterized by the constraint (44). We will minimize, given by (43), over all choices of satisfying (44). Step 4: Show that in minimizing over satisfying (44), we may restrict attention to functions conditions: satisfying the following (46) (47) (48) Observe that as defined in (46) (48) is a convex, strictly increasing, piecewise linear function with two parts: an initial segment which increases at slope, and a second segment which increases at slope. In particular, such a function satisfies Assumption 2. Furthermore, we have, so that. This implies ; thus, multiplying through (48) by yields (44).
10 JOHARI et al.: EFFICIENCY LOSS IN A NETWORK RESOURCE ALLOCATION GAME 1721 for ; thus in that region. We let. Then, we have the following relationship: Fig. 1. Proof of Theorem 8, step 4): Given a price function p (solid line) and Nash equilibrium rate 1, a new price function p (dashed line) is defined according to (49). The last equality follows by observing that since, the solution to occurs at where ; and at all points, we have the relationship. Combining the preceding results, we have, as required. Step 5: The minimum value of over all satisfying (46) (48) is. Wefirst show that given satisfying (46) (48), is given by To very the claim of step 4), we consider any function such that (44) holds. We define a new price function as follows: (49) (See Fig. 1 for an illustration.) Let, and let. Then ; and since,we have by convexity of, so that. Furthermore, since from (44), we have. Finally, we have where the equality follows from the definition of and the inequality follows from (44). Thus, satisfies (46) (48). Observe also that, and, and thus. We now show that. As an intermediate step, we define a new price function as follows: (50) The numerator results by simplying the numerator of (43), when takes the form described by (46) (48). To arrive at the denominator, we note that the solution to occurs at satisfying. Since, we must have and. Simplying, we find (51) The expression, upon simplication, becomes the denominator of (50), as required. Fix and such that, and, and define as in (46). We note here that the constraints and may be equivalently rewritten as, and.define ; from (50), note that for a fixed, is a ratio of two affine functions of, and thus the minimal value of is achieved either when or as.define, and. Then Of course, and, so that (44) is satisfied for. Let denote the cost function associated with. Observe that (by convexity of ), we have for all that, so that. Thus Furthermore, so that. Next, we let denote the cost function associated with. By convexity of, we know (52) (53) We now minimize and over.over, the minimum value of is 2/3, achieved as.over, the minimum value of is 20/27, achieved at. Finally, over, the minimum value of is, achieved at. Since, we conclude
11 1722 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 50, NO. 11, NOVEMBER 2005 that the minimal value of over all satisfying (46) (48) is equal to. This completes the proof of (24), the lower bound in the theorem. We now show that this lower bound is tight. Fix. The preceding argument shows that the worst case occurs for price functions satisfying (46) (48), where and. For fixed, let be the associated price function defined according to (46). Then, we have established that From Lemma 9, we know there exists such that, and where is the ratio of Nash equilibrium aggregate surplus to maximal aggregate surplus for some game with price function and total allocated rate 1 at the Nash equilibrium. We thus have Thus, for sufficiently large, we will have, establishing (25). Theorem 8 shows that in the worst case, aggregate surplus falls by no more than approximately 34% when users are able to anticipate the effects of their actions on the price of the link. Furthermore, this bound is essentially tight. In fact, from the proof of the theorem we see that this ratio is achieved via a sequence of games where the following hold true. 1) The price function has the form given by (46) (48), with,, and. 2) The number of users becomes large. 3) User 1 has linear utility with, and all users have linear utility with, where (for ). The last item follows by substituting the solution (41) in (33), and taking the limit as. (Note that formally, the limits of and should be taken in the correct order; in particular, in the proof we first have, and then.) Note that the price function used to achieve the worst case efficiency loss is not dferentiable. As discussed in Section I, this is the main reason that we allow nondferentiable price functions in Assumption 2. Indeed, some of the results of Section II-A can be simplied we restrict attention only to dferentiable price functions. Nevertheless, we note that even we only consider dferentiable price functions, the worst case efficiency loss remains approximately 34%. This result can be established by approximating the piecewise linear price functions described in (46) (48) by dferentiable price functions. It is interesting to note that the worst case is obtained by considering instances where the price function is becoming steeper and steeper at the Nash equilibrium rate 1, since. This forces the optimal rate at the solution to SYSTEM to approach the Nash equilibrium rate,as we observe from (51); nevertheless, the shortfall between the Nash equilibrium aggregate surplus and the maximal aggregate surplus approaches 34%. IV. INELASTIC SUPPLY VERSUS ELASTIC SUPPLY In this section, we briefly compare the model of this paper (allocation of a resource in elastic supply) with the model of [23] (allocation of a resource in inelastic supply). In [23], a model is considered with a single link having exactly units of rate available to allocate among the users. As in the model of this paper, user submits a bid. The link manager then sets a price ; and user receives an allocation given by As in this paper, the payoff to user is. It is shown in [23] that when users are price anticipating and the link supply is inelastic, the efficiency loss is at most 25% of the maximal aggregate utility. Intuitively, we would like to model a system with an inelastic supply by a cost function which is zero for, and infinite for. Formally, we show in this section that the price function is given by for and, then as the worst case efficiency loss approaches 25% the same value obtained in [23]. While this does not formally establish the result in [23], the limit is intuitively plausible, because as the exponent increases, the price function and associated cost function begin to resemble an inelastic capacity constraint with :For, as ; and for, as. Theorem 10: Suppose that Assumptions 1 3 hold. Suppose also that for all, and that for and.define the function by (54) If is any solution to, and is any Nash equilibrium of the game defined by, then surplus surplus (55) where surplus is defined in (3). Furthermore, is strictly increasing, with as ; and the bound (55) is tight: for fixed, for every, there exists a choice of and a choice of (linear) utility functions,, such that a Nash equilibrium a solution to SYSTEM exist with surplus surplus (56) Proof: We follow the proof of Theorem 8. Steps 1) 4) follow as in that proof, provided we can show that two scalings of the function do not affect our result in step 1), where we replace by, and in step 2), where we replace by, where is the Nash equilibrium rate. Indeed, both these scalings remain valid, since the rescaled price function is still a monomial with the same exponent as,but a dferent constant coefficient. In particular, we may continue to restrict attention to the special case where, with, and where the total Nash equilibrium allocated rate is 1.
12 JOHARI et al.: EFFICIENCY LOSS IN A NETWORK RESOURCE ALLOCATION GAME 1723 From steps 1) 4) of the proof of Theorem 8, we must minimize,defined in (43), for all choices of such that (44) is satisfied, i.e., such that. For, we have and, thus, we require (57) Note that at the maximal aggregate surplus, implies that. Furthermore, for. Thus, is given by From (43), we conclude that is given by We now minimize over the set of satisfying (57). We begin by dferentiating with respect to, and setting the derivative to zero; simplying, this yields the following equation: This equation is quadratic in, and has two solutions and :, and. Both solutions satisfy (57). Let, and.wehave Next, we consider. Note first that. Furthermore, as,, and. Thus, as. Finally, let ; it suffices to show is strictly increasing for. Dferentiating yields As before, it suffices to check that, where.wehave ; ; and. Thus, for all, which implies is strictly increasing for. From the previous lemma, we conclude that the minimum value of over satisfying (57) is given by ; this establishes (55). As in Theorem 8, by construction this bound is tight, so (56) holds as well. The preceding theorem shows that for a particular sequence of price functions which approach an inelastic supply constraint, the efficiency loss gradually decreases from 7/27 (at )to 1/4 (as ). In the limit as, we recover the same efficiency loss as in the earlier work of [23]. However, while we have demonstrated such a limit holds as long as the price functions are monomials, there remains an open question: If the price functions converge (in an appropriate sense) to a fixed capacity constraint, under what conditions does the efficiency loss also converge to 1/4? It is straightforward to check that such a limit cannot always hold. For example, consider price functions of the form specied in (46) (48). Using the expression for given in (50), it is possible to show that by first taking, and then taking, the worst case efficiency loss approaches zero; see (53). V. CONCLUSION To minimize over satisfying (57), we need also to check the endpoint where.if,wefind ; since from the definition of, the minimum value is achieved at either or. For,wedefine, and. We need the following technical lemma. Lemma 11: The functions and are strictly increasing for. Furthermore, for, while. Proof: We begin by noting that. Let ; it suffices to show that is strictly increasing for. Dferentiating yields It suffices to check that, where.wehave ; ; and. This implies for all,so is strictly increasing for. This paper considers a pricing mechanism where the available resources in a network are in elastic supply. For a game where users strategies are the payments they are willing to make, we showed that the efficiency loss is no more than 34% when users are price anticipating, for the setting of a single link (Theorem 8). This result can be extended to general networks, using the same approach as in [23]. We consider a standard multicommodity flow model, where each user has multiple paths available, and each path uses a subset of links in the network. The utility to a user depends on the maximum rate at which he can send through the network. We study a game where users submit individual bids to each link in the network; it is straightforward to establish existence of a Nash equilibrium for such a game. Using techniques similar to the results proven in a network context in [23], it can be shown that the efficiency loss is no more than 34% when users are price anticipating, matching the result of Section III. For details of this network extension, the reader is referred to [24] and [29]. Important questions remain regarding an extension of this work to a dynamic context. While our results suggest that ma-
13 1724 IEEE TRANSACTIONS ON AUTOMATIC CONTROL, VOL. 50, NO. 11, NOVEMBER 2005 nipulation of the market in a static game setting cannot lead to arbitrarily high efficiency loss, such a result does not necessarily imply users will not be able to manipulate an algorithmic implementation of this mechanism (such as those proposed in [3]). Investigation of this point is an open research topic. Critical to any investigation of dynamics is the nature of the information available to the players of the pricing game. In order to compute an optimal strategic decision users need to know not only the current price level, but also the total allocated rate and the derivative of the price (where we have assumed for simplicity that is dferentiable). We postulate that the overhead of actually collecting such detailed information in a large scale communication network is quite high; in fact, in general users do not have knowledge of either the total allocated rate or the derivative of the price at the resource. This raises an important question of information availability when users respond to price signals: users may not react optimally, so what are the users conjectures about how their strategies affect the price? Developing more detailed models for the users response to available price information from the network is a research direction for the future. REFERENCES [1] B. Briscoe, V. Darlagiannis, O. Heckman, H. Oliver, V. Siris, D. Songhurst, and B. Stiller, A market managed multiservice Internet (M3I), Comput. Commun., vol. 26, no. 4, pp , [2] M. Falkner, M. Devetsikiotis, and I. Lambadaris, An overview of pricing concepts for broadband IP networks, IEEE Commun. Surv., vol. 3, no. 2, [3] F. P. Kelly, A. K. Maulloo, and D. K. Tan, Rate control for communication networks: shadow prices, proportional fairness, and stability, J. Oper. Res. Soc., vol. 49, pp , [4] F. P. Kelly, Charging and rate control for elastic traffic, Eur. Trans. Telecommun., vol. 8, pp , [5] A. Mas-Colell, M. D. Whinston, and J. R. Green, Microeconomic Theory. Oxford, U.K.: Oxford Univ. Press, [6] R. Johari and D. K. Tan, End-to-end congestion control for the Internet: delays and stability, IEEE/ACM Trans. Networking, vol. 9, no. 6, pp , Dec [7] F. Kelly, Stability and fairness of end-to-end congestion control, Eur. J. Control, vol. 9, pp , [8] R. Srikant, The Mathematics of Internet Congestion Control. Boston, MA: Birkhäuser, [9] G. Vinnicombe, On the stability of networks operating TCP-like congestion control, in Proc. IFAC World Congr., [10] K. Ramakrishnan, S. Floyd, and D. Black, The addition of explicit congestion notication (ECN) to IP, Internet Engineering Task Force, [11] S. Athuraliya, S. H. Low, V. H. Li, and Q. Yin, REM: active queue management, IEEE Network, vol. 15, no. 3, pp , [12] F. P. Kelly, Models for a self managed Internet, Phil. Trans.: Math., Phys., Eng. Sci., vol. 358, no. 1773, pp , [13] S. Kunniyur and R. Srikant, Analysis and design of an adaptive virtual queue (AVQ) algorithm for active queue management, in Proc. ACM SIGCOMM, 2001, pp [14], End-to-end congestion controls schemes: utility functions, random losses, and ECN marks, IEEE/ACM Transactions on Networking, vol. 11, no. 5, pp , [15] R. J. Gibbens and F. P. Kelly, Resource pricing and the evolution of congestion control, Automatica, vol. 35, pp , [16] A. Czumaj and B. Voecking, Tight bounds for worst-case equilibria, in Proc. 13th Annu. ACM-SIAM Symp. Discrete Algorithms, 2002, pp [17] E. Koutsoupias and C. Papadimitriou, Worst-case equilibria, in Proc. 16th Annu. Symp. Theoretical Aspects of Computer Science, 1999, pp [18] M. Mavronicolas and P. Spirakis, The price of selfish routing, in Proc. 33rd Annu. ACM Symp. Theory of Computing, 2001, pp [19] J. R. Correa, A. S. Schulz, and N. Stier Moses, Selfish routing in capacitated networks, Math. Oper. Res., [20] T. Roughgarden and E. Tardos, How bad is selfish routing?, J. ACM, vol. 49, no. 2, pp , [21] E. Anshelevich, A. Dasgupta, E. Tardos, and T. Wexler, Near-optimal network design with selfish agents, in Proc. 35th Annu. ACM Symp. Theory of Computing, 2003, pp [22] A. Fabrikant, A. Luthra, E. Maneva, C. Papadimitriou, and S. Shenker, On a network creation game, in Proc. 22nd Annu. ACM Symp. Principles of Distributed Computing, 2003, pp [23] R. Johari and J. N. Tsitsiklis, Efficiency loss in a network resource allocation game, Math. Oper. Res., vol. 29, no. 3, pp , [24] R. Johari, S. Mannor, and J. N. Tsitsiklis. (2005) Efficiency loss in a network resource allocation game: The case of elastic supply. ArXiV. [Online] [25] S. Shenker, Fundamental design issues for the future Internet, IEEE J. Select. Areas Commun., vol. 13, no. 7, pp , Sep [26] J. Rosen, Existence and uniqueness of equilibrium points for concave n-person games, Econometrica, vol. 33, no. 3, pp , [27] D. P. Bertsekas, A. Nedic, and A. E. Ozdaglar, Convex Analysis and Optimization. Belmont, MA: Athena Scientic, [28] R. T. Rockafellar, Convex Analysis. Princeton, NJ: Princeton Univ. Press, [29] R. Johari, Efficiency loss in market mechanisms for resource allocation, Ph.D. dissertation, Mass. Inst. Technol., Cambridge, MA, Stanford, CA. Ramesh Johari (M 05) received the A.B. degree in mathematics from Harvard University, Cambridge, MA, the Certicate of Advanced Study in mathematics from the University of Cambridge, Cambridge, U.K., and the Ph.D. in electrical engineering and computer science from the Massachusetts Institute of Technology, Cambridge, in 1998, 1999, and 2004, respectively. He is currently an Assistant Professor of Management Science and Engineering, and by courtesy, Electrical Engineering, at Stanford University, Shie Mannor (S 00 M 03) received the B.Sc. degree in electrical engineering, the B.A. degree in mathematics (both summa cum laude), and the Ph.D. degree in electrical engineering from the Technion Israel Institute of Technology, Haa, in 1996, 1996, and 2002, respectively. During the spring semester of 2002, he was a Lecturer at the Electrical Engineering Department of the Technion. From 2002 to 2004, he was a Postdoctoral Associate at the Massachusetts Institute of Technology, Cambridge. He is currently an Assistant Professor of Electrical and Computer Engineering at McGill University, Montreal, QC, Canada. His research interests include machine learning and pattern recognition, planning and control, multiagent systems, and communications. Dr. Mannor was a Fulbright Scholar in 2002, and he is currently a Canada Research Chair in Machine Learning. John N. Tsitsiklis (F 99) received the B.S. degree in mathematics, and the B.S., M.S., and Ph.D. degrees in electrical engineering, all from the Massachusetts Institute of Technology (MIT), Cambridge, in 1980, 1980, 1981, and 1984, respectively. He is currently a Professor of Electrical Engineering and Computer Science, and a Co-Director of the Operations Research Center at MIT. His research interests are in the fields of systems, optimization, communications, control, and operations research. He has coauthored four books and about 100 journal papers. Dr. Tsitsiklis awards include an Outstanding Paper Award by the IEEE Control Systems Society, the MIT Edgerton Faculty Achievement Award (1989), the Bodossakis Foundation Prize (1995), and the INFORMS/CSTS prize (1997). He is currently a member of the editorial board for the Springer-Verlag Lecture Notes in Control and Information Sciences series, and an Associate Editor of Mathematics of Operations Research.
Inter-Session Network Coding with Strategic Users: A Game-Theoretic Analysis of Network Coding
 Inter-Session Network Coding with Strategic Users: A Game-Theoretic Analysis of Network Coding Amir-Hamed Mohsenian-Rad, Jianwei Huang, Vincent W.S. Wong, Sidharth Jaggi, and Robert Schober arxiv:0904.91v1
Inter-Session Network Coding with Strategic Users: A Game-Theoretic Analysis of Network Coding Amir-Hamed Mohsenian-Rad, Jianwei Huang, Vincent W.S. Wong, Sidharth Jaggi, and Robert Schober arxiv:0904.91v1
CS364A: Algorithmic Game Theory Lecture #14: Robust Price-of-Anarchy Bounds in Smooth Games
 CS364A: Algorithmic Game Theory Lecture #14: Robust Price-of-Anarchy Bounds in Smooth Games Tim Roughgarden November 6, 013 1 Canonical POA Proofs In Lecture 1 we proved that the price of anarchy (POA)
CS364A: Algorithmic Game Theory Lecture #14: Robust Price-of-Anarchy Bounds in Smooth Games Tim Roughgarden November 6, 013 1 Canonical POA Proofs In Lecture 1 we proved that the price of anarchy (POA)
Designing efficient market pricing mechanisms
 Designing efficient market pricing mechanisms Volodymyr Kuleshov Gordon Wilfong Department of Mathematics and School of Computer Science, McGill Universty Algorithms Research, Bell Laboratories August
Designing efficient market pricing mechanisms Volodymyr Kuleshov Gordon Wilfong Department of Mathematics and School of Computer Science, McGill Universty Algorithms Research, Bell Laboratories August
Lecture 5: Iterative Combinatorial Auctions
 COMS 6998-3: Algorithmic Game Theory October 6, 2008 Lecture 5: Iterative Combinatorial Auctions Lecturer: Sébastien Lahaie Scribe: Sébastien Lahaie In this lecture we examine a procedure that generalizes
COMS 6998-3: Algorithmic Game Theory October 6, 2008 Lecture 5: Iterative Combinatorial Auctions Lecturer: Sébastien Lahaie Scribe: Sébastien Lahaie In this lecture we examine a procedure that generalizes
Yao s Minimax Principle
 Complexity of algorithms The complexity of an algorithm is usually measured with respect to the size of the input, where size may for example refer to the length of a binary word describing the input,
Complexity of algorithms The complexity of an algorithm is usually measured with respect to the size of the input, where size may for example refer to the length of a binary word describing the input,
Financial Innovation in Segmented Markets
 Financial Innovation in Segmented Marets by Rohit Rahi and Jean-Pierre Zigrand Department of Accounting and Finance, and Financial Marets Group The London School of Economics, Houghton Street, London WC2A
Financial Innovation in Segmented Marets by Rohit Rahi and Jean-Pierre Zigrand Department of Accounting and Finance, and Financial Marets Group The London School of Economics, Houghton Street, London WC2A
March 30, Why do economists (and increasingly, engineers and computer scientists) study auctions?
 March 3, 215 Steven A. Matthews, A Technical Primer on Auction Theory I: Independent Private Values, Northwestern University CMSEMS Discussion Paper No. 196, May, 1995. This paper is posted on the course
March 3, 215 Steven A. Matthews, A Technical Primer on Auction Theory I: Independent Private Values, Northwestern University CMSEMS Discussion Paper No. 196, May, 1995. This paper is posted on the course
Investing and Price Competition for Multiple Bands of Unlicensed Spectrum
 Investing and Price Competition for Multiple Bands of Unlicensed Spectrum Chang Liu EECS Department Northwestern University, Evanston, IL 60208 Email: changliu2012@u.northwestern.edu Randall A. Berry EECS
Investing and Price Competition for Multiple Bands of Unlicensed Spectrum Chang Liu EECS Department Northwestern University, Evanston, IL 60208 Email: changliu2012@u.northwestern.edu Randall A. Berry EECS
Online Shopping Intermediaries: The Strategic Design of Search Environments
 Online Supplemental Appendix to Online Shopping Intermediaries: The Strategic Design of Search Environments Anthony Dukes University of Southern California Lin Liu University of Central Florida February
Online Supplemental Appendix to Online Shopping Intermediaries: The Strategic Design of Search Environments Anthony Dukes University of Southern California Lin Liu University of Central Florida February
THE TRAVELING SALESMAN PROBLEM FOR MOVING POINTS ON A LINE
 THE TRAVELING SALESMAN PROBLEM FOR MOVING POINTS ON A LINE GÜNTER ROTE Abstract. A salesperson wants to visit each of n objects that move on a line at given constant speeds in the shortest possible time,
THE TRAVELING SALESMAN PROBLEM FOR MOVING POINTS ON A LINE GÜNTER ROTE Abstract. A salesperson wants to visit each of n objects that move on a line at given constant speeds in the shortest possible time,
Appendix: Common Currencies vs. Monetary Independence
 Appendix: Common Currencies vs. Monetary Independence A The infinite horizon model This section defines the equilibrium of the infinity horizon model described in Section III of the paper and characterizes
Appendix: Common Currencies vs. Monetary Independence A The infinite horizon model This section defines the equilibrium of the infinity horizon model described in Section III of the paper and characterizes
Best-Reply Sets. Jonathan Weinstein Washington University in St. Louis. This version: May 2015
 Best-Reply Sets Jonathan Weinstein Washington University in St. Louis This version: May 2015 Introduction The best-reply correspondence of a game the mapping from beliefs over one s opponents actions to
Best-Reply Sets Jonathan Weinstein Washington University in St. Louis This version: May 2015 Introduction The best-reply correspondence of a game the mapping from beliefs over one s opponents actions to
Chapter 10: Mixed strategies Nash equilibria, reaction curves and the equality of payoffs theorem
 Chapter 10: Mixed strategies Nash equilibria reaction curves and the equality of payoffs theorem Nash equilibrium: The concept of Nash equilibrium can be extended in a natural manner to the mixed strategies
Chapter 10: Mixed strategies Nash equilibria reaction curves and the equality of payoffs theorem Nash equilibrium: The concept of Nash equilibrium can be extended in a natural manner to the mixed strategies
Revenue Management Under the Markov Chain Choice Model
 Revenue Management Under the Markov Chain Choice Model Jacob B. Feldman School of Operations Research and Information Engineering, Cornell University, Ithaca, New York 14853, USA jbf232@cornell.edu Huseyin
Revenue Management Under the Markov Chain Choice Model Jacob B. Feldman School of Operations Research and Information Engineering, Cornell University, Ithaca, New York 14853, USA jbf232@cornell.edu Huseyin
Game Theory Fall 2003
 Game Theory Fall 2003 Problem Set 5 [1] Consider an infinitely repeated game with a finite number of actions for each player and a common discount factor δ. Prove that if δ is close enough to zero then
Game Theory Fall 2003 Problem Set 5 [1] Consider an infinitely repeated game with a finite number of actions for each player and a common discount factor δ. Prove that if δ is close enough to zero then
Transport Costs and North-South Trade
 Transport Costs and North-South Trade Didier Laussel a and Raymond Riezman b a GREQAM, University of Aix-Marseille II b Department of Economics, University of Iowa Abstract We develop a simple two country
Transport Costs and North-South Trade Didier Laussel a and Raymond Riezman b a GREQAM, University of Aix-Marseille II b Department of Economics, University of Iowa Abstract We develop a simple two country
MODELING THE ELECTRICITY SPOT MARKETS
 .... MODELING THE ELECTRICITY SPOT MARKETS Özgür İnal Rice University 6.23.2009 Özgür İnal MODELING THE ELECTRICITY SPOT MARKETS 1/27 . Motivation Modeling the game the electricity generating firms play
.... MODELING THE ELECTRICITY SPOT MARKETS Özgür İnal Rice University 6.23.2009 Özgür İnal MODELING THE ELECTRICITY SPOT MARKETS 1/27 . Motivation Modeling the game the electricity generating firms play
1 Answers to the Sept 08 macro prelim - Long Questions
 Answers to the Sept 08 macro prelim - Long Questions. Suppose that a representative consumer receives an endowment of a non-storable consumption good. The endowment evolves exogenously according to ln
Answers to the Sept 08 macro prelim - Long Questions. Suppose that a representative consumer receives an endowment of a non-storable consumption good. The endowment evolves exogenously according to ln
Introducing money. Olivier Blanchard. April Spring Topic 6.
 Introducing money. Olivier Blanchard April 2002 14.452. Spring 2002. Topic 6. 14.452. Spring, 2002 2 No role for money in the models we have looked at. Implicitly, centralized markets, with an auctioneer:
Introducing money. Olivier Blanchard April 2002 14.452. Spring 2002. Topic 6. 14.452. Spring, 2002 2 No role for money in the models we have looked at. Implicitly, centralized markets, with an auctioneer:
Mixed Strategies. Samuel Alizon and Daniel Cownden February 4, 2009
 Mixed Strategies Samuel Alizon and Daniel Cownden February 4, 009 1 What are Mixed Strategies In the previous sections we have looked at games where players face uncertainty, and concluded that they choose
Mixed Strategies Samuel Alizon and Daniel Cownden February 4, 009 1 What are Mixed Strategies In the previous sections we have looked at games where players face uncertainty, and concluded that they choose
Answers to Microeconomics Prelim of August 24, In practice, firms often price their products by marking up a fixed percentage over (average)
 Answers to Microeconomics Prelim of August 24, 2016 1. In practice, firms often price their products by marking up a fixed percentage over (average) cost. To investigate the consequences of markup pricing,
Answers to Microeconomics Prelim of August 24, 2016 1. In practice, firms often price their products by marking up a fixed percentage over (average) cost. To investigate the consequences of markup pricing,
Elements of Economic Analysis II Lecture XI: Oligopoly: Cournot and Bertrand Competition
 Elements of Economic Analysis II Lecture XI: Oligopoly: Cournot and Bertrand Competition Kai Hao Yang /2/207 In this lecture, we will apply the concepts in game theory to study oligopoly. In short, unlike
Elements of Economic Analysis II Lecture XI: Oligopoly: Cournot and Bertrand Competition Kai Hao Yang /2/207 In this lecture, we will apply the concepts in game theory to study oligopoly. In short, unlike
Econ 8602, Fall 2017 Homework 2
 Econ 8602, Fall 2017 Homework 2 Due Tues Oct 3. Question 1 Consider the following model of entry. There are two firms. There are two entry scenarios in each period. With probability only one firm is able
Econ 8602, Fall 2017 Homework 2 Due Tues Oct 3. Question 1 Consider the following model of entry. There are two firms. There are two entry scenarios in each period. With probability only one firm is able
CS364A: Algorithmic Game Theory Lecture #3: Myerson s Lemma
 CS364A: Algorithmic Game Theory Lecture #3: Myerson s Lemma Tim Roughgarden September 3, 23 The Story So Far Last time, we introduced the Vickrey auction and proved that it enjoys three desirable and different
CS364A: Algorithmic Game Theory Lecture #3: Myerson s Lemma Tim Roughgarden September 3, 23 The Story So Far Last time, we introduced the Vickrey auction and proved that it enjoys three desirable and different
On Existence of Equilibria. Bayesian Allocation-Mechanisms
 On Existence of Equilibria in Bayesian Allocation Mechanisms Northwestern University April 23, 2014 Bayesian Allocation Mechanisms In allocation mechanisms, agents choose messages. The messages determine
On Existence of Equilibria in Bayesian Allocation Mechanisms Northwestern University April 23, 2014 Bayesian Allocation Mechanisms In allocation mechanisms, agents choose messages. The messages determine
Public Schemes for Efficiency in Oligopolistic Markets
 経済研究 ( 明治学院大学 ) 第 155 号 2018 年 Public Schemes for Efficiency in Oligopolistic Markets Jinryo TAKASAKI I Introduction Many governments have been attempting to make public sectors more efficient. Some socialistic
経済研究 ( 明治学院大学 ) 第 155 号 2018 年 Public Schemes for Efficiency in Oligopolistic Markets Jinryo TAKASAKI I Introduction Many governments have been attempting to make public sectors more efficient. Some socialistic
Antino Kim Kelley School of Business, Indiana University, Bloomington Bloomington, IN 47405, U.S.A.
 THE INVISIBLE HAND OF PIRACY: AN ECONOMIC ANALYSIS OF THE INFORMATION-GOODS SUPPLY CHAIN Antino Kim Kelley School of Business, Indiana University, Bloomington Bloomington, IN 47405, U.S.A. {antino@iu.edu}
THE INVISIBLE HAND OF PIRACY: AN ECONOMIC ANALYSIS OF THE INFORMATION-GOODS SUPPLY CHAIN Antino Kim Kelley School of Business, Indiana University, Bloomington Bloomington, IN 47405, U.S.A. {antino@iu.edu}
KIER DISCUSSION PAPER SERIES
 KIER DISCUSSION PAPER SERIES KYOTO INSTITUTE OF ECONOMIC RESEARCH http://www.kier.kyoto-u.ac.jp/index.html Discussion Paper No. 657 The Buy Price in Auctions with Discrete Type Distributions Yusuke Inami
KIER DISCUSSION PAPER SERIES KYOTO INSTITUTE OF ECONOMIC RESEARCH http://www.kier.kyoto-u.ac.jp/index.html Discussion Paper No. 657 The Buy Price in Auctions with Discrete Type Distributions Yusuke Inami
January 26,
 January 26, 2015 Exercise 9 7.c.1, 7.d.1, 7.d.2, 8.b.1, 8.b.2, 8.b.3, 8.b.4,8.b.5, 8.d.1, 8.d.2 Example 10 There are two divisions of a firm (1 and 2) that would benefit from a research project conducted
January 26, 2015 Exercise 9 7.c.1, 7.d.1, 7.d.2, 8.b.1, 8.b.2, 8.b.3, 8.b.4,8.b.5, 8.d.1, 8.d.2 Example 10 There are two divisions of a firm (1 and 2) that would benefit from a research project conducted
1 The Solow Growth Model
 1 The Solow Growth Model The Solow growth model is constructed around 3 building blocks: 1. The aggregate production function: = ( ()) which it is assumed to satisfy a series of technical conditions: (a)
1 The Solow Growth Model The Solow growth model is constructed around 3 building blocks: 1. The aggregate production function: = ( ()) which it is assumed to satisfy a series of technical conditions: (a)
PORTFOLIO OPTIMIZATION AND EXPECTED SHORTFALL MINIMIZATION FROM HISTORICAL DATA
 PORTFOLIO OPTIMIZATION AND EXPECTED SHORTFALL MINIMIZATION FROM HISTORICAL DATA We begin by describing the problem at hand which motivates our results. Suppose that we have n financial instruments at hand,
PORTFOLIO OPTIMIZATION AND EXPECTED SHORTFALL MINIMIZATION FROM HISTORICAL DATA We begin by describing the problem at hand which motivates our results. Suppose that we have n financial instruments at hand,
ISSN BWPEF Uninformative Equilibrium in Uniform Price Auctions. Arup Daripa Birkbeck, University of London.
 ISSN 1745-8587 Birkbeck Working Papers in Economics & Finance School of Economics, Mathematics and Statistics BWPEF 0701 Uninformative Equilibrium in Uniform Price Auctions Arup Daripa Birkbeck, University
ISSN 1745-8587 Birkbeck Working Papers in Economics & Finance School of Economics, Mathematics and Statistics BWPEF 0701 Uninformative Equilibrium in Uniform Price Auctions Arup Daripa Birkbeck, University
Microeconomic Theory August 2013 Applied Economics. Ph.D. PRELIMINARY EXAMINATION MICROECONOMIC THEORY. Applied Economics Graduate Program
 Ph.D. PRELIMINARY EXAMINATION MICROECONOMIC THEORY Applied Economics Graduate Program August 2013 The time limit for this exam is four hours. The exam has four sections. Each section includes two questions.
Ph.D. PRELIMINARY EXAMINATION MICROECONOMIC THEORY Applied Economics Graduate Program August 2013 The time limit for this exam is four hours. The exam has four sections. Each section includes two questions.
An Approximation Algorithm for Capacity Allocation over a Single Flight Leg with Fare-Locking
 An Approximation Algorithm for Capacity Allocation over a Single Flight Leg with Fare-Locking Mika Sumida School of Operations Research and Information Engineering, Cornell University, Ithaca, New York
An Approximation Algorithm for Capacity Allocation over a Single Flight Leg with Fare-Locking Mika Sumida School of Operations Research and Information Engineering, Cornell University, Ithaca, New York
Trade Agreements and the Nature of Price Determination
 Trade Agreements and the Nature of Price Determination By POL ANTRÀS AND ROBERT W. STAIGER The terms-of-trade theory of trade agreements holds that governments are attracted to trade agreements as a means
Trade Agreements and the Nature of Price Determination By POL ANTRÀS AND ROBERT W. STAIGER The terms-of-trade theory of trade agreements holds that governments are attracted to trade agreements as a means
Game Theory. Lecture Notes By Y. Narahari. Department of Computer Science and Automation Indian Institute of Science Bangalore, India October 2012
 Game Theory Lecture Notes By Y. Narahari Department of Computer Science and Automation Indian Institute of Science Bangalore, India October 22 COOPERATIVE GAME THEORY Correlated Strategies and Correlated
Game Theory Lecture Notes By Y. Narahari Department of Computer Science and Automation Indian Institute of Science Bangalore, India October 22 COOPERATIVE GAME THEORY Correlated Strategies and Correlated
Does Retailer Power Lead to Exclusion?
 Does Retailer Power Lead to Exclusion? Patrick Rey and Michael D. Whinston 1 Introduction In a recent paper, Marx and Shaffer (2007) study a model of vertical contracting between a manufacturer and two
Does Retailer Power Lead to Exclusion? Patrick Rey and Michael D. Whinston 1 Introduction In a recent paper, Marx and Shaffer (2007) study a model of vertical contracting between a manufacturer and two
ECON Micro Foundations
 ECON 302 - Micro Foundations Michael Bar September 13, 2016 Contents 1 Consumer s Choice 2 1.1 Preferences.................................... 2 1.2 Budget Constraint................................ 3
ECON 302 - Micro Foundations Michael Bar September 13, 2016 Contents 1 Consumer s Choice 2 1.1 Preferences.................................... 2 1.2 Budget Constraint................................ 3
Chapter 7 One-Dimensional Search Methods
 Chapter 7 One-Dimensional Search Methods An Introduction to Optimization Spring, 2014 1 Wei-Ta Chu Golden Section Search! Determine the minimizer of a function over a closed interval, say. The only assumption
Chapter 7 One-Dimensional Search Methods An Introduction to Optimization Spring, 2014 1 Wei-Ta Chu Golden Section Search! Determine the minimizer of a function over a closed interval, say. The only assumption
Econ 101A Final exam Mo 18 May, 2009.
 Econ 101A Final exam Mo 18 May, 2009. Do not turn the page until instructed to. Do not forget to write Problems 1 and 2 in the first Blue Book and Problems 3 and 4 in the second Blue Book. 1 Econ 101A
Econ 101A Final exam Mo 18 May, 2009. Do not turn the page until instructed to. Do not forget to write Problems 1 and 2 in the first Blue Book and Problems 3 and 4 in the second Blue Book. 1 Econ 101A
Martingale Pricing Theory in Discrete-Time and Discrete-Space Models
 IEOR E4707: Foundations of Financial Engineering c 206 by Martin Haugh Martingale Pricing Theory in Discrete-Time and Discrete-Space Models These notes develop the theory of martingale pricing in a discrete-time,
IEOR E4707: Foundations of Financial Engineering c 206 by Martin Haugh Martingale Pricing Theory in Discrete-Time and Discrete-Space Models These notes develop the theory of martingale pricing in a discrete-time,
An Ascending Double Auction
 An Ascending Double Auction Michael Peters and Sergei Severinov First Version: March 1 2003, This version: January 20 2006 Abstract We show why the failure of the affiliation assumption prevents the double
An Ascending Double Auction Michael Peters and Sergei Severinov First Version: March 1 2003, This version: January 20 2006 Abstract We show why the failure of the affiliation assumption prevents the double
Constrained Sequential Resource Allocation and Guessing Games
 4946 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 54, NO. 11, NOVEMBER 2008 Constrained Sequential Resource Allocation and Guessing Games Nicholas B. Chang and Mingyan Liu, Member, IEEE Abstract In this
4946 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 54, NO. 11, NOVEMBER 2008 Constrained Sequential Resource Allocation and Guessing Games Nicholas B. Chang and Mingyan Liu, Member, IEEE Abstract In this
Two-Dimensional Bayesian Persuasion
 Two-Dimensional Bayesian Persuasion Davit Khantadze September 30, 017 Abstract We are interested in optimal signals for the sender when the decision maker (receiver) has to make two separate decisions.
Two-Dimensional Bayesian Persuasion Davit Khantadze September 30, 017 Abstract We are interested in optimal signals for the sender when the decision maker (receiver) has to make two separate decisions.
Game Theory and Economics Prof. Dr. Debarshi Das Department of Humanities and Social Sciences Indian Institute of Technology, Guwahati.
 Game Theory and Economics Prof. Dr. Debarshi Das Department of Humanities and Social Sciences Indian Institute of Technology, Guwahati. Module No. # 06 Illustrations of Extensive Games and Nash Equilibrium
Game Theory and Economics Prof. Dr. Debarshi Das Department of Humanities and Social Sciences Indian Institute of Technology, Guwahati. Module No. # 06 Illustrations of Extensive Games and Nash Equilibrium
ECON 459 Game Theory. Lecture Notes Auctions. Luca Anderlini Spring 2017
 ECON 459 Game Theory Lecture Notes Auctions Luca Anderlini Spring 2017 These notes have been used and commented on before. If you can still spot any errors or have any suggestions for improvement, please
ECON 459 Game Theory Lecture Notes Auctions Luca Anderlini Spring 2017 These notes have been used and commented on before. If you can still spot any errors or have any suggestions for improvement, please
ECE 586BH: Problem Set 5: Problems and Solutions Multistage games, including repeated games, with observed moves
 University of Illinois Spring 01 ECE 586BH: Problem Set 5: Problems and Solutions Multistage games, including repeated games, with observed moves Due: Reading: Thursday, April 11 at beginning of class
University of Illinois Spring 01 ECE 586BH: Problem Set 5: Problems and Solutions Multistage games, including repeated games, with observed moves Due: Reading: Thursday, April 11 at beginning of class
Department of Economics The Ohio State University Final Exam Questions and Answers Econ 8712
 Prof. Peck Fall 016 Department of Economics The Ohio State University Final Exam Questions and Answers Econ 871 1. (35 points) The following economy has one consumer, two firms, and four goods. Goods 1
Prof. Peck Fall 016 Department of Economics The Ohio State University Final Exam Questions and Answers Econ 871 1. (35 points) The following economy has one consumer, two firms, and four goods. Goods 1
GAME THEORY. Department of Economics, MIT, Follow Muhamet s slides. We need the following result for future reference.
 14.126 GAME THEORY MIHAI MANEA Department of Economics, MIT, 1. Existence and Continuity of Nash Equilibria Follow Muhamet s slides. We need the following result for future reference. Theorem 1. Suppose
14.126 GAME THEORY MIHAI MANEA Department of Economics, MIT, 1. Existence and Continuity of Nash Equilibria Follow Muhamet s slides. We need the following result for future reference. Theorem 1. Suppose
THE PUBLIC data network provides a resource that could
 618 IEEE/ACM TRANSACTIONS ON NETWORKING, VOL. 9, NO. 5, OCTOBER 2001 Prioritized Resource Allocation for Stressed Networks Cory C. Beard, Member, IEEE, and Victor S. Frost, Fellow, IEEE Abstract Overloads
618 IEEE/ACM TRANSACTIONS ON NETWORKING, VOL. 9, NO. 5, OCTOBER 2001 Prioritized Resource Allocation for Stressed Networks Cory C. Beard, Member, IEEE, and Victor S. Frost, Fellow, IEEE Abstract Overloads
5. COMPETITIVE MARKETS
 5. COMPETITIVE MARKETS We studied how individual consumers and rms behave in Part I of the book. In Part II of the book, we studied how individual economic agents make decisions when there are strategic
5. COMPETITIVE MARKETS We studied how individual consumers and rms behave in Part I of the book. In Part II of the book, we studied how individual economic agents make decisions when there are strategic
EC487 Advanced Microeconomics, Part I: Lecture 9
 EC487 Advanced Microeconomics, Part I: Lecture 9 Leonardo Felli 32L.LG.04 24 November 2017 Bargaining Games: Recall Two players, i {A, B} are trying to share a surplus. The size of the surplus is normalized
EC487 Advanced Microeconomics, Part I: Lecture 9 Leonardo Felli 32L.LG.04 24 November 2017 Bargaining Games: Recall Two players, i {A, B} are trying to share a surplus. The size of the surplus is normalized
1 Consumption and saving under uncertainty
 1 Consumption and saving under uncertainty 1.1 Modelling uncertainty As in the deterministic case, we keep assuming that agents live for two periods. The novelty here is that their earnings in the second
1 Consumption and saving under uncertainty 1.1 Modelling uncertainty As in the deterministic case, we keep assuming that agents live for two periods. The novelty here is that their earnings in the second
October An Equilibrium of the First Price Sealed Bid Auction for an Arbitrary Distribution.
 October 13..18.4 An Equilibrium of the First Price Sealed Bid Auction for an Arbitrary Distribution. We now assume that the reservation values of the bidders are independently and identically distributed
October 13..18.4 An Equilibrium of the First Price Sealed Bid Auction for an Arbitrary Distribution. We now assume that the reservation values of the bidders are independently and identically distributed
Game Theory and Economics Prof. Dr. Debarshi Das Department of Humanities and Social Sciences Indian Institute of Technology, Guwahati
 Game Theory and Economics Prof. Dr. Debarshi Das Department of Humanities and Social Sciences Indian Institute of Technology, Guwahati Module No. # 03 Illustrations of Nash Equilibrium Lecture No. # 04
Game Theory and Economics Prof. Dr. Debarshi Das Department of Humanities and Social Sciences Indian Institute of Technology, Guwahati Module No. # 03 Illustrations of Nash Equilibrium Lecture No. # 04
13.1 Infinitely Repeated Cournot Oligopoly
 Chapter 13 Application: Implicit Cartels This chapter discusses many important subgame-perfect equilibrium strategies in optimal cartel, using the linear Cournot oligopoly as the stage game. For game theory
Chapter 13 Application: Implicit Cartels This chapter discusses many important subgame-perfect equilibrium strategies in optimal cartel, using the linear Cournot oligopoly as the stage game. For game theory
Comparing Allocations under Asymmetric Information: Coase Theorem Revisited
 Comparing Allocations under Asymmetric Information: Coase Theorem Revisited Shingo Ishiguro Graduate School of Economics, Osaka University 1-7 Machikaneyama, Toyonaka, Osaka 560-0043, Japan August 2002
Comparing Allocations under Asymmetric Information: Coase Theorem Revisited Shingo Ishiguro Graduate School of Economics, Osaka University 1-7 Machikaneyama, Toyonaka, Osaka 560-0043, Japan August 2002
10.1 Elimination of strictly dominated strategies
 Chapter 10 Elimination by Mixed Strategies The notions of dominance apply in particular to mixed extensions of finite strategic games. But we can also consider dominance of a pure strategy by a mixed strategy.
Chapter 10 Elimination by Mixed Strategies The notions of dominance apply in particular to mixed extensions of finite strategic games. But we can also consider dominance of a pure strategy by a mixed strategy.
MAT25 LECTURE 10 NOTES. = a b. > 0, there exists N N such that if n N, then a n a < ɛ
 MAT5 LECTURE 0 NOTES NATHANIEL GALLUP. Algebraic Limit Theorem Theorem : Algebraic Limit Theorem (Abbott Theorem.3.3) Let (a n ) and ( ) be sequences of real numbers such that lim n a n = a and lim n =
MAT5 LECTURE 0 NOTES NATHANIEL GALLUP. Algebraic Limit Theorem Theorem : Algebraic Limit Theorem (Abbott Theorem.3.3) Let (a n ) and ( ) be sequences of real numbers such that lim n a n = a and lim n =
Duopoly models Multistage games with observed actions Subgame perfect equilibrium Extensive form of a game Two-stage prisoner s dilemma
 Recap Last class (September 20, 2016) Duopoly models Multistage games with observed actions Subgame perfect equilibrium Extensive form of a game Two-stage prisoner s dilemma Today (October 13, 2016) Finitely
Recap Last class (September 20, 2016) Duopoly models Multistage games with observed actions Subgame perfect equilibrium Extensive form of a game Two-stage prisoner s dilemma Today (October 13, 2016) Finitely
Ph.D. Preliminary Examination MICROECONOMIC THEORY Applied Economics Graduate Program June 2017
 Ph.D. Preliminary Examination MICROECONOMIC THEORY Applied Economics Graduate Program June 2017 The time limit for this exam is four hours. The exam has four sections. Each section includes two questions.
Ph.D. Preliminary Examination MICROECONOMIC THEORY Applied Economics Graduate Program June 2017 The time limit for this exam is four hours. The exam has four sections. Each section includes two questions.
Class Notes on Chaney (2008)
 Class Notes on Chaney (2008) (With Krugman and Melitz along the Way) Econ 840-T.Holmes Model of Chaney AER (2008) As a first step, let s write down the elements of the Chaney model. asymmetric countries
Class Notes on Chaney (2008) (With Krugman and Melitz along the Way) Econ 840-T.Holmes Model of Chaney AER (2008) As a first step, let s write down the elements of the Chaney model. asymmetric countries
d. Find a competitive equilibrium for this economy. Is the allocation Pareto efficient? Are there any other competitive equilibrium allocations?
 Answers to Microeconomics Prelim of August 7, 0. Consider an individual faced with two job choices: she can either accept a position with a fixed annual salary of x > 0 which requires L x units of labor
Answers to Microeconomics Prelim of August 7, 0. Consider an individual faced with two job choices: she can either accept a position with a fixed annual salary of x > 0 which requires L x units of labor
6.896 Topics in Algorithmic Game Theory February 10, Lecture 3
 6.896 Topics in Algorithmic Game Theory February 0, 200 Lecture 3 Lecturer: Constantinos Daskalakis Scribe: Pablo Azar, Anthony Kim In the previous lecture we saw that there always exists a Nash equilibrium
6.896 Topics in Algorithmic Game Theory February 0, 200 Lecture 3 Lecturer: Constantinos Daskalakis Scribe: Pablo Azar, Anthony Kim In the previous lecture we saw that there always exists a Nash equilibrium
Partial privatization as a source of trade gains
 Partial privatization as a source of trade gains Kenji Fujiwara School of Economics, Kwansei Gakuin University April 12, 2008 Abstract A model of mixed oligopoly is constructed in which a Home public firm
Partial privatization as a source of trade gains Kenji Fujiwara School of Economics, Kwansei Gakuin University April 12, 2008 Abstract A model of mixed oligopoly is constructed in which a Home public firm
Analysis of a highly migratory fish stocks fishery: a game theoretic approach
 Analysis of a highly migratory fish stocks fishery: a game theoretic approach Toyokazu Naito and Stephen Polasky* Oregon State University Address: Department of Agricultural and Resource Economics Oregon
Analysis of a highly migratory fish stocks fishery: a game theoretic approach Toyokazu Naito and Stephen Polasky* Oregon State University Address: Department of Agricultural and Resource Economics Oregon
Pass-Through Pricing on Production Chains
 Pass-Through Pricing on Production Chains Maria-Augusta Miceli University of Rome Sapienza Claudia Nardone University of Rome Sapienza October 8, 06 Abstract We here want to analyze how the imperfect competition
Pass-Through Pricing on Production Chains Maria-Augusta Miceli University of Rome Sapienza Claudia Nardone University of Rome Sapienza October 8, 06 Abstract We here want to analyze how the imperfect competition
Department of Economics The Ohio State University Final Exam Answers Econ 8712
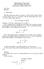 Department of Economics The Ohio State University Final Exam Answers Econ 8712 Prof. Peck Fall 2015 1. (5 points) The following economy has two consumers, two firms, and two goods. Good 2 is leisure/labor.
Department of Economics The Ohio State University Final Exam Answers Econ 8712 Prof. Peck Fall 2015 1. (5 points) The following economy has two consumers, two firms, and two goods. Good 2 is leisure/labor.
A Decentralized Learning Equilibrium
 Paper to be presented at the DRUID Society Conference 2014, CBS, Copenhagen, June 16-18 A Decentralized Learning Equilibrium Andreas Blume University of Arizona Economics ablume@email.arizona.edu April
Paper to be presented at the DRUID Society Conference 2014, CBS, Copenhagen, June 16-18 A Decentralized Learning Equilibrium Andreas Blume University of Arizona Economics ablume@email.arizona.edu April
Game Theory: Normal Form Games
 Game Theory: Normal Form Games Michael Levet June 23, 2016 1 Introduction Game Theory is a mathematical field that studies how rational agents make decisions in both competitive and cooperative situations.
Game Theory: Normal Form Games Michael Levet June 23, 2016 1 Introduction Game Theory is a mathematical field that studies how rational agents make decisions in both competitive and cooperative situations.
An optimal policy for joint dynamic price and lead-time quotation
 Lingnan University From the SelectedWorks of Prof. LIU Liming November, 2011 An optimal policy for joint dynamic price and lead-time quotation Jiejian FENG Liming LIU, Lingnan University, Hong Kong Xianming
Lingnan University From the SelectedWorks of Prof. LIU Liming November, 2011 An optimal policy for joint dynamic price and lead-time quotation Jiejian FENG Liming LIU, Lingnan University, Hong Kong Xianming
Extraction capacity and the optimal order of extraction. By: Stephen P. Holland
 Extraction capacity and the optimal order of extraction By: Stephen P. Holland Holland, Stephen P. (2003) Extraction Capacity and the Optimal Order of Extraction, Journal of Environmental Economics and
Extraction capacity and the optimal order of extraction By: Stephen P. Holland Holland, Stephen P. (2003) Extraction Capacity and the Optimal Order of Extraction, Journal of Environmental Economics and
The mean-variance portfolio choice framework and its generalizations
 The mean-variance portfolio choice framework and its generalizations Prof. Massimo Guidolin 20135 Theory of Finance, Part I (Sept. October) Fall 2014 Outline and objectives The backward, three-step solution
The mean-variance portfolio choice framework and its generalizations Prof. Massimo Guidolin 20135 Theory of Finance, Part I (Sept. October) Fall 2014 Outline and objectives The backward, three-step solution
Outline for today. Stat155 Game Theory Lecture 19: Price of anarchy. Cooperative games. Price of anarchy. Price of anarchy
 Outline for today Stat155 Game Theory Lecture 19:.. Peter Bartlett Recall: Linear and affine latencies Classes of latencies Pigou networks Transferable versus nontransferable utility November 1, 2016 1
Outline for today Stat155 Game Theory Lecture 19:.. Peter Bartlett Recall: Linear and affine latencies Classes of latencies Pigou networks Transferable versus nontransferable utility November 1, 2016 1
arxiv: v1 [math.oc] 16 Jun 2016
![arxiv: v1 [math.oc] 16 Jun 2016 arxiv: v1 [math.oc] 16 Jun 2016](/thumbs/83/87065371.jpg) Impact of storage competition on energy markets James Cruise, Lisa Flatley and Stan Zachary June 20, 2016 arxiv:1606.05361v1 [math.oc] 16 Jun 2016 Abstract We study how storage, operating as a price maker
Impact of storage competition on energy markets James Cruise, Lisa Flatley and Stan Zachary June 20, 2016 arxiv:1606.05361v1 [math.oc] 16 Jun 2016 Abstract We study how storage, operating as a price maker
MA300.2 Game Theory 2005, LSE
 MA300.2 Game Theory 2005, LSE Answers to Problem Set 2 [1] (a) This is standard (we have even done it in class). The one-shot Cournot outputs can be computed to be A/3, while the payoff to each firm can
MA300.2 Game Theory 2005, LSE Answers to Problem Set 2 [1] (a) This is standard (we have even done it in class). The one-shot Cournot outputs can be computed to be A/3, while the payoff to each firm can
Supplement to the lecture on the Diamond-Dybvig model
 ECON 4335 Economics of Banking, Fall 2016 Jacopo Bizzotto 1 Supplement to the lecture on the Diamond-Dybvig model The model in Diamond and Dybvig (1983) incorporates important features of the real world:
ECON 4335 Economics of Banking, Fall 2016 Jacopo Bizzotto 1 Supplement to the lecture on the Diamond-Dybvig model The model in Diamond and Dybvig (1983) incorporates important features of the real world:
Single-Parameter Mechanisms
 Algorithmic Game Theory, Summer 25 Single-Parameter Mechanisms Lecture 9 (6 pages) Instructor: Xiaohui Bei In the previous lecture, we learned basic concepts about mechanism design. The goal in this area
Algorithmic Game Theory, Summer 25 Single-Parameter Mechanisms Lecture 9 (6 pages) Instructor: Xiaohui Bei In the previous lecture, we learned basic concepts about mechanism design. The goal in this area
Essays on Some Combinatorial Optimization Problems with Interval Data
 Essays on Some Combinatorial Optimization Problems with Interval Data a thesis submitted to the department of industrial engineering and the institute of engineering and sciences of bilkent university
Essays on Some Combinatorial Optimization Problems with Interval Data a thesis submitted to the department of industrial engineering and the institute of engineering and sciences of bilkent university
Exercises Solutions: Oligopoly
 Exercises Solutions: Oligopoly Exercise - Quantity competition 1 Take firm 1 s perspective Total revenue is R(q 1 = (4 q 1 q q 1 and, hence, marginal revenue is MR 1 (q 1 = 4 q 1 q Marginal cost is MC
Exercises Solutions: Oligopoly Exercise - Quantity competition 1 Take firm 1 s perspective Total revenue is R(q 1 = (4 q 1 q q 1 and, hence, marginal revenue is MR 1 (q 1 = 4 q 1 q Marginal cost is MC
PAULI MURTO, ANDREY ZHUKOV
 GAME THEORY SOLUTION SET 1 WINTER 018 PAULI MURTO, ANDREY ZHUKOV Introduction For suggested solution to problem 4, last year s suggested solutions by Tsz-Ning Wong were used who I think used suggested
GAME THEORY SOLUTION SET 1 WINTER 018 PAULI MURTO, ANDREY ZHUKOV Introduction For suggested solution to problem 4, last year s suggested solutions by Tsz-Ning Wong were used who I think used suggested
Product Di erentiation: Exercises Part 1
 Product Di erentiation: Exercises Part Sotiris Georganas Royal Holloway University of London January 00 Problem Consider Hotelling s linear city with endogenous prices and exogenous and locations. Suppose,
Product Di erentiation: Exercises Part Sotiris Georganas Royal Holloway University of London January 00 Problem Consider Hotelling s linear city with endogenous prices and exogenous and locations. Suppose,
Price of Anarchy Smoothness Price of Stability. Price of Anarchy. Algorithmic Game Theory
 Smoothness Price of Stability Algorithmic Game Theory Smoothness Price of Stability Recall Recall for Nash equilibria: Strategic game Γ, social cost cost(s) for every state s of Γ Consider Σ PNE as the
Smoothness Price of Stability Algorithmic Game Theory Smoothness Price of Stability Recall Recall for Nash equilibria: Strategic game Γ, social cost cost(s) for every state s of Γ Consider Σ PNE as the
Chapter 1 Microeconomics of Consumer Theory
 Chapter Microeconomics of Consumer Theory The two broad categories of decision-makers in an economy are consumers and firms. Each individual in each of these groups makes its decisions in order to achieve
Chapter Microeconomics of Consumer Theory The two broad categories of decision-makers in an economy are consumers and firms. Each individual in each of these groups makes its decisions in order to achieve
Interest on Reserves, Interbank Lending, and Monetary Policy: Work in Progress
 Interest on Reserves, Interbank Lending, and Monetary Policy: Work in Progress Stephen D. Williamson Federal Reserve Bank of St. Louis May 14, 015 1 Introduction When a central bank operates under a floor
Interest on Reserves, Interbank Lending, and Monetary Policy: Work in Progress Stephen D. Williamson Federal Reserve Bank of St. Louis May 14, 015 1 Introduction When a central bank operates under a floor
Effective Cost Allocation for Deterrence of Terrorists
 Effective Cost Allocation for Deterrence of Terrorists Eugene Lee Quan Susan Martonosi, Advisor Francis Su, Reader May, 007 Department of Mathematics Copyright 007 Eugene Lee Quan. The author grants Harvey
Effective Cost Allocation for Deterrence of Terrorists Eugene Lee Quan Susan Martonosi, Advisor Francis Su, Reader May, 007 Department of Mathematics Copyright 007 Eugene Lee Quan. The author grants Harvey
Fundamental Theorems of Welfare Economics
 Fundamental Theorems of Welfare Economics Ram Singh October 4, 015 This Write-up is available at photocopy shop. Not for circulation. In this write-up we provide intuition behind the two fundamental theorems
Fundamental Theorems of Welfare Economics Ram Singh October 4, 015 This Write-up is available at photocopy shop. Not for circulation. In this write-up we provide intuition behind the two fundamental theorems
Regret Minimization and Security Strategies
 Chapter 5 Regret Minimization and Security Strategies Until now we implicitly adopted a view that a Nash equilibrium is a desirable outcome of a strategic game. In this chapter we consider two alternative
Chapter 5 Regret Minimization and Security Strategies Until now we implicitly adopted a view that a Nash equilibrium is a desirable outcome of a strategic game. In this chapter we consider two alternative
A folk theorem for one-shot Bertrand games
 Economics Letters 6 (999) 9 6 A folk theorem for one-shot Bertrand games Michael R. Baye *, John Morgan a, b a Indiana University, Kelley School of Business, 309 East Tenth St., Bloomington, IN 4740-70,
Economics Letters 6 (999) 9 6 A folk theorem for one-shot Bertrand games Michael R. Baye *, John Morgan a, b a Indiana University, Kelley School of Business, 309 East Tenth St., Bloomington, IN 4740-70,
ECON 301: General Equilibrium V (Public Goods) 1. Intermediate Microeconomics II, ECON 301. General Equilibrium V: Public Goods
 ECON 301: General Equilibrium V (Public Goods) 1 Intermediate Microeconomics II, ECON 301 General Equilibrium V: Public Goods In our last discussion on externality, we found that as long as property rights
ECON 301: General Equilibrium V (Public Goods) 1 Intermediate Microeconomics II, ECON 301 General Equilibrium V: Public Goods In our last discussion on externality, we found that as long as property rights
Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets
 Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets Nathaniel Hendren October, 2013 Abstract Both Akerlof (1970) and Rothschild and Stiglitz (1976) show that
Unraveling versus Unraveling: A Memo on Competitive Equilibriums and Trade in Insurance Markets Nathaniel Hendren October, 2013 Abstract Both Akerlof (1970) and Rothschild and Stiglitz (1976) show that
Endogenous choice of decision variables
 Endogenous choice of decision variables Attila Tasnádi MTA-BCE Lendület Strategic Interactions Research Group, Department of Mathematics, Corvinus University of Budapest June 4, 2012 Abstract In this paper
Endogenous choice of decision variables Attila Tasnádi MTA-BCE Lendület Strategic Interactions Research Group, Department of Mathematics, Corvinus University of Budapest June 4, 2012 Abstract In this paper
Zhen Sun, Milind Dawande, Ganesh Janakiraman, and Vijay Mookerjee
 RESEARCH ARTICLE THE MAKING OF A GOOD IMPRESSION: INFORMATION HIDING IN AD ECHANGES Zhen Sun, Milind Dawande, Ganesh Janakiraman, and Vijay Mookerjee Naveen Jindal School of Management, The University
RESEARCH ARTICLE THE MAKING OF A GOOD IMPRESSION: INFORMATION HIDING IN AD ECHANGES Zhen Sun, Milind Dawande, Ganesh Janakiraman, and Vijay Mookerjee Naveen Jindal School of Management, The University
Online Appendix for Debt Contracts with Partial Commitment by Natalia Kovrijnykh
 Online Appendix for Debt Contracts with Partial Commitment by Natalia Kovrijnykh Omitted Proofs LEMMA 5: Function ˆV is concave with slope between 1 and 0. PROOF: The fact that ˆV (w) is decreasing in
Online Appendix for Debt Contracts with Partial Commitment by Natalia Kovrijnykh Omitted Proofs LEMMA 5: Function ˆV is concave with slope between 1 and 0. PROOF: The fact that ˆV (w) is decreasing in
Optimal Mechanisms for Robust Coordination in Congestion Games
 Optimal Mechanisms for Robust Coordination in Congestion Games Philip N. Brown and Jason R. Marden Abstract Uninfluenced social systems often exhibit suboptimal performance; a common mitigation technique
Optimal Mechanisms for Robust Coordination in Congestion Games Philip N. Brown and Jason R. Marden Abstract Uninfluenced social systems often exhibit suboptimal performance; a common mitigation technique
Bargaining and Competition Revisited Takashi Kunimoto and Roberto Serrano
 Bargaining and Competition Revisited Takashi Kunimoto and Roberto Serrano Department of Economics Brown University Providence, RI 02912, U.S.A. Working Paper No. 2002-14 May 2002 www.econ.brown.edu/faculty/serrano/pdfs/wp2002-14.pdf
Bargaining and Competition Revisited Takashi Kunimoto and Roberto Serrano Department of Economics Brown University Providence, RI 02912, U.S.A. Working Paper No. 2002-14 May 2002 www.econ.brown.edu/faculty/serrano/pdfs/wp2002-14.pdf
February 23, An Application in Industrial Organization
 An Application in Industrial Organization February 23, 2015 One form of collusive behavior among firms is to restrict output in order to keep the price of the product high. This is a goal of the OPEC oil
An Application in Industrial Organization February 23, 2015 One form of collusive behavior among firms is to restrict output in order to keep the price of the product high. This is a goal of the OPEC oil
Game Theory Notes: Examples of Games with Dominant Strategy Equilibrium or Nash Equilibrium
 Game Theory Notes: Examples of Games with Dominant Strategy Equilibrium or Nash Equilibrium Below are two different games. The first game has a dominant strategy equilibrium. The second game has two Nash
Game Theory Notes: Examples of Games with Dominant Strategy Equilibrium or Nash Equilibrium Below are two different games. The first game has a dominant strategy equilibrium. The second game has two Nash
16 MAKING SIMPLE DECISIONS
 247 16 MAKING SIMPLE DECISIONS Let us associate each state S with a numeric utility U(S), which expresses the desirability of the state A nondeterministic action A will have possible outcome states Result
247 16 MAKING SIMPLE DECISIONS Let us associate each state S with a numeric utility U(S), which expresses the desirability of the state A nondeterministic action A will have possible outcome states Result
Maximum Contiguous Subsequences
 Chapter 8 Maximum Contiguous Subsequences In this chapter, we consider a well-know problem and apply the algorithm-design techniques that we have learned thus far to this problem. While applying these
Chapter 8 Maximum Contiguous Subsequences In this chapter, we consider a well-know problem and apply the algorithm-design techniques that we have learned thus far to this problem. While applying these
