Bidding for network size

Transcription

1 MPRA Munih Personal RePE Arhive Bidding for network size Renaud Fouart and Jana Friedrihsen Humboldt University, Berlin, BERA and BCCP, DIW, Berlin, Humboldt University, Berlin, BERA and BCCP 21 June 2016 Online at MPRA Paper No , posted 21 June :01 UTC

2 Bidding for Network Size * Renaud Fouart Jana Friedrihsen June 21, 2016 Abstrat We study a game were two firms ompete on investment in order to attrat onsumers. Below a ertain threshold, investment aims at attrating ex-ante indifferent users. Above this threshold firms also ompete for users loyal to the other firm. We find that, in equilibrium, firms do not hoose their investment deterministially but randomize over two disonneted intervals. These orrespond to ompeting for either the entire population or only the ex-ante indifferent users. While the benefits of attrating users are idential for both firms, the value of remaining passive and not investing at all depends on a firm s loyal base. The firm with the smallest base bids more aggressively to ompensate for its lower outside option and ahieves a monopoly position with higher probability than its ompetitor. Keywords: firms, quality ompetition, all-pay aution, status-quo bias JEL-Code: D43, D44, M13 *This paper originates from Chapter 3 of Jana s PhD thesis. We thank Pio Baake, Hans-Peter Grüner, Volker Noke, Luis Corhón, Dirk Engelmann, Paul Klemperer, Christian Mihel, Mikku Mustonen, Alexander Nesterov, Regis Renault, Jan-Peter Siedlarek, Philipp Zahn, and partiipants at EARIE 2013 (Evora), ECORE Summer Shool 2013 Governane and Eonomi Behavior (Leuven) and in seminars in Berlin, Helsinki, Mannheim and Oxford for helpful omments. All remaining errors are ours. Humboldt-Universität zu Berlin, renaud.fouart@hu-berlin.de DIW and Humboldt-Universität zu Berlin, jana.friedrihsen@hu-berlin.de 1

3 1 Introdution Two firms, equipped with an initial endowment, ompete for a prize of exogenous value by simultaneously providing a level of investment. If both investments are below a ertain threshold, the ompetition is of low intensity : the firm with the highest investment wins the prize, and eah firm keeps its endowment. If at least one firm invests above the threshold, the ompetition is of high intensity : the firm with the highest level of investment wins the prize, keeps its initial endowment, and takes the endowment of the ompetitor. This setup applies to a number of situations were investment an be either inremental or radial. This is the ase for instane in innovation raes, were small innovations help attrating undeided onsumers, and disruptive innovations allow attrating the whole population. In politis, two andidates running a primary ampaign an have low intensity debates, and be able to work with eah other afterwards, or high intensity ampaigns were the winner takes the ontrol of the whole party. 1 Similarly, advertisement an have as an objetive to onvine ex-ante indifferent onsumers, or turn into advertisement wars were most onsumers end up oordinating on one of the firms. 2 Through the paper, we stik to the example of firms ompeting for users, with the initial endowment being eah firm s base of loyal onsumers. The unique equilibrium is in mixed strategies. The intuition is similar to that of an all-pay aution: for every given level of investment of the winning firm, the ompetitor ould win instead by hoosing a marginally higher level. A ruial differene is that investments below the threshold an only win ex-ante indifferent users whereas investments above imply that the prie of winning is obtaining a monopoly position. When the threshold is very high, no firm ever tries to take the endowment of the other: the two firms randomize over the same interval in equilibrium, and make a profit equal to the value of their loyal base. When the threshold is exatly zero, the idea is similar: both firms always ompete at high intensity, randomize over the same interval, and make zero profit. Whenever the threshold is not too high but stritly positive, equilibrium bidding strategies are asymmetri. Firms hoose investments below and above the threshold and therefore expet to sometimes keep their loyal users even if they invest less than 1 In the ase of politial ontests, as noted by Moldovanu and Sela (2001), the runner-up often serves as seond soure and gets rewarded even if she did not win the ontest. 2 The idea that onsumers use the level of advertisement to oordinate on one firm has been developed by Farrell and Katz (1998), Pastine and Pastine (2002) and Bagwell (2007). 2

4 the ompetitor. Hene, even by not investing anything, a firm always keeps its share of loyal onsumers with positive probability, so that eah player makes a stritly positve expeted profit. The higher is the threshold, the higher is the probability mass that the firms put on investments below the threshold, and the probability of one firm obtaining a monopoly position dereases. The support of the equilibrium mixed strategy exhibits a gap just below the minimum investment neessary to attrat the loyal users of the ompetitor. This is beause hoosing an investment just above this threshold does not only inrease the probability of winning, but also the prize of winning, whih is then the whole population instead of only the ex-ante indifferent onsumers. Looking at two polar ases allows a better understanding of this model. (1) If there is no exogenous prize, the only thing a firm an win is the endowment of the opponent: eah firm either invests above the threshold to try and win the endowment of the other, or it does not invest in hope that the other firm does the same. We find that eah firm hooses not to invest with positive probability, and that the one that has more to gain, not more to lose, invests more aggressively. Both firms make positive profits in this ase. (2) If the exogenous prize is stritly positive and firms have no initial endowments, they randomize over a onneted interval. Whether overbidding happens above or below the threshold does not hange anything to the result beause no endowments are to be won by passing the threshold. In this ase, firms make zero profit and invest the same amount in expetation. The existene of an initial endowment of loyal onsumers introdues an antiompetitive element: holding fixed the behavior of the rival firm, a firm with a larger base of loyal onsumers enjoys a higher payoff from not investing at all than a firm with fewer loyal onsumers. Therefore, a firm that starts from a larger loyal base invests less on average, and establishes a monopoly less often than a firm with fewer loyal onsumers. At the same time, the expeted profit of a firm is (weakly) inreasing in the size of its loyal base. In ontrast, it is easy to show that a firm with lower osts would invest more aggressively. By onstrution, our setting is similar to an all pay aution (Baye et al., 1996), with endogenous prizes. Moldovanu and Sela (2001) study the optimal alloation of prizes in a setting of imperfet information where the highest bidder gets the first prize, and the seond bidder the seond prize. Siegel (2009) studies asymmetri players ompeting for a fixed number of prizes. Another approah to multiple prize all-pay aution is the Colonel Blotto game (Roberson, 2006), where onsumers bid separately for different 3

5 prizes. Our approah is different in the sense that the prizes themselves are endogenously determined by the level of investment. If investment is above a ertain threshold, there is only one prize to be won, but there are two prizes for smaller investments. 3 The endogeneity of the prizes in our setup omes from the well-known fat that onsumers sometimes are biased in favour of ertain options. Consumers may experiene swithing osts (Klemperer, 1987), or they may inspet ompeting firms in a ertain order while bearing a searh ost to observe an additional option (Arbatskaya, 2007, Armstrong et al., 2009). The fat that firms an either be nek-on-nek and ompete or provide an innovation that makes it a monopolist is also a well-known feature of innovation models (see for instane Aghion et al., 2005). We proeed as follows: we introdue the model in Setion 2 and provide the most important properties of the equilibrium strategies in the simultaneous investment game in Setion 3. We formally present the equilibrium in Setion 4. We disuss the impat of the different parameters on the equilibrium bidding strategies in Setion 5. We onlude in Setion 6. For those results that do not follow diretly from the text, formal proofs are olleted in the appendix. 2 Model setup There are two firms, A and B, whih ompete for users from a population of mass one. This population onsists of three types of users, a, b, and m. Types a and b our with frequeny α and β, respetively, in the population and the remaining part are of type m, = 1 α β. We assume that eah type of onsumer exists α, β, > 0. The struture of the game and frequenies of types are ommon knowledge. Eah firm i {A, B} has the goal to maximize its network size n i, orresponding to the share of its users in the population. To attrat users, eah firm hooses its investment K i 0. The unit ost of investment is for both firms. 4 The payoff of firm i is: (1) Π i (n i, K i ) = n i K i, for i {A, B} 3 Many of our results an be generalized to n-player games where there are n prizes for small investments and one prize for investments above the threshold. 4 Allowing for asymmetri osts ompliates the analysis but leaves our main finding intat. Having a ost advantage makes a firm more likely to monopolize the market but unless the ost differene is very large, both firms provide positive investment in equilibrium and the firm with fewer loyal ustomers dominates ex post more often. 4

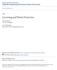
6 K A 1 n A = 1 n B = 0 γ n A = α + n B = β n A = 0 n B = 1 n A = α n B = β + γ 1 K B Figure 1: Network sizes for given investments Below a threshold γ, we assume firms ompete for the share of ex-ante indifferent users only. Above the threshold, the firm with the highest investment wins the entire population. The objetive of the paper is to desribe a general lass of games with similar payoff strutures, regardless of whether it omes from onsumer behaviour or other soures. However, we provide onsumers utility funtions that orrespond to this situation in Appendix B. For every level of investment, the orresponding network sizes are: (i) n i = 1 and n j = 0 if K i > K j and K i γ. (ii) n A = α + and n B = β if K B < K A < γ. (iii) n A = α and n B = β + if K A < K B < γ. We assume that onsumers split identially between the firms if K i = K j ; this onerns only onsumers of type m if K i = K j < γ, and it applies to all onsumers if K i = K j γ. For eah ombination of investments by firms A and B, Figure 1 states the network sizes in the equilibrium resulting in the user subgame. If both firms hoose investments within the square in the lower left of the figure, K A < γ, K B < γ, the investments are not high enough for loyal users to onsider the ompetitor. Thus, the resulting equilibrium features ompeting networks. The firm whih invests more obtains the larger network independent of the relative sizes of the loyal base. 5

7 If at least one of the two firms invests γ or more, the equilibrium is a monopoly. If firm B hooses an investment of γ or above, this is suffiient to ompensate loyal users of firm A for swithing to firm B if all others join firm B too (and vie versa). The ompetitor with the lower investment does not attrat any user in this ase. 3 Equilibrium properties We now derive some general properties of the equilibrium investments for firms A and B. The game faed by the two firms resembles an all-pay aution where the bids are the investment levels and the prize of winning is the share of users joining the firm. If the investment (i.e., the bid) exeeds the threshold γ, the network size of the winning firm and thereby the valuation of winning inreases disontinuously beause at this point the investment is just high enough to attrat loyal users from the ompetitor in addition to new users. Obviously, it is never a best response for either firm to provide an investment greater than 1, the utility from attrating all users normalized by the ost. If one firm hooses an investment above 1, the other firm would best respond by hoosing zero. For invest- ments up to 1, overbidding is in general profitable, though. Thus, if γ 1, both firms want to marginally overbid the investment of the ompetitor up to 1 and hoose a zero investment thereafter. Suppose instead γ < 1. If one firm hooses an investment of γ or above, the other firm an provide slightly more so as to attrat the entire population. If one firm provides an investment below γ, the other firm again prefers to slightly overbid the given investment to any investment below or equal to it. In this ase, loyal users do not swith. As an be expeted from the literature on omplete information all-pay autions, the game does not have a pure-strategy equilibrium. We haraterize the main properties of the equilibrium strategies in the following Lemma. Lemma 1. The following properties always hold in equilibrium: (i) There is no equilibrium in pure strategies. (ii) If one firm invests K with stritly positive probability, the other firm does not invest the exat same level with stritly positive probability. (iii) The support of both firms investment is either ontinuous with the same onneted support, or ontinuous over the same two disonneted supports, (0, δ) and (γ, K). 6

8 (iv) No firm bids a level of investment K {0, γ} with stritly positive probability. The formal proof is in Appendix A. The first property derives from the fat that marginally overbidding over a ertain investment of the ompetitor is always profitable. If firm A hooses a stritly positive investment with ertainty, firm B an marginally overbid and win with ertainty so that firm A would be better off by hoosing zero. If any firm bids zero with ertainty, the other an make a stritly positive profit by marginally overbidding, or bidding exatly γ. But then the other firm ould ensure a positive profit by marginally overbidding. The intuition behind the seond property is that, if one firm invests a ertain level K with stritly positive probability, the other firm has an inentive to marginally overbid. Hene, at least one firm must not have an atom at K. The third property is reminisent of the literature on prie dispersion, and in partiular Lemma 1 of Burdett and Judd (1983). For investments stritly below γ, there is no gap in the support of the mixed strategy, beause no one wants to invest at the lowest level of the upper disonneted interval, as it would give the same expeted gain as bidding as the upper level of the lower disonneted interval, for a lower ost. The same holds above γ. The differene with the existing literature omes from the disontinuity at the threshold γ. For investments losely below the threshold γ, a firm might do even better than marginally overbidding by hoosing a disretely higher investment and apturing the entire population than by outbidding the ompetitor at the margin and winning only the indifferent users. Speifially, firm A is better off attrating everyone by investing γ than by slightly overbidding firm B s investment K if K < γ and (2) lim F B(γ ε) γ > F B (K)(α + ) K K > γ lim ε 0 F B (γ ε) F B (K)(α + ). ε 0 An analogous inequality holds for firm B. It implies that if firms bid both below and above γ, they will not hoose investments just below γ. Instead, they will randomize over two disonneted intervals (0, δ) and (γ, K) where δ is determined endogenously. The fourth property desribes the only ases in whih a firm may benefit from hoosing an investment level with stritly positive probability. If, in equilibrium, a firm bids K with stritly positive probability, K must be at the lower bound of the support of the mixed strategy, as the opponent always stritly prefers to bid marginally above than marginally below K. By the third property, one possibility is K = 0, as no firm is al- 7

9 lowed to bid a stritly negative amount. The seond is K = γ, as bidding marginally less than γ implies loosing a disrete amount whenever the opponent bids above γ with stritly positive probability. Given the above properties, it is possible to show that the existene of the initial endowment is antiompetitive. In partiular, both players always make a stritly positive profit. Lemma 2. Both firms make a stritly positive expeted profit in equilibrium. Proof. For γ 1, it is obvious that firms hoose investments below γ with positive probability and this implies positive profits to the ompetitor, as by Lemma 1 K = 0 is always part of the support of the equilibrium mixed strategy. Assume that γ < 1. The proof is by ontradition. Suppose that the expeted profit is zero in equilibrium. For both firms for every investment equal to or above γ F (K) K = 0 F (K) = K and both firms invest up to the maximum investment K = 1. This implies that F (γ) = γ. Suppose one firm hooses investments below γ with positive probability, P i (K i < γ) > 0. Then, for the other firm j i, the expeted payoff from hoosing an investment of zero is stritly positive. Suppose both firms hoose an investment γ with probability γ. Then, the expeted payoff from investing γ is 1 γ γ < 0, and it is a profitable 2 deviation for a firm to play K = 0. Lemma 2 establishes that a firm has a positive reservation utility, i.e., utility from not providing any investment at all. This is linked to the fat that in equilibrium the ompetitor hooses an investment below γ with positive probability. The reservation utility is equal to the utility from the size of the loyal base multiplied by the probability that the ompetitor hooses an investment below γ, i.e., it is Prob(K B < γ)α for firm A and Prob(K A < γ)β for firm B. This implies that firms do not hoose investments up to the level at whih they just break even. Instead at the maximum investment, the expeted profit onditional on this investment is equal to the reservation utility in form of the expeted profit from not investing at all as introdued above. Before we go on to haraterize the equilibrium, we prove that the equilibrium investment behavior of eah firm must ontain an atom at some level of investment if the firms enjoy unequal market positions to start with. This finding is losely linked to 8

10 the previous observation that both firms make positive expeted profits in equilibrium. The firms are symmetri when they invest beause they fae idential ost funtions but they differ with respet to their share of loyal users. Therefore, their bidding behavior for investments below the threshold must differ and these differenes imply ertain mass points. Lemma 3. For any γ < 1, there does not exist an equilibrium without any mass point. Proof. Let us assume without loss of generality that firm A has a larger loyal base than firm B, α > β. Denote the expeted profits by E[Π A ] and E[Π B ] and the share of loyal users of firm i by f i. Suppose the equilibrium is haraterized by distribution funtions F A ( ) and F B ( ) that do not exhibit any mass points. For both firms for every investment equal to or above γ F j (K) K = E[Π i ] F j (K) = E[Π i ] + K. Both firms must hoose the same maximum level of investment K, and therefore they make the same expeted profit E[Π i ] = E[Π]. Moreover, the distribution funtions annot exhibit an atom at this maximum level or at any investment level K (γ, K). For investments below γ F j (K) K + Prob(K j < γ)f i = E[Π] F j (K) = E[Π] + K Prob(K j < γ)f i. Both firms distribution funtions must have the same support and inlude an investment of zero. Thus, Prob(K B < γ)α = E[Π] = Prob(K A < γ)β. Then α > β implies Prob(K B < γ) < Prob(K A < γ). Observe that the densities of both firms investment behavior must oinide for investments below and above γ. For both distribution funtions to integrate to one, this implies that firm A s investment behavior has an atom at zero and firm B s has one at γ. 4 Results We now haraterize the equilibrium of the game for different levels of γ. Let us assume without loss of generality that firm A has a larger loyal base than firm B, α > β. If the threshold is very low, ompetition is intense and one firms establishes a monopoly position with high probability even though market sharing remains a possible outome 9

11 too by Lemma 2. For intermediate levels of the threshold γ, in equilibrium firm A only engages in ompetition below the threshold so that most of the probability mass is distributed on investments below. The smaller firm B, however, gambles for a monopoly position by hoosing investments of γ with positive probability. If the threshold is very high, it is prohibitively ostly to attrat loyal users. Thus, both firms only hoose investments below γ and ompete for ex ante indifferent users. We onsider these three ases in more detail separately. Consider first the ase, where the threshold is low, γ < 1 1 α β+α 2. Then, it is relatively easy to attrat users loyal to the ompetitor, and both firms are in priniple 1 β willing to hoose investments high enough to do so. However, by Lemma 2 both firms must make positive profits in equilibrium and therefore alloate positive probability to investments below γ. We show that in equilibrium both firms randomize over investments in a range not high enough to attrat users loyal to the opposing firm and a range where all users inluding the loyal ones join the firm with the highest investment. In this equilibrium, firm A hooses zero with positive probability beause its larger share of loyal users makes it ompete less aggressively. Proposition 1. If γ < 1 and (γ, 1 γ α 1 β 1 α β+α 2 in equilibrium, both firms randomize uniformly over (0, δ] 1 β < γ, and the distribution funtions are given by ) where δ = γ (1 α)(1 α β) 1 α β+α 2 F A (K) = F B (K) = K + 1 α β (1 β)γ 1 α β+α 2 (α β)γ (1 α β+α 2 ) if K [0, δ] if δ < K γ K + (1 α)αγ if γ < K K 1 α β+α 2 1 if K > K K if K (0, δ] 1 α β if δ < K < γ (1 α)γ 1 α β+α 2 K + (1 α)αγ if γ K K 1 α β+α 2 1 if K > K Firm B hooses γ with positive probability. Firm A hooses 0 with positive probability. Both firms make an expeted profit of F B (δ)α>0. Firm B invests more in expetation and beomes a market leader with higher probability than firm A. The formal proof is in Appendix A. We represent the equilibrium strategies in Figure 2. For low values of the threshold γ, firms have an inentives to sometimes bid aggres- 10

12 sively and win the endowment of the opponent. We know from the previous setion however that ompetition is never perfet, as both firms always make a stritly positive profit in equilibrium. Both firms strategies are symmetri, exept for the level of investments they play with stritly positive probability. For eah stritly positive investment between 0 and δ, it must hold that (3) f A (K) = f B (K) =, where = 1 α β. This is, by overbidding at a marginal ost, a firm inreases its probability of winning a share of the onsumers by, so that the marginal benefit of overbidding is also equal to and the firm is indifferent between all levels of investment in the support. For eah level of investment between γ and the maximum of the support K, it must hold that (4) f A (K) = f B (K) =. This is beause, above γ, the prize to be won is the whole population, and the marginal benefit of overbidding must equal the ost. Therefore, the slopes of the umulative density funtions F are steeper below γ as illustrated in Figure 2. From Lemma 1 we know that both firms bid over the same intervals and no firm has an atom at the maximum bid K. Then the expeted profit of both firms bidding the maximum K must be idential. For this to be the ase, as α > β, it must hold that firm A invests below γ with higher probability. The only possibility for this is that it invests exatly zero with stritly positive probability, while firm B invests exatly γ with stritly positive probability. Therefore F A is above F B for investments below γ, and both umulative densities oinide for investments above γ. A onsequene of these equilibrium strategies is that firm B, having the smallest endowment, invests more aggressively and wins more often in expetation. This is not simply a uriosity deriving from the mixed strategy equilibrium but the same intuition holds for probabilisti investments that lead to a pure strategy equilibrium (see Appendix C for details). Neither firm an gain by deviating from their equilibrium strategies, and the mixed strategy we haraterize is the unique equilibrium of the game. For the parameter values orresponding to Proposition 1, both firms make the same expeted profit, even if firm A starts with an advantage in terms of loyal base. To understand the logi, it is helpful to onsider the problem of firm A: to maximize its profit, 11

13 F (K) 1 F A (δ) F B (δ) γ α(1 β) 1 α β+α 2 F B (δ)α F A (δ)β 1 α β δ γ K max K 1 α β+α 2. 1 β Figure 2: Cumulative distribution funtions if α < γ < 1 K max = 1 γ 1 α. Dashed: firm A, Gray solid: firm B. 1 α β+α 2 it must be the ase that there is no obvious overbidding strategy for firm B. Hene, firm A wants to make firm B indifferent among all options in the support. In order to do so, firm B must believe that there is a suffiiently high probability P that firm A will bid below γ. Similarly, firm B wants firm A to be indifferent among all options in the support. For firm A to be indifferent between investments above and below γ, it must believe that firm B invests below γ with a suffiiently high probability P. However, as α > β, it must hold that P < P, the mixed strategy of firm A must be less aggressive in order to make firm B indifferent. In other words, firm A is trapped by the small loyal base of firm B: as firm A wants firm B to invest with some probability below γ (to benefit from the loyal base α), it must ompensate firm B by not investing too aggressively. This is not a ommitment problem: at equilibrium, by definition, both firm A and firm B are indifferent among the options in the support. Moreover, even if one of the two firms ould ommit ex-ante to a mixed strategy (using a randomization devie), the one that would maximize eah firm s expeted surplus is the equilibrium one. Consider now a variant of the previous equilibrium, where the threshold is suffiiently large for firm A not to find it worthwhile to attrat B s loyal users but B sill wants to attrat A s loyal users. This asymmetry arises beause firm A is more ontent with its larger base of loyal users, and B is more aggressive to ompensate for its initially inferior market position. 12

14 Proposition 2. If 1 1 α β+α 2 1 β δ = γ α < γ < 1 β, both firms randomize uniformly over (0, δ), where, and the distribution funtions are given by F A (K) = F B (K) = K + 1 β γ if K [0, δ] 1 if K δ K if K (0, δ] K if δ K γ 1 if K γ Firm B invests more in expetation than firm A and beomes a market leader more often. The expeted profit of firm B is 1 γ and the expeted profit of firm A is α > 1 γ. The formal proof is in Appendix A. This result is a variant of Proposition 1, where it is too ostly for firm A to attrat the loyal users of type B. Below γ, it is still the ase that both density funtions satisfy (5) f A (K) = f B (K) =. However, above γ, only firm B invests. As there is no interest to bid stritly above γ if no other firm does so, firm B puts a probability mass at γ, while firm A puts a stritly positive probability mass at 0. In this ase, the expeted profits are not idential. Firm A benefits from its larger base, invests less and makes a higher expeted profit. The asymmetry here is therefore twofold: one firm is more aggressive and wins more often, but the other firm is the one that atually makes the highest profit in expetation. Consider finally the onstellation where both firms keep their investments below the threshold γ. Then, neither firm questions the existene of the ompetitor but ompetition onerns only the share of ex ante indifferent users and determines who will have a dominant market position in the end. Even though the two firms have different shares of loyal users, they behave identially and both firms dominate the market with equal probability. Proposition 3. If γ > 1 β both firms randomize ontinuously over the interval [0, ]. The density is f(k) = for all [0, ]. The expeted profit of firm B is β and the expeted profit of firm A is α > β. 13

15 Proof. We prove that in equilibrium neither firm hooses investments at γ or above so that lim ε 0 F (γ ε) = 1 and both firms keep their loyal users for sure. 5 Neither firm hooses an investment that is high enough to attrat users loyal to the opposing firm. The outside option for both firms is to keep only their own loyal users and get a payoff equal to its share of biased users α respetively β. The valuation of winning is then the value of getting the new users in addition, i.e.,, so that in equilibrium, both players randomize ontinuously on [0, ] aording to the following umulative distribution funtion F (K) = K for all K [0, ] 1 for K It is straightforward that eah firm is indifferent between all investments in [0, ]. None of the two firms hooses zero with positive probability by the same argument as in Proposition 1. The expeted payoff to firm A and B is equal to α and β, respetively. By deviating to an investment at γ, suffiient to apture the entire population, a firm would make an expeted profit of F ( ) γ = 1 γ < 1 (1 β) = β < α suh that this deviation is not profitable. The expeted investment in equilibrium equals E[K i ] = 0 xdx = 1 for i = A, B 2 per firm. In total, the two firms invest. Sine equilibrium mixed strategies and investments are idential, both firms have the same probability of winning whih equals 1. By the properties of the mixed strategy equilibrium, the expeted profit of eah firm 2 equals its expeted profit onditional on investing zero whih is its endowment of loyal users. 5 Disussion Given the properties of the equilibrium (see Setion 3), it is easy to see that for eah value of the threshold γ the equilibrium desribed in Setion 4 is unique. This means that, for all values of the threshold γ, the equilibrium is a mixed strategy were the firm 5 For γ > 1 ompetition for the entire population is not profitable even if the suess probability was one. For 1 β < γ < 1 ompeting for everyone is profitable if the suess probability is high enough. However, in equilibrium, this is not the ase. Thus, we analyze the two ases jointly. 14

16 with the smallest endowment bids the most aggressively, wins more often and makes (weakly) lower profit. Corollary 1. In expetation, the firm B with the smallest loyal base establishes a monopoly position more often than firm A. The formal proof is in Appendix A. It derives from omputing the respetive probabilities of winning for both firms in eah equilibrium. It is important to note that the nature of this equilibrium is not similar to the mixed strategy one would find alongside two pure strategies if the game were depited as a two-by-two matrix. In the latter ase, following any small perturbation of one players strategy, best responses lead to one of the pure strategy equilibria. In our paper, onsider a level of investment K < γ that both players bid with density f(k ) = at equilibrium. If player A hooses to put slightly more density at K, say f(k ) = φ >, player B would like to put more weight on the investment level marginally above K, as the marginal investment above K yields expeted benefit φ stritly higher than the expeted ost. This in turn would stritly derease the expeted profit of firm A, who would be stritly better off by going bak to the equilibrium strategy. In the present setion, we disuss two important fators that influene the equilibrium bidding strategies: the role of loyal onsumers and of the threshold γ. 5.1 The role of loyal onsumers To better understand the mehanism behind the model, let us now onentrate on two polar ases, 1 and 0. When the shares of onsumers loyal to either firm go to zero, α 0, β 0, the population finally onsists only of new users, 1, and investments are hosen to only ompete for these ex-ante indifferent onsumers. Thus, there is no partiular interest in bidding exatly γ and the endogenously determined δ onverges to γ. There is no gap in the support of the equilibrium distributions of firms investments, and both firms make zero profit in expetation. This means that, without a loyal base, our game is nothing else than a lassi all-pay aution. When the sum of the shares of onsumers loyal to either firm goes to one, firms ompete for the endowment of their opponent only beause 0, and there are no exante indifferent onsumers. This an be interpreted as a rae for innovation: If no firm innovates, eah firm keeps her loyal onsumers. One one of the two firms manages to provide a suessful innovation, all onsumers oordinate on the best one (the highest 15

17 level of investment). This means that all stritly positive investments that lie below γ are wasted beause these are failed innovation attempts. Using our results from the previous setion, we an see that only two equilibria exists depending on the size of the innovation threshold relative to the ost of innovating. The onditions for Proposition 2 are never satisfied if = 0. In the equilibrium with a low threshold, γ < α, the support below γ ollapses as δ goes to zero. Both firm invest zero with positive probability, but firm A does so more often. Firm B invests γ with stritly positive probability and both firms randomize over (γ, 1 γ). If the threshold is instead high, γ > α, both firms stop investing and keep their share of loyal onsumers beause investments above γ are too expensive and there is nothing to win for investments below γ. Hene, when all onsumers are loyal, ompetition is less intense, and both firms remain idle with stritly positive probability. We immediately see that a first positive effet of inreasing on expeted investment is that it inreases the upper bound of the lower bidding strategy δ, while keeping onstant the mass distributed on investments in the interval [0, δ] (exept for K = 0). This does not mean however that a higher share of ex-ante indifferent onsumers always inreases expeted investment at the margin. Figure 3 illustrates the influene of on the different elements of equilibrium bidding strategies, for parameter values orresponding to Proposition 1. The aggregate effet is shown in the panel on the lefthand side of the Figure. We observe that the expeted bid of the firm with the smallest initial endowment B initially dereases with, and only omes bak to its initial level when the share of ex-ante indifferent onsumers goes to 1. The impat is muh more positive for the firm with the highest initial endowment A. To understand the logi, we show the influene of the share of ex-ante indifferent users on the bidding strategies in the panel on the right-hand side of Figure 3. We see that δ onverges to γ as the share of ex-ante indifferent users goes to 1, as bidding above or below γ beomes irrelevant. The two other effets are however ambiguous. First, the maximum bid K initially dereases with, beause the presene of more ex-ante indifferent onsumers limits the interest of bidding above γ. Seond, the probability of bidding exatly γ (for firm B) dereases with, making this firm bid less aggressively. As P (K B = γ) = P (K A = 0), this implies that the effet goes in the other diretion for the firm with the highest share of loyal onsumers A. 16

18 E(K B ), E(K A ) δ, P (K B = γ), K 9 K 5 E(K B ) γ = 5 P (K B = γ) δ 1 E(K A ) Figure 3: Impat of the share of ex-ante indifferent onsumers, with = 0.1, γ = 5 and α = 3β. Left panel: equilibrium investment. Right panel: bidding strategies. 5.2 The impat of the threshold level on expeted investment. As in the previous subsetion, it is instrutive to onsider two polar ases. For a threshold exatly equal to zero, all ompetition is for the entire population, and firms bid aggressively, in a setup idential to the lassi all-pay aution. For γ very high, we are in the ase of Proposition 3; both firms bid in the way well known from the lassi all-pay aution with the twist that the prie equals only. Sine both firms have shares of loyal onsumers, bidding is less aggressive and both firms obtain stritly positive expeted profits. For intermediate values of γ, we illustrate the effet of γ on expeted investments in Figure 4. The vertial dotted lines represent the values of γ that delimit the zones orresponding to Propositions 1 to 3 of the paper. When the investment threshold γ is small but stritly positive (part (i) of the graph, orresponding to Proposition 1) both firms ompete for loyal users of their ompetitors. If firms were to ompete for these loyal users with ertainty, both would be willing to invest up to K = 1 to win the ompetition. The range of investments for whih the density is zero is [δ, γ]. Lowering the threshold, inreases ompetition: the higher is the threshold γ, the less probability mass 17

19 both firms assign to investments above γ. As long as γ < 1 β, the highest investment below γ whih is still inluded in the mixed strategy, δ, is lower than the maximum investment whih would be hosen if the two firms agreed to ompete only for new users. The probability mass on higher investment levels overompensates this so that in total investments are higher when firms ompete for the entire population. This explains why both E(K A ) and E(K B ) derease with γ, and why the gap between the two inreases, as A beomes proportionally more often idle when the threshold γ inreases. In the intermediate part (ii) of Figure 4 orresponding to Proposition 2, the impat of γ on expeted investments is ambiguous. For these intermediate values, the firm with the highest initial endowment A starts to invest muh more aggressively. This is beause for these values, and as opposed to Proposition 1, the probability mass P (K A ) = 0 = P (K = B) = γ dereases with the threshold γ, whih implies that the firms beome more and more symmetri in their bidding strategies, and less and less symmetri in their expeted profits. When γ reahes the level at whih firms deide to only ompete for ex-ante indifferent users, the expeted investments in both types of equilibrium are the same and the expeted level of investment is ontinuous in γ. As γ inreases furhte,r the investments remain onstant beause firms ompete only for new users and therefore bidding behavior is independent of γ. This orresponds to the part (iii) of the Figure, and to Proposition 3. 6 Conlusion When two firms ompete in investment to obtain a disrete prize, it is well known that the outome is a mixed strategy where eah firm wins with a ertain probability. In the presene of a loyal base of onsumer and of an investment threshold, we find that if there are differenes in the probabilities of one or the other firm dominating, the one that has the lowest loyal base has the higher hane of being suessful. This firm ompetes more aggressively beause its outside option of remaining a nihe in a shared market is less attrative than it is for the ompetitor. If only large investments are suessful innovations in the sense that they an attrat onsumers loyal to the ompetitor, firms trade off small investments with low returns with high investments that promise a high return but they do not hoose intermediate level of investment. We find that the pres- 18

20 E(K A ), E(K B ) 5 γ = 1 1 α β+α 2 1 β γ = 1 β 4 E(K B ) E(K A ) 1 2 (i) (ii) 8 9 (iii) γ Figure 4: Expeted equilibrium investment, with α = 0.4, β = 0.1 and = 0.1. ene of loyal users in the market introdues an antiompetitive element that allows both firms to make positive profits in expetation. Referenes AGHION, P., BLOOM, N., BLUNDELL, R., GRIFFITH, R. and HOWITT, P. (2005). Competition and innovation: an inverted-u relationship*. The Quarterly Journal of Eonomis, 120 (2), ARBATSKAYA, M. (2007). Ordered searh. The RAND Journal of Eonomis, 38 (1), ARMSTRONG, M., VICKERS, J. and ZHOU, J. (2009). Prominene and onsumer searh. The RAND Journal of Eonomis, 40 (2), BAGWELL, K. (2007). The eonomi analysis of advertising. Handbook of Industrial Organization, 3, BAYE, M. R., KOVENOCK, D. and DE VRIES, C. G. (1996). The all-pay aution with omplete information. Eonomi Theory, 8 (2),

21 BURDETT, K. and JUDD, K. L. (1983). Equilibrium prie dispersion. Eonometria: Journal of the Eonometri Soiety, pp FARRELL, J. and KATZ, M. L. (1998). The effets of antitrust and intelletual property law on ompatibility and innovation. Antitrust Bulletin, 43, 609. JIA, H. (2008). A stohasti derivation of the ratio form of ontest suess funtions. Publi Choie, 135 (3-4), KLEMPERER, P. (1987). Markets with onsumer swithing osts. The quarterly journal of eonomis, pp MOLDOVANU, B. and SELA, A. (2001). The optimal alloation of prizes in ontests. Amerian Eonomi Review, pp PASTINE, I. and PASTINE, T. (2002). Consumption externalities, oordination, and advertising. International Eonomi Review, 43 (3), ROBERSON, B. (2006). The olonel blotto game. Eonomi Theory, 29 (1), SIEGEL, R. (2009). All-pay ontests. Eonometria, 77 (1),

22 Appendix A Proofs A.1 Proof of Lemma 1 Proof. (i) Suppose firm A hooses any investment K > 0 with ertainty. Then, firm B an invest at any K B = K + ε and win with ertainty so that firm A would be better off by hoosing zero. Suppose firm A invests zero with probability 1. Then, firm B makes a profit arbitrarily lose to max{1 α, 1 γ} by either marginally overbidding A s investment of zero or investing γ to win the entire population. But then firm A ould ensure a positive profit by in turn marginally overbidding B s investment so that this annot be an equilibrium either. Thus, the equilibrium must be in mixed strategies. (ii) Suppose firm A bids K A = K with stritly positive probability, P A (K ) > 0. Hene, by marginally overbidding K B = K + ɛ, firm B gets a stritly higher profit of at least P A (K ) ɛ. Hene, two firms never have an atom at the same level of investment beause both would have a strit gain by marginally overbidding the other. (iii) Suppose there is a gap in the support of firm i s strategy between some K and K (0, γ), where F i (K ) = F i (K ) and K < K. Firm j always stritly prefers to invest K than K, as the expeted benefit is the same and the expeted ost is stritly lower. This implies that firm j also stritly prefers K, whih violates the ondition that a firms has the same expeted profit over the support of her mixed strategy. The same reasoning applies to any K and K > γ. It does not hold however if K < γ and K γ. This is why, if there is a gap in the support of the equilibrium strategy, it must be between a K < γ and K γ. Define K i as the lower bound of the support of firm i s investment strategy below γ. If K j = K i is in the support of firm j, then by (ii), at least one of the firms is stritly better off by bidding exatly 0, as the expeted probability of having the lower bid would be idential. This implies that the ontinuous support must start at zero. Similarly, define K i as the lower bound of the support of firm i s investment strategy above γ. If K j = K i is in the support of firm j, then by (ii), at least one of the firms is 21

23 stritly better off by bidding exatly γ, as the expeted probability of having the lower bid would be idential. The supports of both firms strategies are idential, beause no firm wants to bid stritly above the upper bound of the other firm s support, no firm an bid below zero, and no firm has an inentive to bid just below γ. (iv) Suppose firm A bids K A = K {0, γ} with stritly positive probability, P A (K ) > 0. At equilibrium, this bid must also be in the support of firm B, unless it is exatly equal to γ. Else, firm A ould bid a lower amount and keep the same expeted gain for a lower ost. If the investment is in the support of firm B, firm B stritly prefers to bid K B = K + ɛ than K B = K ɛ, as the benefit disretely inreases just above K. If K = 0, this is possible, as firm B annot bid a stritly negative amount. Else, this is only possible if the support of the equilibrium investment of firm B displays a gap below K. By (iii), this is only possible at K = γ. A.2 Proof of Proposition 1 Proof. For every investment of firm B below γ whih is ontained in the support of the equilibrium strategy, the following ondition has to hold: (6) F B (K) + lim ε 0 F B (γ ε)α K = lim ε 0 F B (γ ε)α F B (K) = K and for every investment equal to or above γ (7) F B (K) K = lim ε 0 F B (γ ε)α F B (K) = K + lim ε 0 F B (γ ε)α If firm A hooses zero with positive probability, firm B s mixed strategy must not ontain an atom at zero. However, firm B must also be indifferent between all investment levels in the support of its equilibrium mixed strategy. Denote B s expeted profit by E[Π B ]. Then, for all K < γ (8) F A (K) + lim ε 0 F A (γ ε)β K = E[Π B ] F A (K) = K + E[Π B] lim ε 0 F A (γ ε)β 22

24 For every investment at γ or above having a lower investment than the ompetitor implies also losing their share of favorably biased users. (9) F A (K) K = E[Π B ] F A (K) = K + E[Π B ] From Lines (6) to (9) follows that firm A s and firm B s distribution funtions have the same slopes. This is true in both the low and the high investment range. Sine the slope is higher for investments below γ than for investments above γ, there exists δ (0, γ) suh that for both firms (10) F A (K) = F A (δ) and F B (K) = F B (δ) for all K [δ, γ) and therefore lim ε 0 F A (γ ε) = F A (δ) and lim ε 0 F B (γ ε) = F B (δ). Neither firm has an inentive to stritly exeed the maximum investment of the other firm. This would inrease ost but not inrease the probability of winning. Thus, the maximum investment hosen by eah firm must be idential in equilibrium, i.e., there exists a unique K suh that F A (K) = F B (K) = 1 and for all ε > 0, F A (K ε) < 1 and F B (K ε) < 1. Sine the distribution funtions of firms A and B also have idential slopes for K γ, the distribution funtions of both firms are idential for K γ: (11) F A (K) = F B (K) for all K γ Combining Equations (7), (9), and (11) yields E[Π B ] = F B (δ)α. Starting with Line (8) and plugging in yields for K < γ (12) F A (K) = K + F B(δ)α We solve (12) for F B (δ) and obtain F A(δ)β F B (δ) = F A (δ) + β α α δ We plug in from Line (6) and solve for F A (δ) to obtain ( α (13) F A (δ) = δ ( + β) + 1 ) + β 23

25 The flat part in the distribution funtions (Equation (10)) implies together with the different shares of biased users that firm B hooses an investment equal to γ with a positive probability while firm A s strategy has an atom at zero. Sine the two firms annot have an atom at the same investment level, and sine neither firm has an inentive to hoose δ with positive probability, the distribution funtion of firm A must be ontinuous in δ and γ. In addition, at γ the distribution funtions of both firms take idential values. Thus, the following holds (14) F A (δ) = F A (γ) = F B (γ) Sine F B (K) is linear for K δ, we an rewrite (7) as (15) F B (γ) = γ + δα Taking Line (14) and plugging in from Line (13) on the left-hand side and from Line (15) on the right-hand side, we arrive at (16) It is easily verified that ( α δ ( + β) β ( + β) δ = γ + α α( + β) ) = γ + δα = γ (1 α) + α 2 (1 α) < + α 2 δ < γ Finally, we derive the maximum investment levels. Suppose K > γ. Sine the distribution funtions stay onstant at one for all investment levels above the maximum level hosen, we obtain the following ondition (17) K + F B (δ)α = 1 K = 1 (1 α) δ = 1 γ ( + α 2 ) where δ has been derived in Equation (16). Rewriting (17) yields the maximum investment level K = 1 γ 1 α + α 2. 24

26 As by assumption α + β + = 1, we replae = 1 α β in the above results to state Proposition 1. For the derivation of the maximum investment, we have assumed K > γ. This is indeed true if (18) 1 γ 1 α + α > γ γ < 1 + α β Using the distribution funtions, we observe that F A (δ) > F B (δ) so that firm B has a higher investment than firm A more often than the reverse. We ompute expeted investments as E[K A ] = E[K B ] = δ 0 K xdx + xdx γ = (1 α)2 γ 2 2(+α 2 ) ( ( α((1+α)γ α)) 2 δ 0 xdx + K γ 2 (+α 2 ) 2 γ 2 ) xdx + Prob(K B = γ)γ ( ) = (1 α)2 γ ( α((1+α)γ α)) 2 γ 2 + (α β)γ2 2(+α 2 ) (+α 2 ) 2 +α 2 It is easily verified that E[K A ] < E[K B ]. By the properties of the mixed strategy equilibrium, the expeted profit of eah firm equals its expeted profit onditional on investing zero whih is its endowment of loyal users multiplied with the probability of the ompetitor investing below γ. A.3 Proof of Proposition 2. Proof. In the following, we derive δ (0, γ) suh that both firms randomize over (0, δ), firm A hooses zero with positive probability and firm B hooses γ with positive probability. In this equilibrium firm A hooses investments below or equal to δ with ertainty, i.e., F A (δ) whereas firm B also hooses γ suh that F B (δ) < 1. Sine firm B ould ensure profit 1 γ by deviating to hoosing γ, the distribution funtion of firm A must fulfill for all K δ (19) F A (K) + β K = 1 γ F A (K) = K + 1 β γ 25

27 By assumption γ < 1 β and thus 1 β γ > 0. Note that hoosing γ also yields an expeted profit equal to 1 γ for firm B. Firm A obtains an expeted profit equal to its share of loyal users multiplied by the probability that B hooses an investment invests less than γ, F B (δ)α. For the distribution funtion of firm B and investments K δ the following must hold: F B (K) + α K = α F B (K) = K The investment level δ is suh that the distribution funtion of firm A just reahes 1 at this level (20) δ + 1 β γ = 1 δ = γ α If γ < 1 β, then δ <. Finally, we derive the probability with whih firm B hooses γ. From Line (19) also Prob(K B = γ) = 1 δ = β γ = 1 β γ Prob(K A = 0) = 1 β γ = Prob(K B = γ) By γ < 1 β, it holds that Prob(K B = γ) > 0. Moreover, > 0 +β > β (1 α) 2 > β(1 α) 1 α β+α 2 > α αβ 1 α β + α2 1 β > α and therefore so that Prob(K B = δ) < 1. By γ > 1 γ > 1 1 β 1+α β γ > 1 1 α β + α 2 γ > α 1 β firm A does indeed not want to deviate to hoosing γ: 1 β 1+α β γ( + α) > + α2 α2 + γα > 1 γ F B(δ)α > 1 γ 26