Appendix for: Price Setting in Forward-Looking Customer Markets
|
|
|
- Theodore Hutchinson
- 5 years ago
- Views:
Transcription
1 Appendix for: Price Setting in Forward-Looking Customer Markets Emi Nakamura and Jón Steinsson Columbia University Appendix A. Second Order Approximations Appendix A.. A Derivation of a nd Order Approximation to the Firm s Value It is straightforward to show that the steady state price with full commitment is pz) = S, where variables without subscripts denote steady state values. Notice furthermore that equation ) in the paper implies that C = )cz) and equation ) in the paper implies that β)p = pz). A second order Taylor series approximation of the value of the firm around the steady state of the solution to the firm s problem with commitment is given by E 0 β t [cz)p t z) pz)) + pz)c tz) cz)) + p t z) pz))c t z) cz)) pz) S S t S)c t z) cz)) + cz) p β t t z) pz))m 0,t β t ) + ] pz) c β t t z) cz))m 0,t β t ) + ex. terms + O ξ 3 ), A.) where ex. terms stands for terms that are exogenous to the firm s decision problem, ξ stands for a vector of the exogenous variables and O ξ 3 ) denotes higher order terms. The exposition of our results is simplified if we make a change of variables. Let ĉ t z) = logc t z)/cz)) and define hatted versions of all other variables in the same way. Making use of the fact that c t z) = cz) + ĉ t z) + ) ĉtz) + O ξ 3 ),
2 we can rewrite equation A.) as E 0 [ pz)cz)β t ˆp t z) + ) ˆp tz) + ĉ t z) + ĉtz) ) + ˆp t z)ĉ t z) Ŝ t ĉ t z) +ˆp t z) ˆM 0,t + ĉtz) ˆM 0,t ] + ex. terms + O ξ 3 ).A.) Appendix A.. A Derivation of a nd Order Approximation to the Consumer Demand Curve Notice that consumer demand given by equation ) in the paper may be rewritten as P t C t t c t z) c t z)) t = p t z) + E t [M t,t+ P t+ Ct+ c t+ z) c t z)) t+ t+ ] A second order Taylor series approximation of this equation around the steady state of the solution to the firm s problem with commitment is given by. P t P ) + P C C t C) P cz) c t z) cz)) + P cz) c t z) cz)) P cz) P t P )c t z) cz)) + + P cz) c t z) cz)) P C cz) C t C)c t z) cz)) + P cz) c t z) cz)) t ) = p t z) pz)) β P cz) E t c t+ z) cz)) + s.o.ex.terms + O ξ, 3 ), A.3) where s.o.ex.terms denotes second order exogenous terms and O ξ, 3 ) denotes terms that are third order or higher) in ξ,. The norm ξ, is simply meant to denote the standard Euclidian distance norm in ξ, ) space. As in the case of the expression for the value of the firm, we find it convenient to rewrite equation A.3) in terms of the hatted variables and subsitute the E t ĉ t+ z) term our for a E tˆp t+ z) term. This yields ĉ t z) + ĉtz) ) ĉ t z) + )ĉtz) ˆP t Ĉt + ˆP t ĉ t z) + Ĉtĉ t z) ĉ t z)ˆ t = β)ˆp t z) ˆp tz) βe tˆp t+ z) + s.o.ex.terms + O ξ, A.4) 3 ),
3 Appendix B. Proofs of Propositions Appendix B.. Proposition Proof: We can rearrange equation 5) in the paper so that it says that β ĉtz) β ĉtz) β β E tĉ t+ z) = ˆp t z) β ĉtz) + + ) β)ĉtz) β ĉtz) ˆΥ t β ˆp tz) β ˆP t + Ĉt ˆP t ĉ t z) ) Ĉtĉ t z) + s.o.ex.terms + O ξ, 3 ). Now notice that equation 4) in the paper may be written [ ) E 0 pz)cz)β t β ĉtz) β ĉtz) β β ĉt+z) + ˆp t z) + ) ˆp tz) + ĉtz) + ˆp t z)ĉ t z) Ŝ t ĉ t z) +ˆp t z) ˆM 0,t + ] ĉtz) ˆM 0,t pz)cz) β ĉ0z) + ex. terms + O ξ, 3 ). Substituting consumer demand into this expression now yields [ E 0 pz)cz)β t ĉ t z) + β )ĉtz) + )ĉ t z) ˆΥ t + ˆp t z) ˆP t ĉ t z) )) Ĉtĉ t z) + ˆp tz) + ĉtz) + ˆp t z)ĉ t z) Ŝ t ĉ t z) +ˆp t z) ˆM 0,t + ] ĉtz) ˆM 0,t pz)cz) β ĉ0z) + ex. terms + O ξ, 3 ). If we now multiply this expression by ) β), use consumer demand to substitute for ĉ t z) and simplify, we get that [ ] E 0 pz)cz)β t ˆp t z) + ) ˆΥ tˆp t z) + )Ŝtˆp t z) + pz)cz) ˆp 0 z) +ex. terms + O ξ, 3 ). B.) Setting the derivative of this with respect to ˆp t z) for t equal to zero shows that the firm s optimal pricing policy under full commitment to a state-contingent rule for t is ˆp t z) = Ŝt + ˆΥ t up to an error of order O ξ, ). 3
4 Appendix B.. Proposition Proof: A derivation analogous to the derivation of expression B.) yields that the objective of the firm at time t can be written as E t j=0 pz)cz)β j [ ] ˆp t+j z) + ) ˆΥ t+j ˆp t+j z) + )Ŝt+j ˆp t+j z) + pz)cz) ˆp t z) +ex. terms + O ξ, 3 B.) ). We seek a Markov perfect equilibrium that is accurate up to a residual of order O ξ, ). The definition of a Markov perfect equilibrium implies that the strategies of the firms are functions of only the pay-off relevant state of the economy. In our model, the state of the economy at time t is ĉ t z), Ŝt, ˆΥ t ). However, given our approximation, ĉ t z) contributes only terms of order O ξ, ) since it is multiplied by in consumer demand. This implies that, up to a residual of order O ξ, ), the stretegies of the firm are functions of only Ŝt, ˆΥ t ). Since these two variables are i.i.d., the firm can correctly assume that its decisions at time t have no effect on outcomes in any period T t +. The firm can therefore simply maximize expression B.) with respect to the current period price ˆp t z). This yields ˆp t z) = + Ŝt + ˆΥ t, B.3) up to an error of order O ξ, ). Appendix B.3. Proposition 3 Proof: We must show that the firm does not have a profitable deviation when it is setting p t z) = p c tz). The potential benefit from deviating at this point is a higher price in the current period. Denote this benefit by Π d t Π c t which could be negative). The loss is the change in future profits associated with playing the Markov perfect equilibrium in future periods rather than p t+j z) = p c t+jz). Denote the expected loss in the period after the deviation by E[Π c + Π m +] and the per period loss in subsequent periods by E[Π c Π m ]. The firm will refrain from deviating in the current period if Π d t Π c t < βe[π c + Π m +] + β E[Π c Π m ]/ β). This condition will hold for all β > β t where β t is implicitely defined by Π d t Π c t = β t E[Π c + Π m +] + β t E[Πc Π m ]/ β t ). The firm will never deviate if 4
5 β > β = max β t. If Π d t Π c t is negative, β = 0. It is relatively easy to show that β is independent of. Appendix B.4. Proposition 4 Proof: First, we show that the profit maximizing price rule assuming that prices can only be changed in odd numbered periods is given by equation 0) in the paper. The value of the firm s expected profits from period t on are given by expression B.). The firm maximizes this expression with respect to ˆp t subject to the constraint ˆp t z) = ˆp t+ z). We can use this constraint to eliminate ˆp t+ z) in expression B.) and rewrite it ignoring terms that are exogenous to the firm s time t problem. This yields [ ] ) + β) pz)cz) ˆp t z) + ) ˆΥ tˆp t z) + )Ŝtˆp t z) + ˆp t z) +ex. terms + O ξ, 3 ).B.4) Maximizing this with respect to ˆp t z) yields equation 0) in the paper. Next, we show that the value expected profits in future periods from adhering to the price path stated in the proposition is greater than from playing the Markov perfect equilibrium. The value of the expected future profits is equal to E t j= pz)cz)β j [ ] ˆp t+j z) + )Ŝt+j + ˆΥ t+j )ˆp t+j z) + ex. terms + O ξ, 3 ). Using equation 8) in the paper we can derive that, ignoring exogenous terms and terms of higher than second order, the value of the expected profits of a firm if it plays the Markov perfect equilibrium in all future periods is E t Π m β t+ = pz)cz) β [ ) + varŝt + ˆΥ t )]. Similarly, using equation 0) in the paper we can derive that the value of the expected profits of a firm that prices according the the rule in the proposition is larger than or equal 5
6 to [ [ min E t Π F Ŝ t+ ˆΥ t+ = min pz)cz)β ) ] + + β t Ŝ t+ ˆΥ t ) + β) + β) Ŝt + ˆΥ t ) [ ) ]] +pz)cz) β + + β β ) + β) + β) varŝt + ˆΥ t ) [ ) ] β β + β) = pz)cz) + β ) + β) + β) varŝt + ˆΥ t ) Comparing these expressions we get that minŝt+ ˆΥ t E t Π F t+ > E t Π m t+ if > ) + β β β + β varŝt + ˆΥ t ). Given this condition an argument analogous to the one given in the proof of Proposition 3 implies that the firm does not have a profitable deviation while it is setting its price according to equation 0) in the paper as long as β > β. Appendix B.5. Proposition 5 We must show that the portion of the price path described in the proposition that is played in equilibrium is the best feasible price path from the firm s perspective. Once we have shown this, an argument analogous to the proof of Proposition 3 implies that the firm does not have a profitable deviation from this price path. We begin by deriving the function in our model that correponds to Rx t, µ t, t ) in Athey et al. 004). Given the consumer s demand curve equation 5) one can view the decision the consumer makes at each point in time as a decision about what he expects prices to be in the next period. To see this, notice that we can rewrite equation 5) as ˆp t z) = β ĉtz) β ĉtz) β β E tĉ t+ z) + β ˆp tz) + β ĉtz) + ) β)ĉtz) ˆP t Ĉt + ˆP t + ) β) Ĉt + ) ˆΥ t ĉ t z) + s.o.ex.terms + O ξ, 3 ). Notice furthermore that ĉ t z) = ˆp t z) + ˆP t + Ĉt + O ξ, ). 6 B.5)
7 Using this fact, we can rewrite the consumer s demand curve as ˆp t z) = β ĉtz) β ĉtz) β + β E tˆp t+ z) + β ˆp tz) + β ˆp tz) ˆP tˆp t z) Ĉtˆp t z)) + ) ) β) ˆp tz) ˆP tˆp t z) Ĉtˆp t z)) ˆP t Ĉt ˆP t + ) β) Ĉt + ) ˆΥ t ˆp t z) + s.o.ex.terms + O ξ, 3 ). Notice that once the consumer has chosen what to expect about the firm s price in period t +, this equation determines his demand. One can therefore view the consumer s decision at each point given the form of the demand curve as a choice about what to expect about the firm s price in the next period. In equilibrium, the consumer will have rational expectations. We have used this fact by writing the consumer s expectation as E tˆp t+. However, more generally, we can denote the consumer s expectation about ˆp t at time t as x t. Using this notation, the consumer s demand curve becomes ˆp t z) = β ĉtz) β ĉtz) β + β x t+ + β ˆp tz) + β ˆp tz) ˆP tˆp t z) Ĉtˆp t z)) + ) ) β) ˆp tz) ˆP tˆp t z) Ĉtˆp t z)) ˆP t Ĉt ˆP t + ) β) Ĉt + ) ˆΥ t ˆp t z) + s.o.ex.terms + O ξ, 3 ). B.6) Next, notice that the second order approximation of the value of the firm equation 4) may be written E 0 pz)cz)β t [ ˆp t z) + β ĉtz) + ˆp tz) + ĉtz) + ˆp t z)ĉ t z) +ex. terms + O ξ 3 ) ) β ĉtz) Ŝ t ĉ t z) + ˆp t z) ˆM 0,t + ] ĉtz) ˆM 0,t β ĉtz) Using equation B.6) to eliminate the first two terms in this expression, equation B.5) to eliminate ĉ t z) and multiplying the resulting expression by β) ) gives [ E 0 pz)cz)β t ˆp t z) βx t+ + ] ˆp t + )Ŝt + ˆΥ t )ˆp t z) +ex. terms+o ξ, 3 ). B.7) 7
8 Collecting the terms in the sum that involve ˆp t z), x t and ˆΦ t = Ŝt + ˆΥ t we can define Rx t, ˆp t z), Ŝt) = ˆp t z) x t )ˆp t z) + )ˆΦ tˆp t z) B.8) for t. This is the function in our model that corresponds to Rx t, µ t, t ) in Athey et al. 004). Mapping our notation into the notation used by Athey et al. 004) we get that: x t = x t, µ t = ˆp t z) and t = ˆΦ t. In the notation used by Athey et al. 004), the firm s objective function is Rx t, µ t, t ) = µ t x t )µ t + ) t µ t. Notice that this function satisfies all the conditions required for the propositions in Athey et al. 004) to be valid. Specifically, R x x t, µ t, t ) = < 0, R µ x t, µ t, t ) = > 0 and R µµ x t, µ t, t ) = ) < 0. The main difference between our results and the results in Athey et al. 004) is that they consider a model in which Rx t, µ t, t ) is the social welfare function, i.e. it is the objective of all the agents in the model. The fact that Rx t, µ t, t ) in Athey et al. 004) is the social welfare function entails that the resulting policy is socially optimal. Here we use the objective of the firm as our Rx t, µ t, t ), which means that the resulting policy is not socially optimal but rather the best policy from the perspective of the firm. The proofs in Athey et al. 004) do not rely on Rx t, µ t, t ) being a social welfare function. Only their interpretation as solving for the socially optimal policy relies on this. Given equation B.8) and the following monotone hazard conditions: P ˆΦ t ))/pˆφ t ) is strictly decreasing in ˆΦ t and P ˆΦ t )/pˆφ t ) is strictly increasing in ˆΦ t, Proposition in Athey et al. 004) shows that the pricing policy that is optimal from the perspective of the firm is static. Here pˆφ t ) and P ˆΦ t ) denote the pdf and cdf of ˆΦ t, respectively. We assume that ˆΦ t [ˆΦ, ˆΦ]. Furthermore, Proposition in Athey et al. 004) shows that the firm s best pricing policy is either a constant price or it is a policy of bounded discretion, i.e., ˆp ˆΦ; z) if ˆΦ [ˆΦ, ˆΦ ] ˆpz) = ˆp ˆΦ ; z) if ˆΦ [ˆΦ, ˆΦ] 8 B.9)
9 where ˆp ˆΦ; z) denotes the static best response of a firm with a desired price equal to ˆΦ and ˆΦ ˆΦ ˆΦ. To complete the description of the policy most prefered by the firm, we must calculate four things: ) Under what conditions does the firm prefer a constant price? ) What is the optimal constant price from the firm s perspective? 3-4) When the firm prefers to set its price according to equation B.9), what is the optimal cutoff point ˆΦ and what is the firm s static best response ˆp ˆΦ; z)? The remainder of this section draws heavily on appendix D in Athey et al. 004). First, notice that the static best reponse of the firm solves Rˆpz) E ˆpz), ˆpz), ˆΦ) = 0. The solution is ˆp ˆΦ, z) = + ˆΦ. If the firm s pricing policy is of the form B.9), then B.0) E ˆpz) = ˆΦ ˆΦ ˆp ˆΦ, z)pˆφ)dˆφ + ˆΦ ˆp ˆΦ, z)pˆφ)dˆφ. Using equation B.0) to plug in for ˆp ˆΦ, z) in this equation we get that E ˆpz) = ˆΦ ˆΦ )pˆφ)dˆφ. ˆΦ Athey et al. 004) show that the objective of the firm, RE ˆpz), ˆpz), ˆΦ)pˆΦ)dˆΦ may be written RE ˆpz), ˆp ˆΦ, z), ˆΦ) + ˆΦ ˆΦ RˆΦE ˆpz), ˆp ˆΦ, z), ˆΦ)[ P ˆΦ)]dˆΦ + RˆΦE ˆpz), ˆp ˆΦ, z), ˆΦ)[ P ˆΦ)]dˆΦ. ˆΦ Since RˆΦE ˆpz), ˆpz), ˆΦ) = )ˆpz), this expression simplifies to ˆΦ ˆΦ ˆΦ )pˆφ)dˆφ + ) ˆΦ ˆΦ ˆΦ[ P ˆΦ)]dˆΦ + ) ˆΦ [ P ˆΦ)]dˆΦ + ex. terms. ˆΦ Differentiating this with respect to ˆΦ and setting the resulting expression equal to zero yields pˆφ)dˆφ + ) [ P ˆΦ)]dˆΦ = 0, ˆΦ ˆΦ 9
10 which is equivalent to [ P ˆΦ )] + ) [ P ˆΦ)]dˆΦ = 0. ˆΦ When ˆΦ < ˆΦ, P ˆΦ ) > 0, so this last equation is equivalent to P ˆΦ) pˆφ) + ) ˆΦ pˆφ) P ˆΦ ) dˆφ = 0. B.) Notice that the second term on the left hand side of this equaiton is the conditional mean of P ˆΦ))/pˆΦ) over the interval [ˆΦ, ˆΦ]. Since P ˆΦ))/pˆΦ) is strictly decreasing in ˆΦ monotone hazard assumption), its conditional mean is also strictly decreasing in ˆΦ. This implies that equation B.) has at most one interior solution. Since the expression on the left hand side of equation B.) is decreasing in both and ˆΦ, it is furthermore the case that ˆΦ is decreasing in. We have shown that equation B.) has at most one interior solutions. To show that such a solution in fact exists we must show that the left hand side of this equation is negative for ˆΦ close ˆΦ and positive for ˆΦ = ˆΦ. Notice that when ˆΦ ˆΦ, P ˆΦ))/pˆΦ) 0. This implies that for > 0 and ˆΦ close enough to ˆΦ, the left hand side of equation B.) is strictly less than zero. When ˆΦ = ˆΦ, equation B.) is not defined. However, ˆΦ = ˆΦ is a solution to the equation above equation B.). However, since the expression on the left hand side of that equation is strictly negative for ˆΦ < ˆΦ in the neighborhood of ˆΦ, this is not a local maximum. Athey et al. 004) show that at ˆΦ = ˆΦ the left hand side of equation B.) becomes ˆΦ. Since ˆΦ < 0, this is positive for 0, ˆΦ). So, there is an interior solution in this case. When > ˆΦ there is no interior solution to equation B.). This implies that for this range of the firm s best policy is a constant price. Finally, when > ˆΦ the firm chooses its constant price to maximize ˆΦ RE ˆpz), ˆpz), ˆΦ)pˆΦ)dˆΦ subject to E ˆpz) = ˆpz). The solution to this problem is ˆpz) = 0. 0
11 References Athey, S., Atkeson, A., Kehoe, P. J., 005. The optimal degree of discretion in monetary policy. Econometrica 73 5),
Appendix: Common Currencies vs. Monetary Independence
 Appendix: Common Currencies vs. Monetary Independence A The infinite horizon model This section defines the equilibrium of the infinity horizon model described in Section III of the paper and characterizes
Appendix: Common Currencies vs. Monetary Independence A The infinite horizon model This section defines the equilibrium of the infinity horizon model described in Section III of the paper and characterizes
Appendix for Growing Like China 1
 Appendix for Growing Like China 1 Zheng Song (Fudan University), Kjetil Storesletten (Federal Reserve Bank of Minneapolis), Fabrizio Zilibotti (University of Zurich and CEPR) May 11, 2010 1 Equations,
Appendix for Growing Like China 1 Zheng Song (Fudan University), Kjetil Storesletten (Federal Reserve Bank of Minneapolis), Fabrizio Zilibotti (University of Zurich and CEPR) May 11, 2010 1 Equations,
Class Notes on Chaney (2008)
 Class Notes on Chaney (2008) (With Krugman and Melitz along the Way) Econ 840-T.Holmes Model of Chaney AER (2008) As a first step, let s write down the elements of the Chaney model. asymmetric countries
Class Notes on Chaney (2008) (With Krugman and Melitz along the Way) Econ 840-T.Holmes Model of Chaney AER (2008) As a first step, let s write down the elements of the Chaney model. asymmetric countries
The Neoclassical Growth Model
 The Neoclassical Growth Model 1 Setup Three goods: Final output Capital Labour One household, with preferences β t u (c t ) (Later we will introduce preferences with respect to labour/leisure) Endowment
The Neoclassical Growth Model 1 Setup Three goods: Final output Capital Labour One household, with preferences β t u (c t ) (Later we will introduce preferences with respect to labour/leisure) Endowment
The New Keynesian Model
 The New Keynesian Model Noah Williams University of Wisconsin-Madison Noah Williams (UW Madison) New Keynesian model 1 / 37 Research strategy policy as systematic and predictable...the central bank s stabilization
The New Keynesian Model Noah Williams University of Wisconsin-Madison Noah Williams (UW Madison) New Keynesian model 1 / 37 Research strategy policy as systematic and predictable...the central bank s stabilization
Recently the study of optimal monetary policy has shifted from an
 Implementation of Optimal Monetary Policy Michael Dotsey and Andreas Hornstein Recently the study of optimal monetary policy has shifted from an analysis of the welfare effects of simple parametric policy
Implementation of Optimal Monetary Policy Michael Dotsey and Andreas Hornstein Recently the study of optimal monetary policy has shifted from an analysis of the welfare effects of simple parametric policy
Online Appendix for Debt Contracts with Partial Commitment by Natalia Kovrijnykh
 Online Appendix for Debt Contracts with Partial Commitment by Natalia Kovrijnykh Omitted Proofs LEMMA 5: Function ˆV is concave with slope between 1 and 0. PROOF: The fact that ˆV (w) is decreasing in
Online Appendix for Debt Contracts with Partial Commitment by Natalia Kovrijnykh Omitted Proofs LEMMA 5: Function ˆV is concave with slope between 1 and 0. PROOF: The fact that ˆV (w) is decreasing in
1 Answers to the Sept 08 macro prelim - Long Questions
 Answers to the Sept 08 macro prelim - Long Questions. Suppose that a representative consumer receives an endowment of a non-storable consumption good. The endowment evolves exogenously according to ln
Answers to the Sept 08 macro prelim - Long Questions. Suppose that a representative consumer receives an endowment of a non-storable consumption good. The endowment evolves exogenously according to ln
Online Appendix Optimal Time-Consistent Government Debt Maturity D. Debortoli, R. Nunes, P. Yared. A. Proofs
 Online Appendi Optimal Time-Consistent Government Debt Maturity D. Debortoli, R. Nunes, P. Yared A. Proofs Proof of Proposition 1 The necessity of these conditions is proved in the tet. To prove sufficiency,
Online Appendi Optimal Time-Consistent Government Debt Maturity D. Debortoli, R. Nunes, P. Yared A. Proofs Proof of Proposition 1 The necessity of these conditions is proved in the tet. To prove sufficiency,
Lecture 2: The Neoclassical Growth Model
 Lecture 2: The Neoclassical Growth Model Florian Scheuer 1 Plan Introduce production technology, storage multiple goods 2 The Neoclassical Model Three goods: Final output Capital Labor One household, with
Lecture 2: The Neoclassical Growth Model Florian Scheuer 1 Plan Introduce production technology, storage multiple goods 2 The Neoclassical Model Three goods: Final output Capital Labor One household, with
Problem set Fall 2012.
 Problem set 1. 14.461 Fall 2012. Ivan Werning September 13, 2012 References: 1. Ljungqvist L., and Thomas J. Sargent (2000), Recursive Macroeconomic Theory, sections 17.2 for Problem 1,2. 2. Werning Ivan
Problem set 1. 14.461 Fall 2012. Ivan Werning September 13, 2012 References: 1. Ljungqvist L., and Thomas J. Sargent (2000), Recursive Macroeconomic Theory, sections 17.2 for Problem 1,2. 2. Werning Ivan
Ramsey s Growth Model (Solution Ex. 2.1 (f) and (g))
 Problem Set 2: Ramsey s Growth Model (Solution Ex. 2.1 (f) and (g)) Exercise 2.1: An infinite horizon problem with perfect foresight In this exercise we will study at a discrete-time version of Ramsey
Problem Set 2: Ramsey s Growth Model (Solution Ex. 2.1 (f) and (g)) Exercise 2.1: An infinite horizon problem with perfect foresight In this exercise we will study at a discrete-time version of Ramsey
Monetary Economics Final Exam
 316-466 Monetary Economics Final Exam 1. Flexible-price monetary economics (90 marks). Consider a stochastic flexibleprice money in the utility function model. Time is discrete and denoted t =0, 1,...
316-466 Monetary Economics Final Exam 1. Flexible-price monetary economics (90 marks). Consider a stochastic flexibleprice money in the utility function model. Time is discrete and denoted t =0, 1,...
Monetary Economics Basic Flexible Price Models
 Monetary Economics Basic Flexible Price Models Nicola Viegi July 26, 207 Modelling Money I Cagan Model - The Price of Money I A Modern Classical Model (Without Money) I Money in Utility Function Approach
Monetary Economics Basic Flexible Price Models Nicola Viegi July 26, 207 Modelling Money I Cagan Model - The Price of Money I A Modern Classical Model (Without Money) I Money in Utility Function Approach
Department of Economics The Ohio State University Final Exam Answers Econ 8712
 Department of Economics The Ohio State University Final Exam Answers Econ 872 Prof. Peck Fall 207. (35 points) The following economy has three consumers, one firm, and four goods. Good is the labor/leisure
Department of Economics The Ohio State University Final Exam Answers Econ 872 Prof. Peck Fall 207. (35 points) The following economy has three consumers, one firm, and four goods. Good is the labor/leisure
Answers to Microeconomics Prelim of August 24, In practice, firms often price their products by marking up a fixed percentage over (average)
 Answers to Microeconomics Prelim of August 24, 2016 1. In practice, firms often price their products by marking up a fixed percentage over (average) cost. To investigate the consequences of markup pricing,
Answers to Microeconomics Prelim of August 24, 2016 1. In practice, firms often price their products by marking up a fixed percentage over (average) cost. To investigate the consequences of markup pricing,
Department of Economics The Ohio State University Final Exam Answers Econ 8712
 Department of Economics The Ohio State University Final Exam Answers Econ 8712 Prof. Peck Fall 2015 1. (5 points) The following economy has two consumers, two firms, and two goods. Good 2 is leisure/labor.
Department of Economics The Ohio State University Final Exam Answers Econ 8712 Prof. Peck Fall 2015 1. (5 points) The following economy has two consumers, two firms, and two goods. Good 2 is leisure/labor.
Introducing nominal rigidities. A static model.
 Introducing nominal rigidities. A static model. Olivier Blanchard May 25 14.452. Spring 25. Topic 7. 1 Why introduce nominal rigidities, and what do they imply? An informal walk-through. In the model we
Introducing nominal rigidities. A static model. Olivier Blanchard May 25 14.452. Spring 25. Topic 7. 1 Why introduce nominal rigidities, and what do they imply? An informal walk-through. In the model we
market opportunity line fair odds line Example 6.6, p. 120.
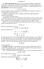 September 5 The market opportunity line depicts in the plane the different combinations of outcomes and that are available to the individual at the prevailing market prices, depending on how much of an
September 5 The market opportunity line depicts in the plane the different combinations of outcomes and that are available to the individual at the prevailing market prices, depending on how much of an
Topic 7. Nominal rigidities
 14.452. Topic 7. Nominal rigidities Olivier Blanchard April 2007 Nr. 1 1. Motivation, and organization Why introduce nominal rigidities, and what do they imply? In monetary models, the price level (the
14.452. Topic 7. Nominal rigidities Olivier Blanchard April 2007 Nr. 1 1. Motivation, and organization Why introduce nominal rigidities, and what do they imply? In monetary models, the price level (the
1 Continuous Time Optimization
 University of British Columbia Department of Economics, International Finance (Econ 556) Prof. Amartya Lahiri Handout #6 1 1 Continuous Time Optimization Continuous time optimization is similar to dynamic
University of British Columbia Department of Economics, International Finance (Econ 556) Prof. Amartya Lahiri Handout #6 1 1 Continuous Time Optimization Continuous time optimization is similar to dynamic
Macro II. John Hassler. Spring John Hassler () New Keynesian Model:1 04/17 1 / 10
 Macro II John Hassler Spring 27 John Hassler () New Keynesian Model: 4/7 / New Keynesian Model The RBC model worked (perhaps surprisingly) well. But there are problems in generating enough variation in
Macro II John Hassler Spring 27 John Hassler () New Keynesian Model: 4/7 / New Keynesian Model The RBC model worked (perhaps surprisingly) well. But there are problems in generating enough variation in
Production and Inventory Behavior of Capital *
 ANNALS OF ECONOMICS AND FINANCE 8-1, 95 112 (2007) Production and Inventory Behavior of Capital * Yi Wen Research Department, Federal Reserve Bank of St. Louis E-mail: yi.wen@stls.frb.org This paper provides
ANNALS OF ECONOMICS AND FINANCE 8-1, 95 112 (2007) Production and Inventory Behavior of Capital * Yi Wen Research Department, Federal Reserve Bank of St. Louis E-mail: yi.wen@stls.frb.org This paper provides
Financial Fragility and the Exchange Rate Regime Chang and Velasco JET 2000 and NBER 6469
 Financial Fragility and the Exchange Rate Regime Chang and Velasco JET 2000 and NBER 6469 1 Introduction and Motivation International illiquidity Country s consolidated nancial system has potential short-term
Financial Fragility and the Exchange Rate Regime Chang and Velasco JET 2000 and NBER 6469 1 Introduction and Motivation International illiquidity Country s consolidated nancial system has potential short-term
Comparing Allocations under Asymmetric Information: Coase Theorem Revisited
 Comparing Allocations under Asymmetric Information: Coase Theorem Revisited Shingo Ishiguro Graduate School of Economics, Osaka University 1-7 Machikaneyama, Toyonaka, Osaka 560-0043, Japan August 2002
Comparing Allocations under Asymmetric Information: Coase Theorem Revisited Shingo Ishiguro Graduate School of Economics, Osaka University 1-7 Machikaneyama, Toyonaka, Osaka 560-0043, Japan August 2002
1 The Solow Growth Model
 1 The Solow Growth Model The Solow growth model is constructed around 3 building blocks: 1. The aggregate production function: = ( ()) which it is assumed to satisfy a series of technical conditions: (a)
1 The Solow Growth Model The Solow growth model is constructed around 3 building blocks: 1. The aggregate production function: = ( ()) which it is assumed to satisfy a series of technical conditions: (a)
Course Handouts - Introduction ECON 8704 FINANCIAL ECONOMICS. Jan Werner. University of Minnesota
 Course Handouts - Introduction ECON 8704 FINANCIAL ECONOMICS Jan Werner University of Minnesota SPRING 2019 1 I.1 Equilibrium Prices in Security Markets Assume throughout this section that utility functions
Course Handouts - Introduction ECON 8704 FINANCIAL ECONOMICS Jan Werner University of Minnesota SPRING 2019 1 I.1 Equilibrium Prices in Security Markets Assume throughout this section that utility functions
Econ 8602, Fall 2017 Homework 2
 Econ 8602, Fall 2017 Homework 2 Due Tues Oct 3. Question 1 Consider the following model of entry. There are two firms. There are two entry scenarios in each period. With probability only one firm is able
Econ 8602, Fall 2017 Homework 2 Due Tues Oct 3. Question 1 Consider the following model of entry. There are two firms. There are two entry scenarios in each period. With probability only one firm is able
Working Paper Series. This paper can be downloaded without charge from:
 Working Paper Series This paper can be downloaded without charge from: http://www.richmondfed.org/publications/ On the Implementation of Markov-Perfect Monetary Policy Michael Dotsey y and Andreas Hornstein
Working Paper Series This paper can be downloaded without charge from: http://www.richmondfed.org/publications/ On the Implementation of Markov-Perfect Monetary Policy Michael Dotsey y and Andreas Hornstein
Supplementary Material for: Belief Updating in Sequential Games of Two-Sided Incomplete Information: An Experimental Study of a Crisis Bargaining
 Supplementary Material for: Belief Updating in Sequential Games of Two-Sided Incomplete Information: An Experimental Study of a Crisis Bargaining Model September 30, 2010 1 Overview In these supplementary
Supplementary Material for: Belief Updating in Sequential Games of Two-Sided Incomplete Information: An Experimental Study of a Crisis Bargaining Model September 30, 2010 1 Overview In these supplementary
Inflation. David Andolfatto
 Inflation David Andolfatto Introduction We continue to assume an economy with a single asset Assume that the government can manage the supply of over time; i.e., = 1,where 0 is the gross rate of money
Inflation David Andolfatto Introduction We continue to assume an economy with a single asset Assume that the government can manage the supply of over time; i.e., = 1,where 0 is the gross rate of money
Bank Leverage and Social Welfare
 Bank Leverage and Social Welfare By LAWRENCE CHRISTIANO AND DAISUKE IKEDA We describe a general equilibrium model in which there is a particular agency problem in banks. The agency problem arises because
Bank Leverage and Social Welfare By LAWRENCE CHRISTIANO AND DAISUKE IKEDA We describe a general equilibrium model in which there is a particular agency problem in banks. The agency problem arises because
The Costs of Losing Monetary Independence: The Case of Mexico
 The Costs of Losing Monetary Independence: The Case of Mexico Thomas F. Cooley New York University Vincenzo Quadrini Duke University and CEPR May 2, 2000 Abstract This paper develops a two-country monetary
The Costs of Losing Monetary Independence: The Case of Mexico Thomas F. Cooley New York University Vincenzo Quadrini Duke University and CEPR May 2, 2000 Abstract This paper develops a two-country monetary
PAULI MURTO, ANDREY ZHUKOV
 GAME THEORY SOLUTION SET 1 WINTER 018 PAULI MURTO, ANDREY ZHUKOV Introduction For suggested solution to problem 4, last year s suggested solutions by Tsz-Ning Wong were used who I think used suggested
GAME THEORY SOLUTION SET 1 WINTER 018 PAULI MURTO, ANDREY ZHUKOV Introduction For suggested solution to problem 4, last year s suggested solutions by Tsz-Ning Wong were used who I think used suggested
Department of Economics The Ohio State University Final Exam Questions and Answers Econ 8712
 Prof. Peck Fall 016 Department of Economics The Ohio State University Final Exam Questions and Answers Econ 871 1. (35 points) The following economy has one consumer, two firms, and four goods. Goods 1
Prof. Peck Fall 016 Department of Economics The Ohio State University Final Exam Questions and Answers Econ 871 1. (35 points) The following economy has one consumer, two firms, and four goods. Goods 1
Product Di erentiation: Exercises Part 1
 Product Di erentiation: Exercises Part Sotiris Georganas Royal Holloway University of London January 00 Problem Consider Hotelling s linear city with endogenous prices and exogenous and locations. Suppose,
Product Di erentiation: Exercises Part Sotiris Georganas Royal Holloway University of London January 00 Problem Consider Hotelling s linear city with endogenous prices and exogenous and locations. Suppose,
Supplemental Materials for What is the Optimal Trading Frequency in Financial Markets? Not for Publication. October 21, 2016
 Supplemental Materials for What is the Optimal Trading Frequency in Financial Markets? Not for Publication Songzi Du Haoxiang Zhu October, 06 A Model with Multiple Dividend Payment In the model of Du and
Supplemental Materials for What is the Optimal Trading Frequency in Financial Markets? Not for Publication Songzi Du Haoxiang Zhu October, 06 A Model with Multiple Dividend Payment In the model of Du and
Department of Mathematics. Mathematics of Financial Derivatives
 Department of Mathematics MA408 Mathematics of Financial Derivatives Thursday 15th January, 2009 2pm 4pm Duration: 2 hours Attempt THREE questions MA408 Page 1 of 5 1. (a) Suppose 0 < E 1 < E 3 and E 2
Department of Mathematics MA408 Mathematics of Financial Derivatives Thursday 15th January, 2009 2pm 4pm Duration: 2 hours Attempt THREE questions MA408 Page 1 of 5 1. (a) Suppose 0 < E 1 < E 3 and E 2
On Existence of Equilibria. Bayesian Allocation-Mechanisms
 On Existence of Equilibria in Bayesian Allocation Mechanisms Northwestern University April 23, 2014 Bayesian Allocation Mechanisms In allocation mechanisms, agents choose messages. The messages determine
On Existence of Equilibria in Bayesian Allocation Mechanisms Northwestern University April 23, 2014 Bayesian Allocation Mechanisms In allocation mechanisms, agents choose messages. The messages determine
1 Optimal Taxation of Labor Income
 1 Optimal Taxation of Labor Income Until now, we have assumed that government policy is exogenously given, so the government had a very passive role. Its only concern was balancing the intertemporal budget.
1 Optimal Taxation of Labor Income Until now, we have assumed that government policy is exogenously given, so the government had a very passive role. Its only concern was balancing the intertemporal budget.
Advanced Macroeconomics
 Advanced Macroeconomics Chapter 5: Government: Expenditures and public finances Günter W. Beck University of Mainz December 14, 2010 Günter W. Beck () Advanced Macroeconomics December 14, 2010 1 / 16 Overview
Advanced Macroeconomics Chapter 5: Government: Expenditures and public finances Günter W. Beck University of Mainz December 14, 2010 Günter W. Beck () Advanced Macroeconomics December 14, 2010 1 / 16 Overview
Homework # 8 - [Due on Wednesday November 1st, 2017]
![Homework # 8 - [Due on Wednesday November 1st, 2017] Homework # 8 - [Due on Wednesday November 1st, 2017]](/thumbs/93/112043254.jpg) Homework # 8 - [Due on Wednesday November 1st, 2017] 1. A tax is to be levied on a commodity bought and sold in a competitive market. Two possible forms of tax may be used: In one case, a per unit tax
Homework # 8 - [Due on Wednesday November 1st, 2017] 1. A tax is to be levied on a commodity bought and sold in a competitive market. Two possible forms of tax may be used: In one case, a per unit tax
1 No capital mobility
 University of British Columbia Department of Economics, International Finance (Econ 556) Prof. Amartya Lahiri Handout #7 1 1 No capital mobility In the previous lecture we studied the frictionless environment
University of British Columbia Department of Economics, International Finance (Econ 556) Prof. Amartya Lahiri Handout #7 1 1 No capital mobility In the previous lecture we studied the frictionless environment
A Note on Optimal Taxation in the Presence of Externalities
 A Note on Optimal Taxation in the Presence of Externalities Wojciech Kopczuk Address: Department of Economics, University of British Columbia, #997-1873 East Mall, Vancouver BC V6T1Z1, Canada and NBER
A Note on Optimal Taxation in the Presence of Externalities Wojciech Kopczuk Address: Department of Economics, University of British Columbia, #997-1873 East Mall, Vancouver BC V6T1Z1, Canada and NBER
Sharing the Burden: Monetary and Fiscal Responses to a World Liquidity Trap David Cook and Michael B. Devereux
 Sharing the Burden: Monetary and Fiscal Responses to a World Liquidity Trap David Cook and Michael B. Devereux Online Appendix: Non-cooperative Loss Function Section 7 of the text reports the results for
Sharing the Burden: Monetary and Fiscal Responses to a World Liquidity Trap David Cook and Michael B. Devereux Online Appendix: Non-cooperative Loss Function Section 7 of the text reports the results for
Information Acquisition under Persuasive Precedent versus Binding Precedent (Preliminary and Incomplete)
 Information Acquisition under Persuasive Precedent versus Binding Precedent (Preliminary and Incomplete) Ying Chen Hülya Eraslan March 25, 2016 Abstract We analyze a dynamic model of judicial decision
Information Acquisition under Persuasive Precedent versus Binding Precedent (Preliminary and Incomplete) Ying Chen Hülya Eraslan March 25, 2016 Abstract We analyze a dynamic model of judicial decision
1 Dynamic programming
 1 Dynamic programming A country has just discovered a natural resource which yields an income per period R measured in terms of traded goods. The cost of exploitation is negligible. The government wants
1 Dynamic programming A country has just discovered a natural resource which yields an income per period R measured in terms of traded goods. The cost of exploitation is negligible. The government wants
The Cagan Model. Lecture 15 by John Kennes March 25
 The Cagan Model Lecture 15 by John Kennes March 25 The Cagan Model Let M denote a country s money supply and P its price level. Higher expected inflation lowers the demand for real balances M/P by raising
The Cagan Model Lecture 15 by John Kennes March 25 The Cagan Model Let M denote a country s money supply and P its price level. Higher expected inflation lowers the demand for real balances M/P by raising
Transport Costs and North-South Trade
 Transport Costs and North-South Trade Didier Laussel a and Raymond Riezman b a GREQAM, University of Aix-Marseille II b Department of Economics, University of Iowa Abstract We develop a simple two country
Transport Costs and North-South Trade Didier Laussel a and Raymond Riezman b a GREQAM, University of Aix-Marseille II b Department of Economics, University of Iowa Abstract We develop a simple two country
Aggregation with a double non-convex labor supply decision: indivisible private- and public-sector hours
 Ekonomia nr 47/2016 123 Ekonomia. Rynek, gospodarka, społeczeństwo 47(2016), s. 123 133 DOI: 10.17451/eko/47/2016/233 ISSN: 0137-3056 www.ekonomia.wne.uw.edu.pl Aggregation with a double non-convex labor
Ekonomia nr 47/2016 123 Ekonomia. Rynek, gospodarka, społeczeństwo 47(2016), s. 123 133 DOI: 10.17451/eko/47/2016/233 ISSN: 0137-3056 www.ekonomia.wne.uw.edu.pl Aggregation with a double non-convex labor
Eco504 Fall 2010 C. Sims CAPITAL TAXES
 Eco504 Fall 2010 C. Sims CAPITAL TAXES 1. REVIEW: SMALL TAXES SMALL DEADWEIGHT LOSS Static analysis suggests that deadweight loss from taxation at rate τ is 0(τ 2 ) that is, that for small tax rates the
Eco504 Fall 2010 C. Sims CAPITAL TAXES 1. REVIEW: SMALL TAXES SMALL DEADWEIGHT LOSS Static analysis suggests that deadweight loss from taxation at rate τ is 0(τ 2 ) that is, that for small tax rates the
Chapter 9 Dynamic Models of Investment
 George Alogoskoufis, Dynamic Macroeconomic Theory, 2015 Chapter 9 Dynamic Models of Investment In this chapter we present the main neoclassical model of investment, under convex adjustment costs. This
George Alogoskoufis, Dynamic Macroeconomic Theory, 2015 Chapter 9 Dynamic Models of Investment In this chapter we present the main neoclassical model of investment, under convex adjustment costs. This
Arrow-Debreu Equilibrium
 Arrow-Debreu Equilibrium Econ 2100 Fall 2017 Lecture 23, November 21 Outline 1 Arrow-Debreu Equilibrium Recap 2 Arrow-Debreu Equilibrium With Only One Good 1 Pareto Effi ciency and Equilibrium 2 Properties
Arrow-Debreu Equilibrium Econ 2100 Fall 2017 Lecture 23, November 21 Outline 1 Arrow-Debreu Equilibrium Recap 2 Arrow-Debreu Equilibrium With Only One Good 1 Pareto Effi ciency and Equilibrium 2 Properties
Economics 101. Lecture 3 - Consumer Demand
 Economics 101 Lecture 3 - Consumer Demand 1 Intro First, a note on wealth and endowment. Varian generally uses wealth (m) instead of endowment. Ultimately, these two are equivalent. Given prices p, if
Economics 101 Lecture 3 - Consumer Demand 1 Intro First, a note on wealth and endowment. Varian generally uses wealth (m) instead of endowment. Ultimately, these two are equivalent. Given prices p, if
Notes on Macroeconomic Theory. Steve Williamson Dept. of Economics Washington University in St. Louis St. Louis, MO 63130
 Notes on Macroeconomic Theory Steve Williamson Dept. of Economics Washington University in St. Louis St. Louis, MO 63130 September 2006 Chapter 2 Growth With Overlapping Generations This chapter will serve
Notes on Macroeconomic Theory Steve Williamson Dept. of Economics Washington University in St. Louis St. Louis, MO 63130 September 2006 Chapter 2 Growth With Overlapping Generations This chapter will serve
Solutions to Problem Set 1
 Solutions to Problem Set Theory of Banking - Academic Year 06-7 Maria Bachelet maria.jua.bachelet@gmail.com February 4, 07 Exercise. An individual consumer has an income stream (Y 0, Y ) and can borrow
Solutions to Problem Set Theory of Banking - Academic Year 06-7 Maria Bachelet maria.jua.bachelet@gmail.com February 4, 07 Exercise. An individual consumer has an income stream (Y 0, Y ) and can borrow
5. COMPETITIVE MARKETS
 5. COMPETITIVE MARKETS We studied how individual consumers and rms behave in Part I of the book. In Part II of the book, we studied how individual economic agents make decisions when there are strategic
5. COMPETITIVE MARKETS We studied how individual consumers and rms behave in Part I of the book. In Part II of the book, we studied how individual economic agents make decisions when there are strategic
Macroeconomics 2. Lecture 6 - New Keynesian Business Cycles March. Sciences Po
 Macroeconomics 2 Lecture 6 - New Keynesian Business Cycles 2. Zsófia L. Bárány Sciences Po 2014 March Main idea: introduce nominal rigidities Why? in classical monetary models the price level ensures money
Macroeconomics 2 Lecture 6 - New Keynesian Business Cycles 2. Zsófia L. Bárány Sciences Po 2014 March Main idea: introduce nominal rigidities Why? in classical monetary models the price level ensures money
B. Online Appendix. where ɛ may be arbitrarily chosen to satisfy 0 < ɛ < s 1 and s 1 is defined in (B1). This can be rewritten as
 B Online Appendix B1 Constructing examples with nonmonotonic adoption policies Assume c > 0 and the utility function u(w) is increasing and approaches as w approaches 0 Suppose we have a prior distribution
B Online Appendix B1 Constructing examples with nonmonotonic adoption policies Assume c > 0 and the utility function u(w) is increasing and approaches as w approaches 0 Suppose we have a prior distribution
MFE Macroeconomics Week 8 Exercises
 MFE Macroeconomics Week 8 Exercises 1 Liquidity shocks over a unit interval A representative consumer in a Diamond-Dybvig model has wealth 1 at date 0. They will need liquidity to consume at a random time
MFE Macroeconomics Week 8 Exercises 1 Liquidity shocks over a unit interval A representative consumer in a Diamond-Dybvig model has wealth 1 at date 0. They will need liquidity to consume at a random time
Online Appendix for The Political Economy of Municipal Pension Funding
 Online Appendix for The Political Economy of Municipal Pension Funding Jeffrey Brinkman Federal eserve Bank of Philadelphia Daniele Coen-Pirani University of Pittsburgh Holger Sieg University of Pennsylvania
Online Appendix for The Political Economy of Municipal Pension Funding Jeffrey Brinkman Federal eserve Bank of Philadelphia Daniele Coen-Pirani University of Pittsburgh Holger Sieg University of Pennsylvania
Extraction capacity and the optimal order of extraction. By: Stephen P. Holland
 Extraction capacity and the optimal order of extraction By: Stephen P. Holland Holland, Stephen P. (2003) Extraction Capacity and the Optimal Order of Extraction, Journal of Environmental Economics and
Extraction capacity and the optimal order of extraction By: Stephen P. Holland Holland, Stephen P. (2003) Extraction Capacity and the Optimal Order of Extraction, Journal of Environmental Economics and
ECON Micro Foundations
 ECON 302 - Micro Foundations Michael Bar September 13, 2016 Contents 1 Consumer s Choice 2 1.1 Preferences.................................... 2 1.2 Budget Constraint................................ 3
ECON 302 - Micro Foundations Michael Bar September 13, 2016 Contents 1 Consumer s Choice 2 1.1 Preferences.................................... 2 1.2 Budget Constraint................................ 3
1 Two Period Exchange Economy
 University of British Columbia Department of Economics, Macroeconomics (Econ 502) Prof. Amartya Lahiri Handout # 2 1 Two Period Exchange Economy We shall start our exploration of dynamic economies with
University of British Columbia Department of Economics, Macroeconomics (Econ 502) Prof. Amartya Lahiri Handout # 2 1 Two Period Exchange Economy We shall start our exploration of dynamic economies with
On Quality Bias and Inflation Targets: Supplementary Material
 On Quality Bias and Inflation Targets: Supplementary Material Stephanie Schmitt-Grohé Martín Uribe August 2 211 This document contains supplementary material to Schmitt-Grohé and Uribe (211). 1 A Two Sector
On Quality Bias and Inflation Targets: Supplementary Material Stephanie Schmitt-Grohé Martín Uribe August 2 211 This document contains supplementary material to Schmitt-Grohé and Uribe (211). 1 A Two Sector
STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics. Ph. D. Comprehensive Examination: Macroeconomics Fall, 2010
 STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics Fall, 2010 Section 1. (Suggested Time: 45 Minutes) For 3 of the following 6 statements, state
STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics Fall, 2010 Section 1. (Suggested Time: 45 Minutes) For 3 of the following 6 statements, state
Chapter 4. Consumer and Firm Behavior: The Work-Leisure Decision and Profit Maximization
 Chapter 4 Consumer and Firm Behavior: The Work-Leisure Decision and Profit Maximization The Representative Consumer Preferences Goods: The Consumption Good and Leisure The Utility Function More Preferred
Chapter 4 Consumer and Firm Behavior: The Work-Leisure Decision and Profit Maximization The Representative Consumer Preferences Goods: The Consumption Good and Leisure The Utility Function More Preferred
Market Liquidity and Performance Monitoring The main idea The sequence of events: Technology and information
 Market Liquidity and Performance Monitoring Holmstrom and Tirole (JPE, 1993) The main idea A firm would like to issue shares in the capital market because once these shares are publicly traded, speculators
Market Liquidity and Performance Monitoring Holmstrom and Tirole (JPE, 1993) The main idea A firm would like to issue shares in the capital market because once these shares are publicly traded, speculators
Fiscal policy and minimum wage for redistribution: an equivalence result. Abstract
 Fiscal policy and minimum wage for redistribution: an equivalence result Arantza Gorostiaga Rubio-Ramírez Juan F. Universidad del País Vasco Duke University and Federal Reserve Bank of Atlanta Abstract
Fiscal policy and minimum wage for redistribution: an equivalence result Arantza Gorostiaga Rubio-Ramírez Juan F. Universidad del País Vasco Duke University and Federal Reserve Bank of Atlanta Abstract
Mean-Variance Analysis
 Mean-Variance Analysis Mean-variance analysis 1/ 51 Introduction How does one optimally choose among multiple risky assets? Due to diversi cation, which depends on assets return covariances, the attractiveness
Mean-Variance Analysis Mean-variance analysis 1/ 51 Introduction How does one optimally choose among multiple risky assets? Due to diversi cation, which depends on assets return covariances, the attractiveness
Intro to Economic analysis
 Intro to Economic analysis Alberto Bisin - NYU 1 The Consumer Problem Consider an agent choosing her consumption of goods 1 and 2 for a given budget. This is the workhorse of microeconomic theory. (Notice
Intro to Economic analysis Alberto Bisin - NYU 1 The Consumer Problem Consider an agent choosing her consumption of goods 1 and 2 for a given budget. This is the workhorse of microeconomic theory. (Notice
Online Shopping Intermediaries: The Strategic Design of Search Environments
 Online Supplemental Appendix to Online Shopping Intermediaries: The Strategic Design of Search Environments Anthony Dukes University of Southern California Lin Liu University of Central Florida February
Online Supplemental Appendix to Online Shopping Intermediaries: The Strategic Design of Search Environments Anthony Dukes University of Southern California Lin Liu University of Central Florida February
Final Exam II (Solutions) ECON 4310, Fall 2014
 Final Exam II (Solutions) ECON 4310, Fall 2014 1. Do not write with pencil, please use a ball-pen instead. 2. Please answer in English. Solutions without traceable outlines, as well as those with unreadable
Final Exam II (Solutions) ECON 4310, Fall 2014 1. Do not write with pencil, please use a ball-pen instead. 2. Please answer in English. Solutions without traceable outlines, as well as those with unreadable
Department of Economics The Ohio State University Midterm Questions and Answers Econ 8712
 Prof. James Peck Fall 06 Department of Economics The Ohio State University Midterm Questions and Answers Econ 87. (30 points) A decision maker (DM) is a von Neumann-Morgenstern expected utility maximizer.
Prof. James Peck Fall 06 Department of Economics The Ohio State University Midterm Questions and Answers Econ 87. (30 points) A decision maker (DM) is a von Neumann-Morgenstern expected utility maximizer.
Financial Economics Field Exam August 2011
 Financial Economics Field Exam August 2011 There are two questions on the exam, representing Macroeconomic Finance (234A) and Corporate Finance (234C). Please answer both questions to the best of your
Financial Economics Field Exam August 2011 There are two questions on the exam, representing Macroeconomic Finance (234A) and Corporate Finance (234C). Please answer both questions to the best of your
1. Introduction of another instrument of savings, namely, capital
 Chapter 7 Capital Main Aims: 1. Introduction of another instrument of savings, namely, capital 2. Study conditions for the co-existence of money and capital as instruments of savings 3. Studies the effects
Chapter 7 Capital Main Aims: 1. Introduction of another instrument of savings, namely, capital 2. Study conditions for the co-existence of money and capital as instruments of savings 3. Studies the effects
Fundamental Theorems of Welfare Economics
 Fundamental Theorems of Welfare Economics Ram Singh October 4, 015 This Write-up is available at photocopy shop. Not for circulation. In this write-up we provide intuition behind the two fundamental theorems
Fundamental Theorems of Welfare Economics Ram Singh October 4, 015 This Write-up is available at photocopy shop. Not for circulation. In this write-up we provide intuition behind the two fundamental theorems
QI SHANG: General Equilibrium Analysis of Portfolio Benchmarking
 General Equilibrium Analysis of Portfolio Benchmarking QI SHANG 23/10/2008 Introduction The Model Equilibrium Discussion of Results Conclusion Introduction This paper studies the equilibrium effect of
General Equilibrium Analysis of Portfolio Benchmarking QI SHANG 23/10/2008 Introduction The Model Equilibrium Discussion of Results Conclusion Introduction This paper studies the equilibrium effect of
PROBLEM SET 7 ANSWERS: Answers to Exercises in Jean Tirole s Theory of Industrial Organization
 PROBLEM SET 7 ANSWERS: Answers to Exercises in Jean Tirole s Theory of Industrial Organization 12 December 2006. 0.1 (p. 26), 0.2 (p. 41), 1.2 (p. 67) and 1.3 (p.68) 0.1** (p. 26) In the text, it is assumed
PROBLEM SET 7 ANSWERS: Answers to Exercises in Jean Tirole s Theory of Industrial Organization 12 December 2006. 0.1 (p. 26), 0.2 (p. 41), 1.2 (p. 67) and 1.3 (p.68) 0.1** (p. 26) In the text, it is assumed
Financial Frictions Under Asymmetric Information and Costly State Verification
 Financial Frictions Under Asymmetric Information and Costly State Verification General Idea Standard dsge model assumes borrowers and lenders are the same people..no conflict of interest. Financial friction
Financial Frictions Under Asymmetric Information and Costly State Verification General Idea Standard dsge model assumes borrowers and lenders are the same people..no conflict of interest. Financial friction
Trade on Markets. Both consumers' initial endowments are represented bythesamepointintheedgeworthbox,since
 Trade on Markets A market economy entails ownership of resources. The initial endowment of consumer 1 is denoted by (x 1 ;y 1 ), and the initial endowment of consumer 2 is denoted by (x 2 ;y 2 ). Both
Trade on Markets A market economy entails ownership of resources. The initial endowment of consumer 1 is denoted by (x 1 ;y 1 ), and the initial endowment of consumer 2 is denoted by (x 2 ;y 2 ). Both
Nominal Debt as a Burden on Monetary Policy
 Nominal Debt as a Burden on Monetary Policy Javier Díaz-Giménez Giorgia Giovannetti Ramon Marimon Pedro Teles November, 2007 Abstract We characterize the optimal sequential choice of monetary policy in
Nominal Debt as a Burden on Monetary Policy Javier Díaz-Giménez Giorgia Giovannetti Ramon Marimon Pedro Teles November, 2007 Abstract We characterize the optimal sequential choice of monetary policy in
Assets with possibly negative dividends
 Assets with possibly negative dividends (Preliminary and incomplete. Comments welcome.) Ngoc-Sang PHAM Montpellier Business School March 12, 2017 Abstract The paper introduces assets whose dividends can
Assets with possibly negative dividends (Preliminary and incomplete. Comments welcome.) Ngoc-Sang PHAM Montpellier Business School March 12, 2017 Abstract The paper introduces assets whose dividends can
Game Theory Fall 2006
 Game Theory Fall 2006 Answers to Problem Set 3 [1a] Omitted. [1b] Let a k be a sequence of paths that converge in the product topology to a; that is, a k (t) a(t) for each date t, as k. Let M be the maximum
Game Theory Fall 2006 Answers to Problem Set 3 [1a] Omitted. [1b] Let a k be a sequence of paths that converge in the product topology to a; that is, a k (t) a(t) for each date t, as k. Let M be the maximum
The objectives of the producer
 The objectives of the producer Laurent Simula October 19, 2017 Dr Laurent Simula (Institute) The objectives of the producer October 19, 2017 1 / 47 1 MINIMIZING COSTS Long-Run Cost Minimization Graphical
The objectives of the producer Laurent Simula October 19, 2017 Dr Laurent Simula (Institute) The objectives of the producer October 19, 2017 1 / 47 1 MINIMIZING COSTS Long-Run Cost Minimization Graphical
1 Unemployment Insurance
 1 Unemployment Insurance 1.1 Introduction Unemployment Insurance (UI) is a federal program that is adminstered by the states in which taxes are used to pay for bene ts to workers laid o by rms. UI started
1 Unemployment Insurance 1.1 Introduction Unemployment Insurance (UI) is a federal program that is adminstered by the states in which taxes are used to pay for bene ts to workers laid o by rms. UI started
EconS 424 Strategy and Game Theory. Homework #5 Answer Key
 EconS 44 Strategy and Game Theory Homework #5 Answer Key Exercise #1 Collusion among N doctors Consider an infinitely repeated game, in which there are nn 3 doctors, who have created a partnership. In
EconS 44 Strategy and Game Theory Homework #5 Answer Key Exercise #1 Collusion among N doctors Consider an infinitely repeated game, in which there are nn 3 doctors, who have created a partnership. In
Interpolation. 1 What is interpolation? 2 Why are we interested in this?
 Interpolation 1 What is interpolation? For a certain function f (x we know only the values y 1 = f (x 1,,y n = f (x n For a point x different from x 1,,x n we would then like to approximate f ( x using
Interpolation 1 What is interpolation? For a certain function f (x we know only the values y 1 = f (x 1,,y n = f (x n For a point x different from x 1,,x n we would then like to approximate f ( x using
STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics. Ph. D. Comprehensive Examination: Macroeconomics Spring, 2016
 STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics Spring, 2016 Section 1. Suggested Time: 45 Minutes) For 3 of the following 6 statements,
STATE UNIVERSITY OF NEW YORK AT ALBANY Department of Economics Ph. D. Comprehensive Examination: Macroeconomics Spring, 2016 Section 1. Suggested Time: 45 Minutes) For 3 of the following 6 statements,
Sequential Investment, Hold-up, and Strategic Delay
 Sequential Investment, Hold-up, and Strategic Delay Juyan Zhang and Yi Zhang February 20, 2011 Abstract We investigate hold-up in the case of both simultaneous and sequential investment. We show that if
Sequential Investment, Hold-up, and Strategic Delay Juyan Zhang and Yi Zhang February 20, 2011 Abstract We investigate hold-up in the case of both simultaneous and sequential investment. We show that if
Sequential Investment, Hold-up, and Strategic Delay
 Sequential Investment, Hold-up, and Strategic Delay Juyan Zhang and Yi Zhang December 20, 2010 Abstract We investigate hold-up with simultaneous and sequential investment. We show that if the encouragement
Sequential Investment, Hold-up, and Strategic Delay Juyan Zhang and Yi Zhang December 20, 2010 Abstract We investigate hold-up with simultaneous and sequential investment. We show that if the encouragement
Sentiments and Aggregate Fluctuations
 Sentiments and Aggregate Fluctuations Jess Benhabib Pengfei Wang Yi Wen June 15, 2012 Jess Benhabib Pengfei Wang Yi Wen () Sentiments and Aggregate Fluctuations June 15, 2012 1 / 59 Introduction We construct
Sentiments and Aggregate Fluctuations Jess Benhabib Pengfei Wang Yi Wen June 15, 2012 Jess Benhabib Pengfei Wang Yi Wen () Sentiments and Aggregate Fluctuations June 15, 2012 1 / 59 Introduction We construct
Bailouts, Time Inconsistency and Optimal Regulation
 Federal Reserve Bank of Minneapolis Research Department Sta Report November 2009 Bailouts, Time Inconsistency and Optimal Regulation V. V. Chari University of Minnesota and Federal Reserve Bank of Minneapolis
Federal Reserve Bank of Minneapolis Research Department Sta Report November 2009 Bailouts, Time Inconsistency and Optimal Regulation V. V. Chari University of Minnesota and Federal Reserve Bank of Minneapolis
Does Capitalized Net Product Equal Discounted Optimal Consumption in Discrete Time? by W.E. Diewert and P. Schreyer. 1 February 27, 2006.
 1 Does Capitalized Net Product Equal Discounted Optimal Consumption in Discrete Time? by W.E. Diewert and P. Schreyer. 1 February 27, 2006. W. Erwin Diewert, Paul Schreyer Department of Economics, Statistics
1 Does Capitalized Net Product Equal Discounted Optimal Consumption in Discrete Time? by W.E. Diewert and P. Schreyer. 1 February 27, 2006. W. Erwin Diewert, Paul Schreyer Department of Economics, Statistics
Money in an RBC framework
 Money in an RBC framework Noah Williams University of Wisconsin-Madison Noah Williams (UW Madison) Macroeconomic Theory 1 / 36 Money Two basic questions: 1 Modern economies use money. Why? 2 How/why do
Money in an RBC framework Noah Williams University of Wisconsin-Madison Noah Williams (UW Madison) Macroeconomic Theory 1 / 36 Money Two basic questions: 1 Modern economies use money. Why? 2 How/why do
Transactions and Money Demand Walsh Chapter 3
 Transactions and Money Demand Walsh Chapter 3 1 Shopping time models 1.1 Assumptions Purchases require transactions services ψ = ψ (m, n s ) = c where ψ n s 0, ψ m 0, ψ n s n s 0, ψ mm 0 positive but diminishing
Transactions and Money Demand Walsh Chapter 3 1 Shopping time models 1.1 Assumptions Purchases require transactions services ψ = ψ (m, n s ) = c where ψ n s 0, ψ m 0, ψ n s n s 0, ψ mm 0 positive but diminishing
On the 'Lock-In' Effects of Capital Gains Taxation
 May 1, 1997 On the 'Lock-In' Effects of Capital Gains Taxation Yoshitsugu Kanemoto 1 Faculty of Economics, University of Tokyo 7-3-1 Hongo, Bunkyo-ku, Tokyo 113 Japan Abstract The most important drawback
May 1, 1997 On the 'Lock-In' Effects of Capital Gains Taxation Yoshitsugu Kanemoto 1 Faculty of Economics, University of Tokyo 7-3-1 Hongo, Bunkyo-ku, Tokyo 113 Japan Abstract The most important drawback
Capital Constraints, Lending over the Cycle and the Precautionary Motive: A Quantitative Exploration
 Capital Constraints, Lending over the Cycle and the Precautionary Motive: A Quantitative Exploration Angus Armstrong and Monique Ebell National Institute of Economic and Social Research 1. Introduction
Capital Constraints, Lending over the Cycle and the Precautionary Motive: A Quantitative Exploration Angus Armstrong and Monique Ebell National Institute of Economic and Social Research 1. Introduction
Does Retailer Power Lead to Exclusion?
 Does Retailer Power Lead to Exclusion? Patrick Rey and Michael D. Whinston 1 Introduction In a recent paper, Marx and Shaffer (2007) study a model of vertical contracting between a manufacturer and two
Does Retailer Power Lead to Exclusion? Patrick Rey and Michael D. Whinston 1 Introduction In a recent paper, Marx and Shaffer (2007) study a model of vertical contracting between a manufacturer and two
Macro Consumption Problems 33-43
 Macro Consumption Problems 33-43 3rd October 6 Problem 33 This is a very simple example of questions involving what is referred to as "non-convex budget sets". In other words, there is some non-standard
Macro Consumption Problems 33-43 3rd October 6 Problem 33 This is a very simple example of questions involving what is referred to as "non-convex budget sets". In other words, there is some non-standard
